Abstract
In this paper, an arbitrary Lagrangian–Eulerian local discontinuous Galerkin (ALE-LDG) method for Hamilton–Jacobi equations will be developed, analyzed and numerically tested. This method is based on the time-dependent approximation space defined on the moving mesh. A priori error estimates will be stated with respect to the \(\mathrm {L}^{\infty }\left( 0,T;\mathrm {L}^{2}\left( \Omega \right) \right) \)-norm. In particular, the optimal (\(k+1\)) convergence in one dimension and the suboptimal (\(k+\frac{1}{2}\)) convergence in two dimensions will be proven for the semi-discrete method, when a local Lax–Friedrichs flux and piecewise polynomials of degree k on the reference cell are used. Furthermore, the validity of the geometric conservation law will be proven for the fully-discrete method. Also, the link between the piecewise constant ALE-LDG method and the monotone scheme, which converges to the unique viscosity solution, will be shown. The capability of the method will be demonstrated by a variety of one and two dimensional numerical examples with convex and noneconvex Hamiltonian.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper deals with the development and analysis of a moving mesh discontinuous Galerkin (DG) method to solve time-dependent Hamilton–Jacobi equations
augmented with suitable initial data \(u(\mathbf{x},0) = u_0(\mathbf{x})\) and boundary conditions. The domain \(\Omega \in \mathbb {R}^d\) is bounded. The relevant solution for the problem (1.1) is the viscosity solution introduced by Crandall and Lions [9]. In the same paper it was proven that there exists a unique bounded and continuous viscosity solution for the problem (1.1). Nevertheless, it should be noted that the derivatives of the unique viscosity solution can be discontinuous, regardless of the smoothness of the initial condition.
The equations of motion in many physical models are related to the Hamilton–Jacobi equations. For instance Hamilton–Jacobi equations with viscosity terms occur in front propagation problems, which are applied in models for crystal growth or flame propagation (cf. Sethian [27]). In some situations, it is advantageous to solve numerically motion related equations by an arbitrary Lagrangian–Eulerian (ALE) approach. Especially, in the context of moving boundaries problems with incompressible flows the ALE approach has some advantages (cf. Calderer and Masud [4]). The ALE approach was rigorously described by Donea et al. [11]. It allows to move the mesh along specific mesh generating points like in the Lagrangian approach or to fix the mesh like in the Eulerian approach. The implementation and mathematical description of the ALE approach be ensured by a mapping which connects the physical domain with a suitable reference configuration. The mapping provides a description of the grid velocity field. It should be noted that the mapping may produce a geometric error, when the numerical method was chosen unsuitable. To overcome this issue, the ALE method should satisfy the geometric conservation law (GCL). Guillard and Farhat analyzed in [13] the significance of the GCL and the destabilizing effect of the geometric error.
Otherwise, the Runge–Kutta (RK) DG approach enables the development of high order methods with certain desirable computational properties like parallelization capability or the ability to handle a complex mesh topology (cf. Cockburn and Shu [8]). Nevertheless, the development of discontinuous Galerkin methods for solving the Hamilton–Jacobi equations is delicate, since the Hamilton–Jacobi equations in general are not in the divergence form. In order to overcome this issue the close relation between the Hamilton–Jacobi equations (1.1) and conservation laws is often used to develop high order numerical methods for solving the problem (1.1). The essentially non-oscillatory (ENO) and weighted essentially non-oscillatory (WENO) schemes by Jiang, Peng, Osher and Shu [14, 25] or the DG method by Hu, Lepsky, Li and Shu [15, 16, 18, 19] are examples of high order methods which are adapted from numerical schemes for conservation laws. The DG method of Hu et al. was extended to a moving mesh method by Mackenzie and Nicola [23]. However, the system of conservation laws which arises from the problem (1.1) is in general weakly hyperbolic. This structure could force the convergence to a physically not relevant solution. Therefore, from this point of view, a method for directly solving the Hamilton–Jacobi equations is desirable.
In the following a few DG methods for solving directly the Hamilton–Jacobi equations are mentioned. Cheng and Shu developed in [5] a DG method. The method is stabilized by a certain numerical flux, which is motivated by the discretization and stabilization of a DG method for conservation laws with a source term. However, the numerical flux is not enough to ensure the convergence to the viscosity solution. Thus, an additional entropy correction procedure is adopted in the method. Cheng and Shu’s approach was combined with the central DG approach for conservation laws to develop a central DG method for solving the Hamilton–Jacobi equations by Li and Yakovlev [20]. A limiter has been developed to ensure that the method can handle problems with a nonconvex Hamiltonian. Another approach has been introduced by Yan and Osher [29]. They replaced the Hamiltonian by a numerical flux which is evaluated in the interior of each cell. The arguments of the numerical flux function are calculated by upwind schemes. The solutions of these upwind schemes are approximating the partial derivatives of the numerical solution. This approach is similar to the local Discontinuous Galerkin approach developed by Cockburn and Shu [7] for solving systems of convection–diffusion equations, since the PDE is locally dissected. For this reason, Yan and Osher’s method is called local DG (LDG) for solving directly the Hamilton–Jacobi equations. All these DG methods were tested by numerical experiments. These experiments demonstrate the stability and the optimal accuracy of the methods. In addition, the stability and a suboptimal error estimate with respect to the \(\mathrm {L}^{2}\)-norm were proven for the central DG method in [20] when a linear Hamiltonian is investigated. Likewise, for the semi-discrete formulations of Cheng and Shu’s DG method as well as Yan and Osher’s LDG method the optimal error estimate in the \(\mathrm {L}^{2}\)-norm was proven by Xiong et al. [28]. “In this context the term optimal error estimate” has to be understood with respect to the approximation properties of the test function space.” There are also DG methods for solving directly the Hamilton–Jacobi equations in the context of front propagation problems in the literature. For instance, Barth and Sethian developed in [1] a Petrov–Galerkin DG method on triangular meshes with an adaptive mesh refinement technique and Bokanowski, Cheng and Shu developed an explicit RK-DG method in [3] for these kind of problems.
The aim of this paper is to combine the ALE and the DG approach to develop an ALE–DG method for directly solving the Hamilton–Jacobi equations. It should be mentioned that there are already ALE–DG methods with different strategies to describe the ALE kinematic in the literature, for example, in the context of problems with compressible viscous flows, these kind of methods were developed by Lomtev et al. [22], Nguyen [24] or Persson et al. [26]. In [17] Klingenberg, Schnücke and Xia developed an ALE–DG method for one dimensional conservation laws. In the same paper, the ALE kinematic is described by local affine linear mappings which ensure the satisfaction of the GCL for any time discretization method higher or equal to first order. In the present paper, in the one dimensional case, the ALE approach, developed in [17], is combined with Yan and Osher’s LDG approach [29] and a new ALE method for directly solving the Hamilton–Jacobi equations is developed. The new ALE method is called ALE-LDG method. The ALE-LDG method has a local structure like the DG methods for static meshes and we will prove that the method satisfies the GCL for any time discretization method higher or equal to first order. A two dimensional extension of the method is designed for triangular meshes, since each triangle element can be mapped by a local affine linear mapping to a time-independent reference triangle element. This allows the same description of the ALE kinematic as in the one dimensional case. In particular, it follows that the GCL is satisfied for any time discretization method higher or equal to second order. Furthermore, a priori error estimates with respect to the \(\mathrm {L}^{\infty }\left( 0,T;\mathrm {L}^{2}\left( \Omega \right) \right) \)-norm will be proven for the one and two dimensional semi-discrete methods. Also it will be shown that the first order piecewise constant ALE-LDG method is a monotone scheme. The last point is important, since in [10] Crandall and Lions proved that monotone schemes for the problem (1.1) converge to the unique viscosity solution. In numerical experiments it will be observed that our one and two dimensional ALE-LDG methods are stable and optimally accurate with respect to the approximation properties of the test function spaces for the methods.
This paper is organized as follows: In Sect. 2, the ALE kinematic, the semi-discrete one and two dimensional ALE-LDG methods and some auxiliary lemmas are presented. In particular, the GCL is discussed and it is shown that the fully-discrete piecewise constant ALE-LDG method is a monotone scheme. Afterward, in Sect. 3, an optimal a priori error estimates for the semi-discrete one dimensional ALE-LDG method and an suboptimal a priori error estimates for the semi-discrete two dimensional ALE-LDG method are proven with respect to the \(\mathrm {L}^{\infty }\left( 0,T;\mathrm {L}^{2}\left( \Omega \right) \right) \)-norm. Section 4 contains numerical results for a variety of problems to demonstrate the accuracy and capabilities of the ALE-LDG methods. Finally, some concluding remarks are given in Sect. 5.
1.1 Constants and Notation
In the present paper, vectors, vector valued functions and matrices are denoted by bold letters. Scalar quantities are denoted by regular letters. The set \(K\left( t\right) \) denotes a time-dependent interval in one dimension and a time-dependent simplex cell with the edges \(e_{K\left( t\right) }^{\nu }\), \(\nu =1,2,3\), in two dimensions. Volume integrals with respect to \(K\left( t\right) \) and surface integrals with respect to the edges \(e_{K\left( t\right) }^{\nu }\), \(\nu =1,2,3\), are denoted by the bracket notation. Hence, for all \(v,w\in \mathrm {L}^{2}\left( K\left( t\right) \right) \cap \mathrm {L}^{2}\left( \partial K\left( t\right) \right) \) and \(\nu =1,2,3\) the notations \(\left( v,w\right) _{K\left( t\right) }:=\int _{K\left( t\right) }vw \, d\mathbf x \), \(\left\langle v,w\right\rangle _{e_{K\left( t\right) }^{\nu }}:=\int _{e_{K\left( t\right) }^{\nu }}vw\,d\varvec{\Gamma }\) and \(\left\langle v,w\right\rangle _{\partial K\left( t\right) }:=\sum _{\nu =1}^{3}\left\langle v,w\right\rangle _{e_{K\left( t\right) }^{\nu }}\) are applied. Furthermore, to avoid confusion with different constants, C denotes a positive constant, which is independent of the mesh size and the numerical solution for the problem (1.1). Note, that the constant may depend on the exact solution of the problem (1.1) and may have a different value in each occurrence.
2 The ALE-LDG Method
In this section, we introduce the ALE-LDG method for directly solving the Hamilton–Jacobi equations, state some auxiliary lemmas which will be used to prove the a priori error estimates in the upcoming sections, discuss the GCL for the method and show that the forward Euler piecewise constant ALE-LDG method is a monotone scheme which converges to the unique viscosity solution according to Crandall and Lions [10].
2.1 Preliminaries
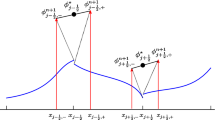
We assume that at any time level \(t_{n}\), \(n =0,\ldots ,L\), regular families of triangular meshes \(\mathcal {T}_{n}\) with the same mesh topology are given. We say that the triangular mesh \(\mathcal {T}_{n}\) at time level \(t_{n}\) and the triangular mesh \(\mathcal {T}_{n+1}\) at time level \(t_{n+1}\) have the same mesh topology, if they have the same numbers of vertices and triangles and the same connectivity. Henceforth for each time level \(t_n\) the vectors \(\mathbf{v}_{1}^{n},\mathbf{v}_{2}^{n},\mathbf{v}_{3}^{n}\) denote the vertices of the cell \(K^{n} \in \mathcal {T}_{n}\). We connect the vertices of two arbitrary cells \(K^{n}\in \mathcal {T}_{n}\) and \(K^{n+1}\in \mathcal {T}_{n+1}\) for all \(t\in \left[ t_{n},t_{n+1}\right] \) and \(\ell =1,2,3\) by time-dependent straight lines
In Fig. 1 the connection of two cells at different time levels is illustrated. The straight lines (2.1) provide for any \(t\in \left[ t_{n},t_{n+1}\right] \) time-dependent cells
where \(e_{K\left( t\right) }^{\nu }\), \(\nu =1,2,3\), are the edges of the time-dependent cell \(K\left( t\right) \). Note that in this context \(\text {int}\left( \cdot \right) \) and \(\text {conv}\left( \cdot \right) \) denote the interior and the convex hull of a set. The family of all sets containing the cells (2.2) is denoted by \(\mathcal {T}_{\left( t\right) }\) for any \(t\in \left[ t_{n},t_{n+1}\right] \). Furthermore, for any cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\), the diameter is denoted by \(h_{K\left( t\right) }\) and the radius of the largest ball, contained in \(K\left( t\right) \), is denoted by \(\rho _{K\left( t\right) }\). The meshsize of the tessellations is given by \(h\left( t\right) :=\underset{K\left( t\right) \in \mathcal {T}_{\left( t\right) }}{\text {max}}h_{K\left( t\right) }\). In order to state a priori error estimates for the ALE-LDG method, we define a global length
and assume that there exists a constant \(\kappa \), independent of h, such that for all \(t\in \left[ 0,T\right] \)
Additionally, we assume that \(\mathcal {T}_{\left( t\right) }\) is a regular triangulation of the domain \(\Omega \), which satisfies the properties:
-
(A1)
For all \(t\in \left[ 0,T\right] \) holds: The family \(\mathcal {T}_{\left( t\right) }\) covers exactly \(\overline{\Omega }\), such that \(\overline{\Omega }=\bigcup _{K^{n}\in \mathcal {T}_{\left( t\right) }}\overline{K\left( t\right) }\).
-
(A2)
There are constants \(\sigma >0\) and \(\tau >0\), independent of the mesh parameter, such that for all \(t\in \left[ 0,T\right] \) holds:
$$\begin{aligned} \frac{h_{K\left( t\right) }}{\rho _{K\left( t\right) }}\le \sigma \quad \text {and}\quad \frac{h\left( t\right) }{h_{K\left( t\right) }}\le \tau ,\quad \forall K\left( t\right) \in \mathcal {T}_{\left( t\right) }. \end{aligned}$$
In addition, we define for any cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) the matrix
and assume that \(J_{K\left( t\right) }>0\). It should be noted that the boundary faces of the mesh are not changing in time for the compactly supported problem and could move with the periodic speed for the periodic boundary problem.
Next, we define for any cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) the following time-dependent affine linear mapping
where \(\mathcal {K}\) is the reference cell given by.
The mapping provides the local representation of the grid velocity field for the ALE-LDG method, since the grid velocity field is in a point \(\mathbf{x}=\varvec{\chi }_{K\left( t\right) }\left( \varvec{\xi },t\right) \) defined by
where \({\mathbf{W}}_{K\left( t\right) }:=\left( \frac{d}{dt}{\mathbf{A}}_{K\left( t\right) }\right) \left( {\mathbf{A}}_{K\left( t\right) }\right) ^{-1}\). It should be noted that the Eq. (2.7) yields for all \(\mathbf{x}\in K(t)\)
where \(\text {tr}\left[ {\mathbf{W}}_{K\left( t\right) }\right] \) denotes the trace of the matrix \({\mathbf{W}}_{K\left( t\right) }\). Moreover, the mapping supplies the following finite element approximation space
where the index \(d\in \left\{ 1,2\right\} \) denotes the spatial dimension, \(P^{k}\left( \mathcal {K}\right) \) denotes the space of polynomials in \(\mathcal {K}\) of degree at most k and
Henceforth, we omit the label \(|_{K\left( t\right) }\) in (2.10), if it is clear which cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) is under consideration. The space \(\mathcal {V}_{h,d}(t)\) is finite dimensional, since \(P^{k}\left( \mathcal {K}\right) \) has the dimension \(\frac{\left( k+d\right) !}{d!k!}\). In general the functions from the space \(\mathcal {V}_{h,d}(t)\) are discontinuous along the interface of two adjacent cells. Certainly, the functions could exist two different traces on any interior interface, since the functions are polynomials in the interior of the cells and the cells have Lipschitz boundaries. Therefore, we define for a function \(v\in \mathcal {V}_{h,d}(t)\), an arbitrary cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) and all \(\nu =1,2,3\) the following limits
where the vector \(\mathbf {n}_{K\left( t\right) }^{\nu }\) is the outward normal of the cell \(K\left( t\right) \) with respect to the edge \(e_{K\left( t\right) }^{\nu }\). Accordingly, the cell average and jump of v along the edge \(e_{K\left( t\right) }^{\nu }\) are defined by
In the following, we present some auxiliary lemmas which are related to the space (2.9). This requires the introduction of a broken \(\mathrm {L}^{2}\left( \partial \mathcal {T}_{\left( t\right) }\right) \)-norm given by
where \(v\in \mathrm {L}^{2}\left( \partial K(t)\right) \) for all \(K(t)\in \mathcal {T}_{\left( t\right) }\). This notation allows to state the following lemma. The proof of the lemma ensues by a result from approximation theory (c.f. Ciarlet [6, pp. 140–141, Theorem 3.2.6.]). Hence, it is skipped in this paper.
Lemma 2.1
Suppose \(d\in \left\{ 1,2\right\} \). Then, for all \(v\in \mathcal {V}_{h,d}(t)\), there exists a constant C, independent of v and h, such that
Furthermore, the test functions provide the following ALE transport equation.
Lemma 2.2
Let \(d\in \left\{ 1,2\right\} \) and \(u:\Omega \times \left[ 0,T\right] \rightarrow {\mathbb {R}}\) be a sufficiently smooth function in any cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). Then for all \(v\in \mathcal {V}_{h,d}(t)\) holds the transport equation
Proof
In the following, the functions \(u^{*}\) and \(v^{*}\) are defined by (2.10). It is \(\left( u^{*},\partial _{t}v^{*}\right) _{\mathcal {K}}=0\), for all functions \(v\in \mathcal {V}_{h,d}(t)\), since the test functions are time-independent polynomials on the reference cell. Furthermore, the chain rule formula supplies \(\partial _{t}u^{*}=\partial _{t}u+\varvec{\omega }\cdot \nabla u\). Hence, the integration by substitution formula provides for all functions \(v\in \mathcal {V}_{h,d}(t)\)
Next, by Jacobi’s formula (cf. Bellman [2]) and (2.8) follows
where \(\text {adj}\left( {\mathbf{A}}_{K\left( t\right) }\right) \) denotes the adjoint matrix of \({\mathbf{A}}_{K\left( t\right) }\). Finally, we obtain the transport Eq. (2.13) by (2.14), (2.15) and the integration by substitution formula. \(\square \)
It should be noted that the equality (2.14) does not hold, if the test function v is a polynomial with time-dependent coefficients on the reference cell.
Next, for \(d\in \left\{ 1,2\right\} \) and a cell \(K(t)\in \mathcal {T}_{\left( t\right) }\), we define the \(\mathrm {L}^{2}\)-projection \(\mathcal {P}_{h}\left( u\right) \) of a function \(u\in \mathrm {L}^{2}\left( \Omega \right) \) into the test function space \(\mathcal {V}_{h,d}\left( t\right) \) by
The \(\mathrm {L}^{2}\)-projection satisfies the following interpolation inequalities. A proof of these inequalities can be found in Ciarlet [6, pp. 124–125, Theorem 3.1.6.]).
Lemma 2.3
Let \(d\in \left\{ 1,2\right\} \) and \(u\in \mathrm {H}^{k+1}\left( \Omega \right) \). Then there exists a constant C, such that
where the constant C depends on u, but it is independent of h.
2.2 Notes About the One Dimensional Setup
In the one dimensional case, we assume that at any time level \(t_{n}\), \(n=1,\ldots ,L\), the distribution of the mesh generating points \(\left\{ x_{j-\frac{1}{2}}^{n}\right\} _{j=1}^{N}\) is given. We connect these points for all \(j=1,\ldots ,N\) by time-dependent straight lines
Note that for any time point t the points \(x_{\frac{1}{2}}\left( t\right) \) and \(x_{N+\frac{1}{2}}\left( t\right) \) are not changing in time for the compactly supported problem and could move with the same speed \(\frac{d}{dt}x_{\frac{1}{2}}\left( t\right) =\frac{d}{dt}x_{N+\frac{1}{2}}\left( t\right) \) for the periodic boundary problem. The straight lines (2.18) provide for any \(t\in \left[ t_{n},t_{n+1}\right] \) and all \(j=1,\ldots ,N\) the cells
Like in the two dimensional case, a time-dependent affine linear mapping to a reference cell can be defined for any cell (2.19). The mapping allows to characterize the local grid velocity field and to define a finite element space in the same manner as in (2.7) and (2.9). In particular, the grid velocity is for all \(t\in \left[ t_{n},t_{n+1}\right] \) and \(x\in K_{j}(t)\) given by
Moreover, Lemmas 2.1 and 2.2 hold also for the one dimensional test function space \(\mathcal {V}_{h,1}\left( t\right) \). Nevertheless, for a function \(v\in \mathcal {V}_{h,1}(t)\), the left as well as right limit, the cell average and the jump in an interface point are denoted by
In addition, in one dimension, surface integrals reduce to pointwise evaluations. Thus, the broken \(\mathrm {L}^{2}\left( \partial \mathcal {T}_{\left( t\right) }\right) \)-norm is defined by
In order to prove that the a priori error in the \(\mathrm {L}^{\infty }\left( 0,T;\mathrm {L}^{2}\left( \Omega \right) \right) \)-norm for the one dimensional ALE-LDG method behaves as \(\mathcal {O}\left( h^{k+1}\right) \), we apply for any cell \(K_{j}\left( t\right) \), \(j=1,\ldots ,N\), the Gauss–Radau projections besides the \(\mathrm {L}^{2}\)-projection. For \(k\ge 1\), we define the Gauss–Radau projections \(\mathcal {P}^{\pm }_{h}\left( u\right) \) of a function \(u\in \mathrm {L}^{2}\left( \Omega \right) \) into \(\mathcal {V}_{h,1}(t)\) by
and
where the function \(v|_{K_{j}\left( t\right) }^{*}\) is defined by (2.10). Next, we combine the \(\mathrm {L}^{2}\)-projection with the Gauss–Radau projections and define the \(\mathcal {Q}\)-projection \(\mathcal {Q}_{h}\left( u\right) \) of a function \(u\in \mathrm {L}^{2}\left( \Omega \right) \) into the test function space \(\mathcal {V}_{h,1}(t)\) by
where the function \(H(\partial _{x}u,x)\) is the Hamiltonian in (1.1). It should be noted that Lemma 2.3 holds for the \(\mathcal {Q}\)-projection, too. Moreover, in order to evaluate the time derivative of the \(\mathcal {Q}\)-projection, we apply the following lemma, which was proven by Klingenberg et al. [17].
Lemma 2.4
Let \(u:\Omega \times \left[ 0,T\right] \rightarrow {\mathbb {R}}\) be a sufficiently smooth function. Then holds
2.3 The One-Dimensional Semi-discrete Method
In the following, we derive the one-dimensional semi-discrete ALE-LDG method for an arbitrary \(t\in \left[ t_{n},t_{n+1}\right] \) a cell \(K_{j}\left( t\right) \). We would like to approximate the solution u of the problem (1.1) by a function
where \(\left\{ \phi _{0}^{j}\left( x,t\right) ,\ldots ,\phi _{k}^{j}\left( x,t\right) \right\} \) is a basis of the space \(\mathcal {V}_{h,1}\left( t\right) \) in the cell \(K_{j}(t)\). The coefficients \(u_{0}^{j}\left( t\right) ,\ldots ,u_{k}^{j}\left( t\right) \) in (2.24) will be the unknowns of the method. In order to determine these coefficients, we plug (2.24) in the PDE (1.1), multiply the equation by a test function \(v \in \mathcal {V}_{h,1}(t)\) and apply the transport Eq. (2.13) as well as the integration by parts formula. This results in the equation
The function \(u_{h}\) is in general discontinuous along the interface of two adjacent cells and thus \(\partial _{x}u_{h}\) is merely defined in the interior of the cells. Therefore, we replace the integral with the Hamiltonian and the terms in cell boundary points by
where \(\widehat{G}\left( \omega ,p_{1},p_{2},x\right) \) is a local Lax–Friedrichs flux given by
with \(D_{j}:=\left. \left[ \min \left( p_{1},p_{2}\right) ,\max \left( p_{1},p_{2}\right) \right] \right| _{K_{j}\left( t\right) }\). The variables \(p_{1}\) and \(p_{2}\) in (2.26) are used to approximate \(\partial _{x}u_{h}\). We obtain these variables by solving two auxiliary equations. Finally, the semi-discrete method can be written as:
Problem
(The 1D semi-discrete ALE-LDG method) Find functions \(u_{h},p_{1},p_{2}\in \mathcal {V}_{h,1}(t)\), such that for all \(v,v_{1},v_{2}\in \mathcal {V}_{h,1}(t)\) and \(j=1,\ldots ,N\) holds
Note that the functions \(u_{h}\), \(p_{1}\) and \(p_{2}\) are time-dependent, since in each cell \(K_{j}\left( t\right) \) the ALE-LDG solution \(u_{h}\) is given by (2.24) and the functions \(p_{1}\), \(p_{2}\) approximate \(\partial _{x}u_{h}\). Moreover, it should be noted that the Eq. (2.28a) is for all \(v\in \mathcal {V}_{h,1}(t)\) and all \(j=1,\ldots ,N\) equivalent to
The equivalence follows from the transport Eq. (2.13).
2.4 The Two-Dimensional Semi-discrete Method
In this section, we derive the two-dimensional semi-discrete ALE-LDG method for the time interval \(\left[ t_{n},t_{n+1}\right] \) and the cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). The description of the two dimensional semi-discrete ALE-LDG method follows similar to the description of the one dimensional method. However, the two dimensional ALE-LDG method is a system of five equations, since a two dimensional Hamiltonian depends on more variables than its one dimensional analogue. First of all, in each cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\), we approximate the solution of the problem (1.1) by the two dimensional analogue of the function (2.24). In order to determine the unknowns, we proceed as in the one dimensional case. We plug the approximation in the PDE (1.1), multiply the equation by a test function \(v \in \mathcal {V}_{h,2}(t)\) and apply the transport Eq. (2.13) as well as the integration by parts formula. Then we obtain a two dimensional analogue of the Eq. (2.25) and replace the integral with the Hamiltonian as well as the terms in the surface integrals by
where \(\mathbf {n}_{K\left( t\right) }=\left( n_{K\left( t\right) ,x},n_{K\left( t\right) ,y}\right) ^{T}\) denotes the outward unit normal along the cell boundary \(\partial K\left( t\right) \) and the two dimensional local Lax–Friedrichs flux is for all \(\mathbf{x}\in K\left( t\right) \) given by
where
and
with
The variables \(p_{1}\) as well as \(p_{2}\) in (2.30) are used to approximate \(\partial _{x}u_{h}\) and the variables \(q_{1}\) as well as \(q_{2}\) are used to approximate \(\partial _{y}u_{h}\). We obtain these variables by solving four additional equations. Finally, the semi-discrete ALE-LDG method in two dimensions can be written as:
Problem
(The 2D semi-discrete ALE-LDG method) Seek functions \(u_{h},p_{1},p_{2},q_{1},q_{2}\in \mathcal {V}_{h,2}(t)\), such that for all \(v,v_{1},v_{2},w_{1},w_{2}\in \mathcal {V}_{h,2}(t)\) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) holds
The functions \(u_{h}^{+,i}\) and \(u_{h}^{-,i}\), \(i=x,y\), are given by
where for \(i=x,y\) the vector \(n_{K\left( t\right) ,i}\) denotes the i-component of the outward unit normal \(\mathbf {n}_{K\left( t\right) }\)
Note that the functions \(u_{h}\), \(p_{1}\), \(p_{2}\), \(q_{1}\) and \(q_{2}\) are time-dependent, since in each cell \(K\left( t\right) \) the ALE-LDG solution \(u_{h}\) is given by the two dimensional analogue of the function (2.24), the functions \(p_{1}\), \(p_{2}\) approximate \(\partial _{x}u_{h}\) and the functions \(q_{1}\), \(q_{2}\) approximate \(\partial _{y}u_{h}\). Furthermore, note that by the transport Eq. (2.13) for all \(v\in \mathcal {V}_{h,2}(t)\) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) follows that the Eq. (2.33a) is equivalent to
Finally, some important connections to other numerical methods should be mentioned.
Remark 2.1
-
(i)
The ALE-LDG methods (2.28) and (2.33) coincide with Yan and Osher’s LDG methods in [29], when a static mesh is used.
-
(ii)
The one dimensional ALE-LDG method (2.28) is equivalent to the ALE–DG method for conservation laws in [17], when a linear Hamiltonian with constant coefficients is investigated.
-
(iii)
When we plug the function (2.24) in the PDE (1.1), multiply the equation by a test function \(v \in \mathcal {V}_{h,1}(t)\) and apply the transport Eq. (2.13), it follows
$$\begin{aligned} 0=\frac{d}{dt}\left( u_{h},v\right) _{K_{j}\left( t\right) }+\left( \omega u_{h},\partial _{x}v\right) _{K_{j}\left( t\right) }+\left( H\left( \partial _{x}u_{h},x\right) -\omega \partial _{x}u_{h},v\right) _{K_{j}\left( t\right) }. \end{aligned}$$Next, we replace the function \(H\left( p,x\right) -\omega \partial _{x}p\) by the numerical flux \(\widehat{F} = \widehat{G} - \omega \frac{p_1+p_2}{2}\). Note that the numerical flux \(\widehat{F}\) is consistent with \(H\left( p,x\right) -\omega \partial _{x}p\). Hence, the one dimensional ALE-LDG method (2.28) can also be applied with the equation
$$\begin{aligned} 0=\frac{d}{dt}\left( u_{h},v\right) _{K_{j} \left( t\right) }-\left( \left( \partial _{x}\omega \right) u_{h},v\right) _{K_{j}\left( t\right) } +\left( \widehat{F}\left( \omega ,p_{1},p_{2},x\right) ,v\right) _{K_{j} \left( t\right) }, \end{aligned}$$(2.35)instead of (2.28a). The ALE method with (2.35) satisfies the same a priori error estimates as the ALE-LDG method (2.28). This can be proven by the same analysis as in Sect. 3. Numerically, the ALE method with (2.35) produces similar results as the ALE-LDG method (2.28). Nevertheless, to short this paper a discussion of the ALE method with (2.35) will be skipped. Similarly, a two dimensional analogue of the Eq. (2.35) can be used to replace the Eq. (2.33a) in the two dimensional ALE-LDG method (2.33).
2.5 The GCL for the ALE-LDG Method
The ALE mapping (2.6) can be the source of geometric errors in the moving mesh method. In order to control these geometric errors, the method should satisfy the GCL. The term GCL was introduced by Lombard and Thomas [21]. A moving mesh method respects the GCL, if it provides for constant initial data the right solution at the upcoming time level. In the context of conservation laws is the GCL satisfied, if the method preserves constant states. In other words, a moving mesh method for conservation laws satisfies the GCL, if for all \(n=0,\ldots ,L-1\) holds:
If the initial value problem (1.1) is investigated with the special Hamiltonian \(H=H\left( p,q\right) \), \(p,q\in {\mathbb {R}}\), and constant initial data \(u_{0}\in {\mathbb {R}}\), the unique viscous solution will be the function \(u=u_{0}-H\left( \mathbf{0}\right) t\). This observation motivates the following definition.
Definition 2.1
A moving mesh method for the Hamilton–Jacobi equations (1.1) with the Hamiltonian \(H=H\left( p,q\right) \) satisfies the GCL, if for all \(n=0,\ldots ,L-1\) holds:
In the following, we analyze the ALE-LDG method with respect to the GCL. Therefore, in order to find a criteria for the accomplishment of the GCL, we assume that \(u_{h}=1-H\left( \mathbf{0}\right) t\) is the approximate solution given by the ALE-LDG method. Then by the Eqs. (2.33b), (2.33c), (2.33d) and (2.33e) follows \(p_{1}=0\), \(p_{2}=0\), \(q_{1}=0\) and \(q_{2}=0\). Thus, (2.33a) and the integration by parts formula provide for all \(v\in \mathcal {V}_{h,2}(t)\) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\)
Next, we obtain by the substitution formula
since \(J_{K(t)}\) and \(\nabla \cdot \varvec{\omega }\) are independent of spatial variables by (2.5) and (2.8). Thus, \(u_{h}=1-H\left( \mathbf{0}\right) t\) can only be the solution of the semi-discrete ALE-LDG method, if the ordinary differential equation (ODE) (2.37) is satisfied. Hence, the semi-discrete ALE-LDG method satisfies the GCL, if the ODE (2.37) is satisfied. Since \(u_{h}=1-H\left( \mathbf{0}\right) t\) is constant in space, it holds the equation \(u_{h}^{*}=u_{h}\). Moreover, the test functions \(v^{*}\) are time-independent polynomials on the reference cell \(\mathcal {K}\) and it follows \(\left( \nabla \cdot \varvec{\omega }\right) J_{K(t)}\in P^{1}\left( \left[ t_{n},t_{n+1}\right] \right) \) by (2.8). Hence, the ODE in (2.37) can be solved exactly by any second order time discretization method. Therefore, we proved the following result for the two dimensional fully discrete ALE-LDG method.
Proposition 2.5
Consider the problem (1.1) with the Hamiltonian \(H=H\left( p,q\right) \), \(p,q\in {\mathbb {R}}\). Then the ODE (2.37) is satisfied for any time discretization method which is higher or equal to second order. Thus, the two dimensional fully discrete ALE-LDG method (2.33) satisfies the geometric conservation when these kind of time discretization methods are applied.
For the one dimensional ALE-LDG method, we obtain by (2.20) the ODE
Furthermore, it holds \(J_{K(t)}=h_{j}(t)\) in the one dimensional case. Hence, we proved the following result.
Proposition 2.6
Consider the problem (1.1) with the Hamiltonian \(H=H\left( p\right) \), \(p\in {\mathbb {R}}\). Then the ODE (2.38) is satisfied for any time discretization method, which is higher or equal to first order. Thus, the two dimensional fully discrete ALE-LDG method (2.28) satisfies the geometric conservation when these kind of time discretization methods are applied. In particular, the method satisfies the geometric conservation law for any high order single step method in which the stage order is equal or higher than first order.
2.6 The Forward Euler Piecewise Constant ALE-LDG Method
In this section, we consider the two dimensional forward Euler ALE-LDG method for the Hamiltonian \(H=H\left( p,q\right) \), \(p,q\in {\mathbb {R}}\). The one dimensional method can be analyzed by similar arguments.
In the following, we consider an arbitrary cell \(K(t) \in \mathcal {T}_{(t)}\). The outward unit normals of K(t) along the edges \(e^{\nu }_{K(t)}\), \(\nu =1,2,3\), are denoted by \(\mathbf {n}^{\nu }_{K(t)}=(n^{\nu }_{K(t),x},n^{\nu }_{K(t),y})^T\), \(\nu =1,2,3\). The neighboring cells along the edges \(e^{\nu }_{K(t)}\), \(\nu =1,2,3\), are denoted by \(K_{\nu }\left( t\right) \). The Lebesgue measure of the cell K(t) is \(\left| K(t)\right| =\frac{1}{2}J_{K(t)}\). In addition, the lengths of the edges are denoted by \(\ell _{K(t)}^{\nu }\), \(\nu =1,2,3\). Let \(\overline{u}_{K^{n}}^{n}\) be the piecewise constant approximation for the solution u of the problem (1.1) at time level \(t_{n}\) in an arbitrary cell \(K^{n}\in \mathcal {T}_{n}\). Then the Eqs. (2.33b) as well as (2.33c) provide
and by the Eqs. (2.33d) as well as (2.33e) follows
Next, we obtain by (2.15) and the second order accurate midpoint quadrature method
where \(t_{n+\frac{1}{2}}:=\frac{1}{2}\left( t_{n}+t_{n+1}\right) \) and \(\left| K^{n+\frac{1}{2}}\right| :=\left| K\left( \frac{1}{2}\left( t_{n}+t_{n+1}\right) \right) \right| \). The second order accurate midpoint quadrature method is also used to evaluate the surface integrals \(\left\langle \varvec{\omega }^{n},\mathbf {n}_{K^{n}}^{\nu }\right\rangle _{e_{K^{n}}^{\nu }}\), \(\nu =1,2,3\), since the grid velocity field is linear in the spatial variables. Hence, we obtain for all \(\nu =1,2,3\)
where \(\overline{\mathbf{v}}_{\nu }^{n}\) is the midpoint of the edge \(e^{\nu }_{K(t)}\). Next, by (2.39), (2.40), (2.41), (2.42), (2.43) and (2.44) the forward Euler piecewise constant ALE-LDG method can be written as
where for all \(a_{0},a_{1},a_{2},a_{3}\in {\mathbb {R}}\)
with
and
It should be noted that the function \(\mathcal {H}\left( a_{0},a_{1},a_{2},a_{3}\right) \) is increasing in all its arguments, if the following CFL condition is satisfied
where \(c_{0}:=\max \left\{ \left| \nabla \cdot \varvec{\omega }\left( \mathbf{x},t\right) \right| :\mathbf{x}\in K_{j}(t),\ t\in \left[ t_{n},t_{n+1}\right] \right\} \). Hence, (2.45) is a monotone scheme, if the CFL condition above is satisfied. Thus the forward Euler piecewise constant ALE-LDG method converges to the unique viscous solution according to Crandall and Lions [10].
3 A Priori Error Estimates
In this section, we prove a priori error estimates for the one and two dimensional semi-discrete ALE-LDG method. It should be noted that these a priori error estimates are merely valid when the initial value problem (1.1) has a smooth solution. Moreover, the a priori error will be estimated in the sense of the global length h given by (2.3). We will proceed as follows: First of all, we would like to use the ALE–DG solution \(u_{h}\) as test function in the Eqs. (2.28a) and (2.33a). Admittedly, this is not possible, since the transport Eq. (2.13) cannot be used for test functions with time-dependent coefficients like (2.24). Thus, the equivalent Eqs. (2.29) and (2.34) need to be applied. Afterward, in order to compensate the nonlinear nature of the Hamiltonian in the problem (1.1), the Taylor formula is used. Finally, we apply interpolation, inverse and trace inequalities to estimate the remainders of the Taylor expansion. Therefore, we need the following a priori assumptions
and
where the constants \(C_{\mathcal {H}_{1}}\) and \(C_{\mathcal {H}_{2}}\) are independent of \(u_{h}\) and h. First of all, we would like to mention that the a priori assumptions are merely necessary when a nonlinear Hamiltonian is investigated in the problem (1.1). Furthermore, the assumptions (3.1a) and (3.1b) make sense, since \(p_{1}\), \(p_{2}\) approximate \(\partial _{x}u_{h}\) and \(q_{1}\), \(q_{2}\) approximate \(\partial _{y}u_{h}\). It should be noted that these a priori assumptions are slightly different from the a priori assumption which was applied by Xiong et al. [28] to prove a priori error estimates for Yan and Osher’s LDG method. Nevertheless, the a priori assumptions above supply
The inequality (3.2) corresponds to the a priori assumption in [28]. Furthermore, we assume that the Hamiltonian in the problem (1.1) and the grid velocity field given by (2.7) and (2.20) are sufficiently smooth and have bounded derivatives. These assumptions and the mean value theorem provide the upcoming lemma.
Lemma 3.1
Suppose \(u\in \mathrm {W}^{1,\infty }\left( 0,T;\mathrm {H}^{2}\left( \Omega \right) \right) \), the Hamiltonian \(H\in \mathcal {C}^{2}\left( {\mathbb {R}}^{2}\times \Omega \right) \) as well as the grid velocity field \(\varvec{\omega }=\left( \omega _{1},\omega _{2}\right) ^{T}\) are bounded and have bounded derivatives. Furthermore, suppose \(K(t)\in \mathcal {T}_{(t)}\) is an arbitrary cell and \(\beta _{K\left( t\right) }\) is either (2.31) or (2.32). Then there exists constants \(C_{1}^{\star }\), \(C_{2}^{\star }\) and \(C_{3}^{\star }\) independent of h and \(u_{h}\), such that for \(\sigma =p\), \(\tau =1\), \(\beta _{K\left( t\right) }=\lambda _{K\left( t\right) }\) or \(\sigma =q\), \(\tau =2\), \(\beta _{K\left( t\right) }=\mu _{K\left( t\right) }\)
if \(\partial _{\sigma }H\left( \nabla u,\mathbf{x}\right) -\omega _{\tau }\left( \mathbf{x},t\right) >0\) in the cell \(K\left( t\right) \),
if \(\partial _{\sigma }H\left( \nabla u,\mathbf{x}\right) -\omega _{\tau }\left( \mathbf{x},t\right) <0\) in the cell \(K\left( t\right) \),
if \(\partial _{\sigma }H\left( \nabla u,\mathbf{x}\right) -\omega _{\tau }\left( \mathbf{x},t\right) \) changes the sign in the cell \(K\left( t\right) \). In addition, there exists a constant \(C_{4}^{\star }\), such that for \(\nu =1,2,3\) holds
where \(K_{\nu }(t)\), \(\nu =1,2,3\), are the adjacent cells of K(t).
Proof
We merely prove the estimates for the function \(\partial _{p}H\left( p,q,\mathbf{x}\right) -\omega _{1}\left( \mathbf{x},t\right) \). The estimates for the function \(\partial _{q}H\left( p,q,\mathbf{x}\right) -\omega _{2}\left( \mathbf{x},t\right) \) can be proven similar.
Henceforth, \(K(t)\in \mathcal {T}_{(t)}\) is an arbitrary cell. First of all, it should be noted that there exists at least one point \((\hat{p},\hat{q},{\hat{\mathbf{x}}})\in D_{K(t)}\times E_{K(t)}\times \overline{K(t)}\) with
since the function \(\left| \partial _{p}H\left( p,q,\mathbf{x}\right) -\omega _{1}\left( \mathbf{x},t\right) \right| \) is continuous in the domain \(D_{K(t)}\times E_{K(t)}\times \overline{K(t)}\).
Afterward, we run a case analysis started with the case: \(\partial _{p}H(\nabla u,\mathbf{x})-\omega _{1}\left( \mathbf{x},t\right) >0\), for all \(\mathbf{x}\in K(t)\). It follows by the reverse triangle inequality and (3.7)
The mean value theorem and the a priori assumptions (3.1a), (3.1b) as well as (3.2) provide that the right hand side of (3.8) behaves as \(\mathcal {O}\left( h\right) \), since the Hamiltonian \(H\in \mathcal {C}^{2}\left( {\mathbb {R}}^{2}\times \Omega \right) \) and the grid velocity field \(\varvec{\omega }=\left( \omega _{1},\omega _{2}\right) ^{T}\) are bounded and have bounded derivatives. This proves the inequality (3.3).
Next, we consider the case: \(\partial _{p}H(\nabla u,\mathbf{x})-\omega _{1}\left( \mathbf{x},t\right) <0\), for all \(\mathbf{x}\in K(t)\). We obtain by the reverse triangle inequality and (3.7)
By the same arguments as in the previous case, follows that the right hand side of (3.9) behaves as \(\mathcal {O}\left( h\right) \). Hence, we obtain the inequality (3.4).
Finally, we consider the case: \(\partial _{p}H(\nabla u,\mathbf{x})-\omega _{1}\left( \mathbf{x},t\right) \) changes the sign in the cell \(K\left( t\right) \). Then, there exists at least one point \({\tilde{\mathbf{x}}}\in K\left( t\right) \), such that \(\partial _{p}H(\nabla u,\hat{\mathbf{x}})-\omega _{1}\left( \hat{\mathbf{x}},t\right) =0\). Therefore, we obtain by the Taylor formula and the mean value theorem for all \(\mathbf{x}\in K(t)\)
Moreover, by the reverse triangle inequality and (3.7) follows
The inequality (3.10) yields (3.5), since the right hand side of the inequality (3.10) behaves as \(\mathcal {O}\left( h\right) \). This follows by the same arguments as in the previous cases.
It left to prove the inequality (3.6). In the following, for all \(\nu =1,2,3\) the edge shared by the cell K(t) and its adjacent cell \(K_{\nu }(t)\) is denoted by \(e_{K\left( t\right) }^{\nu }\). First of all, it should be noted that there exists points \((\hat{p},\hat{q},{\hat{\mathbf{x}}})\in D_{K(t)}\times E_{K(t)}\times \overline{K\left( t\right) }\) and \((\hat{p}_{\nu },\hat{q}_{\nu },{\hat{\mathbf{x}}}_{\nu })\in D_{K_{\nu }\left( t\right) }\times E_{K_{\nu }\left( t\right) }\times \overline{K_{\nu }\left( t\right) }\) such that for \(\nu =1,2,3\)
since the function \(\left| \partial _{p}H\left( p,q,\mathbf{x}\right) -\omega _{1}\left( \mathbf{x},t\right) \right| \) is continuous. Thus, we obtain by the reverse triangle inequality and the Eq. (3.11) for any point \(\mathbf{x}_{K\left( t\right) }^{\nu }\in e_{K\left( t\right) }^{\nu }\), \(\nu =1,2,3\), the estimate
The right hand side of the inequality (3.12) behaves as \(\mathcal {O}\left( h\right) \). This follows by the same arguments as in the previous case analysis. Hence, it follows \(\left| \lambda _{K(t)}-\lambda _{K_{\nu }(t)}\right| \le Ch\). This completes the proof of Lemma 3.1. \(\square \)
The next estimates give information about the relationship between the quantities \(\partial _{x}u_{h}\), \(p_{1}\), \(p_{2}\) and \(\partial _{y}u_{h}\), \(q_{1}\), \(q_{2}\).
Lemma 3.2
Let \(u\in \mathrm {W}^{1,\infty }\left( 0,T;\mathrm {H}^{k+1}\left( \Omega \right) \right) \) be the exact solution of the initial value problem (1.1). Suppose, for any \(t\in \left[ 0,T\right] \), there exists a partition of the domain \(\Omega \) with the properties (A1) as well as (A2) and the condition (2.4) is satisfied for the global length h given by (2.3). Let \(u_{h}\) be the solution of the semi-discrete ALE-LDG method (2.33) with the test function space (2.9) given by piecewise polynomials. Then there exists a constant C, independent of \(u_{h}\) and h, such that
where \(\varphi _{h}:=u_{h}-\mathcal {P}_{h}\left( u\right) \) and \(\mathcal {P}_{h}\left( u\right) \) is the \(\mathrm {L}^{2}\)-projection of the given function u.
Proof
The integration by parts formula and the Eq. (2.33b) provide for any cell \(K(t)\in \mathcal {T}_{\left( t\right) }\) and all \(v\in \mathcal {V}_{h,2}(t)\)
We would like to sum the Eq. (3.15) over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). In the course of this, the surface integrals along the edges of the cells need to be analyzed carefully. Therefore, first, we investigate merely the cells \(K_{\nu }\left( t\right) \), \(\nu =1,2,3\), which share the edges \(e_{K\left( t\right) }^{\nu }\), \(\nu =1,2,3\), with \(K\left( t\right) \) and analyze the Eq. (3.15) summed over these cells. The outward normals of the cell \(K\left( t\right) \) along the edges \(e_{K\left( t\right) }^{\nu }\) are denoted by \(\mathbf {n}_{K(t)}^{\nu }=(n_{K(t),x}^{\nu },n_{K(t),y}^{\nu })^{T}\). Then the outward normals of the cells \(K_{\nu }\left( t\right) \) along the edges \(e_{K\left( t\right) }^{\nu }\) satisfy \(\mathbf {n}_{K_{\nu }(t)}^{\nu }=-\mathbf {n}_{K(t)}^{\nu }\). Hence, for \(\nu =1,2,3\) and \(i=x,y\) follows
Therefore, we obtain for all \(v\in \mathcal {V}_{h,2}(t)\) and \(\nu =1,2,3\)
where \(e_{K\left( t\right) }^{\nu ,c}=\partial K\left( t\right) {\setminus } e_{K\left( t\right) }^{\nu }\), \(e_{K_{\nu }\left( t\right) }^{\nu ,c}:=\partial K\left( t\right) {\setminus } e_{K\left( t\right) }^{\nu }\) and
Hence, the surface integrals at the cell interfaces can be summarized in the shape of (3.19), when the Eq. (3.15) is summed over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). Furthermore, the surface integrals at the boundary faces canceled out, since the problem (1.1) is considered with periodic boundary conditions. Therefore, since the function u is sufficiently smooth, we obtain for all \(v\in \mathcal {V}_{h,2}(t)\) the inequality
when the Eq. (3.15) is summarized over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) and the notation
is used. Next, we plug the test function \(v=\partial _{x} u_{h}-p_{1}\) into the inequality (3.20) and apply the Cauchy–Schwarz inequality, Young’s inequality, the inverse inequalities (2.12) and the interpolation inequalities (2.17). This results in
Finally, it should be noted that we obtain similar estimates as (3.22) for the quantities \(\left\| \partial _{x}u_{h}-p_{2}\right\| _{\mathrm {L}^{2}\left( \Omega \right) }^{2}\), \(\left\| \partial _{y}u_{h}-q_{1}\right\| _{\mathrm {L}^{2}\left( \Omega \right) }^{2}\) and \(\left\| \partial _{y}u_{h}-q_{2}\right\| _{\mathrm {L}^{2}\left( \Omega \right) }^{2}\) when we apply the same analysis as above with the Eqs. (2.33c), (2.33d) and (2.33e). These estimates supply the desired estimates (3.13) and (3.14). \(\square \)
The inequalities (3.13) and (3.14) yield for all \(t\in \left[ 0,T\right] \)
Moreover, it should be noted that the bounds and inequalities in Lemmas 3.1 and 3.2 hold also in one dimension. In particular, Lemma 3.2 can be applied with the \(\mathcal {Q}\)-projection instead of the \(\mathrm {L}^{2}\)-projection. Thus, there is no harm to apply these results in the proof of the a priori error estimates for the one dimensional ALE-LDG method.
3.1 An Optimal Error Estimate for the One Dimensional Method
In this section we prove the following a priori error estimate.
Theorem 3.3
Let \(u\in \mathrm {W}^{1,\infty }\left( 0,T;\mathrm {H}^{k+2}\left( \Omega \right) \right) \) be the exact solution of the initial value problem (1.1), the Hamiltonian \(H\in \mathcal {C}^{2}\left( {\mathbb {R}}\times \Omega \right) \) and the grid velocity \(\omega \) given by (2.20) be bounded and have bounded derivatives. Furthermore, for any time level \(t\in \left[ 0,T\right] \), there exists a regular partition of the domain \(\Omega \), which covers the whole domain \(\Omega \), and the condition (2.4) is satisfied for the global length h given by (2.3). Let \(u_{h}\) be the solution of the semi-discrete ALE-LDG method (2.28) with the test function space (2.9) given by piecewise polynomials of degree \(k\ge 2\) and the initial data \(\mathcal {Q}_{h}\left( u_{0}\right) \). Then there exists a constant C independent of \(u_{h}\) and h, such that
Proof
First of all, we define the quantities
Then the error function \(e_{h}:=u-u_{h}\) and the quantity \(\partial _{x}u-\frac{p_{1}+p_{2}}{2}\) can be written as
The solution u of the initial value problem (1.1) is assumed to be smooth. Hence, the integration by parts formula provides for all \(v\in \mathcal {V}_{h,1}\left( t\right) \) and \(j=1,\ldots ,N\)
Next, for all \(j=1,\ldots ,N\), we subtract the equation (2.28b) or (2.28c) from the Eq. (3.25) and plug the test function \(v=\varphi _{h}\) in the result. This yields the error equations
where we used that \(\left( \psi _{h},\partial _{x}\varphi _{h}\right) _{K\left( t\right) }=0\) by (2.16) as well as (2.21a) and we used that \(u_{j-\frac{1}{2}}^{-}=u_{j-\frac{1}{2}}^{+}\) for all \(j=1,\ldots ,N\), since the exact solution u is smooth.
Moreover, we obtain the error equation
by summarizing the Eqs. (3.26a) and (3.26b) multiplied with \(\frac{1}{2}\).
Before the Eq. (3.26) can be used to state the next error equation, we need to make some preparations. First of all, we define the quantities
Then we obtain by the mean value theorem for all \(t\in \left[ 0,T\right] \) and \(j=1,\ldots ,N\)
since the grid velocity is assumed to be bounded and has bounded derivatives. The integration by parts formula and Lemma 2.4 provide
since \(\left( \overline{\omega }_{j}\psi _{h}, \partial _{x}\varphi _{h}\right) _{K_{j}(t)}=0\) by (2.16) and (2.21a). Next, the transport Eq. (2.13) supplies
The Taylor formula yields
where \(\Theta \) is a value between \(\partial _{x}u\) and \(\frac{p_{1}+p_{2}}{2}\). Furthermore, since the solution u of the initial value problem (1.1) is assumed to be smooth, for all \(v\in \mathcal {V}_{h,1}\left( t\right) \) and \(j=1,\ldots ,N\) holds
First of all, we subtract the Eq. (2.29) from Eq. (3.31), plug the test function \(v=\varphi _{h}\) in the result and subtract the Eq. (3.26c) multiplied by \(\overline{\omega }_{j}\). Then, we apply the Eqs. (3.28), (3.29) and (3.30) and obtain the error equation
where
In the following, we will prove that the quantities (3.33) summed from \(j=1\) to N behave as \(\mathcal {O}\left( h^{k+1}\right) \).
First of all, Young’s inequality, the inverse inequalities (2.12), the interpolation estimates (2.17) and the inequality (3.27) for the grid velocity provide
since the grid velocity is assumed to be bounded with bounded derivatives and the initial value problem (1.1) is investigated with periodic boundary conditions. In the same matter, we obtain
by Young’s inequality, the inverse inequalities (2.12), the interpolation estimates (2.17) and the inequality (3.27) for the grid velocity. Furthermore, the a priori assumption (3.2), the Cauchy–Schwarz inequality, Young’s inequality, the inverse inequalities (2.12), (3.23) and the interpolation inequalities (2.17) supply
since the Hamiltonian is assumed to be bounded and has bounded derivatives. The quantity (3.33d) deserves more attention. A careful case analysis determined by the sign of the function \(\partial _{p}H\left( \partial _{x}u,x\right) -\omega \left( x,t\right) \) in the cells \(K_{j}\left( t\right) \), \(j=1,\ldots ,N\), is necessary. The case analysis will provide the inequality
In order to avoid confusion, we skip the details of the case analysis and prove the inequality (3.37) separated from this proof at the end of this section.
Finally, we sum the Eq. (3.32) from \(j=1\) to N, apply (3.34), (3.35), (3.36), (3.37) and Gronwall’s inequality. This results in the estimate
Then, (3.38) and the interpolation inequality (2.17) yield for all \(t\in \left[ 0,T\right] \) an \(\mathrm {L}^{2}\)-estimate for the error function \(e_{h}\). The maximum of the \(\mathrm {L}^{2}\)-estimate over the interval \(\left[ 0,T\right] \) supplies the desired error estimate. This completes the proof of Theorem 3.3. \(\square \)
It remains to prove the inequality (3.37).
Lemma 3.4
Suppose the same assumptions as in Theorem 3.3. Then there exists a constant C, independent of \(u_{h}\) and h, such that it holds the inequality (3.37).
Proof
We prove the inequality (3.37) in two steps. In the first step, we run a case analysis determined by the sign of the function \(\partial _{p}H\left( \partial _{x}u,x\right) -\omega \left( x,t\right) \) and different families of consecutive cells \(\left\{ K_{j}(t)\right\} _{j=j_{1}}^{j_{2}}\) with \(1\le j_{1}\le j_{2} \le N\). The case analysis provides estimates for the quantity (3.33d) summed over the consecutive cells. In the final step, we apply these estimates to estimate the quantity (3.33d) summed over all cells.
Case 1 We consider an arbitrary family of consecutive cells \(\left\{ K_{j}(t)\right\} _{j=j_{1}}^{j_{2}}\) with \(1\le j_{1}\le j_{2} \le N\) and \(\partial _{p}H(\partial _{x}u,x)-\omega \left( x,t\right) \) changes the sign in each cell \(K_{j}\left( t\right) \), \(j=j_{1},\ldots ,j_{2}\). First of all, for any cell \(K_{j}(t)\), \(j=j_{1},\ldots ,j_{2}\), we subtract the Eq. (3.26a) multiplied by \(\frac{\lambda _{j}}{2}\) and the Eq. (3.26b) multiplied by \(-\frac{\lambda _{j}}{2}\) from the equation (3.33d). This provides

Since the quantities \(\left| \partial _{p}H\left( \partial _{x} u,x\right) -\omega \left( x,t\right) \right| \) and \(\lambda _{j}\) are bounded by \(C_{3}^{\star }h\) according to the inequality (3.5) in Lemma 3.1, it follows
by the inequality (3.27) for the grid velocity. Therefore, Young’s inequality and a summation from \(j=j_{1}\) to \(j_{2}\) of the Eq. (3.39) supply
Case 2 We consider an arbitrary family of consecutive cells \(\left\{ K_{j}(t)\right\} _{j=j_{1}}^{j_{2}}\) with \(1\le j_{1}\le j_{2} \le N\) and \(\partial _{p}H\left( \partial _{x}u,x\right) -\omega \left( x,t\right) >0\) for each cell \(K_{j}\left( t\right) \), \(j=j_{1},\ldots ,j_{2}\). Then we obtain \(\mathcal {Q}_{h}=\mathcal {P}_{h}^{-}\). Thus, by (2.21b) it follows \(\psi _{h,j-\frac{1}{2}}^{-}=0\) for all \(j=j_{1},\ldots ,j_{2}\). We subtract the Eq. (3.26a) multiplied by \(\lambda _{j}\) from the Eq. (3.33d) and obtain
According to the inequality (3.5) in Lemma 3.1, the quantities \(\lambda _{j_{2}-1}\) as well as \(\lambda _{j_{1}+1}\) are bounded by \(C_{3}^{\star }\), since \(\partial _{p}H\left( \partial _{x}u,x\right) -\omega \left( x,t\right) \) changes the sign in the cells \(K_{j_{1}-1}\left( t\right) \) and \(K_{j_{2}+1}\left( t\right) \). Likewise, according to the inequality (3.6) in Lemma 3.1, the quantities \(\left| \lambda _{j}-\lambda _{j-1}\right| \) is bounded \(C_{4}^{\star }h\) for all \(j=j_{1},\ldots ,j_{2}\). Therefore, the summation by parts formula provides
Furthermore, by the inequality (3.3) in Lemma 3.1 and the inequality (3.27) for the grid velocity follows
Next, we sum the Eq. (3.41) from \(j=j_{1}\) to \(j_{2}\) and apply Young’s inequality, the inequality (3.3) in Lemma 3.1 and (3.42) as well as (3.43). This results in the inequality (3.40), since \(-\sum _{j=j_{1}}^{j_{2}}\frac{\lambda _{j}}{2}\left( [\![\varphi _{h}]\!] _{j-\frac{1}{2}}\right) ^{2}\le 0\).
Case 3 We consider an arbitrary family of consecutive cells \(\left\{ K_{j}(t)\right\} _{j=j_{1}}^{j_{2}}\) with \(1\le j_{1}\le j_{2} \le N\) and \(\partial _{p}H\left( \partial _{x}u,x\right) -\omega (x,t)<0\) for each cell \(K_{j}\left( t\right) \), \(j=j_{1},\ldots ,j_{2}\). In this case, we obtain \(\mathcal {Q}_{h}=\mathcal {P}_{h}^{+}\). Thus, by (2.21b) it follows \(\psi _{h,j-\frac{1}{2}}^{+}=0\) for all \(j=j_{1},\ldots ,j_{2}\). We subtract the Eq. (3.26b) multiplied by \(-\lambda _{j}\) from the Eq. (3.33d). This results in an equation of the type (3.41). Moreover, we obtain by the inequality (3.4) in Lemma 3.1 and the inequality (3.27) for the grid velocity
Hence, (3.44) and the same arguments as in case 2) supply the inequality (3.40).
Finally, we sum the Eq. (3.33d) from \(j=1\) to N and apply the inverse inequalities (2.12), the interpolation estimates (2.17) as well as the inequality (3.40). Then, since we obtained the inequality (3.40) in the cases (1), (2), (3) and the initial value problem (1.1) is considered with periodic boundary conditions, we obtain
It should be noted, that in the Eq. (3.45) each boundary term has been counted at most twice. This does not affect the error estimate. \(\square \)
3.2 A Suboptimal Error Estimate for the Two Dimensional Method
In this section we prove the following a priori error estimate.
Theorem 3.5
Let \(u\in \mathrm {W}^{1,\infty }\left( 0,T;\mathrm {H}^{k+1}\left( \Omega \right) \right) \) be the exact solution of the initial value problem (1.1), the Hamiltonian \(H\in \mathcal {C}^{2}\left( {\mathbb {R}}^{2}\times \Omega \right) \) and the grid velocity field \(\varvec{\omega }=\left( \omega _{1},\omega _{2}\right) ^{T}\) be bounded and have bounded derivatives. Furthermore, for any \(t\in \left[ 0,T\right] \), there exists a partition of the domain \(\Omega \) with the properties (A1) as well as (A2) and the condition (2.4) is satisfied for the global length h given by (2.3). Let \(u_{h}\) be the solution of the semi-discrete ALE-LDG method (2.33) with the test function space (2.9) given by piecewise polynomials of degree \(k\ge 3\) and the initial data \(\mathcal {P}_{h}\left( u_{0}\right) \). Then there exists a constant C independent of \(u_{h}\) and h, such that
Proof
In this proof, we apply the notation (3.21) as in the proof of the Lemma 3.2. Hence, the error function \(e_{h}:=u-u_{h}\) can be written as \(e_{h}=\psi _{h}-\varphi _{h}\). Moreover, we define
Then the quantities \(\partial _{x}u-\frac{p_{1}+p_{2}}{2}\) and \(\partial _{y}u-\frac{q_{1}+q_{2}}{2}\) can be written as
It is assumed that the exact solution of the initial value problem (1.1) is smooth. Thus, the integration by parts formula provides for all \(v,w\in \mathcal {V}_{h,2}(t)\) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\)
Next, we subtract the Eqs. (2.33b) or (2.33c) from the Eq. (3.47a) and the Eqs. (2.33d) or (2.33e) from the Eq. (3.47b) and plug in the results the test function \(v=\varphi _{h}\). This results for all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) in the error equations
since \(\left( \psi _{h},\partial _{x}\varphi _{h}\right) _{K\left( t\right) }=0\) and \(\left( \psi _{h},\partial _{y}\varphi _{h}\right) _{K\left( t\right) }=0\) by (2.16) the exact solution u is smooth such that \(u^{\text {int}_{K\left( t\right) }}=u^{\text {ext}_{K\left( t\right) }}\).
Henceforth, we define for \(s =1,2\)
The mean value theorem provides for all \(t\in \left[ 0,T\right] \) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\)
Furthermore, we sum the Eqs. (3.48a) as well as (3.48b) and multiply the result by \(\frac{1}{2}\overline{\omega }_{K(t),1}\). In the same manner we sum the Eqs. (3.48c) as well as (3.48d) and multiply the result by \(\frac{1}{2}\overline{\omega }_{K(t),2}\). This provides the additional error equations
Before the Eq. (2.33a) can be used to state the next error equation, we need to make some preparations. First of all, it should be noted that the function \(\varphi _{h}\) has time-dependent coefficients on the reference cell. Nevertheless, by a simple calculation it can be shown that \(\partial _{t}\varphi _{h}\in \mathcal {V}_{h,2}\left( t\right) \). Hence, the transport Eq. (2.13) with the test function \(v=1\) and the Eq. (2.16) provide
In addition, it follows
by the transport Eq. (2.13) with the test function \(v=1\). Next, the Taylor formula supplies
where \(\Theta _{1}\) is a value between \(\partial _{x}u\) as well as \(\frac{p_{1}+p_{2}}{2}\) and \(\Theta _{2}\) is a value between \(\partial _{y}u\) as well as \(\frac{q_{1}+q_{2}}{2}\).
Moreover, since u is a smooth solution of the initial value problem (1.1), it follows for all \(v\in \mathcal {V}_{h,2}(t)\) and all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\)
Next, we subtract the Eq. (2.34) from the Eq. (3.54) and plug the test function \(v=\varphi _{h}\) in the result. Then, we apply the equations (3.51) as well as (3.52) and the Taylor expansion (3.53) to rewrite the result for all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) as follows
where for \(s=1,2\) and \(i=x,y\)
The next steps in the proof of Theorem 3.5 are similar as in the proof of Theorem 3.3. First, we estimate the quantities (3.56). It follows,
by the inequality (3.49) for the grid velocity and the same analysis as in the proof of Theorem 3.3. Moreover, we will prove that it holds
We would like to mention that it is not straightforward to derive the estimate (3.58), since an intensive case analysis is required. At the end of this section, we sketch the basic steps in the proof by presenting the evaluation of the most important case. Furthermore, it should be noted that the constants in (3.57) and (3.58) are independent of \(u_{h}\) and h.
Next, the Eq. (3.55) is summed over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) and the inequalities (3.57), (3.58) and Gronwall’s inequality are applied. This provides the inequality
The inequality (3.59) and the interpolation inequality (2.17) yield for any \(t\in \left[ 0,T\right] \) a \(\mathrm {L}^{2}\)-estimate of the error \(e_{h}\). Finally, we obtain the desired error estimate by taking the maximum of the \(\mathrm {L}^{2}\)-estimate over all \(t\in \left[ 0,T\right] \). \(\square \)
In the following the basic ideas to prove the inequality (3.58) are sketched.
Lemma 3.6
Suppose the same assumptions as in Theorem 3.5. Then there exists a constant C, independent of \(u_{h}\) and h, such that it holds the inequality (3.58).
Proof
We sketch the proof for the quantity \(\sum _{K(t)\in \mathcal {T}_{(t)}}b_{3}\left( \omega _{1,K(t)},u,u_{h},p_{1},p_{2}\right) \) the quantity \(\sum _{K(t)\in \mathcal {T}_{(t)}}b_{4}\left( \omega _{2,K(t)},u,u_{h},q_{1},q_{2}\right) \) can be estimated similar by applying the error Eqs. (3.48c) and (3.48d).
The proof of the inequality follows in two steps. First, the cell interfaces need to be analyzed carefully by a case analysis. Afterward, we apply the results of the case analysis to estimate the Eq. (3.56c) summed over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). The case analysis is determined by the sign of the function \(\partial _{p}H\left( \nabla u,\mathbf{x}\right) -\omega _{1}\left( \mathbf{x},t\right) \) in two adjacent cells. Seven different cases appear, since \(H\in \mathcal {C}^{2}\left( {\mathbb {R}}^{2}\times \Omega \right) \) and the grid velocity is continuous in the spatial variables. The evaluation of these cases ensues similar as in the proof of Lemma 3.4. We multiply the error Eq. (3.48) by the parameter (2.31) and add or subtract the result from the quantity (3.56a). In this paper, we show merely the analysis of the case: The function \(\partial _{p}H\left( \nabla u,\mathbf{x}\right) -\omega _{1}\left( \mathbf{x},t\right) \) is positive in both cells. This is the most important case, since a loss of accuracy appears in this case. All the other cases can be analyzed by similar arguments.
At first, we obtain for an arbitrary cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\)
where we multiplied the Eq. (3.48a) by \(\lambda _{K(t)}\) and subtract the result from the quantity (3.56c). By the inequality (3.3) in Lemma 3.1 and the inequality (3.49) for the grid velocity follows
Hence, by applying the Cauchy–Schwarz inequality and Young’s inequality, the volume integral in (3.60) can be estimated as follows
Next, we would like to estimate the quantity (3.56a) summed over two adjacent cells. Therefore, henceforth, \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\) is an arbitrary cell. We apply the same notation as in the proof of Lemma 3.2 for the adjacent cells, edges and outward normals of the cell \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\). However, in this proof, we fix the index \(\nu \in \left\{ 1,2,3\right\} \) and analyze only the situation along the edge \(e_{K\left( t\right) }^{\nu }\) which is shared by the cell \(K\left( t\right) \) and the adjacent cell \(K_{\nu }\left( t\right) \). We start with the analysis of the surface integrals, which appear by the Eq. (3.60), when the quantity (3.56a) is summed over the cells \(K\left( t\right) \) and \(K_{\nu }\left( t\right) \). Then, since \(\mathbf {n}_{K(t)}^{\nu }=-\mathbf {n}_{K_{\nu }(t)}^{\nu }\) along the \(e_{K\left( t\right) }^{\nu }\), it follows
where \(e_{K\left( t\right) }^{\nu ,c}:=\partial K\left( t\right) {\setminus } e_{K\left( t\right) }^{\nu }\), \(e_{K_{\nu }\left( t\right) }^{\nu ,c}:=\partial K_{\nu }\left( t\right) {\setminus } e_{K\left( t\right) }^{\nu }\) and
The function \(S_{\pm }\left( \psi _{h},\varphi _{h},n_{K\left( t\right) ,x}\right) \) is defined as follows: If \(n_{K\left( t\right) ,x}^{\nu }>0\), it is by (3.16a)
and if \(n_{K\left( t\right) ,x}^{\nu }<0\), it is by (3.16b)
It is assumed that the Hamiltonian and the grid velocity have bounded derivatives. Thus, there exists a constant \(C_{1}\), which is independent of \(u_{h}\) and h, such that \(\left| \lambda _{K\left( t\right) }\right| +\left| \lambda _{K_{\nu }\left( t\right) }\right| \le C_{1}\). Furthermore, by the inequality (3.6) in Lemma 3.1 holds \(\left| \lambda _{K_{1}\left( t\right) }-\lambda _{K_{2}\left( t\right) }\right| \le C_{4}^{\star }h\). Therefore, we obtain by Young’s inequality
It should be noted that in the other cases the surface integrals can be summarized in a similar matter as in the Eq. (3.63). Furthermore, the estimates (3.62) and (3.67) can be derived. Hence, when we sum the quantity (3.56a) over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\), the surface integrals at the cell interfaces can be summarized in the shape of (3.65) and (3.66). Moreover, the surface integrals at the boundary faces canceled out, since the problem (1.1) is investigated with periodic boundary conditions. Thus, a summation of the quantity (3.56c) over all cells \(K\left( t\right) \in \mathcal {T}_{\left( t\right) }\), the estimates (3.62) as well as (3.67), the inverse inequalities (2.12) and the interpolation inequalities (2.17) provide
Note that in the inequality (3.67) an extra h to control the loss of accuracy by the inverse inequalities (2.12) is missing. Thus, the interpolation estimates (2.17) provide merely the suboptimal order \(h^{2k+1}\) instead of the optimal order \(h^{2k+2}\). Furthermore, in the Eq. (3.68) each boundary term has been counted at most twice. This does not affect the error estimate. \(\square \)
4 Numerical Experiments
In this section, we display the performance of the ALE-LDG method for the Hamilton Jacobi equations with convex and noneconvex Hamiltonian in one and two dimension. For the two-dimensional problem, triangular meshes are used in our simulation. We adopt TVD Runge–Kutta methods (c.f. Gottlieb and Shu [12]) for the time discretization, which are convex combinations of the forward Euler method. Thus, by an adequate adjustment of the CFL condition, the results for the forward Euler discretization can be extended to TVD Runge–Kutta methods. We obtain the optimal order of accuracy on the moving grids as the static grids when the approximation space (2.9) is defined by \(P^k\) polynomials on the reference cell.
Example 4.1
Variable coefficient linear Hamiltonian equation
with periodic boundary condition and initial condition \(u(x,0)=\sin (x)\). The exact solution is
In Table 1 we compare the convergence history of the ALE-LDG method by using piecewise \(P^2\) and \(P^3\) polynomial elements with different cell numbers N at \(t=1\) on the static uniform grid and the moving grid \(x_{j+\frac{1}{2}}(t^n ) = x_{j+\frac{1}{2}}(0) + 0.4 \sin (t^n)\sin (x_{j+\frac{1}{2}}(0))\) respectively. The moving grid starts from an uniform grid initially. And we use the notations \(u_h^S\) and \(u_h^M\) for the numerical solutions on the static and moving grid respectively. It can be seen that numerically the optimal convergence order can be obtained for both grids.
Example 4.2
Nonsmooth variable coefficient linear Hamiltonian equation
with periodic boundary condition and initial condition \(u(x,0)=\sin (x)\).
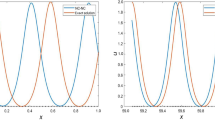
For this example, there will be a shock forming in the derivative \(\partial _{x}u\) at \(x = \frac{\pi }{2}\) and a rarefaction wave forming at \(x = \frac{3\pi }{2}\). Figure 2 shows the ALE-LDG solutions \(u_h^S\) and \(u_h^M\) at time \(t = 1\) with piecewise quadratic polynomial approximations. The same grids are adopted as in the last example. We find that both numerical solutions converge to the viscosity solution.
Example 4.3
One-dimensional Burgers’ equation
with periodic boundary condition and initial condition \(u(x,0)=-\cos (x)\).
The solution is smooth till the discontinuous derivative develops at \(t=1\). In Table 2, we show the \(L^2\) and \(L^\infty \) errors of \(u_h^S\) and \(u_h^M\) on the static and moving grids at time \(t=0.8\) when the solution is still smooth. The moving grid is the same as in the first example. The expected optimal order is obtained for \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) and \(P^3\) polynomial basis. For \(t = 1.6\) after the singularity develops, we show the numerical solutions \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) polynomial approximation in Fig. 3. The singularity is clearly resolved for both cases.
Another example is the Burgers’ equation
with nonsmooth initial condition
and periodic boundary condition. This is a benchmark problem to check the convergence of the numerical solution to the viscosity solution. In Fig. 4 we plot the ALE-LDG solutions \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) polynomial approximations at time \(t=1\) after the shock in derivative forms. Both numerical solutions converge to the viscosity solution.
Example 4.4
One-dimensional nonconvex Hamiltonian equation
with periodic boundary condition and initial condition \(u(x,0)=-\cos (x)\).
This example is designed to check the convergence of the numerical solution to the viscosity solution for a nonconvex Hamiltonian problem. In Fig. 5 we plot the ALE-LDG solutions \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) polynomial approximations at time \(t=\frac{1.5}{\pi ^2}\) after the shock in the derivative \(\partial _{x}u\) forms. The moving grid is defined as \(x_{j+\frac{1}{2}}(t^n ) = x_{j+\frac{1}{2}}(0) + 0.8 \sin (t^n)\sin (2\pi x_{j+\frac{1}{2}}(0))\). It shows that both numerical solutions converge to the viscosity solution.
Example 4.5
Two-dimensional Burgers’ equation
with periodic boundary condition and initial condition \(u(x,0)=-\cos (\frac{x+y}{2})\).
Similar as the one-dimensional Burgers’ equation, the solution is smooth till the discontinuous derivative develops at \(t=1\). In Table 3, we show the \(L^2\) and \(L^\infty \) errors of ALE-LDG solutions \(u_h^S\) and \(u_h^M\) on the static and moving grids at time \(t=0.8\). The moving grid is defined as
where \((x_j,y_j)\) are the vertices of the triangular mesh. The moving mesh starts from an uniform criss triangular mesh with N cells in each direction. The uniform mesh is also adopted for the numerical solution \(u_h^S\). The expected optimal order is obtained for \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) and \(P^3\) polynomial basis. For \(t = 1.6\) after the singularity develops in the partial derivatives \(\partial _{x}u\) and \(\partial _{y}u\), we show that the numerical solutions \(u_h^S\) and \(u_h^M\) with piecewise \(P^2\) polynomial approximation in Fig. 6. For both numerical solutions, the singularity is clearly resolved.
5 Conclusions
In this paper, an ALE-LDG method for solving Hamilton–Jacobi equations with time-dependent approximation spaces was developed. In the one dimensional case, the description of the ALE kinematic ensues by local time-depending affine linear mappings. This approach ensures that the ALE-LDG method satisfies the GCL for any time discretization method higher or equal to first order. An optimal a priori error estimate was proven for the semi-discrete ALE-LDG method. The two dimensional method is designed for moving triangular meshes, since on these meshes the ALE kinematic can be described similar as in one dimension. Nevertheless, the two dimensional method satisfies the GCL merely for any time discretization method higher or equal to second order. A suboptimal a priori error estimate was proven for the two dimensional semi-discrete ALE-LDG method. Furthermore, in both dimensions, the forward Euler piecewise constant ALE-LDG methods can be written as a monotone scheme.
Numerically, the one and two dimensional ALE-LDG methods were tested for two moving mesh scenarios in a variety of one and two dimensional examples. The first scenario described the situation of static fixed mesh. In the second scenario the grid point distribution was given by a certain formula. The methods preformed in both scenarios well. The stability, convergence and optimal accuracy was demonstrated in all test examples.
It should be noted that in the numerical computations a specific moving mesh methodology was not used and the mesh motion was predetermined. Hence, in a future work, a moving mesh methodology for the methods needs to be developed. Furthermore, a detailed investigation of problems with a nonconvex Hamiltonian and applications of the methods in the context of front propagation problems are worthwhile.
References
Barth, T.J., Sethian, J.A.: Numerical schemes for the Hamilton–Jacobi and level set equations on triangulated domains. J. Comput. Phys. 145, 1–40 (1998)
Bellman, R.: Introduction to Matrix Analysis, Volume 19 of Classics in Applied Mathematics, 2nd edn. SIAM, Philadelphia (1987)
Bokanowski, O., Cheng, Y., Shu, C.-W.: A discontinuous Galerkin scheme for front propagation with obstacles. Numer. Math. 126, 1–31 (2014)
Calderer, R., Masud, A.: A multiscale stabilized ALE formulation for incompressible flows with moving boundaries. Comput. Mech. 46, 185–197 (2010)
Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for directly solving the Hamilton–Jacobi equations. J. Comput. Phys. 223, 398–415 (2007)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems, Volume 40 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2002). Reprint of the 1978 original [North-Holland, Amsterdam; MR0520174 (58 #25001)]
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection–diffusion systems. SIAM J. Numer. Anal. 35, 2440–2463 (1998)
Cockburn, B., Shu, C.-W.: Runge–Kutta discontinuous Galerkin methods for convection-dominated problems. J. Sci. Comput. 16, 173–261 (2001)
Crandall, M.G., Lions, P.-L.: Viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 277, 1–42 (1983)
Crandall, M.G., Lions, P.-L.: Two approximations of solutions of Hamilton–Jacobi equations. Math. Comput. 43, 1–19 (1984)
Donea, J., Huerta, A., Ponthot, J.-P., Rodríguez-Ferran, A.: Arbitrary Lagrangian–Eulerian methods. In: Stein, E., De Borst, R., Hughes, T.J.R. (eds.) Encyclopedia of Computational Mechanics, Volume 1: Fundamentals, vol. 1, pp. 413–437. Wiley, New York (2004)
Gottlieb, S., Shu, C.-W.: Total variation diminishing Runge–Kutta schemes. Math. Comput. 67, 73–85 (1998)
Guillard, H., Farhat, C.: On the significance of the geometric conservation law for flow computations on moving meshes. Comput. Methods Appl. Mech. Eng. 190, 1467–1482 (2000)
Jiang, G.-S., Peng, D.: Weighted ENO schemes for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 2126–2143 (2000)
Hu, C., Shu, C.-W.: A discontinuous Galerkin finite element method for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 666–690 (1999)
Hu, C., Lepsky, O., Shu, C.-W.: The effect of the least square procedure for discontinuous Galerkin methods for Hamilton–Jacobi equations. In: Cockburn, B., Karniadakis, G.E., Shu, C.-W. (eds.) Discontinuous Galerkin Methods, Volume 11 of the Series Lecture Notes in Computational Science and Engineering, pp. 343–348. Springer, Berlin (2000)
Klingenberg, C., Schnücke, G., Xia, Y.: Arbitrary Lagrangian–Eulerian discontinuous Galerkin method for conservation laws: analysis and application in one dimension. Math. Comput. 86, 1203–1232 (2017)
Lepsky, O., Hu, C., Shu, C.-W.: Analysis of the discontinuous Galerkin method for Hamilton–Jacobi equations. Appl. Numer. Math. 33, 423–434 (2000)
Li, F., Shu, C.-W.: Reinterpretation and simplified implementation of a discontinuous Galerkin method for Hamilton–Jacobi equations. Appl. Math. Lett. 18, 1204–1209 (2005)
Li, F., Yakovlev, S.: A central discontinuous Galerkin method for Hamilton–Jacobi equations. J. Sci. Comput. 45, 404–428 (2010)
Lombard, C.K., Thomas, P.D.: Geometric conservation law and its application to flow computations on moving grids. AIAA J. 17, 1030–1037 (1979)
Lomtev, I., Kirby, R.M., Karniadakis, G.E.: A discontinuous Galerkin ALE method for compressible viscous flows in moving domains. J. Comput. Phys. 155, 128–159 (1999)
Mackenzie, J.A., Nicola, A.: A discontinuous Galerkin moving mesh method for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 29, 2258–2282 (2007)
Nguyen, V.-T.: An arbitrary Lagrangian–Eulerian discontinuous Galerkin method for simulations of flows over variable geometries. J. Fluids Struct. 26, 312–329 (2010)
Osher, S., Shu, C.-W.: High-order essentially non-oscillatory schemes for Hamilton–Jacobi equations. SIAM J. Numer. Anal. 28, 907–922 (1991)
Persson, P.-O., Bonet, J., Peraire, J.: Discontinuous Galerkin solution of the Navier–Stokes equations on deformable domains. Comput. Methods Appl. Mech. Eng. 198, 1585–1595 (2009)
Sethian, J.A.: Curvature and the evolution of fronts. Commun. Math. Phys. 101, 487–499 (1985)
Xiong, T., Shu, C.-W., Zhang, M.: A priori error estimates for semi-discrete discontinuous Galerkin methods solving nonlinear Hamilton–Jacobi equations with smooth solutions. Int. J. Numer. Anal. Model. 10, 154–177 (2013)
Yan, J., Osher, S.: A local discontinuous Galerkin method for directly solving Hamilton–Jacobi equations. J. Comput. Phys. 230, 232–244 (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
Research supported by NSFC Grant Nos. 11471306 and 11371342.
Rights and permissions
About this article
Cite this article
Klingenberg, C., Schnücke, G. & Xia, Y. An Arbitrary Lagrangian–Eulerian Local Discontinuous Galerkin Method for Hamilton–Jacobi Equations. J Sci Comput 73, 906–942 (2017). https://doi.org/10.1007/s10915-017-0471-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-017-0471-2