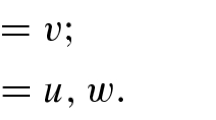Superconvergence of Local Discontinuous Galerkin Method for One-Dimensional Linear Schrödinger Equations

Abstract

In this paper, we study the superconvergence properties of the LDG method for the one-dimensional linear Schrödinger equation. We build a special interpolation function by constructing a correction function, and prove the numerical solution is superclose to the interpolation function in the $L^{2}$ norm. The order of superconvergence is $2k+1$, when the polynomials of degree at most k are used. Even though the linear Schrödinger equation involves only second order spatial derivative, it is actually a wave equation because of the coefficient i. It is not coercive and there is no control on the derivative for later time based on the initial condition of the solution itself, as for the parabolic case. In our analysis, the special correction functions and special initial conditions are required, which are the main differences from the linear parabolic equations. We also rigorously prove a $(2k+1)$-th order superconvergence rate for the domain, cell averages, and the numerical fluxes at the nodes in the maximal and average norm. Furthermore, we prove the function value and the derivative approximation are superconvergent with a rate of $(k+2)$-th order at the Radau points. All theoretical findings are confirmed by numerical experiments.

1 Introduction

In this paper, we consider the local discontinuous Galerkin (LDG) method for the one-dimensional linear Schrödinger equation

$$\begin{aligned} \begin{aligned}&\text{ i }u_{t}+u_{xx}=0, \quad (x,t)\in [0,2\pi ]\times (0,T]\\&u(x,0)=u_{0}(x), \end{aligned} \end{aligned}$$

(1.1)

where u(x, t) is a complex function, $u_{0}(x)$ is a sufficiently smooth function and $\text{ i }^{2} = -1$. We will consider the periodic boundary condition $u(0,t)=u(2\pi ,t)$ and mixed boundary condition $u(0,t)=g_{0}(t)$, $u_{x}(2\pi ,t)=g_{1}(t)$. We study the superconvergence property of the LDG method for Eq. (1.1).

Discontinuous Galerkin (DG) methods, first introduced in 1973 by Reed and Hill [18], are a class of finite element methods using completely discontinuous, piecewise polynomials as the basis functions. It was originally aimed at solving hyperbolic conservation laws containing only first order spacial derivatives, e.g. [1, 3,4,5]. The LDG method developed from DG method, was designed to solve partial differential equations (PDEs) with higher than first order spatial derivatives. Cockburn and Shu constructed the first LDG method to solve the convection diffusion equation containing second order spatial derivatives in [6]. The idea of the LDG method is that reformulate the equation as a first-order system such that the DG method can be applied. Recently, Rivière and Wheeler proposed a first DG method for the acoustic wave equation in its original second-order formulation, which is based on a nonsymmetric interior penalty formulation and requires additional stabilization terms for optimal convergence [20, 21]. The symmetric interior penalty DG method for second-order scalar wave equation was developed and analyzed by Grote, Schneebeli and Schötzau in [12]. We make reference to [2, 15, 19, 22, 25, 26, 28] for more details and the development of the DG and LDG method.

Our contribution here is to study the superconvergence phenomena of the LDG method for the one-dimensional linear Schrödinger equation. In [24], Xu and Shu developed the LDG methods to solve generalized nonlinear schrödinger equations and proved the stability of the method. Later, they obtained $(k+1)$-th order convergence rate for linear schrödinger equations in [27]. We refer the reader to [14, 16] for the accuracy of LDG method for nonlinear schrödinger equations. As for the superconvergence behavior of finite element methods (FEM) for Schrödinger equation, very little previous work had been done. In [17], Lin and Liu obtained the second order gradient superconvergence rate for the initial boundary value problem of Schrödinger equation by linear finite elements. The global superconvergence of the anisotropic linear triangular finite element for nonlinear Schrödinger equation was derived in [23]. Both [17, 23] only work for linear approximation space. Recently, in [8,9,10,11], Cao and Zhang studied superconvergence properties of DG and LDG method for linear hyperbolic and parabolic equations. When piecewise polynomials of degree at most k were used as the basis functions, they provided a strict mathematical proof of the $(2k+1)$-th order superconvergence rate for the domain and cell averages as well as the numerical fluxes at mesh points. They also proved the superconvergence rate was $(k+2)$-th order for the function value approximation and $(k+1)$-th order for the derivative approximation at Radau points.

In this paper, we aim at achieving the same superconvergence results of the parabolic equations in [11] for the one-dimensional linear Schrödinger equation. The linear Schrödinger equation, even though it involves only second order spatial derivative, is actually a wave equation because of the coefficient i. It is not coercive and there is no control on the derivative for later time based on the initial condition of the solution itself, as for the parabolic case. To be more specific, we shall rigorously prove a $(2k+1)$-th order superconvergence rate of the LDG solution for the domain, cell averages and the numerical fluxes at nodes of the mesh. Moreover, we also prove the function value and the derivative approximation are superconvergent with a rate of $(k+2)$-th order at the Radau points. To the best of our knowledge, no previous results in the literature show the above superconvergence properties of the LDG method for Eq. (1.1).

The main step to obtain superconvergence is to construct a correction function. Based on the energy stability for the variables (the exact solution u and the auxiliary variable $q=u_{x}$) [27], we construct correction functions to result in the super-closeness (with order $2k+1$) between the LDG solutions and special interpolations, which are defined by the Gauss–Radau projections of the exact solutions and the correction functions. The idea of the correction functions has been successfully applied to the DG and LDG method for linear hyperbolic and parabolic equations, e.g. [8, 9, 11]. However, it is more complicated to construct correction functions for Schrödinger equation due to the complex exact solution of Eq. (1.1). We shall construct the complex valued correction functions for both variables. Moreover, special initial conditions are required in our analysis, which are quite different from parabolic equations. We then prove the superconvergence properties by use of the correction functions.

This paper is organized as follows. In Sect. 2, we present some notations adopted throughout the paper. In Sect. 3, we consider the LDG scheme for the one-dimensional linear Schrödinger equation. The correction function is constructed in Sect. 4, which is the most characteristic and innovative part of this paper. Section 5 present how to construct the suitable initial discretization. In Sect. 6, the superconvergence results are proved. The numerical examples to demonstrate the accuracy are given in Sect. 7. We conclude our results in Sect. 8.

2 Notations

In this section, we will introduce some notations to be used in the analysis of the superconvergence properties for the Eq. (1.1). They are slightly different from the real valued space.

2.1 Symbols

Let $W^{m,p}(D)$ be the Sobolev space on sub-domain $D\subset \varOmega$, which is equipped with the norm $\Vert \cdot \Vert _{m,p,D}$ and semi-norm $|\cdot |_{m,p,D}$. $A\lesssim B$ indicates that $A \le CB$, where C is a positive constant independent of the exact solution u and the mesh size h. For any r, $\lfloor r\rfloor$ stands for the maximal integer no more than r, and $\lceil r\rceil$ stands for the minimal integer no less than r. Denote $\mathbb {Z}_{r}=\{1,\cdots ,r\}$ for any positive integer r.

2.2 Function Spaces

We first introduce the partition of the domain $\varOmega =[0, 2\pi ]$. Let $0=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N+\frac{1}{2}}=2\pi$ be a subdivision of $\bar{\varOmega }$. We denote the length of $\tau _{j} = (x_{j-\frac{1}{2}},x_{j+\frac{1}{2}})$ by $h_{j} = x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}$ and set $\bar{h}_{j}=h_{j}/2$. Let $x_{j}=(x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}})/2$ be the center of the cell and denote $h = \max \limits _{j\in \mathbb {Z_{N}}} h_{j}$. We assume that the mesh is quasi-uniform in the sense that $h\le Ch_{j}$ for $j\in \mathbb {Z_{N}}$. Then the finite element space is defined by

$$\begin{aligned} {}_c{V_{h}} = \{v: v\mid _{\tau _{j}}\in P^{k}(\tau _{j}), \quad j\in \mathbb {Z_{N}}\}, \end{aligned}$$

where $P^{k}(\tau _{j})$ denotes the space of polynomials of degree at most k on $\tau _{j}$. Note that functions in ${}_c{V_{h}}$ are complex valued functions since the solution of the linear Schrödinger Eq. (1.1) is complex valued.

2.3 Inner Products and Norms in the Complex Space

Let $w^{*}$ be the conjugate of w and define the inner product and the conjugate of the inner product by

$$\begin{aligned} (v,w)_{j}=\int _{\tau _{j}}vw^{*}dx,\quad (w,v)^{*}_{j}=(v,w)_{j}. \end{aligned}$$

The definitions of the $L^{p}$-norm over $\tau _{j}$ and in the domain $\varOmega$ are given as

$$\begin{aligned} \Vert v\Vert _{0,p,\tau _{j}}^{p}=\int _{\tau _{j}}|v|^{p}dx, \quad \Vert v\Vert _{0,p,\varOmega }^{p}=\sum _{j \in \mathbb {Z}_{N}} \Vert v\Vert _{0,p,\tau _{j}}^{p} \end{aligned}$$

in the case $1\le p < \infty$, and in the case $p=\infty$

$$\begin{aligned} \Vert v\Vert _{0,\infty ,\tau _{j}}=Inf\{K: |v|\le K, a.e.x\in \tau _{j}\}, \quad \Vert v\Vert _{0,\infty ,\varOmega }=\max \limits _{j \in \mathbb {Z}_{N}} \Vert v\Vert _{0,\infty ,\tau _{j}}. \end{aligned}$$

The $W^{m,p}$-norm over $\tau _{j}$ and in the domain $\varOmega$ are defined as

$$\begin{aligned} \Vert v\Vert _{m,p,\tau _{j}}^{p}=\sum _{l=0}^{m} \Vert D^{l}v\Vert ^{p}_{0,p,\tau _{j}}, \quad \Vert v\Vert _{m,p,\varOmega }^{p}=\sum _{j \in \mathbb {Z}_{N}} \Vert v\Vert _{m,p,\tau _{j}}^{p} \end{aligned}$$

in the case $1\le p < \infty$, and in the case $p=\infty$

$$\begin{aligned} \Vert v\Vert _{m,\infty ,\tau _{j}}= \max \limits _{0\le l \le m} \Vert D^{l}v\Vert _{0,\infty ,\tau _{j}} , \quad \Vert v\Vert _{m,\infty ,\varOmega }=\max \limits _{j \in \mathbb {Z}_{N}} \Vert v\Vert _{m,\infty ,\tau _{j}}. \end{aligned}$$

If $p=2$, we set $\Vert v\Vert _{m,2,D} = \Vert v\Vert _{m,D}$ and $|v|_{m,2,D}= |v|_{m,D}$, where $D \subset \varOmega$.

2.4 Projection

We will consider two Gauss–Radau projections $P_{h}^{-}$, $P_{h}^{+}$ into ${}_c{V_{h}}$ defined by

$$\begin{aligned}&(P_{h}^{-}v,w)_{j}=(v,w)_{j},\quad P_{h}^{-}v(x_{j+\frac{1}{2}}^{-})=v(x_{j+\frac{1}{2}}^{-}),\quad \forall w\in P^{k-1}, \end{aligned}$$

(2.1)

$$\begin{aligned}&(P_{h}^{+}v,w)_{j}=(v,w)_{j},\quad P_{h}^{+}v(x_{j-\frac{1}{2}}^{+})=v(x_{j-\frac{1}{2}}^{+}),\quad \forall w\in P^{k-1}. \end{aligned}$$

(2.2)

Note that the special projections are often used to derive the optimal $L^{2}$ error bounds of the DG methods in the literature, e.g. in [27]. Next, we shall focus on the projections $P_{h}^{-}v$, $P_{h}^{+}v$ by the Legendre expansion of v(x, t). In an arbitrary element $\tau _{j}$, $j\in \mathbb {Z}_{N}$, v(x, t) has the following Legendre expansion

$$\begin{aligned} v(x,t)=\sum _{m=0}^{\infty }v_{j,m}(t)L_{j,m}(x), \quad v_{j,m}(t)=\frac{2m+1}{h_{j}}(v,L_{j,m})_{j}, \end{aligned}$$

where $L_{j,m}$ denotes the standard Legendre polynomial of degree m on $\tau _{j}$. Then by the definitions of $P_{h}^{-}v$, $P_{h}^{+}v$, we obtain

$$\begin{aligned} P_{h}^{-}v(x,t)&=-\bar{v}_{j,k}(t)L_{j,k}(x)+\sum _{m=0}^{k}v_{j,m}(t)L_{j,m}(x),\\ P_{h}^{+}v(x,t)&=-\tilde{v}_{j,k}(t)L_{j,k}(x)+\sum _{m=0}^{k}v_{j,m}(t)L_{j,m}(x), \end{aligned}$$

where

$$\begin{aligned} \bar{v}_{j,k}=-v(x_{j+\frac{1}{2}}^{-},t)+ \sum _{m=0}^{k}v_{j,m},\quad \tilde{v}_{j,k}= (-1)^{k+1}v(x_{j-\frac{1}{2}}^{+},t)+ \sum _{m=0}^{k}(-1)^{k+m}v_{j,m}. \end{aligned}$$

(2.3)

Finally, by the orthogonal property of the Legendre polynomials, we can easily get

$$\begin{aligned} (v-P_{h}^{-}v,w)_{j}=\bar{v}_{j,k}(L_{j,k},w)_{j}, \quad (v-P_{h}^{+}v,w)_{j}=\tilde{v}_{j,k}(L_{j,k},w)_{j},\quad \forall w\in {}_c{V_{h}}. \end{aligned}$$

(2.4)

3 The LDG Scheme

In order to define the LDG method, we rewrite the linear Schrödinger Eq. (1.1) into a system of the first order derivatives

$$\begin{aligned} \text{ i }u_{t}+q_{x}=0, \\ q-u_{x}=0. \end{aligned}$$

The LDG scheme to solve (1.1) is as follows: find $u_{h}$, $q_{h} \in {}_c{V_{h}}$ such that for all test functions $\eta$, $\varphi \in {}_c{V_{h}}$, we have

$$\begin{aligned} \text{ i }((u_{h})_{t}, \eta )_{j}-(q_{h} , \eta _{x})_{j} + \hat{q}_{h}\eta ^{*-}|_{j+\frac{1}{2}}-\hat{q}_{h}\eta ^{*+}|_{j-\frac{1}{2}}=0,\end{aligned}$$

(3.1)

$$\begin{aligned} (q_{h},\varphi )_{j}+(u_{h},\varphi _{x})_{j}-\hat{u}_{h}\varphi ^{*-}|_{j+\frac{1}{2}}+\hat{u}_{h}\varphi ^{*+}|_{j-\frac{1}{2}}=0. \end{aligned}$$

(3.2)

Here the $\hat{q}_{h}$, $\hat{u}_{h}$ are the numerical fluxes. For both periodic and mixed boundary conditions, we can choose

$$\begin{aligned} \hat{u}_{h}|_{j+\frac{1}{2}}=u_{h}^{-}|_{j+\frac{1}{2}},\quad \hat{q}_{h}|_{j+\frac{1}{2}}=q_{h}^{+}|_{j+\frac{1}{2}}, \quad j=0,1,\cdots ,N, \end{aligned}$$

(3.3)

where

$$\begin{aligned} u_{h}^{-}|_{\frac{1}{2}}=u_{h}^{-}|_{N+\frac{1}{2}},\quad q_{h}^{+}|_{N+\frac{1}{2}}=q_{h}^{+}|_{\frac{1}{2}} \end{aligned}$$

for periodic boundary condition, and

$$\begin{aligned} u_{h}^{-}|_{\frac{1}{2}}=g_{0}(t),\quad q_{h}^{+}|_{N+\frac{1}{2}}=g_{1}(t) \end{aligned}$$

for mixed boundary conditions. For simplicity, we use the notation

$$\begin{aligned} a^{1}(v,w;\eta )=\sum _{j=1}^{N}a^{1}_{j}(v,w;\eta ),\quad a^{2}(v,w;\varphi )=\sum _{j=1}^{N}a^{2}_{j}(v,w;\varphi ), \end{aligned}$$

where

$$\begin{aligned} a^{1}_{j}(v,w;\eta )= \text{ i }(v_{t}, \eta )_{j}-(w, \eta _{x})_{j} + w^{+}\eta ^{*-}|_{j+\frac{1}{2}}-w^{+}\eta ^{*+}|_{j-\frac{1}{2}},\\ a^{2}_{j}(v,w;\varphi )= (w,\varphi )_{j}+(v,\varphi _{x})_{j}-v^{-}\varphi ^{*-}|_{j+\frac{1}{2}}+v^{-}\varphi ^{*+}|_{j-\frac{1}{2}}. \end{aligned}$$

By the above notation, the LDG scheme (3.1)–(3.2) can be rewritten as

$$\begin{aligned} a^{1}_{j}(u_{h},q_{h};\eta )=0,\quad a^{2}_{j}(u_{h},q_{h};\varphi )=0,\quad \forall \eta ,\varphi \in {}_c{V_{h}}. \end{aligned}$$

Obviously, the LDG scheme is also satisfied when we replace the numerical solutions with the exact solutions u, $q=u_{x}$. Therefore, we obtain the fundamental error equations

$$\begin{aligned} a^{1}_{j}(u-u_{h},q-q_{h};\eta )=0,\quad a^{2}_{j}(u-u_{h},q-q_{h};\varphi )=0,\quad \forall \eta ,\varphi \in {}_c{V_{h}}. \end{aligned}$$

(3.4)

It’s also easily to show the energy functions, for both periodic and mixed boundary conditions,

$$\begin{aligned} \text{ i }(v_{t}, v)+\text{ i }(v_{t}, v)^{*}&= a^{1}(v,w;v)+a^{2}(v,w;w)-a^{1}(v,w;v)^{*}-a^{2}(v,w;w)^{*}\nonumber \\&\quad +\,v^{-}w^{*+}|_{N+\frac{1}{2}}-v^{-}w^{*+}|_{\frac{1}{2}}-v^{*-}w^{+}|_{N+\frac{1}{2}}+v^{*-}w^{+}|_{\frac{1}{2}} , \end{aligned}$$

(3.5)

$$\begin{aligned} (w_{t},w)+(w_{t},w)^{*}&= a^{1}(v,w;-v_{t})+a^{2}(v_{t},w_{t};w)+a^{1}(v,w;-v_{t})^{*}+a^{2}(v_{t},w_{t};w)^{*}\nonumber \\&\quad +\,v_{t}^{-}w^{*+}|_{N+\frac{1}{2}}-v_{t}^{-}w^{*+}|_{\frac{1}{2}}+v_{t}^{*-}w^{+}|_{N+\frac{1}{2}}-v_{t}^{*-}w^{+}|_{\frac{1}{2}}. \end{aligned}$$

(3.6)

It is worthy to point out that applying the energy techniques to obtain the error estimates can be often found in the literature, e.g. in [27]. Here, our superconvergence analysis is also based on the energy functions (3.5)–(3.6), which makes them play key roles in obtaining superconvergence properties.

4 Correction Functions

In this section, we shall construct special correction functions $(W_{u}^{l}, W_{q}^{l})$ for fluxes (3.3) which is the key step to study the superconvergence properties for the LDG solution of Eq. (1.1).

We start with some preliminary works. Define an integral operator $D_{s}^{-1}$ by

$$\begin{aligned} D_{s}^{-1}v(x)=\frac{1}{\bar{h}_{j}}\int _{x_{j-\frac{1}{2}}}^{x}v(\hat{x})d\hat{x}, \quad x\in \tau _{j}, \quad j\in \mathbb {Z}_{N}, \end{aligned}$$

(4.1)

obviously we have $(D_{s}^{-1}v(x))^{'} = v(x)/\bar{h}_{j}$. In each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$, we define

$$\begin{aligned}&F_{1,1}(x)= P_{h}^{+}D_{s}^{-1}L_{j,k}, \quad F_{1,r}(x)= (P_{h}^{+}D_{s}^{-1}P_{h}^{-}D_{s}^{-1})^{r}F_{1,1}, \quad r\ge 2, \end{aligned}$$

(4.2)

$$\begin{aligned}&F_{2,1}(x)= P_{h}^{-}D_{s}^{-1}L_{j,k}, \quad F_{2,r}(x)= (P_{h}^{-}D_{s}^{-1}P_{h}^{+}D_{s}^{-1})^{r}F_{2,1}, \quad r\ge 2, \end{aligned}$$

(4.3)

$$\begin{aligned}&\bar{F}_{1,r}(x)= P_{h}^{-}D_{s}^{-1}F_{1,r},\quad \bar{F}_{2,r}(x)= P_{h}^{+}D_{s}^{-1}F_{2,r}, \quad 1\le r\le \lfloor k/2\rfloor . \end{aligned}$$

(4.4)

A direct calculation derives

$$\begin{aligned} F_{1,r+1}(x)=P_{h}^{+}D_{s}^{-1}\bar{F}_{1,r}(x), \quad F_{2,r+1}(x)=P_{h}^{-}D_{s}^{-1}\bar{F}_{2,r}(x),\quad 1\le r\le \lfloor k/2\rfloor . \end{aligned}$$

(4.5)

It has been proved in [11] that $F_{1,r}$, $F_{2,r}$, $\bar{F}_{1,r}$ and $\bar{F}_{2,r}$ have the following representations

$$\begin{aligned}&F_{1,r}(x)= \sum _{m=k-2r+2}^{k}a_{r,m}(L_{j,m}+L_{j,m-1})(x), \quad 1\le r\le \lceil k/2 \rceil , \end{aligned}$$

(4.6)

$$\begin{aligned}&F_{2,r}(x)= \sum _{m=k-2r+2}^{k}b_{r,m}(L_{j,m}-L_{j,m-1})(x), \quad 1\le r\le \lceil k/2 \rceil , \end{aligned}$$

(4.7)

$$\begin{aligned}&\bar{F}_{1,r}(x)= \sum _{m=k-2r+2}^{k}\alpha _{r,m}(L_{j,m}-L_{j,m-1})(x), \quad 1\le r\le \lfloor k/2 \rfloor , \end{aligned}$$

(4.8)

$$\begin{aligned}&\bar{F}_{2,r}(x)= \sum _{m=k-2r+2}^{k}\beta _{r,m}(L_{j,m}+L_{j,m-1})(x), \quad 1\le r\le \lfloor k/2 \rfloor , \end{aligned}$$

(4.9)

where $a_{r,m}$, $b_{r,m}$, $\alpha _{r,m}$ and $\beta _{r,m}$ are some bounded constants independent of the mesh size $h_{j}$. By the properties of Legendre polynomials, we obtain, in each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$,

$$\begin{aligned}&F_{1,r}(x_{j-\frac{1}{2}}^{+})= 0, \quad F_{1,r}\bot P^{k-2r}, \quad \Vert F_{1,r}\Vert _{0,\infty ,\tau _{j}}\lesssim 1, \end{aligned}$$

(4.10)

$$\begin{aligned}&F_{2,r}(x_{j+\frac{1}{2}}^{-})= 0, \quad F_{2,r}\bot P^{k-2r}, \quad \Vert F_{2,r}\Vert _{0,\infty ,\tau _{j}}\lesssim 1, \end{aligned}$$

(4.11)

$$\begin{aligned}&\bar{F}_{1,r}(x_{j+\frac{1}{2}}^{-})= 0,\quad \bar{F}_{1,r}\bot P^{k-2r}, \quad \Vert \bar{F}_{1,r}\Vert _{0,\infty ,\tau _{j}}\lesssim 1, \end{aligned}$$

(4.12)

$$\begin{aligned}&\bar{F}_{2,r}(x_{j-\frac{1}{2}}^{+})= 0, \quad \bar{F}_{2,r}\bot P^{k-2r}, \quad \Vert \bar{F}_{2,r}\Vert _{0,\infty ,\tau _{j}}\lesssim 1. \end{aligned}$$

(4.13)

We are now ready to define the correction functions for all $1 \le l \le k$. From (2.4), we have the following properties in each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$, $\forall w\in {}_c{V_{h}}$,

$$\begin{aligned} (u-P_{h}^{-}u,w)_{j}=\bar{u}_{j,k}(t)(L_{j,k},w)_{j}, \quad (q-P_{h}^{+}q,w)_{j}=\tilde{q}_{j,k}(t)(L_{j,k},w)_{j}, \end{aligned}$$

(4.14)

where $\bar{u}_{j,k}(t)$, $\tilde{q}_{j,k}(t)$ are given by (2.3). Let us denote the derivatives by

$$\begin{aligned} \bar{u}_{j,k}^{(m)} = D_{t}^{m}\bar{u}_{j,k}(t), \quad \tilde{q}_{j,k}^{(m)} = D_{t}^{m}\tilde{q}_{j,k}(t),\quad 0\le m \le \lceil k/2\rceil . \end{aligned}$$

Then we define, at the boundary points,

$$\begin{aligned} W^{l}_{q}(x^{+}_{N+\frac{1}{2}},t) = 0, \quad W^{l}_{u}(x^{-}_{\frac{1}{2}},t) = 0, \quad \forall t\ge 0, \end{aligned}$$

(4.15)

and in each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$,

$$\begin{aligned} W^{l}_{q}(x,t) = \sum _{m=1}^{\lceil l/4 \rceil }w_{q_{1},m}+\sum _{m=1}^{\lfloor l/4+1/2 \rfloor }w_{q_{2},m}+\sum _{m=1}^{\lfloor l/4+1/4 \rfloor }w_{q_{3},m}+\sum _{m=1}^{\lfloor l/4 \rfloor }w_{q_{4},m}, \end{aligned}$$

(4.16)

$$\begin{aligned} W^{l}_{u}(x,t) = \sum _{m=1}^{\lceil l/4 \rceil }w_{u_{1},m}+\sum _{m=1}^{\lfloor l/4+1/2 \rfloor }w_{u_{2},m}+\sum _{m=1}^{\lfloor l/4+1/4 \rfloor }w_{u_{3},m}+\sum _{m=1}^{\lfloor l/4 \rfloor }w_{u_{4},m}, \end{aligned}$$

(4.17)

where

$$\begin{aligned}&w_{q_{1},m} = \text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-3}\bar{u}_{j,k}^{(2m-1)}F_{1,2m-1}, \quad w_{q_{3},m} = \text{ i }^{4m}(-1)^{m}\bar{h}_{j}^{4m-1}\bar{u}_{j,k}^{(2m)}F_{1,2m}, \end{aligned}$$

(4.18)

$$\begin{aligned}&w_{q_{2},m} = \text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-2}\tilde{q}_{j,k}^{(2m-1)}\bar{F}_{2,2m-1}, \quad w_{q_{4},m} = \text{ i }^{4m}(-1)^{m}\bar{h}_{j}^{4m}\tilde{q}_{j,k}^{(2m)}\bar{F}_{2,2m}, \end{aligned}$$

(4.19)

$$\begin{aligned}&w_{u_{1},m} = \text{ i }^{4m}(-1)^{m-1}\bar{h}_{j}^{4m-3}\tilde{q}_{j,k}^{(2m-2)}F_{2,2m-1}, \quad w_{u_{4},m} = \text{ i }^{4m}(-1)^{m}\bar{h}_{j}^{4m}\bar{u}_{j,k}^{(2m)}\bar{F}_{1,2m}, \end{aligned}$$

(4.20)

$$\begin{aligned}&w_{u_{2},m} = \text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-2}\bar{u}_{j,k}^{(2m-1)}\bar{F}_{1,2m-1}, \quad w_{u_{3},m} = \text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-1}\tilde{q}_{j,k}^{(2m-1)}F_{2,2m}. \end{aligned}$$

(4.21)

With the definitions of the correction functions $W^{l}_{q}$, $W^{l}_{u}$ and the properties (4.10)–(4.13) of the functions $F_{1,r}$, $F_{2,r}$, $\bar{F}_{1,r}$ and $\bar{F}_{2,r}$, we can easily prove the following lemma, which is crucial in our analysis later.

Lemma 1

Suppose $W^{l}_{q}$, $W^{l}_{u}$ $\in {}_c{V_{h}}$ are defined by (4.15)–(4.21). Then, for all $\eta$, $\varphi \in {}_c{V_{h}}$,

$$\begin{aligned} W^{l}_{q}(x^{+}_{j-\frac{1}{2}},t) = 0, \quad W^{l}_{u}(x^{-}_{j-\frac{1}{2}},t) = 0, \quad \forall j \in \mathbb {Z}_{N+1}. \end{aligned}$$

(4.22)

Moreover, if $l=4r$,

$$\begin{aligned} \text{ i }((W^{l}_{u})_{t},\eta )_{j}-(W^{l}_{q},\eta _{x})_{j}&= -(w_{q_{1},1},\eta _{x})_{j}+\text{ i }((w_{u_{4},r})_{t},\eta )_{j}, \end{aligned}$$

(4.23)

$$\begin{aligned} (W^{l}_{q},\varphi )_{j}+(W^{l}_{u},\varphi _{x})_{j}&= (w_{u_{1},1},\varphi _{x})_{j} + (w_{q_{4},r},\varphi )_{j}, \end{aligned}$$

(4.24)

if $l=4r+s,s=1,2,3$,

$$\begin{aligned} \text{ i }((W^{l}_{u})_{t},\eta )_{j}-(W^{l}_{q},\eta _{x})_{j}&= -(w_{q_{1},1},\eta _{x})_{j}+\text{ i }((w_{u_{s},r+1})_{t},\eta )_{j}, \end{aligned}$$

(4.25)

$$\begin{aligned} (W^{l}_{q},\varphi )_{j}+(W^{l}_{u},\varphi _{x})_{j}&= (w_{u_{1},1},\varphi _{x})_{j} + (w_{q_{s},r+1},\varphi )_{j}. \end{aligned}$$

(4.26)

Proof

From the properties (4.10)–(4.13) and the definitions (4.18)–(4.21), we get, $\forall j \in \mathbb {Z}_{N}$

$$\begin{aligned}&w_{q_{1},m}(x^{+}_{j-\frac{1}{2}},t)=w_{q_{2},m}(x^{+}_{j-\frac{1}{2}},t)=w_{q_{3},m}(x^{+}_{j-\frac{1}{2}},t)=w_{q_{4},m}(x^{+}_{j-\frac{1}{2}},t)=0,\\&w_{u_{1},m}(x^{-}_{j+\frac{1}{2}},t)=w_{u_{2},m}(x^{-}_{j+\frac{1}{2}},t)=w_{u_{3},m}(x^{-}_{j+\frac{1}{2}},t)=w_{u_{4},m}(x^{-}_{j+\frac{1}{2}},t)=0, \end{aligned}$$

hence, the desired results (4.22) follow from the definitions (4.15)–(4.17). By a direct calculation from (4.6)–(4.9), we obtain, for any integer l, $1\le l \le k$,

$$\begin{aligned} D_{s}^{-1}F_{1,m}(x^{-}_{j+\frac{1}{2}}) =D_{s}^{-1}F_{1,m}(x^{+}_{j-\frac{1}{2}}) =D_{s}^{-1}F_{2,m}(x^{-}_{j+\frac{1}{2}}) =D_{s}^{-1}F_{2,m}(x^{+}_{j-\frac{1}{2}})=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/2 \rfloor }$, and

$$\begin{aligned} D_{s}^{-1}\bar{F}_{1,m}(x^{-}_{j+\frac{1}{2}}) =D_{s}^{-1}\bar{F}_{1,m}(x^{+}_{j-\frac{1}{2}}) =D_{s}^{-1}\bar{F}_{2,m}(x^{-}_{j+\frac{1}{2}}) =D_{s}^{-1}\bar{F}_{2,m}(x^{+}_{j-\frac{1}{2}})=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/2 \rfloor -1}$ in case $l=2r$ and $m\in \mathbb {Z}_{\lfloor l/2 \rfloor }$ in case $l=2r+1$. Noticing the fact that $(D_{s}^{-1}v(x))^{'} = v(x)/\bar{h}_{j}$ and the properties (4.4)–(4.5), we have, by integration by parts and (2.1)–(2.2),

$$\begin{aligned} \text{ i }((w_{u_{1},m})_{t},\eta )_{j}-(w_{q_{2},m},\eta _{x})_{j}&=\text{ i }^{4m+1}(-1)^{m-1}\bar{h}_{j}^{4m-3}\tilde{q}_{j,k}^{(2m-1)}(F_{2,2m-1},\eta )_{j}\\&\quad \ -\text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-2}\tilde{q}_{j,k}^{(2m-1)}(\bar{F}_{2,2m-1},\eta _{x})_{j}\\&=(\text{ i }^{4m+1}+\text{ i }^{4m-1})(-1)^{m-1}\bar{h}_{j}^{4m-3}\tilde{q}_{j,k}^{(2m-1)}(F_{2,2m-1},\eta )_{j}=0,\\ (w_{q_{1},m},\varphi )_{j}+(w_{u_{2},m},\varphi _{x})_{j}&=\text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-3}\bar{u}_{j,k}^{(2m-1)}(F_{1,2m-1},\varphi )_{j}\\&\quad \ +\text{ i }^{4m-1}(-1)^{m-1}\bar{h}_{j}^{4m-2}\bar{u}_{j,k}^{(2m-1)}(\bar{F}_{1,2m-1},\varphi _{x})_{j}\\&=((-1)^{m-1}-(-1)^{m-1})\text{ i }^{4m-1}\bar{h}_{j}^{4m-3}\bar{u}_{j,k}^{(2m-1)}(F_{1,2m-1},\varphi )_{j}=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/4 \rfloor }$ in case $l=4r$, $4r+1$ and $m\in \mathbb {Z}_{\lfloor l/4 \rfloor +1}$ in case $l=4r+2$, $4r+3$. With the same arguments, we have

$$\begin{aligned} \text{ i }((w_{u_{2},m})_{t},\eta )_{j}-(w_{q_{3},m},\eta _{x})_{j}=0,\\ (w_{q_{2},m},\varphi )_{j}+(w_{u_{3},m},\varphi _{x})_{j}=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/4 \rfloor }$ in case $l=4r$, $4r+1$, $4r+2$ and $m\in \mathbb {Z}_{\lfloor l/4 \rfloor +1}$ in case $l=4r+3$, and

$$\begin{aligned} \text{ i }((w_{u_{3},m})_{t},\eta )_{j}-(w_{q_{4},m},\eta _{x})_{j}=0,\\ (w_{q_{3},m},\varphi )_{j}+(w_{u_{4},m},\varphi _{x})_{j}=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/4 \rfloor }$, and

$$\begin{aligned} \text{ i }((w_{u_{4},m})_{t},\eta )_{j}-(w_{q_{1},m+1},\eta _{x})_{j}=0,\\ (w_{q_{4},m},\varphi )_{j}+(w_{u_{1},m+1},\varphi _{x})_{j}=0 \end{aligned}$$

for all $m\in \mathbb {Z}_{\lfloor l/4 \rfloor -1}$ in case $l=4r$ and $m\in \mathbb {Z}_{\lfloor l/4 \rfloor }$ in case $l=4r+s$, $s=1$, 2, 3. After summing over all m, we obtain the desired results (4.23)–(4.26).

Now the special interpolation functions can be defined, in each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$,

$$\begin{aligned} u_{I}^{l} = P_{h}^{-}u - W_{u}^{l}, \quad q_{I}^{l} = P_{h}^{+}q - W_{q}^{l}, \quad 1\le l \le k. \end{aligned}$$

(4.27)

By using (2.1)–(2.2) and (4.22), we have

$$\begin{aligned} u_{I}^{l}(x_{j-\frac{1}{2}}^{-},t) = u(x_{j-\frac{1}{2}}^{-},t), \quad q_{I}^{l}(x_{j-\frac{1}{2}}^{+},t) = q(x_{j-\frac{1}{2}}^{+},t), \quad \forall j\in \mathbb {Z}_{N+1}. \end{aligned}$$

(4.28)

For simplicity, we denote the error between the exact solution and the numerical solution by $e_{u} = u-u_{h}$, $e_{q} = q-q_{h}$, and let $\eta _{u}=u_{I}^{l}-u_{h}$, $\eta _{q}=q_{I}^{l}-q_{h}$ be the error between the interpolation function and the numerical solution. Then we have

$$\begin{aligned} e_{u} = u-u_{I}^{l}+\eta _{u},\quad e_{q} = q-q_{I}^{l}+\eta _{q}. \end{aligned}$$

(4.29)

We will next present a significant result of our superconvergence analysis to end this section.

Lemma 2

Suppose $u\in W^{k+l+3,\infty }(\varOmega )$, $1\le l \le k$ is the solution of (1.1) and $W^{l}_{q}$, $W^{l}_{u} \in {}_c{V_{h}}$ are defined by (4.15)–(4.21), then we have

$$\begin{aligned} \Vert W^{l}_{q}\Vert _{0,\infty ,\tau _{j}} + \Vert W^{l}_{u}\Vert _{0,\infty ,\tau _{j}} \lesssim h^{k+2}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}, \quad \forall j\in \mathbb {Z}_{N}. \end{aligned}$$

(4.30)

Moreover, for all $\eta$, $\varphi \in {}_c{V_{h}}$,

$$\begin{aligned} |\text{ i }((u_{I}^{l}-u)_{t},\eta )_{j}+(W_{q}^{l},\eta _{x})_{j}| \lesssim h^{k+l+1}\Vert u\Vert _{k+l+3,\infty ,\tau _{j}}\Vert \eta \Vert _{0,1,\tau _{j}}, \end{aligned}$$

(4.31)

$$\begin{aligned} |(q_{I}^{l}-q,\varphi )_{j}-(W_{u}^{l},\varphi _{x})_{j}| \lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}\Vert \varphi \Vert _{0,1,\tau _{j}}, \end{aligned}$$

(4.32)

where $u_{I}^{l}$ and $q_{I}^{l}$ are defined by (4.27).

Proof

By the standard approximation theory, if $u\in W^{k+2m+2,\infty }(\varOmega )$,

$$\begin{aligned} |\bar{u}_{j,k}^{(m)}| = |D_{t}^{m}\bar{u}_{j,k}| \lesssim h^{k+1}\Vert u\Vert _{k+1+2m,\infty ,\tau _{j}},\\ |\tilde{q}_{j,k}^{(m)}| = |D_{t}^{m}\tilde{q}_{j,k}| \lesssim h^{k+1}\Vert u\Vert _{k+2+2m,\infty ,\tau _{j}}, \end{aligned}$$

then we have, from the definitions (4.18)–(4.21)

$$\begin{aligned}&\Vert w_{u_{1},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m-2}\Vert u\Vert _{k+4m-2,\infty ,\tau _{j}},&\Vert w_{u_{2},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m-1}\Vert u\Vert _{k+4m-1,\infty ,\tau _{j}}, \end{aligned}$$

(4.33)

$$\begin{aligned}&\Vert w_{u_{3},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m}\Vert u\Vert _{k+4m,\infty ,\tau _{j}},&\Vert w_{u_{4},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m+1}\Vert u\Vert _{k+4m+1,\infty ,\tau _{j}}, \end{aligned}$$

(4.34)

$$\begin{aligned}&\Vert w_{q_{1},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m-2}\Vert u\Vert _{k+4m-1,\infty ,\tau _{j}},&\Vert w_{q_{2},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m-1}\Vert u\Vert _{k+4m,\infty ,\tau _{j}}, \end{aligned}$$

(4.35)

$$\begin{aligned}&\Vert w_{q_{3},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m}\Vert u\Vert _{k+4m+1,\infty ,\tau _{j}},&\Vert w_{q_{4},m}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{k+4m+1}\Vert u\Vert _{k+4m+2,\infty ,\tau _{j}}. \end{aligned}$$

(4.36)

Thus we get (4.30) from the definitions (4.16)–(4.17). In the following discussion, we will focus on showing (4.31)–(4.32). By (4.14), integration by parts, and the definitions of $F_{1,m}$, $F_{2,m}$, we have, $\forall \eta$, $\varphi \in {}_c{V_{h}}$,

$$\begin{aligned} \text{ i }((P_{h}^{-}u-u)_{t},\eta )_{j}=-\text{ i }\bar{u}_{j,k}^{(1)}(L_{j,k},\eta )_{j}=\text{ i }\bar{h}_{j}\bar{u}_{j,k}^{(1)}(F_{1,1},\eta _{x})_{j}=-(w_{q_{1},1},\eta _{x})_{j},\\ (P_{h}^{+}q-q,\varphi )_{j}=-\tilde{q}_{j,k}(L_{j,k},\varphi )_{j}=\bar{h}_{j}\tilde{q}_{j,k}(F_{2,1},\varphi _{x})_{j}=(w_{u_{1},1},\varphi _{x})_{j}. \end{aligned}$$

With the definitions of $u_{I}^{l}$, $q_{I}^{l}$ and (4.23)–(4.26), we obtain

$$\begin{aligned}&\text{ i }((u_{I}^{l}-u)_{t},\eta )_{j}+(W_{q}^{l},\eta _{x})_{j}=-\text{ i }((w_{u_{4},r})_t,\eta )_{j}, \end{aligned}$$

(4.37)

$$\begin{aligned}&(q_{I}^{l}-q,\varphi )_{j}-(W_{u}^{l},\varphi _{x})_{j}=-(w_{q_{4},r},\varphi )_{j} \end{aligned}$$

(4.38)

for $l=4r$ and

$$\begin{aligned}&\text{ i }((u_{I}^{l}-u)_{t},\eta )_{j}+(W_{q}^{l},\eta _{x})_{j}=-\text{ i }((w_{u_{s},r+1})_{t},\eta )_{j}, \end{aligned}$$

(4.39)

$$\begin{aligned}&(q_{I}^{l}-q,\varphi )_{j}-(W_{u}^{l},\varphi _{x})_{j}=-(w_{q_{s},r+1},\varphi )_{j} \end{aligned}$$

(4.40)

for $l=4r+s$, $s=1$, 2, 3. Using the estimates of (4.33)–(4.36), we get the desired results (4.31)–(4.32) for all $l\ge 1$.

5 The Initial Discretization

In this section, we shall consider how to construct the suitable initial discretization such that the initial solution satisfy $\eta _{q}=0$, $\int _{\varOmega }\eta _{u}dx=0$ and $\Vert \eta _{u}\Vert _{0,\varOmega }\lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\varOmega }$. The choice of the initial condition is technical and critical to our superconvergence analysis, and the idea is motivated from Yang and Shu in [29, 30]. However, the addition of the correction functions makes the proof slightly different. Thus we present the detailed process.

Recall the linear error function $a_{j}^{2}(e_{u},e_{q};v)=0$ and the fact that $e_{u} = u-u_{I}^{l}+\eta _{u}$, and $e_{q} = q-q_{I}^{l}+\eta _{q}$, we obtain for all $v \in {}_c{V_{h}}$,

$$\begin{aligned} a_{j}^{2}(\eta _{u},\eta _{q};v)=a_{j}^{2}(u_{I}^{l}-u,q_{I}^{l}-q;v)= \left\{ \begin{array}{l} -(w_{q4,r},v)_{j}, \quad l=4r,\\ -(w_{qs,r+1},v)_{j}, \quad l=4r+s,s=1,2,3. \end{array} \right. \end{aligned}$$

Here for the last step we use the properties of (2.1), (4.28), (4.38) and (4.40). Without loss of generality, we only consider $l=4r$. If $\eta _{q}=0$ and by the definition of $a_{j}^{2}(\cdot ,\cdot ;\cdot )$, the above equation turns out to be

$$\begin{aligned} (\eta _{u},v_{x})_{j}-\eta _{u}^{-}v^{*-}|_{j+\frac{1}{2}} +\eta _{u}^{-}v^{*+}|_{j-\frac{1}{2}}=-(w_{q4,r},v)_{j}. \end{aligned}$$

(5.1)

Integrating (5.1) by parts yields

$$\begin{aligned} ((\eta _{u})_{x},v)_{j}+(\eta _{u}^{+}-\eta _{u}^{-}) v^{*+}|_{j-\frac{1}{2}}=(w_{q4,r},v)_{j}. \end{aligned}$$

(5.2)

If we choose $v=L_{j,m}+L_{j,m+1}$, $\text{ i }(L_{j,m}+L_{j,m+1})$, $m=0$, 1, $\cdots$, k in (5.2), then it is not difficult to obtain $(\eta _{u})_{x}$, which can be uniquely determined in the cell $\tau _{j}$, $j\in \mathbb {Z}_{N}$. Now we can easily get the following lemma.

Lemma 3

Suppose $\eta _{q}=0$, then $(\eta _{u})_{x}$ exists and is unique in each cell $\tau _{j}$, $j\in \mathbb {Z}_{N}$. Moreover, we have

$$\begin{aligned} \Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}\lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}. \end{aligned}$$

(5.3)

Proof

The existence and uniqueness of $(\eta _{u})_{x}$ can be obtained directly by the above analysis. Taking $v=(\eta _{u})_{x}-(-1)^{k}aL_{j,k}$ in (5.2), where $a=(\eta _{u})_{x}^{+}|_{j-\frac{1}{2}}$ such that $v(x_{j-\frac{1}{2}}^{+})=0$, we obtain

$$\begin{aligned} ((\eta _{u})_{x},(\eta _{u})_{x})_{j}&=(w_{q4,r},(\eta _{u})_{x}-(-1)^{k}aL_{j,k})_{j}\\&\lesssim \Vert w_{q4,r}\Vert _{0,\tau _{j}}(\Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}+|a|\Vert L_{j,k}\Vert _{0,\tau _{j}})\\&\lesssim \Vert w_{q4,r}\Vert _{0,\tau _{j}}(\Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}+h_{j}^{-\frac{1}{2}}\Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}h_{j}^{\frac{1}{2}})\\&\lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}\Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}. \end{aligned}$$

Here we use Cauchy–Schwarz inequality for the second step, the inverse inequality for the third step, and the estimate (4.36) for the last step. By dividing both sides of the above inequality by $\Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}}$, we get

$$\begin{aligned} \Vert (\eta _{u})_{x}\Vert _{0,\tau _{j}} \lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}, \quad j\in \mathbb {Z}_{N}. \end{aligned}$$

Thus, the proof is completed.

Now we present how to construct $\eta _{u}(x,0)$ with the help of Lemma 3 and $\int _{\varOmega }\eta _{u}dx=0$. Noticing the fact that

$$\begin{aligned} \eta _{u}(x,0)=\eta _{u}(x_{j+\frac{1}{2}}^{-},0) -\int _{x}^{x_{j+\frac{1}{2}}}(\eta _{u})_{y}(y,0)dy,\quad x\in \tau _{j}, \end{aligned}$$

(5.4)

we only need to determine the value $\eta _{u}(x_{j+\frac{1}{2}}^{-},0)$, since $(\eta _{u})_{x}$ can be obtained by Lemma 3. For simplicity, we just consider the situation $l=4r$ and other cases can be proved by the same arguments. Choosing $v=1$ in the Eq. (5.1), we get

$$\begin{aligned} \eta _{u}(x_{j+\frac{1}{2}}^{-},0)-\eta _{u} (x_{j-\frac{1}{2}}^{-},0)=(w_{q4,r},1)_{j}(0). \end{aligned}$$

Summing over j yields

$$\begin{aligned} \eta _{u}(x_{j+\frac{1}{2}}^{-},0)=\eta _{u}(x_{\frac{1}{2}}^{-},0) +S_{j}, \end{aligned}$$

(5.5)

where

$$\begin{aligned} S_{j}=\sum _{m=1}^{j}\int _{\tau _{m}}w_{q4,r}dx(0), \quad \Vert S_{j}\Vert _{0,\infty ,\tau _{j}}\lesssim \sum _{m=1}^{j}h_{m}h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{m}}. \end{aligned}$$

(5.6)

Here for the second inequality we use the estimate (4.36). Due to $\int _{\varOmega }\eta _{u}dx=0$ and the representation (5.4), we obtain

$$\begin{aligned} \sum _{j=1}^{N}\biggl (h_{j}\eta _{u}(x_{j+\frac{1}{2}}^{-},0) -\int _{\tau _{j}}\int _{x}^{x_{j+\frac{1}{2}}}(\eta _{u})_{y}(y,0) dydx\biggr )=0. \end{aligned}$$

Keeping in mind that $\sum _{j=1}^{N}h_{j}=|\varOmega |$ and using (5.5), we get,

$$\begin{aligned} \eta _{u}(x_{\frac{1}{2}}^{-},0)=\frac{-1}{|\varOmega |} \sum _{j=1}^{N}h_{j}S_{j}+\frac{1}{|\varOmega |} \sum _{j=1}^{N}B_{j}, \end{aligned}$$

(5.7)

where

$$\begin{aligned} B_{j}=\int _{\tau _{j}}\int _{x}^{x_{j+\frac{1}{2}}}(\eta _{u})_{y}(y,0)dydx, \quad j \in \mathbb {Z}_{N}. \end{aligned}$$

(5.8)

In light of the estimate (5.3) of $(\eta _{u})_{x}$ in Lemma 3, we have

$$\begin{aligned} \Vert B_{j}\Vert _{0,\infty ,\tau _{j}}\lesssim h_{j}h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\tau _{j}}, \quad j \in \mathbb {Z}_{N}. \end{aligned}$$

(5.9)

Plugging (5.7) into (5.5), then plugging (5.5) into (5.4), we obtain

$$\begin{aligned} \eta _{u}(x,0)&=\frac{-1}{|\varOmega |}\sum _{j=1}^{N}h_{j}S_{j} +\frac{1}{|\varOmega |}\sum _{j=1}^{N}B_{j}+S_{j} -\int _{x}^{x_{j+\frac{1}{2}}}(\eta _{u})_{y}(y,0)dy,\quad x \in \tau _{j}. \end{aligned}$$

(5.10)

Combining (5.3), (5.6), and (5.9), we can easily get the following estimates.

Lemma 4

If $\eta _{q}=0$ and $\int _{\varOmega }\eta _{u}dx=0$, then $\eta _{u}$ exists and is unique in each cell $\tau _{j}$, $j\in \mathbb {Z}_{N}$. Moreover, we have

$$\begin{aligned} \Vert \eta _{u}\Vert _{0,\varOmega }\lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\varOmega }. \end{aligned}$$

(5.11)

Algorithm for Initial Condition

Now we are ready to implement the initial discretization. Without loss of generality, we only consider the case $l=4r$. If $l=4r+s$, $s=1$, 2, 3, we only need to replace $w_{q4,r}$ by $w_{qs,r+1}$ in the following process.

• (1) Use (5.2) to find $(\eta _{u})_{x}$.

• (2) Compute $S_{j}$ in each cell from (5.6).

• (3) Work out $B_{j}$ from the expression of $(\eta _{u})_{x}$ and (5.8).

• (4) In each element $\tau _{j}$, calculate $\eta _{u}$ by (5.10).

• (5) Figure out $u_{h}=u_{I}^{l}-\eta _{u}$, where $u_{I}^{l}$ is defined by (4.27). We refer to [11] for the details how to compute $u_{I}^{l}$.

6 Superconvergence

In this section, we will discuss the superconvergence properties for the Eq. (1.1), which is the main part in our paper. Various errors shall be studied, such as the domain, cell average, and the errors at the nodes and Radau points. We first analyse the errors between the special interpolation functions $(u_{I}^{l},q_{I}^{l})$ and the LDG solutions $(u_{h},q_{h})$.

6.1 Superconvergence for the Interpolation Function

Theorem 5

Assume that $u\in W^{k+l+6,\infty }(\varOmega )$, $1\le l \le k$ is the exact solution of (1.1), and $u_{h}$, $q_{h}$ are the numerical solutions of LDG scheme (3.1)–(3.2) with the initial conditions $q_{h}(\cdot ,0) = q_{I}^{l}(\cdot ,0)$ and $\int _{\varOmega }(u_{I}^{l}-u_{h})(x,0)dx = 0$, where $u_{I}^{l}$, $q_{I}^{l}\in {}_c{V_{h}}$ are defined by (4.27). Then for the periodic and mixed boundary conditions, it holds that

$$\begin{aligned} \Vert (u^{l}_{I}-u_{h})_{t}\Vert _{0,\varOmega }(t)&\lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega }, \quad \forall t\ge 0,\end{aligned}$$

(6.1)

$$\begin{aligned} \Vert q^{l}_{I}-q_{h}\Vert _{0,\varOmega }(t)&\lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega }, \quad \forall t\ge 0. \end{aligned}$$

(6.2)

Proof

Noticing the linear error functions (3.4) and the notation (4.29), we get, for all v, $w \in {}_c{V_{h}}$,

$$\begin{aligned}&a^{1}(\eta _{u},\eta _{q};v)=a^{1}(u^{l}_{I}-u,q^{l}_{I}-q;v)=\sum _{j=1}^{N}\text{ i }((u_{I}^{l}-u)_{t},v)_{j}+(W_{q}^{l},v_{x})_{j},\\&a^{2}(\eta _{u},\eta _{q};v)=a^{2}(u^{l}_{I}-u,q^{l}_{I}-q;v)=\sum _{j=1}^{N}(q_{I}^{l}-q,v)_{j}-(W_{u}^{l},v_{x})_{j},\\&a^{1}((\eta _{u})_{t},(\eta _{q})_{t};v)=a^{1}((u^{l}_{I}-u)_{t},(q^{l}_{I}-q)_{t};v)=\sum _{j=1}^{N}\text{ i }((u_{I}^{l}-u)_{tt},v)_{j}+((W_{q}^{l})_{t},v_{x})_{j},\\&a^{2}((\eta _{u})_{t},(\eta _{q})_{t};v)=a^{2}((u^{l}_{I}-u)_{t},(q^{l}_{I}-q)_{t};v)=\sum _{j=1}^{N}((q_{I}^{l}-q)_{t},v)_{j}-((W_{u}^{l})_{t},v_{x})_{j}. \end{aligned}$$

Here we use the properties (2.1)–(2.2) and (4.28). By the same line of reasoning used to prove (4.31)–(4.32) and $\text{ i }u_{t}=-u_{xx}$, we have

$$\begin{aligned}&|a^{1}(\eta _{u},\eta _{q};v)|=|a^{1}(u^{l}_{I}-u,q^{l}_{I}-q;v)|\lesssim h^{k+l+1}\Vert u\Vert _{k+l+3,\infty ,\varOmega }\Vert v\Vert _{0,1,\varOmega }, \end{aligned}$$

(6.3)

$$\begin{aligned}&|a^{2}(\eta _{u},\eta _{q};v)|=|a^{2}(u^{l}_{I}-u,q^{l}_{I}-q;v)|\lesssim h^{k+l+1}\Vert u\Vert _{k+l+2,\infty ,\varOmega }\Vert v\Vert _{0,1,\varOmega }, \end{aligned}$$

(6.4)

$$\begin{aligned}&|a^{1}((\eta _{u})_{t},(\eta _{q})_{t};v)|=|a^{1}((u^{l}_{I}-u)_{t},(q^{l}_{I}-q)_{t};v)|\lesssim h^{k+l+1}\Vert u\Vert _{k+l+5,\infty ,\varOmega }\Vert v\Vert _{0,1,\varOmega }, \end{aligned}$$

(6.5)

$$\begin{aligned}&|a^{2}((\eta _{u})_{t},(\eta _{q})_{t};v)|=|a^{2}((u^{l}_{I}-u)_{t},(q^{l}_{I}-q)_{t};v)|\lesssim h^{k+l+1}\Vert u\Vert _{k+l+4,\infty ,\varOmega }\Vert v\Vert _{0,1,\varOmega }. \end{aligned}$$

(6.6)

Note that the choice of the numerical fluxes and the property (4.28), we have, for $m=0$, 1,

$$\begin{aligned} (\partial _{t}^{m}\eta _{u})^{-}(\eta _{q}^{*})^{+}|_{N+\frac{1}{2}}=(\partial _{t}^{m}\eta _{u})^{-}(\eta _{q}^{*})^{+}|_{\frac{1}{2}},\quad (\partial _{t}^{m}\eta _{u})^{-}(\eta _{q}^{*})^{+}_{t}|_{N+\frac{1}{2}}=(\partial _{t}^{m}\eta _{u})^{-}(\eta _{q}^{*})_{t}^{+}|_{\frac{1}{2}} \end{aligned}$$

(6.7)

for both periodic and mixed boundary conditions. Then choosing $v=\eta _{u}$, $w=\eta _{q}$ in the energy function (3.6), we obtain

$$\begin{aligned} \frac{d}{dt}\Vert \eta _{q}\Vert _{0,\varOmega }^{2}&=|a^{1}(\eta _{u},\eta _{q};-(\eta _{u})_{t})+a^{2}((\eta _{u})_{t},(\eta _{q})_{t};\eta _{q})+a^{1}(\eta _{u},\eta _{q};-(\eta _{u})_{t})^{*}\\&\quad +\,a^{2}((\eta _{u})_{t},(\eta _{q})_{t};\eta _{q})^{*}|\\&\lesssim h^{k+l+1}\Vert u\Vert _{k+l+4,\infty ,\varOmega }(\Vert (\eta _{u})_{t}\Vert _{0,1,\varOmega }+\Vert \eta _{q}\Vert _{0,1,\varOmega })\\&\lesssim h^{k+l+1}\Vert u\Vert _{k+l+4,\infty ,\varOmega }(\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }+\Vert \eta _{q}\Vert _{0,\varOmega }). \end{aligned}$$

Integrating the above inequality with respect to time between 0 and t, we obtain

$$\begin{aligned} \Vert \eta _{q}\Vert _{0,\varOmega }^{2}(t)\lesssim th^{k+l+1}\Vert u\Vert _{k+l+4,\infty ,\varOmega }(\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }(t)+\Vert \eta _{q}\Vert _{0,\varOmega }(t)). \end{aligned}$$

(6.8)

Here we use the special choice of initial condition $\eta _{q}(x,0)=0$. By taking $v=(\eta _{u})_{t}$, $w=(\eta _{q})_{t}$ in (3.5), we obtain

$$\begin{aligned} \text{ i }((\eta _{u})_{tt}, (\eta _{u})_{t})+\text{ i }((\eta _{u})_{tt}, (\eta _{u})_{t})^{*}&= a^{1}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{u})_{t})+a^{2}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{q})_{t})\nonumber \\&\quad -\,a^{1}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{u})_{t})^{*}-a^{2}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{q})_{t})^{*}. \end{aligned}$$

(6.9)

Here we use the property (6.7) again. Integrating the second term of the right-hand side by parts over the interval [0, t] yields

$$\begin{aligned} \int _{0}^{t}a^{2}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{q})_{t})dt&=\sum _{j=1}^{N}\int _{0}^{t}((q_{I}^{l}-q)_{t},(\eta _{q})_{t})_{j}-((W_{u}^{l})_{t},(\eta _{q})_{tx})_{j}dt\\&=\sum _{j=1}^{N}((q_{I}^{l}-q)_{t},\eta _{q})_{j}|_{0}^{t}-\sum _{j=1}^{N}((W_{u}^{l})_{t},(\eta _{q})_{x})_{j}|_{0}^{t}\\&\quad \ -\sum _{j=1}^{N}\int _{0}^{t}((q_{I}^{l}-q)_{tt},\eta _{q})_{j}-((W_{u}^{l})_{tt},-(\eta _{q})_{x})_{j}dt. \end{aligned}$$

Then by the same arguments used in Lemma 2, we obtain

$$\begin{aligned} \left| \int _{0}^{t}a^{2}((\eta _{u})_{t},(\eta _{q})_{t};(\eta _{q})_{t})dt\right| \lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega }\Vert \eta _{q}\Vert _{0,\varOmega }(t). \end{aligned}$$

We then integrate (6.9) with respect to time between 0 and t and obtain, from (6.5),

$$\begin{aligned}&\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }^{2}(t)\lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega } (\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }(t)\nonumber \\&\quad +\,\Vert \eta _{q}\Vert _{0,\varOmega }(t)) + \Vert (\eta _{u})_{t}\Vert _{0,\varOmega }^{2}(0). \end{aligned}$$

(6.10)

Now we analyse $\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }(0)$. From the error functions (3.4) and $\eta _{q}(\cdot ,0)=0$ , we have

$$\begin{aligned} 0=a^{1}_{j}(e_{u},e_{q};v)(0)&=a^{1}_{j}(u-u_{I}^{l},q-q_{I}^{l};v)(0)+a^{1}_{j}(\eta _{u},\eta _{q};v)(0)\\&=\text{ i }((\eta _{u})_{t},v)_{j}(0)+\text{ i }((u-u_{I}^{l})_{t},v)_{j}(0)-(W_{q}^{l},v_{x})_{j}(0). \end{aligned}$$

Here we use the properties (2.2) and (4.28). By (4.37) and (4.39), it is not difficult to obtain, in each element $\tau _{j}$, $j\in \mathbb {Z}_{N}$,

$$\begin{aligned} (\eta _{u})_{t}(x,0)=-(w_{u_{4},r})_{t}(x,0) \end{aligned}$$

in case $l=4r$ and

$$\begin{aligned} (\eta _{u})_{t}(x,0)=-(w_{u_{s},r+1})_{t}(x,0) \end{aligned}$$

in case $l=4r+s$, $s=1$, 2, 3. By (4.33)–(4.34), we have

$$\begin{aligned} \Vert (\eta _{u})_{t}\Vert _{0,\varOmega }(0) \lesssim \Vert (\eta _{u})_{t}\Vert _{0,\infty ,\varOmega }(0)\lesssim h^{k+l+1}\Vert u\Vert _{k+l+3,\infty ,\varOmega }. \end{aligned}$$

(6.11)

Combining (6.8), (6.10), and (6.11) and using Young’s inequality, we get

$$\begin{aligned} \Vert (\eta _{u})_{t}\Vert _{0,\varOmega }(t)\lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega },\\ \Vert \eta _{q}\Vert _{0,\varOmega }(t)\lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega }. \end{aligned}$$

The proof is completed.

By the aid of Theorem 5, we proceed to study the superconvergence properties of the error $\eta _{u}$, which will be presented in the following theorem.

Theorem 6

Assume that the conditions of Theorem 5 are satisfied. Then for the periodic and mixed boundary conditions,

$$\begin{aligned} \Vert u^{l}_{I}-u_{h}\Vert _{0,\varOmega }(t) \lesssim (1+t)h^{k+l+1}\Vert u\Vert _{k+l+6,\infty ,\varOmega }, \quad \forall t\ge 0. \end{aligned}$$

(6.12)

Proof

Noticing the special initial conditions, we see that (6.12) is true in the case $t=0$ by Lemma 4. Thus we only consider $t>0$. By taking $v=\eta _{u}$, $w=\eta _{q}$ in (3.5) and with similar arguments to prove (6.8), we obtain

$$\begin{aligned} \Vert \eta _{u}\Vert _{0,\varOmega }^{2}(t)\lesssim \Vert \eta _{u}\Vert _{0,\varOmega }^{2}(0)+ th^{k+l+1}\Vert u\Vert _{k+l+3,\infty ,\varOmega }(\Vert \eta _{u}\Vert _{0,\varOmega }(t)+\Vert \eta _{q}\Vert _{0,\varOmega }(t)). \end{aligned}$$

Applying Young’s inequality and the results of Theorem 5, we complete the proof.

Remark 7

We remark that we obtain the supercloseness between the LDG solution $(u_{h},q_{h})$ and the special interpolation function $(u_{I}^{k},q_{I}^{k})$ if we choose $l=k$ in Theorems 5 and 6, which achieves a superconvergence rate of $(2k+1)$-th order. The significant results will be frequently used to prove the $(2k+1)$-th superconvergence rate for the domain and cell averages as well as the numerical fluxes at mesh nodes.

6.2 Superconvergence of Numerical Fluxes at Nodal Points

In this subsection, we provide the superconvergence results for the numerical fluxes at mesh nodes.

Theorem 8

Assume that $u\in W^{2k+6,\infty }(\varOmega )$, $k\ge 1$ is the exact solution of (1.1), and $u_{h}$, $q_{h}$ are the numerical solutions of LDG scheme (3.1)–(3.2) with the initial condition $q_{h}(\cdot ,0) = q_{I}^{k}(\cdot ,0)$ and $\int _{\varOmega }(u_{I}^{k}-u_{h})(x,0)dx = 0$, where $u_{I}^{k}$, $q_{I}^{k}\in {}_c{V_{h}}$ are defined by (4.27). Then for the periodic and mixed boundary conditions, it holds that,

$$\begin{aligned} e_{u,n}&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },&e_{q,n}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },\end{aligned}$$

(6.13)

$$\begin{aligned} \Vert e_{u}\Vert _{*}&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },&\Vert e_{q}\Vert _{*}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \end{aligned}$$

(6.14)

where

$$\begin{aligned}&e_{u,n}=\max \limits _{j\in \mathbb {Z}_{N}}|(\hat{u}-\hat{u}_{h})(x_{j+\frac{1}{2}},t)|,&\Vert e_{u}\Vert _{*}=\left( \frac{1}{N}\sum _{j=1}^{N}\left| (\hat{u}-\hat{u}_{h})(x_{j+\frac{1}{2}},t)\right| ^{2}\right) ^{\frac{1}{2}},\\&e_{q,n}=\max \limits _{j\in \mathbb {Z}_{N}}|(\hat{q}-\hat{q}_{h})(x_{j-\frac{1}{2}},t)|,&\Vert e_{q}\Vert _{*}=\left( \frac{1}{N}\sum _{j=1}^{N}\left| (\hat{q}-\hat{q}_{h})(x_{j-\frac{1}{2}},t)\right| ^{2}\right) ^{\frac{1}{2}}. \end{aligned}$$

Proof

We obtain (6.14) by following the same logical in Theorem 4.4 of [11]. For (6.13), we first consider periodic boundary condition. Assume that $\eta _{u}(x,t)$ has the following representation

$$\begin{aligned} \eta _{u}(x,t)=\eta _{u}(x_{j},t)+s_{u}(x,t)\frac{x-x_{j}}{h_{j}},\quad x\in \tau _{j},\quad t>0. \end{aligned}$$

(6.15)

From the definition of $a_{j}^{2}(\cdot ,\cdot ;\cdot )$, we obtain

$$\begin{aligned} 0=a_{j}^{2}(e_{u},e_{q};v)&=a_{j}^{2}(\eta _{u},\eta _{q};v) +a_{j}^{2}(u-u_{I}^{k},q-q_{I}^{k};v)\\&=(\eta _{q},v)_{j}-((\eta _{u})_{x},v)_{j} +a_{j}^{2}(u-u_{I}^{k},q-q_{I}^{k};v), \end{aligned}$$

where $v=s_{u}(x,t)\frac{x-x_{j-\frac{1}{2}}}{h_{j}}$. By (6.2) and (6.4), we get

$$\begin{aligned} |((\eta _{u})_{x},v)_{j}|&=|(\eta _{q},v)_{j}+a_{j}^{2}(u-u_{I}^{k},q-q_{I}^{k};v)|\nonumber \\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }\Vert v\Vert _{0,\tau _{j}}. \end{aligned}$$

(6.16)

Denote $\mathbf {Re}v(x,t)$ to be the real part of v(x, t), and $\mathbf {Im}v(x,t)$ to be the imaginary part of v(x, t). Rewrite $s_{u}(x,t)=s_{1}(x,t)+\text{ i }s_{2}(x,t)$, where $s_{1}(x,t)=\mathbf {Re}s_{u}(x,t)$, $s_{2}(x,t)=\mathbf {Im}s_{u}(x,t)$. Then by direct calculation, we get

$$\begin{aligned} (\mathbf {Re}(\eta _{u})_{x},\mathbf {Re}v)_{j}&=\int _{\tau _{j}}s_{1}(x,t)\frac{x-x_{j-\frac{1}{2}}}{h_{j}}\frac{d}{dx}(s_{1}(x,t)\frac{x-x_{j}}{h_{j}})=\frac{1}{4h_{j}}\int _{\tau _{j}}s_{1}^{2}dx\\&\quad + \frac{s_{1}^{2}(x_{j+\frac{1}{2}},t)}{4},\\ (\mathbf {Im}(\eta _{u})_{x},\mathbf {Im}v)_{j}&=\int _{\tau _{j}}s_{2}(x,t)\frac{x-x_{j-\frac{1}{2}}}{h_{j}}\frac{d}{dx}(s_{2}(x,t)\frac{x-x_{j}}{h_{j}})=\frac{1}{4h_{j}}\int _{\tau _{j}}s_{2}^{2}dx\\&\quad + \frac{s_{2}^{2}(x_{j+\frac{1}{2}},t)}{4}. \end{aligned}$$

Here the last equation can be found in [7]. From (6.16), we obtain

$$\begin{aligned} \Vert s_{1}\Vert _{0,\tau _{j}}^{2}&\lesssim h_{j}|(\mathbf {Re}(\eta _{u})_{x},\mathbf {Re}v)_{j}|\lesssim h_{j}|((\eta _{u})_{x},v)_{j}|\\&\lesssim (1+t)h^{2k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega }\Vert v\Vert _{0,\tau _{j}}. \end{aligned}$$

By the same arguments, we get

$$\begin{aligned} \Vert s_{2}\Vert _{0,\tau _{j}}^{2}\lesssim (1+t)h^{2k+2} \Vert u\Vert _{2k+6,\infty ,\varOmega }\Vert v\Vert _{0,\tau _{j}}. \end{aligned}$$

Thus

$$\begin{aligned} \Vert s_{u}\Vert _{0,\tau _{j}}^{2}=\Vert s_{1}\Vert _{0, \tau _{j}}^{2}+\Vert s_{2}\Vert _{0,\tau _{j}}^{2} \lesssim (1+t)h^{2k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega }\Vert v\Vert _{0,\tau _{j}}. \end{aligned}$$

Since $\Vert v\Vert _{0,\tau _{j}}\lesssim \Vert s_{u}\Vert _{0,\tau _{j}}$, the above inequality becomes

$$\begin{aligned} \Vert s_{u}\Vert _{0,\tau _{j}}\lesssim (1+t)h^{2k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

By the inverse inequality, we have

$$\begin{aligned} \Vert s_{u}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{-\frac{1}{2}}\Vert s_{u}\Vert _{0,\tau _{j}} \lesssim (1+t)h^{2k+\frac{3}{2}}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

(6.17)

On the other hand, choose $v=1$ in the equation $a_{j}^{2}(e_{u},e_{q};v)=0$ to obtain

$$\begin{aligned} \eta _{u}^{-}|_{j+\frac{1}{2}}-\eta _{u}^{-}|_{j-\frac{1}{2}}=e_{u}^{-}|_{j+\frac{1}{2}}-e_{u}^{-}|_{j-\frac{1}{2}}=\int _{\tau _{j}}e_{q}dx=\int _{\tau _{j}}\eta _{q}+W_{q}^{k}dx. \end{aligned}$$

Here for the first step we use (4.28) and for the last step we use property (2.2) of the Gauss–Radau projection. Then

$$\begin{aligned} \eta _{u}^{-}|_{j+\frac{1}{2}}&=\eta _{u}^{-}|_{\frac{1}{2}}+\sum _{m=1}^{j}\int _{\tau _{m}}\eta _{q}+W_{q}^{k}dx. \end{aligned}$$

(6.18)

By the representation of (6.15), we have

$$\begin{aligned} \eta _{u}(x_{j},t)&=\eta _{u}(x_{0},t) +\frac{1}{2}s_{u}(x_{\frac{1}{2}}^{-},t) -\frac{1}{2}s_{u}(x_{j+\frac{1}{2}}^{-},t)+\sum _{m=1}^{j}\int _{\tau _{m}}(\eta _{q}+W_{q}^{k})(x,t)dx.\ \end{aligned}$$

(6.19)

From the definitions (4.10)–(4.13) and the orthogonal properties of Legendre polynomials, we have, for $m=0$, 1

$$\begin{aligned} \int _{\tau _{j}}\partial _{t}^{m}W_{u}^{l}(x,t)dx=\int _{\tau _{j}}\partial _{t}^{m}w_{u_{4},r}(x,t)dx \end{aligned}$$

(6.20)

in case $l=4r$, and

$$\begin{aligned} \int _{\tau _{j}}\partial _{t}^{m}W_{u}^{l}(x,t)dx=\int _{\tau _{j}}\partial _{t}^{m}w_{u_{s},r+1}(x,t)dx \end{aligned}$$

(6.21)

in case $l=4r+s$, $s=1$, 2, 3. By (4.33)–(4.34), for all $1\le l \le k$ we have,

$$\begin{aligned} \left| \int _{\tau _{j}}\partial _{t}^{m}W_{u}^{l}(x,t)dx \right| \lesssim h^{k+l+2}\Vert u\Vert _{k+l+1+2m,\infty ,\tau _{j}}, \quad m=0,1,\quad \forall t\ge 0. \end{aligned}$$

(6.22)

By the same arguments, we also get

$$\begin{aligned} \left| \int _{\tau _{j}}\partial _{t}^{m}W_{q}^{l}(x,t)dx\right| \lesssim h^{k+l+2}\Vert u\Vert _{k+l+2+2m,\infty ,\tau _{j}}, \quad m=0,1,\quad \forall t\ge 0. \end{aligned}$$

(6.23)

Choosing $v=1$ in the equation $a^{1}(e_{u},e_{q};v)=0$, we obtain, by the periodic boundary condition,

$$\begin{aligned} \sum _{j=1}^{N}\text{ i }\int _{\tau _{j}}(\eta _{u}+W_{u}^{k})_{t}dx= \sum _{j=1}^{N}\text{ i }\int _{\tau _{j}}(e_{u})_{t}dx=e_{q}^{+}|_{\frac{1}{2}}-e_{q}^{+}|_{N+\frac{1}{2}}= 0. \end{aligned}$$

Integrating the above equation with respect to time over [0, t] and by the special initial condition $\int _{\varOmega }\eta _{u}(x,0)dx=0$, we get

$$\begin{aligned} \sum _{j=1}^{N}\int _{\tau _{j}}\eta _{u}(x,t)dx= \sum _{j=1}^{N}\int _{\tau _{j}}W_{u}^{k}(x,0)-W_{u}^{k}(x,t)dx, \end{aligned}$$

Due to the representation of (6.15), we have

$$\begin{aligned}&\sum _{j=1}^{N}\left( h_{j}\eta _{u}(x_{j},t)+\int _{\tau _{j}}s_{u}(x,t)\frac{x-x_{j}}{h_{j}}dx\right) \\&\quad = \sum _{j=1}^{N}\int _{\tau _{j}}W_{u}^{k}(x,0)-W_{u}^{k}(x,t)dx. \end{aligned}$$

Combining (6.17) and (6.19), we have

$$\begin{aligned} |\eta _{u}(x_{0},t)|&\lesssim \Vert s_{u}\Vert _{0,\infty ,\varOmega }+\Vert \eta _{q}\Vert _{0,\varOmega }(t)+\sum _{j=1}^{N}\left| \int _{\tau _{j}}W_{u}^{k}dx(0)\right| \\&\quad +\sum _{j=1}^{N}\left| \int _{\tau _{j}}W_{u}^{k}dx(t)\right| +\sum _{j=1}^{N}\left| \int _{\tau _{j}}W_{q}^{k}dx(t)\right| \\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Then by (6.19), we have

$$\begin{aligned} |\eta _{u}(x_{j},t)|&\lesssim \Vert s_{u}\Vert _{0,\infty ,\varOmega }+ |\eta _{u}(x_{0},t)|+\Vert \eta _{q}\Vert _{0,\varOmega }(t)+\sum _{m=1}^{j}\left| \int _{\tau _{m}}W_{q}^{k}dx(t)\right| \\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \quad \forall j \in \mathbb {Z}_{N}. \end{aligned}$$

Note that $u(x_{j+\frac{1}{2}}^{-},t)=u_{I}^{k}(x_{j+\frac{1}{2}}^{-},t)$, we get

$$\begin{aligned} |(u-u_{h})(x_{j+\frac{1}{2}}^{-},t)|&=|(u_{I}^{k}-u_{h})(x_{j+\frac{1}{2}}^{-},t)|\lesssim \Vert \eta _{u}\Vert _{0,\infty ,\varOmega }\\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \quad \forall j\in \mathbb {Z}_{N}, \end{aligned}$$

then the first inequality of (6.13) follows directly. Assume that $\eta _{q}(x,t)$ has the following representation

$$\begin{aligned} \eta _{q}(x,t)=\eta _{q}(x_{j},t)+s_{q}(x,t)\frac{x-x_{j}}{h_{j}},\quad x\in \tau _{j}, \quad j\in \mathbb {Z}_{N}. \end{aligned}$$

(6.24)

From the definition of $a_{j}^{1}(\cdot ,\cdot ;\cdot )$, we obtain

$$\begin{aligned} 0=a_{j}^{1}(e_{u},e_{q};v)&=a_{j}^{1}(\eta _{u},\eta _{q};v) +a_{j}^{1}(u-u_{I}^{k},q-q_{I}^{k};v)\\&=\text{ i }((\eta _{u})_{t},v)_{j}+((\eta _{q})_{x},v)_{j} +a_{j}^{1}(u-u_{I}^{k},q-q_{I}^{k};v), \end{aligned}$$

where $v=s_{q}(x,t)\frac{x-x_{j+\frac{1}{2}}}{h_{j}}$. From (6.1) and (6.3), we have

$$\begin{aligned} |((\eta _{q})_{x},v)_{j}|&=|-\text{ i }((\eta _{u})_{t},v)_{j}-a_{j}^{1}(u-u_{I}^{k},q-q_{I}^{k};v)|\\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }\Vert v\Vert _{0,\tau _{j}}. \end{aligned}$$

By similar arguments, it is not difficult to get

$$\begin{aligned}&\Vert s_{q}\Vert _{0,\infty ,\tau _{j}}\lesssim h^{-\frac{1}{2}}\Vert s_{q}\Vert _{0,\tau _{j}} \lesssim (1+t)h^{2k+\frac{3}{2}}\Vert u\Vert _{2k+6,\infty ,\tau _{j}},\\&|\eta _{q}(x_{j},t)| \lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \quad \forall j \in \mathbb {Z}_{N}. \end{aligned}$$

Then, in light of (6.24), we have

$$\begin{aligned} |(q-q_{h})(x_{j-\frac{1}{2}}^{+},t)|=|(q_{I}^{k}-q_{h})(x_{j-\frac{1}{2}}^{+},t)|&\lesssim \Vert \eta _{q}\Vert _{0,\infty ,\varOmega }\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Thus we obtain (6.13) is true for periodic boundary condition. Next, we will analyze the mixed boundary conditions. Since $\eta _{u}^{-}|_{\frac{1}{2}}=0$ for mixed boundary conditions, the representation of (6.18) yields that

$$\begin{aligned} |\eta _{u}(x_{j+\frac{1}{2}}^{-},t)|&\lesssim \sum _{m=1}^{j}\int _{\tau _{m}}|\eta _{q}|dx+\sum _{m=1}^{j}\left| \int _{\tau _{m}}W_{q}^{k}dx\right| \\&\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Here we use Theorem 5 and the estimates (6.23). In light of the representation (6.15), we have

$$\begin{aligned} \eta _{u}(x_{j},t)=\eta _{u}(x_{j+\frac{1}{2}}^{-},t) -\frac{1}{2}s_{u}(x_{j+\frac{1}{2}}^{-},t), \end{aligned}$$

which yields that

$$\begin{aligned} \Vert \eta _{u}(x,t)\Vert _{0,\infty ,\varOmega }\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Here we use the estimate (6.17). Similarly, choose $v=1$ in the equation $a_{j}^{1}(e_{u},e_{q};v)=0$ to obtain

$$\begin{aligned} \eta _{q}^{+}|_{j-\frac{1}{2}}-\eta _{q}^{+}|_{j+\frac{1}{2}} =e_{q}^{+}|_{j-\frac{1}{2}}-e_{q}^{+}|_{j+\frac{1}{2}} =\text{ i }\int _{\tau _{j}}(e_{u})_{t}dx =\text{ i }\int _{\tau _{j}}(\eta _{u})_{t} +(W_{u}^{k})_{t}dx. \end{aligned}$$

Then

$$\begin{aligned} \eta _{q}^{+}|_{j+\frac{1}{2}}&=\eta _{q}^{+}|_{\frac{1}{2}} -\text{ i }\sum _{m=1}^{j}\int _{\tau _{m}}(\eta _{u})_{t}dx -\text{ i }\sum _{m=1}^{j}\int _{\tau _{m}}(W_{u}^{k})_{t}dx. \end{aligned}$$

Since $\eta _{q}^{+}|_{N+\frac{1}{2}}=0$ for mixed boundary conditions, the estimates (6.22) and (6.1) give that

$$\begin{aligned} |\eta _{q}(x_{\frac{1}{2}}^{+},t)|\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

By similar arguments, we have

$$\begin{aligned} \Vert \eta _{q}(x,t)\Vert _{0,\infty ,\varOmega }\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Note that $u(x_{j+\frac{1}{2}}^{-},t)=u_{I}^{k}(x_{j+\frac{1}{2}}^{-},t)$ and $q(x_{j-\frac{1}{2}}^{+},t)=q_{I}^{k}(x_{j-\frac{1}{2}}^{+},t)$, we get

$$\begin{aligned} e_{u,n}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \quad e_{q,n}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

for mixed boundary conditions. The proof is completed.

6.3 Superconvergence for the Domain and Cell Averages

In this subsection, we study the superconvergence properties for the domain and cell averages.

Theorem 9

Assume that the conditions of Theorem 8 are satisfied, then, for the periodic and mixed boundary conditions, we have, $\forall t>0$,

$$\begin{aligned}&\Vert e_{u}\Vert _{c}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },\quad \Vert e_{u}\Vert _{d}\lesssim h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },\end{aligned}$$

(6.25)

$$\begin{aligned}&\Vert e_{q}\Vert _{c}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },\quad \Vert e_{q}\Vert _{d}\lesssim h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega } , \end{aligned}$$

(6.26)

where

$$\begin{aligned}&\Vert e_{u}\Vert _{d}=\left| \frac{1}{2\pi }\int _{0}^{2\pi }(u-u_{h})(x,t)dx\right| ,\\&\Vert e_{u}\Vert _{c}=\left( \frac{1}{N}\sum _{j=1}^{N}\biggl |\frac{1}{h_{j}}\int _{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}(u-u_{h})(x,t)dx\biggr |^{2}\right) ^{\frac{1}{2}}, \end{aligned}$$

similarly, the domain average $\Vert e_{q}\Vert _{d}$ and the cell average $\Vert e_{q}\Vert _{c}$ of $q-q_{h}$ can be defined in the same way. Moreover, for the periodic boundary condition, there holds

$$\begin{aligned} \Vert e_{q}\Vert _{d}=0. \end{aligned}$$

(6.27)

Proof

From the properties (2.1)–(2.2) of $P^{+}_{h},P^{-}_{h}$, we can obtain

$$\begin{aligned} \int _{\tau _{j}}(u-u_{h})(x,t)dx=\int _{\tau _{j}}(u_{I}^{k}-u_{h})(x,t)dx+\int _{\tau _{j}}W_{u}^{k}(x,t)dx, \end{aligned}$$

(6.28)

where $W_{u}^{k}$ is defined by (4.17). Choosing $l=k$ in Theorem 6 and by the estimate (6.22), we obtain

$$\begin{aligned} \Vert e_{u}\Vert _{c}\lesssim \Vert u_{I}^{k}-u_{h}\Vert _{0,\varOmega }+h^{2k+1}\Vert u\Vert _{2k+1,\infty ,\varOmega } \lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Summing over all j in (6.28), we obtain

$$\begin{aligned} \Vert e_{u}\Vert _{d}\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

The proof of $\Vert e_{q}\Vert _{d}$ and $\Vert e_{q}\Vert _{c}$ can be obtained by the same arguments. In addition, note that $a_{j}^{2}(e_{u},e_{q};1)=0$, we have

$$\begin{aligned} \int _{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}(q-q_{h})(x,t)dx=(u-u_{h})(x_{j+\frac{1}{2}}^{-},t)-(u-u_{h})(x_{j-\frac{1}{2}}^{-},t). \end{aligned}$$

Summing over all j and by the periodic boundary condition, we obtain

$$\begin{aligned} \int _{0}^{2\pi }(q-q_{h})(x,t)dx=0, \end{aligned}$$

which yields (6.27).

6.4 Superconvergence of the Function Value Approximation at Radau Points

In this subsection, we will study the superconvergence phenomena for the function value at Radau points. The notations $R_{j,m}^{l}$, $R_{j,m}^{r}$, $m\in \mathbb {Z}_{k}$ stand for the k interior left and right Radau points in the interval $\tau _{j}$, $j\in \mathbb {Z}_{N}$. Namely, $R_{j,m}^{l}$, $m\in \mathbb {Z}_{k}$ are zeros of $L_{j,k}+L_{j,k+1}$ except for $x_{j-\frac{1}{2}}$, and $R_{j,m}^{r}$, $m\in \mathbb {Z}_{k}$ are zeros of $L_{j,k+1}-L_{j,k}$ except for $x_{j+\frac{1}{2}}$.

Theorem 10

Assume that the conditions of Theorem 8 are satisfied, then for the periodic and mixed boundary conditions, it holds that,

$$\begin{aligned} e_{u,r}\lesssim (1+t)h^{k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega },\quad e_{q,l}\lesssim (1+t)h^{k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega }, \end{aligned}$$

(6.29)

where

$$\begin{aligned} e_{u,r}=\max \limits _{(j,m)\in \mathbb {Z}_{N}\times \mathbb {Z}_{k}}|(u-u_{h})(R_{j,m}^{r},t)|,\quad e_{q,l}=\max \limits _{(j,m)\in \mathbb {Z}_{N}\times \mathbb {Z}_{k}}|(q-q_{h})(R_{j,m}^{l},t)|. \end{aligned}$$

(6.30)

Proof

From the proof of Theorem 8, we know that

$$\begin{aligned} \Vert \eta _{u}(x,t)\Vert _{0,\infty ,\varOmega }\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega },\quad \Vert \eta _{q}(x,t)\Vert _{0,\infty ,\varOmega }\lesssim (1+t)h^{2k+1}\Vert u\Vert _{2k+6,\infty ,\varOmega }. \end{aligned}$$

Thus the desired results can be obtained by the same arguments used in Theorem 4.6 of [11].

6.5 Superconvergence of the Derivative Approximation at Radau Points

This subsection will prove the superconvergence results for the derivative approximation at Radau points.

Theorem 11

Assume that the conditions of Theorem 8 are satisfied. For the periodic and mixed boundary conditions, we have

$$\begin{aligned} {(e_{u,l})_{x}\lesssim (1+t)h^{k+2}\Vert u\Vert _{2k+6,\infty ,\varOmega }}. \end{aligned}$$

(6.31)

Moreover, if $k\ge 2$, we have

$$\begin{aligned} (e_{q,r})_{x}\lesssim (1+t\sqrt{h})h^{k+2}\Vert u\Vert _{k+8,\infty ,\varOmega }. \end{aligned}$$

(6.32)

Here

$$\begin{aligned} (e_{u,l})_{x}=\max \limits _{(j,m)\in \mathbb {Z}_{N}\times \mathbb {Z}_{k}}|(u-u_{h})_{x}(R_{j,m}^{l},t)|,\quad (e_{q,r})_{x}=\max \limits _{(j,m)\in \mathbb {Z}_{N}\times \mathbb {Z}_{k}}|(q-q_{h})_{x}(R_{j,m}^{r},t)|. \end{aligned}$$

Proof

In light of the LDG scheme (3.2), we have

$$\begin{aligned} (q_{h},v)_{j}&=-(u_{h},v_{x})_{j} + u_{h}^{-}v^{*-}|_{j+\frac{1}{2}}-u_{h}^{-}v^{*+}|_{j-\frac{1}{2}}\nonumber \\&=((u_{h})_{x},v)_{j}+(u_{h}^{+}-u_{h}^{-})v^{*+}|_{j-\frac{1}{2}}. \end{aligned}$$

(6.33)

Note that $u_{h}$ can be expressed as

$$\begin{aligned} u_{h}(x,t)=u_{h}(x_{j+\frac{1}{2}}^{-},t) + \sum _{m=1}^{k}\biggl (c_{m}(t)+\text{ i }d_{m}(t)\biggr )\biggl (L_{j,m}(x)-L_{j,m-1}(x)\biggr ), \quad \forall j\in \mathbb {Z}_{N}, \end{aligned}$$

where $c_{m}(t)$, $d_{m}(t)$ are real coefficients. Obviously,

$$\begin{aligned} (u_{h})_{x}(x,t)=\sum _{m=1}^{k}\biggl (c_{m}(t)+\text{ i }d_{m}(t)\biggr )\biggl (L_{j,m}^{'}(x)-L_{j,m-1}^{'}(x)\biggr ). \end{aligned}$$

(6.34)

Define $D_{x}^{-1}q_{h}(x,t)=\int _{x_{j-\frac{1}{2}}}^{x}q_{h}(\hat{x},t)d\hat{x}$, $x\in \tau _{j}$, which implies that $D_{x}^{-1}q_{h}(x,t)\in P^{k+1}(\tau _{j})$. Similarly, let

$$\begin{aligned} D_{x}^{-1}q_{h}(x,t)=D_{x}^{-1}q_{h}(x_{j+\frac{1}{2}}^{-},t)+\sum _{m=1}^{k+1}\biggl (b_{m}(t)+\text{ i }f_{m}(t)\biggr )\biggl (L_{j,m}(x)-L_{j,m-1}(x)\biggr ), \end{aligned}$$

where $b_{m}(t)$, $f_{m}(t)$ are real coefficients. Thus we obtain

$$\begin{aligned} q_{h}(x,t)=\sum _{m=1}^{k+1}\biggl (b_{m}(t)+\text{ i }f_{m}(t)\biggr )\biggl (L_{j,m}^{'}(x)-L_{j,m-1}^{'}(x)\biggr ). \end{aligned}$$

(6.35)

By taking $v=L_{j,m}+L_{j,m-1}$, $m\in \mathbb {Z}_{k}$ in (6.33) and the representations (6.34)–(6.35), we have

$$\begin{aligned} b_{m}(t)+\text{ i }f_{m}(t)=c_{m}(t)+\text{ i }d_{m}(t),\quad m=1,2, \cdots ,k. \end{aligned}$$

Here we use the orthogonality of the Legendre polynomials

$$\begin{aligned} \int _{\tau _{j}}(L_{j,m}^{'}-L_{j,m-1}^{'})(L_{j,n}+L_{j,n-1})dx=\left\{ \begin{aligned}&0,\quad m\ne n,\\&2,\quad m=n. \end{aligned} \right. \end{aligned}$$

Then we get the relationship between $(u_{h})_{x}$ and $q_{h}$,

$$\begin{aligned} q_{h}(x,t)=(u_{h})_{x}(x,t)+\biggl (b_{k+1}(t)+\text{ i }f_{k+1}(t)\biggr )\biggl (L_{j,k+1}^{'}(x)-L_{j,k}^{'}(x)\biggr ), \end{aligned}$$

which yields that

$$\begin{aligned} q_{h}(R_{j,m}^{l},t)=(u_{h})_{x}(R_{j,m}^{l},t). \end{aligned}$$

Thus we obtain

$$\begin{aligned} (u-u_{h})_{x}(R_{j,m}^{l},t)=(q-q_{h})(R_{j,m}^{l},t). \end{aligned}$$

By Theorem 10, we can obtain (6.31). With similar arguments, we also have

$$\begin{aligned} (q_{h})_{x}(R_{j,m}^{r},t)=-\text{ i }(u_{h})_{t}(R_{j,m}^{r},t), \end{aligned}$$

which implies that

$$\begin{aligned} (q-q_{h})_{x}(R_{j,m}^{r},t)=-\text{ i }(u-u_{h})_{t}(R_{j,m}^{r},t). \end{aligned}$$

When $k\ge 2$, choose $l=2$ in (6.1) to obtain

$$\begin{aligned} \Vert (\eta _{u})_{t}\Vert _{0,\infty ,\varOmega }\lesssim h^{-\frac{1}{2}}\Vert (\eta _{u})_{t}\Vert _{0,\varOmega }\lesssim (1+t)h^{k+\frac{5}{2}}\Vert u\Vert _{k+8,\infty ,\varOmega }. \end{aligned}$$

Then following the same logic as in Theorem 4.6 of [11], we get

$$\begin{aligned} |(u-u_{h})_{t}(R_{j,m}^{r},t)|\lesssim (1+t\sqrt{h})h^{k+2}\Vert u\Vert _{k+8,\infty ,\varOmega }. \end{aligned}$$

Thus (6.32) follows.

Remark 12

We remark that for another choice of numerical fluxes, namely, $\hat{u}_{h}=u_{h}^{+}$, $\hat{q}_{h}=q_{h}^{-}$, we can also define the corresponding correction functions and obtain all of the superconvergence results we have proved in previous sections. Since all the technical details are identical with the arguments used in the case of fluxes (3.3), we omit them here for the sake of saving space. Thus, we know that all of the superconvergence results are true for the mixed boundary conditions $u_{x}(0,t)=g_{0}(t)$, $u(2\pi ,t)=g_{1}(t)$.

7 Numerical Results

In this section, we provide numerical examples to illustrate our theoretical findings developed in the precious sections. Since the program for testing the examples for $k=1$, 2 is similar to $k = 3$, 4, we just present the results of $k=3$, 4 to save space.

Example 7.1

We consider the following problem

$$\begin{aligned}&\text{ i }u_t+u_{xx}=0, \quad (x,t) \in [0,2\pi ]\times (0,1],\\&u(x,0)= \text{ exp }(2\text{ i }x) + 3\text{ exp }(\text{ i }x), \quad x \in [0,2\pi ], \end{aligned}$$

with the periodic boundary condition, where the exact solution is

$$\begin{aligned} u(x,t)=\text{ exp }(\text{ i }(2x-4t))+3\text{ exp }(\text{ i }(x-t)). \end{aligned}$$

Fig. 1

Error curves for $k=3$ with periodic boundary conditions (left: u, right: q)

Fig. 2

Error curves for $k=4$ with periodic boundary conditions (left: u, right: q)

We use the LDG scheme (3.1)–(3.2) with $k = 3$, 4 to solve the problem, and the time discretization is the ninth order strong-stability preserving (SSP) Runge–Kutta method [13]. We take (3.3) as the choice of numerical fluxes and the initial solution is obtained by the same method as mentioned in Sect. 1. In our experiments, we use piecewise uniform meshes, which are constructed by equally dividing $[0,\frac{3\pi }{4}]$ and $[\frac{3\pi }{4},2\pi ]$ into N / 2 subintervals, $N=4$, 8, $\cdots$, 128. We test our numerical solutions at the final time $t=1$ with time step $\varDelta t = 0.001h_{min}^{2}$ in $k=3$, 4, where $h_{min}=3\pi /2N$ in this case. The relevant error curves are shown in Figs. 1 and 2 with log–log scale.

Fig. 3

Error curves for $k=3$ with mixed boundary conditions (left: u, right: q)

Fig. 4

Error curves for $k=4$ with mixed boundary conditions (left: u, right: q)

From Figs. 1 and 2, we observe that the LDG solution $(u_{h},q_{h})$ is superconvergent to the special interpolation function $(u_{I}^{k},q_{I}^{k})$, with a convergence rate of $(2k+1)$-th order; a $(2k+1)$-th superconvergence rate for the cell average of $u-u_{h}$ and $q-q_{h}$ as well as the domain average of $u-u_{h}$; the error for the domain average of $q-q_{h}$ reaches the machine precision; the average and maximum errors of $u-\hat{u}_{h}$ and $q-\hat{q}_{h}$ is superconvergent with a $(2k+1)$-th order at nodes of the mesh; both the function value error $u-u_{h}$ at right Radau points and its derivative error $(u-u_{h})_{x}$ at interior left Radau points all converge with a rate $(k+2)$-th order, the same rate for $q-q_{h}$ at left Radau points and $(q-q_{h})_{x}$ at interior right Radau points. These results are consistent with our theoretical findings in Theorems 5–11.

Example 7.2

In this example, we consider the model problem with mixed boundary conditions

$$\begin{aligned}&\text{ i }u_t+u_{xx}=0, \quad \quad \quad (x,t)\in [0,2\pi ]\times (0,0.2],\\&u(x,0)= \text{ exp }(3\text{ i }x), \quad x \in [0,2\pi ],\\&u(0,t)=\text{ exp }(-9\text{ i }t), \quad u_{x}(2\pi ,t)=3\text{ i }\text{ exp }(\text{ i }(6\pi -9t)), \quad t \in [0,0.2], \end{aligned}$$

where the exact solution is $u(x,t)=\text{ exp }(\text{ i }(3x-9t))$.

Similarly, the problem is solved by LDG scheme (3.1)–(3.2) with $k = 3$, 4. Time discretization is the fourth order Runge–Kutta method. We use the uniform meshes. The numerical fluxes is taken by (3.3) and the initial solution is obtained by the same method as mentioned in Sect. 1. In order to obtain the accuracy dominated by the spacial discretization, we take the time step $\varDelta t = 0.001h^{2}$ for $k=3$, and $\varDelta t = 0.001h^{3}$ for $k=4$, where $h=2\pi /N$ in this case. The corresponding error curves are shown in Figs. 3 and 4 with log–log scale.

Figures 3 and 4 show that the LDG solutions are superclose to the interpolation functions defined by (4.27), with a $(2k+1)$-th convergence rate; for both u and the auxiliary variable $q=u_{x}$, domain and cell averages are $(2k+1)$-th superconvergent as well as the numerical fluxes at all nodes in the maximal and average norm; both the function value error and derivative approximation at Radau points converge with a rate $(k+2)$-th order. These results are consistent with our theoretical findings in Theorems 5–11.

8 Concluding Remarks

We have developed the superconvergence properties of the LDG method for the one-dimensional linear Schrödinger equation. We build a special interpolation function by constructing a correction function, and prove supercloseness between the interpolation function and the numerical solution in the $L^{2}$ norm, with a order of $2k+1$. We prove the LDG solutions are superconvergent for the numerical fluxes at the nodes, with a convergence rate of $(2k+1)$-th order in the maximal and average norm. We also prove a $(2k+1)$-th order superconvergence rate for the domain and cell averages. Moreover, we find the function value and derivative approximation at the Radau points are superconvergent with a rate of $(k+2)$-th order. All theoretical findings are confirmed by numerical examples.