Vertex-Centered Linearity-Preserving Schemes for Nonlinear Parabolic Problems on Polygonal Grids

Abstract

On arbitrary polygonal grids, a family of vertex-centered finite volume schemes are suggested for the numerical solution of the strongly nonlinear parabolic equations arising in radiation hydrodynamics and magnetohydrodynamics. We define the primary unknowns at the cell vertices and derive the schemes along the linearity-preserving approach. Since we adopt the same cell-centered diffusion coefficients as those in most existing finite volume schemes, it is required to introduce some auxiliary unknowns at the cell centers in the case of nonlinear diffusion coefficients. A second-order positivity-preserving algorithm is then suggested to interpolate these auxiliary unknowns via the primary ones. All the schemes lead to symmetric and positive definite linear systems and their stability can be rigorously analyzed under some standard and weak geometry assumptions. More interesting is that these vertex-centered schemes do not have the so-called numerical heat-barrier issue suffered by many existing cell-centered or hybrid schemes (Lipnikov et al. in J Comput Phys 305:111–126, 2016). Numerical experiments are also presented to show the efficiency and robustness of the schemes in simulating nonlinear parabolic problems.

1 Introduction

We consider the following parabolic equation

$$\begin{aligned} \frac{\partial u}{\partial t}-{\mathrm{div}} (\kappa (u) \nabla u ) =S,\quad \hbox {in}\ \varOmega , \end{aligned}$$

(1)

where $\kappa (u)$ denotes the diffusion coefficient that is possibly a strongly nonlinear function of u, S is the source or sink term and $\varOmega$ is an open bounded connected polygonal domain in ${\mathbb {R}}^2$. For simplicity of exposition, here we only consider the isotropic diffusion, i.e. $\kappa (u)$ is a scalar, and the extension to the case of full diffusion tensor is almost straightforward. Besides, we assume that the above equation is equipped with proper initial and boundary conditions so that the resulting problem is well-posed.

Equations in the form of (1) arise in many applications such as radiation hydrodynamics (RHD), magnetohydrodynamics (MHD), reservoir modeling, and so on. For example, in RHD, (1) is coupled with hydrodynamics that are usually simulated using Lagrange or ALE algorithms, where u stands for temperature or radiation energy. In this case, the diffusion coefficient is closely related to some cell-centered quantities such as density and energy, taking a strongly nonlinear form of $\kappa (u)\varpropto u^{\alpha }$ with $\alpha =5/2$ or 3. Diffusion coefficients in a cell-centered form are natural in these applications. Moreover, the meshes are generally skewed and distorted because of the movements of the fluids and at the same time, a variety of discontinuities, such as multi-materials, shocks and radiation waves, are usually presented. Finite volume discretizations of such systems are very popular among the scientists and engineers due to their nice properties such as simplicity and local conservation. A desirable scheme should be capable of handling all the aforementioned difficulties and possesses good numerical properties as many as possible.

The key ingredient in the numerical solution of (1) through finite volume approach is the discretization of the diffusion operator therein. In recent decades, numerous efforts have been devoted to this topic, which results in a great many diffusion schemes that can be roughly classified as cell-centered schemes, hybrid schemes, mixed schemes, nonlinear positivity-preserving schemes and so on. The reader is referred to [8, 10, 12, 18] for some recent developments. Here we just mention some recent works confined to RHD and MHD. The authors in [23] updated a nonlinear cell-centered scheme [15] to solve a nonlinear heat conduction equation in MHD on moving Voronoi meshes. For non-equilibrium radiation diffusion equations, a moving mesh finite difference method was studied in [35], and two 1D finite point schemes were proposed in [21] where the authors also discussed the extension to 2D rectangular grids. A three-temperature radiation-hydrodynamics code [31] was developed based on a diffusion scheme that is a combination of a nonlinear two-point flux approximation [29] and an efficient nodal interpolation algorithm [14]. A non-overlapping domain decomposition algorithm combined with a linearity-preserving hybrid scheme was studied in [36].

Recently, it has been pointed out in [25] that many existing finite volume schemes for nonlinear parabolic equations, including the mimetic finite difference schemes [4, 6], suffer the so-called heat-barrier issue (addressed in the following section). More explicitly, any schemes based on the harmonic averaging of cell-centered diffusion coefficients will break down when some of these coefficients go to zero or their ratio grows, which results in totally wrong numerical solution profiles in some strongly nonlinear problems such as the propagation of a nonlinear heat wave in a cold media. A new mimetic scheme with a remedy technique, i.e., a staggered discretization of diffusion coefficients, was then suggested in [25] to overcome this problem. A similar work can be found in [17]. Our numerical experiments indicate that all the cell-centered and hybrid linearity-preserving schemes we studied before suffer the same problem. To overcome the heat-barrier issue is among the main motivations of the present work.

In this paper, we keep in our mind the applications of RHD and MHD, and focus on constructing pure vertex-centered schemes for (1), using only the cell-centered diffusion coefficients, a simple and natural choice to couple with Lagrange or ALE hydrodynamics. All the derivations are conducted according to the linearity-preserving criterion, i.e., each step of the derivation is exact in the sense whenever the solution is piecewise linear and the diffusion coefficient is piecewise constant with respect to the mesh. This procedure looks a bit like the famous patch test [22] in finite element method or the consistence condition in some finite volume schemes [10]. Although at the present we do not know whether the linearity-preserving property is sufficient or necessary for the convergence of finite volume schemes, it is a simple tool for us to derive some cell-centered or hybrid schemes [14, 16, 33, 37, 39]. In [34], we suggested a vertex-centered linearity-preserving scheme for linear anisotropic diffusion problems where only the unknowns defined at cell vertices are involved. The construction of this scheme is based on two types of meshes: a primary mesh and its dual counterpart, which is similar to the finite volume element method (FVEM) [2, 7, 24, 27, 41] and DDFV schemes [8, 19]. Actually, this scheme can be viewed as a direct extension of FVEM and it reduces to the lower-order finite volume element scheme on triangular meshes [34]. By comparison, DDFV schemes are not pure vertex-centered ones since they have both cell-centered and vertex-centered unknowns. Here we further develop the idea to construct a family of finite volume schemes for the nonlinear parabolic equations. Both the vertex-centered and cell-centered unknowns are introduced and the cell-centered ones are only required in the evaluation of cell-centered nonlinear diffusion coefficients. By interpolating the cell-centered unknowns via vertex-centered ones, the final schemes become pure vertex-centered. These new schemes have many good numerical properties, for example, they are locally conservative, linearity-preserving, coercive on arbitrary polygonal grids with star-shaped cells, and capable of handing arbitrary discontinuities. Moreover, they have local stencil and always lead to symmetric and positive definite linear systems. Most interesting is that they do not suffer the numerical heat-barrier issue.

To our knowledge, there exists no linear finite volume scheme (leading to linear systems for the linear equations) that preserves solution positivity unconditionally. The present vertex-centered schemes are linear ones, so they may produce negative solutions at cell vertices when the analytic solution is near zero. As far as the application in RHD and MHD is concerned, what really matters is not the positivity of the vertex-centered unknowns, but the positivity of the cell-centered ones. For this purpose, we suggest a second-order algorithm to interpolate the cell-centered unknowns by the vertex-centered ones. On polygonal meshes with star-shaped cells, this interpolation algorithm is a positivity-preserving one, that is, it produces non-negative cell-centered values provided that all the vertex-centered values involved are non-negative. As for the positivity of the vertex-centered unknowns, it is guaranteed by simply truncating the negative values, which is a traditional practice and has also a certain mathematical foundation [26].

The rest part of this paper is organized as follows. In Sect. 2, the numerical heat-barrier issue is addressed by a 1D example. The construction of the new vertex-centered schemes is discussed in Sect. 3 and the stability of the schemes is proved in Sect. 4. A number of numerical experiments are presented in Sect. 5 and some concluding remarks are given in the last section.

2 The Numerical Heat-Barrier Issue

In this section, we employ the 1D problem to illustrate the so-called numerical heat-barrier issue arising in the numerical solution of strongly nonlinear parabolic problems by some existing cell-centered or hybrid finite volume schemes. Consider the following 1D counterpart of (1),

$$\begin{aligned} \frac{\partial u}{\partial t}-\frac{\partial }{\partial x}\left( \kappa (u)\frac{\partial u}{\partial x}\right) =S,\quad (x,t)\in (0, a)\times (0, T], \end{aligned}$$

(2)

where u(0, t), u(a, t) and u(x, 0) are the given Dirichlet boundary data and initial data, respectively.

Let $0=x_0<x_1<\cdots <x_m=a$ be a uniform partition of [0, a] with mesh size $h=x_i-x_{i-1}=a/m$. The partition of [0, T] is also uniform and the mesh size is $\varDelta t=t_n-t_{n-1}=T/N$ where $t_n=n \varDelta t$. Denote by $x_{i-1/2}$ the midpoint or cell center of cell $[x_{i-1},\ x_{i}]$ and F the so-called flux, defined by

$$\begin{aligned} F=-\kappa (u)\frac{\partial u}{\partial x}. \end{aligned}$$

$u_i^n$ and $u_{i-1/2}^n$ are respectively the approximations of u at $(x_i,t_n)$ and $(x_{i-1/2},t_n)$, while $F_i^n$ and $F_{i-1/2}^n$ can be understood in an analogous sense.

2.1 Hybrid and Cell-Centered Schemes

From now on, all the derivation is conducted according to the linearity-preserving criterion. Integrating (2) over the control volume $[x_{i-1},x_i]$, using the backward Euler time-stepping and by the fundamental theorem of calculus, we obtain the following finite volume equation

$$\begin{aligned} \frac{h}{\varDelta t}\left( u_{i-\frac{1}{2}}^{n}-u_{i-\frac{1}{2}}^{n-1}\right) +F_{i,l}^{n}-F_{i-1,r}^{n}=\int _{x_{i-1}}^{x_i}Sdx, \end{aligned}$$

(3)

where $F_{i,l}^{n}$ (resp. $F_{i-1,r}^{n}$) denotes the approximation of F at $x_i$ (resp. $x_{i-1}$) from the left (resp. right) side, given by

$$\begin{aligned} \displaystyle F_{i,l}^{n}=-\frac{2}{h}\kappa \left( u_{i-\frac{1}{2}}^{n}\right) \left( u_{i}^{n}-u_{i-\frac{1}{2}}^{n}\right) ,\quad \displaystyle F_{i-1,r}^{n}=-\frac{2}{h}\kappa \left( u_{i-\frac{1}{2}}^{n}\right) \left( u_{i-\frac{1}{2}}^{n}-u_{i-1}^{n}\right) . \end{aligned}$$

(4)

Usually, it is required that the flux should be continuous at the mesh vertex $x_i$ so that $F_{i,l}^{n}=F_{i,r}^{n}$, which leads to the local conservation equation below

$$\begin{aligned} -\frac{2}{h}\kappa \left( u_{i-\frac{1}{2}}^{n}\right) \left( u_{i}^{n}-u_{i-\frac{1}{2}}^{n}\right) =-\frac{2}{h}\kappa \left( u_{i+\frac{1}{2}}^{n}\right) \left( u_{i+\frac{1}{2}}^{n}-u_{i}^{n}\right) . \end{aligned}$$

(5)

If $u_i^{n}$ and $u_{i-1/2}^{n}$ are all treated as primary unknowns, then (3)–(5) constitute a hybrid scheme for (2), which is the 1D counterpart of some 2D hybrid linearity-preserving schemes, such as those in [6, 28, 37, 39].

If only the cell-centered unknowns $u_{i-1/2}^{n}(1\le i \le m)$ are treated as primary unknowns, then by eliminating the vertex-centered unknowns from (4) and (5) we get

$$\begin{aligned} \displaystyle F_{i,l}^{n}=-\frac{1}{h}\kappa _i^{n}\left( u_{i+\frac{1}{2}}^{n}-u_{i-\frac{1}{2}}^{n}\right) ,\quad \displaystyle F_{i-1,r}^{n}=-\frac{1}{h}\kappa _{i-1}^{n}\left( u_{i-\frac{1}{2}}^{n}-u_{i-\frac{3}{2}}^{n}\right) , \end{aligned}$$

(6)

where

$$\begin{aligned} \kappa _i^{n}=\frac{2\kappa (u_{i-\frac{1}{2}}^{n})\kappa (u_{i+\frac{1}{2}}^{n})}{\kappa (u_{i-\frac{1}{2}}^{n})+\kappa (u_{i+\frac{1}{2}}^{n})},\quad 1\le i\le m-1. \end{aligned}$$

(7)

Substituting (6) into (3) yields a cell-centered finite volume scheme. Some existing 2D cell-centered schemes, such as those in [1, 5, 14, 16, 20, 33], reduce to this scheme on uniform square meshes.

2.2 A Vertex-Centered Scheme

In this approach, only vertex-centered unknowns $u_{i}^{n}(1\le i \le m-1)$ are treated as primary unknowns. Recall that the flux is assumed to be continuous over the whole domain. By choosing $[x_{i-1/2},x_{i+1/2}]$ to be the control volume and following the same derivation of (3), we have

$$\begin{aligned} \frac{h}{\varDelta t}\left( u_{i}^{n}-u_{i}^{n-1}\right) +F_{i+\frac{1}{2}}^{n}-F_{i-\frac{1}{2}}^{n}=\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}Sdx, \end{aligned}$$

(8)

where $F_{i\pm 1/2}^{n}$ denote the approximations of F at the cell centers $x_{i\pm 1/2}$. Note that both the solution and the diffusion coefficient are usually assumed to be smooth inside each cell $[x_{i-1},x_i]$. Thus, we directly obtain

$$\begin{aligned} \displaystyle F_{i+\frac{1}{2}}^{n}=-\frac{1}{h}\kappa \left( u_{i+\frac{1}{2}}^{n}\right) \left( u_{i+1}^{n}-u_{i}^{n}\right) ,\quad \displaystyle F_{i-\frac{1}{2}}^{n}=-\frac{1}{h}\kappa \left( u_{i-\frac{1}{2}}^{n}\right) \left( u_{i}^{n}-u_{i-1}^{n}\right) . \end{aligned}$$

(9)

Here, the cell-centered unknowns $u_{i-1/2}^{n}(1\le i\le m)$ appear only in the evaluation of diffusion coefficients and can be interpolated by the vertex-centered ones via the formula below

$$\begin{aligned} u_{i\pm \frac{1}{2}}^{n}=\frac{1}{2}\left( u_{i\pm 1}^{n}+u_{i}^{n}\right) . \end{aligned}$$

(10)

Substituting (10) and (9) into (8) leads to a classical vertex-centered finite volume scheme.

2.3 A Numerical Example

For (2), let

$$\begin{aligned} a=3,\quad \kappa (u)=u^3, \quad S=0,\quad u(0,t)=\root 3 \of {3c^2t+\epsilon },\quad u(3,t)=\root 3 \of {\epsilon },\quad u(x,0)=\root 3 \of {\epsilon }, \end{aligned}$$

(11)

where c and $\epsilon$ are two positive parameters. When $\epsilon =0$, (2) has the following analytic solution

$$\begin{aligned} u(x,t)=\left\{ \begin{array}{ll} \root 3 \of {3c(ct-x)},&{}\quad x<ct,\\ 0,&{}\quad \hbox {otherwise}. \end{array} \right. \end{aligned}$$

(12)

This example is taken from [25]. Since the hybrid scheme and the cell-centered scheme in Sect. 2.1 are equivalent, we simply use the cell-centered version and at the same time, use also the vertex-centered scheme (8)–(10) for comparison. As done in [25], we choose $c=0.4$, $\epsilon =10^{-9}$, $h=1/30$ and $\varDelta t=0.4h^2$. Obviously, in this case (12) can approximately serve as the exact solution since $\epsilon$ is small.

Fig. 1

Solution profiles at $t=5.0$ (left cell-centered scheme; right vertex-centered scheme)

The profiles of the numerical solution and the approximate analytic solution (12) are depicted in Fig. 1, where we can see that the cell-centered scheme produces a totally wrong solution while the result of the vertex-centered scheme is quite good. The solution profile for the cell-centered scheme indicates that the heat wave seems to be blocked so that it cannot propagate at a right speed. As was already pointed out by some authors [3, 17, 25], the reason for this is due to the harmonic averaging of the cell-centered diffusion coefficients given in (7). More explicitly, we deduce from (7) that

$$\begin{aligned} \kappa _i^{n}\approx 2\kappa \left( u_{i+\frac{1}{2}}^{n}\right) , \quad \hbox {if}\quad \kappa \left( u_{i-\frac{1}{2}}^{n}\right)>> \kappa \left( u_{i+\frac{1}{2}}^{n}\right) >0, \end{aligned}$$

which implies that when one of the two cell-centered diffusion coefficients $\kappa (u_{i- 1/2}^{n})$ and $\kappa (u_{i+ 1/2}^{n})$ goes to zero or their ratio grows large, vertex $x_i$ will act like a barrier preventing the heat conducing from one neighbor cell to the other. As a result, for any cell-centered or hybrid scheme that can reduce to (3) and (6) in 1D case, some special techniques, such as those in [17, 25], have to be employed to overcome this difficult. By comparison, for the vertex-centered scheme (8)–(10), no such harmonic averaging is involved so that it does not suffer the same issue, which indicates that the vertex-centered scheme might provide an alternative solution to the heat-barrier issue. In the following, we shall derive 2D linearity-preserving schemes without any harmonic averaging over the diffusion coefficients.

3 A Family of Vertex-Centered Linearity-Preserving Schemes

3.1 The Meshes and Unknowns

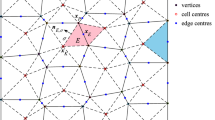
We first partition $\varOmega$ into a number of non-overlapped polygonal cells that constitute the so-called primary mesh, whose cell edges, edge midpoints and cell centers are shown by solid line segments, hollow squares and hollow circles in Fig. 2, respectively. The center of a primary cell can be any point inside the cell. Each primary cell is further partitioned into several quadrilateral subcells by connecting the cell center with the edge midpoints. All subcells sharing a common vertex of the primary mesh form a cell of the dual mesh, which is shown by dashed line segments in Fig. 2. Obviously, the dual mesh makes sense under the following geometric assumption:

(H1):

Every primary cell is star-shaped with respect to its cell center, i.e., any ray that starts from the cell center intersects the cell boundary only once.

At each primary vertex in ${{\overline{\varOmega }}}\setminus \overline{\varGamma }_D$ where $\varGamma _D$ denotes the Dirichlet boundary, we introduce a primary unknown, shown by the solid points in Fig. 2. A finite volume equation will be constructed associated with each primary unknown. For linear problems, there is no need to introduce any auxiliary unknowns. However, for the nonlinear problems, since we plan to use the same cell-centered diffusion coefficients as those in cell-centered or hybrid schemes, we have to introduce some auxiliary unknowns defined at cell centers. To get a pure vertex-centered scheme, these cell-centered unknowns will be interpolated by the vertex-centered ones.

Fig. 2

The primary mesh (solid line) and dual mesh (dashed line)

3.2 The Flux Discretization

Throughout, all the derivations are conducted under the following assumptions:

• 1. The solution and the diffusion coefficient are smooth inside each primary cell and the former is even continuous on the whole domain ${{\overline{\varOmega }}}$. The possible discontinuities of the solution gradient and the diffusion coefficient are only allowed to appear on the edges of the primary mesh.

• 2. The normal component of the flux $\mathbf{F}=-\kappa (u)\nabla u$ is continuous across all interior edges of the primary mesh.

These assumptions are standard and the same as those for the derivation of cell-centered and hybrid finite volume schemes. Note that the first assumption implies the continuity of the normal component of the flux across all interior edges of the dual mesh, which is explicitly maintained in the present vertex-centered schemes. As for the second assumption, it is just involved implicitly and will be discussed later.

To facilitate the exposition, we introduce some notations, some of which are also shown in Fig. 3.

• K, a generic primary cell with $n_K$ edges; its center, measure, diameter (the maximal distance of two arbitrary points in ${\overline{K}}$) and set of edges are denoted as ${\varvec{x}}_K$, |K|, $h_K$ and $\mathcal {E}_K$, respectively.

• $\mathcal {M}$, the set of primary cells in ${{\overline{\varOmega }}}$ with mesh size $h=\max _{K\in \mathcal {M}}h_K$.

• $\sigma$, a generic primary edge of K whose two endpoints, measure and midpoint are denoted as $\mathbf{x}_{\nu }$, ${\varvec{x}}_{\nu ^+}$, $|\sigma |$ and ${\varvec{x}}_{\sigma }$, respectively. In addition, it is always assumed that ${\varvec{x}}_{\nu }$ points anticlockwisely to the other one ${\varvec{x}}_{\nu ^+}$ along $\partial K$. In this context, we sometimes use notation $[\nu ,\nu ^+]$ to replace $\sigma$.

• $K_{\nu }^*$, a generic dual cell associated with primary vertex ${\varvec{x}}_{\nu }$ whose outward unit normal vector along the boundary of the dual cell is denoted as ${\varvec{n}}_{\nu }^*$.

• $\sigma _K^*$, a generic dual edge connecting ${\varvec{x}}_K$ and ${\varvec{x}}_{\sigma }$.

• ${\varvec{n}}_{K,\sigma }^*$, a unit vector normal to $\sigma _K^*$ whose direction is fixed once and for all. Moreover, for simplicity, we assume that all ${\varvec{n}}_{K,\sigma }^*(\sigma \in \mathcal {E}_K)$ inside K are oriented clockwisely.

• $u_{\nu }^{n}, u_{\nu ^+}^{n}, u_K^{n}$, the unknowns defined respectively at ${\varvec{x}}_{\nu }$, ${\varvec{x}}_{\nu ^+}$ and ${\varvec{x}}_{K}$ when $t=t_{n}$.

• $F_{K,\sigma ^*}^{n}$, the approximation of $\int _{\sigma _{K}^*}{\varvec{F}}\cdot {\varvec{n}}_{K,\sigma }^* ds$ on time level $t=t_{n}$.

Generally speaking, each quantity related to the dual mesh is distinguished by a star superscript. Throughout, the hollow letters ${{{\mathbb {A}}}}, {{\mathbb {F}}}, {{\mathbb {U}}}, \cdots$ will be used to denote rectangular matrices with a number of columns greater than one while the bold ones ${\varvec{F}}, {\varvec{x}}, {\varvec{n}},\cdots$ will represent vectors.

Fig. 3

Notations related to a primary cell (left) and a dual cell (right)

The main part of the finite volume discretization of the parabolic equation (1) is to obtain the flux approximation. For this purpose, we first gather all the $n_K$ flux approximations $F_{K,\sigma ^*}^{n}, \sigma \in \mathcal {E}_K$ into a group and manipulate them together. Then, we seek the following local algebraic system

$$\begin{aligned} {\varvec{F}}_K^{n}={{\mathbb {A}}}_K^n \delta {\varvec{U}}_K^{n}, \end{aligned}$$

(13)

where ${{\mathbb {A}}}_K^n$ is the so-called cell matrix of size $n_K\times n_K, {\varvec{F}}_K^{n}=(F_{K,\sigma ^*}^{n} )^T_{\sigma \in \mathcal {E}_K}$ and ${\delta \varvec{U}}_K^{n}=(u_{\nu ^+}^{n}-u_{\nu }^{n})^T_{[\nu ,\nu ^+]\in \mathcal {E}_K}$ are two vectors of size $n_K$, containing all the flux approximations inside K and all the successive differences of the primary unknowns along $\partial K$, respectively. Obviously, once the cell matrix ${{\mathbb {A}}}_K^n$ is specified, all the $n_K$ flux approximations inside K are obtained by (13).

In the linearity-preserving approach, (13) is required to be exact for piecewise affine solutions and piecewise constant diffusion coefficients with respect to the primary mesh. Thus, by setting $u=x, y$ and $\kappa (u)= \kappa (u_K^{n})$ in (13), we have

$$\begin{aligned} \kappa (u_K^{n}){\widetilde{{\mathbb {F}}}}_K={{\mathbb {A}}}_K^n {\mathbb {X}}_K, \end{aligned}$$

(14)

where ${\widetilde{{\mathbb {F}}}}_K$ and ${{\mathbb {X}}}_K$ are two $n_K\times 2$ matrices, given by

$$\begin{aligned} {\widetilde{{\mathbb {F}}}}_K=\left( -|\sigma _K^*|{\varvec{n}}_{K,\sigma }^*\right) ^T_{\sigma \in \mathcal {E}_K},\quad {\mathbb {X}}_K=({\varvec{x}}_{\nu ^+}-{\varvec{x}}_{\nu })^T_{[\nu ,\nu ^+]\in \mathcal {E}_K}. \end{aligned}$$

(15)

If all $n_K\times n_K$ entries of the cell matrix ${{\mathbb {A}}}_K^n$ are treated as unknowns, then (14) provides only $n_K\times 2$ equations. Therefore, the cell matrix ${\mathbb {A}}_K^n$ that satisfies (14) is not unique and different cell matrices may result in different schemes. The key ingredient in the present work is to find a symmetric and positive definite (SPD) matrix ${\mathbb {A}}_K^n$ through an algebraic approach such that (14) is fulfilled.

3.2.1 A Direct Algorithm for ${{\mathbb {A}}}_K^n$

The first algorithm for ${{\mathbb {A}}}_K^n$ is a direct one and was suggested in [34] for the solution of diffusion equations. Here we give a simple description of this algorithm in order to facilitate the exposition of the new and indirect algorithm. Under assumption (H1), we have the identity (see Lemma 3.1 in [34])

$$\begin{aligned} {\widetilde{{\mathbb {F}}}}_K^T{{\mathbb {X}}}_K=|K|{{\mathbb {I}}}_2, \end{aligned}$$

(16)

where ${{\mathbb {I}}}_2$ denotes the $2\times 2$ identity matrix. This formula is actually a variant of some existing geometric identities, see, e.g., (2.17) in [11] or (3.7) in [39]. Multiplying (16) with $\kappa (u_K^{n})/|K|{\widetilde{{\mathbb {F}}}}_K$ yields

$$\begin{aligned} \frac{\kappa (u_K^{n})}{|K|}{\widetilde{{\mathbb {F}}}}_K{\widetilde{{\mathbb {F}}}}_K^T{{\mathbb {X}}}_K=\kappa (u_K^{n}){\widetilde{\mathbb {F}}}_K, \end{aligned}$$

which implies that, if we choose

$$\begin{aligned} {\mathbb {A}}_K^n=\frac{\kappa (u_K^{n})}{|K|} {\widetilde{{\mathbb {F}}}}_K{\widetilde{{\mathbb {F}}}}_K^T, \end{aligned}$$

(14) will be satisfied. However, cell matrix of this type is only semi-positive definite. Motivated by [6, 32, 37], we suggested that a stabilized term should be added so that

$$\begin{aligned} {\mathbb {A}}_K^n=\frac{\kappa (u_K^{n})}{|K|} {\widetilde{{\mathbb {F}}}}_K{\widetilde{{\mathbb {F}}}}_K^T +\gamma _K{\mathbb {C}}_K{\mathbb {C}}_K^T, \end{aligned}$$

(17)

where

$$\begin{aligned} {{\mathbb {C}}}_K={{\mathbb {I}}}_{K}-\frac{1}{|K|} {\widetilde{{\mathbb {F}}}}_K{{\mathbb {X}}}_K^T, \end{aligned}$$

(18)

$\gamma _K$ is a positive parameter and ${{\mathbb {I}}}_{K}$ the $n_K\times n_K$ identity matrix. By (24), the add of the stabilized term does not destroy the linear-preserving property (14).

Theorem 1

(Theorem 3.1 in [34]) The cell matrix ${{\mathbb {A}}}_K^n$, defined by (17) and (18), satisfies (14) and is SPD.

3.2.2 An Indirect Algorithm for ${{\mathbb {A}}}_K^n$

In the indirect algorithm, we obtain ${{\mathbb {A}}}_K^n$ by evaluating its inverse first. Starting from an equivalent version of (16), i.e.,

$$\begin{aligned} {{\mathbb {X}}}_K^T{\widetilde{{\mathbb {F}}}}_K=|K|{{\mathbb {I}}}_2 \end{aligned}$$

(19)

and following the derivation of (17), we get

$$\begin{aligned} \left( {\mathbb {A}}_K^n\right) ^{-1}=\frac{1}{\kappa (u_K^{n})|K|}{ {{\mathbb {X}}}}_K{ {{\mathbb {X}}}}_K^T +{\widehat{\gamma }}_K{{\mathbb {C}}}_K^T{{\mathbb {C}}}_K, \end{aligned}$$

(20)

where ${{\mathbb {C}}}_K$ is defined by (18) and ${\widehat{\gamma }}_K$ denotes a positive parameter.

Theorem 2

The cell matrix ${{\mathbb {A}}}_K^n$, defined by (20) and (18), is SPD and satisfies (14).

Proof

$\left( {\mathbb {A}}_K^n\right) ^{-1}$ is obviously symmetric and semi-positive definite. Suppose that ${\varvec{v}}^T\left( {\mathbb {A}}_K^n\right) ^{-1}{\varvec{v}}$ $=0$ for some $\varvec{v}$. Noticing that ${\widehat{\gamma }}_K>0$ and $\kappa (u_K^n)>0$, we have

$$\begin{aligned} {{\mathbb {X}}}_K^T{\varvec{v}}=\varvec{0}, \quad {{\mathbb {C}}}_K{\varvec{v}}=\left( {{\mathbb {I}}}_{K} -\frac{1}{|K|}{\widetilde{{\mathbb {F}}}}_K{{\mathbb {X}}}_K^T\right) {\varvec{v}}=\varvec{0}, \end{aligned}$$

which leads to $\varvec{v}=\varvec{0}$ and proves that $\left( {\mathbb {A}}_K^n\right) ^{-1}$ (and in turn ${\mathbb {A}}_K^n$) is SPD, here $\varvec{0}$ denotes a generic zero vector. From (18) and (19), we have

$$\begin{aligned} {\mathbb {C}}_K{\widetilde{{\mathbb {F}}}}_K= \left( {{\mathbb {I}}}_{K}-\frac{1}{|K|}{\widetilde{{\mathbb {F}}}}_K{{\mathbb {X}}}_K^T\right) {\widetilde{{\mathbb {F}}}}_K={\widetilde{{\mathbb {F}}}}_K-{\widetilde{{\mathbb {F}}}}_K={\mathbb {O}}. \end{aligned}$$

(21)

It follows from (20) that

$$\begin{aligned} \left( {\mathbb {A}}_K^n\right) ^{-1}{\widetilde{{\mathbb {F}}}}_K=\frac{1}{\kappa (u_K^{n})|K|}{ {{\mathbb {X}}}}_K{ {{\mathbb {X}}}}_K^T{\widetilde{{\mathbb {F}}}}_K= \frac{1}{\kappa (u_K^{n})}{ {{\mathbb {X}}}}_K, \end{aligned}$$

which leads to (14) and completes the proof.

Here we must point out that, generally speaking, algorithms (17) and (20) produce different families of ${\mathbb {A}}_K^n$. Theoretically, we have the following result.

Theorem 3

(17) and (20) generate an identical cell matrix ${\mathbb {A}}_K^n$ if and only if

$$\begin{aligned} {\gamma }_K{\widehat{\gamma }}_K{\mathbb {C}}_K{\mathbb {C}}_K^T{{\mathbb {C}}}_K={{\mathbb {C}}}_K. \end{aligned}$$

(22)

Moreover, a necessary condition for (22) is that all the positive eigenvalues of ${\mathbb {C}}_K^T{{\mathbb {C}}}_K$ are identical and equal to $1/({\gamma }_K{\widehat{\gamma }}_K)$.

Proof

If the undetermined parameters ${\gamma }_K$ and ${\widehat{\gamma }}_K$ can be properly chosen such that (20) is identical to (17), then we have

$$\begin{aligned} \left( \frac{\kappa (u_K^{n})}{|K|}{\widetilde{{\mathbb {F}}}}_K{\widetilde{{\mathbb {F}}}}_K^T+{\gamma }_K{\mathbb {C}}_K{\mathbb {C}}_K^T\right) \left( \frac{1}{\kappa (u_K^{n})|K|}{ {{\mathbb {X}}}}_K{ {{\mathbb {X}}}}_K^T+{\widehat{\gamma }}_K{{\mathbb {C}}}_K^T{{\mathbb {C}}}_K\right) ={{\mathbb {I}}}_K. \end{aligned}$$

(23)

Notice that

$$\begin{aligned} {\mathbb {C}}_K^T{\mathbb {X}}_K=\left( {{\mathbb {I}}}_{K}-\frac{1}{|K|}{{\mathbb {X}}}_K{\widetilde{{\mathbb {F}}}}_K^T\right) {\mathbb {X}}_K={\mathbb {X}}_K-{\mathbb {X}}_K={\mathbb {O}} \end{aligned}$$

(24)

and

$$\begin{aligned} {\mathbb {C}}_K^2=\left( {{\mathbb {I}}}_{K}-\frac{1}{|K|}{\widetilde{{\mathbb {F}}}}_K{{\mathbb {X}}}_K^T\right) {\mathbb {C}}_K={\mathbb {C}}_K. \end{aligned}$$

Then, by (16), (18) and (21), we can simplify (23) to reach (22). Now, let $\lambda _i$ be a positive eigenvalue of ${\mathbb {C}}_K^T{\mathbb {C}}_K$ so that ${\mathbb {C}}_K^T{\mathbb {C}}_K\varvec{\xi }_i=\lambda _i\varvec{\xi }_i$ for some $\varvec{\xi }_i\ne \varvec{0}.$ It follows from (22) that ${\gamma }_K{\widehat{\gamma }}_K\lambda _i {\mathbb {C}}_K\varvec{\xi }_i ={\mathbb {C}}_K\varvec{\xi }_i,$ which implies $\lambda _i=1/({\gamma }_K{\widehat{\gamma }}_K)$ since ${\mathbb {C}}_K \varvec{\xi }_i\ne \varvec{0}$. The proof is complete.

Remark 1

• (i) If K is a triangle cell and its cell center $\varvec{x}_K$ is chosen to be the barycenter, then by straightforward calculations, we find that ${\mathbb {C}}_K$ is a $3\times 3$ matrix with all entries equal to 1 / 3. Thus (22) holds if we choose ${\gamma }_K{\widehat{\gamma }}_K=1$.

• (ii) If K is a polygonal cell, then (22) will generally not hold. For example, suppose that K is a trapezoid with vertices $(0,0), (h,0), (\alpha h, h)$ and (0, h), where $0<\alpha <1$ and $h>0$. The cell center is chosen to be ${\varvec{x}}_K=((1+\alpha )h/4,h/2)$. By straightforward calculations, we have

  $$\begin{aligned} {\mathbb {C}}_K=\frac{1}{2(1+\alpha )}\left( \begin{array}{cccc} 2\alpha &{}\quad 1-\alpha &{}\quad 2\alpha &{}\quad 1-\alpha \\ 0&{}\quad 1+\alpha &{}\quad 0 &{}\quad 1+\alpha \\ 2&{}\quad \alpha -1&{}\quad 2 &{}\quad \alpha -1\\ 0&{}\quad 1+\alpha &{}\quad 0&{}\quad 1+\alpha \end{array} \right) . \end{aligned}$$

  Using Maple software, we find that the four eigenvalues of ${\mathbb {C}}_K^T{\mathbb {C}}_K$ are

  $$\begin{aligned} 0,\ 0,\ 1,\ 1+\frac{2(1-\alpha )^2}{(1+\alpha )^2}. \end{aligned}$$

  By Theorem 1, it is impossible for (17) and (20) to produce an identical cell matrix in this case.

We admit that the indirect algorithm involves some extra computations. However, as a reward, it allows for a simple estimate of the minimal eigenvalue of ${\mathbb {A}}_K^n$, which is required in the stability analysis of the schemes.

3.3 The Finite Volume Equation and the Boundary Discretization

For a vertex ${\varvec{x}}_{\nu }\in {{\overline{\varOmega }}}\setminus \overline{\varGamma }_D$, let $\mathcal{M}_{\nu }$ (resp. $\mathcal {E}_{\nu }$) be the set of primary cells (resp. edges in primary mesh) sharing ${\varvec{x}}_{\nu }$. Integrating (1) over the dual cell ${ K}_\nu ^*$, using the divergence theorem and by the backward Euler time-stepping, we obtain the following finite volume equation

$$\begin{aligned} \left| { K}_\nu ^*\right| \frac{u_{\nu }^{n}-u_{\nu }^{n-1}}{\varDelta t}+\sum _{K\in \mathcal{M}_{\nu }}\sum \limits _{\sigma \in \mathcal {E}_K\cap \mathcal {E}_{\nu }}\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) F_{K,\sigma ^*}^{n}=|{ K}_\nu ^*|S^{n}_K, \end{aligned}$$

(25)

where

$$\begin{aligned} S^{n}_K=\frac{1}{|{ K}_\nu ^*|}\int _{{ K}_\nu ^*} S^n\,\mathrm {d}{\varvec{x}},\quad S^n=S({\varvec{x}}, t_n), \end{aligned}$$

$F_{K,\sigma ^*}^{n}$ is given by (13) and (17) (or (20)). Note that a factor $\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) (=1 \ \hbox {or}\ -1)$ is added to assure the true flux orientation. We mention that any higher order time discretization such as the Crank-Nicolson method can be easily integrated into the above finite volume algorithm.

The discretization of the boundary conditions is the same as the lower-order finite volume element method [24]. Here, we just give a brief description. There are no finite volume equations associated with the vertices on the Dirichlet boundary, and the Dirichlet boundary data are inserted into $\delta {\varvec{U}}_K^{n}$ in the local system (13). By comparison, there is one finite volume equation associated with each vertex on the Neumann boundary. In this case, the dual cell for each vertex on the Neumann boundary has some edges located on the boundary and the Neumann boundary data (or the flux data) are directly integrated into the finite volume equation (25). The discretization of the mixed boundary condition can be considered analogously.

3.4 The Discussion on Local Conservation of the Flux

Since we define a unique flux approximation for a dual cell edge, the local conservation with respect to the dual mesh is always guaranteed. However, for the primary mesh, the conservation of the flux is never touched because we do not require in the present approach the fluxes across the primary cell edges. Actually the new schemes do have a compatible definition of fluxes across primary cell edges that assures the later local conservation. Here we just give a sketch.

Without loss of generality, suppose that $\varvec{x}_{\nu }$ is an interior vertex. Let $n_{\nu }$ denote the number of edges in $\mathcal {E}_{\nu }$ and define

$$\begin{aligned} F_{\sigma }\approx \int _{{\varvec{x}}_{\nu }{\varvec{x}}_{\sigma }}{\varvec{F}}\cdot {\varvec{n}}_{\sigma } ds,\quad \sigma \in \mathcal {E}_{\nu }, \end{aligned}$$

where ${\varvec{n}}_{\sigma }$ is the unit vector normal to $\sigma$ and oriented anticlockwisely with respect to $\varvec{x}_{\nu }$. Similar to (25), we can easily establish a finite volume equation on each subcell sharing ${\varvec{x}}_{\nu }$, leading to $n_{\nu }$ linear equations for unknowns $F_{\sigma }$ whose coefficient matrix is given by

$$\begin{aligned} \left( \begin{array}{ccccc} -1&{}\quad 1&{}\quad 0&{}\quad \cdots &{}\quad 0\\ 0&{}\quad -1&{}\quad 1&{}\quad \cdots &{}\quad 0\\ \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad \cdots \\ 1&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad -1 \end{array} \right) \quad \end{aligned}$$

Obviously, the summation of these $n_{\nu }$ equations yields (25) and only $n_{\nu }-1$ of them are linearly independent so that we need one more equation.

For a primary cell $K\in {\mathcal{M}}_{\nu }$, we can compute a discrete gradient $\nabla _K u$ from all the fluxes $F_{K,\sigma ^*}^{n}$(viewed as known quantities) through a least squares approach. From this discrete gradient, we obtain flux approximations across the edge of K, given by

$$\begin{aligned} F_{K,\sigma }=\left| \varvec{x}_{\nu }\varvec{x}_{\sigma }\right| (-\varLambda _K\nabla _K u)\cdot {\varvec{n}}_{\sigma },\quad \sigma \in \mathcal {E}_{\nu }\cap \mathcal {E}_K,\quad K\in \mathcal{M}_{\nu }. \end{aligned}$$

Using a least squares approach once again, we obtain the following equation

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}_{\nu }}F_{\sigma }=\frac{1}{2}\sum _{K\in \mathcal{M}_{\nu }}\sum _{\sigma \in \mathcal {E}_K\cap \mathcal {E}_{\nu }}F_{K,\sigma }. \end{aligned}$$

(26)

Replacing any of the $n_{\nu }$ equations derived in the first step with the above equation, we obtain $n_{\nu }$ linearly independent equations, by which $F_{\sigma }(\sigma \in \mathcal {E}_{\nu })$ can be uniquely determined. It is easy to see that the above algorithm is compatible with (25) and the fluxes defined on dual cell edges.

3.5 The Interpolation of the Cell-Centered Unknowns

From the previous discussion, we can see that the cell-centered unknowns $u_K^{n}$ appear in the evaluation of diffusion coefficients for nonlinear parabolic problems. In order to get a pure vertex-centered scheme, they must be evaluated via the vertex-centered ones. Since the solution and the diffusion coefficient are assumed to be smooth inside each primary cell, we have many choices to design a second-order interpolation algorithm, such as the least squares interpolation [9] and the first-order Taylor expansion algorithm [20]. However, these interpolation algorithms are generally not positivity-preserving, which will cause serious problems in some cases such as $\kappa (u)\propto u^{5/2}$. Here we suggest a second-order positivity-preserving algorithm under assumption (H1).

We recall once again that, in the linearity-preserving discretization, the derivation must be exact whenever the diffusion coefficient is piecewise constant and the solution is piecewise linear with respect to the primary mesh. In this context, the steady-state counterpart of (1) reduces to a harmonic equation on each primary mesh cell. Thus, our main idea to design the interpolation algorithm is to solve the harmonic equation on a single primary cell through a finite volume approach.

For simplicity, let the vertices of cell K be denoted as ${\varvec{x}}_i(1\le i\le n_K)$ which are ordered anticlockwisely, see Fig. 4. In addition, denote by $S_i$ the area of triangle $\varvec{x}_K\varvec{x}_i\varvec{x}_{i+1}$. For edge ${\varvec{x}}_i{\varvec{x}}_{i+1}$ of K, under assumption (H1), it is always possible for us to find a certain $j(i)\in \{1,2,\cdots , n_K\}$, such that

$$\begin{aligned} {\varvec{n}}_i:=\mathcal{R}\left( {\varvec{x}}_{i+1}-{\varvec{x}}_i\right) =\alpha _i\left( {\varvec{x}}_{j(i)}-{\varvec{x}}_K\right) +\beta _i \left( {\varvec{x}}_{j(i)+1}-{\varvec{x}}_K\right) \end{aligned}$$

(27)

and

$$\begin{aligned} \alpha _i\ge 0,\quad \beta _i\ge 0, \end{aligned}$$

(28)

Fig. 4

The stencil and notations for the interpolation algorithm

where $\mathcal R$ denotes a rotation operator that rotates a vector clockwise to its normal direction. The geometric meaning of the above algorithm is that the normal vector ${\varvec{n}}_i$ is located between ${\varvec{x}}_{j(i)}-{\varvec{x}}_K$ and ${\varvec{x}}_{j(i)+1}-{\varvec{x}}_K$, see Fig. 4. By direct calculations, we have

$$\begin{aligned} \begin{array}{l} \displaystyle \alpha _i=\frac{{\varvec{n}}_i\cdot \mathcal{R}\left( {\varvec{x}}_{j(i)+1}-{\varvec{x}}_K\right) }{\left( {\varvec{x}}_{j(i)}-{\varvec{x}}_K\right) \cdot \mathcal{R}\left( {\varvec{x}}_{j(i)+1}-{\varvec{x}}_K\right) }=\frac{\left| \varvec{n}_i\right| \left| {\varvec{x}}_{j(i)+1}-{\varvec{x}}_K\right| \sin \theta _{j(i)}^2}{2S_{j(i)}},\\ \displaystyle \beta _i=\frac{{\varvec{n}}_i\cdot \mathcal{R}\left( {\varvec{x}}_{j(i)}-{\varvec{x}}_K\right) }{\left( {\varvec{x}}_{j(i)+1}-{\varvec{x}}_K\right) \cdot \mathcal{R}\left( {\varvec{x}}_{j(i)}-{\varvec{x}}_K\right) }=\frac{\left| \varvec{n}_i\right| \left| {\varvec{x}}_{j(i)}-{\varvec{x}}_K\right| \sin \theta _{j(i)}^1}{2S_{j(i)}}, \end{array} \end{aligned}$$

(29)

where $\theta _{j(i)}^1$(resp. $\theta _{j(i)}^2$) denotes the angle between $\varvec{n}_i$ and $\varvec{x}_{j(i)}-\varvec{x}_K$(resp. $\varvec{x}_{j(i)+1}-\varvec{x}_K$). Obviously,

$$\begin{aligned} \theta _{j(i)}^1\ge 0,\quad \theta _{j(i)+1}^1\ge 0, \quad \theta _{j(i)}^1+\theta _{j(i)}^2=\angle \varvec{x}_{j(i)+1}\varvec{x}_K\varvec{x}_{j(i)}<\pi , \end{aligned}$$

which implies (28). Since $\varvec{n}_i\ne \varvec{0}$, a direct consequence of (28) is

$$\begin{aligned} \alpha _i+\beta _i>0. \end{aligned}$$

(30)

As will be seen clear, (28) and (30) are very important in assuring the positivity-preserving property and second-order accuracy of the interpolation algorithm. It follows from (27) that

$$\begin{aligned} \nabla u\cdot {{\varvec{n}}}_i=\alpha _i\left( u({\varvec{x}}_{j(i)},t)-u({\varvec{x}}_K,t)\right) +\beta _i\left( u({\varvec{x}}_{j(i)+1},t)-u({\varvec{x}}_K,t)\right) +O(h_K^2). \end{aligned}$$

Integrating the harmonic equation $\varDelta u=0$ over K, using the divergence theorem and the above formula, we obtain

$$\begin{aligned} u({\varvec{x}}_K,t)\sum _{i=1}^{n_K}(\alpha _i+\beta _i)= \sum _{i=1}^{n_K}\left( \alpha _iu({\varvec{x}}_{j(i)},t)+ \beta _iu({\varvec{x}}_{j(i)+1},t)\right) {+O(h_K^2)}, \end{aligned}$$

which leads to the following interpolation formula

$$\begin{aligned} u_K^n=\frac{1}{\sum _{i=1}^{n_K}(\alpha _i+\beta _i)} \sum _{i=1}^{n_K}\left( \alpha _iu_{j(i)}^n+\beta _iu_{j(i)+1}^n\right) , \end{aligned}$$

(31)

where $u_l^n(l=j(i),j(i)+1)$ denotes the approximation of u at $({\varvec{x}}_l,t_n)$ and $u_K^n$ the approximation of $u({\varvec{x}}_K,t_n)$. Theoretically, we have the following result.

Theorem 4

Under assumption (H1), the interpolation algorithm (31) is a positivity-preserving one. If it is assumed further that $u\in C^2( K)\cap C^0({\overline{K}})$ and $u_i^n=u({\varvec{x}}_i,t_n)+O(h_K^2)(1\le i\le n_K)$, then (31) has a second-order accuracy.

Proof

For simplicity of exposition, set $\varpi =1 /\sum _{i=1}^{n_K}(\alpha _i+\beta _i)$. From (28) and (30), we have

$$\begin{aligned} 0 \le \varpi {\alpha }_i< 1,\quad 0 \le \varpi {\beta }_i< 1. \end{aligned}$$

(32)

Thus, (31) is a positivity-preserving one, i.e., the fact that $u_{j(i)}^n$ and $u_{j(i)+1}^n$ are all nonnegative guarantees the nonnegativity of $u_K^n$. By Taylor expansion, we have

$$\begin{aligned} u_l^n=u({\varvec{x}}_l,t_n)+O(h_K^2)=u(\varvec{x}_K,t_n)+\nabla u(\varvec{x}_K,t_n)\cdot \left( \varvec{x}_l-\varvec{x}_K\right) +R_l, \end{aligned}$$

where $l=j(i),j(i)+1$ and the remainder $R_l=O(h_K^2)$. It follows from (31) and (27) that

$$\begin{aligned} \begin{array}{ll} \displaystyle u_K^n-u(\varvec{x}_K,t_n)&{}\displaystyle =\varpi \sum _{i=1}^{n_K}\nabla u(\varvec{x}_K,t_n)\cdot \left( {\alpha }_i\left( \varvec{x}_{j(i)}-\varvec{x}_K\right) + {\beta }_i\left( \varvec{x}_{j(i)+1}-\varvec{x}_K\right) \right) \\ &{}\quad \displaystyle +\varpi \sum _{i=1}^{n_K}\left( \alpha _iR_{j(i)}+ {\beta }_iR_{j(i)+1}\right) \\ \ &{} \displaystyle =\varpi \nabla u(\varvec{x}_K,t_n)\cdot \sum _{i=1}^{n_K}\mathcal{R}\left( {\varvec{x}}_{i+1}-{\varvec{x}}_i\right) +\varpi \sum _{i=1}^{n_K}\left( {\alpha }_iR_{j(i)}+ {\beta }_iR_{j(i)+1}\right) \\ \ &{}\displaystyle =\varpi \sum _{i=1}^{n_K}\left( \alpha _iR_{j(i)}+{\beta }_iR_{j(i)+1}\right) . \end{array} \end{aligned}$$

Using (32) once again, we have $u_K^n-u(\varvec{x}_K,t_n)=O(h_K^2)$, which completes the proof.

4 Stability of the Vertex-Centered Schemes

Throughout this section, we shall assume that (1) is imposed with a homogenous Dirichlet boundary condition. The discrete $L^2$ and $H^1$ norms employed in the analysis are defined respectively by

$$\begin{aligned} \Vert u_h^n\Vert _{0,\mathcal {M}} =\left\{ \sum _{{\varvec{x}}_{\nu }\in \overline{\varOmega }}|K_{\nu }^*|\left( u_{\nu }^n\right) ^2\right\} ^{1/2} \end{aligned}$$

(33)

and

$$\begin{aligned} |u_h^n|_{1,\mathcal {M}}=\left\{ \sum _{K\in \mathcal {M}}\sum _{\sigma \in \mathcal {E}_K}(u_{\nu ^+}^n-u_{\nu }^n)^2\right\} ^{1/2} =\left\{ \sum _{K\in \mathcal {M}}\Vert \delta {\varvec{U}}_K^n\Vert ^2\right\} ^{1/2}, \end{aligned}$$

(34)

where $\Vert \cdot \Vert$ denotes the Euclidean vector norm, and $u_h^n$ is the discrete function whose nodal value at primary vertex ${\varvec{x}}_{\nu }$ is $u_{\nu }^n$.

Moreover, in addition to (H1), we introduce the following assumptions.

(H2):

There exists a positive constant $\underline{\alpha }$, independent of mesh size h, such that

$$\begin{aligned} |K|\ge \underline{\alpha } h_K^2, \quad \forall K\in \mathcal {M}. \end{aligned}$$

(35)

(H3):

For the matrix ${{\mathbb {C}}}_K$ defined by (18), there exists a positive constant $\underline{\lambda }$, independent of h, such that

$$\begin{aligned} \Vert {{\mathbb {C}}}^T_K{{\mathbb {C}}}_K {\varvec{v}}\Vert ^2\ge \underline{\lambda } \Vert {{\mathbb {C}}}_K{\varvec{v}}\Vert ^2,\quad \forall K\in \mathcal {M}. \end{aligned}$$

(36)

Here, we remark that (H3) can actually be removed since (H1) implies (H3) with $\underline{\lambda }= 1$. The proofs of such a fact for triangular and quadrilateral grids were given in page 139-140 of [34], while the proof for general polygonal grids involves tedious details and will not be presented here.

Lemma 1

(Discrete Gronwall inequality [42]) Suppose that a nonnegative sequence $\{w_n, n=1, \cdots ,N\}$ satisfies

$$\begin{aligned} w_n\le A+B\varDelta t\sum _{k=1}^{n}w_k,\quad 1\le n\le N, \end{aligned}$$

where $N\varDelta t=T$, A and B are nonnegative constants. Then,

$$\begin{aligned} \max _{1\le n\le N}w_n\le Ae^{2BT}, \end{aligned}$$

where $\varDelta t$ is sufficiently small such that $B\varDelta t\le 1/2$.

Lemma 2

(Lemma 4.1 in [34]) For the two matrices ${{\mathbb {X}}}_K$ and $\widetilde{{\mathbb {F}}}_K$ defined in (15), we have

$$\begin{aligned} \Vert {{\mathbb {X}}}_K{\varvec{v}}\Vert \le \sqrt{n_K}\;h_K\Vert {\varvec{v}}\Vert ,\quad \Vert \widetilde{{\mathbb {F}}}_K{\varvec{v}}\Vert \le \sqrt{n_K}\;h_K\Vert {\varvec{v}}\Vert , \quad \forall {\varvec{v}}\in {{\mathbb {R}}}^2,\quad \forall K\in \mathcal {M}. \end{aligned}$$

(37)

Theorem 5

Assume that $\kappa (u)\ge {\underline{\kappa }}$ and ${{\mathbb {A}}}_K^n$ is defined by (17) or (20). Then, under assumptions (H1), (H2) and (H3), we have

$$\begin{aligned} {\varvec{v}}^T{{\mathbb {A}}}_K^n{\varvec{v}}\ge {{\underline{\varrho }}}_K \Vert {\varvec{v}}\Vert ^2, \quad \forall {\varvec{v}}\in {{\mathbb {R}}}^{n_K}, \quad \forall K\in \mathcal {M}, \end{aligned}$$

(38)

where ${{\underline{\varrho }}}_K$ is a positive constant, independent of h, given by

$$\begin{aligned} {{\underline{\varrho }}}_K=\frac{\gamma _K{\underline{\lambda }}\;{\underline{\alpha }}^2 \;\underline{\kappa }}{n_K(2n_K{\underline{\kappa }}+\gamma _K{\underline{\alpha }}\;{\underline{\lambda }})}, \quad \hbox {for}\ \ (17) \end{aligned}$$

(39)

and

$$\begin{aligned} {{\underline{\varrho }}}_K=\frac{{\underline{\alpha }}^2 \;\underline{\kappa }}{n_K{\underline{\alpha }}+2{{{\widehat{\gamma }}}}_K\;\underline{\kappa }\left( {\underline{\alpha }}^2+n_K^2\right) }, \quad \hbox {for}\ \ (20). \end{aligned}$$

(40)

Proof

(39) was proved in Lemma 4.3 of [34] under assumptions (H1), (H2) and (H3), and what remains is to prove (40). For any ${\varvec{v}}\in {{\mathbb {R}}}^{n_K}$, from (20), we have

$$\begin{aligned} {\varvec{v}}^T\left( {\mathbb {A}}_K^n\right) ^{-1}{\varvec{v}}\displaystyle \le \frac{1}{{\underline{\kappa }}|K|}\Vert {{\mathbb {X}}}^T_K{\varvec{v}} \Vert ^2+{{{\widehat{\gamma }}}}_K\Vert {{\mathbb {C}}}_K{\varvec{v}}\Vert ^2. \end{aligned}$$

(41)

By (15),

$$\begin{aligned} \Vert {{\mathbb {X}}}^T_K{\varvec{v}}\Vert ^2\le \Vert {\varvec{v}}\Vert ^2 \sum _{\sigma \in \mathcal {E}_K}\Vert {\varvec{x}}_{\nu ^+}-{\varvec{x}}_{\nu }\Vert ^2\le n_Kh_K^2\Vert {\varvec{v}}\Vert ^2. \end{aligned}$$

(42)

It follows from (18) and Lemma 2 and that

$$\begin{aligned} \Vert {\mathbb {C}}_K {\varvec{v}}\Vert ^2\le 2\Vert {\varvec{v}}\Vert ^2+\frac{2}{|K|^2}\Vert {\widetilde{{\mathbb {F}}}}_K{\mathbb {X}}_K^T{\varvec{v}}\Vert ^2\le 2\left( 1+\frac{n_K^2h_K^4}{|K|^2}\right) \Vert {\varvec{v}}\Vert ^2. \end{aligned}$$

(43)

Substituting (42) and (43) into (41) and by (H2), we have

$$\begin{aligned} \begin{array}{rl} \displaystyle {\varvec{v}}^T\left( {\mathbb {A}}_K^n\right) ^{-1}{\varvec{v}}\displaystyle &{}\displaystyle \le \frac{n_Kh_K^2}{{\underline{\kappa }}|K|}\Vert {\varvec{v}}\Vert ^2+2{{{\widehat{\gamma }}}}_K\left( 1+\frac{n_K^2h_K^4}{|K|^2}\right) \Vert {\varvec{v}}\Vert ^2\\ &{} \displaystyle \le \left( \frac{n_K}{{\underline{\alpha }}\;{\underline{\kappa }}}+2{{{\widehat{\gamma }}}}_K+\frac{2{{{\widehat{\gamma }}}}_Kn_K^2}{{{\underline{\alpha }}}^2}\right) \Vert {\varvec{v}}\Vert ^2 \end{array} \end{aligned}$$

and in turn we obtain (38) with (40), which concludes the proof.

It is interesting to note from the above argumentation that (H3) is not required in the proof of (40).

Theorem 6

Assume that $\kappa (u)\ge {\underline{\kappa }}$ and (1) is imposed with a homogenous Dirichlet boundary condition. Then, under assumptions (H1), (H2) and (H3), there exists a positive constant C, dependent only on T, such that

$$\begin{aligned} \Vert u_h^{n}\Vert ^2_{0,\mathcal{M}}+\min _{K\in \mathcal{M}} {{\underline{\varrho }}}_K\varDelta t\sum _{n=1}^N|u_h^n|_{1,\mathcal{M}}\le C\left( \Vert u_h^0\Vert _{0,\mathcal{M}}^2+\varDelta t\sum _{n=1}^N\Vert S^n\Vert ^2_{0}\right) , \end{aligned}$$

(44)

where $1\le n\le N$, $\varDelta t\le 1/2$, $\Vert \cdot \Vert _0$ denotes the standard $L^2$ norm and $u_h^0$ is the discrete function that coincides with initial data $u(\varvec{x},0)$ at primary vertices.

Proof

Notice that $u_{\nu }^{n}=0$ if $\varvec{x}_{\nu }\in \partial \varOmega$. Then, multiplying both sides of (25) with $u_{\nu }^{n}$ and summing over all the dual cells, we have

$$\begin{aligned} \begin{array}{l} \displaystyle \sum _{{\varvec{x}}_{\nu }\in {{\overline{\varOmega }}}}\left| { K}_\nu ^*\right| u_{\nu }^{n}\frac{u_{\nu }^{n}-u_{\nu }^{n-1}}{\varDelta t}+\sum _{{\varvec{x}}_{\nu }\in {{\overline{\varOmega }}}}\sum _{K\in \mathcal{M}_{\nu }}\sum \limits _{\sigma \in \mathcal {E}_K\cap \mathcal {E}_{\nu }}\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) u_{\nu }^{n}F_{K,\sigma ^*}^{n}\\ \quad \displaystyle =\sum _{{\varvec{x}}_{\nu }\in {{\overline{\varOmega }}}}|{ K}_\nu ^*|u_{\nu }^{n}S^{n}_K. \end{array} \end{aligned}$$

(45)

For the first term in the left-hand side of (45),

$$\begin{aligned} \begin{array}{rl} \displaystyle \sum _{{\varvec{x}}_{\nu }\in {\overline{\varOmega }}}\left| { K}_\nu ^*\right| u_{\nu }^{n}\frac{u_{\nu }^{n}-u_{\nu }^{n-1}}{\varDelta t}&{}\displaystyle =\frac{1}{2\varDelta t} \sum _{{\varvec{x}}_{\nu }\in {\overline{\varOmega }}}\left| { K}_\nu ^*\right| \left[ \left( u_{\nu }^{n}\right) ^2-\left( u_{\nu }^{n-1}\right) ^2 +\left( u_{\nu }^{n}-u_{\nu }^{n-1}\right) ^2\right] \\ \ &{} \displaystyle \ge \frac{1}{2\varDelta t}\left( \Vert u_h^n\Vert _{0,\mathcal{M}}^2-\Vert u_h^{n-1}\Vert _{0,\mathcal{M}}^2\right) . \end{array} \end{aligned}$$

(46)

For the second term in the left-hand side of (45), by shifting the summation to primary cells, we have

$$\begin{aligned} \begin{array}{rl} \displaystyle \sum _{{\varvec{x}}_{\nu }\in {\overline{\varOmega }}} \sum _{K\in \mathcal{M}_{\nu }}\sum \limits _{\sigma \in \mathcal {E}_K\cap \mathcal {E}_{\nu }}\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) u_{\nu }^n F_{K,\sigma ^*}^n&{}\displaystyle =\sum _{K\in \mathcal {M}} \sum _{\sigma \in \mathcal {E}_K}\left( u_{\nu ^+}^n-u_{\nu }^n\right) F_{K,\sigma ^*}^n\\ &{}\displaystyle =\sum _{K\in \mathcal {M}}\left( \delta {\varvec{U}}_K^n\right) ^T {\varvec{F}}_K^n, \end{array} \end{aligned}$$

where we have used

$$\begin{aligned} \left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) u_{\nu }^n+\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu ^+}^*\right) u_{\nu ^+}^n=\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu ^+}^*\right) \left( u_{\nu ^+}^n-u_{\nu }^n\right) \end{aligned}$$

and $\varvec{n}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu ^+}^*=1$ (see the orientations of the relevant vectors in Fig. 3). It follows from (13), (38) and (34) that

$$\begin{aligned}&\displaystyle \sum _{{\varvec{x}}_{\nu }\in {\overline{\varOmega }}} \sum _{K\in \mathcal{M}_{\nu }}\sum \limits _{\sigma \in \mathcal {E}_K\cap \mathcal {E}_{\nu }}\left( {\varvec{n}}_{K,\sigma }^*\cdot {\varvec{n}}_{\nu }^*\right) u_{\nu }^n F_{K,\sigma ^*}^n =\sum _{K\in \mathcal {M}}\left( \delta {\varvec{U}}_K^n\right) ^T{\mathbb {A}}_K^n\delta {\varvec{U}}^n_K\nonumber \\&\quad \displaystyle \ge \min _{K\in \mathcal{M}} \underline{\varrho }_K|u_h^n|_{1,\mathcal{M}}^2. \end{aligned}$$

(47)

As for the right-hand side of (45), by Cauchy inequality, we have

$$\begin{aligned} \displaystyle \sum _{{\varvec{x}}_{\nu }\in {\overline{\varOmega }}}|{ K}_\nu ^*|u_{\nu }^{n}S^{n}_K&\displaystyle \le \frac{1}{2}\sum _{{\varvec{x}}_{\nu }\in \overline{\varOmega }}|{ K}_\nu ^*|\left( u_{\nu }^{n}\right) ^2+\frac{1}{2}\sum _{{\varvec{x}}_{\nu }\in \overline{\varOmega }}|{ K}_\nu ^*|\left( \frac{1}{|{ K}_\nu ^*|}\int _{K^*_{\nu }}S^nd{\varvec{x}}\right) ^2\nonumber \\&\displaystyle \le \frac{1}{2} \Vert u_h^n\Vert _{0,{\mathcal{M}}}^2+\frac{1}{2}\Vert S^n\Vert _0^2. \end{aligned}$$

(48)

Substituting (46), (47) and (48) into (45) yields

$$\begin{aligned} \frac{1}{\varDelta t}\left( \Vert u_h^n\Vert _{0,\mathcal{M}}^2-\Vert u_h^{n-1}\Vert _{0,\mathcal{M}}^2\right) +2\min _{K\in \mathcal{M}} {{\underline{\varrho }}}_K|u_h^n|_{1,\mathcal{M}}^2 \le \Vert u_h^n\Vert _{0,\mathcal{M}}^2+\Vert S^n\Vert _0^2, \end{aligned}$$

$n=1,2,\cdots , N,$ which implies

$$\begin{aligned} \Vert u_h^n\Vert _{0,\mathcal{M}}^2+2\min _{K\in \mathcal{M}} {\underline{\varrho }}_K\varDelta t\sum _{k=1}^n|u_h^k|_{1,\mathcal{M}}^2 \le \Vert u_h^{0}\Vert _{0,\mathcal{M}}^2+\varDelta t\sum _{n=1}^N\Vert S^n\Vert _0^2+\varDelta t\sum _{k=1}^n\Vert u_h^k\Vert _{0,\mathcal{M}}^2. \end{aligned}$$

(49)

By the discrete Gronwall inequality, we have

$$\begin{aligned} \Vert u_h^n\Vert _{0,\mathcal{M}}^2 \le e^{2T}\left( \Vert u_h^{0}\Vert _{0,\mathcal{M}}^2 +\varDelta t\sum _{n=1}^N\Vert S^n\Vert _0^2\right) , \end{aligned}$$

(50)

where $\varDelta t\le 1/2$. Substituting (50) into the right-hand side of (49) gives (44) and completes the proof.

Based on the above stability result, a first-order error estimate in the discrete $H^1$ norm can be obtained through a discrete functional approach, see, e.g., subsection 6.1 in [38].

5 Numerical Experiments

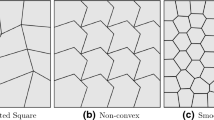
In this section, we shall investigate the numerical performance of the vertex-centered linearity-preserving schemes given by (25). For simplicity, the two schemes with the cell matrix ${\mathbb {A}}_K^n$ given by the direct algorithm (17) and the indirect algorithm (20) will be denoted as VLPS-D and VLPS-I, respectively. The corresponding parameters are chosen as follows:

$$\begin{aligned} \gamma _K=\frac{1}{100}\hbox {trace}\left( \frac{\kappa (u_K^{n})}{|K|}{\widetilde{{\mathbb {F}}}}_K{\widetilde{{\mathbb {F}}}}_K^T\right) ,\quad {\widehat{\gamma }}_K=\hbox {trace}\left( \frac{1}{\kappa (u_K^{n})|K|}{ {{\mathbb {X}}}}_K{ {{\mathbb {X}}}}_K^T\right) . \end{aligned}$$

At the same time, the $Q_1$ finite volume element method ($Q_1$-FVEM) [24] is employed for comparison. Since the numerical behaviors of VLPS-D and VLPS-I are quite similar and the former was thoroughly investigated in [34], we mainly present the results of VLPS-I and $Q_1$-FVEM, and the results of VLPS-D are only given in those cases where $Q_1$-FVEM fails or cannot be readily implemented. All mesh types used in the numerical experiments are shown in Fig. 5. In addition, errors of the schemes are calculated in both discrete $L^2$ and $H^1$ norms, defined respectively by

$$\begin{aligned} E_u(h)=\Vert e_h^n\Vert _{0,\mathcal{M}}, \quad E_q(h)=|e_h^n|_{1,\mathcal{M}}, \end{aligned}$$

where $e_h^n=u({\varvec{x}},t)-u_h^n$. The convergence rates are obtained by the formula

$$\begin{aligned} {\log [E_{\alpha }(h_2)/E_{\alpha }(h_1)]}/{\log (h_2/h_1)}, \end{aligned}$$

where $\alpha =u,q$ and $h_i(i=1,2)$ denote the mesh sizes of the two successive meshes. Throughout, without special mention, the cell center is chosen to be the geometric one whose coordinates are simple averages of those of the cell vertices. Moreover, all computations are performed in double precision, and BICGSTAB is used for solving linear systems with stopping tolerance $1.0E{-}15$, while the possible nonlinear iteration is carried out by the fixed-point method with stopping tolerance $1.0E{-}10$.

Fig. 5

Mesh types used in the numerical experiments. a Triangular mesh, b Kershaw mesh, c locally refined mesh, d random mesh, e skewed mesh and f polygonal mesh

5.1 Linear Elliptic Problem with a Discontinuity

For a finite volume scheme to be used in radiation hydrodynamics, the ability to deal with discontinuities is a fundamental requirement. Here we consider the linear elliptic equation $-\hbox {div}(\kappa \nabla u)=S$ on $\varOmega =[0,1]^2$ with a pure Dirichlet boundary condition. The diffusion coefficient is discontinuous and defined by $\kappa (x,y)=1$ for $x <0.5$ and $\kappa (x,y)=k$ for $x >0.5$, where k is a parameter. The exact solution is chosen to be

$$\begin{aligned} u(x,y)=\left\{ \begin{array}{ll} \displaystyle 1+x+y+(x-0.5)^2e^{x+y},&{}\quad x\le 0.5,\\ \displaystyle \frac{3k-1}{2k}+\frac{x}{k}+y+(x-0.5)^2e^{x+y},&{}\quad x>0.5 \end{array} \right. \end{aligned}$$

and S is determined by u accordingly. We set $k=0.001$ so that the solution gradient has a strongly discontinuity across the vertical line $x=0.5$. Since the mesh lines must be aligned with the discontinuity, we simply test the schemes on the mesh types (a), (b) and (c) in Fig. 5. The results are presented respectively in Tables 1, 2, and 3, where optimal convergence rates, i.e., second-order for the discrete $L^2$ errors and first-order for the discrete $H^1$ errors, can be seen for three schemes. We mention that it was proved in [34] that all vertex-centered linearity-preserving schemes reduce to the $P_1$ finite volume element scheme [24] on triangular meshes, which is confirmed by the identical results of $P_1$-FVEM and VLPS-I in Table 1. Moreover, on mesh type (b), VLPS-I performs a little better than $Q_1$-FVEM, and superconvergence of the discrete $H^1$ error for VLPS-I can be obviously observed. We find that mesh type (b) belongs to the so-called $h^2$-parallelogram meshes whose cells approach parallels as $h\rightarrow 0$. Supperconvergence of the flux usually appears on this type of meshes. In addition, we present at the last rows of Tables 1 and 2 the CPU times, which shows that the computational costs of VLPS-I and $Q_1$-FVEM (resp. $P_1$-FVEM) on quadrilateral meshes (resp. triangular meshes) are almost the same.

Table 1 Results of the schemes on triangular mesh

Table 2 Results of the schemes on Kershaw mesh

Table 3 Results of the schemes on locally refined mesh

5.2 Nonlinear Parabolic Problem

We solve the model problem (1) on $\varOmega =[0,1]^2$. The diffusion coefficient and the exact solution are chosen to be $\kappa (u)=1+u^2$ and $u=e^{-t}\sin (\pi (x+2y)/3)$, respectively. The source function, the Dirichlet boundary data and the initial data are determined accordingly. In this example, we use the three mesh types (d), (e) and (f) in Fig. 5. Here we mention that, some cells in mesh type (d) are concave and the traditional $Q_1$-FVEM fails so that some new method must be explored [13]. Recall that, for the new schemes, the cell center can be any point in a cell provided that (H1) holds. Therefore, when a concave cell in mesh type (d) is not star-shaped with respect to its geometric center, we can assure (H1) simply by shifting the cell center to the midpoint of the diagonal that touches the concave angle. This problem is run up to time $t=1$ with time step $\varDelta t=0.4h^2$. The results are presented in Tables 4, 5, and 6, respectively. One can see that, in each table, all involved schemes achieve optimal convergence rates. Besides, on mesh type (e)(another $h^2$-parallelogram mesh), the results of VLPS-I are a little better than those of $Q_1$-FVEM, and superconvergence of the discrete $H^1$ error is also observed for both schemes.

Table 4 Results of the schemes on random mesh

Table 5 Results of the schemes on shewed mesh

Table 6 Results of the schemes on polygonal mesh

5.3 Radiation Diffusion Problem

We solve (1) on a rectangular domain $\varOmega =(0,3)\times (0,1)$. The diffusion coefficient, the source term, the Dirichlet data and the initial data are the same as those in (11). The left and right boundaries are treated as Dirichlet ones while the top and bottom boundaries are imposed with homogeneous flux boundary conditions. This problem was tested in [25] where the authors claimed that many existing finite volume schemes fail on it. Our numerical experiments show that, if no special treatments are made, all the cell-centered and hybrid schemes we studied before suffer the numerical heat-barrier issue and yield solution profiles similar to the black one in the left figure of Fig. 1.

We first partition the computational domain into random quadrilateral grids. Still, we choose $c=0.4$, $\epsilon =10^{-9}$, $\varDelta t=0.4h^2$ and use (12) as the analytic solution. For VLPS-D, the contour(resp. the solutions versus x-coordinates) on $30\times 10$ grid at time level $t=5$ are shown in the left (resp. right) part of Fig. 6, where we can see that this scheme captures the heat wave quite well and maintains fairly good the 1D nature of the solution. The corresponding figures for VLPS-I are similar and then omitted, while $Q_1$-FVEM fails in this example due to the presence of concave cells. The convergence investigation on a sequence of random quadrilateral meshes is presented in Table 7 where one can see that the convergence rates of the discrete $L^2$ errors are less than 1. The convergence behavior of the new schemes in this problem is similar to that of the new mimetic scheme in [25], where the authors pointed out that the slower convergence rate might be caused by the possible lower-order regularity of the exact solution.

Fig. 6

Results for scheme VLPS-D at $t=5.0$ (left contour and grid; right solutions)

Table 7 Convergence investigation on random meshes at $t=5.0$

5.4 Spherical Nonlinear Heat Wave

Consider a spherically symmetric heat wave, propagating in a cold medium and governed by the following nonlinear parabolic equation

$$\begin{aligned} \rho C_{v}\frac{\partial T}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left( r^2\kappa \frac{\partial T}{\partial r}\right) , \end{aligned}$$

(51)

where T stands for the temperature and depends only on the spherical radius r. Here the thermal conduction coefficient obeys the power-law $\kappa =\kappa _0T^n$, where $\kappa _0$ denotes the thermal conductivity at room temperature and n is a constant. Assume that at time $t=0$ a finite amount of energy $E_0$ is instantaneously released at $r=0$. In this case, the analytic solution is obtained by [40] in terms of the radial position of the wave front $r_f$ and the temperature at the center $T_c$,

$$\begin{aligned} T=T_c\left( 1-\frac{r^2}{r_f^2}\right) ^{1/n},\quad r\le r_f;\quad T=0, \quad \hbox {otherwise}, \end{aligned}$$

(52)

where

$$\begin{aligned} T_c=\left[ \frac{n\xi ^2}{2(3n+2)}\right] ^{1/n}\left[ \frac{\rho C_{v}Q^{2/3}}{\kappa _0t}\right] ^{3/(3n+2)},\quad r_f=\xi \left( \frac{\kappa _0t}{\rho C_{v}}Q^n\right) ^{1/(3n+2)}, \end{aligned}$$

(53)

$\xi$ is a dimensionless constant depending only on n, and T obeys the conservation of energy,

$$\begin{aligned} \int _0^{+\infty } 4\pi r^2 Tdr= \frac{E_0}{\rho C_{v}}=Q. \end{aligned}$$

(54)

Substituting (52) and (53) into (54) and through some direct calculations, we have

$$\begin{aligned} 4\pi \xi ^{(3n+2)/n}\left[ \frac{n}{2(3n+2)}\right] ^{1/n}\int _0^1s^2(1-s^2)^{1/n}ds=1, \end{aligned}$$

where $s=r/r_f$. Noticing that

$$\begin{aligned} 2\int _0^1s^2(1-s^2)^{1/n}ds=B\left( \frac{3}{2}, 1+\frac{1}{n}\right) =\frac{\varGamma (\frac{3}{2})\varGamma (1+\frac{1}{n})}{\varGamma (\frac{5}{2} +\frac{1}{n})}, \end{aligned}$$

one reaches

$$\begin{aligned} \displaystyle \xi =\left( \frac{3n+2}{2^{n-1}n\pi ^n}\right) ^{1/(3n+2)}\left[ \frac{\varGamma (\frac{5}{2}+\frac{1}{n})}{\varGamma (\frac{3}{2})\varGamma (1+\frac{1}{n})}\right] ^{n/(3n+2)}. \end{aligned}$$

(55)

A number of special cases were used as benchmark examples in the literature, some of which are listed below.

• Case 1 [17, 30]: $n=3$, $\rho C_v=\kappa _0=E_0=1.$

• Case 2 [3, 31]: $n=2$, $\rho C_v=\kappa _0=E_0=1.$

Here, we employ Case 2 to test the new vertex-centered schemes. In order to use the present schemes directly we simply turn to solve the model equation (1) on xy-plane with $u=T, \ \kappa (u)=T^2$ and $S=-T/(8t)$. In this case, the solution is still given by (52) with $r=\sqrt{x^2+y^2}$. The computational domain is chosen to be $[0,1]\times [0,1]$ and the point source is placed at its bottom-left corner. The top and right boundaries are treated as homogeneous Dirichlet ones while the left and bottom boundaries are imposed with homogeneous flux boundary data.

Fig. 7

Results for scheme VLPS-I on $10\times 10$ uniform square mesh at $t=0.3$

Fig. 8

Results for scheme VLPS-I on $20\times 20$ uniform square mesh at $t=0.3$

Fig. 9

Results for scheme VLPS-I on $40\times 40$ uniform square mesh at $t=0.3$

A sequence of uniform square meshes are used, which aims to check how the schemes maintain the spherical symmetry of solution on meshes that do not possess the same symmetry. The simulation starts at $t=1.0E{-}8$ and stops at $t=0.3$. Meanwhile, the time step is a variable one, i.e., it takes $4E{-}10\times h^2$ at the beginning and in the following computation it is enlarged (resp. shortened) 20 % if the number of nonlinear iteration is no more than 5 (resp. greater than 20). The results for VLPS-I on $10\times 10$, $20\times 20$ and $40\times 40$ uniform square meshes are shown in Figs. 7, 8, and 9, respectively. The left parts of the figures show the meshes and contours while the right parts are the solution profiles with respect to the spherical radius r. One can see that the new scheme maintains the spherical symmetry quite well. As for the accuracy, the average convergence rate of discrete $L^2$(resp. $H^1$) errors on these sequence of meshes is approximately 1.48 (resp. 0.56). Similar to the previous example, the reason for the lower-order convergence might be the lower-order regularity of the exact solution. The results for $Q_1$-FVEM and VLPS-D are similar and then omitted.

6 Conclusions

We suggest a family of vertex-centered finite volume schemes for the nonlinear parabolic equations arising in RHD and MHD. The primary unknowns are defined at cell vertices and the derivation of the schemes is performed through a linearity-preserving approach. We use the same cell-centered diffusion coefficients as those in most existing cell-centered or hybrid schemes, which is natural in coupling with some standard numerical methods for hydrodynamics such as Lagrange or ALE algorithms. These new schemes are locally conservative, linearity-preserving, coercive on arbitrary polygonal grids with star-shaped cells, and capable of handing arbitrary discontinuities. They also lead to symmetric and positive definite linear systems. Moreover, unlike many existing cell-centered or hybrid schemes that use only cell-centered diffusion coefficients, it does not suffer the so-called numerical heat-barrier issue, which is confirmed by numerical experiments on some standard benchmark models. One drawback of the present schemes is that they are not positivity-preserving so that they may produce negative values at vertices. Moreover, for the two algorithms of the cell matrix, our numerical experiments show that the indirect algorithm seems more robust since the result is not sensitive to the choice of ${\widehat{\gamma }}_K$. The future works include the investigation of supperconvergence and the extensions to two-dimensional $r-z$ meshes and three-dimensional polyhedral meshes.