Exponentially Accurate Spectral Element Method for Fourth Order Elliptic Problems

Abstract

In this paper, a fully non-conforming least-squares spectral element method for fourth order elliptic problems on smooth domains is presented. The proposed method works for a general fourth order elliptic operator with non-homogeneous data in two dimensions and gives exponentially accurate solutions. We derive differentiability estimates and prove our main stability estimate theorem using a non-conforming spectral element method. We then formulate a numerical scheme using a block diagonal preconditioner. Error estimates are also proven for the proposed method. We provide the computational complexity of our method and present results of numerical simulations that have been performed to validate the theory.

1 Introduction

The h–p version of the finite element method (FEM) for elliptic problems was proposed in the mid-80’s by Babuška et al. [3, 4] for solving problems in structural mechanics. The h–p version simultaneously refines the mesh and increases the polynomial degree achieve optimal convergence. The h–p version of spectral element method (SEM) as compared to FEM employ polynomials of higher degree in order to recover the so called spectral/exponential convergence. It is well established that SEM deliver exponential convergence for elliptic problems with smooth solutions and have been successfully implemented to many practical problems [24, 30]. In this paper we describe an efficient and exponentially accurate least-squares spectral element method for fourth order elliptic problems on smooth domains. Such problems include examples of the classical plate bending problem in the theory of elasticity. This type of boundary value problems arise in structural mechanics, materials science and fluid flow.

Several methods have been proposed and analyzed both theoretically and computationally for fourth order elliptic problems in [7, 9, 13, 28, 34–36, 39–42, 44] (and references cited therein) and have been shown to be very effective. In [9], Ben-Artzi et al. presented a fast direct solver for the Dirichlet biharmonic problem in a rectangle based on the capacitance matrix method of [13, 14]. The resulting linear system is solvable in $O(N^2 \log N)$, where N is the number of grid points in each direction. Bernardi et al. [7] presented some spectral approximations of two-dimensional fourth-order problems. Preconditioning of thin solids in structural mechanical problems was analyzed in [28] using $p-$version FEM. It is shown that the method performs well for modelling many real world problems such as skin of an aircraft, laminated fibre plate, microstructure of composite materials etc. These preconditioners are constructed using classical additive Schwarz method which is essentially a generalization of the block Jacobi method to allow for overlapping of the blocks.

In [34], Shen proposed an efficient spectral-Galerkin method for the second and fourth order equations using Legendre polynomials. The two books by Shen and coworkers [35, 36] deal with many important practical aspects of computations using spectral methods and present the recent research in the subject. Zhang et al. [41] developed nearly optimal solvers for the linear algebraic systems for fourth order problems on arbitrary polygonal domains that are partitioned by unstructured grids in the framework of finite element methods. They proved that such a system can be solved in $O(N\log N)$ operations on an unstructured grid of size N. We refer to the work by Meleshko [29] for a comprehensive history and summary of results available for the biharmonic problem in two dimensions. Recently, Yu et al. [39, 40] proposed spectral element method for mixed inhomogeneous boundary value problems of fourth order and also discussed spectral method for fourth-order problems on quadrilaterals.

The least-squares methods are well suited for the numerical solution of partial differential equations. However, the convergence of the least-squares approach in solving biharmonic problems depends on the convergence of fourth order derivatives which is an essential disadvantage in comparison with the conventional Galerkin or weak formulation approach, where only the convergence of the second order derivatives is required for solving biharmonic problems. Secondly, the resulting coefficient matrices are essentially more ill-conditioned as compared to the Galerkin methods. This can be easily circumvented by properly selected preconditioners. On the other hand, the least-squares methods give rise to symmetric, positive definite matrices and does not require numerical integration. Moreover, least-squares approach can be used for solving problems on complicated geometries.

The least squares spectral element method (LSQ-SEM) is a very promising numerical method developed by Proot et al. [32], and Potanza et al. [31] which combine the least squares formulation with the spectral element approximation. LSQ-SEM combines the generality of finite element methods, the accuracy of the spectral methods and the theoretical and computational advantages of the algorithmic design and implementation into a general mathematical framework. LSQ-SEM has been successfully applied to many interesting problems (see [18–21, 25, 31, 32, 37, 38, 43]). However, their implementation to the fourth order problems has been limited so far.

In [18–20, 37, 38], an exponentially accurate h–p spectral element method was proposed for two dimensional elliptic problems on non-smooth domains using parallel computers. The key ingredients were use of auxiliary mappings and geometrical mesh near corners, proposed originally by Babuška et al. [3, 4]. The analysis of LSQ-SEM for Stokes and Navier-Stokes is given in [31, 32]. Recently, an exponentially accurate nonconforming LSQ-SEM for elliptic problems on unbounded domain is presented in [25]. LSQ-SEM solution of the gas-liquid multi-fluid model coupled with the population balance equation is discussed in [43]. A discrete weighted least-squares method for the Poisson and biharmonic problems on circular and annular domains was presented by Zitnan [44] having smooth solutions. The resulting matrices were preconditioned using algebraic polynomials, suitably chosen collocation (matching) points and weight factors. However, the method is not suitable for problems on irregular domains. For a complete survey of spectral element methods and their applications to elliptic boundary value problems we refer to the monograph by Karniadakis et al. [24] which summarizes the recent developments in the subject.

We choose as our solution the spectral element function which minimizes the sum of a squared norm of the residuals in the partial differential equations and the squared norm of the residuals in the boundary conditions in fractional order Sobolev spaces and enforce continuity by adding a term which measures the jump in the function and its derivatives at inter-element boundaries in fractional Sobolev norms, to the functional being minimized. The method we shall describe is a least-squares collocation method and to obtain our approximate solution we solve the normal equations using preconditioned conjugate gradient method (PCGM). The residuals in the normal equations can be obtained without computing and storing mass and stiffness matrices [37, 38]. A preconditioner is defined for the method which is a block diagonal matrix, where each diagonal block corresponds to an element. It is shown in [23] that there exists a new preconditioner which is a diagonal matrix on each element.

We remark here that after obtaining our approximate solution at the Gauss-Lobatto-Legendre points consisting of non-conforming spectral element functions we can make a correction to it so that the corrected solution is conforming and is an exponentially accurate approximation to the true solution in the $H^2$ norm over the whole domain. These corrections are similar to those for second order elliptic problems described in [33, 38]. However, our computational results do not include these corrections. We also emphasize that for simplicity we consider only curvilinear domains although our results have a more general character. The method works for non self-adjoint problems too. Computational results for a non self-adjoint problem with variable coefficients are provided. Throughout this paper, $\Omega$ will denote a curvilinear domain in $\mathbb {R}^{2}$ and $(x_{1},x_{2})$ will denote the standard Cartesian coordinates. We shall also denote the Cartesian coordinates by (x, y).

The organization of this paper is as follows. In Sect. 2, we introduce the problem under consideration. In Sect.  3, we drive differentiability estimates, define the spectral element functions and prove the stability estimate which is the main result of this paper. Numerical scheme and error estimates are provided in Sects. 4 and 5 respectively. Sections 6 is dedicated to computational results for various test problems on with analytic solutions. Concluding remarks and some outlines for future work are provided in Sect. 7.

2 Preliminaries

Let $\Omega$ denote a curvilinear domain in $\mathbb {R}^2$ with smooth boundary. We shall denote the boundary of $\Omega$ by $\partial \Omega$. Consider the fourth order elliptic problem with non-homogeneous Dirichlet boundary conditions

$$\begin{aligned} \mathcal {L}w=\Delta ^{2}\;w&=f\quad \text{ in }\quad \Omega ,\end{aligned}$$

(2.1a)

$$\begin{aligned} w&=\Phi \quad \text{ on }\quad \partial \Omega ,\end{aligned}$$

(2.1b)

$$\begin{aligned} \frac{\partial w}{\partial \nu }&=\Psi \quad \text{ on }\quad \partial \Omega . \end{aligned}$$

(2.1c)

Here, $\nu$ denotes the outward unit normal vector to the boundary $\partial \Omega$. The data f is analytic on $\bar{\Omega }$ and $\Phi$, $\Psi$ are analytic on $\partial \Omega$. The problem (2.1) describes the vibration of a homogeneous non-clamped isotropic plate with constant thickness. The thickness is assumed to be much smaller that the other two dimensions of the plate.

We need to review a set of function spaces. Let $w(x_1,x_2)$ be a smooth function. By $H^m(\Omega )$, we denote the usual Sobolev space of integer order $m\ge 0$ furnished with the norm

$$\begin{aligned} ||w||^2_{H^{m}(\Omega )}=\sum _{|\alpha |\le m}||\partial ^{\alpha }w||^2_{L^{2}(\Omega )} =\mathop {\int \int }_{\Omega } \sum _{|\alpha |\le m}|\partial ^{\alpha } w|^{2}dx_1 dx_2, \end{aligned}$$

where $\alpha =(\alpha _1,\alpha _2), |\alpha |=\alpha _1+\alpha _2, \partial ^{\alpha }w=\partial ^{\alpha _1}_{x_1}\partial ^{\alpha _2}_{x_2}w=w_{x_{1}^{{\alpha }_{1}} x_{2}^{{\alpha }_{2}}}$ is the distributional (weak) derivative of w. As usual $H^{0}(\Omega )=L^{2}(\Omega )$, and

$$\begin{aligned} H^{2}_{0}(\Omega )=\left\{ w\in {L^{2}(\Omega )}: \partial w, \partial ^2 w \in {L^{2}(\Omega )}\,\,\text{ such } \text{ that }\,\, w=0,\frac{\partial w}{\partial \nu }=0 \,\text {on}\, \partial \Omega \right\} . \end{aligned}$$

A seminorm on $H^m(\Omega )$ is given by

$$\begin{aligned} |w|^2_{H^{m}(\Omega )}=\sum _{|\alpha |= m}||\partial ^{\alpha }w||^2_{L^{2}(\Omega )}. \end{aligned}$$

Further, let

$$\begin{aligned} ||w||^{2}_{H^{s}( I)}=\int _{I} w^{2}dx+\int _{I}\int _{I}\frac{|w(x)-w(x^{\prime })|^{2}}{|x-x^{\prime }|^{1+2s}}dxdx^{\prime } \end{aligned}$$

denote the fractional Sobolev norm of order s, where $0< s < 1$. Here, I denotes an interval contained in $\mathbb {R}$.

We now cite a special case of important regularity result Theorem (7.2.2.3) of Grisvard [22].

Theorem 2.1

(Smooth regularity) Let $w\in H^{2}(\Omega )$ be a solution of

$$\begin{aligned} \Delta ^{2}\;w&=f\quad \text{ in }\quad \Omega ,\\ w&=\Phi \quad \text{ on }\quad \partial \Omega ,\\ \frac{\partial w}{\partial \nu }&=\Psi \quad \text{ on }\quad \partial \Omega . \end{aligned}$$

with $f\in H^{k}(\Omega )$, $\Phi \in H^{k+7/2}(\partial \Omega )$ and $\Psi \in H^{k+5/2}(\partial \Omega )$, $k\ge -1$. Then $w\in H^{k+4}(\Omega )$.

Using this it follows that if $f\in L^{2}(\Omega ), \Phi \in H^{\frac{7}{2}}(\partial \Omega )$ and $\Psi \in H^{\frac{5}{2}}(\partial \Omega )$, then the solution w of (2.1) belongs to $H^{4}(\Omega )$.

Theorem 2.2

(Analytic regularity) For a curvilinear domain $\Omega$ with analytic boundary $\partial \Omega$, if the given data $f,\Phi$ and $\Psi$ are analytic then this implies analyticity of w and the following differentiability estimate

$$\begin{aligned} \displaystyle \int _{{\Omega }}\sum _{|\alpha |\le m}\left| \,\partial _x^\alpha w(x)\right| ^2 dx \le C\,(d^m\,m!)^2 \end{aligned}$$

(2.2)

holds for all integers $m\ge 1$. Here, C and d denote positive constants.

Proof

Since the solution w(x) is analytic in an open neighbourhood of $\bar{\Omega }$. Hence, (2.2) follows. $\square$

3 Stability Estimates

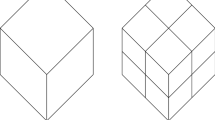
First we divide the domain $\Omega$ into a set of N quadrilaterals $\Omega _1,\Omega _2,\ldots ,\Omega _N$ with smooth sides as shown in Fig. 1. Thus, the boundary $\partial \Omega$ of $\Omega$ is divided into analytic arcs $\bar{\gamma }_{l}, 1\le l\le N$ i.e. $\partial \Omega =\displaystyle {\bigcup _{l\in \mathcal {I}}}\bar{\gamma }_{l}$, where $\mathcal {I}=\{1,2,\ldots ,N\}$. We shall assume that the data f is analytic on $\bar{\Omega }$ and $\Phi ,\Psi$ are analytic on every closed arc $\bar{\gamma }_{l}$ and continuous on $\partial \Omega$. Each of the quadrilaterals $\{\Omega _{l}\}_{l=1,2,\ldots ,N}$ is mapped onto the master square $S=(-1,1)\times (-1,1)$ by a set of analytic maps $\{M_{l}^{-1}\}_{l=1,2,\ldots ,N}$, where $M_{l}$ is from S to $\Omega _{l}$. The map $M_{l}$ is of the form

$$\begin{aligned} x_1=X^{l}(\xi ,\eta ),\quad x_2=Y^{l}(\xi ,\eta ) \end{aligned}$$

with $X^{l}$ and $Y^{l}$ being analytic functions on S. Thus, $M_{l}=(X^{l},Y^{l})$. Let W denote an upper bound on the degree of the approximating polynomial. We shall assume that N is proportional to W. A set of non-conforming spectral element functions which are a sum of tensor products of polynomials in their respective coordinates are defined on the elements in $\Omega$. Let $\Omega _l$ be one of the elements into which $\Omega$ is divided. We now define the spectral element function $u_l$ on $\Omega _l$ by

$$\begin{aligned} u_l(\xi ,\eta )=\sum _{i=0}^{W}\sum _{j=0}^{W}\;\alpha _{i,j}\,\xi ^i\eta ^j\;. \end{aligned}$$

Let $\{\mathcal F_u\}$ denote the spectral element representation of the function u and ${\mathcal S}^{N,W}(\Omega )$ denote the space of spectral element functions $\mathcal F_u$ over the whole domain $\Omega$. To state our main stability theorem we shall define two quadratic forms $\mathcal V^{N,W}\left( \{\mathcal F_u\}\right)$ and $\mathcal U^{N,W}\left( \{\mathcal F_u\}\right)$.

Fig. 1

The domain $\Omega$ and its division into $\Omega _1,\Omega _2,\ldots ,\Omega _N$

Let $\left. {[u]}\right| _{\gamma _{l,i}}$ denote the jump in u across the side $\gamma _{l,i}$. Let the side $\gamma _{l,i}=\gamma _{m,j}$, where $\gamma _{m,j}$ is one of the sides of the element $\Omega _m$. We assume that the side $\gamma _{l,i}$ corresponds to $\xi =1$ and $\gamma _{m,j}$ corresponds to $\xi =-1$. Then, $\left. {[u]}\right| _{\gamma _{l,i}}$ is a function of $\eta$ only. Let $J_{l}(\xi ,\eta )$ is the Jacobian of the mapping $M_{l}$ from S to $\Omega _{l}$ and let $\mathscr {L}_l u_{l}(\xi , \eta ) =\mathcal {L}u_l(M_l(\xi ,\eta ))\sqrt{J_{l}}$. Now we have to approximate

$$\begin{aligned} |\mathcal {L} u_{l}|^{2}_{0,\Omega _{l}}=\int _{\Omega _{l}}\int (\mathcal {L} u_{l})^{2} dx dy. \end{aligned}$$

Hence,

$$\begin{aligned} \int _{\Omega _{l}}\int (\mathcal {L}u_{l})^{2} dx dy=\int _{S}\int (\mathscr {L}_{l}u_{l})^{2} d\xi d\eta . \end{aligned}$$

(3.1)

Let $(\mathscr {L}_{l})^{a}$ denotes a differential operator which is an approximation to $\mathscr {L}_{l}$ in which the coefficients of $\mathscr {L}_{l}$ are replaced by polynomial approximation. Then it is easy to prove that for W large enough

$$\begin{aligned} \sum _{l=l}^{ N} \int _{\Omega _{l}}\int (\mathcal {L}u_{l})^{2} dx dy&=\sum _{l=l}^{ N} \int _{S}\int (\mathscr {L}_{l}u_{l})^{2} d\xi d\eta = \sum _{l=l}^{ N}||\mathscr {L}_{l}u_{l}-(\mathscr {L}_{l})^{a}u_{l}+(\mathscr {L}_{l})^{a}u_{l}||_{0,S}^2,\nonumber \\&\le C\left( \sum _{l=l}^{ N}||(\mathscr {L}_{l})^{a}u_{l}||_{0,S}^2+\sum _{l=l}^{ N}||\mathscr {L}_{l}u_{l}-(\mathscr {L}_{l})^{a}u_{l}||_{0,S}^2\right) ,\nonumber \\&\le C \sum _{l=l}^{ N}\int _{S} \int ((\mathscr {L}_{l})^{a}u_{l})^{2} d\xi d\eta +\varepsilon _{W}\sum _{l=l}^{ N}||u_{l}||^{2}_{4,S}. \end{aligned}$$

(3.2)

Here, C is a constant and $\varepsilon _{W}\rightarrow 0$ as $W\rightarrow \infty$. In fact the rate of the convergence of $\varepsilon _{W}\rightarrow 0$ decays exponentially in W (the rest of the proof is given in Sect. 5). We now define the quadratic form

$$\begin{aligned} {\mathcal V}^{N,W}\left( \{\mathcal F_u\}\right)&=\sum _{l=1}^{N}\mathop {\int _{\Omega _l}}|{\mathcal L} {u}_{l}(x,y)|^{2}dxdy\nonumber \\&\quad \ +\sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }\left( ||[u]||_{0,\gamma _{l,i}}^{2} +\sum _{1\le |\alpha |\le 2}||[(\partial ^{\alpha }{u})]||^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}||[(\partial ^{\alpha }{u})]||^{2}_{1/2,\gamma _{l,i}}\right) \nonumber \\&\quad \ +\sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||{u}_{l}||^{2}_{7/2,\gamma _{s}} +\left| \left| \frac{\partial {u}_{l}}{\partial \nu }\right| \right| ^{2}_{5/2,\gamma _{s}}\right) . \end{aligned}$$

(3.3)

The fractional Sobolev norms used above are as defined in [22].

Since $\gamma _{l,i}$, corresponding to $\xi =1$, is the image of the interval $I=(-1,1)$, in $\eta$ coordinates

$$\begin{aligned} \Vert w\Vert _{\sigma , \gamma _{l,i}}^2 = \Vert w\Vert _{0,I}^2 + \int _I\int _I\frac{\left( w(\eta ) -w(\eta ^{\prime })\right) ^2}{\left( \eta -\eta ^{\prime }\right) ^{1+2\sigma }}d\eta \,d\eta ^{\prime } \end{aligned}$$

(3.4)

for $0< \sigma < 1$. Moreover,

$$\begin{aligned} \Vert w\Vert _{1+\sigma ,\gamma _{l,i}}^2=\Vert w\Vert _{0,I}^2+\left\| \,\frac{\partial w}{\partial \eta } \,\right\| _{\sigma ,I}^2\;. \end{aligned}$$

(3.5)

Next, we define the quadratic form

$$\begin{aligned} \mathcal U^{N,W}(\{\mathcal F_u\})=\sum _{l=1}^{N}\mathop {\int }_{S=(M_l)^{-1}(\Omega _l)} \displaystyle \sum _{0\le |\alpha |\le 4}\left| \,\partial ^\alpha u_l\,\right| ^2\,d\xi d\eta \;. \end{aligned}$$

(3.6)

We now state our main stability estimate theorem.

Theorem 3.1

Consider the fourth order elliptic boundary value problem (2.1). Then

$$\begin{aligned} \mathcal U^{N,W}(\{\mathcal F_u\})\le C(\ln W)^4\mathcal V^{N,W}(\{\mathcal F_u\}). \end{aligned}$$

At the same time there exists a constant K (using trace theorems) such that

$$\begin{aligned} \frac{1}{K}\mathcal V^{N,W}(\{\mathcal F_u\})\le \mathcal U^{N,W}(\{\mathcal F_u\})\le C(\ln W)^4\mathcal V^{N,W}(\{\mathcal F_u\}). \end{aligned}$$

Proof

By Lemma 3.2, there exists $\{\mathcal F_v\}$ such that $w=u+v\in H^{4}(\Omega )$. Using Minkowski’s inequality, we can write the following estimate

$$\begin{aligned} \sum _{l=1}^{N}||{u}_{l}||^{2}_{4,S}&\le C\left( \sum _{l=1}^{N}||{u}_{l}+{v}_{l}||^{2}_{4,S}+\sum _{l=1}^{N}||{v}_{l}||^{2}_{4,S}\right) . \end{aligned}$$

(3.7)

Hence, by regularity result stated in Theorem 2.1, the estimate

$$\begin{aligned} \sum _{l=1}^{N}||{u}_{l}||^{2}_{4,S}\le&C\left( \sum _{l=1}^{N}||\mathcal {L}{u}_{l}||^{2}_{4,\Omega _l}+||w||^{2}_{\frac{7}{2},\partial \Omega }+\left| \left| \frac{\partial w}{\partial \nu } \right| \right| ^{2}_{\frac{5}{2},\partial \Omega }+ \sum _{l=1}^{N}||{v}_{l}||^{2}_{4,\Omega _l}\right) \end{aligned}$$

(3.8)

holds.

Inserting the results from Lemma 3.1 and 3.2 in Eq. (3.8), the desired result follows. $\square$

3.1 Technical Results

Lemma 3.1

Let $\{\mathcal F_u\}\in {\mathcal S}^{N,W}(\Omega )$. Then there exists $\{\mathcal F_v\}$ such that $v_{l}\in H^{4}(S)$, for $l=1,2,\ldots ,N$ and $u+v\in H^{4}(\Omega )$. Moreover, the estimate

$$\begin{aligned}&\sum _{l=1}^{N} ||{v}_{l}||_{4,S}^{2}\\&\quad \ \le C(\ln W)^{4}\sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }\left( ||[u]||_{0,\gamma _{l,i}}^{2} +\sum _{1\le |\alpha |\le 2}||[(\partial ^{\alpha }{u})]||^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}||[(\partial ^{\alpha }{u})]||^{2}_{1/2,\gamma _{l,i}}\right) \\&\qquad \ +\epsilon _{W} \sum _{l=1}^{N}||u_{l}(\xi ,\eta )||^{2}_{4,S} \end{aligned}$$

holds. Here, $\epsilon _{W}$ is exponentially small in W.

Proof

Proof of Lemma 3.1 is very similar to the proof of Lemma 7.1 of [18] and we omit the details. $\square$

Lemma 3.2

Let $w=u+v\in H^{4}(\Omega )$. Here, $\{\mathcal F_u\}\in {\mathcal S}^{N,W}(\Omega )$ and $\{\{{v}_{l}(\xi ,\eta )\}_{l}\}$ is as defined in Lemma 3.1. Then the estimate

$$\begin{aligned}&||w||^{2}_{\frac{7}{2},\partial \Omega }+\left| \left| \frac{\partial w}{\partial \nu } \right| \right| ^{2}_{\frac{5}{2},\partial \Omega }\\&\quad \le C(\ln W)^{4}\left( \sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||u||_{\frac{7}{2},\gamma _{s}} +\left| \left| \frac{\partial u}{\partial \nu }\right| \right| ^{2}_{\frac{5}{2},\gamma _{s}}\right) \right. \\&\qquad \ \left. +\sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }\left( ||[u]||_{0,\gamma _{l,i}}^{2} +\sum _{1\le |\alpha |\le 2}||[(\partial ^{\alpha }{u})]||^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}||[(\partial ^{\alpha }{u})]||^{2}_{1/2,\gamma _{l,i}}\right) \right) \\&\qquad \ +\epsilon _{W}\sum _{l=1}^{N}||u_{l}(\xi ,\eta )||^{2}_{4,S}. \end{aligned}$$

holds. Here, $\epsilon _{W}$ is exponentially small in W.

Proof

By the Lemma 3.1, there exists $\{\mathcal F_v\}$ such that $v_{l}\in H^{4}(S)$, for $l=1,2,\ldots ,N$ and $u+v\in H^{4}(\Omega )$. Using Minkowski’s inequality, the following estimate

$$\begin{aligned} ||w||^{2}_{\frac{7}{2},\partial \Omega }+\left| \left| \frac{\partial w}{\partial \nu } \right| \right| ^{2}_{\frac{5}{2},\partial \Omega }&\le C\sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||u+v||_{\frac{7}{2},\gamma _{s}} +\left| \left| \frac{\partial u}{\partial \nu }+\frac{\partial v}{\partial \nu }\right| \right| ^{2}_{\frac{5}{2},\gamma _{s}}\right) \nonumber \\&\le C\sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||u||_{\frac{7}{2},\gamma _{s}} +\left| \left| \frac{\partial u}{\partial \nu }\right| \right| ^{2}_{\frac{5}{2},\gamma _{s}}+||v||_{\frac{7}{2},\gamma _{s}}+\left| \left| \frac{\partial v}{\partial \nu }\right| \right| ^{2}_{\frac{5}{2},\gamma _{s}}\right) . \end{aligned}$$

(3.9)

holds.

Applying trace theorem, we obtain

$$\begin{aligned} ||w||^{2}_{\frac{7}{2},\partial \Omega }+\left| \left| \frac{\partial w}{\partial \nu } \right| \right| ^{2}_{\frac{5}{2},\partial \Omega }\le C\left( \sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||u||_{\frac{7}{2},\gamma _{s}} +\left| \left| \frac{\partial u}{\partial \nu }\right| \right| ^{2}_{\frac{5}{2},\gamma _{s}}\right) +\sum _{l=1}^{N} ||{v}_{l}||_{4,S}^{2}\right) . \end{aligned}$$

(3.10)

Using the result from Lemma 3.1 in Eq. (3.10), we get the final result. $\square$

4 Numerical Scheme

Let $f_{l}=f(X^l(\xi ,\eta ), Y^l(\xi ,\eta ))$, for $1\le l\le N$. Let $\tilde{f}_l(\xi ,\eta )$ denote the polynomial of degree $2W-1$ in $\xi$ and $\eta$ which is the orthogonal projection of $f_{l}(\xi ,\eta )$ into the space of polynomials of degree $2W-1$ with respect to the usual inner product on $H^4(S)$. Let $\gamma _{l,i}=\gamma _{i}\cap \partial \Omega _{l}$ be the image of $\xi =-1$ under the mapping $M_{l}:S\rightarrow \Omega _{l}$. Let $\Phi (X^l(-1,\eta ),Y^l(-1,\eta )) =\Phi _{l}(\eta )$ and let $\tilde{\Phi }_{l}(\eta )$ denote the orthogonal projection of $\Phi _{l} (\eta )$ into the space of polynomials of degree $2W-1$ in $\eta$ with respect to the usual inner product in $H^{4}(-1,1)$. Let $\Psi (X^l(-1,\eta ),Y^l(-1,\eta ))=\Psi _l(\eta )$ and let $\tilde{\Psi }_{l}(\eta )$ denote the orthogonal projection of $\Psi _{l}(\eta )$ into the space of polynomials of degree $2W-1$ in $\eta$ with respect to the usual inner product in $H^4(-1,1)$. Let $J_l$ denote the Jacobian of the mapping $M_l$ as before. Define

$$\begin{aligned} \tilde{F}_{l}(\xi ,\eta )=\tilde{f}_l(\xi ,\eta )\sqrt{J_l}\quad \text{ and }\quad {\mathscr {L}_l}u_{l}(\xi ,\eta )=\mathcal {L}u_l(M_l(\xi ,\eta ))\sqrt{J_{l}}. \end{aligned}$$

We now define the least-squares functional

$$\begin{aligned} \mathcal {R}^{N,W}\left( \{\mathcal F_u\}\right)&=\sum _{l=1}^{N}||(\mathscr {L}_{l})^{a}{u}_{l} -\tilde{F}_l||_{0,S}^{2}\nonumber \\&\quad \ +\sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega } \left( ||[u]||_{0,\gamma _{l,i}}^{2} +\sum _{1\le |\alpha |\le 2}||[(\partial ^{\alpha }{u})^{a}]||^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}||[(\partial ^{\alpha }{u})^{a}]||^{2}_{1/2,\gamma _{l,i}}\right) \nonumber \\&\quad \ +\sum _{\gamma _{s}\subseteq \partial \Omega }\left( ||{u}_{l}-\tilde{\Phi }_{l}||^{2}_{{7/2},\gamma _{s}} +\left| \left| \left( \frac{\partial {u}_{l}}{\partial \nu }\right) ^{a}-\tilde{\Psi }_{l}\right| \right| ^{2}_{{5/2}, \gamma _{s}}\right) . \end{aligned}$$

(4.1)

Our numerical scheme may now be formulated as

Theorem 4.1

Find $\mathcal F_s\in {\mathcal S}^{N,W}(\Omega )$ which minimizes the functional $\mathcal R^{N,W}(\{\mathcal F_u\})$ over all $\mathcal F_u\in {\mathcal S}^{N,W}(\Omega )$.

This functional $\mathcal {R}^{N,W}\left( \{\mathcal F_u\}\right)$ is closely related to quadratic form in the stability estimate in Theorem 3.1. Using quadratures we can exactly evaluate the functional $\mathcal {R}^{N,W}\left( \{\mathcal F_u\}\right)$. Thus, we find a solution which minimizes the sum of $L^2$ norm of residuals in the partial differential equation and fractional Sobolev norm of the residuals in the boundary conditions and enforce continuity by a adding a term which measures the sum of the squares of the jumps in the function and its derivatives at the inner-element boundaries in appropriates Sobolev norm.

Now

$$\begin{aligned} \mathcal R^{N,W}(U+\epsilon V)=\mathcal R^{N,W}(U)+2\epsilon V^t(SU-TG)+o(\epsilon ^2) \end{aligned}$$

for all V, where U is a vector assembled from the values of $\{(u_{l}(\xi ,\eta ))\}$.

Similarly V is a vector assembled and G is assembled from the data. Here S and T denote matrices. Thus we have to solve $SU-TG=0$.

The method is essentially a least-squares method and the normal equations can be solved using the preconditioned conjugate gradient method (PCGM). To be able to do so we must be able to compute the residuals in the Normal equation inexpensively. Let the normal equations be

$$\begin{aligned} A^TAU=A^TG. \end{aligned}$$

Thus at each iteration of the PCGM we have to compute the action of a matrix on a vector. The feasibility of such a process depends on the ability to compute $A^TAU$ efficiently and inexpensively for any vector U. As in [18–20] it can be shown that $A^TAU$ can be computed inexpensively without computing the mass and stiffness matrices.

However, in addition to this it is imperative that we should be able to construct an effective preconditioner for the matrix $A^TA$ so that the condition number of the preconditioned system is as small as possible. If this can be done then it will be possible to compute $(A^TA)^{-1}G$ efficiently using the PCGM for any vector G.

4.1 Parallelization and Preconditioning

This quadratic form $\mathcal {V}^{N, W}(\{\mathcal F_v\})$ is equivalent to the functional $\mathcal {R}^{N,W} (\{\mathcal F_v\})$ with zero data. Define a quadratic form $\mathscr {U}^{N,W}(\{\mathcal F_v\})$, where

$$\begin{aligned} \mathscr {U}^{N,W}(\{\mathcal F_v\})=\sum _{l=1}^{N}||\check{v}_{l}||^{2}_{H^{4}(S)}. \end{aligned}$$

(4.2)

Here, $\mathscr {U}^{N,W}(\{\mathcal F_v\})$ is the preconditioner for $\mathcal {V}^{N,W}(\{\mathcal F_v\})$. Now, we find the estimate of condition number of the preconditioner $\mathscr {U}^{N,W}(\{\mathcal F_v\})$.

Using Theorem 3.1, the following result holds

$$\begin{aligned} \frac{1}{ C (\log W)^{4}}\mathscr {U}^{N,W}(\{\mathcal F_v\})\le \;\mathcal {V}^{N,W}(\{\mathcal F_v\})\le K \mathscr {U}^{N,W}(\{\mathcal F_v\})\;, \end{aligned}$$

(4.3)

where K is a constant. From (4.3), we observe that the condition number of the preconditioned system is $O({(\log W)^{4}})$. Now $\check{v}_{l}$ is defined in terms of Legendre polynomials in $\xi$ and $\eta$. The form of $\check{v}_{l}$ is

$$\begin{aligned} \check{v}_{l}(\xi ,\eta )=\sum _{i=0}^{W}\sum _{j=0}^{W} a_{i,j} L_{i}( \xi ) L_{j}( \eta ). \end{aligned}$$

(4.4)

The coefficients $a_{i,j}$ are arranged lexicographically in i and j. The detail of the computation of preconditioner is given in [17, 23]. Each element is mapped to a single processor for ease of parallelism. During the PCGM process, communication between neighbouring processors is confined to the interchange of information consisting of the value of function and its derivatives at inter-element boundaries. In addition we need to compute two global scalars to update the approximate solution and the search direction. Hence inter-processor communication is quite small.

5 Error Estimates

In this section we obtain the error estimates for the proposed method. If u is smooth then the proposed method gives spectral accuracy in W, however if u is analytic then the method gives exponential accuracy in W. The optimal rate of convergence with respect to $W_{dof}$, the number of degrees of freedom is also provided.

Let $\{\mathcal F_{z}\}$ minimize $\mathcal R^{N,W}(\{\mathcal F_u\})$ over all $\{\mathcal F_{u}\}\in {\mathcal S}^{N,W}(\Omega )$. We write one more representation for $\{\mathcal F_{z}\}$ as $\{\mathcal F_{z}\}=\left\{ \left\{ z_l(\xi ,\eta )\right\} _{l=1}^{N}\right\}$.

Consider a typical quadrilateral $\Omega _{l}$ into which $\Omega$ is divided. Let

$$\begin{aligned} U_l(\xi ,\eta )=u(M_{l}(\xi ,\eta )), \end{aligned}$$

where the general form of the mapping $M_{l}=(X^{l}(\xi ,\eta ),Y^{l}(\xi ,\eta ))$ from S to $\bar{\Omega }_{l}$ has been defined in [4]. Then the following has been proved in Lemma 5.1 of [4].

Theorem 5.1

(Lemma 5.1 of [4]) If $U_l$ is analytic on $\bar{S}$ then for some constant C and d independent of l and $|\alpha |=m$, $m=1,2,\ldots$, we have

$$\begin{aligned} \left| D^\alpha U_{l}(\xi ,\eta )\right| \le C m! d^m. \end{aligned}$$

Our main theorem on error estimates is now stated.

Theorem 5.2

Let $\{\mathcal F_{z}\}$ minimize $\mathcal R^{N,W}(\{\mathcal F_u\})$ over all $\{\mathcal F_{u}\}\in {\mathcal S}^{N,W}(\Omega )$. Then there exist a constant $C_s$ such that

$$\begin{aligned} \mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le C_{s} W^{-2s+12} \;(\mathbf I ). \end{aligned}$$

(5.1)

Here, $\mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right)$ is as defined in (3.3) and $(\mathbf I )=\displaystyle {\sum _{l=1}^{N}}||U_l||_{s,S}^2$.

Proof

Here, $U_{l}(\xi ,\eta )=u(M_l(\xi ,\eta ))$. Then using the results on approximation theory as in Section 5 of [4] it follows that there exists a polynomial $\phi _{l}(\xi ,\eta )$ of degree W in each variable separately such that

$$\begin{aligned} ||U_l-\phi _l||^{2}_{m,S}\le C_{s} W^{4+2m-2s}||U_l||^{2}_{s,S} \end{aligned}$$

(5.2)

for $0\le m\le 4$ and all $W> s$, where $C_{s}= C e^{2s}$. Hence

$$\begin{aligned} ||U_l-\phi _l||^{2}_{4,S}\le C_{s} W^{-2s+12} ||U_l||^{2}_{s,S}. \end{aligned}$$

(5.3)

Let $\tilde{f}_{l}$ be the polynomial of degree $(2W-1)$ in each variable separately which is the orthogonal projection of $f_{l}$ in $H^{4}(S)$ into the space of polynomials of degree $(2W-1)$. Then

$$\begin{aligned} ||f_l-\tilde{f}_l||^{2}_{0,S}\le C_{t} (2W-1)^{-2t+12} ||U_l||^{2}_{t,S}. \end{aligned}$$

(5.4)

Next, we examine the error committed in the boundary data. Let $\Phi _{l}(\eta )=\Phi (X^{l}(-1,\eta ), Y^{l}(-1,\eta ))$ for $-1\le \eta \le 1$. Let $\tilde{\Phi }_{l}(\eta )$ be the polynomial of degree $(2W-1)$ in each variable separately which is the orthogonal projection of $\Phi _{l}(\eta )$ in $H^{4}(-1,1)$ into the space of polynomials of degree $(2W-1)$. Then we have

$$\begin{aligned} ||\Phi _l-\tilde{\Phi }_l||^{2}_{7/2,\gamma _{s}}\le C_{t} (2W-1)^{-2t+12} ||U_l||^{2}_{t,S} \end{aligned}$$

(5.5)

for $t< 2W-1$.

Let $\Psi _{l}(\eta )=\Psi (X^{l}(-1,\eta ), Y^{l}(-1,\eta ))$ for $0\le \eta \le 1$. Let $\tilde{\Psi }_{l}(\eta )$ be the polynomial of degree $(2W-1)$ in each variable separately which is the orthogonal projection of $\Psi _{l}(\eta )$ in $H^{4}(-1,1)$ into the space of polynomials of degree $(2W-1)$. Then we have

$$\begin{aligned} ||\Psi _{l}-\tilde{\Psi }_{l}||^{2}_{5/2,\gamma _{s}}\le C_{t} (2W-1)^{-2t+12} ||U_l||^{2}_{t,S} \end{aligned}$$

(5.6)

for $t< 2W-1$.

Now consider the set of functions $\{\phi _l(\xi ,\eta )\}$. We wish to show $\mathcal {R}^{N,W}(\{\phi _l(\xi ,\eta )\})$ as defined in (3.3) is exponentially small in W. It remains then to estimate the terms

$$\begin{aligned} \mathcal {R}^{N,W}(\{\mathcal F_{\phi }\})&= \sum _{l=1}^{N}\left| \left| (\mathscr {L}_{l})^a{\phi }_{l}(\xi ,\eta ) -\tilde{f}_l(\xi ,\eta )\right| \right| ^{2}_{0,S}\nonumber \\&\quad \ +\sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }\left( \left| \left| [{\phi }]\right| \right| ^{2}_{0,\gamma _{l,i}} +\sum _{1\le |\alpha |\le 2}\left| \left| [(\partial ^{\alpha }{\phi })^a]\right| \right| ^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}\left| \left| [(\partial ^{\alpha }{\phi })^a]\right| \right| ^{2}_{1/2,\gamma _{l,i}}\right) \nonumber \\&\quad \ +\sum _{\gamma _{s}\subseteq \partial \Omega }\left( \left| \left| (\phi _{l})^a(-1,\eta ) -\tilde{\Phi }_l(\eta )\right| \right| ^{2}_{{7/2},\gamma _{s}}+\left| \left| \left( \frac{\partial {\phi }_{l}}{\partial \varvec{\nu }}\right) ^a(-1,\eta )-\tilde{\Psi }_{l}(\eta )\right| \right| ^{2}_{{5/2},\gamma _{s}}\right) . \end{aligned}$$

(5.7)

Let $\mathscr {L}_{l}$ denote the differential operator with analytic coefficients such that

$$\begin{aligned} \mathop {\int \int }_{\Omega _{l}}\left( \Delta ^2 u(x,y)\right) dxdy=\mathop {\int \int }_{S}(\mathscr {L}_{l} u(\xi ,\eta ))^2 d\xi d\eta , \end{aligned}$$

where

$$\begin{aligned} \mathscr {L}_{l}u(\xi ,\eta )&=\mathcal {A}_{l}u_{\xi \xi \xi \xi }+\mathcal {B}_{l}u_{\xi \xi \xi \eta } +\mathcal {C}_{l}u_{\xi \xi \eta \eta }+\mathcal {D}_{l}u_{\xi \eta \eta \eta }+\mathcal {E}_{l}u_{\eta \eta \eta \eta } +\mathcal {F}_{l}u_{\xi \xi \xi }+\mathcal {G}_{l}u_{\xi \xi \eta }\\&\quad \ +\mathcal {H}_{l}u_{\xi \eta \eta }+\mathcal {I}_{l}u_{\eta \eta \eta }+\mathcal {J}_{l}u_{\xi \xi } +\mathcal {K}_{l}u_{\xi \eta }+\mathbb {L}_{l}u_{\eta \eta }+\mathcal {M}_{l}u_{\xi }+\mathcal {N}_{l}u_{\eta } +\mathcal {O}_{l}u. \end{aligned}$$

We can show as in [4] that there exists constants C and d such that

$$\begin{aligned} |D^{\alpha _{1}}_{\xi }D^{\alpha _{2}}_{\eta }\mathcal {A}_{l}|\le C d^{m} m! \end{aligned}$$

for all $(\xi ,\eta )\in S, |\alpha |\le m$. Similarly, we can estimate all other coefficients of $\mathscr {L}_{l}$. Now,

$$\begin{aligned} (\mathscr {L}_{l})^{a}u(\xi ,\eta )&=(\mathcal {A}_{l})^{a}u_{\xi \xi \xi \xi }+(\mathcal {B}_{l})^{a}u_{\xi \xi \xi \eta } +(\mathcal {C}_{l})^{a}u_{\xi \xi \eta \eta }+(\mathcal {D}_{l})^{a}u_{\xi \eta \eta \eta }+(\mathcal {E}_{l})^{a}u_{\eta \eta \eta \eta }\\&\quad \ +(\mathcal {F}_{l})^{a}u_{\xi \xi \xi } \,{+}\,(\mathcal {G}_{l})^{a}u_{\xi \xi \eta }\,{+}\,(\mathcal {H}_{l})^{a}u_{\xi \eta \eta }\,{+}\,(\mathcal {I}_{l})^{a}u_{\eta \eta \eta } \,{+}\,(\mathcal {J}_{l})^{a}u_{\xi \xi }\,{+}\,(\mathcal {K}_{l})^{a}u_{\xi \eta }\\&\quad \ +(\mathbb {L}_{l})^{a}u_{\eta \eta }+(\mathcal {M}_{l})^{a}u_{\xi }+(\mathcal {N}_{l})^{a}u_{\eta }+(O_{l})^{a}u. \end{aligned}$$

Here, $(\mathcal {A}_{l})^{a}$ is the orthogonal projection of $\mathcal {A}_{l}$ in $H^4(S)$ into the space of polynomials of degree $W-1$. The other coefficients of $(\mathscr {L}_{l})^{a}$ are obtained in a similar way. Therefore,

$$\begin{aligned} |\mathcal {A}_{l}-(\mathcal {A}_{l})^a|\le \sqrt{C_{s}}\;(W-1)^{-s+6}\;(C d^s s!). \end{aligned}$$

Same relation holds for all other coefficients. Now

$$\begin{aligned}&\left| \left| (\mathscr {L}_{l})^a \phi _l-\tilde{f}_{l}\right| \right| ^{2}_{0,S}\\&\quad \le 3\left( \left| \left| \mathscr {L}_{l}U_l-(\mathscr {L}_{l})^a U_l\right| \right| ^{2}_{0,S}+\left| \left| (\mathscr {L}_{l})^a U_l -(\mathscr {L}_{l})^a \phi _l\right| \right| ^{2}_{0,S}+\left| \left| f_l-\tilde{f}_l\right| \right| ^{2}_{0,S} \right) . \end{aligned}$$

Hence,

$$\begin{aligned} ||(\mathscr {L}_{l})^a \phi _l-\tilde{f}_l||^{2}_{0,S}\le C_{s}\;W^{-2s+12}\; ||U_l||^{2}_{s,S}. \end{aligned}$$

Finally, we show how to estimate the jump term (at inter-element boundary)

$$\begin{aligned} \left| \left| [{\phi }]\right| \right| ^{2}_{0,\gamma _{l,i}} +\sum _{1\le |\alpha |\le 2}\left| \left| [(\partial ^{\alpha }{\phi })^a]\right| \right| ^{2}_{0,\gamma _{l,i}} +\sum _{|\alpha |=3}\left| \left| [(\partial ^{\alpha }{\phi })^a]\right| \right| ^{2}_{1/2,\gamma _{l,i}} \end{aligned}$$

for any $\gamma _{l,i}\subseteq \bar{\Omega }{\setminus }\partial \Omega$.

The other boundary terms can be handled in a similar fashion. Clearly, $\gamma _{l,i}$ is a side which is common to $\Omega _{m}$ and $\Omega _{n}$ for some m and n. Let us assume that $\gamma _{l,i}$ is the image of the side $\xi =1$ of the square S under the mapping $M_{m}$ and $\xi =-1$ of the square S under the mapping $M_{n}$. Then

$$\begin{aligned} \left| \left| [\phi ]\right| \right| ^{2}_{0,\gamma _{l,i}}&=\int _{-1}^{1}\left( \phi _{m}(1,\eta )-\phi _{n}(-1,\eta ) \right) ^{2} \; d\eta \le C_{s}\;\left( W^{-2s+12}(Cd^s s!)^{2}\right) . \end{aligned}$$

Now,

$$\begin{aligned} \left| \left| [(\phi )^{a}_{x}]\right| \right| ^{2}_{0,\gamma _{l,i}}= & {} \left| \left| \left( (\phi _{m})_{\xi }(\hat{\xi }_{m})_{x} +(\phi _{m})_{\eta }(\hat{\eta }_{m})_{x}\right) (1,\eta )\right. \right. \\&\left. \left. -\left( (\phi _{n})_{\xi }(\hat{\xi }_{n})_{x} +(\phi _{n})_{\eta }(\hat{\eta }_{n})_{x}\right) (-1,\eta )\right| \right| _{0,(-1,1)}^{2}. \end{aligned}$$

Also,

$$\begin{aligned} (U_{m})_{x}(1,\eta )&=\Big ((U_{m})_{\xi }(\xi _{m})_{x}+(U_{m})_{\eta }(\eta _{m})_{x}\Big )(1,\eta ),\\ (U_{n})_{x}(-1,\eta )&=\Big ((U_{n})_{\xi }(\xi _{n})_{x}+(U_{n})_{\eta }(\eta _{n})_{x}\Big )(-1,\eta ). \end{aligned}$$

Moreover,

$$\begin{aligned} (U_{m})_{x}(1,\eta )=(U_{n})_{x}(-1,\eta ). \end{aligned}$$

Now $(\xi _{m})_{x},(\eta _{m})_{x},(\xi _{m})_{y}$ and $(\eta _{m})_{y}$ are analytic functions of $\xi$ and $\eta$ and satisfy

$$\begin{aligned} |D^{\alpha _{1}}D^{\alpha _{2}}((\xi _{m})_{x})|\le C d^{m} m! \end{aligned}$$

for $(\xi ,\eta )\in S$ and $|\alpha |\le m$. Similar estimates hold for the functions $(\eta _{m})_{x}$, $(\xi _{m})_{y}$ and $(\eta _{m})_{y}$. So we can show

$$\begin{aligned} \left| \left| \left( (\xi _{m})_{x}-(\hat{\xi })_{x}\right) \right| \right| ^{2}_{0,(-1,1)} \le C_{s}\;\left( W^{-2s+12}(C d^{s} s!)^{2}\right) . \end{aligned}$$

Combining all these estimates, we conclude that

$$\begin{aligned} \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{x}]||^{2}_{0,\gamma _{l,i}}\le C_{s}\;\left( W^{-2s+12}\;(\mathbf I )\right) . \end{aligned}$$

Similarly, we can show that

$$\begin{aligned} \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{y}]||^{2}_{0,\gamma _{l,i}}\le C_{s}\;\left( W^{-2s+12}\;(\mathbf I )\right) , \end{aligned}$$

and

$$\begin{aligned} \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }\sum _{|\alpha |=2}\left| \left| [(\partial ^{\alpha }{\phi })^a]\right| \right| ^{2}_{0,\gamma _{l,i}} \le C_{s}\;\left( W^{-2s+12}\;(\mathbf I )\right) . \end{aligned}$$

Finally, we estimate the term $||[(\phi )^{a}_{xxx}]||^{2}_{1/2,\gamma _{l,i}}$. We have

$$\begin{aligned} ||[(\phi )^{a}_{xxx}]||^{2}_{1/2,\gamma _{l,i}}=||(\phi _m)^{a}_{xxx}(1,\eta ) -(\phi _n)^{a}_{xxx}(-1,\eta )||^{2}_{1/2,(-1,1)}, \end{aligned}$$

where

$$\begin{aligned} (\phi _j)^{a}_{xxx}&=(\phi _j)_{\xi \xi \xi }(\hat{\xi }_j)^{3}_{x}+3(\phi _j)_{\xi \xi \eta }(\hat{\xi }_j)^{2}_{x}(\hat{\eta }_j)_{x} +3(\phi _j)_{\xi \eta \eta }(\hat{\xi }_j)_{x}(\hat{\eta }_j)^{2}_{x}+(\phi _j)_{\eta \eta \eta }(\hat{\eta }_j)^{3}_{x} \\&\quad \ +3(\phi _j)_{\xi \xi }(\hat{\xi }_j)_{x}(\hat{\xi }_j)_{xx} +3(\phi _j)_{\xi \eta }((\hat{\xi }_j)_{xx}(\hat{\eta })_{x}+(\hat{\xi }_j)_{x}(\hat{\eta }_j)_{xx}) \\&\quad \ +3(\phi _j)_{\eta \eta }(\hat{\eta }_j)_{x}(\hat{\eta }_j)_{xx}+(\phi _j)_{\xi }(\hat{\xi }_j)_{xxx}+(\phi _j)_{\eta }(\hat{\eta }_j)_{xxx}. \end{aligned}$$

for $j=m,n$. We have

$$\begin{aligned} (U_{m})_{xxx}(1,\eta )&=\left( (U_{m})_{\xi \xi \xi }({\xi }_m)^{3}_{x}+3(U_{m})_{\xi \xi \eta }({\xi }_{m})^{2}_{x}({\eta }_{m})_{x} +3(U_{m})_{\xi \eta \eta }({\xi }_{m})_{x}({\eta }_{m})^{2}_{x}\right. \\&\quad \ +(U_{m})_{\eta \eta \eta }({\eta }_{m})^{3}_{x} +3(U_{m})_{\xi \xi }({\xi }_{m})_{x}({\xi })_{xx}+3(U_{m})_{\xi \eta }(({\xi }_{m})_{xx}({\eta }_{m})_{x}\\&\quad \ +({\xi }_{m})_{x}({\eta }_{m})_{xx}) +3(U_{m})_{\eta \eta }({\eta }_{m})_{x}({\eta }_{m})_{xx}+(U_{m})_{\xi }({\xi }_{m})_{xxx}\\&\quad \ \left. +\,(U_{m})_{\eta }({\eta }_{m})_{xxx}\right) (1,\eta ). \end{aligned}$$

and

$$\begin{aligned} (U_{n})_{xxx}(-1,\eta )&=\left( (U_{n})_{\xi \xi \xi }({\xi }_n)^{3}_{x}+3(U_{n})_{\xi \xi \eta }({\xi }_{n})^{2}_{x} ({\eta }_{n})_{x}+3(U_{n})_{\xi \eta \eta }({\xi }_{n})_{x}({\eta }_{n})^{2}_{x}\right. \\&\quad \ \left. +\,(U_{n})_{\eta \eta \eta }({\eta }_{n})^{3}_{x} +3(U_{n})_{\xi \xi }({\xi }_{n})_{x}({\xi }_{n})_{xx}+3(U_{n})_{\xi \eta }(({\xi }_{n})_{xx}({\eta }_{n})_{x} \right. \\&\quad \ +\,({\xi }_{n})_{x}({\eta }_{n})_{xx})+3(U_{n})_{\eta \eta }({\eta }_{n})_{x}({\eta }_{n})_{xx}+(U_{n})_{\xi }({\xi }_{n})_{xxx}\\&\quad \ \left. +\,(U_{n})_{\eta }({\eta }_{n})_{xxx}\right) (-1,\eta ). \end{aligned}$$

Moreover,

$$\begin{aligned} (U_{m})_{xxx}(1,\eta )=(U_{n})_{xxx}(-1,\eta ) \end{aligned}$$

and

$$\begin{aligned} ||ab||_{1/2,(-1,1)}\le ||a||_{1,\infty ,(-1,1)}||b||_{1/2,(-1,1)}. \end{aligned}$$

Now, $(\xi _m)^{3}_{x}$, $(\xi _m)^{2}_{x} (\eta _m)_{x}$, $(\xi _m)_{x} (\eta _m)^{2}_{x}$, $(\eta _m)^{3}_{x}$, $(\xi _m)_{x}(\xi _m)_{xx}$, $(\eta _m)_{x}(\xi _m)_{xx}$, $(\xi _m)_{x}(\eta _m)_{xx}$, $(\eta _m)_{x}(\eta _m)_{xx}$, $(\xi _m)_{xxx}$ and $(\eta _m)_{xxx}$ are analytic functions of $\xi$ and $\eta$ on S and satisfy

$$\begin{aligned} |D^{\alpha _{1}}_{\xi }D^{\alpha _{2}}_{\eta }((\xi _{m})^{3}_{x})|\le C d^{m} m! \end{aligned}$$

for $(\xi ,\eta )\in S$ and $|\alpha |\le m$. All other terms can be estimated similarly. So we can show that

$$\begin{aligned} \left| \left| (\xi _m)^{3}_{x}-(\hat{\xi }_m)^{3}_{x}\right| \right| ^{2}_{1/2,(-1,1)} \le C_{s} (W^{-2s+12}\;(Cd^{s}s!)^{2}). \end{aligned}$$

Putting all these estimate together we conclude that

$$\begin{aligned} \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{xxx}]||^{2}_{1/2,\gamma _{l,i}}\le C_{s} \; W^{-2s+12}\;(\mathbf I ). \end{aligned}$$

Similarly,

$$\begin{aligned} \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{xxy}]||^{2}_{1/2,\gamma _{l,i}}\le C_{s} \; W^{-2s+12}\;(\mathbf I ),\\ \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{xyy}]||^{2}_{1/2,\gamma _{l,i}}\le C_{s} \; W^{-2s+12}\;(\mathbf I ),\\ \sum _{\gamma _{l,i}\subseteq \overline{\Omega }{\setminus }\partial \Omega }||[(\phi )^{a}_{yyy}]||^{2}_{1/2,\gamma _{l,i}}\le C_{s} \; W^{-2s+12}\;(\mathbf I ). \end{aligned}$$

Hence, we can conclude that

$$\begin{aligned} \mathcal {R}^{N,W}(\{\mathcal F_{\phi }\})\le C_{s} \; W^{-2s+12}\;(\mathbf I ). \end{aligned}$$

Let $\{\mathcal F_{z}\}$ minimizes $\mathcal {R}^{N,W}(\{\mathcal F_{u}\})$ over all $\{\mathcal F_{u}\}\in \mathcal {S}^{N,W}$. Then we have

$$\begin{aligned} \mathcal {R}^{N,W}(\{\mathcal F_{\phi }\})=\mathcal {R}^{N,W}(\{\mathcal F_{z}\})+{\mathcal V}^{N,W}\left( \{\mathcal F_{\phi -z}\}\right) . \end{aligned}$$

Therefore, we conclude that

$$\begin{aligned} {\mathcal V}^{N,W}\left( \{\mathcal F_{\phi -z}\}\right) \le \mathcal {R}^{N,W} (\{\mathcal F_{\phi }\})\le C_{s} \; W^{-2s+12}\;(\mathbf I )\;. \end{aligned}$$

Hence, using stability theorem 3.1, we obtain

$$\begin{aligned} \sum _{l=1}^{N}||\phi _{l}(\xi ,\eta )-z_{l}(\xi ,\eta )||_{4,S}\le \;C_{s} \; W^{-2s+12}\;(\mathbf I )\;. \end{aligned}$$

(5.8)

It is easy to show that

$$\begin{aligned} \sum _{l=1}^{N}||\phi _{l}(\xi ,\eta )-U_{l}(\xi ,\eta )||_{4,S}\le \;C_{s} \; W^{-2s+12}\;(\mathbf I )\;. \end{aligned}$$

(5.9)

Combining the results (5.8) and (5.9), we obtain

$$\begin{aligned} \sum _{l=1}^{N}||U_{l}(\xi ,\eta )-z_{l}(\xi ,\eta )||_{4,S}\le \;C_{s} \; W^{-2s+12}\;(\mathbf I )\;, \end{aligned}$$

(5.10)

which is the desired result. $\square$

Theorem 5.3

Let $\{\mathcal F_{z}\}$ minimize $\mathcal R^{N,W}(\{\mathcal F_u\})$ over all $\{\mathcal F_{u}\}\in {\mathcal S}^{N,W}(\Omega )$. If u is analytic then there exist constants C and b (independent of N) such that

$$\begin{aligned} \mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le Ce^{-bW}. \end{aligned}$$

(5.11)

Here, $\mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right)$ is as defined in (3.3).

Proof

Combining Theorem 5.1 and 5.2, we obtain

$$\begin{aligned} \mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le \;C_{s} \; W^{-2s+12}\;(s! \,d^s)^2\;, \end{aligned}$$

(5.12)

for $W>s$.

Applying Stirling’s formula

$$\begin{aligned} n!\sim \sqrt{2\pi n}\, n^n\, e^{-n} \end{aligned}$$

in Eq. (5.12) and choosing $s=\gamma W$ with $0<\gamma <1$, implies

$$\begin{aligned} \mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le C W^{12} (2\pi \gamma W) (d\gamma )^{2\gamma W}. \end{aligned}$$

Select $\gamma$ so that $(d\gamma )<1$. Then there exists a constant $b>0$ such that the following result holds:

$$\begin{aligned} \mathcal E^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le C e^{-b \,W}. \end{aligned}$$

$\square$

Remark 5.1

After having obtained the non-conforming spectral element solution we can make a correction to it so that the corrected solution is conforming and the error in the $H^2$ norm is exponentially small in W. These corrections are similar to those for second order problems as explained in [33, 37].

Let us now estimate the error in terms of number of degrees of freedom. There are O(1) number of elements in $\Omega$ and each element has $O(W^{2})$ degrees of freedom.

Theorem 5.4

Let $\{\mathcal F_{z}\}$ minimize $\mathcal R^{N,W}(\{\mathcal F_u\})$ over all $\{\mathcal F_{u}\}\in {\mathcal S}^{N,W}(\Omega )$. Then there exist constants C and b (independent of N and W) such that

$$\begin{aligned} \mathcal U^{N,W}\left( \{\mathcal F_{(z-U)}\}\right) \le Ce^{-bW_{dof}^{1/2}}. \end{aligned}$$

(5.13)

Here, $\mathcal U^{N,W}\left( \{\mathcal F_{(z-U)}\}\right)$ is as defined in (5) and $W_{dof}=dim({\mathcal S}^{N,W}(\Omega ))=\#$ degrees of freedom.

6 Numerical Results

Let $u_{approx.}$ be the spectral element solution obtained from the minimization problem and $u_{exact}$ be the exact solution. Then the relative error is defined as

$$\begin{aligned} ||E||_{rel} (\%)=\frac{||u_{approx.}-u_{exact}||_{H^{2}}}{||u_{exact}||_{H^{2}}}\times 100. \end{aligned}$$

The numerical results presented in this Section have been obtained with a FORTRAN90 code. All our computations are carried out using a 372-node HPC cluster which is based on Intel Xeon Quadcore processors with a total of 2944 cores having a peak performance of 34.5 TF. In all examples of this section we have mapped each element onto a single processor. The library used for inter processor communication is Message Passing Interface (MPI). To show the exponential rate of convergence the relative error is plotted on a $\log -$scale.

We perform the PCGM until a stopping criterion on the relative norm of the residual vector for the normal equations becoming less than $\epsilon$, a specified number, is satisfied. Since we would need to perform $O\left( \frac{\sqrt{\kappa }}{2}|\log \left( \frac{2}{\epsilon }\right) |\right)$ iterations of the PCGM to satisfy the stopping criterion, we would need to perform $O(W(\ln W)^2)$ iterations of the PCGM to obtain the approximate solution to an accuracy of $O(e^{-bW})$. Here, $\kappa$ denotes condition number of the preconditioner. Each iteration requires $O(W^3)$ operation-time on a parallel computer with O(N) processors. Thus, the method requires $O(W^{4}(\ln W)^2)$ operation-time on a parallel computer with O(N) processors to compute the solution to an accuracy of $O(e^{-bW})$.

Let $\Omega =S$ be the master square with boundary $\partial \Omega$. In all our examples we have used three different meshes with uniform mesh size $h=2.0,1.0$ and 0.5 in each direction (corresponds to $N=1,4$ and 16 respectively).

Remark 6.1

In general singularities arise at the corners for 2D square domain. However, we choose our data selectively so that the solution is not singular at the corners.

Example 6.1

(Biharmonic problem with Dirichlet boundary conditions): Consider the biharmonic problem with Dirichlet BCs on $\Omega =(-1,1)^2$,

$$\begin{aligned} \Delta ^{2} w&= f \quad \text{ in }\quad \Omega ,\\ w&= g \quad \text{ on }\quad \partial \Omega \\ \frac{\partial w}{\partial \nu }&= h \quad \text{ on }\quad \partial \Omega . \end{aligned}$$

We choose f, g and h such that the exact solution is

$$\begin{aligned} w(x,y)=x^4 e^y. \end{aligned}$$

Results are presented in the Table 1 and the corresponding plots are shown in Fig. 3. A uniform mesh of size $h=1$ is used which corresponds to the Mesh 2 (Fig. 2). In Fig. 3a, the relative error is plotted against W. Fig. 3c contains iterations vs. W and shows growth of iterations almost $O(W(\log (W))^2)$ with increase in polynomial order. This is in agreement with our condition number estimates obtained in [23]. It is clear that the error decays exponentially and satisfies (5.1). Relative error as a function of iterations is shown in Fig. 3b. It validate the result which require $O(W(\log W)^2)$ iterations to achieve the accuracy of $O(e^{-bW})$ (Fig. 4).

Fig. 2

The domain $\Omega =S=(-1,1)^{2}$ with uniform refinements a Mesh 1, b Mesh 2, c Mesh 3

Fig. 3

a Error vs. W, b error vs. iterations ($\log$ scale), c iterations vs. W ($\log$ scale), for Example 6.1

Fig. 4

a Exact solution, b approximate solution for $W=10$ in Example 6.1

Table 1 Performance of the method for Example 6.1 on Mesh 2

Example 6.2

(Homogeneous boundary conditions): In order to demonstrate the efficiency of the method and to compare our scheme with those existing in the literature, we now consider the biharmonic problem:

$$\begin{aligned} -\Delta w+2\Delta ^{2} w&= f \quad \text{ in }\quad \Omega =(-1,1)^2,\\ w&= 0 \quad \text{ on }\quad \partial \Omega ,\\ \frac{\partial w}{\partial \nu }&= 0 \quad \text{ on }\quad \partial \Omega , \end{aligned}$$

and test the performance of our method. Consider the case when the exact solution is

$$\begin{aligned} w(x,y)= (1-x^2)^2) (1-y^2)^2. \end{aligned}$$

In this case we have homogeneous boundary conditions. This example was reported in [9]. Table 2 summarizes the results. Comparing Tables 2 and 3, it can be observed that:

Table 2 Performance of the method for Example 6.2 on Mesh 1

Table 3 Table from Ben-Artzi et al. [9]

• 1. Ben-Artzi et al. achieved $10^{-10}$ accuracy with grid point $n=256$ while our proposed method LSQ-SEM obtain $10^{-13}$ accuracy with total grid point $n=5$.

• 2. The proposed method takes only $1.3 \times 10^{-2}$ second to achieve $3.2\times 10^{-15}$ accuracy.

• 3. As expected we received zero error up to the machine accuracy, however, with much fewer degree of freedom as compared to 3, this is in agreement with the fact that our method is exact for polynomials.

• 4. Plots among various parameters are plotted in Fig. 5. It is clear from the plots that the method give accuracy up to machine precision for polynomial solutions and is very effective in comparison to other methods.

• 5. The graphs of exact solution and approximate solution for $W=10$ are given in Fig. 6.

Fig. 5

a Error vs. W, b error vs. iterations ($\log$ scale), c iterations vs. W ($\log$ scale) for Example 6.2

Fig. 6

a Exact solution, b approximate solution for $W=10$ in Example 6.2

Example 6.3

(Non-homogeneous boundary conditions): We consider an additional example by choosing our exact solution as

$$\begin{aligned} w(x,y)=\sin {x}\,e^{y} \end{aligned}$$

This solves the equation

$$\begin{aligned} -\Delta w+\Delta ^{2} w = f (x,y)\quad \text{ in }\quad \Omega =(-1,1)^2, \end{aligned}$$

with non-zero boundary conditions where the forcing term $f(x,y)=0$. Performance of the method on Mesh 2 (Fig. 2) is presented in Table 4.

Table 4 Performance of the method for Example 6.3 on Mesh 2

Plots of relative error and iterations against polynomial orders and other parameters are depicted in Fig. 7. The relative error decays rapidly to $\approx 10^{-7}$ when $W=8$. The error profile is nearly a straight line for $W=2,\ldots ,10$. This shows exponential convergence (Fig. 8).

Fig. 7

a Error vs. W, b error vs. iterations ($\log -\log$ scale), c iterations vs. W ($\log$ scale) for Example 6.3

Fig. 8

a Exact solution, b approximate solution for $W=10$ in Example 6.3

Example 6.4

(Non-separable biharmonic problem): In Table 5 we report results of numerical simulations of our solver on Mesh 3 of Fig. 2 for a non-separable biharmonic problem in $\Omega =(0,1)^2$ (see also [1, 9]) with exact solution

$$\begin{aligned} w(x,y)=x^3 \log (1+y) + \frac{y}{1+x}. \end{aligned}$$

Table 5 Performance of the method for Example 6.4 on Mesh 3

Comparing the Tables 5 and 6, we can easily see that

Table 6 Performance of the method from Altas et al. [1]

• 1. Altas et al. [1] obtained $10^{-10}$ accuracy for mesh size $32\times 32$ while LSQ-SEM achieve $10^{-11}$ accuracy with mesh 3 for $W=8$.

• 2. The proposed method takes only 0.4387 second to achieve $10^{-11}$ accuracy.

• 3. Plots for various parameters are presented in Fig. 9. Percentage relative error against polynomial degrees and iterations is plotted in Figs. 9a, b respectively on a $\log$-scale.

  Fig. 9

  

  a Error vs. W, b error vs. iterations ($\log -\log$ scale), c iterations versus W ($\log$ scale) for Example 6.4

• 4. The graphs of exact solution and approximate solution for $W=10$ are given in Fig. 10.

  Fig. 10

  

  a Exact solution, b approximate solution for $W=10$ in Example 6.4

• 5. It is evident from the graphs the approximate solutions converge exponentially to the exact solution.

Remark 6.2

It is clear from these examples that the method is efficient in dealing problems with homogeneous as well as non-homogeneous boundary conditions.

Example 6.5

(Periodic boundary conditions): In our next example we take $\Omega =(-1,1)^2$ and solve (2.1). We choose f, g and h such that the exact solution is

$$\begin{aligned} w(x,y)=\sin ^{2}(2\pi x) \sin ^{2}(2\pi y). \end{aligned}$$

This example was considered in [1, 9, 12]. The source term is $\Delta ^2 w(x,y)$ and the boundary conditions are zeros on the four sides of the square. Table 7 depicts the numerical results.

Table 7 Performance of the method for Example 6.5 on Mesh 3

Here, we are comparing our result in Table 7 from Tables 8 and 9. The observations are as follows:

Table 8 Table from Shen [34]

Table 9 Table from Bialecki et al. [11]

• 1. Shen [34] and Bialecki et al. [11] achieved the accuracy $10^{-12}$ for $W=32$ while LSQ-SEM obtain $10^{-13}$ accuracy for $W=12$.

• 2. In Fig. 11a, relative error is plotted against polynomial order W on a $\log -$scale. The curve is almost a straight line and it confirms the theoretical estimates obtained.

• 3. In Fig. 11b, the error is drawn as a function of iterations on a $\log$ scale. It satisfy the criteria to achieve the $O(e^{-b W})$ accuracy with $O(W(\log (W))^2)$ iteration.

• 4. In Fig. 11c, iteration is plotted against polynomial order W on a $\log -$scale. The growth of the iterations is almost $O(W(\log (W))^2)$.

• 5. The graphs of exact solution and approximate solution for $W=10$ are given in Fig. 12.

Fig. 11

a Error vs. W, b error vs. iterations ($\log$ scale), c iterations vs. W ($\log$ scale) for Example 6.5

Fig. 12

a Exact solution, b approximate solution for $W=12$ in Example 6.5

7 Conclusions

In this article we have presented a fully non-conforming least-squares spectral element method for fourth order elliptic problems on smooth domains. It is shown that the condition number of the preconditioned system is $O((\ln W)^{4})$. It is also clear from giving test problems that the error in the computed solution decays exponentially in W, the number of elements in the mesh. The computational complexity of the method is $O(W^{4}(\ln W)^2)$ operations on a parallel computer with O(N) processors.

Numerical results for a number of test problems on rectangular domains with analytic solutions confirm the estimates obtained for the error and computational complexity. The algorithm is quite simple and easy to implement on parallel computers since the bottlenecks of our algorithm are matrix-vector multiplications. The method works for variable coefficient problems too and can be extended to three dimensional problems with less efforts. We plan to develop numerical schemes for fourth order problems with various types of singularities on polygonal and polyhedral domains in future work.