The Inverse Power Method for the $p(x)$-Laplacian Problem

Abstract

We present an inverse power method for the computation of the first homogeneous eigenpair of the $p(x)$-Laplacian problem. The operators are discretized by the finite element method. The inner minimization problems are solved by a globally convergent inexact Newton method. Numerical comparisons are made, in one- and two-dimensional domains, with other results present in literature for the constant case $p(x)\equiv p$ and with other minimization techniques (namely, the nonlinear conjugate gradient) for the $p(x)$ variable case.

1 Introduction

In this paper we consider the generalization of the $p$-Laplacian eigenvalue problem with homogeneous Dirichlet boundary conditions

$$\begin{aligned} -\Delta _p u(x)=\eta _p \left|u(x)\right|^{p-2}u(x) \end{aligned}$$

(1)

where $\Delta u(x)={{\mathrm{div}}}(\left|\nabla u(x)\right|^{p-2}\nabla u(x))$, $\varOmega$ is a bounded domain in $\mathbb {R}^m$, $u\in W^{1,p}_0(\varOmega )$ and $p>1$, to the case with variable exponent $p(x)$.

The $p$-Laplacian operator appears in several mathematical models that describe nonlinear problems in physics and mechanics [7, 9]. Examples include fluid dynamics [11], modeling of non-Newtonian fluids and glaciology [4, 10, 12, 20, 27, 28], turbulent flows [15], climatology [16], nonlinear diffusion (where the equation is called the $N$-diffusion equation, see Ref. [29] for the original article and Ref. [21] for some current developments), flows through porous media [30], power law materials [5] and torsional creep [24].

The $p$-Laplacian operator where $p$ is replaced by $p(x)$, $1<p^-\le p(x)\le p^+<+\infty$, is deeply related to generalized Lebesgue and Sobolev spaces, which have been vigorously studied and whose theory has been ripe for applications to PDEs. The common assumption in literature is that the exponent $p(x)$ is a measurable function and $1/p(x)$ is globally log-Hölder continuous [17]. There have been many contributions to nonlinear elliptic problems associated with the $p(x)$-Laplacian from various view points (see Ref. [1, 2, 14] and Ref. [22] for a survey), whereas there are much less contributions to parabolic problems [3] and eigenvalue problems [18].

If $p$ is constant, it is well known that the smallest eigenvalue satisfies

$$\begin{aligned} \underline{\eta _p}=\inf _{\mathop {u\ne 0}\limits ^{u\in W^{1,p}_0(\varOmega )}} \frac{\int _\varOmega \left|\nabla u\right|^p\mathrm{d}x}{\int _\varOmega \left|u\right|^p\mathrm{d}x}. \end{aligned}$$

(2)

The trivial generalization of quotient (2) to the case $p=p(x)$ yields a problem in which the homogeneity is lost, that is if $u$ is a minimizer then $\omega u$, $\omega \ne 0$, is not. In Ref. [19], the homogeneity is restored considering

$$\begin{aligned} \underline{\lambda }=\inf _{\mathop {u\ne 0}\limits ^{u\in W^{1,p(x)}_0(\varOmega )}} \frac{\left\| \nabla u\right\| _{p(x)}}{\left\| u\right\| _{p(x)}}, \end{aligned}$$

where the norm $\left\| \cdot \right\| _{p(x)}$ is the so called Luxemburg norm

$$\begin{aligned} \left\| u\right\| _{p(x)}=\inf _{\gamma >0}\left\{ \gamma :\int _\varOmega \left|\frac{u(x)}{\gamma }\right|^{p(x)} \frac{\mathrm{d}x}{p(x)}\le 1\right\} . \end{aligned}$$

(3)

The use of $\mathrm{d}x/p(x)$ (rather than the classical $\mathrm{d}x$) just simplifies the equations a little (see Ref. [19]). The corresponding Euler–Lagrange equation is

$$\begin{aligned} -{{\mathrm{div}}}\left( \left|\frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\right|^{p(x)-2} \frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\right) =\lambda T\left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|^{p(x)-2} \frac{u(x)}{\left\| u\right\| _{p(x)}}, \end{aligned}$$

(4)

where

$$\begin{aligned} T=\frac{\int _\varOmega \left|\frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\right|\mathrm{d}x}{\int _\varOmega \left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|\mathrm{d}x}. \end{aligned}$$

We notice that in the constant case $p(x)\equiv p$, since $p\left\| u\right\| _{p}^p=\left\| u\right\| _{L^p}^p$,

$$\begin{aligned} (\lambda ,u)\ \text {eigenpair for~(4)} \Leftrightarrow (\lambda ^p,u/\root p \of {p})\ {\text {eigenpair for~(1)}} \end{aligned}$$

(5)

with $\left\| u\right\| _{p}=\left\| u/\root p \of {p}\right\| _{L^p}=1$.

Although some different numerical methods for the eigenvalue problem with constant $p$ are available, see Ref. [7, 9, 13], to the knowledge of the authors the first numerical method, based on the nonlinear conjugate gradient method, for computing

$$\begin{aligned} \underline{\lambda }^2=\varLambda =\inf _{\mathop {u\ne 0}\limits ^{u\in W^{1,p(x)}_0(\varOmega )}} \frac{\left\| \nabla u\right\| _{p(x)}^2}{\left\| u\right\| _{p(x)}^2} \end{aligned}$$

(6)

and the corresponding minimizer was proposed by the first author in Ref. [6], where only the case $p(x)\ge 2$ was considered. Here we use a preconditioned quadratic model for the minimization problem, either with the exact Hessian, if $p(x)\ge 2$, or with a modified Hessian, otherwise. The new method turns out to be more general, more robust and faster (see the numerical experiments in Table 3, Sect. 3) than the previous one.

2 The Inverse Power Method for a Nonlinear Eigenproblem

Given $R:\mathbb {R}^n\rightarrow \mathbb {R}_+$ and $S:\mathbb {R}^n\rightarrow \mathbb {R}_+$ convex, differentiable, even and positively 2-homogeneous functionals, with the further assumption that $S(u)=0$ only if $u=0$, then the critical points $u^*$ of $F(u)=R(u)/S(u)$ satisfy

$$\begin{aligned} \nabla _u F(u^*)=\nabla _u R(u^*)-\frac{R(u^*)}{S(u^*)}\nabla _u S(u^*)=0. \end{aligned}$$

If we define $r(u)=\nabla _u R(u)$, $s(u)=\nabla _u S(u)$ and $\varLambda ^*=\frac{R(u^*)}{S(u^*)}$, then the critical point $u^*$ satisfies the nonlinear eigenproblem

$$\begin{aligned} r(u^*)-\varLambda ^*s(u^*)=0. \end{aligned}$$

(7)

If $R(u)=\langle u,Au\rangle$, where $A:\mathbb {R}^n\rightarrow \mathbb {R}^n$ is linear and $S(u)=\langle u,u\rangle$, $\langle \cdot ,\cdot \rangle$ being the scalar product in $\mathbb {R}^n\times \mathbb {R}^n$, the standard linear eigenproblem is retrieved. The generalization of the inverse power method for the computation of the smallest eigenvalues is the following algorithm:

• 1. take ${\tilde{u}}^0$ random and compute $u^0=\displaystyle \frac{{\tilde{u}^{0}}}{S({\tilde{u}}^{0})^{1/2}}$ and $\varLambda ^0=F(u^0)=R(u^0)$

• 2. repeat

  • ${\tilde{u}}^{k}=\displaystyle \arg \min _u\{R(u)-\langle u,s(u^{k-1})\rangle \}$

  • $u^{k}=\displaystyle \frac{{\tilde{u}^{k}}}{S({\tilde{u}}^{k})^{1/2}}$

  • $\varLambda ^{k}=F(u^{k})=R(u^k)$

  • until convergence

It is proven [23] that the sequence $\{(u^k,\varLambda ^k)\}_k$ produced by the algorithm satisfies $F(u^k)<F(u^{k-1})$ and converges to an eigenpair $(u^*,\varLambda ^*)$ for problem (7), with $u^*$ a critical point of $F$.

Let now $u(x)$ be a linear combination of basis functions

$$\begin{aligned} u(x)=\sum _{j=1}^nu_j\phi _j(x), \end{aligned}$$

with $u=(u_1,\ldots ,u_n)^\mathrm{T}$ the vector of coefficients, and let us apply the algorithm described above to the case

$$\begin{aligned} R(u)=\left\| \sum _{j=1}^nu_j\nabla \phi _j(\cdot )\right\| ^{2},\quad S(u)=\left\| \sum _{j=1}^nu_j\phi _j(\cdot )\right\| ^{2} \end{aligned}$$

In our numerical experiments, the set of functions $\{\phi _j(x)\}_{j=1}^n$ will be a proper set of finite element basis functions. With abuse of notation, we will write for short $R(u)=\left\| \nabla u\right\| _{p(x)}^2$ and $S(u)=\left\| u\right\| _{p(x)}^2$.

We remind that the algorithm does not guarantee the convergence to the smallest eigenvalue. On the other hand, it is possible to apply it to different initial guesses and then take the smallest eigenvalue.

2.1 Initial Values and Exit Criteria

Although ${\tilde{u}}^0$ can be chosen randomly, it is clear that the more it is close to $u^*$, the faster the algorithm converges. In order to speed up the convergence, we use a continuation technique over $p(x)$, starting from $p(x)\equiv 2$ for which the solution is known at least for common domains $\varOmega$. By employing a convex combination

$$\begin{aligned} p^m(x)=2\cdot (1-\theta _m)+p(x)\cdot \theta _m,\quad \theta _m=\sqrt{\frac{m}{M}},\quad m=0,1,\ldots ,M, \end{aligned}$$

(8)

the $m$th problem is solved by providing as initial condition the solution of the $(m-1)$th problem.

For the minimization problem (called inner problem)

$$\begin{aligned} {\tilde{u}}^{k}=\displaystyle \arg \min _u\{R(u)-\langle u,s(u^{k-1})\rangle \},\quad \text {given}\, u^{k-1} \end{aligned}$$

we use an iterative method as well. Since the inverse power method, at convergence, ensures

$$\begin{aligned} r(u^{k-1})-\varLambda ^{k-1}s(u^{k-1})\approx 0 \Rightarrow r\left( \frac{u^{k-1}}{\varLambda ^{k-1}}\right) -s(u^{k-1})\approx 0, \end{aligned}$$

and (at each iteration)

$$\begin{aligned} r({\tilde{u}}^k)-s(u^{k-1})=0, \end{aligned}$$

a good choice for the initial value of ${\tilde{u}}^k$ is $u^{k-1}/\varLambda ^{k-1}$. By the proof of Lemma 3.1 in Ref. [23], we know that the descent in $F$ is guaranteed not only for the exact solution of the inner problem but also for any vector ${\bar{u}}^{k}$ which satisfies the condition

$$\begin{aligned} R({\bar{u}}^k)-\langle {\bar{u}}^k,s(u^{k-1})\rangle < R\left( \frac{u^{k-1}}{F(u^{k-1})}\right) -\left\langle \frac{u^{k-1}}{F(u^{k-1})},s(u^{k-1})\right\rangle . \end{aligned}$$

Since $F(u^{k-1})=\varLambda ^{k-1}$, $u^{k-1}/F(u^{k-1})$ is precisely the above suggested choice for the initial value of ${\tilde{u}}^k$. Therefore, in principle, starting from this value, the use of a descent method for the inner problem would require a single step in order to guarantee the descent in $F$. More realistically, this means that far from convergence (for instance during the continuation technique) it makes no sense to solve the inner problem too accurately. For this reason, an exit criterion could encompass both a relatively large tolerance and a relatively small maximum number of iterations.

A classical exit criterion for the inverse power method is

$$\begin{aligned} \left|\varLambda ^{k}-\varLambda ^{k-1}\right|\le \mathrm{tol}\cdot \left|\varLambda ^{k}\right| \end{aligned}$$

(9)

for a given tolerance $\mathrm{tol}$. As soon as it is satisfied, we assume that $\varLambda ^k\approx \varLambda ^*$ and thus

$$\begin{aligned} r(u^{k})-\varLambda ^{k}s(u^k)\approx 0. \end{aligned}$$

(10)

We call the left hand side residual; clearly, its infinity norm could be used as a different exit criterion.

2.2 Approximation of the Luxemburg Norm

If $u(x)$ is not zero almost everywhere, then its Luxemburg norm $\gamma$ is implicitly defined by

$$\begin{aligned} F(u,\gamma )=\int _\varOmega \left|\frac{u(x)}{\gamma }\right|^{p(x)} \frac{\mathrm{d}x}{p(x)}-1=0. \end{aligned}$$

(11)

Hereafter we remove the integration domain $\varOmega$ from the notation. The derivative with respect to $\gamma$ of $F(u,\gamma )$ is

$$\begin{aligned} \partial _\gamma F(u,\gamma )= -\frac{1}{\gamma }\int \left|\frac{u(x)}{\gamma }\right|^{p(x)}\mathrm{d}x \end{aligned}$$

(12)

and thus Newton’s method can be easily applied. For a given $u(x)$, $F(u,\gamma )$ is a monotonically decreasing convex ${\fancyscript{C}}^2$ function in $\gamma$. This guarantees the convergence of Newton’s method whenever the initial guess $\gamma _0>0$ is chosen such that $F(u,\gamma _0)\ge 0$.

For the initial guess $\gamma _0$, we use the following estimates

$$\begin{aligned} \gamma _0= \left\{ \begin{aligned}&\left( \int \frac{\left|u(x)\right|^{p(x)}}{p(x)}\mathrm{d}x\right) ^{\frac{1}{p_{\max }}}&\text {if }\int \frac{\left|u(x)\right|^{p(x)}}{p(x)}\mathrm{d}x&\ge 1\\&\left( \int \frac{\left|u(x)\right|^{p(x)}}{p(x)}\mathrm{d}x\right) ^{\frac{1}{p_{\min }}}&\text {if }\int \frac{\left|u(x)\right|^{p(x)}}{p(x)}\mathrm{d}x&<1 \end{aligned}\right. \end{aligned}$$

where $p_{\max }=\max p(x)$ and $p_{\min }=\min p(x)$. In fact, if we consider the first case,

$$\begin{aligned} F(u,\gamma _0)&= \int \left|\frac{u(x)}{\gamma _0}\right|^{p(x)} \frac{\mathrm{d}x}{p(x)}-1\ge \int \frac{\left|u(x)\right|^{p(x)}}{\gamma _0^{p_{\max }}} \frac{\mathrm{d}x}{p(x)}-1\\&= \frac{1}{\int \frac{\left|u(x)\right|^{p(x)}}{p(x)}\mathrm{d}x} \int \left|u(x)\right|^{p(x)} \frac{\mathrm{d}x}{p(x)}-1=0. \end{aligned}$$

2.3 The Inner Problem

In the inverse power method, we need to solve the inner problem

$$\begin{aligned} {\tilde{u}}^{k}=\displaystyle \arg \min _uf(u)=\displaystyle \arg \min _u\{R(u)-\langle u,s(u^{k-1})\rangle \},\quad \text {given}\, u^{k-1}. \end{aligned}$$

We first compute $\langle v,s(u)\rangle =\langle v,\nabla _u S(u)\rangle$ for given vectors $u$ and $v$. Since $\gamma (u)=\left\| u\right\| _{p(x)}$ is implicitly defined by $F(u,\gamma (u))=0$, the differentiation of implicit functions leads to

$$\begin{aligned} \langle v,\nabla _u F(u,\gamma (u))\rangle =\langle v,\partial _u F(u,\gamma (u))\rangle + \langle v,\partial _\gamma F(u,\gamma (u))\nabla _u\gamma (u)\rangle =0, \end{aligned}$$

from which

$$\begin{aligned} \langle v,\nabla _u\left\| u\right\| _{p(x)}\rangle =\langle v,\nabla _u\gamma (u)\rangle =- \frac{\langle v,\partial _u F(u,\gamma (u))\rangle }{\partial _\gamma F(u,\gamma (u))}. \end{aligned}$$

By recalling that, in general,

$$\begin{aligned} \partial _{u_i}\left( \int g(u(x))\mathrm{d}x\right) = \int g'(u(x))\phi _i(x)\mathrm{d}x, \end{aligned}$$

for $v(x)=\sum _{j=1}^nv_j\phi _j(x)$ we have

$$\begin{aligned} \left\langle v,\partial _{u_i}\left( \int g(u(x))\mathrm{d}x\right) \right\rangle = \int g'(u(x))v(x)\mathrm{d}x \end{aligned}$$

and thus

$$\begin{aligned} \langle v,\partial _u F(u,\gamma )\rangle =\int \left|\frac{u(x)}{\gamma }\right|^{p(x)-2} \frac{u(x)}{\gamma }\frac{v(x)}{\gamma }\mathrm{d}x. \end{aligned}$$

By employing (12) we get

$$\begin{aligned} \langle v,\nabla _u \left\| u\right\| _{p(x)}\rangle =\frac{\int \left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|^{p(x)-2} \frac{u(x)}{\left\| u\right\| _{p(x)}}v(x)\mathrm{d}x}{\int \left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|^{p(x)}\mathrm{d}x}, \end{aligned}$$

from which

$$\begin{aligned} \langle v,s(u)\rangle =\langle v,2\left\| u\right\| _{p(x)}\nabla _u\left\| u\right\| _{p(x)}\rangle = 2\frac{\int \left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|^{p(x)-2} u(x)v(x)\mathrm{d}x}{\int \left|\frac{u(x)}{\left\| u\right\| _{p(x)}}\right|^{p(x)}\mathrm{d}x}. \end{aligned}$$

(13)

Given $u^{k-1}$ of unitary Luxemburg norm, the problem reduces to find the minimizer of

$$\begin{aligned} f(u)&= R(u)-\langle u,s(u^{k-1})\rangle \nonumber \\&= \left\| \nabla u\right\| _{p(x)}^2-2\frac{\int \left|u^{k-1}(x)\right|^{p(x)-2} u^{k-1}(x)u(x)\mathrm{d}x}{\int \left|u^{k-1}(x)\right|^{p(x)}\mathrm{d}x} \end{aligned}$$

(14)

We use a line search method based on the sufficient decrease condition. If $u_\mathrm{c}$ is the solution at the current iteration, its update is

$$\begin{aligned} u_+=u_\mathrm{c}+\delta d, \end{aligned}$$

(15)

where $d$ is a descent direction, i.e. $\langle \nabla _u f(u_\mathrm{c}),d\rangle < 0$, and $\delta$ is such that

$$\begin{aligned} f(u_\mathrm{c}+\delta d)< f(u_\mathrm{c})+\alpha \delta \langle \nabla _u f(u_\mathrm{c}),d\rangle \end{aligned}$$

(16)

with $\alpha =10^{-4}$. Condition (16) is usually called Armijo’s rule.

2.3.1 The Quadratic Model for the Inner Problem, $p(x)\ge 2$

We first consider the case $p(x)\ge 2$ and approximate $f(u)$ in (14) with a quadratic model

$$\begin{aligned} f(u)\approx f(u_\mathrm{c})+\langle \nabla _u f(u_\mathrm{c}),u-u_\mathrm{c}\rangle + \frac{1}{2}\langle u-u_\mathrm{c},H(u_\mathrm{c})(u-u_\mathrm{c})\rangle \end{aligned}$$

where $H(u_\mathrm{c})$ is the exact Hessian of $f$ at the current iteration $u_\mathrm{c}$. For $p(x)\ge 2$, $R(u)$ is twice continuously differentiable and convex, i.e. the Hessian of $f$ is symmetric positive definite. Therefore

$$\begin{aligned} \nabla _u f(u_+)\approx \nabla _u f(u_\mathrm{c})+H(u_\mathrm{c})(u_+-u_\mathrm{c})=0 \Leftrightarrow u_+-u_\mathrm{c}=-H(u_\mathrm{c})^{-1}\nabla _u f(u_\mathrm{c}) \end{aligned}$$

and hence the descent direction is $d=-H(u_\mathrm{c})^{-1}\nabla _u f(u_\mathrm{c})$. If condition (16) is not satisfied for a given $\delta$, then it is repeatedly reduced (backtracking) until the condition is satisfied, using a quite standard cubic polynomial model for $p(\delta )=f(u_c+\delta d)$ (see Ref. [26]).

Let us compute $\nabla _u f(u)$ and $H(u)v$, for a given $v\in \mathbb {R}^n$. With the arguments used to obtain (13), we immediately have

$$\begin{aligned} r_i(u)=\partial _{u_i}R(u)= 2\frac{\left\| \nabla u\right\| _{p(x)}\int \left|\frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\right|^{p(x)-2} \frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\cdot \nabla \phi _i(x)\mathrm{d}x}{\int \left|\frac{\nabla u(x)}{\left\| \nabla u\right\| _{p(x)}}\right|^{p(x)}\mathrm{d}x} \end{aligned}$$

(17)

where here $\cdot$ denotes the scalar product in $\mathbb {R}^m\times \mathbb {R}^m$. Since $u^{k-1}$ has unitary Luxemburg norm,

$$\begin{aligned} \partial _{u_i} f(u)=2\frac{K\int \left|\frac{\nabla u}{K}\right|^{p-2} \frac{\nabla u}{K}\cdot \nabla \phi _i}{\int \left|\frac{\nabla u}{K}\right|^{p}}- 2\frac{\int \left|u^{k-1}\right|^{p-2} u^{k-1}\phi _i}{\int \left|u^{k-1}\right|^{p}} \end{aligned}$$

(18)

where we set $K=\left\| \nabla u\right\| _{p(x)}$ and omitted the dependency on $x$ in the integrals in order to reduce the notation. By introducing

$$\begin{aligned} N_i(u)=\int \left|\frac{\nabla u}{K}\right|^{p-2}\nabla u\cdot \nabla \phi _i,\quad D(u)=\int \left|\frac{\nabla u}{K}\right|^p \end{aligned}$$

the $i$th row of $H(u)v$ is

$$\begin{aligned} (H(u)v)_i&= 2\frac{D(u)\langle v,\nabla _u N_i(u)\rangle - N_i(u)\langle v,\nabla _u D(u)\rangle }{D(u)^2}\\&= 2\frac{\int (p-2)\left|\frac{\nabla u}{K}\right|^{p-4}\frac{\nabla u}{K}\cdot \frac{\nabla vK-\nabla u\langle v,\nabla _u K\rangle }{K^2}\nabla u\cdot \nabla \phi _i+\left|\frac{\nabla u}{K}\right|^{p-2}\nabla v\cdot \nabla \phi _i}{D(u)}+\\&\quad -\,2\frac{N_i(u)\int p\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \frac{\nabla vK-\nabla u\langle v,\nabla _u K\rangle }{K^2}}{D(u)^2}\\&= 2\frac{\int (p-2)\left|\frac{\nabla u}{K}\right|^{p-4}\frac{\nabla u}{K}\cdot \nabla v \frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)}+\\&\quad -\,2\frac{\langle v,\nabla _u K\rangle \int (p-2)\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)} +2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\nabla v\cdot \nabla \phi _i}{D(u)}+\\&\quad -\,2\frac{\frac{N_i(u)}{K}\int p\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v}{D(u)^2}+ 2\frac{\frac{N_i(u)}{K}\langle v,\nabla _u K\rangle \int p\left|\frac{\nabla u}{K}\right|^{p}}{D(u)^2}. \end{aligned}$$

By using again (13), the inner product $\langle v,\nabla _u K\rangle$ can be recast as

$$\begin{aligned} \langle v,\nabla _u K\rangle =\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v}{D(u)} \end{aligned}$$

and the $i$th row of $H(u)v$ becomes

$$\begin{aligned} (H(u)v)_i&= 2\frac{\int (p-2)\left|\frac{\nabla u}{K}\right|^{p-4}\frac{\nabla u}{K}\cdot \nabla v \frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)}+\nonumber \\&\quad -\,2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v\int (p-2)\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)^2}+\nonumber \\&\quad +\,2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\nabla v\cdot \nabla \phi _i}{D(u)}+\nonumber \\&\quad -\,2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla \phi _i \int p\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v}{D(u)^2}+\nonumber \\&\quad +\,2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla \phi _i \int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v \int p\left|\frac{\nabla u}{K}\right|^{p}}{D(u)^3}. \end{aligned}$$

(19)

The reason for computing the action of $H(u)$ to a vector is that $H(u)$ is not a sparse matrix, even if finite elements are used. Therefore, the descent direction $-H(u_c)^{-1}\nabla _u f(u_c)$ is computed through an iterative method such as the preconditioned conjugate gradient method, which only requires the action of $H(u_c)$ to a vector $v$. A good choice for the preconditioner in computing ${\tilde{u}^{k}}$ can be suggested by the modified gradient

$$\begin{aligned} \partial _{u_i} f_{c}(u)=2\frac{\displaystyle \int \left|\frac{\nabla u_c}{K_c}\right|^{p-2} \nabla u\cdot \nabla \phi _i}{\displaystyle \int \left|\frac{\nabla u_c}{K_c}\right|^{p}}- 2\frac{\int \left|u^{k-1}\right|^{p-2} u^{k-1}\phi _i}{\int \left|u^{k-1}\right|^{p}} \end{aligned}$$

and the corresponding modified Hessian $H_c$, whose entries are

$$\begin{aligned} 2\frac{\displaystyle \int \left|\frac{\nabla u_c}{K_c}\right|^{p-2}\nabla \phi _j\cdot \nabla \phi _i}{\displaystyle \int \left|\frac{\nabla u_c}{K_c}\right|^{p}}. \end{aligned}$$

(20)

In fact, this preconditioner turns out to be sparse in case the basis functions $\{\phi _j(x)\}$ correspond to a finite element method. It is possible to use a fixed preconditioner for each iteration of the inverse power method (and not a preconditioner for each iteration of the inner problem), starting from the modified gradient

$$\begin{aligned} \partial _{u_i} f^{k-1}(u)=2\frac{\displaystyle \int \left|\frac{\nabla u^{k-1}}{K^{k-1}}\right|^{p-2} \nabla u\cdot \nabla \phi _i}{\displaystyle \int \left|\frac{\nabla u^{k-1}}{K^{k-1}}\right|^{p}}- 2\frac{\int \left|u^{k-1}\right|^{p-2} u^{k-1}\phi _i}{\int \left|u^{k-1}\right|^{p}} \end{aligned}$$

and the corresponding modified Hessian $H_{k-1}$, whose entries are

$$\begin{aligned} 2\frac{\displaystyle \int \left|\frac{\nabla u^{k-1}}{K^{k-1}}\right|^{p-2}\nabla \phi _j\cdot \nabla \phi _i}{\displaystyle \int \left|\frac{\nabla u^{k-1}}{K^{k-1}}\right|^{p}}. \end{aligned}$$

(21)

Once the modified Hessian is computed, it is factorized by Choleski’s method and the triangular factors are inverted in order to get the preconditioned conjugate gradient iterations.

2.3.2 The Quadratic Model for the Inner Problem, $p(x)\ge p^->1$

If, for some values of $x$, $p(x)$ is less than two and $\nabla u(x)$ is zero, than the first and the third term in the Hessian (19) are not defined, while the gradient (18) is still well defined, in the sense that

$$\begin{aligned} \left|\nabla u(x)\right|^{p(x)-2}\nabla u(x)\cdot \nabla \phi _i(x)=0 \quad {\text {if}}\quad \nabla u(x)=0. \end{aligned}$$

We can consider (see Ref. [9]) the modified Hessian arising from

$$\begin{aligned} N_i^{\varepsilon _n}(u)=\int \left( \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-2}{2}}\nabla u\cdot \nabla \phi _i,\quad D(u)=\int \left|\frac{\nabla u}{K}\right|^p \end{aligned}$$

where $\varepsilon _n$ is a small quantity, possibly depending on the number $n$ of basis functions $\phi _j(x)$

$$\begin{aligned}&2\frac{\int (p-2)\left( \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-4}{2}}\frac{\nabla u}{K}\cdot \nabla v \frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)}+\\&\quad -\,2\frac{\int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v \int (p-2)\left( \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-2}{2}}\frac{\nabla u}{K}\cdot \nabla \phi _i}{D(u)^2}+\\&\quad +\,2\frac{\int \left( \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-2}{2}}\nabla v\cdot \nabla \phi _i}{D(u)}+\\&\quad -\,2\frac{\int \left( \varepsilon _n^2+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-2}{2}}\frac{\nabla u}{K}\cdot \nabla \phi _i \int p\left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v}{D(u)^2}+\\&\quad +\,2\frac{\int \left( \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2\right) ^{\frac{p-2}{2}}\frac{\nabla u}{K}\cdot \nabla \phi _i \int \left|\frac{\nabla u}{K}\right|^{p-2}\frac{\nabla u}{K}\cdot \nabla v \int p\left|\frac{\nabla u}{K}\right|^{p}}{D(u)^3} \end{aligned}$$

We notice that, in this way, the integrand function of the first term above side is equal to zero where $\nabla u(x)=0$, and well defined otherwise, even without $\varepsilon ^2_n$. Therefore we replace

$$\begin{aligned} \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2 \end{aligned}$$

with

$$\begin{aligned} \left( 1-{{\mathrm{sign}}}\left|\nabla u\right|^2\right) +\left|\frac{\nabla u}{K}\right|^2 \end{aligned}$$

in that term. Indeed, such a modification is useful in the numerical implementation of $f$, its gradient and its exact Hessian, even in the case $p(x)\ge 2$, for the evaluation of terms (see, for instance, the second, the fourth and the fifth above) like

$$\begin{aligned} \left|z\right|^{p-2}z, \end{aligned}$$

which can be numerically computed as

$$\begin{aligned} \left( (1-{{\mathrm{sign}}}\left|z\right|^2)+\left|z\right|^2\right) ^{\frac{p-2}{2}}z. \end{aligned}$$

On the other hand, if $\nabla u(x)=0$, the third term in the Hessian above is not defined without $\varepsilon _n^2$, but it is well defined if $\nabla u(x)\ne 0$. Therefore, we replace

$$\begin{aligned} \varepsilon ^2_n+\left|\frac{\nabla u}{K}\right|^2 \end{aligned}$$

in the third term of the Hessian above and in the corresponding modified Hessian (see (20)) with

$$\begin{aligned} \varepsilon ^2_n\cdot \left( 1-{{\mathrm{sign}}}\left|\nabla u\right|^2\right) +\left|\frac{\nabla u}{K}\right|^2. \end{aligned}$$

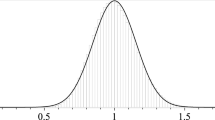
When $p(x)\rightarrow 1^+$ for some values of $x$, the eigenvalue problem is numerically quite difficult. This is due not only to the fact that the exact Hessian does not exist, but also to the high derivatives of the solution at the boundaries. In fact, as reported in Fig. 1 for the case of $p$ constant, when $p \rightarrow 1^+$ the first eigenfunction on the ball converges to its characteristic function (see Ref. [25]).

3 Numerical Results

3.1 Details of the Algorithm

For the computation of the Luxemburg norm, Newton’s method is stopped when the relative difference of two successive solutions is smaller then $10\cdot \varepsilon$, where $\varepsilon$ is the machine precision.

From our numerical experience, we found that a number of continuation steps in (8) chosen as

$$\begin{aligned} M=\left\{ \begin{aligned}&\left\lceil \frac{\max p(x)}{2}\right\rceil&\text {if}\, \min p(x)\ge 2\\&\left\lceil -3\log (\min p(x)-1)\right\rceil&\text {if}\, \min p(x)< 2 \end{aligned}\right. \end{aligned}$$

provides a satisfactory behavior. Moreover, the $m$th problem in (8) is solved with tolerance

$$\begin{aligned} \mathrm{tol}_m=\mathrm{tol}_0\cdot (1-\theta _m)+\mathrm{tol}\cdot \theta _m \end{aligned}$$

where $\mathrm{tol}_0=100\cdot \mathrm{tol}$ and $\mathrm{tol}$ is the tolerance in the exit criterion (9) for the inverse power method. It is chosen proportional to $h^{r+1}$, where $r$ is the degree of the finite element piecewise polynomial basis. The same tolerance is used for inner problem (14). Four exit criteria are used. Since we use (modified) Newton’s method, if the infinity norm of the descent direction $\delta d$ in (15) is smaller than $\mathrm{tol}\cdot \left\| u_c\right\| _{\infty }$ already with $\delta =1$, we stop the iterations. Then we consider the ratio between the relative change in $f(u_+)$ and the relative change in $u_+$. If

$$\begin{aligned} \left\| {\frac{\nabla _u f(u_+)\circ u_+}{f(u_+)}}\right\| _{\infty } \le \mathrm{tol}, \end{aligned}$$

where $\circ$ denotes Hadamard’s product, we stop the iterations. We stop the iterations if the method stagnates, that is if $\Vert \delta d\Vert _\infty \le 0.1\cdot \mathrm{tol} \cdot \Vert u_c\Vert _\infty$, too. Finally, we fix the maximum number of iterations to 10. The value of $\varepsilon _n$ for the modified Hessian is $10^{-5}$.

3.2 One-Dimensional Case

We implemented and run the one-dimensional case in GNU Octave 3.8, using piecewise linear basis functions $\phi _j(x)$ and approximating the arising integrals by midpoint quadrature formulas.

The initial solution $u^0(x)$ corresponding to $p(x)\equiv p=2$ is the (piecewise linear interpolation of the) first eigenfunction of

$$\begin{aligned} -u''(x)=\eta _2 u(x),\quad x_0<x<x_1 \end{aligned}$$

normalized in order to have $\left\| u^0\right\| _{2}=1$, that is

$$\begin{aligned} u^0(x)=\frac{2}{\sqrt{x_1-x_0}}\sin \left( \frac{x-x_0}{x_1-x_0}\pi \right) ,\quad \eta _2=\underline{\eta _2}=\left( \frac{\pi }{x_1-x_0}\right) ^2. \end{aligned}$$

The first test aims at comparing our results with the analytical solution, which is known for constant values of $p(x)\equiv p$ in the interval $(-1,1)$ (see, for instance, Ref. [8])

$$\begin{aligned} \underline{\eta _p}=\left( \frac{2\root p \of {p-1}(\pi /p)}{2\sin (\pi /p)}\right) ^p \end{aligned}$$

Table 1 reports the eigenvalue $\underline{\lambda }^p$, computed with 101 basis functions, and the relative difference with the corresponding analytical value $\underline{\eta _p}$ [see (5)]. Figure 1 shows the eigenfunction $u(x)$ for different values of constant $p$. In the limit $p \rightarrow 1^+$ it tends to an almost constant function with steep gradients at the boundaries due to the homogeneous boundary conditions, whereas in the limit $p \rightarrow +\infty$ the eigenfunction resembles the absolute value of a linear function (non differentiable at the origin).

Fig. 1

First eigenfunctions for some values of constant $p(x)\equiv p$

Table 1 Values of $\underline{\lambda }^p$ and relative error with respect to $\underline{\eta _p}$ for some values of constant $p(x)\equiv p$, in the interval $(-1,1)$

Figure 2 reports the first eigenfunction for two cases. In the first one (left), $p(x)=28+26\cos (2\pi x)$, in the second one (right) $p(x)$ is discontinuous, $p(x)=1.1$ if $x<0$ and $p(x)=10$ otherwise. The second case, although does not satisfy the log-Hölder continuity usually required to the exponent, was chosen as a limit case to check the robustness of the method. The values of $\underline{\lambda }$ for the two cases are about $0.94548$ and $1.25999$, respectively; the corresponding eigenfunctions are reported in the second row of plots. The values of residuals (10) in infinity norm are $0.0018$ and $0.64$, respectively. The second residual is not so small. In fact, the first part of the numerical residual contains terms like $\left|\nabla u(x)\right|^{p(x)-1}$ [see (17)], with $\nabla u(x)$ close to zero where $p(x)$ is close to one. Those terms are approximated by $\left|\nabla u(x)+{\fancyscript{O}}(h)\right|^{p-1}$, where $h$ the mesh size, which can be quite far from their exact values. A possible confirmation of such an explanation is the fact that the maximum of the residual is taken at $\bar{x}=0.04$, where $\nabla u(\bar{x})\approx 0$ and $p(\bar{x})=1.1$. Similar values of the residuals were observed for the smaller values of $p$ in the constant case.

3.3 Two-Dimensional Cases

We implemented and run the algorithm with FreeFem$++$ 3.23, using piecewise quadratic elements for $u(x,y)$ and piecewise constant elements for $p(x,y)$, in order to better manage discontinuous functions $p(x,y)$.

3.3.1 The Rectangle

The initial solution $u^0(x,y)$ corresponding to $p(x,y)\equiv p=2$ is the first eigenfunction of

$$\begin{aligned} -\nabla ^2u(x,y)=\eta _2 u(x,y),\quad x_0<x<x_1,\ y_0<y<y_1 \end{aligned}$$

normalized to have $\left\| u^0\right\| _{2}=1$, that is

$$\begin{aligned} u^0(x,y)&= \sqrt{\frac{8}{(x_1-x_0)(y_1-y_0)}} \sin \left( \frac{x-x_0}{x_1-x_0}\pi \right) \sin \left( \frac{y-y_0}{y_1-y_0}\pi \right) \\ \eta _2&= \underline{\eta _2}=\left( \frac{\pi }{x_1-x_0}\right) ^2+\left( \frac{\pi }{y_1-y_0}\right) ^2. \end{aligned}$$

Fig. 2

$p(x)=28+26\cos (2\pi x)$ (left) and $p(x)=1.1$ if $x<0$ and $p(x)=10$ if $x\ge 0$ (right) and the corresponding eigenfunctions (bottom)

For some constant values of $p(x)\equiv p$, Ref. [13], Table 4, $p$-version] reports the values of the eigenvalues $\underline{\lambda }^p$ with six significant digits for the unit square and Ref. [9, Table 2] reports the values for a wider range of $p$. In Table 2 we compare our results for $p=1.5,2,2.5$ and $4.0$ computed on a regular mesh with $26\times 26$ vertices and 1,250 triangles. We find that our results are closer to those obtained by the $p$-version of FEM algorithm used in Ref. [13] than to those obtained in Ref. [9].

In order to test the code performance, we compared our new minimization method [called precNewton(10) in Table 3] with the FreeFem++ function NLCG, which implements the nonlinear conjugate gradient minimization method (see Table 3). In a first example, taken from Ref. [6, Section 2.2], $p_1(x,y)=5+3\sin (3\pi x)$. Here, differently than in Ref. [6], we implemented a preconditioner for the NLCG method based on modified Hessian (21) and set the maximum number of iterations to 10. Therefore, the method is denoted precNLCG(10) in Table 3. In a second example we checked the case $p_2(x,y)=4.5+3\sin (3\pi x)$, in which $p_2(x,y)$ assumes values less than two. As shown in Table 3, our method outperforms the preconditioned NLCG in terms of CPU time (with comparable residuals).

Table 2 Values of $\underline{\lambda }^p$ for some values of constant $p(x)\equiv p$

Table 3 Comparison for the cases $p_1(x,y)=5+3\sin (3\pi x)$ and $p_2(x,y)=4.5+3\sin (3\pi x)$

As a final test, we considered a discontinuous case with

$$\begin{aligned} p_3(x,y)={\left\{ \begin{array}{ll} 1.1&{}\quad \text {if}\, x^2+y^2\le 1\\ 10&{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

The corresponding eigenfunction $u(x,y)$ is shown in Fig. 3. Its shape resembles that of the one-dimensional case (see Fig. 2, right).

Fig. 3

Eigenfunction for $p_3(x,y)$. $\underline{\lambda }= 4.3491$, residual 0.16

3.3.2 The Disk

We computed the eigenvalues for the disk for some constant values of $p(x)\equiv p$, namely $p=1.5,2,2.5$ and 4. The initial solution $u^0(x,y)$ corresponding to $p(x,y)\equiv p=2$ is the normalized first eigenfunction of

$$\begin{aligned} -\nabla ^2u(x,y)=\eta _2 u(x,y),\quad x^2+y^2< r^2 \end{aligned}$$

that is

$$\begin{aligned} u^0(x,y)=\frac{\tilde{u}^0(x,y)}{\left\| \tilde{u}^0\right\| _{2}},\quad \tilde{u}^0(x,y)=J_0\left( j_{0,1}\frac{\sqrt{x^2+y^2}}{r}\right) , \quad \eta _2=\underline{\eta _2}=\left( \frac{j_{0,1}}{r}\right) ^2 \end{aligned}$$

where $J_0$ is the Bessel function of the first kind of order zero and $j_{0,1}\approx 2.40482555769577$ is its first zero, computed by the commands

in GNU Octave 3.8. In Table 4 we compare our results for the unit disk ($r=1$), on a mesh with 2,032 vertices and 3,912 triangles, with those provided in Ref. [9, Table 1] (there reported with five or six significant digits). We notice that for $p(x)\equiv 2$, the analytical solution is $j_{0,1}^2\approx 5.7832$ and that our value is more accurate.

Table 4 Values of $\underline{\lambda }^p$ for some values of constant $p(x)\equiv p$

3.3.3 The Annulus

The initial solution $u^0(x,y)$ corresponding to $p(x,y)\equiv p=2$ for the annulus is the normalized first eigenfunction of

$$\begin{aligned} -\nabla ^2u(x,y)=\eta _2 u(x,y),\quad a^2<x^2+y^2<b^2 \end{aligned}$$

that is

$$\begin{aligned} u^0(x,y)=\frac{\tilde{u}^0(x,y)}{\left\| \tilde{u}^0\right\| _{2}},\quad \eta _2=\underline{\eta _2}=\left( \frac{k_{0,1}}{a}\right) ^2 \end{aligned}$$

where

$$\begin{aligned} \tilde{u}^0(x,y)=J_0(k_{0,1})Y_0\left( k_{0,1}\frac{\sqrt{x^2+y^2}}{a}\right) - Y_0(k_{0,1})J_0\left( k_{0,1}\frac{\sqrt{x^2+y^2}}{a}\right) \end{aligned}$$

If we choose $a=0.5$ and $b=1$, then $k_{0,1}\approx 3.12303091959569$ is the first zero of

$$\begin{aligned} J_0(z)Y_0\left( z\frac{b}{a}\right) -Y_0(z)J_0\left( z\frac{b}{a}\right) \end{aligned}$$

computed by the commands

and $Y_0$ being the Bessel function of the second kind of order zero.

The eigenvalues in Table 5 were obtained on a mesh with 1,502 vertices and 2,780 triangles. The exact value of $\underline{\eta _2}$ for the analytical known case $p(x)\equiv 2$ is $4k_{0,1}^2$.

Table 5 Values of $\underline{\lambda }^p$ for some values of constant $p(x)\equiv p$

4 Conclusions

We described an effective method for the computation of the first eigenpair of the $p(x)$-Laplacian problem. The numerical results, in one- and two-dimensional domains, agree well with those analytical or numerical available in literature for the constant case $p(x)\equiv p$. The main contribution of the present work is a fast and reliable method for the general case of variable exponent $p(x)\ge p^->1$, applied for the first time to some test problems in the critical range $p(x)<2$ somewhere in the domain.