1 Discovery of Second Sound and Its Basic Properties

The proposition that heat in liquid \(^4\)He below the \(\lambda \)-point propagates as a wave can be attributed to Tisza [1], who also calculated the velocity of such a heat wave (for comprehensive historical context, see [2]). The existence of such a heat, or entropy, wave is based on the phenomenological two-fluid description of superfluid \(^4\)He, which for historical reasons is called He II. The two-fluid model, introduced by Tisza [3] and further developed on a more rigorous basis by Landau [4,5,6], states that He II can be thought of as consisting of two fluids—a normal fluid and a superfluid—each possessing an independent density and velocity field (\(\rho _n\), \(v_\text {n}\) and \(\rho _s\), \(v_\text {s}\), respectively) with total density and mass flow given by the sum of the components. The normal component has finite entropy and viscosity, both of which vanish for the superfluid component. Landau predicted that there should exist two different types of waves in superfluid helium: ordinary sound and heat waves which he called second sound, similar in nature to the heat waves proposed by Tisza.

The usual longitudinal sound mode in fluids, representing a propagating density wave, also exists in He II and is termed first sound. Here the normal and superfluid components oscillate in phase, so that the temperature, corresponding to the ratio of their densities, remains approximately constant. In the second sound mode, however, the normal and superfluid components oscillate in anti-phase with each other so that the total density \(\rho =\rho _n+\rho _s\) and pressure remain constant. Because the entire entropy content is carried by the normal fluid, second sound can be considered to be an entropy or temperature wave. The existence of the theoretically predicted second sound was subsequently confirmed experimentally by Peshkov [7], who also confirmed [8] the validity of Landau’s calculation of the speed of second sound at very low temperature. Second sound in He II can be generated and detected by various means and will be discussed in more detail below, but perhaps the simplest method is to generate it by applying an ac voltage of frequency f across a resistive heater and to detect it by a sensitive thermometer at frequency 2f.

Since its discovery, second sound in He II has been extensively investigated. Its observed velocity at low amplitude \(u_{20}\) at the saturated vapor pressure, based on experiments of several low temperature research groups, is accurately known and has been conveniently tabulated by Donnelly and Barenghi [9]. By lowering the temperature below \(T_\lambda \), \(u_{20}\) quickly rises from zero to about 20 m/s and displays two extrema—a very shallow maximum at 1.65 K and a minimum at around 1.1 K—and then, it rises toward its theoretical zero-temperature limit of \(u_{10}/\sqrt{3}\), where \(u_{10}\approx 240\) m/s [9] is the first sound velocity.

The velocity of a second sound traveling wave depends on its amplitude and, to a first approximation, can be written as

$$\begin{aligned} u_2 = u_{20} (1 + \beta \varDelta T ); \quad \beta =\frac{\partial }{\partial T} \ln \left( u_{20}^3 \frac{C}{T}\right) . \end{aligned}$$
(1)

Here, \(\varDelta T\) is the wave amplitude, \(u_{20}\) is the velocity of a wave of infinitesimal amplitude, and C denotes the heat capacity per unit mass of liquid helium at constant pressure. The sign of the nonlinearity coefficient \(\beta \) [10] depends on the temperature T and pressure p [10, 11]. Under saturated vapor pressure, where most experiments are performed, \(\beta \) is positive at \(T < T_\mathrm{inv} = 1.88\) K, passes through zero and becomes negative for \( T_\mathrm{inv}< T < T_\lambda \). It follows that the wave energy can flow both toward higher and lower frequencies, leading in particular to the formation of the acoustic analog of giant oceanic (rogue) waves which can endanger shipping. While realistic controlled experiments on rogue waves are not feasible, second sound provides an excellent, laboratory-accessible, model system of nonlinear wave interactions believed to be involved in their generation. It is indeed easy to experimentally adjust \(\beta \) simply by changing the temperature, which makes second sound an ideal candidate for testing nonlinear wave interactions, in particular wave turbulence. These interesting applications of second sound are, however, beyond the scope of this review—for details, see [12, 13] and references therein.

Dispersion of second sound, significant only very slightly (of order 1 \(\upmu \)K) below the superfluid transition, is extremely weak [14] and in connection with investigations of quantum turbulence, can be neglected.

We note that Lu and Kojima observed second sound at low frequencies of order 1 Hz in superfluid \(^3\)He-B [15]. By using a cylindrical cavity, they measured the speed of second sound, of order 1 cm/s, at various pressures. Second sound in superfluid \(^3\)He-B is, however, strongly attenuated and to the best of our knowledge was not yet attempted to use in experimental investigation of quantum turbulence in this quantum fluid.

2 Quantized Vortices, Quantum Turbulence and Their Interaction with Second Sound

The idea of quantized circulation belongs to Onsager [16]. It was further developed by Feynman [17] and experimentally confirmed by Vinen [18]. Quantized vortex lines exist in the superfluid component of He II and can be viewed as hollow Angström-sized tubes with fixed circulation \(\kappa = h/m_4 \approx 0.997 \times 10^{-7}\) m\(^{2}\)s\(^{-1}\), where h is the Planck constant and \(m_4\) denotes the mass of a \(^4\)He atom. Unlike a classical vortex, which decays due to viscous forces, the superflow around an isolated vortex line is persistent: By the quantization of circulation, the vortex is topologically protected.

According to classical fluid mechanics, a container filled with an ordinary viscous fluid rotates as a solid body at constant angular velocity \(\Omega \) about the vertical axis. In rotating He II, the superfluid component becomes threaded by a hexagonal lattice of rectilinear singly quantized vortex lines with areal density \(n_{\mathrm{{v}}} = 2\Omega /\kappa \) and on length scales larger that the mean inter-vortex distance \(\ell =1/\sqrt{L}\) mimics solid body rotation. Here L is the vortex line density, i.e., the total length of quantized vortex lines in a unit volume of He II.

An isothermal He II sample with no quantized vortices would support two independent velocity fields. In practice, quantized vortex lines are always present in the superfluid component of a macroscopic sample of He II [19, 20], and interact with the phonons and rotons that make up the normal fluid. These quasiparticles are scattered off the vortex cores, giving rise to a mutual friction force acting on the vortex lines as they move with respect to the normal fluid. As a result, the normal and the superfluid velocity fields are no longer independent.

Mutual friction can be described via its action on second sound which is attenuated by vortex lines. Hall and Vinen [21, 22] studied second sound in rotating He II and found that the second sound is unaltered (in the first approximation) if the wave propagates in the direction parallel to the vortex lines; however, if the wave propagates in the direction perpendicular to the vortex lines, the amplitude of the wave is attenuated.

These experimental results are consistent with a mutual friction force (per unit volume) of the form [21, 22]

$$\begin{aligned} {\mathbf {F}}_\text {ns}=B \frac{\rho _s \rho _n}{\rho } {\hat{{\varvec{\Omega }}}} \times [{\varvec{\Omega }} \times (\overline{{\mathbf {v}}_s}-\overline{{\mathbf {v}}_n})] + B' \frac{\rho _s \rho _n}{\rho } {\varvec{\Omega }} \times (\overline{{\mathbf {v}}_s}-\overline{{\mathbf {v}}_n}) \end{aligned}$$
(2)

where \(\overline{{\mathbf {v}}_s}\) and \(\overline{{\mathbf {v}}_n}\) are velocity fields averaged over fluid volumes containing many vortex lines, \(\varvec{\Omega }\) is the angular velocity of the container and \({{\varvec{\hat{\Omega }}}}\) is the unit vector in the direction of \(\varvec{\Omega }\). The experimentally observed quantities B and \(B'\) are weakly frequency dependent, but their values are well known and tabulated [9].

Measurements of second sound signals in rotating containers showed a dependence of the attenuation on the angle \(\theta \) between the vortex lattice and the direction of propagation of the second sound [23, 24]. Assuming that all vortices point in the same direction, we can write \(\varvec{\Omega } = \frac{1}{2}\kappa L{{\varvec{\hat{\Omega }}}}\) (i.e., the macroscopic superfluid vorticity \(\varvec{\omega }= 2\varvec{\Omega }\) and \(|\varvec{\omega }| = \kappa L\)). Neglecting the non-dissipative terms in the mutual friction, Eq. (2) reduces to

$$\begin{aligned} \mathbf {F}_\text {ns} = -B\kappa \frac{\rho _s\rho _n}{2\rho }L\left( \overline{\mathbf {v}_n} - \overline{\mathbf {v}_s}\right) \sin ^2\theta , \end{aligned}$$
(3)

which is usually referred to as the “sine squared law”.

Quantum turbulence can be loosely defined as the most general form of motion of quantum fluids displaying superfluidity [25]. In this review, we consider quantum turbulence in He II at finite temperatures above 1 K, where it can be studied (and generated) by second sound. Quantized vortices in the superfluid component usually take the form of a dynamic tangle that coexists with classical-like turbulent flow of the normal component, making up what is usually called quantum turbulence (i.e., turbulent flow of a quantum fluid). In this sense, quantized vortices are not a necessary ingredient of quantum turbulence, as one can imagine a two-fluid flow of He II consisting of turbulent normal flow and potential superflow. Indeed, in the hypothetical case of a macroscopic sample of He II free of quantized vortices [19] (i.e., without mutual friction coupling the two velocity fields), in an isothermal flow the normal and superfluid components move independently. This kind of flow cannot be probed by second sound. In practice, however, remnant vortices always exist in macroscopic samples of He II and extrinsic nucleation of quantized vorticity is easily triggered even by low flow velocities of order 1 cm/s [19, 26, 27].

3 Experimental Determination of Vortex Line Density Using Second Sound

The intensity of quantum turbulence is usually quantified by the vortex line density L, i.e., by the total length of a vortex line in a unit volume. This quantity is, however, not directly detected by the second sound attenuation in the experiment. In view of the “sine squared law”, Eq. (3), one has to assume how the vortices in the tangle are arranged as the detected attenuation, i.e., the vortex line density, is scaled by \(\left\langle \sin ^2\theta \right\rangle \) [28]. As was already discussed, two limiting cases regarding the vortex lattice correspond to \(\left\langle \sin ^2\theta \right\rangle = 1\) or 0 for second sound wave propagating perpendicularly or along the vortex lattice, respectively. Experimentally, more relevant edge cases are a fully isotropic tangle, for which \(\left\langle \sin ^2\theta \right\rangle = 2/3\) and the case of planar vortex loops lying in planes parallel with the second sound propagation direction (a case important for thermal counterflow, see Sect. 4) for which \(\left\langle \sin ^2\theta \right\rangle = 1/2\).

Experimentally, one can measure the damping of a high-frequency second sound beam propagating through a region of turbulence [29]. However, a more common experimental arrangement is based on the measurement of the damping constant of a resonator where a second sound standing wave is created, with the turbulence to be studied created inside the resonator. The use of a second sound standing wave greatly improves the signal-to-noise ratio; however, it introduces another potential complication. The energy dissipation due to the mutual friction is given by \(\mathbf {F}_\text {ns}\cdot \left( {\mathbf {v}}_\text {n} - \mathbf v_\text {s}\right) \), which is a spatially dependent quantity for a standing wave inside the resonator. Second sound attenuation therefore samples the vortex tangle inside the resonator unevenly, and in fact can be used to detect inhomogeneous distributions of vortex lines [30]. The effective vortex line density \(L_n\) (obtained using Eq. (5) below) seen by the nth second sound mode is given by (for a one-dimensional resonator and assuming symmetry around the center of the resonator)

$$\begin{aligned} L_n = \langle {L(x)} \rangle _x - \frac{1}{D}\int _0^D L(x)\cos (2\pi nx) {\text {d}}x, \end{aligned}$$
(4)

where L(x) is the “true” distribution and the integration is over the entire one-dimensional resonator of length D; \(\left\langle \cdot \right\rangle _x\) denotes spatial averaging. The mode dependence of \(L_n\) is given by the appropriate Fourier component of L(x). For sufficiently high n, the Fourier component can be neglected (due to the convergence of the Fourier series) and \(L_n\) is simply the mean vortex line density in the resonator. Note that knowing \(L_n\), the inverse problem can be solved and the variation of L(x) could, in principle, be probed by measuring \(L_n\) for different modes of the resonator. However, this technique is experimentally challenging as it requires multiple high-quality low-lying modes of the second sound resonator.

In most of the Prague experiments [26, 28, 31, 32], earlier experiments by Donnelly’s group in Eugene [33,34,35] and recent experiments in Tallahassee [36,37,38,39], the second sound transducers and receivers of identical construction are mounted flush in the opposing walls of the channel. They consist of a porous (pores of roughly 100 nm) membrane with one gold-plated side in contact with the channel body. A circular brass electrode is spring loaded against the other side of the membrane, thus forming a capacitor with one vibrating plate. The membranes and the channel are held at a bias voltage, typically \(V_\text {bias} \approx 100\) V, while the backing electrodes are held near ground. The porous membrane of typically 10 mm in diameter induces a second sound wave by oscillating and displacing only the viscous normal component of helium, thereby causing higher local concentration of normal component and hence higher temperature. To create a second sound wave, the membrane of the transducer is actuated by sine-wave voltage, created by a function generator, connected to the backing brass electrode. The channel walls constitute a resonator for such wave, which is detected using the receiver placed across the resonator, as an oscillating current measured using a lock-in amplifier between the backing electrode and the ground, induced by the oscillating biased membrane.

It can be shown [26], that the vortex line density of a homogeneous and isotropic tangle inside a one-dimensional resonator of the length D (if second sound propagates across the channel then D is its width) is

$$\begin{aligned} L \cong \frac{3u_{2}}{B \kappa D}\ln \left( \frac{1 + p^2P + \sqrt{2p^2P + p^4P^2}}{1 + P + \sqrt{2P + P^2}}\right) \simeq \frac{6\pi \varDelta _0}{B\kappa }\left( \frac{a_0}{a} - 1\right) \,. \end{aligned}$$
(5)

Here, \(p = a_0 / a\), \(a_0\) is the amplitude when there is no flow in the channel and a is the amplitude with the flow; \(P = 1 - \cos (2 \pi D \varDelta _0 / u_{2})\); \(\varDelta _0\) is the full width at the half-maximum height of the second sound resonance peak measured in quiescent He II. \(D \varDelta _0 / u_{2}\) is assumed to be small. For inhomogeneous tangles, Eq. (5) gives \(L_n\) in Eq. (4) for a particular resonance mode used. The simplified version of Eq. (5) becomes an overestimate of L (by less than 10% at the typical highest experimentally achievable \(L\approx 10^7\) cm\(^{-2}\)), however, in view of other uncertainties associated with second sound attenuation, this over-estimation can typically be neglected. First, the usual assumption of an isotropic tangle can cause, in view of Eq. (3), an error of the order of 10%. Second, this method of obtaining L is necessarily relative, as it compares two levels of attenuation: the calculated value L is relative to the remnant vorticity present in the quiescent state, which is not directly accessible with second sound attenuation. Inferences about the remnant vortex line density [40] \(L_R\) can be made by comparing the attenuation before turbulence is created and after it decays [32] with typical values of \(L_R\) of order \(10^2\) cm\(^{-2}\).

To measure L using Eq. (5), one requires only the resonance amplitude a and not the entire resonance peak. Typically, the amplitude is measured by a lock-in amplifier with the resonator tuned to one of its resonance frequencies. However, physical processes of creation and decay of quantum turbulence typically cause sufficiently large and abrupt changes in the temperature that can overwhelm its control in the cryostat. Moreover, a longitudinal thermal gradient of up to a few mK is naturally associated with quantum turbulence created in the particular He II channel flow under scrutiny, which causes a frequency shift of the second sound resonance, as shown in Fig. 1 for the case of thermal counterflow. This invalidates the time-resolved measurements of the second sound amplitude at fixed frequency. We are aware of two ways to overcome this difficulty.

Fig. 1
figure 1

Increased attenuation of a second sound resonance (the upper and lower families of curves represent the in-phase and quadrature responses of the lock-in amplifier) with increasing flow velocity (and thus increasing vortex line density). The shift in the central frequency is caused by the temperature increase. The data shown were measured in a \(7\times 7\) mm\(^2\) channel at the temperature 1.95 K in thermal counterflow with heat flux as indicated in the figure (Color figure online)

Full size image
Fig. 2
figure 2

Real amplitude from the off-resonant complex amplitude. (left) The second sound resonance in the plane of the complex amplitude (the color corresponds to the real resonant amplitude) with superimposed typical trajectory (i.e., a time-dependent signal) measured with fixed excitation frequency. (right) Close-up of the fixed-frequency measurement. The background color field indicates the real resonant amplitude corresponding to the complex off-resonant amplitude. The color mapping in the left and right panels is the same. The arrows in the right panel indicate the time evolution of the signal (Color figure online)

Full size image

One may consider the shape of the resonance peak in the plane of the complex amplitude \({\tilde{a}}\). By plotting the amplitude of the second sound signal in the complex plane in the vicinity of the resonance for different attenuation levels, see Fig. 2, one obtains a set of (distorted) circles. For a fixed attenuation, these curves do not depend on the slight temperature shift. The complex amplitude of the second sound signal at fixed attenuation level (i.e., constant vortex line density) subject to changes in temperature or frequency (sufficiently small not to affect mutual friction parameters significantly), will move only along the “circle” corresponding to the particular level of attenuation. By measuring the resonances beforehand, one can calibrate, by suitable interpolation, a patch of the complex plane to obtain the correct real amplitude a from the off-resonant complex amplitude \({\tilde{a}}\). For more information regarding the implementation of this method, see Refs. [41, 42].

Therefore, it is clear that deviating too far from the central frequency decreases the resolution. Another difficulty arises when the resonance peaks are disturbed (e.g., by neighboring spurious resonances)—the circles of the complex amplitude can cross, and thus, it is not possible to uniquely assign a real resonant amplitude to the complex amplitude. These difficulties limit the applicability of the compensation method only to a neighborhood of the central frequency of the resonance (typically about the width of the resonance) that depends on the particular shape of the resonance peak.

The Gainesville group recently developed a tracking system to overcome the difficulty of temperature changes occurring during the experiment. Their tracking method uses a feedback loop to adjust the frequency of the driving ac voltage to minimize the detected quadrature component and hence track the resonance. When the resonance frequency is shifted while measuring L, the tracking system ensures that oscillation takes place at the resonance frequency. For details, we direct the reader to Ref. [43].

Fig. 3
figure 3

Illustration of three types of quantum two-fluid flows of He II. Thermal counterflow is most easily generated by placing a heat source at the closed end of a channel which is open to the helium bath at the other end. Coflow is any flow generated by classical means, for example pressure-driven steady flows or flows generated by towed grids, i.e., flows where the two components are not forced differently. The last type of flow, pure superflow, is analogous to thermal counterflow but only the superfluid component flows through the channel, on average. The flow occurs upon forcing He II by pressure through a superleak—a porous filter which is impenetrable to the viscous normal component but allows a through-flow of the inviscid superfluid component (Color figure online)

Full size image

4 Second Sound Investigations of Channel Flows of He II

Using mechanical and/or thermal drives, a variety of two-fluid channel flows can be generated, as illustrated in Fig. 3. Classical-like mechanical forcing (e.g., the action of compressing bellows or towing a grid through stationary helium) results in a coflow, the closest analog to classical viscous channel flows, in which the normal fluid and superfluid move, on average, with the same mean velocity in the same direction. Quite generally, the two components of He II can also be made to flow, on average, relative to each other, a situation called counterflow. In the special case of counterflow, termed thermal counterflow, when one side of the channel is heated and the opposite one is open to the helium bath and there is no net mass flow, both components move relative to the channel walls in opposite directions. In another special case called pure superflow, only a net flow of the superfluid component occurs in the channel, while the normal component remains (on average) stationary. Pure superflows can be generated both mechanically (e.g., by compressing bellows, as for coflow) and thermally (as for counterflow), in both cases using superleaks. All these types of quantum turbulent channel flows have been investigated by second sound attenuation. Here we review only the basic experimental findings.

For thermal counterflow, the mass transport by the flow vanishes, i.e., \(\rho _s \overline{\mathbf {v}_s} + \rho _n \overline{\mathbf {v}_n} = 0\). The entropy deposited into He II by the heat flux per unit area \(\dot{q}\) is carried away by the normal fluid with velocity \(v_n=\dot{q}/(ST\rho )\), where S is the specific entropy of He II. From the last two equations it follows that the counterflow velocity \(v_\mathrm{ns} = |v_n - v_s |\) is \(v_\mathrm{ns} = \dot{q} / (\rho _s ST)\). For coflow and pure superflow, the channel flow velocity is given by the experimental boundary conditions, e.g., by the rate of volumetric compression of a bellows used to drive the flow.

Second sound is uniquely suited for the study of quantum turbulence in channel flows as the channel itself is typically used as the second sound resonator. Second sound attenuation allows a simple and non-intrusive way of measuring vortex line density in steady flows and also turbulent dynamics in non-stationary flows, the most important example of which being the free decay. In addition, by utilizing multiple resonance modes the spatial distribution of the vortex line density inside the channel can be studied, although this technique has so far received little attention.

4.1 Quantum Turbulence in Steady Flows

When the quantum turbulence is allowed to remain in a steady state for a sufficiently long time, the most straightforward and reliable way to measure the vortex line density is by measuring the full resonance curve, as sketched in Fig. 1. Having access to the entire resonance curve eliminates problems with the central frequency moving due to possible temperature shifts.

In channel flows, this technique has been extensively used to characterize the relationship between the suitably defined flow velocity for the particular flow (i.e., the mass flow velocity or the counterflow velocity) and the steady-state vortex line density.

Historically, the first quantum turbulent flow to be extensively studied was the thermal counterflow investigated by Vinen [44,45,46,47]. He used a Eureka wire heater for generating the second sound and a phosphor bronze wire resistance thermometer to detect it. He found that in its steady state the second sound suffers a fairly severe total attenuation of the form \(\zeta =\zeta _0+\zeta '(W)\), where \(\zeta _0\) is the residual attenuation in the absence of the longitudinal heat current through the channel, which was translated to vortex line density through Eq. (5). In particular, it was found that in the steady state, L scales with \(v_\text {ns}\) as

$$\begin{aligned} L = \gamma ^2(v_\text {ns}- v_\text {c})^2, \end{aligned}$$
(6)

where \(\gamma \) is a temperature dependent parameter and \(v_\text {c}\) is small (typically of the order of 1 mm/s) critical velocity below which no turbulence is observed.

For an unbounded system, any two flows with the same mean \(v_\text {ns}\) can be transformed into each other by a Galilean transformation. Thus it is not surprising that the steady-state relationship (6) can be immediately generalized to any flow with forced nonzero mean \(v_\mathrm{ns}\), such as the pure superflow, and this has indeed been observed [26]. Real systems, however, are finite and the velocity of individual components with respect to the system walls could, in principle, be important. It is thus remarkable that the parameter \(\gamma \) was found to be very similar for pure superflow and thermal counterflow in strongly turbulent flows (i.e., the TII state of thermal counterflow [48]). Contrary to the weak geometrical dependence of \(\gamma \), there is evidence that the scaling of the critical velocity \(v_\text {c}\) with system size is different for pure superflow and thermal counterflow [26], but further detailed measurements of second sound attenuation for very low drives in thermal counterflow and pure superflow in channels of different dimensions are clearly needed.

The situation drastically changes when the components’ mean velocities are not forced to differ, such as the case of bellows-driven coflow [27]. For this quasi-classical flow, it was found that

$$\begin{aligned} L \propto v^{3/2}, \end{aligned}$$
(7)

where v is now the mass flow velocity. Introducing the quantum length scale—inter-vortex distance \(\ell = L^{-1/2}\), Eq. (7) can be rewritten as \(\ell \propto v^{-3/4}\), which resembles the well-known scaling of the classical Kolmogorov dissipation length scale \(\eta \) with the Reynolds number \(\text {Re}\), i.e., \(\eta \propto \text {Re}^{-3/4}\). Indeed, it holds quite generally that quasi-classical quantum turbulence can be consistently described by connecting the rate of energy dissipation of the flow \(\epsilon \) with the vortex line density by the use of the effective kinematic viscosity \(\nu _\text {eff}\) [49, 50]

$$\begin{aligned} \epsilon =-\frac{{\text {d}}E}{{\text {d}}t}= \nu _\mathrm{eff}(\kappa L)^2, \end{aligned}$$
(8)

i.e., the classical vorticity is identified with the quantity \(\kappa L\) in full analogy with the rotating bucket. As will be shown later, the quasi-classical relationship (8) is particularly important for the decay of quantum turbulence (where, in fact, it was historically introduced [49]).

One aspect of steady-state second sound measurements that has so far received insufficient attention is the use of multiple modes of the resonator to map out inhomogeneous distribution of vortex line density. For a simple rectangular channel-like resonator (i.e., with a cosine-shaped standing second sound wave), the effective vortex line density seen by the nth resonance mode is given by Eq. (4). So far, this method has been used [30] only with the two lowest modes for the case of pressure-driven coflow, where evidence was found of increased vortex line density near the walls and a homogenizing effect of an upstream grid was observed. This technique, however, clearly holds greater promise than has so far been experimentally realized and is currently being thoroughly tested in ongoing experiments in Prague.

4.2 Quantum Turbulence in Non-steady Flows

Second sound attenuation has been fruitfully utilized to study the dynamical behavior of vortex line density in non-steady quantum flows, in particular the free decay. The temporal decay of vortex line density has been extensively studied in all three types of channel flow (Fig. 3). The experimental methodology is identical for all flows: The amplitude of the second sound standing wave is measured at resonance for a chosen resonance mode (usually at a fixed frequency), which is then used to calculate time-dependent vortex line density via Eq. (5). For time-resolved measurements, it is crucial that the observed changes in the second sound signal are due to changes in vortex line density and not due to shifts of the resonance frequency caused by changing temperature. Thus a good temperature stability in the cryostat is important for successful measurement (usually the stability of the order of 0.1 mK) and, especially for thermally driven counterflow, some compensation procedure, such as the one described in Sect. 2, is often necessary.

For time-dependent measurements, the changing attenuation of second sound is accurately reflected only at timescales larger than the natural second sound response time\(t_\text {char}^\text {ss}\), given by the time-dependent inverse of the second sound resonance width (i.e., product of the quality factor and the time it takes for second sound to propagate across the resonator). This sets the smallest resolvable timescale. Typically, \(t_\text {char}^\text {ss} \le 100\) ms.

The understanding of the dynamical behavior of vortex line density in coflows and counterflows has been historically developed along somewhat different lines and we will briefly discuss them in turn.

4.2.1 Quasi-classical and Coflow Decay

A particularly important class of experiments concerns decaying quantum turbulence in He II generated by a towed grid in channels of square cross section. The experiments were performed during the 1990s in Donnelly’s group in Oregon [35, 51, 52], followed by Ihas’ group in Gainesville [43] and recently by Guo’s group in Tallahassee [53]. These experiments revealed that the decaying vortex line density is complementary to a classical fluid dynamical problem of great interest—indeed, the temporal decay of turbulent energy (and vorticity) in the absence of sustained production is the topic of many textbooks and reviews. Over a wide range of times, the observed decay follows \(L \propto (t-t_0)^{-3/2}\), where \(t_0\) is the virtual origin time and \(t=0\) marks the beginning of the decay. This relation is fully consistent with the quasi-classical picture given by Eq. (8).

We shall not discuss the complex temporal decay of L displaying several subsequent decay regimes; we direct the reader to a review by Skrbek and Sreenivasan [54]. Recently, decaying grid turbulence has been probed simultaneously by second sound attenuation and by the visualization of the normal fluid flow by using neutral excimer He* molecules [38], which allowed for the experimental confirmation [53] of the theoretically predicted [55] temperature dependent intermittency enhancement in quantum turbulence.

Quasi-classical decay was observed also in pressure-driven coflow [56] and as a late decay regime in both pure superflow and thermal counterflow [32]. The second sound data from the late quasi-classical decay and steady-state scaling of coflow allows one to determine the effective kinematic viscosity \(\nu _\mathrm{eff}\) of turbulent He II [27, 50, 57]. The recent visualization study [38] of the quasi-classical decay of thermal counterflow combined with vortex line density measurements provided an independent check of Eq. (8). The data from different experiments display general agreement, despite significant scatter, indicating that the effective viscosity is a well defined parameter.

4.2.2 Dynamical Behavior of Counterflows

In his pioneering experiments, Vinen [44] investigated both steady state and, by photographing the oscilloscope screen, also the transient behavior of counterflow quantum turbulence. He also introduced a phenomenological model of counterflow turbulence based on the concept of a random vortex tangle characterized by a single variable, the (approximately homogeneous and isotropic) vortex line density L [44]. He argued that L obeys the following equation (now called the Vinen equation):

$$\begin{aligned} \frac{{\text {d}}L}{{\text {d}}t}= \frac{\rho _n B}{2\rho } \chi _1 v_\mathrm{ns} L^{3/2}- \frac{\kappa }{2\pi } \chi _2 L^2+g(v_\mathrm{ns}), \end{aligned}$$
(9)

where \(\chi _1\) and \(\chi _1\) are undetermined dimensionless constants and B is the (dimensionless) mutual friction parameter, tabulated by Donnelly and Barenghi [9]. The arguments leading to Eq. (9) are dimensional; however, the equation was later derived on a number of assumptions from the laws of vortex dynamics in the local induction approximation by Schwarz [58]. The first two terms on the right-hand side describe the production and the decay of turbulence, while the unspecified function \(g=g(v_\mathrm{ns})\) was included to account for the observation of a small critical velocity \(v_{c}\) of the order of 1 mm/s (see Eq. (6)). Vinen’s approach accounts fairly well for most of the phenomena observed in steady-state counterflow turbulence in relatively wide channels of order 1 cm.

While the Vinen equation quantitatively describes the steady-state of counterflow turbulence (i.e., \(L\propto v_\text {ns}^2\)), the temporal decay of L in counterflow turbulence was a long-standing puzzle. Indeed, this equation predicts inverse time dependence \(L(t)\propto 1/t\) which was rarely observed, for example, in the case when spatially inhomogeneous turbulence was created by a pair of ultrasonic transducers and detected by a pulsed ion technique [59] or for low starting L [39]. Most experiments displayed the predicted \(t^{-1}\) decay for very short time, often followed by a well-pronounced temporary increase in vortex line density (the so-called bump) and a classical-like \(t^{-3/2}\) decay at later times. Various explanations of the bump have not been convincing [28, 60, 61], and the satisfactory understanding was achieved only recently. In short, following Gao et al. [39], there are two length scales at which the energy is injected. At small scales, the energy is taken from the mean flow by the ballooning of favorably oriented vortex loops and Kelvin waves via the action of mutual friction [58]; this small-scale energy injection induces a “quantum peak” [62] in the turbulent energy spectrum located near the quantum scale \(\ell \). Additionally, there is a largescale injecting mechanism acting on the scale of the size of the system, i.e., the channel width D. This energy would normally be distributed along a classical Richardson cascade following a classical K41 spectrum, however, in the case with an imposed difference between the normal and superfluid mean velocities, which pulls eddies in the two components apart, there is additional dissipation across all scales and the spectrum is steeper than the classical K41; the exact roll-off exponent depends on the temperature and heat flux [36, 63]. When the counterflow is switched off and the decay starts, the quasi-classical spectrum is established (it takes roughly the turnover time of the large eddies) and energy flow to the inter-vortex scale resumes. The quasi-classical spectrum is established only in finite time, during which the quantum peak in the energy spectrum decays to be subsequently partially replenished by the restored energy flux, thus resulting in temporary increase in L, experimentally seen as a bump in its temporal decay.

For completeness, let us note here that in thermal counterflow the tangle is found to be slightly anisotropic [33] and depolarizes during the decay [28].

In pure superflow, the normal fluid is not directly forced but can be entrained by the turbulent superflow at large scales, although its mean through-flow is blocked by the superleaks. It is thus plausible that the pure superflow energy spectrum is closer to a quasi-classical one and the energy flux to small scales is suppressed to a lesser degree, which would translate to a less pronounced bump, in accordance with experimental observation [32].

It is now clear that a simple dynamical equation of the type of Eq. (9) cannot fully account for the wealth of experimentally observed phenomena; however, finding a simple closure that connects vortex line density and flow velocity would be useful (e.g., for numerical calculations based on continuous models such as the HVBK [25] or for engineering calculations of heat transfer, where the vortex line density is the source of the impedance to the heat flow). Recently, there has been progress on theoretical and numerical grounds [64,65,66] with several new proposals for the dynamical equation for the vortex line density.

It follows from very recent second sound experiments in square-wave modulated thermal counterflow [31] that a dynamical equation of the form of Eq. (9) is suitable for the description of the growth of turbulence for relatively low densities of the tangle. For the higher densities, no currently available dynamical equation accurately accounts for the experimental time dependence of vortex line density.

At the same time, our recent experiments [31] revealed that the region of validity of Eq. (9), as derived by Schwarz [58], is greater than perhaps expected. In particular, in the regions of \(L\simeq 10^5\) cm\(^{-2}\), Eq. (9) accurately describes the growth of turbulence even though the “bump” observed during the decay invalidates any first-order differential equation for L without explicit time dependence. Moreover, the agreement with experiments (including early decay) can be significantly improved if the ratio of the RMS curvature of vortex lines to the inter-vortex distance, as introduced and termed \(c_2\) by Schwarz [58], is allowed to vary. In fact, Ref. [31] provides an experimental estimation of the curvature parameter \(c_2\), which is found to be in very good agreement with numerical results in both absolute value and temperature dependence. This is remarkable, as the local induction approximation introduced by Schwarz neglects non-local interactions between vortex lines and, moreover, turbulence in the normal fluid is not taken into account.

We close the discussion of non-steady counterflow by estimating the time scales of two parasitic effects that may obscure the intrinsic dynamics of L(t). Indeed, to study strongly non-stationary flows, one needs to thoroughly understand all underlying physical processes triggered in the channel by switching on and off the applied heat flux. It is useful to describe these processes by their characteristic times.

1. Kinetic characteristic time. In steady-state counterflow in a channel of length \(L_{c}\), both the normal and superfluid components of He II move, carrying kinetic energy. Neglecting the flow generated in the bath outside the channel and the turbulent velocity inside the channel, it takes time \(t_\mathrm{char}^\mathrm{kin}\) to gain this kinetic energy from the heater, which can be estimated from the energy balance as [31]

$$\begin{aligned} t_\mathrm{char}^\mathrm{kin}= \frac{\rho _n}{2 \rho _s \rho S^2 T^2} L_{c} \dot{q}. \end{aligned}$$
(10)
Fig. 4
figure 4

Kinetic (solid lines) and thermal (dashed lines) characteristic timescales given by Eqs. (10) and (11), respectively, for \(L_c = 21\) cm and a channel of \(7\times 7\) mm cross section. Dependencies for the three experimental temperatures 1.45, 1.65 and 1.95 K are shown (lines from top to bottom). The thermal time constant has been calculated assuming heat input was changed from zero to the value indicated (i.e., the worst-case scenario) (Color figure online)

Full size image

2. Thermal characteristic time. Following [67], let us consider a switch of the applied heat input to the channel heater from \(\dot{q}_1\) to \(\dot{q}_2\). As shown already by Vinen [44], for high enough L a steady-state counterflow is accompanied by a temperature gradient, i.e., \(\dot{q} = \zeta (T) \nabla T^{1/3}\), where for any temperature \(\zeta \simeq \mathrm{const}\). Assuming a linear temperature profile and the open end of the channel at constant (i.e., bath) temperature, the excess heat contained in the channel is \(Q = C \rho A L_{c} |\varDelta T_2-\varDelta T_1|\) where \(\varDelta T = L_c \nabla T\) and \(L_c\) is the length of the channel. The specific heat, C, is assumed to be constant for the small (order of few mK) temperature changes. It can be shown [31, 67] that the time required to either conduct the excess heat away or supply it by the heater is given by

$$\begin{aligned} t_\mathrm{char}^\mathrm{th}= \frac{3C \rho |\varDelta T_2-\varDelta T_1|}{4 \zeta } L_{c}^{4/3}. \end{aligned}$$
(11)

For illustration purposes, Fig. 4 shows the calculated characteristic times \(t_\mathrm{char}^\mathrm{kin}\) and \(t_\mathrm{char}^\mathrm{th}\) for a particular case of one experimental channel used in Prague, 21 cm long and of square 0.7 cm cross section, for various applied heat fluxes at different temperatures. Estimated times \(t_\mathrm{char}^\mathrm{kin}\), \(t_\mathrm{char}^\mathrm{th}\) and \(t_\mathrm{char}^{ss}\) are generally rather short, of order 10 ms, the typical time constant of the lock-in amplifier. This, in turn, must be chosen based on the frequency and quality factor of the second sound resonance used for direct measurement of L in the channel. The processes described above ought to work simultaneously and in parallel. The actual limitation to the experiment is therefore given roughly by the longest time constant (i.e., the slowest process) for a given experimental configuration, typically 50 ms. It should be noted, however, that the thermal time constant can become significant for the cases of thermal counterflow with a “hot chamber” at the closed end of the channel [44].

5 Second Sound Investigations of Oscillatory Flows of He II

5.1 Quantum Turbulence Generated by Oscillating Objects

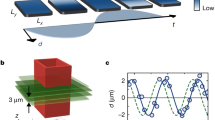
In a series of ongoing experiments, a quartz tuning fork is placed inside a cylindrical second sound resonator cavity [68]. In these experiments, the velocity of the tuning fork, v, is gradually increased and its damping is inferred, while the second sound resonance is simultaneously monitored.

Figure 5 shows the dependence of the inferred vortex line density and drag coefficient against the velocity of a 31 kHz tuning fork at 1.6 K. The vortex line density was inferred using Eq. (5), by setting \(A_{0}\) = 0.4402 mV, \(\varDelta f_{0}\) = 5.3658 Hz and B(1.6 K) = 1.194. The drag coefficient is defined as \(C_D = 2F/A\rho v^{2}\), where \(A = WL\) is the cross-sectional area of the fork perpendicular to the direction of motion.

Fig. 5
figure 5

Vortex line density (triangles, right axis) inferred from the second sound attenuation and the corresponding drag coefficient (circles, left axis) versus tuning fork velocity. Note that when the drag coefficient starts deviating from the laminar dependence \(C_{D} \propto v^{-1}\) (dashed line), the vortex line density detected by the second sound sensors starts to increase (Color figure online)

Full size image

The response exhibits the onset of extra damping when the velocity of the fork’s prongs exceeds 0.5 ms\(^{-1}\), marking the formation of some flow instability due to its motion. Attenuation of the simultaneously monitored 5th resonant mode of second sound increases at about the same velocity, indicating the production of quantized vortex lines and the development of quantum turbulence.

Although an exact determination of L in this case is complicated due to the presumably non-homogeneous structure of the produced vortex tangle, this kind of experiment is important in understanding the formation of quantum turbulence since it allows one to determine in which component of He II any instabilities first occurs. Indeed, very recent systematic measurements of high-Stokes-number flows of He II due to the oscillatory motion of various oscillators: a vibrating wire resonator, quartz tuning forks, double paddle and a torsionally oscillating disk, show that, depending on the temperature and geometry of the flow, either type of instability (i.e., classical-like instabilities in the normal flow or Donnelly–Glaberson instability in the superflow) may occur first, and moreover, a crossover caused by the temperature dependence of the viscosity of the normal fluid component may occur [69]. Measurements of second sound attenuation due to flows generated by various oscillating objects are ongoing, and ought to shed light on the complex processes leading to the transition to quantum turbulence in oscillatory flows of He II.

5.2 Quantum Turbulence Generated and Detected by Second Sound

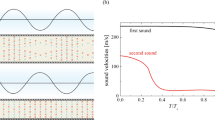
In this last section, we show that second sound can be used not only as a tool to probe quantum turbulence in He II, but that an intense enough second sound wave can also generate it. Indeed, Kotsubo and Swift [70, 71] used second sound resonators driven by a Peshkov transducer [72], in which superfluid is pumped through a stationary superleak made of compressed \(\mathrm {Al_2O_3}\) powder. The pump was bellows-driven by a stationary superconducting magnet exerting pressure against a superconducting plate attached to the moving end of the bellows. This method allows for the high-amplitude second sound needed to create quantum turbulence to be generated inside the resonator and, moreover, does not add any dc counterflow field within the resonator. The amplitude of the second sound was measured by a carbon composition resistor sanded down to a thickness of less than 50 \(\upmu \)m, calibrated by driving the resonator on resonance with a known power output of an additional heater.

Measurements were taken on some of the second sound resonance frequencies in the resonator by stepping the drive level in small increments, while measuring the carbon resistor response using a lock-in amplifier. Quantum turbulence was clearly indicated as the region where the measured response no longer increased linearly with the drive amplitude. One remarkable feature was the independence of the second sound amplitude on drive level in the turbulent state. The authors suggested that once the critical velocity is exceeded, almost all of the additional energy delivered by the transducer goes into the vortex tangle, however, in the light of today’s understanding of quantum turbulence it is likely that the normal fluid inside the resonator was also driven into the turbulent state. The authors also measured the critical velocity for several low lying modes and found its square root frequency dependence, in accordance with the frequency dependence of the critical velocity for the transition to quantum turbulence in various oscillatory flows, as well as hysteretic behavior of this transition.

Quantum turbulence in a similar resonator can also be generated when resonant second sound is thermally driven by a resistive heater, and the temperature amplitude in the second sound resonance measured by a sensitive thermometer on the opposite side of the resonator, as it was done by Chagovets [73]. Again, a typical flat top Lorentzian response was observed.

Recently, miniaturization of second sound probes has led Roche and coworkers in Grenoble to the design and construction of a novel micromachined device, based on a Cr heater and Al transition edge thermometer. This noninvasive (0.1 mm) device has opened new possibilities of exploring the properties of superfluid turbulence and has been used to perform measurements of the vorticity spectrum in superfluid helium [74, 75]. Such devices are promising, especially for studies of vortex line density fluctuations or non-homogeneous distributions of vorticity.

6 Future Prospects and Conclusions

We have seen that second sound can be used not only as a probe to investigate quantized vorticity, quantum flows and turbulence in He II but also to generate these flows. We believe that the full potential of second sound as an investigative tool has yet to be fully realized and it should be exploited. For example, the vortex dynamics—generation and decay—of quantum turbulence generated by high-amplitude second sound clearly calls for further investigation, as such quantum turbulence is free of mean flows of both normal and superfluid components. Of particular interest are both the temporal growth and decay of such quantum turbulence. In the Prague Laboratory, such an experiment is now underway, with the resonator equipped with an additional pair of low-amplitude second sound transducers placed in the middle of its long axis, perpendicular to the longitudinally generated second sound resonance, which is excited by an ac heater. As quantum turbulence forms in the vicinity of the antinodes of the second sound wave, various low-lying longitudinal modes ought to generate different turbulent regions. Results of this experiment will be published and discussed in detail, elsewhere.

Other examples include spherical or cylindrical counterflow, where very recent preliminary computer simulations seem to predict the existence of a peculiar flow phase diagram, with the temperature dependent region of quantum turbulence bounded both from below and from above by critical velocities [41, 76]. In a more general sense, the list of future experiments includes second sound studies of unbounded quantum turbulence in He II.

We conclude that second sound—theoretically predicted and experimentally confirmed soon after the discovery of superfluidity as a peculiar temperature or entropy wavelike motion supported in the two-fluid superfluid \(^4\)He—thanks to its ability to detect quantized vortices, has been utilized for more than half a century since the pioneering experiments of Vinen as an efficient tool to investigate quantum flows and turbulence in He II. The aim of this article is not to review all of the important contributions by many investigators, and due to limited space, we have only outlined and discussed selected experiments, with an emphasis on nearly two decades’ worth of second sound attenuation experiments in our Prague Laboratory. Despite the long history of various second sound experiments, this experimental tool still brings new and unexpected results, especially if combined with other complementary experimental techniques such as the various methods of flow visualization, various theoretical approaches and ever more powerful numerical simulations in the framework of complex models.