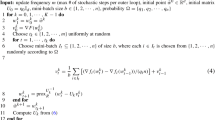1 Introduction

Nowadays, deep learning has been widely applied in various fields, and it performs well in such scenarios as computer vision [1], speech recognition [2, 3], word processing [4], and malware detection [5]. In supervised learning, we assume that there are n input-output samples \(\{(x_{i},y_{i})\}_{i=1}^{n}\) and P(x, y) is the true relationship between inputs and outputs. Ideally, the expected risk is defined as:

$$\begin{aligned} F(\omega )=\int l(\omega ) d P(x,y) ={\mathbb {E}} [l(\omega )], \end{aligned}$$

where \(\omega \in \mathbb {R}^d\) and \(l(\omega )\) is the loss function that measures the distance between the prediction and the real value y. We aim to minimize \(F(\omega )\). While the information about P is not complete, in practice, there is a formula that involves an estimate of the expected risk F. It is defined as the empirical risk function:

$$\begin{aligned} f(\omega )=\dfrac{1}{n}\sum _{i=1}^{n}f_{i}(\omega ), \end{aligned}$$

where each \(f_{i}(\omega ):\mathbb {R}^d \rightarrow \mathbb {R}\) is the loss function corresponding to the i-th sample. Hence, the following optimization problem ERM that minimizes the sum of loss functions over samples from a finite training set appears frequently in deep learning:

$$\begin{aligned} \mathop {\min }\limits _\omega f(\omega )=\dfrac{1}{n} \sum \limits _{i=1}^{n} f_{i}(\omega ). \end{aligned}$$
(1)

The full gradient descent algorithm [6] is a classical algorithm to solve (1), and the update rule for \(k=0,1,2,\cdots \) can be described as:

$$\begin{aligned} \omega _{k+1}=\omega _{k}-\alpha _{k} \nabla f(\omega _{k})=\omega _{k}-\dfrac{\alpha _{k}}{n} \sum _{i=1}^{n} \nabla f_{i}(\omega _{k}). \end{aligned}$$

Because of the structure of \(f(\omega )\), \(\nabla f(\omega )\) is the average sum of every loss function gradient \(\nabla f_{i}(\omega )\), which is corresponding to i-th sample. However, the calculation of \(\nabla f(\omega )\) is challenging when n is extremely large. A modification of the full gradient descent is the stochastic gradient descent method (SGD) [7,8,9] with the iteration update:

$$\begin{aligned} \omega _{k+1}=\omega _{k}-\alpha _{k}g_{k}, \end{aligned}$$

where \(g_{k}\) covers the choices

$$\begin{aligned} g_{k}=\left\{ \begin{aligned}&\nabla f_{i_{k}}(\omega _{k}), i_{k} \text { is randomly selected from } \{1,2,\cdots ,n \},\\&\dfrac{1}{|S|} \sum _{i\in S}\nabla f_{i}(\omega _{k}) , S \text { is a mini-batch of }\, n\, \text { samples}. \end{aligned} \right. \end{aligned}$$

The calculation of \(g_{k}\), as the estimate of full gradient \(\nabla f(\omega _{k})\), is much cheaper than \(\nabla f(\omega _{k})\). Based on the above basic framework, there are two main classes of SGD variants. One is the accelerated methods [10,11,12]. The other one is adaptive learning rate methods like AdaGrad [13], AdaDelta [14], RMSProp [15] and Adam [16].

Though the expectation of \(g_{k}\) equals to full gradient \(\nabla f(\omega _{k})\), randomly different choices of \(g_{k}\) may yield the variance, which causes the slow convergence rate of SGD. In fact, the convergence rate of SGD is sublinear under certain conditions, which is slower than full gradient descent methods. Hence, another important class, variance reduction SGD, is proposed to improve the convergence rate. Le Roux et al. [18] proposed the stochastic average gradient (SAG) that gets a reduction of variance for SGD, which leads to a linear convergence rate when each \(f_{i}(\omega )\) is smooth and strongly convex, but the estimation of the gradient is biased. Johnson and Zhang [19] proposed the stochastic variance reduced gradient (SVRG) which also accelerates the convergence rate while it needs to compute the gradient of all samples after every m SGD iterations. The SAGA method proposed by Defazio, Bach and Lacoste-Julien [20] makes a trade-off between time and space. It needs to store the gradients of all samples in a table and consequently only updates the gradient of one sample at each iteration. Nguyen, Liu, Scheinberg and Taká et al. [21] proposed the stochastic recursive gradient algorithm(SARAH) which is a new variance reducing stochastic gradient algorithm. For strongly convex case, it has the linear convergence rate. Though it doesn’t require a storage of the past gradients, the estimation of gradient is not unbiased.

As is known to all, the conjugate gradient method (CG) [22, 23], as another important method in classical optimization, often performs better than full gradient descent methods. Moreover, the calculation of CG methods is similar to full gradient descent methods. The four classical nonlinear CG methods are FR [24], PRP [25, 26], HS [27] and DY [28]. In recent years, other efficient CG algorithms [29, 30] are proposed. More details about the CG can be found in [17, 31].

It is natural to adapt the CG method in deep learning because of its advantages. Adaptations of conjugate gradients specifically for neural networks have been proposed earlier, such as the scaled conjugate gradient algorithm [32]. The CG method with mini-batch version has been used successfully for training of neural networks [33]. Recently, a kind of stochastic conjugate gradient algorithm with variance reduction (CGVR) [35] is proposed. The main feature of CGVR is that it calculates a stochastic gradient g together with FR conjugate parameter to compose the search direction in each iteration. But after every m iterations, it requires to calculate the full gradient to correct the stochastic gradient. To get an efficient performance, it needs a huge computational consumption. Inspired by SAGA, in this paper we aim to propose a new variance reduction stochastic conjugate gradient algorithm named as SCGA. It is expected that it has satisfactory numerical performance and less computational cost.

The remainder of this paper is organized as follows. In Sect. 2, we briefly review the variance reduction stochastic gradient descent algorithm, named SAGA. In Sect. 3, a new stochastic conjugate gradient algorithm, called SCGA, is introduced in detail and its linear convergence rate is proved. In Sect. 4, a series of experiments are conducted to compare SCGA with other algorithms. Then, it is summarized in Sect. 5.

2 Brief review of the SAGA algorithm

The SAGA algorithm [20] is a stochastic gradient descent method with variance reduction like SVRG. But compared with SVRG, SAGA doesn’t need to compute the full gradients after every m SGD iterations. It only needs to restore the full gradient. To some sense, it makes to a trade-off between time and space. At each iteration, SAGA computes only the gradient of one randomly chosen sample j and then updates j-th entry of the restored full gradient while all other entries remains unchanged. Then SAGA uses the following stochastic vector \(g_k\) to approximate full gradients.

$$\begin{aligned} g_{k}=\nabla f_{j}(\omega _{k})-\nabla f_{j}(\omega _{[j]})+\dfrac{1}{n} \sum _{i=1}^{n} \nabla f_{i}(\omega _{[i]}), \end{aligned}$$

where \(\omega _{[j]}\) represents the latest iterate at which \(\nabla f_{j}\) was evaluated. And \(\nabla f_{j}(\omega _{[j]})\) is the gradient of the j-th sample at iterate \(\omega _{[j]}\).

From taking the expectation of \(g_{k}\) above, with respect to all choices of random index \(j \in \{1,2,\cdots ,n\}\), it follows that the expectation of \(g_k\) is exactly \(\nabla f(\omega _{k})\), which means this approximation \(g_k\) is an unbiased estimate of full gradients. Also, such unbiased estimate of gradient in SAGA [20] is proved obtaining a reduced variance. Benefiting from the variance reduction, SAGA obtains a linear rate of convergence for strongly convex functions. While its computation cost of each iteration is the same as the basic SGD algorithm.

3 A new stochastic conjugate gradient algorithm

As a stochastic conjugate gradient algorithm, although CGVR accelerates the convergence rate of SGD by reducing the variance of the gradient estimates. It requires to calculate the full gradient to correct the stochastic gradient after every m SGD iterations, which leads to high computation cost. Inspired by SAGA, we propose a new stochastic conjugate gradient algorithm called SCGA to overcome the above-mentioned disadvantages.

3.1 The framework of the new algorithm

We adapt the CG algorithm from SAGA to obtain the SCGA in Algorithm 1. At the initialization step, we compute full gradient at initial iterate and store it into a matrix, named \(\nabla f (\omega _{[0]})=\left[ \nabla f_1(\omega _{0}),\nabla f_2(\omega _{0}), \cdots , \nabla f_n(\omega _{0})\right] \). Consequently, at each iteration, we randomly choose a subset \(S\in \{1,2,\cdots ,n\}\), called a mini-batch of samples, and define the subsampled function \(f_{S}(\omega )\) as

$$\begin{aligned} f_{S}(\omega )=\frac{1}{|S|} \sum _{i \in S} f_{i}(\omega ), \end{aligned}$$

where \(|S |\) denotes the number of elements in the mini-batch S. After \(S_{k}\) is randomly chosen, at the current iterate \(\omega _k\), we don’t need to compute the full gradient, but every gradient of the samples in \(S_k\), i.e. \(\nabla f_j(\omega _{j}), \forall j\in S_k\), then get the average of them, named as \(\nabla f_{S_{k}}(\omega _{k})\). Also, at the last stored iterate, we compute the average gradient on \(S_k\)

$$\begin{aligned} \mu _{S_k}= & {} \dfrac{1}{|S_k|}\sum _{j \in S_k} \nabla f_{j}(\omega _{[k-1]}), \end{aligned}$$
(2)

and the full gradient

$$\begin{aligned} \mu _{k-1}= & {} \dfrac{1}{n}\sum _{i=1}^{n} \nabla f_{i}(\omega _{[k-1]}). \end{aligned}$$
(3)

Then using the two gradients \(\mu _{S_{k}}\) and \(\mu _{k-1}\) at the last restored iterate, we correct \( \nabla f_{S_{k}}\) at the current iterate to obtain the new stochastic gradient

$$\begin{aligned} g_{k}=\nabla f_{S_{k}}(\omega _{k})- \mu _{S_{k}}+\mu _{k-1}. \end{aligned}$$
(4)

It is tempting to conclude \(\mathbb {E}[g_{k}]=\nabla f(\omega _{k})\), which means that (4) is an unbiased estimate of gradient \(\nabla f(\omega _{k})\).

In addition, such estimate of gradient can be proved have a reducing variance. In fact, considering the variance of gradient

$$\begin{aligned} V&= \mathbb {E}\left[ \Vert g_k - \nabla f(w_k)\Vert ^2\right]&= \mathbb {E}[\Vert g_k\Vert ^2]-\Vert \nabla f(\omega _k)\Vert ^2, \end{aligned}$$
(5)

from Lemma 4, we see that

$$\begin{aligned} \mathbb {E}[\Vert g_{k}\Vert ^2] \le 4 \Lambda [f(\omega _{k})-f(\omega _{*})+f({\omega }_{[k]})-f(\omega _*)]. \end{aligned}$$

Intuitively, as \(\omega _k\rightarrow w_*\) and \(\omega _{[k]}\rightarrow \omega _*\) the variance goes to zero asymptotically.

After obtaining the gradients of samples \(\nabla f_j(\omega _{j})\), \(\forall j\in S_k\), we update the corresponding entries of the stored matrix \(\nabla f ({\omega }_{[k]})=\left[ \nabla f_1(\omega _{[k]}),\nabla f_2(\omega _{[k]}), \cdots , \nabla f_n(\omega _{[k]})\right] \), while other entries remain unchanged. That is \(\nabla f_{j}(\omega _{[k]})\leftarrow \nabla f_{j}(\omega _{k}), \forall j \in S_{k} \). SCGA has the similar way of determining stochastic gradients with SAGA. But compared with CGVR, it does not need to compute the full gradient in each iteration instead to compute a mini-batch gradients each time. Based on this, it is reasonable to expect that SCGA consumes less computation cost than CGVR.

figure a

To get the stochastic conjugate gradient direction, the conjugate parameter \(\beta \) can be chosen as FR

$$\begin{aligned} \beta _{k}^{FR}=\frac{\Vert g_{k}\Vert ^2}{\Vert g_{k-1}\Vert ^2}. \end{aligned}$$
(6)

Though the convergence of FR method has been well established, their numerical results are not good. And PR method, which defines the parameter \(\beta _k\) as follows:

$$\begin{aligned} \beta _k^{PR} = \frac{g_k^T(g_k-g_{k-1})}{g_{k-1}^Tg_{k-1}}, \end{aligned}$$
(7)

is generally believed to be one of the most efficient CG method in practical computation because it essentially restarts if a bad direction occurs. But in theory it may not converge. To combine the advantages of these CG methods, our stochastic conjugate gradient algorithm SCGA chooses a hybrid version between FR and PR:

$$\begin{aligned} \beta _{k}^{FR+PR}=\left\{ \begin{array}{ccc} &{} -\beta _{k}^{FR} &{} \quad if \ \ \beta _k^{PR}<-\beta _k^{FR}, \\ &{} \beta _{k}^{PR} &{} \quad if \ \ |\beta _k^{PR}|\le \beta _k^{FR}, \\ &{} \beta _{k}^{FR} &{} \quad if \ \ \beta _k^{PR}>\beta _k^{FR}. \end{array} \right. \end{aligned}$$
(8)

Note that \(|\beta _k^{FR+PR} |\le \beta _k^{FR}\). Moreover, for any \(\beta _k\) satisfying \(|\beta _k|\le \beta _k^{FR}\) we prove the convergence of SCGA in the following subsection.

In order to get an appropriate step size \(\alpha _{k}\), we introduce the inexact line search and require \(\alpha _{k}\) satisfy the stochastic version of the strong Wolfe conditions

$$\begin{aligned} f_{S_k}(\omega _{k}+\alpha _{k}p_{k})\le & {} f_{S_k}(\omega _{k}) + c_{1} \alpha _{k} \nabla f_{S_k}(\omega _{k})^{T} p_{k}, \end{aligned}$$
(9)
$$\begin{aligned} |g_{k+1}^{T}p_{k}|\le & {} -c_{2}g_{k}^{T}p_{k} . \end{aligned}$$
(10)

where \(0< c_1< c_2 < 1\). In addition, The SCGA algorithm is implemented with step size \(\alpha _{k}\) that satisfies condition (10) with \(0<c_{2}<1/2\). It can be shown that SCGA with FR generates the descent direction \(p_{k}\) satisfying

$$\begin{aligned} -\frac{1}{1-c_{2}} \le \frac{g_{k}^{T}p_{k}}{\Vert g_{k}\Vert ^2} \le \dfrac{2c_{2}-1}{1-c_{2}}. \end{aligned}$$

Besides, the above bounds inequality also holds for any \(\beta _k\) satisfying \(|\beta _k|\le \beta _k^{FR}\). The similar proof details can be referred to Lemma 3.1 of [22].

3.2 The convergence analysis of SCGA

We analyze the convergence of SCGA in Alogrithm 1 with any \(\beta _k\) satisfying \(|\beta _k|\le \beta _k^{FR}\). This convergence result leads to SCGA with the hybrid of FR and PR preserves its efficiency and assures its convergence.

The convergence analysis uses the same assumptions in CGVR as follows:

Assumption 1

The SCGA algorithm is implemented with a step size \(\alpha _{k}\) that satisfies \(\alpha _{k}\in [\alpha _{1},\alpha _{2}],0<\alpha _{1}<\alpha _{2}\) and condition (10) with \(c_{2}\le 1/5\).

Assumption 2

The function \(f_{i}\) is twice continuously differentiable for each \(1\le i\le n\), and there exists constants \(0<\lambda \le \Lambda \) such that

$$\begin{aligned}\lambda I \preceq \nabla ^{2}f_{i}(\omega )\preceq \Lambda I \end{aligned}$$

for all \(\omega \in \mathbb {R}^{d} \).

The Assumption 2 indicates that f is also strongly convex and \(\nabla f\) is Lipschitz continuous.

Assumption 3

There exists \(\hat{\beta } <1\) such that

$$\begin{aligned} \beta _{k}=\frac{\Vert g_{k}\Vert ^2}{\Vert g_{k-1}\Vert ^2} \le \hat{\beta } . \end{aligned}$$

Using these assumptions, the following lemmas are directly derived. Lemma 1 and Lemma 2 estimate the lower bound of \(\Vert \nabla f(\omega ) \Vert \) and the upper bound of \(\mathbb {E} [\Vert p_k\Vert ^2]\). They are the same as Lemma 5 [34] and Theorem 2 of [35].

Lemma 1

Suppose that f is continuously differentiable and strongly convex with parameter \(\lambda \). Let \(\omega _{*}\) be the unique minimizer of f. Then, for any \(\omega \in \mathbb {R}^{d}\), we have

$$\begin{aligned} \Vert \nabla f(\omega )\Vert ^2 \ge 2\lambda (f(\omega )-f(\omega _{*})). \end{aligned}$$

Lemma 2

Suppose that Assumptions 1 and 3 hold for Algorithm 1. Then, for any k, we have

$$\begin{aligned} \mathbb {E}[\Vert p_{k}\Vert ^2] \le \eta (k) \mathbb {E}[\Vert g_{0}\Vert ^2], \end{aligned}$$
(11)

where

$$\begin{aligned} \eta (k)=\frac{2}{1-\hat{\beta }} \hat{\beta }^{k}-\frac{1+\hat{\beta }}{1-\hat{\beta }} \hat{\beta }^{2k}. \end{aligned}$$

Lemma 3

According to Algorithm 1, for any k, we have

$$\begin{aligned} \mathbb {E}[\alpha _{k} g_{k}^{T} p_{k}] \le - \alpha _{1} \left\| \nabla f(\omega _{k})\right\| ^{2} +\dfrac{1}{4} \alpha _{2} \hat{\beta }^{k} \mathbb {E}[\left\| g_{0}\right\| ^{2}]. \end{aligned}$$

Proof

By the definition of \(p_k = - g_{k} + \beta _{k} p_{k-1}\), we obtain

$$\begin{aligned} \mathbb {E}[\alpha _{k} g_{k}^{T} p_{k}]&= \mathbb {E}[ - \alpha _{k} \left\| g_{k}\right\| ^{2}] + \mathbb {E}[ \alpha _{k} \beta _{k} g_{k}^{T} p_{k-1}]\\&\le \mathbb {E}[- \alpha _{k} \left\| g_{k}\right\| ^{2}] + \mathbb {E}[ - \alpha _{k} \beta _{k} c_{2} g_{k-1}^{T} p_{k-1}]\\&\le \mathbb {E}[- \alpha _{k} \left\| g_{k}\right\| ^{2}] + \frac{c_{2}}{1-c_{2}}\mathbb {E}[\alpha _{k} \beta _{k} \left\| g_{k-1} \right\| ^{2}]\\&\le \mathbb {E}[- \alpha _{1} \left\| g_{k}\right\| ^{2}] + \frac{c_{2}}{1-c_{2}} \mathbb {E}[\alpha _{2} \hat{\beta } \left\| g_{k-1} \right\| ^{2}]\\&\le - \alpha _{1}\mathbb {E}[ \left\| g_{k}\right\| ^{2}] + \frac{1}{4} \alpha _{2} \hat{\beta } \mathbb {E}[ \left\| g_{k-1} \right\| ^{2}]\\&\le - \alpha _{1} \left\| \mathbb {E}[ g_{k}] \right\| ^{2} + \frac{1}{4} \alpha _{2} \hat{\beta } \mathbb {E}[ \left\| g_{k-1} \right\| ^{2}]\\&= - \alpha _{1} \left\| \nabla f(\omega _{k})\right\| ^{2} +\dfrac{1}{4} \alpha _{2} \hat{\beta } \mathbb {E}[\left\| g_{k-1}\right\| ^{2}]. \end{aligned}$$

The first inequality uses the strong Wolfe condition (10), the second one uses the lower bound \(-\frac{1}{1-c_2}\) of \(\frac{g_k^T p_k}{\left\| g_{k}\right\| ^2}\). Then by using Assumption 1 (\(\alpha _{k}\in [\alpha _{1},\alpha _{2}]\)) and Assumption 3 (\(\beta _{k} \le \hat{\beta }\)), it yields the third inequality. Note that the monotonically increasing property of the function \(\frac{x}{1-x} \) with \(x \ne 1\) which implies \(\frac{c_2}{1-c_2} \le \frac{1}{4}\) with \( c_2\le \frac{1}{5}\), so the fourth inequality holds. It is easy to know \(\mathbb {E}[ \left\| g_{k}\right\| ^{2}] \ge \left\| \mathbb {E}[ g_{k}] \right\| ^{2}\), which deduces the last inequality.

Furthermore, according to Assumption 3 and taking expectation, it holds that \(\mathbb {E}[\left\| g_{k}\right\| ^{2}] \le \hat{\beta } \mathbb {E}[\left\| g_{k-1}\right\| ^{2}]\), and consequently, \(\mathbb {E}[\left\| g_{k}\right\| ^{2}] \le \hat{\beta }^k \mathbb {E}[\left\| g_{0}\right\| ^{2}]\), which implies the conclusion. \(\square \)

In the following Lemma 4, we estimates the upper bound of \(\mathbb {E}[\Vert g_{k}\Vert ^2]\).

Lemma 4

Let \(\omega _{*}\) be the unique minimizer of f. Taking expectation with respect to \(S_{k}\) of \(\Vert g_{k}\Vert ^2\) in (4), we obtain

$$\begin{aligned} \mathbb {E}[\Vert g_{k}\Vert ^2] \le 4 \Lambda [f(\omega _{k})-f(\omega _{*})+f({\omega }_{[k]})-f(\omega _*)]. \end{aligned}$$
(12)

Proof

Given any mini-batch S , considering the function

$$\begin{aligned} h_{S}(\omega )=f_{S}(\omega )-f_{S}(\omega _{*})-\nabla f_{S}(\omega _{*})^{T}(\omega -\omega _{*}), \end{aligned}$$

we know that \(h_{S}(\omega _{*})=\mathop {\min }\limits _\omega h_{S}(\omega )\) since \(\nabla h_{S}(\omega _{*})=0\). Therefore,

$$\begin{aligned} 0=h_{S}(\omega _{*})&\le \mathop {\min }\limits _\eta [h_{S}(\omega - \eta \nabla h_{S}(\omega ))]\\&\le \mathop {\min }\limits _\eta \left[ h_{S}(\omega )-\eta \Vert \nabla h_{S}(\omega ) \Vert ^2 + \dfrac{1}{2} \Lambda \eta ^2 \Vert \nabla h_{S}(\omega ) \Vert ^2 \right] \\&=h_{S}(\omega )-\dfrac{1}{2\Lambda }\Vert \nabla h_{S}(\omega ) \Vert ^2. \end{aligned}$$

That is,

$$\begin{aligned} \Vert \nabla f_{S}(\omega )-\nabla f_{S}(\omega _{*})\Vert ^2 \le 2\Lambda \left[ f_{S}(\omega )-f_{S}(\omega _{*}) -\nabla f_{S}(\omega _{*})^{T}(\omega -\omega _{*})\right] . \end{aligned}$$

By taking expectation with respect to S on the above inequality, we obtain

$$\begin{aligned} \mathbb {E}\left[ \Vert \nabla f_{S}(\omega )-\nabla f_{S}(\omega _{*})\Vert ^2\right]&\le 2\Lambda [f(\omega )-f(\omega _{*})]. \end{aligned}$$
(13)

In case of that \(k\ne 0\), taking expectation with respect to \(S_k\) on norm of \(g_k\) in (4), we obtain

$$\begin{aligned}&\mathbb {E}\left[ \Vert g_{k}\Vert ^2 \right] \nonumber \\&\quad = \mathbb {E} \left[ \Vert \nabla f_{S}(\omega _{k})-\mu _{S}+ \mu \Vert ^2 \right] \nonumber \\&\quad = \mathbb {E} \left[ \Vert \nabla f_{S}(\omega _{k}) - \nabla f_{S}(\omega _{*}) + \nabla f_{S}(\omega _{*}) -\mu _{S}+ \mu \Vert ^2 \right] \nonumber \\&\quad \le 2 \mathbb {E}\left[ \Vert \nabla f_{S}(\omega _{k})-\nabla f_{S}(\omega _{*})\Vert ^2\right] +2 \mathbb {E} \left[ \Vert \mu _{S}-\nabla f_{S}(\omega _{*}) - \mu \Vert ^2 \right] \nonumber \\&\quad = 2 \mathbb {E}\left[ \Vert \nabla f_{S}(\omega _{k})-\nabla f_{S}(\omega _{*})\Vert ^2\right] +2 \mathbb {E} \left[ \Vert \mu _{S}-\nabla f_{S}(\omega _{*}) - \mathbb {E}\left[ \mu _{S}-\nabla f_{S}(\omega _{*} ) \right] \Vert ^2 \right] \nonumber \\&\quad \le 2 \mathbb {E}\left[ \Vert \nabla f_{S}(\omega _{k})-\nabla f_{S}(\omega _{*})\Vert ^2\right] +2 \mathbb {E} \left[ \Vert \mu _{S}-\nabla f_{S}(\omega _{*}) \Vert ^2 \right] \nonumber \\&\quad \le 4 \Lambda \left[ f(\omega _k)-f(\omega _*) + f(\tilde{\omega }_{k})-f(\omega _*)\right] , \end{aligned}$$
(14)

where \(\Lambda \) is the positive constant in Assumption 2. The first inequality uses \(\Vert a-b \Vert ^2 \le 2 \Vert a \Vert ^2 +2\Vert b \Vert ^2\). The second inequality uses \(\mathbb {E} \Vert \xi - \mathbb {E} \xi \Vert ^2 = \mathbb {E} \Vert \xi \Vert ^2 -\Vert \mathbb {E} \xi \Vert ^2 \le \mathbb {E} \Vert \xi \Vert ^2 \) for any random vector \(\xi \). The third inequality uses (13).

In case of that \(k=0\), then \(g_0=\mu _0=\nabla f(\omega _0)\).

$$\begin{aligned} \mathbb {E}\left[ \Vert g_{0}\Vert ^2 \right] = \Vert \nabla f(\omega _0)\Vert ^2 = \Vert \nabla f(\omega _0)-\nabla f(\omega _*)\Vert ^2 \le 2 \Lambda [f(\omega _0)- f(\omega _*)]. \end{aligned}$$
(15)

The above inequality uses Assumption 2. Note that \(\omega _{[0]}=\omega _0\). Thus, for \(k=0\) also satisfies (12), which together with (14) comes to the conclusion. \(\square \)

Finally, we present the convergence rate of SCGA. It can achieve a linear convergence rate for strongly convex function.

Theorem 1

Suppose that Assumptions 1, 2 and 3 hold. Let \(\omega _{*}\) be the unique minimizer of f. Then, for all \(k \ge 0\), we have

$$\begin{aligned} \mathbb {E}[f(\omega _{k+1})-f(\omega _{*})]\le C\xi ^{k+1}\mathbb {E}[f(\omega _{0})-f(\omega _{*})], \end{aligned}$$

where parameters \(\xi \) and C are given by

$$\begin{aligned} \xi= & {} 1-2\alpha _{1}\lambda <1,\\ C= & {} 1+\dfrac{\alpha _{2} \Lambda (1-\hat{\beta })+4\alpha _{2}^{2} \Lambda ^{2}}{2(\xi -\hat{\beta })(1-\hat{\beta })}, \end{aligned}$$

assuming that we choose \(\alpha _{1} <\dfrac{1-\hat{\beta }}{2\lambda }\).

Proof

By Assumption 2, the function \(f_{S_{k}}(\omega _{k})\) satisfies

$$\begin{aligned} \lambda I \preceq \nabla ^2 f_{S_{k}}(\omega _{k}) \preceq \Lambda I. \end{aligned}$$

That is for all \(k \in \mathbb {N}\), the following inequality holds

$$\begin{aligned} f_{S_{k}}(\omega _{k+1}) \le f_{S_{k}}(\omega _{k}) + \nabla f_{S_{k}}(\omega _{k})^{T} (\omega _{k+1}-\omega _{k}) +\dfrac{\Lambda }{2}\left\| \omega _{k+1}-\omega _{k}\right\| ^{2}. \end{aligned}$$

With \(w_{k+1} = w_{k} + \alpha _{k} p_k\), the above inequality also can be written as

$$\begin{aligned} f_{S_{k}}(\omega _{k+1})-f_{S_{k}}(\omega _{k})&\le \alpha _{k} g_k^{T}p_{k}+\dfrac{1}{2}\alpha _{k}^{2}\Lambda \left\| p_{k}\right\| ^2. \end{aligned}$$

Taking expectation in this relation conditioned on \(S_k\), this yields

$$\begin{aligned}&\mathbb {E}[f(\omega _{k+1})]-f(\omega _{k})\\&\quad \le \mathbb {E}[\alpha _{k} g_{k}^{T} p_{k}] + \dfrac{1}{2} \Lambda \mathbb {E}[\alpha _{k}^{2} \left\| p_{k}\right\| ^2]\\&\quad \le - \alpha _{1} \left\| \nabla f(\omega _{k})\right\| ^{2} +\dfrac{1}{4} \alpha _{2} \hat{\beta }^{k} \mathbb {E}[\left\| g_{0}\right\| ^{2}] +\dfrac{1}{2} \Lambda \mathbb {E}[\alpha _{2}^{2} \left\| p_{k}\right\| ^2]\\&\quad \le -\alpha _{1} \left\| \nabla f(\omega _{k})\right\| ^{2} +(\dfrac{1}{4} \alpha _{2} \hat{\beta }^{k} + \dfrac{1}{2} \alpha _{2}^{2} \Lambda \eta (k)) \mathbb {E}[\left\| g_{0}\right\| ^{2}]\\&\quad \le -2 \alpha _{1} \lambda [f(\omega _{k})-f(\omega _{*})] + (\frac{1}{2}\alpha _{2} \Lambda \hat{\beta }^{k} + \alpha _{2}^{2} \Lambda ^{2} \eta (k)) [f(\omega _{0})-f(\omega _{*})]. \end{aligned}$$

The second inequality uses Assumptions 1 and Lemma 3, the third inequality uses Lemma 2, and the last one uses Lemma 1 and (15).

Subtracting \(f(\omega _{*})\) from both sides of the above inequality, taking total expectations, and rearranging, this yields

$$\begin{aligned} \mathbb {E}[f(\omega _{k+1})-f(\omega _{*})]&\le (1-2 \alpha _{1} \lambda ) \mathbb {E}[f(\omega _{k})-f(\omega _{*})]\\ {}&\quad + \left( \frac{1}{2}\alpha _{2} \Lambda \hat{\beta }^{k} + \alpha _{2}^{2} \Lambda ^{2} \eta (k)\right) \mathbb {E}[f(\omega _{0})-f(\omega _{*})]. \end{aligned}$$

For the convenience of discussion, we define

$$\begin{aligned} \xi =1-2 \alpha _{1} \lambda ,\ \ \varphi (k) = \frac{1}{2}\alpha _{2} \Lambda \hat{\beta }^{k} + \alpha _{2}^{2} \Lambda ^{2} \eta (k), \ \ \Delta _{k}=\mathbb {E}[f(\omega _{k})-f(\omega _{*})]. \end{aligned}$$

Then the above inequality can be written as

$$\begin{aligned} \Delta _{k+1} \le \xi \Delta _{k} + \varphi (k) \Delta _{0}. \end{aligned}$$

We further obtain

$$\begin{aligned} \Delta _{k+1}&\le \xi \left( \xi \Delta _{k-1}+ \varphi (k-1) \Delta _{0}\right) + \varphi (k) \Delta _{0} \\&=\xi ^{2} \Delta _{k-1}+[\xi \varphi (k-1) + \varphi (k)] \Delta _{0}\\&\vdots \\&\le [\xi ^{k+1} + \sum \limits _{i=0}^{k} \xi ^{k-i} \varphi (i)] \Delta _{0}. \end{aligned}$$

We now compute \(\sum \limits _{i=0}^{k} \xi ^{k-i} \varphi (i)\),

$$\begin{aligned} \sum \limits _{i=0}^{k} \xi ^{k-i} \varphi (i)&=\xi ^{k} \frac{1}{2}\alpha _{2} \Lambda \sum \limits _{i=0}^{k}\left( \dfrac{\hat{\beta }}{\xi }\right) ^{i} + \xi ^{k} \dfrac{2 \alpha _{2}^{2} \Lambda ^{2}}{1-\hat{\beta }} \sum \limits _{i=0}^{k}\left( \dfrac{\hat{\beta }}{\xi }\right) ^{i}- \xi ^{k}\dfrac{ \alpha _{2}^{2} \Lambda ^{2} (1+\hat{\beta })}{1-\hat{\beta }}\sum \limits _{i=0}^{k} \left( \dfrac{\hat{\beta }^{2}}{\xi }\right) ^{i}\\&= \xi ^{k} \frac{1}{2}\alpha _{2} \Lambda \frac{1-\left( \frac{\hat{\beta }}{\xi }\right) ^{k+1}}{1-\frac{\hat{\beta }}{\xi }} + \dfrac{\xi ^{k}2\alpha _{2}^{2} \Lambda ^{2}}{1-\hat{\beta }} \frac{1-\left( \frac{\hat{\beta }}{\xi }\right) ^{k+1}}{1-\frac{\hat{\beta }}{\xi }}\\&\quad - \xi ^{k} \dfrac{ \alpha _{2}^{2} \Lambda ^{2} (1+\hat{\beta })}{1-\hat{\beta }} \frac{1-\left( \frac{\hat{\beta }^{2}}{\xi }\right) ^{k+1}}{1-\frac{\hat{\beta }^{2}}{\xi }}\\&\le \xi ^{k} \frac{1-\left( \frac{\hat{\beta }}{\xi }\right) ^{k+1}}{1-\frac{\hat{\beta }}{\xi }} \left( \frac{1}{2}\alpha _{2} \Lambda + \dfrac{2 \alpha _{2}^{2} \Lambda ^{2}}{1-\hat{\beta }} \right) \\&\le \xi ^{k} \frac{1}{1-\frac{\hat{\beta }}{\xi }} \left( \frac{1}{2}\alpha _{2} \Lambda + \dfrac{2 \alpha _{2}^{2} \Lambda ^{2}}{1-\hat{\beta }} \right) \\&=\xi ^{k+1} \dfrac{\alpha _{2} \Lambda (1-\hat{\beta })+4\alpha _{2}^{2} \Lambda ^{2}}{2(\xi -\hat{\beta })(1-\hat{\beta })} \end{aligned}$$

The first and second inequality uses \(\alpha _{1} <\dfrac{1-\hat{\beta }}{2\lambda }\) which implies that \(\xi>\hat{\beta }>\hat{\beta }^{2}\). Then, we obtain

$$\begin{aligned} \mathbb {E}[f(\omega _{k+1})-f(\omega _{*})]\le C\xi ^{k+1}\mathbb {E}[f(\omega _{0})-f(\omega _{*})]. \end{aligned}$$

\(\square \)

4 Experiments

In this section we perform a series of experiments to validate the effectiveness of SCGA presented in Algorithm 1.

First, we conduct Algorithm 1 with different \(\beta _k\) options: Option I and Option II. The comparison results on data set ijcnn1 are shown in Fig. 1, where the four sub-figures are corresponding to the four different models introduced in Sect. 4.1. We can see that Algorithm 1 with Option II performs much faster than that with Option I. This is consistent with our theoretical analysis before. Also, similar performance can be found on other data sets of Table 3.

Fig. 1
figure 1

Performance comparison of Algorithm 1 with Option I and Option II on ijcnn1 data set using four learning models shown in (16) (17) (18) and (19). (The x-axis represents the number of iterations. The y-axis represents base-10 logarithm of loss values.)

Full size image

Because of the better performance of Option II, we choose Option II for Algorithm 1, named as SCGA. Table 1 lists all the compared algorithms in the following experiments.

Table 1 Algorithms in the comparison
Full size table

For a fair comparison, we use the same code base for each algorithm, just changing the main update rule. Each algorithm has its step size parameter chosen so as to give the fastest convergence. The parameters of compared algorithms and loss functions are listed in Table 2.

Table 2 Parameters in algorithms
Full size table

4.1 Machine learning models and data sets

We evaluate algorithms on the following popular machine learning models including regression and classification problems.

  1. (1)

    ridge regression (ridge)

    $$\begin{aligned} \mathop {\min }\limits _\omega \dfrac{1}{n} \sum _{i=1}^{n} (y_{i}-x_{i}^{T}\omega )^2 +\lambda \Vert \omega \Vert ^2_{2} \end{aligned}$$
    (16)
  2. (2)

    logistic regression (logistic)

    $$\begin{aligned} \mathop {\min }\limits _\omega \dfrac{1}{n} \sum _{i=1}^{n} \ln (1+\exp (-y_{i}x_{i}^{T}\omega )) +\lambda \Vert \omega \Vert ^2_{2} \end{aligned}$$
    (17)
  3. (3)

    L2-regularized L1-loss SVM (hinge)

    $$\begin{aligned} \mathop {\min }\limits _\omega \dfrac{1}{n} \sum _{i=1}^{n} (1-y_{i}x_{i}^{T}\omega )_{+} +\lambda \Vert \omega \Vert ^2_{2} \end{aligned}$$
    (18)
  4. (4)

    L2-regularized L2-loss SVM (sqhinge)

    $$\begin{aligned} \mathop {\min }\limits _\omega \dfrac{1}{n} \sum _{i=1}^{n} ((1-y_{i}x_{i}^{T}\omega )_{+})^2+\lambda \Vert \omega \Vert ^2_{2} \end{aligned}$$
    (19)

where \(x_{i} \in \mathbb {R}^{d}\) and \(y_{i} \in \mathbb {R}\) is the i-th sample data. And the data matrix X for all dimensions is scaled into the range of \([-1,+1]\) by the max-min scaled in the preprocessing stage. These four models are convex, nonconvex or nonsmooth.

The data sets are presented in Table 3. The first five are the binary classification of large-scale data sets, where the first three,a9a, cod-rna and ijcnn1, are from the LIBSVM data websiteFootnote 1, the next two, quantum and protein, are from the KDD Cup 2004 websiteFootnote 2. The remaining six data sets are regression problems. The details of data sets bodyfat, housing, pyrim, \(space\_ga\) and triazines can be also found in the LIBSVM data website. The last one, Average Localization Error (ALE) in sensor node localization process in WSNs data set, can be found in UCI Machine Learning Repository websiteFootnote 3.

Table 3 Data sets used in comparison
Full size table

4.2 Numerical comparison results

In the first experiment, we compare the convergence of SCGA with several SGD type algorithms on two kinds of data sets. Fig. 2 shows the convergence of these algorithms on five binary-classification large-scale data sets. Fig. 3 presents the results on six regression data sets. From Fig. 2 we see that SCGA has the fastest convergence on almost all of the four models, even when the loss value reaches a notably small value. In Fig. 3, SCGA makes loss drops fast at first and goes down fast to the minimum. In general, SCGA reduces the variance and smoothly converges faster than SGD, SAGA and its mini-batch version.

Fig. 2
figure 2

Performance of SCGA compared with SGD type algorithms. On binary classification large-scale data sets a9a, cod-rna, ijcnn1, quantum and protein for four machine learning models shown in (16) (17) (18) and (19).(The x-axis represents numbers of iterations. The y-axis represents base-10 logarithm of loss values.)

Full size image

In the second experiment, we compare the two stochastic conjugate gradient algorithms, SCGA and CGVR [35]. Because CGVR requires computations of full gradient, while SCGA does not. Thus we measure the computational cost by the number of gradient computations divided by n instead of iterations.

We evaluate these two algorithms on the data sets in Table 3, including classification and regression. For classification data sets, a9a, cod-rna, ijcnn1, quantum and protein, we conduct the algorithms on four machine learning models shown in (16) (17) (18) and (19). From the results, SCGA can be seen to perform similar to CGVR, only with a slight advantage. For these data sets, we do not present the comparison plots. On the other hand, for regression data sets, i.e., the last six data sets in Table 3, we use ridge regression model to evaluate their performance. Fig. 4 plots the logarithm of loss errors with respect to their computational cost. Both of SCGA and CGVR can rapidly goes down initially as expected, but SCGA converges to a better level in pyrim and triazines data sets.

Overall, SCGA is competitive with CGVR and clearly more advantageous than the SGD type algorithms.

Fig. 3
figure 3

Performance of SCGA compared with SGD type algorithms. On ridge regression model for data sets bodyfat, housing, pyrim,space_ga, triazines and ALE in sensor node localization process in WSNs. (The x-axis represents numbers of iterations. The y-axis represents base-10 logarithm of loss values.)

Full size image
Fig. 4
figure 4

Performance comparisons of SCGA and CGVR. On ridge regression model for data sets bodyfat, housing, pyrim,space_ga, triazines and ALE in sensor node localization process in WSNs data sets. (The x-axis represents computational cost measured by the number of gradient computations divided by n.The y-axis represents base-10 logarithm of loss values.)

Full size image

5 Conclusion

In this paper, we propose a new stochastic conjugate gradient algorithm with variance reduction, named SCGA. At each iteration, SCGA only computes the gradients of mini-batch samples then updates them into the stored full gradient, instead of computing full gradients in CGVR. We prove that SCGA with a class of FR choices obtain a convergence rate for strongly convex function. Moreover, among the class of FR choices, we introduce a choice to SCGA, which is a hybrid of FR and PR, shown in Option II of Algorithm 1. From a series of experiments, it demonstrates that SCGA converges faster than SGD type algorithms. And compared with CGVR, SCGA is a competitive algorithm, especially for some regression problems.