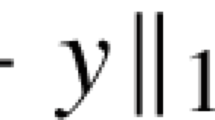On a class of bilevel linear mixed-integer programs in adversarial settings

Abstract

We consider a class of bilevel linear mixed-integer programs (BMIPs), where the follower’s optimization problem is a linear program. A typical assumption in the literature for BMIPs is that the follower responds to the leader optimally, i.e., the lower-level problem is solved to optimality for a given leader’s decision. However, this assumption may be violated in adversarial settings, where the follower may be willing to give up a portion of his/her optimal objective function value, and thus select a suboptimal solution, in order to inflict more damage to the leader. To handle such adversarial settings we consider a modeling approach referred to as $\alpha$-pessimistic BMIPs. The proposed method naturally encompasses as its special classes pessimistic BMIPs and max–min (or min–max) problems. Furthermore, we extend this new modeling approach by considering strong-weak bilevel programs, where the leader is not certain if the follower is collaborative or adversarial, and thus attempts to make a decision by taking into account both cases via a convex combination of the corresponding objective function values. We study basic properties of the proposed models and provide numerical examples with a class of the defender–attacker problems to illustrate the derived results. We also consider some related computational complexity issues, in particular, with respect to optimistic and pessimistic bilevel linear programs.

1 Introduction

Bilevel programs form a class of optimization problems that are suitable for modeling hierarchical settings with two independent decision-makers, namely, the leader and the follower, who are also often referred to as the upper- and lower-level decision-makers, respectively [5, 15]. The involved decision-makers may be collaborative or conflicting. The latter situation often arises in military and law-enforcement applications, e.g., defender–attacker, attacker–defender and interdiction models [8, 24, 36].

In bilevel programs the leader decides first. In response to the leader’s decision, the follower solves the lower-level optimization problem that is parameterized by the leader’s decisions, e.g., the right-hand sides of the follower’s constraints are functions of the leader’s decision variables. On the other hand, the leader’s objective function is affected by the follower’s response; most typically it includes a term that is a function of the follower’s decision variables.

There are two approaches for modeling the follower’s response in bilevel programs [13]: the optimistic formulation assumes that if there are multiple optimal solutions to the follower’s problem for a given decision by the leader, then the follower selects the solution that is the most favorable for the leader. On the contrary, the pessimistic formulation assumes that the follower selects the least favorable solution for the leader. One should note that in the case of max–min (or min–max) problems, optimistic and pessimistic cases coincide.

Bilevel programming is closely related to static Stackelberg leader-follower game [10, 31]. Furthermore, it provides a flexible modeling approach for decentralized decision-making in several important application domains including hazardous material transportation [20, 37], network design [12] and interdiction [24, 30, 36], revenue management [14], traffic planning [26, 28], energy [6, 32, 33], computational biology [9, 29] and defense [8]. For more details on bilevel optimization and its applications we refer the reader to a survey in [13] and the references therein.

In this paper we focus on a broad class of bilevel linear mixed-integer programs (BMIPs):

$$\begin{aligned} \hbox {[BMIP]}: \quad {\hbox {``}}{\mathop {\max }\limits _{x}}{\hbox {''}}\quad&c^{\top } x+d^{\top }_{1}y&\\ \text {subject to} \quad&x \in {\mathbb {X}},&\\ \quad&y\in \mathop {{{\mathrm{argmax}}}}\limits _y \quad d_2^{\top } y&\\&\text {subject to} \quad Ax+By \le h,&\\&\qquad \,\, \qquad \,\, y\in {\mathbb {R}}_+^{n_2},&\end{aligned}$$

where ${\mathbb {X}} \subseteq \mathbb {Z}^{n_1-k}_+\times \mathbb {R}^{k}_+$, $A \in {\mathbb {R}}^{m_2\times n_1}$, $B\in {\mathbb {R}}^{m_2\times n_2}$, $h\in {\mathbb {R}}^{m_2}$, $c\in {\mathbb {R}}^{n_1}$, $d_1\in {\mathbb {R}}^{n_2}$ and $d_2\in {\mathbb {R}}^{n_2}$. The leader’s and the follower’s decision variables are denoted by x and y, respectively. The leader’s problem is a linear mixed-integer program (MIP).

In the remainder of the paper we make the following assumptions that are relatively standard in the bilevel optimization literature:

A1::

${\mathbb {X}}\ne \emptyset$ and ${\mathbb {X}}=\widehat{\mathbb {X}}\cap \big (\mathbb {Z}^{n_1-k}_+\times \mathbb {R}^{k}_+\big )$, where $\widehat{\mathbb {X}}$ is a polytope.

A2::

For every feasible leader’s decision $x\in {\mathbb {X}}$ the corresponding follower’s feasible set is non-empty, i.e., $\{ y\in \mathbb {R}^{n_2}_+:\ By \le h-Ax\}\ne \emptyset$ for any $x\in {\mathbb {X}}$, and bounded.

Following the notation used in some of the bilevel optimization literature [16], we use “$\max$” (with quotes) in the leader’s objective function of BMIP to emphasize that there are two possible cases of the bilevel program. Indeed, the pessimistic formulation of BMIP is given by:

$$\begin{aligned} \text{[ }\mathrm {BMIP}^\mathrm {pes}\text{] } \quad \max \limits _{x \in {\mathbb {X}}}&\big \{ c^\top x+ \min \limits _{y \in H(x)} d_1^\top y \big \}, \end{aligned}$$

(1)

$$\begin{aligned} \text {where}&H(x) = {{\mathrm{argmax}}}\{ d_2^\top y : \ Ax+By \le h,\ y\in \mathbb {R}^{n_2}_+\}, \end{aligned}$$

(2)

and H(x) denotes the lower-level (follower’s) rational reaction set for a given x. Note that (1) involves a minimization problem over optimal solutions of the follower’s problem for a given leader’s decision.

On the other hand, the optimistic BMIP is formulated by simply eliminating the $\min$ operator from the objective function (1) that is:

$$\begin{aligned} \text{[ }\mathrm {BMIP}^\mathrm {opt}\text{] } \quad \max \limits _{x \in {\mathbb {X}},\ y \in H(x)}&c^\top x+d_1^\top y \end{aligned}$$

(3)

Given the leader’s decision x, we denote by f(x) and $f^p(x)$ the optimistic and pessimistic objective function values of the leader, respectively. Similarly, we denote by $f^*$ and $f^*_p$, the optimal objective function values of the leader in the optimistic and pessimistic cases, respectively.

Note that if $k=n_1$, then BMIP reduces to a bilevel linear program (BLP). Bilevel programming, in particular, BMIPs and BLPs, where for a given leader’s decision the corresponding follower’s problem reduces to a linear program (LP) as in (2), is a well-studied area of optimization with a host of algorithmic and theoretical developments; see, e.g., [2, 4, 5, 13, 15]. In particular, it is known that, in contrast to polynomially solvable single-level LPs, BLPs are $\textit{NP}$-hard optimization problems [18]. Furthermore, due to the fact that the follower’s problem in (2) is an LP, BMIPs can be reformulated as single-level linear MIPs [3], which consequently can be solved either via standard MIP solvers or by using some specialized approaches [4, 13, 15]. Bilevel problems that involve integrality restrictions for the follower’s variables, see, e.g., some recent results in [11, 17, 34], are outside the scope of the current paper.

In view of our brief discussion above, the contributions of this paper are as follows:

$\bullet$ First, we consider computational complexity of BLPs in the context of optimistic and pessimistic solutions (see Sect. 2). In particular, we establish that even if an optimal optimistic (or pessimistic) solution to BLP is known, then the problem of finding an optimal pessimistic (or optimistic) solution to the same BLP remains an $\textit{NP}$-hard problem. Moreover, we show that even if one of the optimal solutions (either pessimistic or optimistic) to BLP is known, then it is still an $\textit{NP}$-hard problem to identify a leader’s solution that is, first, optimal for both optimistic and pessimistic BLPs, and, second, provides the same objective function value in both cases (if such solution exists).

$\bullet$ Second, we propose a generalization of pessimistic BMIPs, where the follower might willingly give up a portion of his¹ optimal objective function value, and thus select a suboptimal solution in order to inflict more damage to the leader (see Sect. 3). We refer to our proposed models as $\alpha$-pessimistic BMIPs, where parameter $\alpha$ controls the sub-optimality level of the follower and mimics constant-factor approximation ideas that are often used in the literature, see, e.g., [19, 35]. Clearly, such situations may arise in adversarial and interdiction settings, e.g., military and law-enforcement applications, which is the main motivation behind this study. (We illustrate our results with an example of the defender–attacker problem in Sect. 5.2.) Thus, the leader should be more conservative or guarded when she faces a follower that is $\alpha$-suboptimal. Our model naturally encompasses as its special classes both pessimistic BMIPs and max–min (or min–max) problems. In particular, for $\alpha =1$ the proposed approach corresponds to pessimistic BMIPs, while the case of $\alpha =0$ reduces $\alpha$-pessimistic BMIPs to max–min problems. The latter corresponds to the worst-case scenario for the leader, where the follower completely disregards his objective function and is focused on disrupting the leader’s performance. Therefore, the proposed model can be viewed as an approach for the leader to balance her level of conservatism through the value of parameter $\alpha$ in adversarial settings where the leader is not completely confident regarding the follower’s commitment to his objective function. We refer the reader for more detailed discussion on these issues in Sect. 3. We study the structural properties of $\alpha$-pessimistic BMIPs and illustrate its relationships with optimistic and pessimistic BMIPs.

$\bullet$ Third, we incorporate the proposed model of a sub-optimal adversarial follower into the context of strong-weak BMIP models [1, 10, 39], which is an extension of the ideas behind optimistic and pessimistic BMIPs (see Sect. 4). Specifically, in a strong-weak approach we model a partially collaborative follower by assuming that the leader’s objective function is a convex combination of the leader’s objective functions in the optimistic and pessimistic cases. Furthermore, the coefficients in this summation can be interpreted as the probabilities of cooperation or non-cooperation of the follower, respectively. That is, the leader is not certain if the follower is either collaborative or adversarial, and thus attempts to make a “robust” decision by taking into account both situations. Our approach, referred to as the strong-$\alpha$-weak model, can be viewed as a natural generalization of the strong-weak model from [10, 39] as it assumes that the follower may be $\alpha$-pessimistic, which allows us to consider more general types of adversarial followers including those that completely disregard their objective functions. Thus, our approach naturally links optimistic, pessimistic and max–min models within a unified framework. Another related question when comparing the strong-$\alpha$-weak model against either purely optimistic or pessimistic cases of BMIP is that how much the decision-maker (i.e., the leader) “loses” in terms of the obtained objective function value if the follower is, in fact, either optimistic or $\alpha$-pessimistic, respectively. In Sect. 4 we derive some bounds for such “losses.”

Finally, in Sect. 5 we consider an application of BMIPs, namely, a class of defender–attacker models. We illustrate our theoretical results from Sects. 3 and 4 with numerical examples and provide some insights into the links between optimistic, pessimistic and strong-weak modeling approaches.

2 Computational complexity: optimistic versus pessimistic cases

It is well-known that any linear mixed 0–1 programming problem can be reduced to a BLP instance [3]. Therefore, BLPs are strongly NP-hard [21]. We refer the reader to [18], which provides a brief survey on computational complexity of BLPs, in particular, with respect to issues related to polynomially solvable classes of the problem and inapproximability results.

BLPs are among the simplest classes of bilevel programs, which implies that the computational complexity results established in this section hold for more general bilevel optimization problems. Specifically, our main focus is on the following research questions:

• If the decision-maker knows an optimistic (pessimistic) solution to a BLP, does it simplify the problem of finding a pessimistic (optimistic) solution to the same BLP?

• How difficult is it to identify a leader’s solution that is optimal to both optimistic and pessimistic cases (assuming that such solution exists) when one of the optimal solutions (either pessimistic or optimistic) is known?

In our derivations below we exploit the SUBSET SUM problem that is known to be $\textit{NP}$-complete [19].

SUBSET SUM: Given a set of positive integers $S = \{s_1, s_2, \ldots , s_n\}$, and a positive integer K, does there exist a subset $S'\subseteq S$ such that $\sum _{i:\ s_i \in S'} s_i=K\ ?$

Next, consider the following BLP instance:

$$\begin{aligned} \quad \quad \text {``}\min \limits _{x}\text {''} \quad&\quad \sum _{i=1}^n s_ix_i+Kx_{n+1}+\sum _{i=1}^n v_i +Mu&\end{aligned}$$

(4a)

$$\begin{aligned} \text {s.t.}&\quad \sum _{i=1}^n s_ix_i+Kx_{n+1} \ge K,&\end{aligned}$$

(4b)

$$\begin{aligned}&\quad 0\le x_i \le 1, \quad i=1,\ldots ,n+1,&\end{aligned}$$

(4c)

$$\begin{aligned}&\quad (v,u)\in \mathop {{{\mathrm{argmax}}}}\limits _{v,u} \quad \sum _{i=1}^n v_i+(u-v_{n+1})&\end{aligned}$$

(4d)

$$\begin{aligned}&\quad \text {s.t.} \quad v_i\le 1-x_i, \quad \quad \ i=1,\ldots ,n,&\end{aligned}$$

(4e)

$$\begin{aligned}&\qquad \quad \quad v_i\le x_i, \quad \quad \quad \quad i=1,\ldots ,n,&\end{aligned}$$

(4f)

$$\begin{aligned}&\qquad \quad \quad 0 \le u \le x_{n+1},&\end{aligned}$$

(4g)

$$\begin{aligned}&\qquad \quad \quad u-v_{n+1}\le 1-x_{n+1},&\end{aligned}$$

(4h)

$$\begin{aligned}&\qquad \quad \quad u-v_{n+1}\le x_{n+1},&\end{aligned}$$

(4i)

$$\begin{aligned}&\qquad \quad \quad v_i\ge 0,\quad \ i=1,\ldots ,n+1.&\end{aligned}$$

(4j)

where M is a sufficiently large positive constant parameter.

Lemma 1

The following statements hold for model (4):

• (i) $x^*=(0,\ldots ,0,1)^\top$, $u^*=v^*_1=\cdots =v^*_{n+1}=0$ is an optimal optimistic solution, and $f^*=K$.

• (ii) $f^*_p=K$ iff the answer to the considered instance of the SUBSET SUM problem is “yes.”

• (iii) there exists a leader’s decision $x^*$ such that $f^*=f(x^*)=f^p(x^*)=f^*_p=K$, i.e., $x^*$ is optimal for both optimistic and pessimistic cases, iff the answer to the considered instance of the SUBSET SUM problem is “yes.”

Proof

• (i) Observe that $f^*\ge K$ due to (4b). Then it is easy to check that $x^*_1=\cdots =x^*_n=0, \ x^*_{n+1}=1$, and $u^*=v^*_1=\cdots =v^*_{n+1}=0$ is an optimal optimistic solution with $f^*= K$.

• (ii) $\Longleftarrow$ Suppose the answer to the SUBSET SUM problem is “yes.” Consider the leader’s solution, where $\bar{x}_{n+1}=0$, and $\bar{x}_i=1$ if $s_i\in S'$ or $\bar{x}_i=0$, otherwise, for $i=1,\ldots ,n$. From (4e), (4f) and (4g), $\bar{u}=\bar{v}_1=\cdots =\bar{v}_n=\bar{v}_{n+1}=0$ is the respective solution of the follower, and so $f^*_p=K$.

  $\Longrightarrow$ Let $f^*_p=K$ and $\bar{x}$ be an optimal pessimistic solution of the leader. Then, from (4a) and (4b), $\bar{u}=\bar{v}_1=\cdots =\bar{v}_n=0$. Therefore, $\bar{x}_1\ldots ,\bar{x}_n \in \{0,1\}$. Note that if $\bar{x}_{n+1}>0$ then the follower implements the solution that maximizes the leader’s objective, that is $\bar{u}=\bar{x}_{n+1}>0$ and $\bar{v}_{n+1}=\bar{u}-\min \{1-\bar{x}_{n+1},\bar{x}_{n+1}\}$, which is a contradiction. Therefore, $\bar{x}_{n+1}=0$. The required result follows if we let $s_i\in S'$ iff $\bar{x}_i=1$, $i=1,\ldots ,n$.

• (iii) From (ii), $f^* = f^*_p=K$ iff the answer to the SUBSET SUM problem is “yes.” Note that the same solution of the leader, i.e., $\bar{x}_{n+1}=0$, and $\bar{x}_i=1$ if $s_i\in S'$ or $\bar{x}_i=0$, otherwise, for $i=1,\ldots ,n$, is constructed in both directions of (ii), and this solution is also optimal in the optimistic case. $\square$

Note that constraints of the form (4e)–(4f) are often used for linking lower- and upper-level variables while proving theoretical results in bilevel programming [3, 21]. For example, in [21] such constraints are exploited for showing that linear max–min programs are strongly $\textit{NP}$-hard. The main novelty of our reduction is in using constraints of the form (4g)–(4i) and the corresponding additional terms in the objective functions (4a) and (4d), which allows us to obtain the following results based on Lemma 1:

Proposition 1

The problem of finding an optimal pessimistic solution of BLP remains NP-hard even if an optimal optimistic solution of the same BLP is known.

Proposition 2

Checking whether there exists a leader’s decision $x^*$, that

• (a) is optimal for both optimistic and pessimistic cases of BLP, and

• (b) simultaneously provides the same objective function values for both cases,

  is $\textit{NP}$-complete even if an optimal optimistic solution is known.

Proposition 3

Checking whether the BLP has multiple optimal optimistic solutions is $\textit{NP}$-hard.

Another interesting observation from Lemma 1(i) is given in the following remark.

Remark 1

Consider an instance of BLP given by (4) and let the follower be adversarial, while the leader makes a decision $x^*_1=\cdots =x^*_n=0, \ x^*_{n+1}=1$ by assuming a cooperative follower, i.e., an optimistic case. In response, the adversarial follower would implement $u=v_{n+1}=1$. Thus, $f^p(x^*)=K+M$, while $f^*_p=K$ by Lemma 1 if the answer to the instance of the SUBSET SUM problem is “yes”. Consequently, $f^p(x^*)-f^*_p = M$, which is a positive constant parameter. Therefore, if the leader assumes an optimistic case of BLP, while the follower is adversarial, i.e., the considered BLP is pessimistic, then the difference in the objective function values of the obtained solutions can be arbitrarily large.

In order to extend Proposition 1 we also analyze complexity of BLP when an optimal pessimistic solution is known. Consider another instance of BLP given by:

$$\begin{aligned} \quad \quad \text {``} \min \limits _{x}\text {''}\quad&\sum _{i=1}^n s_ix_i+(K+M)x_{n+1}+\frac{2M}{n}\sum _{i=1}^n (v_i+u_i)&\end{aligned}$$

(5a)

$$\begin{aligned} \text {s.t.}&\quad \sum _{i=1}^n s_ix_i+Kx_{n+1} \ge K,&\end{aligned}$$

(5b)

$$\begin{aligned}&\quad 0\le x_i \le 1, \quad i=1,\ldots ,n+1,&\end{aligned}$$

(5c)

$$\begin{aligned}&\quad (v,u)\in \mathop {{{\mathrm{argmax}}}}\limits _{v,u} \quad \sum _{i=1}^n (u_i-v_i)&\end{aligned}$$

(5d)

$$\begin{aligned}&\quad \text {s.t.} \quad u_i-v_i\le 1-x_i, \quad \quad \ i=1,\ldots ,n,&\end{aligned}$$

(5e)

$$\begin{aligned}&\qquad \quad u_i-v_i\le x_i, \quad \quad \quad \quad \ \; i=1,\ldots ,n,&\end{aligned}$$

(5f)

$$\begin{aligned}&\qquad \quad 0 \le v_i \le 1-x_{n+1}, \quad \ i=1,\ldots ,n,&\end{aligned}$$

(5g)

$$\begin{aligned}&\qquad \quad u_i\ge 0,\quad \quad \quad \quad \quad \qquad \ i=1,\ldots ,n,&\end{aligned}$$

(5h)

where M is a sufficiently large positive constant parameter.

Lemma 2

The following statements hold for model (5):

• (i) $\bar{x}=(0,\ldots ,0,1)^\top$, $\bar{v}_1=\cdots =\bar{v}_n=\bar{u}_1=\cdots =\bar{u}_{n}=0$ is an optimal pessimistic solution with $f_p^*=K+M$.

• (ii) $f^*=K$ iff the answer to the considered instance of the SUBSET SUM problem is “yes.”

Proof

• (i) Let $\bar{x}$ be a feasible solution of the leader with $\bar{x}_{n+1}=1$. Then, it is optimal for the leader to set $\bar{x}_1=\cdots =\bar{x}_{n}=0$. Thus, $f^p(\bar{x})=K+M$. Similarly, let $\widetilde{x}$ be a feasible solution of the leader with $0\le \widetilde{x}_{n+1}<1$. Then, in the pessimistic case, the follower can set $v_i=1-\widetilde{x}_{n+1}$ for all $i=1,\ldots ,n$, while having (5e)–(5f) satisfied. Therefore, $f^p(\widetilde{x})\ge K+M\widetilde{x}_{n+1}+2M(1-\widetilde{x}_{n+1})=K+2M-M\widetilde{x}_{n+1}>K+M$, which implies the necessary result.

• (ii) $\Longleftarrow$ Suppose the answer to the instance of the SUBSET SUM problem is “yes.” Consider the leader’s solution, where $x^*_{n+1}=0$, and ${x}^*_i=1$ if $s_i\in S'$ and ${x}^*_i=0$, otherwise, for $i=1,\ldots ,n$. In the optimistic case, the follower sets $u^*_i=v^*_i=0$ for all $i=1,\ldots ,n$. Thus, $f^*=f(x^*)=K$. $\Longrightarrow$ Let $f^*=K$ and $x^*$ be the corresponding optimal optimistic solution of the leader. Then, from (5a) and (5b), we conclude that $x^*_{n+1}=0$ and the follower’s optimistic solution is $u_1^*=\cdots =u_n^*={v}^*_1=\cdots ={v}^*_n=0$. Therefore, ${x}^*_1,\ldots ,{x}^*_n \in \{0,1\}$. Finally, the required statement follows by setting $s_i\in S'$ iff ${x}^*_i=1$, $i=1,\ldots ,n$. $\square$

Based on Lemma 2 we immediately obtain the following result:

Proposition 4

The problem of finding an optimal optimistic solution of BLP remains $\textit{NP}$-hard even if an optimal pessimistic solution of the same BLP is known.

Another observation from Lemma 2 is similar in spirit to the earlier remark. Specifically:

Remark 2

Suppose that the follower is collaborative, i.e., BLP is optimistic, but the leader makes a decision $\bar{x}_1=\cdots =\bar{x}_{n}=0, \ \bar{x}_{n+1}=1$ by assuming an adversary follower, i.e., pessimistic BLP. In response to the leader’s decision, the collaborative follower implements $u^*_i=v^*_i=0$ for all $i=1,\ldots ,n$. Thus, $f(\bar{x})=K+M$. Assume that the answer to the considered instance of the SUBSET SUM problem is “yes.” Consequently, $f^*=K$ and $f(\bar{x})-f^* = M$, which implies that if the leader assumes a pessimistic BLP while the follower is collaborative, then the difference in the objective function values of the obtained solutions can be arbitrarily large.

3 Suboptimal response to the leader’s decision: adversarial follower

Constraint (2) requires that the follower always implements one of his optimal solutions in response to each leader’s decision. In this section, we consider a more general non-cooperative (adversarial) setting, where the follower, in order to inflict more “damage” to the leader, can give up a portion of his optimal objective function value by selecting a suboptimal solution. Specifically, we propose modeling such settings by defining a suboptimal lower-level reaction set for a given leader’s decision x of the following form:

$$\begin{aligned} H_{\alpha }(x) = \{ y'\in \mathbb {R}^{n_2}_+: \ d^\top _2y' \ge \alpha d^\top _2y+(1-\alpha )L,\ y \in H(x),\ Ax+By' \le h \}, \end{aligned}$$

(6)

where parameter $\alpha \in [0,1]$ controls the suboptimality level of the follower. In (6) we assume that the follower’s objective function is bounded from below by a fixed constant L for any decision of the leader.

Then, the pessimistic BMIP generalizes to:

$$\begin{aligned} \text{[ }\alpha \text{- }\mathrm {BMIP}^\mathrm {pes}\text{] } \quad \max \limits _{x \in {\mathbb {X}}}&\ \big \{c^Tx+ \min \limits _{y \in H_{\alpha }(x)}d_1^\top y\big \}, \end{aligned}$$

(7)

which is referred to as $\alpha$-pessimistic BMIP. By comparing (1) and (7), observe that the $\alpha$-pessimistic BMIP is obtained from the pessimistic BMIP by enlarging the follower’s reaction set. Specifically, if $y\in H(x)$, then $y\in H_\alpha (x)$ for any $\alpha \in [0,1]$ due to the assumption on L. Therefore, $H(x)\subseteq H_\alpha (x)$ for any leader’s decision $x\in {\mathbb {X}}$. In general, $H_{\alpha _1}(x)\subseteq H_{\alpha _2}(x)$ for any $\alpha _1\ge \alpha _2$ and $\alpha _1,\alpha _2\in [0,1]$. Simply speaking, by introducing set $H_{\alpha }(\cdot )$, which is a generalization of the lower-reaction set $H(\cdot )$, we allow the follower to have more flexibility than in standard pessimistic BMIPs to select a solution that is more damaging to the leader’s objective function value.

One of the main motivations behind the proposed definition of $H_{\alpha }(\cdot )$ is to mimic constant-factor approximation ideas that are often used in the literature, see, e.g., [19, 35]. For example, the reaction set of the form (6) naturally arises when $L=0$ (e.g., the follower’s objective function is non-negative) and the follower applies an $\alpha$-approximation algorithm instead of an exact method. (In Sect. 4 we exploit such ideas to provide some approximation guarantees in the context of the strong-weak model.)

Our modeling framework allows for two possible interpretations. In the first one, the follower sets the value of $\alpha$, which is also known to the leader, and optimizes against the leader’s objective while also ensuring that his decision achieves $\alpha$-optimality with respect to his own objective function. In the other interpretation, the follower does not set $\alpha$, but when making the upper-level decisions, the leader takes into account the case where the follower may select an $\alpha$-suboptimal solution. Thus, $\alpha$ is set by the leader to make conservative or guarded upper-level decisions in anticipation of the follower’s suboptimal response.

Observe that if $\alpha =1$, then $H_1(x)=H(x)$ and $\alpha$-pessimistic BMIP reduces to standard pessimistic BMIP, where the follower responds to the leader’s decision optimally. Conversely, if $\alpha =0$, then the follower completely disregards his own objective function, and merely focuses on minimizing the leader’s benefit. In this case, $\alpha$-pessimistic BMIP reduces to a standard max–min problem, where both decision-makers have the same objective function, but their goals are in opposite directions, i.e.,

$$\begin{aligned} \max _{x \in {\mathbb {X}}} \Big \{c^\top x + \min _{y\in \mathbb {R}^{n_2}_+} \{d_1^\top y:Ax+B y \le h\}\Big \} \end{aligned}$$

(8)

Max–min problems of the form (8) arise in a variety of application domains [13, 27]. For example, the classical shortest path network interdiction problem, see, e.g., [24], is a special class of (8), where the leader (interdictor) selects a decision (e.g., removes a set of nodes and/or edges) in order to maximally increase the length of the shortest path for the follower (evader), who travels on a given network between two fixed nodes, i.e., an origin and a destination node.

The discussion above implies that the $\alpha$-pessimistic BMIP contains both the pessimistic BMIP and the max–min problem as its special cases, and thus can be viewed as their natural generalization. More importantly, we believe that the proposed modeling approach can be leveraged to address the following issues:

$\bullet$ In adversarial settings, the standard max–min approach given by (8) is used to provide the worst-case analysis for the decision-maker. This approach is commonly used in the related literature including the defender–attacker, attacker–defender and interdiction models. Such analysis assumes that the follower’s sole objective is to disrupt the leader’s performance to the maximum possible extent. On the other hand, the proposed $\alpha$-pessimistic approach allows to capture settings where, in addition to disrupting the leader’s objective function, the follower has an alternative goal. For example, in the defender–attacker models the follower may want to maximize his probability of survival after the attack. Clearly, he may sacrifice some of this objective in order to inflict more damage to the leader and the parameter $\alpha$ allows the leader to control this trade-off.

$\bullet$ The max–min model given by (8) often arises in the symmetric data/information scenarios. For example, in interdiction applications such assumption implies that both the leader and the follower have the same cost parameters. On the other hand, the pessimistic BMIP is capable of modeling more general asymmetric scenarios, see, e.g., [7], which, in turn, can be exploited by the leader to improve her objective function value in comparison to the conservative max–min approach that captures the worst-case scenario for the leader. However, in practice the leader may not be completely confident about the objective function of the follower. Thus, the parameter $\alpha$ allows the decision-maker, i.e., the leader, to control her level of conservatism.

$\bullet$ In practice it is also conceivable that the follower may not be a rational decision-maker or have bounded rationality and thus, he may implement a suboptimal solution. The parameter $\alpha$ allows the leader to control her level of conservatism in such cases. Admittedly, the actual value of $\alpha$ may be unknown to the leader. However, by performing the sensitivity analysis with respect to $\alpha$, the leader can obtain deeper insights into her possible solution strategies. Furthermore, we also explore potential leader’s “losses” when $\alpha$ is misspecified, see our further discussion at the end of this section.

Next, we provide some theoretical results in the context of the proposed modeling approach. Let $x^*$ and $\bar{x}^\alpha$ be the leader’s optimal solutions in the optimistic (3) and $\alpha$-pessimistic (7) BMIP formulations, respectively. Given the leader’s decision $x \in {\mathbb {X}}$, let w(x), $y^p(x)$ and $y^\alpha (x)$ be the corresponding follower’s decisions in the optimistic, pessimistic and $\alpha$-pessimistic cases, respectively. Thus, $w(x)\in H(x)$, $y^p(x)\in H(x)$ and $y^\alpha (x)\in H_\alpha (x)$. Also, denote by $f_\alpha ^p(x)$ the objective function value of the leader in the $\alpha$-pessimistic case and let $f_\alpha ^{*} = f_\alpha ^p(\bar{x}^\alpha )$. Note that $f^p_1(x)= f^p(x)$ and $f^*_1=f^*_p$; furthermore, $f^*_0$ is the optimal objective function value of (8).

Proposition 5

$f^*\ge f^*_p\ge f^p(\bar{x}^\alpha )\ge f_\alpha ^{*}$ for any $\alpha \in [0,1]$.

Proposition 6

$f_\alpha ^{*}$ and $f^p_\alpha (x)$ are non-decreasing in $\alpha \in [0,1]$.

The proofs of the above two propositions are omitted as they hold by the definitions (2) and (6), which imply that $H(x)\subseteq H_\alpha (x)$.

Proposition 7

$f^p_{\alpha }(x)$ is convex in $\alpha \in [0,1]$ for any $x\in {\mathbb {X}}$.

Proof

Consider $\alpha = \theta \alpha _1 + (1-\theta )\alpha _2$ for $\theta \in [0,1]$. Let $\widetilde{y}=\theta y^{\alpha _1}(x)+(1-\theta )y^{\alpha _2}(x)$ for $x \in {\mathbb {X}}$. Observe that $\widetilde{y} \ge 0$ and

$$\begin{aligned} Ax +B\widetilde{y} =&\ Ax +B\left( \theta y^{\alpha _1}(x)+(1-\theta )y^{\alpha _2}(x) \right) \\ =&\ \theta \left( Ax+B y^{\alpha _1}(x) \right) +(1-\theta )\left( Ax+B y^{\alpha _2}(x) \right) \le \theta h+(1-\theta )h=h. \end{aligned}$$

Furthermore, let $y \in H(x)$. As $y^{\alpha _1}(x)\in H_{\alpha _1}(x)$ and $y^{\alpha _2}(x)\in H_{\alpha _2}(x)$, then:

$$\begin{aligned} d_2^\top \widetilde{y}=&\ \theta d^\top _2y^{\alpha _1}(x)+(1-\theta )d_2^\top y^{\alpha _2}(x)\\ \ge&\ \theta \left( \alpha _1 d_2^\top y+(1-\alpha _1)L\right) +(1-\theta )\left( \alpha _2 d_2^\top y+(1-\alpha _2)L\right) =\alpha d_2^\top y +(1-\alpha ) L, \end{aligned}$$

which implies that $\widetilde{y} \in H_{\alpha }(x)$ and $d_1^\top \widetilde{y}\ge d_1^\top y^\alpha (x)$. The latter inequality holds by the definition of $y^\alpha (x)$. Therefore:

$$\begin{aligned} f^p_{\alpha }(x)=\,&c^\top x +d_1^\top y^\alpha (x)\le c^\top x +d_1^\top \widetilde{y}=\,c^\top x+d_1^\top \left( \theta y^{\alpha _1}(x)+(1-\theta )y^{\alpha _2}(x)\right) \\ =\,&\theta \left( c^\top x+d_1^\top y^{\alpha _1}(x)\right) +(1-\theta )\left( c^\top x+d_1^\top y^{\alpha _2}(x)\right) = \theta f^p_{\alpha _1}(x)+ (1-\theta )f^p_{\alpha _2}(x), \end{aligned}$$

which concludes the proof. $\square$

Corollary 1

$f^*_\alpha$ is convex in $\alpha \in [0,1]$.

Proof

It follows directly from the fact that $\bar{x}^\alpha \in {\mathbb {X}}$ and $f^*_\alpha =f^p_\alpha (\bar{x}^\alpha )$. $\square$

Corollary 2

For $\alpha \in [0,1]$ and $x \in {\mathbb {X}}$, $f^p_\alpha (x)\le \alpha f^p_1(x)+(1-\alpha )f^p_0(x)$ and $f_\alpha ^*\le \alpha f_p^*+(1-\alpha )f_0^*$.

Next, given $x^*$ we define $\Delta _\alpha$ as

$$\begin{aligned} \Delta _\alpha (x^*)=f_\alpha ^{*}-f_\alpha ^p(x^*), \end{aligned}$$

(9)

i.e., the leader’s “loss” when she implements optimal optimistic solution $x^*$, while the follower is $\alpha$-pessimistic. In other words, the leader can be viewed as “over-optimistic” about the follower’s response to her decisions. The dependence of $\Delta _\alpha$ on $x^*$ can be omitted if $x^*$ is a unique optimal optimistic solution, and the latter is assumed below. Clearly, by its definition $\Delta _\alpha \ge 0$. The above properties of $\alpha$-pessimistic solutions allow us to establish some additional lower and upper bounds on $\Delta _\alpha$.

Proposition 8

Let $0 \le \alpha _1\le \alpha _2 \le 1$ and $\alpha = \theta \alpha _1 + (1-\theta )\alpha _2$ for $\theta \in [0,1]$. Then:

$$\begin{aligned} \max \left\{ 0,\theta \Delta _{\alpha _1}+(1-\theta )\Delta _{\alpha _2}-(1-\theta )(f_{\alpha _2}^*-f_{\alpha _1}^*)\right\} \ \le \ \Delta _\alpha \ \le \ \Delta _{\alpha _1}+ (1-\theta )(f_{\alpha _2}^*-f_{\alpha _1}^*). \end{aligned}$$

(10)

Proof

Recall that $x^*$ denotes an optimal optimistic solution for the leader. From Propositions 6 and 7:

$$\begin{aligned} \Delta _\alpha =&f_\alpha ^*-f^p_\alpha (x^*) \ge f^*_{\alpha _1} - \theta f^p_{\alpha _1}(x^*) - (1-\theta )f^p_{\alpha _2}(x^*) \\ =&\theta \Delta _{\alpha _1}+(1-\theta ) f^*_{\alpha _1} - (1-\theta )f^p_{\alpha _2}(x^*) =\theta \Delta _{\alpha _1}+(1-\theta )\Delta _{\alpha _2}-(1-\theta )(f_{\alpha _2}^*-f_{\alpha _1}^*). \end{aligned}$$

Recall that $\Delta _\alpha$ is nonnegative by its definition. Thus, the left inequality in (10) follows. By using Propositions 6 and Corollary 1, we have the following:

$$\begin{aligned} \Delta _\alpha =&f_\alpha ^*-f^p_\alpha (x^*) \le \theta f_{\alpha _1}^* + (1-\theta ) f_{\alpha _2}^* - f^p_{\alpha _1}(x^*)\\ =&\Delta _{\alpha _1}-(1-\theta ) f^*_{\alpha _1} + (1-\theta )f_{\alpha _2}^*=\Delta _{\alpha _1}+ (1-\theta )(f_{\alpha _2}^*-f_{\alpha _1}^*), \end{aligned}$$

which provides the right inequality in (10). $\square$

Corollary 3

$\Delta _\alpha \le \Delta _{0}+ \alpha (f^*_p-f_0^*)$ for any $\alpha \in [0,1]$.

In general, $\Delta _\alpha$ is not monotone in $\alpha$. However, from Propositions 7 and Corollary 1, it follows that $\Delta _\alpha$ is equal to the difference of two convex functions, i.e., $\Delta _\alpha$ is a d.c. function [22].

Next, for $0\le \alpha _1\le \alpha _2\le 1$ given $\bar{x}^{\alpha _1}$ we define $\delta _{\alpha _1,\alpha _2}$ as

$$\begin{aligned} \delta _{\alpha _1,\alpha _2}(\bar{x}^{\alpha _1})=f_{\alpha _2}^{*}-f^p_{\alpha _2}(\bar{x}^{\alpha _1}), \end{aligned}$$

(11)

i.e., the leader’s “loss,” who implements optimal $\alpha _1$-pessimistic solution $\bar{x}^{\alpha _1}$, while the follower is $\alpha _2$-pessimistic. In other words, the leader can be viewed as conservative and “over-pessimistic” about the follower’s response to her decisions. The dependence of $\delta _{\alpha _1,\alpha _2}$ on $\bar{x}^{\alpha _1}$ can be omitted if $\bar{x}^{\alpha _1}$ is either unique or provides the same value of $f^p_{\alpha _2}$, and the latter is assumed below.

Proposition 9

Let $0 \le \alpha _1< \alpha _2 \le 1$. Then

$$\begin{aligned} 0\le \delta _{\alpha _1,\alpha _2}\le f^*_{\alpha _2}-f^*_{\alpha _1}\le \frac{\alpha _2-\alpha _1}{1-\alpha _1}\cdot \left( f_p^*-f^*_{\alpha _1}\right) . \end{aligned}$$

(12)

Proof

By definition $\delta _{\alpha _1,\alpha _2} \ge 0$. Next, from Propositions 5 and 6 along with Corollary 1, we have the following inequalities:

$$\begin{aligned} \delta _{\alpha _1,\alpha _2}= & {} f_{\alpha _2}^{*}-f^p_{\alpha _2}(\bar{x}^{\alpha _1})\le f_{\alpha _2}^{*}-f^*_{\alpha _1}\le \left( \frac{1-\alpha _2}{1-\alpha _1}\right) f^*_{\alpha _1}\\&+\left( \frac{\alpha _2-\alpha _1}{1-\alpha _1}\right) f^*_p-f^*_{\alpha _1}\le \frac{\alpha _2-\alpha _1}{1-\alpha _1}\cdot \left( f_p^*-f^*_{\alpha _1}\right) . \end{aligned}$$

$\square$

Corollary 4

$\delta _{0,\alpha } \le f^{*}_\alpha -f_0^{*}$ and $\delta _{\alpha ,1} \le f^{*}_p-f_\alpha ^{*}$ for any $\alpha \in [0,1]$.

In this section, we mostly focus on the “max–max” BMIPs, i.e., both the leader’s and the follower’s optimization problems involve maximization objectives. For other possible cases of BMIPs, the structural results obtained in this section should be modified by simple adjustments, which are rather straightforward in view of the provided derivations.

For example, in the case of “min–max” BMIPs the definition of $\Delta _\alpha$ and $\delta _{\alpha _1,\alpha _2}$ should be changed to $\Delta _\alpha =f_\alpha ^p(x^*)-f_\alpha ^{*}$ and $\delta _{\alpha _1,\alpha _2}=f^p_{\alpha _2}(\bar{x}^{\alpha _1})-f_{\alpha _2}^{*}$, respectively. The corresponding bounds in Propositions 8 and 9 as well as their corollaries can be modified accordingly. Finally, we note that some additional discussion on this issue is also provided in Sect. 5, where we describe an application example of BMIP that involve “min–max” problems.

To illustrate some basic properties of $\alpha$-pessimistic BMIP developed in this section, we consider the following example:

$$\begin{aligned}&\max _{{\mathbf {x}}\in \{0,1\}^2} \quad f(x,y)=15x_1 + 10x_2 + 2y_1 + y_2 \end{aligned}$$

(13a)

$$\begin{aligned}&\text {subject to} \quad x_1 + x_2 \le 1, \end{aligned}$$

(13b)

$$\begin{aligned}&{\mathbf {y}} \in {{\mathrm{argmax}}}_{{\mathbf {y}}\in {{\mathbb {R}}}_+^2} \{y_1 + y_2\ : \ 3x_1+6x_2\le y_1+y_2\le 10x_1+12x_2, \ y_1 \ge 3x_2\} \end{aligned}$$

(13c)

Table 1 The follower’s decisions and the leader’s objective function values for each leader’s decision. We assume $L=0$ in (6). Note that for $\alpha =0$, i.e., the max–min problem, the leader implements ${\mathbf {x}}^3$

Observe that in (13) the leader has only three feasible actions given in Table 1. The corresponding follower’s feasible regions are illustrated in Fig. 1. Furthermore, Table 1 provides optimal solutions in the optimistic, pessimistic and $\alpha$-pessimistic cases, where we assume that $L=0$ in the definition of $H_\alpha (x)$ given by (6).

According to Fig. 2a, the leader’s optimal $\alpha$–pessimistic decision is $\mathbf x ^3$ for $0\le \alpha \le 0.4$ and $\mathbf x ^2$ for $0.4\le \alpha \le 1$. This figure also shows that for $\alpha =1$, both decisions result in the same objective function value, which corresponds to an optimal pessimistic solution. In Fig. 2b the leader’s optimal objective function value in optimistic, pessimistic and $\alpha$–pessimistic cases is depicted; furthermore, we provide the value of $\alpha f_p^*+(1-\alpha )f_0^*$, which is an upper bound for $f_\alpha ^*$ according to Corollary 2.

Fig. 1

Follower’s feasible regions for leader’s decisions $\mathbf x ^2$ and $\mathbf x ^3$. Note that $\mathbf x ^1=(0,0)^\top$ and $\mathbf w (\mathbf x ^1)=\mathbf y ^p(\mathbf x ^1)=\mathbf y ^\alpha (\mathbf x ^1)=(0,0)^\top$

Fig. 2

Illustration of structural results for a BMIP example given by (13)

Figure 2c illustrates the value of $\delta _{0,\alpha }$, i.e., the “loss” of a conservative decision-maker, who implements optimal 0-pessimistic solution $\bar{x}^{0}$ (i.e., a solution of the max–min problem, where the follower’s objective function is completely ignored), while the follower is, in fact, $\alpha$-pessimistic. It is intuitive that for smaller values of $\alpha$ this “loss” is reasonably small. However, it is interesting to observe that for values of $\alpha$ close to 1, the “loss” of the leader’s is also rather small, which illustrates the fact that the value of $\delta _{\alpha _1,\alpha _2}$ does not necessarily increase if the difference $\alpha _2-\alpha _1$ increases. In Fig. 2c we also depict the value of $f_\alpha ^*-f^*_0$, which is an upper bound for $\delta _{0,\alpha }$ according to Corollary 4. For smaller values of $\alpha$ the quality of this upper bound is rather good; however, as $\alpha$ increases its quality deteriorates. Both of these observations are rather intuitive as $f^*_\alpha$ is a non-decreasing function (see Proposition 6), while by its definition $\delta _{\alpha _1,\alpha _2}$ should be relatively small for sufficiently small values of $\alpha _2-\alpha _1$ (recall that $\delta _{\alpha ,\alpha }=0$).

Figure 2d is similar in spirit to Fig. 2c. Specifically, we first depict the value of $\delta _{\alpha ,1}=f_{1}^{*}-f^p_{1}(\bar{x}^{\alpha })=f_p^{*}-f^p(\bar{x}^{\alpha })$, i.e., the “loss” of the conservative decision-maker, who implements optimal $\alpha$-pessimistic solution $\bar{x}^{\alpha }$, while the follower is, in fact, simply pessimistic. Figure 2d demonstrates that in the considered example, the decision-maker does not lose anything by being conservative as $\delta _{\alpha ,1}=0$ for all values of $\alpha$. Clearly, this is not necessarily the case in general. In Fig. 2d we also provide the value of $f^{*}_p-f_\alpha ^{*}$, which is an upper bound for $\delta _{\alpha ,1}$ according to Corollary 4. The quality of this upper bound is relatively poor for smaller values of $\alpha$, but improves as $\alpha$ gets closer to 1. Such behavior is intuitive if one recalls the definition of $\delta _{\alpha ,1}$ in (11) and observes that the value of $1-\alpha$ decreases as $\alpha$ increases. Some additional numerical illustrations of the developed theoretical results are provided in Sect. 5, where we consider an application example of BMIP.

Concluding this section, we note that our approach has connections to $\epsilon$-regularized version of general bilevel problems, see, e.g., [25], where the follower’s response is assumed to return an objective function value that is within $\epsilon$ from optimal. However, such studies typically consider more general functional forms of the upper- and lower-level optimization problems (not linear as in our case) and they primarily derive stability and existence results. Thus, the motivation behind studying such classes of problems is different from ours.

4 Strong-$\alpha$-weak response to the leader’s decision

The optimistic and pessimistic (also often referred to as strong and weak, see [10]) formulations of BMIP model two extreme cases of possible relationships between the leader and the follower. As discussed in detail in Sect. 1, the leader assumes that the follower is fully cooperative in the optimistic formulation; whereas in the pessimistic formulation, the leader expects an adversarial response from the follower.

To generalize these two approaches, Aboussoror and Loridan [1] define the term strong-weak Stackelberg problem to model partial cooperation between the leader and the follower. They integrate the optimistic and pessimistic formulations through a weighted summation of the leader’s objective functions in the optimistic and pessimistic cases. The coefficients in this summation are set by the leader and can be interpreted as the probabilities of cooperation or non-cooperation of the follower, respectively. In a similar manner, Cao and Leung [10] describe a BLP with partial cooperation for the linear version of the strong-weak Stackelberg problem. They reformulate the bilevel model as a single-level model using penalty coefficients, and present a numerical example, where the follower’s optimal approach is to cooperate partially. In other words, in some cases the follower could achieve the optimization of his interests when he partially cooperates with the leader [10]. Zheng et al. [39] show that the leader’s optimal value function is piece-wise linear and monotone in the weight coefficient measuring the follower’s level of cooperation (see our related discussion of Propositions 10 and 11 below). They also present an exact penalty method to solve the strong-weak BLP for every fixed weight.

In this section, we generalize the strong–weak BLP by considering an $\alpha$-pessimistic follower considered in Sect. 3. Similar to the strong-weak approach described in the previous paragraph, we also use a weight coefficient to integrate those two extremes. Specifically, given $\alpha \in [0,1]$ and cooperation coefficient $\gamma \in [0,1]$, the leader solves the following optimization problem:

$$\begin{aligned} \text{[ }(\gamma ,\alpha )\text{- }\mathrm {BMIP}\text{] } \quad \max \limits _{x \in {\mathbb {X}}} \ \left\{ c^\top x + (1-\gamma ) \min \limits _{y \in H_{\alpha }(x)} d_1^\top y + \gamma \max \limits _{y \in H(x)} d_1^\top y \right\} , \end{aligned}$$

(14)

where at one extreme the follower might fully cooperate with the leader, see the last term in (14), but at the other extreme, he might give up $1-\alpha$ portion of his optimal objective function value in order to inflict more damage to the leader, see the second term in (14).

It is important to note that $(\gamma ,\alpha )$-$\mathrm {BMIP}$ contains as its special cases the max–min problem (8) as well as the pessimistic and optimistic models given by (1) and (3), respectively. Formally, if $\alpha =1$ then $(\gamma ,\alpha )$-$\mathrm {BMIP}$ reduces to the strong-weak formulation from [10, 39], where (0, 1)-BMIP corresponds to the pessimistic BMIP, while $(1,\alpha )$-BMIP reduces to the optimistic BMIP for any $\alpha \in [0,1]$. On the other hand, if $\alpha =0$, then the second term in the objective function of $(\gamma ,\alpha )$-$\mathrm {BMIP}$, namely, the one that optimizes over $y\in H_{\alpha }(x)$, corresponds to the solution of the max–min problem (8). Thus, the proposed approach, further referred to as the strong-$\alpha$-weak problem, can be viewed as a natural generalization of the strong-weak approach, where we consider more general types of adversarial followers by using $\alpha \in [0,1]$.

Let $\bar{x}^{\alpha }_{\gamma }$ be the leader’s optimal solution to $(\gamma ,\alpha )$-$\mathrm {BMIP}$. Recall from Sect. 3 that $x^*$ and $\bar{x}^\alpha$ are the leader’s optimal solutions in the optimistic and $\alpha$-pessimistic formulations, respectively. Thus, $\bar{x}^{\alpha }_{1}=x^*$ and $\bar{x}^{\alpha }_{0}=\bar{x}^\alpha$. Furthermore, denote by $f^*_{\gamma ,\alpha }$ the optimal objective function value of $(\gamma ,\alpha )$-$\mathrm {BMIP}$, that is $f^*_{\gamma ,\alpha } = f^{\gamma ,\alpha }(\bar{x}^{\alpha }_{\gamma })$. Next, we analyze basic properties of $f^*_{\gamma ,\alpha }$.

Proposition 10

For any $\alpha \in [0,1]$, $f^*_{\gamma ,\alpha }$ is non-decreasing in $\gamma \in [0,1]$.

Remark 3

It is rather straightforward to show that for any $\gamma _1$ and $\gamma _2$, such that $1\ge \gamma _1\ge \gamma _2\ge 0$, we have

$$\begin{aligned} f^*\ge f^*_{\gamma _1,1} \ge f^*_{\gamma _2,1}\ge f_p^*. \end{aligned}$$

Therefore, if there exists a leader’s optimal solution $\widetilde{x}$ that is optimal for both optimistic and pessimistic cases of ${\mathrm {BMIP}}$ and ensures that $f^*=f(\widetilde{x})=f^p(\widetilde{x})=f^*_p$, then this solution is obtained by solving $(\gamma ,\alpha )$-$\mathrm {BMIP}$ for any $\gamma \in [0,1]$ and $\alpha =1$. Thus, $f^*=f^*_{\gamma ,1}=f^*_p$ for any $\gamma \in [0,1]$. On the other hand, if the decision-maker solves the optimistic and pessimistic cases of BMIP separately, then it is not guaranteed that such solution is obtained. In other words, the equality $f^*=f^*_p$ can be checked by solving the optimistic and pessimistic cases of ${\mathrm {BMIP}}$ separately. However, the corresponding leader’s solutions $x^*$ and $\bar{x}^1$ are not necessarily optimal for $\mathrm {BMIP}^\mathrm {pes}$and $\mathrm {BMIP}^\mathrm {opt}$, respectively. This observation can be viewed as another advantage of the strong-weak approach, in particular, when the decision-maker is not aware if the follower is collaborative or adversarial.

Proposition 11

For any $\alpha \in [0,1]$, $f^*_{\gamma ,\alpha }$ is convex in $\gamma \in [0,1]$.

Proof

Let $0 \le \gamma _1\le \gamma _2 \le 1$, and $\gamma = \theta \gamma _1 + (1-\theta )\gamma _2$ for $\theta \in [0,1]$. Then:

$$\begin{aligned} f^*_{\gamma ,\alpha }=\,&c^\top \bar{x}^\alpha _\gamma + (1-\gamma ) d_1^\top y^{\alpha }(\bar{x}^\alpha _\gamma )+\gamma d_1^\top w(\bar{x}^\alpha _\gamma )\\ =&\ \theta \left( c^\top \bar{x}^\alpha _\gamma + (1-\gamma _1) d_1^\top y^{\alpha }(\bar{x}^\alpha _\gamma )+\gamma _1 d_1^\top w(\bar{x}^\alpha _\gamma )\right) \\&+(1-\theta )\left( c^\top \bar{x}^\alpha _\gamma + (1-\gamma _2) d_1^\top y^{\alpha }(\bar{x}^\alpha _\gamma )+\gamma _2 d_1^\top w(\bar{x}^\alpha _\gamma )\right) \\ \le&\ \theta \left( c^\top \bar{x}^\alpha _{\gamma _1} + (1-\gamma _1) d_1^\top y^{\alpha }(\bar{x}^\alpha _{\gamma _1})+ \gamma _1 d_1^\top w(\bar{x}^\alpha _{\gamma _1})\right) \\&+(1-\theta )\left( c^\top \bar{x}^\alpha _{\gamma _2} + (1-\gamma _2) d_1^\top y^{\alpha }(\bar{x}^\alpha _{\gamma _2})+\gamma _2 d_1^\top w(\bar{x}^\alpha _{\gamma _2})\right) \nonumber \\ \le&\ \theta f^*_{\gamma _1,\alpha } + (1-\theta ) f^*_{\gamma _2,\alpha }, \end{aligned}$$

which implies the required result. $\square$

If $\alpha =1$, then, as mentioned earlier, the proposed strong-$\alpha$-weak model given by $(\gamma ,\alpha )$-$\mathrm {BMIP}$ reduces to the strong-weak model from the literature, and the structural results derived in Propositions 10 and 11 are equivalent to those shown in [39]. However, our derivations demonstrate that these results, namely, the non-decreasing and convexity properties of $f^*_{\gamma ,\alpha }$, also hold for the case when the follower is $\alpha$-pessimistic for any $\alpha \in [0,1]$. Furthermore:

Proposition 12

For any $\gamma \in [0,1]$, $f^*_{\gamma ,\alpha }$ is convex in $\alpha \in [0,1]$.

Proof

Let $0 \le \alpha _1\le \alpha _2 \le 1$, and $\alpha = \theta \alpha _1 + (1-\theta )\alpha _2$ for $\theta \in [0,1]$. Let $\widetilde{y}=\theta y^{\alpha _1}(\bar{x}^\alpha _\gamma )+(1-\theta )y^{\alpha _2}(\bar{x}^\alpha _\gamma )$. As in the proof of Proposition 7, we can show that $\widetilde{y} \in H_{\alpha }(\bar{x}^\alpha _\gamma )$ and $d_1^\top \widetilde{y}\ge d_1^\top y^\alpha (\bar{x}^\alpha _\gamma )$. Then,

$$\begin{aligned} f^*_{\gamma ,\alpha }=&c^\top \bar{x}^\alpha _\gamma + (1-\gamma ) d_1^\top y^{\alpha }(\bar{x}^\alpha _\gamma )+ \gamma d_1^\top w(\bar{x}^\alpha _\gamma )\le c^\top \bar{x}^\alpha _\gamma + (1-\gamma ) d_1^\top \widetilde{y}+ \gamma d_1^\top w(\bar{x}^\alpha _\gamma ) \\ =&\ \theta \left( c^\top \bar{x}^\alpha _\gamma + (1-\gamma ) d_1^\top y^{\alpha _1}(\bar{x}^\alpha _\gamma )+ \gamma d_1^\top w(\bar{x}^\alpha _\gamma )\right) \\&+(1-\theta )\left( c^\top \bar{x}^\alpha _\gamma + (1-\gamma ) d_1^\top y^{\alpha _2}(\bar{x}^\alpha _\gamma )+\gamma d_1^\top w(\bar{x}^\alpha _\gamma )\right) \\ \le&\theta f^*_{\gamma ,\alpha _1} + (1-\theta ) f^*_{\gamma ,\alpha _2}, \end{aligned}$$

which concludes the proof. $\square$

One natural question that arises when comparing the strong-$\alpha$-weak model against either optimistic or pessimistic cases of BMIP is that how much the leader “loses” in terms of the obtained objective function value if the follower is, in fact, either optimistic or $\alpha$-pessimistic, respectively. Next, we provide bounds on these differences. First, we derive an upper bound for the difference between $f^*$, i.e., the optimal objective value of the leader in the optimistic formulation, and $f(\bar{x}^\alpha _\gamma )$, i.e., the objective value of the leader if she implements $\bar{x}^{\alpha }_\gamma$ in the optimistic case.

Proposition 13

For any $\gamma \in [0,1]$ and $\alpha \in [0,1]$, $f^*-f(\bar{x}^\alpha _\gamma )\le (1-\gamma ) \left( d^\top _1w(x^*)-d^\top _1y^\alpha (x^*)\right)$

Proof

$$\begin{aligned} f(\bar{x}^\alpha _\gamma )=&\ c^\top \bar{x}^\alpha _\gamma +d_1^\top w(\bar{x}^\alpha _\gamma )\nonumber \\ =&\ c^\top \bar{x}^\alpha _\gamma +\gamma d_1^\top w(\bar{x}^\alpha _\gamma ) +(1-\gamma ) d_1^\top y^\alpha (\bar{x}^\alpha _\gamma ) +(1-\gamma ) d^\top _1w(\bar{x}^\alpha _\gamma )-(1-\gamma ) d^\top _1y^\alpha (\bar{x}^\alpha _\gamma ) \\ \ge&\ c^\top x^*+\gamma d_1^\top w(x^*) +(1-\gamma ) d^\top _1y^\alpha (x^*)+(1-\gamma ) d_1^\top w(\bar{x}^\alpha _\gamma ) -(1-\gamma ) d^\top _1y^\alpha (\bar{x}^\alpha _\gamma ) \\ \ge&\ c^\top x^*+\gamma d_1^\top w(x^*) +(1-\gamma ) d^\top _1y^\alpha (x^*) \\ =&\ c^\top x^*+d_1^\top w(x^*) -(1-\gamma ) \left( d_1^\top w(x^*) -d^\top _1y^\alpha (x^*)\right) \\ =&f^*-(1-\gamma ) \left( d^\top _1w(x^*)-d^\top _1y^\alpha (x^*)\right) , \end{aligned}$$

where the last inequality follows from the fact that $d^\top _1w(\bar{x}^\alpha _\gamma )\ge d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )$. $\square$

Moreover, our next result shows that if c and $d_1$ are nonnegative, then $\bar{x}^\alpha _\gamma$ provides a $\gamma$-approximate solution to the optimistic BMIP. In other words, the decision-maker has some guaranteed quality of the obtained solution if the follower turns out to be collaborative.

Corollary 5

If $c\in {\mathbb {R}}^{n_1}_{+}$ and $d_1 \in {\mathbb {R}}^{n_2}_{+}$, then $f(\bar{x}^\alpha _\gamma )\ge \gamma f^*$.

Proof

$$\begin{aligned} f(\bar{x}^\alpha _\gamma )\ge&f^*-(1-\gamma ) \left( d^\top _1w(x^*)-d^\top _1y^\alpha (x^*)\right) \ge \ f^*+(1-\gamma ) \left( -d^\top _1w(x^*)\right) \\ \ge&\ f^*+(1-\gamma ) \left( -d^\top _1w(x^*)-c^\top x^*\right) =f^*+(1-\gamma ) (-f^*)=\gamma f^*. \end{aligned}$$

$\square$

Next, we consider an adversarial follower. In particular, we derive an upper bound for the difference between $f^*_{\alpha }$, i.e., the optimal objective function value of the leader in the $\alpha$-pessimistic formulation, and $f_{\alpha }^{p}(\bar{x}^\alpha _\gamma )$, i.e., the objective function value of the leader if she implements $\bar{x}^{\alpha }_\gamma$ in the $\alpha$-pessimistic case.

Proposition 14

For $0\le \alpha \le 1$ and $0\le \gamma \le 1$, we have that $f_\alpha ^* - f^p_\alpha (\bar{x}^\alpha _\gamma )\le \gamma \left( d^\top _1w(\bar{x}^\alpha _\gamma )-d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )\right)$.

Proof

$$\begin{aligned} f^p_\alpha (\bar{x}^\alpha _\gamma )=&\ c^\top \bar{x}^\alpha _\gamma +d_1^\top y^\alpha (\bar{x}^\alpha _\gamma )\\ =&\ c^\top \bar{x}^\alpha _\gamma +\gamma d_1^\top w(\bar{x}^\alpha _\gamma ) +(1-\gamma ) d_1^\top y^\alpha (\bar{x}^\alpha _\gamma ) +\gamma d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )-\gamma d^\top _1w(\bar{x}^\alpha _\gamma ) \\ \ge&\ c^\top \bar{x}^\alpha +\gamma d_1^\top w(\bar{x}^\alpha ) +(1-\gamma ) d_1^\top y^\alpha (\bar{x}^\alpha ) +\gamma d^\top _1y(\bar{x}^\alpha _\gamma )-\gamma d^\top _1w(\bar{x}^\alpha _\gamma ) \\ =&\ c^\top \bar{x}^\alpha +d_1^\top y(\bar{x}^\alpha )+\gamma d_1^\top w(\bar{x}^\alpha ) -\gamma d_1^\top y^\alpha (\bar{x}^\alpha ) +\gamma d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )-\gamma d^\top _1w(\bar{x}^\alpha _\gamma ) \\ \ge&\ f_\alpha ^*-\gamma \left( d^\top _1w(\bar{x}^\alpha _\gamma )-d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )\right) ,\nonumber \end{aligned}$$

where the last inequality follows from the fact that $d_1^\top w(\bar{x}^\alpha ) \ge d_1^\top y^\alpha (\bar{x}^\alpha )$. $\square$

Note that finding $\bar{x}^\alpha _\gamma$ is an $\textit{NP}$-hard problem. However, given $\bar{x}^\alpha _\gamma$ the values of $d^\top _1w(\bar{x}^\alpha _\gamma )$ and $d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )$ can be computed by solving linear programming problems. Therefore, the upper bound for $f_\alpha ^* - f^p_\alpha (\bar{x}^\alpha _\gamma )$ given by Proposition 14 can be obtained in polynomial time after finding $\bar{x}^\alpha _\gamma$.

Corollary 6

If $c\in {\mathbb {R}}^{n_1}_{+}$ and $d_1 \in {\mathbb {R}}^{n_2}_{+}$, then $f^p_\alpha (\bar{x}^\alpha _\gamma )\ge f_\alpha ^*-\gamma f(\bar{x}^\alpha _\gamma )\ge f_\alpha ^*-\gamma f^*$.

Proof

It follows from Proposition 14 that

$$\begin{aligned} f^p_\alpha (\bar{x}^\alpha _\gamma )\ge&\ f_\alpha ^*-\gamma \left( d^\top _1w(\bar{x}^\alpha _\gamma )-d^\top _1y^\alpha (\bar{x}^\alpha _\gamma )\right) \ge f_\alpha ^*+\gamma \left( -d^\top _1w(\bar{x}^\alpha _\gamma )\right) \\ \ge&\ f_\alpha ^*+\gamma \left( -d^\top _1w(\bar{x}^\alpha _\gamma )-c^\top \bar{x}^\alpha _\gamma \right) = f_\alpha ^*-\gamma f(\bar{x}^\alpha _\gamma )\ge f_\alpha ^*-\gamma f^*,&\end{aligned}$$

which concludes the proof. $\square$

For the example given by (13), Fig. 3 illustrates the bounds obtained in Proposition 14 and Corollary 6. Clearly, the quality of the former bound is better, which is not surprising given the provided derivations. On the other hand, it is also worth mentioning that the quality of the bounds improves as $\alpha$ and $\gamma$ approach one and zero, respectively. This observation is rather intuitive as (0, 1)-BMIP corresponds to the pessimistic case of BMIP.

Fig. 3

Illustration of Proposition 14 and Corollary 6 for a BMIP example given by (13)

Assume that there exist a positive lower bound $L_\alpha ^*$ for $f_\alpha ^*$ and a finite upper bound $U^*$ for $f^*$, that is,

$$\begin{aligned} 0<L^*_\alpha \le f_\alpha ^*\le f^*\le U^*<+\infty .\end{aligned}$$

(15)

Then we have the following result, which is similar in spirit to Corollary 5:

Corollary 7

If $c\in {\mathbb {R}}^{n_1}_{+}$, $d_1 \in {\mathbb {R}}^{n_2}_{+}$ and $f_\alpha ^*>0$, then for a given $\bar{\gamma } \in [0,1]$, define $\gamma = (1-\bar{\gamma })\frac{L^*_\alpha }{U^*}$. Then $f_\alpha ^p(\bar{x}^\alpha _\gamma )\ge \bar{\gamma } f_\alpha ^*$ and $f(\bar{x}^\alpha _\gamma )\ge {\gamma } f^*$.

Proof

By using Corollary 6, we have

$$\begin{aligned} f^p_\alpha (\bar{x}^\alpha _\gamma )\ge&f_\alpha ^*-\gamma f^*\\&=f_\alpha ^*-(1-\bar{\gamma })\cdot \frac{L_\alpha ^*}{U^*}\cdot f^*\ge f_\alpha ^*-(1-\bar{\gamma })\cdot L_\alpha ^*\ge f_\alpha ^*-(1-\bar{\gamma })\cdot f_\alpha ^*\\&= \bar{\gamma }f^*_\alpha , \end{aligned}$$

where we use (15) in the obtained inequalities. $\square$

The above results provide the leader with some estimates of her loses in cases when the follower is either optimistic or $\alpha$-pessimistic. In particular, under some assumptions $\bar{x}^\alpha _\gamma$ provides simultaneously a $\gamma$-approximate solution to the optimistic BMIP and $\bar{\gamma }$-approximate solution to the $\alpha$-pessimistic BMIP. Note that the relationship between $\gamma$ and $\bar{\gamma }$ through some lower and upper bounds for $f_\alpha ^*$ and $f^*$ is rather intuitive given our earlier observations in Remarks 1 and 2.

5 Numerical illustrations

In this section, we provide additional illustrations of the proposed modeling approach using a class of defender–attacker problems. In our numerical experiments we solve single-level reformulations of our models using CPLEX 12.4 [23].

5.1 Single-level reformulations

We reformulate $\mathrm {BMIP}^\mathrm {opt}$, $\mathrm {BMIP}^\mathrm {pes}$, $\alpha$-$\mathrm {BMIP}^\mathrm {pes}$and $(\gamma ,\alpha )$-$\mathrm {BMIP}$ as single-level mixed-integer programs with constraints that enforce primal feasibility, dual feasibility, and complementary slackness for the follower’s linear program. It is a standard approach in the bilevel optimization literature, which can be applied as long as the follower’s problem is an LP, see, e.g., [3] for more detailed discussion in the case of optimistic bilevel programs. The fact that both $\alpha$-$\mathrm {BMIP}^\mathrm {pes}$ and $(\gamma ,\alpha )$-$\mathrm {BMIP}$ admit single-level MIP reformulations can be viewed as another advantage of the proposed modeling approach.

For completeness of the discussion we first present the standard single-level formulation for $\mathrm {BMIP}^\mathrm {opt}$, see, e.g., [3]:

$$\begin{aligned} \text{[ }\mathrm {BMIP}^\mathrm {opt}\text{] }: \max&\quad c^\top x+d_1^\top y \end{aligned}$$

(16a)

$$\begin{aligned} \text {s.t.}&x \in \mathbb {X} \end{aligned}$$

(16b)

$$\begin{aligned}&By \le h-Ax&(\lambda ) \end{aligned}$$

(16c)

$$\begin{aligned}&By \ge h-Ax - M_\lambda (e-u_\lambda )&\end{aligned}$$

(16d)

$$\begin{aligned}&\lambda \le M_\lambda u_\lambda&\end{aligned}$$

(16e)

$$\begin{aligned}&B^\top \lambda \ge d_2&(y) \end{aligned}$$

(16f)

$$\begin{aligned}&B^\top \lambda \le d_2 + M_y(e-u_y) \end{aligned}$$

(16g)

$$\begin{aligned}&y \le M_yu_y \end{aligned}$$

(16h)

$$\begin{aligned}&u_\lambda \in \{0,1\}^{m_2},u_y \in \{0,1\}^{n_2},\ y,\lambda \ge 0, \end{aligned}$$

(16i)

where e is the vector of all ones of appropriate dimensions, i.e., $e=(1,\ldots ,1)^\top$, while $M_\lambda$ and $M_y$ are sufficiently large positive constants. Constraints (16c)–(16i) ensure that $y \in H(x)$ by enforcing primal feasibility, dual feasibility, and complementary slackness conditions for the follower’s LP given the leader’s decision x. In particular, $\lambda$ is the set of dual variables corresponding to constraints (16c) in the follower’s LP, while 0–1 variables $u_\lambda$ and $u_y$ are used to linearize the complementary slackness conditions.

Next, we present the single-level reformulation for $(\gamma ,\alpha )$-$\mathrm {BMIP}$:

$$\begin{aligned} \text{[ }(\gamma ,\alpha )\text{- }\mathrm {BMIP}\text{] }: \max \,&c^\top x+\gamma d_{1}^{\top } y+(1-\gamma )d_{1}^{\top } y'&\end{aligned}$$

(17a)

$$\begin{aligned} \text {s.t.} \,&(\text {16b})-(\text {16i}) \nonumber \\&By' \le h-Ax (\mu ) \end{aligned}$$

(17b)

$$\begin{aligned}&By' \ge h-Ax - M_\mu (e-u_\mu ) \end{aligned}$$

(17c)

$$\begin{aligned}&\mu \le M_\mu u_\mu \end{aligned}$$

(17d)

$$\begin{aligned}&d^\top _2y'\ge \alpha d^\top _2y+(1-\alpha )L (\zeta )\end{aligned}$$

(17e)

$$\begin{aligned}&d^\top _2y'\le \alpha d^\top _2y+(1-\alpha )L + M_\zeta (1-u_\zeta ),&\end{aligned}$$

(17f)

$$\begin{aligned}&\zeta \le M_\zeta u_\zeta ,&\end{aligned}$$

(17g)

$$\begin{aligned}&d_2\zeta -B^\top \mu \le d_1, (y')\end{aligned}$$

(17h)

$$\begin{aligned}&d_2\zeta -B^\top \mu \ge d_1 -M_{y'}(e-u_{y'}),&\end{aligned}$$

(17i)

$$\begin{aligned}&y' \le M_{y'} u_{y'},&\end{aligned}$$

(17j)

$$\begin{aligned}&u_\mu \in \{0,1\}^{m_2},u_{y'} \in \{0,1\}^{n_2},\ u_\zeta \in \{0,1\},\ y',\mu , \zeta \ge 0, \end{aligned}$$

(17k)

where $M_\mu$, $M_\zeta$, $M_{y'}$ are sufficiently large positive constants. Constraints (17b)–(17k) impose that the follower chooses a solution $y' \in H_{\alpha }(x)$ that provides the minimum $d^\top _1y'$ for the leader. The main ideas behind formulation (17) is similar to those used in deriving (16). In particular, y and $y'$ are variables representing the optimistic and the $\alpha$-pessimistic responses of the follower, respectively. Also, $\zeta$ and $\mu$ are the dual variables corresponding to constraints in $H_\alpha (x)$, see (6), given the leader’s decision x.

If $\gamma =0$ and $\alpha =1$ in formulation (17), then we obtain a single-level reformulation for the pessimistic BMIP. Furthermore, if $\gamma > 0$ and $\alpha =1$, then we obtain a single-level reformulation for the strong-weak bilevel linear program [10]. Note that Zeng [38] provides similar reformulations for the strong-weak BMIP. Thus, model (17) generalizes the formulations presented in Zeng [38] by considering follower’s $\alpha$-suboptimal response to the leader, i.e., the strong-$\alpha$-weak approach considered in Sect. 4.

5.2 Defender–attacker problem (DAP)

There are a number of defender–attacker models proposed in the related literature, see some examples in [8] and the references therein. In this section we consider a class of such models, where the defender (leader) runs a set of facilities J. Facility $j\in J$ has a certain value (e.g., capacity) given by $c_j$ and can be fully protected by spending $k_j$ units of the defender’s resource. The total defense budget is K units. The attacker (follower) can destroy $y_j\in [0,1]$ portion of the facility j by spending $b_{j}y_{j}$ units. The attacker’s goal is to minimize the leader’s total value after the attack (i.e., maximize damage) subject to a budget constraint of B units. If $y_j$ portion of the facility value is destroyed, then the defender has to spend $r_jy_j$ units to recover its full value. The defender’s objective is to minimize the total recovery cost. We formulate the considered class of pessimistic DAPs as:

$$\begin{aligned} \text{[pes-DAP] } \quad \min \limits _{x \in \mathbb {X}} \ \max \limits _{y \in H(x)}&\sum _{j \in J} r_{j}y_{j}\\ \text {subject to} \,&H(x) = {{\mathrm{argmax}}}\left\{ \sum _{j \in J} c_jy_{j} : y \in {\mathbb {Y}}, y_j \le 1-x_j, \ j \in J \right\} , \end{aligned}$$

where ${\mathbb {X}} \subseteq \{x \in \{0,1\}^{|J|}\ :\ \sum _{j \in J}k_jx_j \le K\}$ and ${\mathbb {Y}} = \{y \in [0,1]^{|J|}\ :\ \sum _{j \in J} b_{j}y_{j} \le B\}$. The leader’s decision variable, $x_{j}$, is equal to 1 iff facility j is protected and 0, otherwise. The follower’s decision variable, $y_{j} \in [0,1]$, represents the destroyed portion of facility j. Given $\alpha \in [0,1]$ and $\gamma \in [0,1]$, $(\gamma ,\alpha )$–DAP can be formulated as:

$$\begin{aligned} \text{[ }(\gamma ,\alpha )\text{-DAP] } \quad \min \limits _{x \in {\mathbb {X}}} \ \left\{ (1-\gamma ) \max \limits _{y \in H_{\alpha }(x)} \sum _{j \in J} r_{j}y_{j} + \gamma \min \limits _{y \in H(x)} \sum _{j \in J} r_{j}y_{j} \right\} , \end{aligned}$$

where the suboptimal reaction set of the attacker is defined as:

$$\begin{aligned} H_{\alpha }(x) = \{ y'\in {\mathbb {Y}}:\ \sum _{j \in J} c_jy'_{j} \ge \alpha \sum _{j \in J} c_jy_{j}, \ y \in H(x), \ y'_j \le 1-x_j, \ j \in J\}. \end{aligned}$$

Next, we illustrate some of the structural properties derived in Sects. 3 and 4. We consider a DAP instance with 10 facilities. Parameters of the instance include the recovery cost vector ${\mathbf {r}} = [19\ 21\ 25\ 29\ 31\ 35\ 36\ 40\ 43\ 58]^\top$, the capacity vector ${\mathbf {c}}=[10\ 10\ 10\ 9\ 8\ 7\ 6\ 5\ 4\ 3]^\top$, facility protection cost $k_j= 1$ and destruction cost $b_j=1$ for all $j=1,\ldots ,10$, the total defense budget $K=2$ and the attacker’s budget is $B=1$. Furthermore, the defender has two additional logical constraints of the form: $x_1+x_2+x_3\le 1$ and $x_9\le x_1$, which are incorporated into the constraint set defining ${\mathbb {X}}$.

Fig. 4

Illustration of structural results with a DAP instance from Sect. 5.2. Note that the leader’s problem involves minimization, which requires some minor adjustments in the corresponding statements of Sect. 3, see related discussion in Sects. 3 and 5.2. The term “LB” in b stands for the lower bound of $\Delta _\alpha$ in Proposition 8. c and d are analogous to Fig. 2c, d respectively

Fig. 5

Illustration of Propositions 13 and 14 with a DAP instance from Sect. 5.2 for $\alpha =0.7$. Note that the leader’s problem involves minimization

Recall that our example (13) is a “max–max” BMIP. On the other hand, the considered class of DAPs involves minimization of the leader’s objective function. As briefly discussed in Sect. 3, some simple adjustments are necessary when we apply the results from Sects. 3 and 4 to the considered class of DAPs. For example, $f_\alpha ^*$ is non-increasing with respect to $\alpha$ instead of non-decreasing as stated in Proposition 6. Alternatively, one could obtain maximization version of DAP by simply changing the signs of $r_j$’s, and thus, directly apply the results of Sects. 3 and 4.

Figure 4 illustrates various structural properties established in Sect. 3. In particular, it is interesting to observe in Fig. 4a that the value of $\Delta _{\alpha }$ decreases as $\alpha$ increases. This result is rather intuitive if one recalls that $H_{\alpha _1}(x)\subseteq H_{\alpha _2}(x)$ for $\alpha _1\ge \alpha _2$, i.e., the follower has more flexibility in making the decision less favorable for the leader for smaller values of $\alpha$. Figure 4b depicts $\Delta _{\alpha }$ along with its upper and lower bounds derived in Proposition 8 and Corollary 3. Figure 4c, d are analogous to Fig. 2c, d, respectively.

Figure 5 illustrates Propositions 13 and 14 established in Sect. 4. The obtained graphics match the intuition behind $(\gamma ,\alpha )$-BMIP model and the derived results. For example, in Fig. 5a the depicted functions coincide for $\gamma =1$, which, in fact, should be expected as $(1,\alpha )$-BMIP corresponds to optimistic BMIP for any $\alpha \in [0,1]$. Similarly, in Fig. 5b the depicted functions also coincide for $\gamma =0$ as $(0,\alpha )$-BMIP corresponds to $\alpha$-pessimistic BMIP. Finally, the quality of the bounds from Propositions 13 and 14 is better for larger and smaller values of $\gamma$ in Fig. 5a, b, respectively. These observations are natural if one recalls the motivation behind $(\gamma ,\alpha )$-BMIP model, in particular, the fact that the objective function of $(\gamma ,\alpha )$-BMIP is a convex combination of the follower’s optimistic and $\alpha$-pessimistic responses to the leader’s decision.

6 Concluding remarks

In this paper we study relationships between optimistic and pessimistic BLPs and BMIPs, where the follower’s optimization problem is a linear program. First, we focus on theoretical computational complexity issues for BLPs. Perhaps, the most interesting complexity result obtained in this paper is the fact that even if an optimal optimistic (or pessimistic) solution of BLP is known, then the problem of finding an optimal pessimistic (or optimistic) solution for the same BLP remains an $\textit{NP}$-hard problem. Second, we propose a generalization of pessimistic bilevel linear problems, referred to as $\alpha$-pessimistic BMIPs, where the follower might willingly give up a portion of his optimal objective function value, and thus select a suboptimal solution in order to inflict more damage to the leader. It is important to note that our techniques allow the decision-maker to consider more general types of adversarial followers. In particular, $\alpha$-pessimistic BMIPs naturally encompasses as their special classes both pessimistic BMIPs and max–min (or min–max) problems. Furthermore, we incorporate the proposed approach into a class of strong-weak models that capture settings, where the leader is not certain if the follower is either collaborative or adversarial, and thus attempts to make a robust decision by taking into account the follower’s responses in both situations. Finally, we study structural properties of the proposed mathematical models and illustrate the obtained results using insightful numerical examples.

There is a number of possible avenues for future research directions. In particular, we believe that the most interesting ones include issues related to generalizations of the proposed models for bilevel problems that involve integrality restrictions for the follower’s decision variables and more general classes of objective functions at both levels.