Geometric Structure of the Traveling Waves for 1D Degenerate Parabolic Equation

Abstract

We clarify the geometric structure of non-negative traveling waves for the spatial one-dimensional degenerate parabolic equation $U_{t}=U^{p}(U_{xx}+\mu U)-\delta U$. This equation has a nonlinear term with a parameter $p>0$ and the cases $0<p<1$ and $p>1$ have been investigated in the author’s previous studies. It has been pointed out that the classifications of the traveling waves for these two cases are not the same and thus a bifurcation phenomenon occurs at $p=1$. However, the classification of the case $p=1$ remains open since the conventional approaches do not work for this case, which have prevented us to understand how the traveling waves bifurcate. The difficulty for the case $p=1$ is that the corresponding ordinary differential equation through the Poincaré compactification has the non-hyperbolic equilibrium at infinity and we need to estimate the asymptotic behaviors of the trajectories near it. In this paper, we solve this problem by using a new asymptotic approach, which is completely different from the asymptotic analysis performed in the previous studies, and clarify the structure of the traveling waves in the case of $p=1$. We then discuss the rich structure of traveling waves of the equation from a geometric point of view.

1 Introduction

In this paper, we consider non-negative traveling waves in a space one-dimensional degenerate parabolic equation

$$\begin{aligned} U_{t}=U(U_{xx}+\mu U)-\delta U, \quad t>0, \quad x\in {\mathbb {R}}, \end{aligned}$$

(1)

with $\mu >0$ and $\delta =0$ or 1. Equation (1) is a special case of the following equation with $p=1$:

$$\begin{aligned} U_{t}=U^{p}(U_{xx}+\mu U)-\delta U, \quad t>0, \quad x\in {\mathbb {R}}. \end{aligned}$$

(2)

Here we briefly explain some background of Eq. (2). For $\delta =0$, Eq. (2) is closely related to the time evolution problem for plane curves. More precisely, the cases $0<p<1$ and $p>1$ of (2) are related to the problems of the motion of an expanding curve and of curve shortening respectively (see for example [13] and references therein). From the mathematical point of view, the derivation of the blow-up rate of the blow-up solutions of (2) for $p\ge 2$ has been actively studied (see, e.g., [1,2,3, 16] and references therein). By applying Type I rescaling as used in [7,8,9,10, 16], we can obtain the case $\delta =1$ in (2). In addition to this, from the behavior of the traveling wave with $\delta =1$ in (2), we can derive a lower bound for the blow-up rate of (2) with $\delta =0$ for $p\ge 2$. See e.g. [3, 16] and references therein.

The first author gave results on the classifications of the shapes and asymptotic forms of all non-negative traveling waves with $0<p<1$ and $p>1$ for both $\delta =0$ and $\delta =1$ in (2) (see [7,8,9,10]). Note that the results for $p\in 2{\mathbb {N}}$ and $0<p<1$ are given in [8, 10] and [9] respectively, and the former was extended to the case $1<p\in {\mathbb {R}}$ in [7]. It is pointed out in [9] that the bifurcation of the equilibria at infinity occurs at $p=1$, which characterizes the existence of non-negative traveling waves and their bifurcations near $p = 1$. In these studies, a two-dimensional system of ordinary differential equations is derived in terms of traveling wave coordinates, and the Poincaré-type compactification (see below for details) is used to give a classification of all connecting orbits in the system of two-dimensional ordinary differential equations including a point at infinity. That is, by introducing the traveling wave coordinate

$$\begin{aligned} \phi (\xi )=U(t,x), \quad \xi =x-ct, \quad 0<c\in {\mathbb {R}}, \end{aligned}$$

one can derive

(3)

equivalently,

(4)

from Eq. (1), and all dynamics (including a point at infinity) of Eq. (4) can be investigated by using of Poincaré-type compactification. Note that we are interested in the range $\phi \ge 0$ since we are considering non-negative traveling waves. Each connecting orbit (referring to trajectories between finite equilibria or between equilibria at infinity) in (4) corresponds to a traveling wave of (2), and thus the classification of the traveling waves of (2) leads to that of connecting orbits in (4). The shape and asymptotic form of the traveling wave are clarified by studying the dynamical system corresponding to (4) near its finite/infinity equilibria (see Definition 3.13 of [14] for the definition of the equilibria at infinity).

As described in [6, 8, 14, 15], the Poincaré compactification is one of the compactifications of the phase space to analyze dynamical systems near equilibria at infinity, which is the embedding of ${\mathbb {R}}^{n}$ into ${\mathbb {R}}^{n+1}$ in the unit upper hemisphere. Then a point at infinity in the original phase space corresponds to the boundary of a compact manifold. This method has been used, for example, in the analysis of the Liénard equation (see [6] and references therein) and in the reconstruction of ODE blow-up solutions in terms of dynamical systems theory (see [4, 11, 14, 15]). Moreover, in the previous results on the classifications of non-negative traveling waves of (2) with $0<p<1$ and $p>1$ [7,8,9,10], this method plays a central role. In our setting we consider a system of two-dimensional ordinary differential equations corresponding to the case $n=2$, in which case the boundary of the unit upper hemisphere, ${\mathbb {S}}^{1}$, corresponds to the point at infinity of the phase space ${\mathbb {R}}^2$. Moreover, in order to describe the detailed dynamics at infinity, the system is divided into several parts covering ${\mathbb {S}}^{1}$ and each of them is projected into local coordinates. As a result, by combining the dynamics in these local coordinates, we can understand the behavior at infinity (See Appendix A for the details). It is natural to apply the same method for the case $p=1$, i.e., Eq. (1). Once the $p=1$ case is clarified, we obtain the classification of the dynamics of the corresponding two-dimensional system including the dynamics at infinity with the variation of the parameter p, which reveals the geometric structure of non-negative traveling waves in (2). However, there is a significant difference between the case $p\ne 1$ and $p=1$ as pointed out in [9].

For $p\ne 1$, the equilibrium at infinity is hyperbolic and thus we can estimate the dominant asymptotic behavior near it. On the other hand, for $p=1$, the equilibrium at infinity is not hyperbolic and the dynamics near the equilibria has not been clarified. One of the difficulties of this problem is that we need to consider the effect of multiple timescale transformations. If we adopt the approach provided by [7,8,9], a special function called the exponential integral must be evaluated under the multiple time-scale transformations. The previous study [10] examines the relationship between these time-scale transformations carefully and establishes suitable estimates of the integrals including the Lambert W function. This approach essentially relies on the dynamics of the orbit whose initial value belongs to the center manifold of the equilibrium at infinity. On the other hand, for the case $p=1$, we need to investigate all trajectories not on the center manifold and thus we cannot apply the analysis by methods such as [10] to this case. Therefore, it is necessary to develop additional asymptotic studies for the dynamics near the non-hyperbolic equilibrium at infinity. The approach presented in this paper deals with a new relation of dependent and independent variables and with a new estimation of the asymptotic behavior near the non-hyperbolic equilibrium at infinity, which avoids the problem of evaluating the exponential integral with the multiple time-scale transformations which appears in the conventional methods. Our approach allows us not only to obtain the classification of traveling waves at $p=1$ but also to fully understand how the classification of non-negative traveling waves changes as p varies in (2), providing a new perspective as a geometric structure on the “bifurcation of traveling waves” due to parameter changes.

This paper is organized as follows. The next section describes the concept of solution adopted in this paper, which is the same as in [7,8,9], and gives main results for traveling waves. In Sect. 3, all dynamics in the phase space including a point at infinity of (4) are investigated by using of the Poincaré compactification. The proof of the main result is given in Sect. 4. Finally, Sect. 5 gives a concluding remark on the changes of classification of non-negative traveling waves in (2) depending on p and a discussion of the “bifurcation” of traveling waves due to parameter changes.

2 Main Results

Before describing our main results, we provide some prerequisites such as the concept of a solution, which are also given in [7,8,9].

Definition 1

We say that a function $U(t,x) \equiv \phi (\xi )$ is a quasi traveling wave of (1) if the function $\phi (\xi )$ is a solution of (3) on a finite interval or semi-infinite interval, where $\xi =x-ct$ with some positive constant $c>0$.

Definition 2

([7], Definition 2.1) We say that a function $U(t,x) \equiv \phi (\xi )$ is a quasi traveling wave with the singularity of (1) if the function $\phi (\xi )$ is a quasi traveling wave of (1) on a semi-finite such that $U=\phi$ reaches 0 and only right differentiation is possible and it becomes a constant at finite end point of the semi-infinite interval. More precisely, the function $\phi (\xi )$ is a solution of (3) on a semi-infinite interval $( \xi _{-},+\infty )$, where $\phi (\xi ) \in C^{2}(\xi _{-},+\infty ) \cap C^{0}[\xi _{-},+\infty )$ with $|\xi _{-}|<\infty$, and satisfies

$$\begin{aligned} \lim _{\xi \rightarrow \xi _{-} + 0} \phi (\xi ) = 0, \quad \lim _{\xi \rightarrow \xi _{-} +0} |\phi '(\xi )| = C. \end{aligned}$$

This definition also holds for the finite interval with singularities at both ends.

Next, we define the weak traveling wave solution with a singularity of (1). Note that $U=\phi =0$ is an obvious solution in (1).

Definition 3

([7], Definition 2.2) Let $\phi (\xi )$ be a quasi traveling wave with singularity of (1) on a semi-infinite interval $(\xi _{-},\infty )$ satisfying

$$\begin{aligned} \lim _{\xi \rightarrow \xi _{-}+0} \phi '(\xi ) = C \quad \text{ and } \quad \lim _{\xi \rightarrow \xi _{-}+0} \phi (\xi ) =0 \end{aligned}$$

with a positive constant C. Then, we say that a function

$$\begin{aligned} \phi ^{*}(\xi ) = {\left\{ \begin{array}{ll} 0, & \xi \in (-\infty ,\xi _{-}],\\ \phi (\xi ), & \xi \in (\xi _{-},+\infty ) \end{array}\right. } \end{aligned}$$

is a weak traveling wave solution with singularity of (1). Singularity here means having a point $\xi _{-}$ that is not differentiable. The formulation is similar for the case defined on a finite interval with singularities at both ends.

We can check that $\phi =\phi ^{*}(\xi )$ satisfies the following weak form for any $\varphi \in C_{0}^{\infty }({\mathbb {R}})$:

$$\begin{aligned} \int _{{\mathbb {R}}} \left[ c\phi \varphi _{\xi } + (\phi _{\xi })^{2}\varphi - \dfrac{1}{2}\phi ^{2}\varphi _{\xi \xi } -\mu \phi ^{2}\varphi +\delta \phi \varphi \right] \, d\xi =0. \end{aligned}$$

Under these definitions, we now state our main results. Note that $\phi (\xi )=U(\xi )$ and $\phi '(\xi )=\psi (\xi )=U_{\xi }(\xi )$. In the following, the symbol $f(\xi )\sim g(\xi )$ as $\xi \rightarrow a$ implies that

$$\begin{aligned} \lim _{\xi \rightarrow a}\left| \dfrac{f(\xi )}{g(\xi )} \right| =1. \end{aligned}$$

Theorem 1

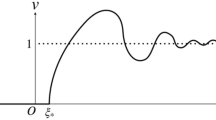
Assume that $\mu >0$ and $\delta =0$. Then, for a given positive constant c, the equation (1) has a family of weak traveling wave solutions with the singularity such that it corresponds to the family of orbits in (4) connecting $(\phi , \psi )=(0, +\infty )$ and $(\phi ,\psi )=(0, 0)$. Each solution $\phi (\xi )$ satisfies the following:

• (i1) $\displaystyle \lim _{\xi \rightarrow \xi _{-} + 0} \phi (\xi ) = \lim _{\xi \rightarrow +\infty } \phi (\xi ) = \lim _{\xi \rightarrow +\infty } \phi '(\xi ) = 0$, $\displaystyle \lim _{\xi \rightarrow \xi _{-} + 0} \phi '(\xi ) =+\infty$ for some $\xi _{-}\in {\mathbb {R}}$.

• (i2) $\phi (\xi )>0$ holds for $\xi \in (\xi _{-},+\infty )$ and $\phi (\xi )=0$ holds for $\xi \in (-\infty , \xi _{-}]$.

• (i3) There exists a constant $\xi _{0}\in (\xi _{-}, +\infty )$ such that the following holds: $\phi '(\xi )>0$ for $\xi \in (\xi _{-}, \xi _{0})$, $\phi '(\xi _{0})=0$ and $\phi '(\xi )<0$ for $\xi \in (\xi _{0}, +\infty )$.

In addition, the asymptotic behaviors of $\phi (\xi )$ and $\phi '(\xi )$ for $\xi \rightarrow \xi _{-}+0$ are

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi (\xi ) \sim -c(\xi -\xi _{-})\log [Ac(\xi -\xi _{-})] + B(\xi -\xi _{-}),\\ \phi '(\xi ) \sim -c\log [Ac(\xi -\xi _{-})] \end{array}\right. } \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0, \end{aligned}$$

(5)

where A, B are constants with $A>0$, and the asymptotic behaviors of $\phi (\xi )$ and $\phi '(\xi )$ for $\xi \rightarrow +\infty$ are

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi (\xi ) \sim \left( \dfrac{\mu }{c}\xi \right) ^{-1},\\ \phi '(\xi ) \sim -\left( \dfrac{\mu }{c}\right) ^{-1}\xi ^{-2}, \end{array}\right. } \quad \mathrm{{as}} \quad \xi \rightarrow +\infty . \end{aligned}$$

(6)

Theorem 2

Assume that $\mu >0$ and $\delta =1$. Then, for a given positive constant c, the equation (1) has two types of weak traveling wave solutions as follows.

• (I) There exists a family of weak traveling wave solutions with the singularity such that it corresponds to the family of orbits in (4) connecting $(\phi , \psi )=(0, +\infty )$ and $(\phi ,\psi )=(\mu ^{-1}, 0)$. Each solution $\phi (\xi )$ satisfies (i2), (i3), and the following:

  • (I1) $\displaystyle \lim _{\xi \rightarrow \xi _{-} + 0} \phi (\xi )=0$, $\displaystyle \lim _{\xi \rightarrow +\infty } \phi (\xi ) = \mu ^{-1}$, $\displaystyle \lim _{\xi \rightarrow \xi _{-} + 0} \phi '(\xi ) =+\infty$, $\displaystyle \lim _{\xi \rightarrow +\infty } \phi '(\xi ) =0$ for some $\xi _-\in {\mathbb {R}}$.

  In addition, the asymptotic behaviors of $\phi (\xi )$ and $\phi '(\xi )$ for $\xi \rightarrow \xi _{-}+0$ are expressed as (5), and the asymptotic behavior of $\phi (\xi )$ for $\xi \rightarrow +\infty$ is

  $$\begin{aligned} \phi (\xi ) \sim {\left\{ \begin{array}{ll} \left( C_{1}e^{\omega _{1}\xi }+C_{2}e^{\omega _{2}\xi }+\dfrac{1}{\mu }\right) , \quad (D>0), \\ \left( (C_{3}\xi +C_{4})e^{\omega \xi }+\dfrac{1}{\mu }\right) ,\quad (D=0), \\ \left( e^{-\frac{\mu c}{2}\xi } \bar{Z}(\xi ) +\dfrac{1}{\mu }\right) ,\quad (D<0), \end{array}\right. } \end{aligned}$$

  (7)

  where $C_{j}$ ($1\le j\le 4$) are some constants and

  $$\begin{aligned}&\omega _{1}=\dfrac{-\mu c+\sqrt{D}}{2}<0, \quad \omega _{2}=\dfrac{-\mu c-\sqrt{D}}{2}<0, \\ &\omega =-\dfrac{\mu c}{2}<0, \quad D=\mu ^{2}c^{2}-4\mu ,\\&\bar{Z}(\xi ) = C_{5}\cdot \sin [\frac{\sqrt{|D|}}{2}\xi ]+ C_{6}\cdot \cos [ \frac{\sqrt{|D|}}{2}\xi ] \end{aligned}$$

  with constants $C_{5},C_{6}$.

• (II) There exists a traveling wave solution such that it corresponds to the orbit in (1) such that it corresponds to the orbit in (4) connecting $(\phi , \psi )=(0, 0)$ and $(\phi ,\psi )=(\mu ^{-1}, 0)$. The solution $\phi (\xi )$ satisfies the following:

  • (II1) $\displaystyle \lim _{\xi \rightarrow -\infty } \phi (\xi ) = \lim _{\xi \rightarrow -\infty } \phi '(\xi )=\lim _{\xi \rightarrow +\infty } \phi '(\xi )=0, \lim _{\xi \rightarrow +\infty } \phi (\xi ) = \mu ^{-1}.$

  • (II2) $\phi (\xi )>0$ holds for $\xi \in {\mathbb {R}}$.

  In addition, the asymptotic behavior of $\phi (\xi )$ for $\xi \rightarrow \infty$ is expressed as (7), and the asymptotic behavior of $\phi (\xi )$ for $\xi \rightarrow -\infty$ is

  $$\begin{aligned} \phi (\xi ) \sim \dfrac{Mc^{2}e^{\frac{1}{c}\xi }}{M(\mu c^{2}+1)e^{\frac{1}{c}\xi }-1} \quad \mathrm{{as}}\quad \xi \rightarrow -\infty , \end{aligned}$$

  (8)

  where $M<0$ is a constant that depends on the initial state $\phi (0)=\phi _{0}$.

3 Dynamics on the Poincaré Disk of (4)

In this section, by using the Poincaré compactification, we study the dynamics on the Poincaré disk $\Phi ={\mathbb {R}}^{2} \cup \{(\phi , \psi ) \mid \Vert (\phi , \psi )\Vert =+\infty \}$. The following discussion is almost the same as for [7, 9], but for the reader’s convenience, we reproduce the details.

3.1 Dynamics Near Finite Equilibria

First, we study the dynamics near finite equilibria of (4). When $\delta =0$, Eq. (4) has no equilibrium. When $\delta =1$, Eq. (4) has an equilibrium $E_{1}: (\phi ,\psi )=(\mu ^{-1},0)$ for $\{\phi >0\}$. Note that the system (4) is singular at $\phi =0$. The Jacobian matrix of the vector field (4) in $E_{1}$ is

$$\begin{aligned} J_{1}= \left( \begin{array}{cc} 0 & 1 \\ -\mu & -c\mu \end{array}\right) . \end{aligned}$$

Then, the behavior of the solution around $E_{1}$ depends on the sign of $D=\mu ^{2}c^{2}-4\mu$. Since $c>0$, $E_{1}$ is a stable node for $D\ge 0$, and is a stable focus (spiral sink) for $D<0$.

Next, we desingularize $\phi =0$ by the time-rescale desingularization:

$$\begin{aligned} ds/d\xi = \phi ^{-1} \end{aligned}$$

(9)

as in [7, 9]. Since we are considering a nonnegative solution, i.e., $\phi \ge 0$, the direction of the time does not change via the desingularization (9) in this region. Then we have

(10)

and we can treat $\phi =0$.

Remark 1

([7], Remark 9) It should be noted that the time scale desingularization (9) is simply multiplying the vector field by $\phi$. Then, except the singularity $\{\phi = 0\}$, the integral curves of the system (vector field) remain the same but are parameterized differently. We refer to Section 7.7 of [12] and references therein for the analytical treatments of desingularization with the time rescaling. In what follows, we use a similar time rescaling (re-parameterization of the solution curves) repeatedly to desingularize the vector fields.

The system (10) has the following equilibrium:

$$\begin{aligned} E_{0}: (\phi , \psi )=(0,0). \end{aligned}$$

The Jacobian matrix of the vector field (10) at $E_{0}$ is

$$\begin{aligned} J_0= \left( \begin{array}{cc} 0 & 0\\ \delta & -c \end{array}\right) . \end{aligned}$$

• For $\delta =0$, we can use the center manifold theory to study the dynamics near $E_{0}$ (for instance, see [5]). Then we obtain the approximation of the (graph of) center manifold as follows:

  $$\begin{aligned} \{ (\phi , \psi ) \mid \psi (s)=-\mu c^{-1}\phi ^{2}+O(\phi ^{4}) \}. \end{aligned}$$

  (11)

  Hence, the dynamics of (10) near $E_{0}$ is topologically conjugate to the dynamics of the following equation:

  $$\begin{aligned} \phi '(s)=-\mu c^{-1}\phi ^{3}+O(\phi ^{5}) \end{aligned}$$

  (12)

• By the same argument as in [7,8,9,10], we can study the dynamics around the equilibrium $E_{0}$ for $\delta = 1$. We conclude that the approximation of the (graph of) center manifold is

  $$\begin{aligned} \left\{ (\phi , \psi ) \mid \psi (s)=c^{-1}\phi -c^{-3}(\mu c^{2}+1)\phi ^{2}+O(\phi ^{3}) \right\} \end{aligned}$$

  (13)

  and the dynamics of (10) near $E_{0}$ is topologically conjugate to the dynamics of the following equation:

  $$\begin{aligned} \phi '(s)=c^{-1}\phi ^{2}-c^{-3}(\mu c^{2}+1)\phi ^{3}+O(\phi ^{4}). \end{aligned}$$

  (14)

These results are equivalent to the results in [7, 9] with $p=1$. Since our interest is the case of $\phi \ge 0$, we will consider the dynamics of this equation on the charts $\overline{U}_{j}$ ($j=1,2$) and $\overline{V}_{2}$. See Appendix A for the definitions and geometric images of $\overline{U}_{j}$ and $\overline{V}_{j}$, which is described similarly in the previous studies [7,8,9]. See also [6, 14, 15].

3.2 Dynamics on the Local Chart $\overline{U}_{2}$

To obtain the dynamics on the chart $\overline{U}_{2}$, we introduce the coordinates $(\lambda , x)$ given by

$$\begin{aligned} \phi =x/\lambda , \quad \psi =1/\lambda , \end{aligned}$$

where $x\ge 0$ and $\lambda \ge 0$. For a geometric image of this coordinates, see Fig. 2. From Eq. (10), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda '(s)=c\lambda +\mu x^{2}-\delta \lambda x,\\ x'(s)=\lambda ^{-1}x+cx+\mu \lambda ^{-1}x^{3}-\delta x^{2}. \end{array}\right. } \end{aligned}$$

(15)

By using the time-scale desingularization $d\tau /ds=\lambda ^{-1}$, we can obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{\tau }=c\lambda ^{2}+\mu \lambda x^{2}-\delta \lambda ^{2} x,\\ x_{\tau }=x+c\lambda x+\mu x^{3}-\delta \lambda x^{2}, \end{array}\right. } \end{aligned}$$

(16)

where $\lambda _{\tau }=d\lambda /d\tau$ and $x_{\tau }=dx/d\tau$. The equilibrium of the system (16) on $\{\lambda =0\}$ is

$$\begin{aligned} E_{2}: (\lambda ,x)=(0,0) \end{aligned}$$

The Jacobian matrix of the vector field (16) at $E_{2}$ is

$$\begin{aligned} \left( \begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \end{aligned}$$

and

$$\begin{aligned} \left. \lambda _{\tau } \phantom {\big |}\right| _{x=0}=c\lambda ^{2}>0, \quad \left. x_{\tau } \phantom {\big |}\right| _{\lambda =0,\, x>0}=x(1+\mu x^{2})>0 \end{aligned}$$

hold. Therefore, $\{\lambda =0\}$ (i.e. the x axis) is the unstable manifold and $\{x=0\}$ (i.e. the $\lambda$ axis) is the center manifold of $E_2$.

3.3 Dynamics on the Local Chart $\overline{V}_{2}$

The change of coordinates

$$\begin{aligned} \phi =-x/\lambda , \quad \psi =-1/\lambda \end{aligned}$$

and the time-rescaling $d\tau /ds = \lambda ^{-1}$ give the projection dynamics of (10) on the chart $\overline{V}_{2}$. Then we obtain the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{\tau }=c\lambda ^{2}-\mu \lambda x^{2}-\delta \lambda ^{2} x,\\ x_{\tau }=-x+c\lambda x-\mu x^{3}-\delta \lambda x^{2}, \end{array}\right. } \end{aligned}$$

(17)

where $\lambda \ge 0$ and $x\le 0$. The equilibrium of the system (17) on $\{\lambda =0\}$ is

$$\begin{aligned} E_{3}: (\lambda ,x)=(0,0). \end{aligned}$$

The Jacobian matrix of the vector field (17) at $E_{3}$ is

$$\begin{aligned} \left( \begin{array}{cc} 0 & 0\\ 0 & -1 \end{array}\right) . \end{aligned}$$

As a dynamical system near the origin of $\overline{V}_{2}$, $\{(\lambda , x) \mid \lambda >0,\, x<0\}$ is topological conjugate to a saddle dynamics, which implies that any trajectory with its initial point on the region $\{(\lambda , x) \mid \lambda >0,\, x<0\}$ does not converge to $(\lambda , x)=(0,0)$. This fact immediately follows from the following relations and the continuity of solutions:

$$\begin{aligned} \left. \lambda _{\tau } \phantom {\big |}\right| _{x=0}=c\lambda ^{2}>0, \quad \left. x_{\tau } \phantom {\big |}\right| _{\lambda =0,\, x<0}= x(-1-\mu x^{2})>0. \end{aligned}$$

3.4 Dynamics and Connecting Orbits on the Poincaré disk

We can also obtain the differential equation on the local coordinate $\overline{U}_{1}$, but it has no equilibrium on $\{\lambda =0\}$. Combining the dynamics on the charts $\overline{U}_{j}$ ($j=1,2$) and $\overline{V}_{2}$, we obtain the whole dynamics on the Poincaré disk $\Phi$ that is equivalent to the dynamics of (4) (or (10)) (see also Fig. 1).

Fig. 1

Schematic pictures of the dynamics on the Poincaré disk. [Left: $\delta =0$.] [Right: $\delta =1$.]

The purpose of this subsection is to prove the existence of connecting orbits (see also Fig. 1). The strategy described in this subsection is the same as for [7,8,9,10]. Before we explain it, we will give some remarks about the Poincaré disk.

Remark 2

([7], Remark 11) In Fig. 1, we need to be careful about the handling of the point $E_{0}$ as stated in [7,8,9,10]. When we consider the parameter s on the disk $\Phi$, $E_{0}$ is the equilibrium of (10). However, under the parameter $\xi$, $E_{0}$ is a point on the line $\{\phi =0\}$ with singularity. We see that $d \phi /d \psi$ takes the same values for (4) and (10) except for the singularity $\{\phi =0\}$, which implies that the trajectories for the parameter s on $\{(\phi , \psi )\in \Phi \mid \phi >0\}$ are the same as that for the parameter $\xi$. This is also the case for the dynamics near the equilibrium at infinity $E_{2}: (\phi , \psi )=(0, +\infty )$.

First, we show the existence of connecting orbits for $\delta = 0$ (see also Fig. 1). Since $\{\phi =0\}$ is invariant in (10), any trajectory on $\{(\phi , \psi ) \in \Phi \mid \phi <0\}$ remains in this domain. Let ${\mathcal {W}}^{cs}(E_{0})$ be a center stable manifold of $E_{0}$ for (10) and ${\mathcal {W}}^{u}(E_{2})$ be an unstable manifold of $E_{2}$ for (10). Then, from the Poincaré-Bendixson theorem, any trajectories that goes to ${\mathcal {W}}^{cs}(E_{0})$ must start from a point on ${\mathcal {W}}^{u}(E_{2})$. That is, in (10), there is a trajectory between $E_{2}:(\phi ,\psi )=(0,+\infty )$ and $E_{0}:(\phi ,\psi )=(0,0)$ such that its initial point is on ${\mathcal {W}}^{u}(E_{2})$ and its end point is on ${\mathcal {W}}^{cs}(E_{0})$. Moreover, we see that such a trajectory obtained in (10) also exists in (4) since $d\phi /d\psi$ takes the same value on the vector fields defined by (4) and (10) as mentioned in Remark 2. Thus, in (4), there is a trajectory between $E_{2}:(\phi ,\psi )=(0,+\infty )$ and $E_{0}: (\phi ,\psi )=(0,0)$ that starts from a point on ${\mathcal {W}}^{u}(E_{2})$ and reaches a point on ${\mathcal {W}}^{cs}(E_{0})$.

Next, we show the existence of connecting orbits for $\delta =1$. Let ${\mathcal {W}}^{cu}(E_{0})$ be a center unstable manifold of $E_{0}$ for (10) and ${\mathcal {W}}^{s}(E_{1})$ be a stable manifold of $E_{1}$ for (10). By applying the Poincaré-Bendixson theorem, we see that any trajectory starting from a point on ${\mathcal {W}}^{cu}(E_{0})$ must go to a point on ${\mathcal {W}}^{s}(E_{1})$, which yields the existence of a connecting orbit between $E_{0}$ and $E_{1}$ in (10). By the same argument as for $\delta =0$, we conclude that there is a connecting orbit between $E_{0}$ and $E_{1}$ in (4) for $\delta =1$. Similarly, we obtain a connecting orbit starting from $E_2$ to $E_{1}$ for $\delta =1$.

From the above, we have the existence of all connecting orbits on the Poincaré disk for both $\delta =0$ and $\delta =1$ as shown in Fig. 1.

4 Proof of Theorems

Each traveling wave in the main results, Theorem 1 and Theorem 2, corresponds to each of connecting orbits shown in Subsection 3.4. We can obtain their shapes and asymptotic behavior except for (5) in a similar way to [7,8,9]. See Appendix B for the details. Therefore, it is sufficient to prove the existence of $\xi _{-}$ in Theorem 1 and to analyze the asymptotic behavior of the corresponding traveling wave as $\xi \rightarrow \xi _{-}+0$. In other words, the problem reduces to the dynamics of (16) near the origin $E_{2}$ as $\tau \rightarrow -\infty$ in $\{\lambda \ge 0, x\ge 0\}$. Letting $\theta =-\tau$, we now consider the asymptotic behavior near $E_2$ in $\{\lambda \ge 0, x\ge 0\}$ of

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{\theta } = -\lambda [c\lambda +\mu x^{2}-\delta \lambda x],\\ x_{\theta } = -x[1+c\lambda +\mu x^{2}-\delta \lambda x], \end{array}\right. } \end{aligned}$$

(18)

as $\theta \rightarrow +\infty$. Recall that $\{\lambda =0\}$ (i.e. x-axis) is a stable manifold and $\{x=0\}$ (i.e. $\lambda$-axis) is a center manifold of $E_2$.

Since the dynamics on the center manifold $\{x=0\}$ is

$$\begin{aligned} \dfrac{d\lambda }{d\theta }=-c\lambda ^{2}, \end{aligned}$$

we get $\lambda (\theta )=(c\theta +a)^{-1}$ with a constant a. Therefore, from the center manifold theorem, $E_2$ is asymptotically stable on $\{\lambda \ge 0, x\ge 0\}$. This implies that there exists some $\eta >0$ such that for every $\Vert (\lambda (0),x(0))\Vert <\eta$ and $\varepsilon >0$ there exists $T>0$ such that

$$\begin{aligned} \Vert (\lambda (\theta ), x(\theta ))\Vert <\varepsilon \end{aligned}$$

holds for all $\theta >T$. In addition, since

$$\begin{aligned} \dfrac{1}{\lambda }\dfrac{d\lambda }{d\theta } -\dfrac{1}{x}\dfrac{dx}{d\theta }=1 \end{aligned}$$

holds in the domain $\{\lambda> 0, x> 0\}$, we obtain

$$\begin{aligned} \dfrac{\lambda (\theta )}{x(\theta )}=Ae^{\theta } \end{aligned}$$

(19)

with $A>0$ as an arbitrary constant. It holds that

$$\begin{aligned} \dfrac{d\lambda }{d\theta } = -\lambda ^{2}[c+\mu A^{-2}e^{-2\theta }\lambda -\delta A^{-1}e^{-\theta }\lambda ] \end{aligned}$$

from (18) and (19), and thus we obtain

$$\begin{aligned} \dfrac{1}{-\lambda ^{2}}\dfrac{d\lambda }{d\theta }= c+A^{-1}e^{-\theta }\lambda [\mu A^{-1}e^{-\theta } -\delta ] \sim c \quad \mathrm{{as}} \quad \theta \rightarrow \infty . \end{aligned}$$

That is, for any $\varepsilon '>0$, there exists $T'>0$ such that

$$\begin{aligned} \left| -\dfrac{1}{\lambda ^{2}}\dfrac{d\lambda }{d\theta }-c \right| \le \varepsilon ' \end{aligned}$$

for all $\theta >T'$. Note that this inequality can be rewritten as follows:

$$\begin{aligned} c-\varepsilon ' \le -\dfrac{1}{\lambda ^{2}}\dfrac{d\lambda }{d\theta }=\dfrac{d}{d\theta }\left( \dfrac{1}{\lambda }\right) \le c+\varepsilon '. \end{aligned}$$

For $T'\le \theta _{0}\le \theta$, we integrate the above inequalities:

$$\begin{aligned} \int _{\theta _{0}}^{\theta } (c-\varepsilon ')\, dr \le \int _{\theta _{0}}^{\theta } \dfrac{d}{dr}\left( \dfrac{1}{\lambda }\right) \, dr \le \int _{\theta _{0}}^{\theta }(c+\varepsilon ')\, dr. \end{aligned}$$

As a result,

$$\begin{aligned} (c-\varepsilon ')\theta -(c-\varepsilon ')\theta _{0}+\dfrac{1}{\lambda (\theta _{0})} \le \dfrac{1}{\lambda (\theta )} \le (c+\varepsilon ')\theta -(c+\varepsilon ')\theta _{0}+\dfrac{1}{\lambda (\theta _{0})} \end{aligned}$$

holds. Let $\alpha$ and $\beta$ be as follows:

$$\begin{aligned} \alpha =-(c-\varepsilon ')\theta _{0}+\dfrac{1}{\lambda (\theta _{0})}, \quad \beta =-(c+\varepsilon ')\theta _{0}+\dfrac{1}{\lambda (\theta _{0})}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} (c-\varepsilon ')\theta +\alpha \le \dfrac{1}{\lambda (\theta )} \le (c+\varepsilon ')\theta +\beta . \end{aligned}$$

(20)

On the other hand, considering the multiple time scale desingularization, we compute

$$\begin{aligned} \dfrac{d\theta }{d\xi } =\dfrac{d\theta }{d\tau }\dfrac{d\tau }{ds}\dfrac{ds}{d\xi }=-1\cdot \lambda ^{-1}\cdot \phi ^{-1} =-1\cdot \lambda ^{-1}\cdot \dfrac{\lambda }{x}=-Ae^{\theta }\lambda ^{-1}. \end{aligned}$$

Therefore, using (20), we get

$$\begin{aligned} -Ae^{\theta } \left[ (c+\varepsilon ')\theta +\beta \right] \le -Ae^{\theta }\dfrac{1}{\lambda (\theta )}=\dfrac{d\theta }{d\xi } \le -Ae^{\theta }\left[ (c-\varepsilon ')\theta +\alpha \right] . \end{aligned}$$

(21)

Since

$$\begin{aligned}&(c+\varepsilon ')<(c-\varepsilon ')\theta +\alpha , \\&e^{\theta }\left[ (c+\varepsilon ')\theta +\beta \right] <ce^{(1+\frac{\varepsilon '}{c})\theta } \end{aligned}$$

hold when $\theta$ is sufficiently large, (21) gives

$$\begin{aligned} -Ace^{(1+\frac{\varepsilon '}{c})\theta }<\dfrac{d\theta }{d\xi } < -Ae^{\theta }(c+\varepsilon '). \end{aligned}$$

(22)

This means that for any $\varepsilon '>0$ there exists some $\tilde{T}>0$ such that for all $\theta >\tilde{T}$ the following holds:

$$\begin{aligned} -Ace^{(1+\frac{\varepsilon '}{c})\theta }<\dfrac{d\theta }{d\xi } < -Ae^{\theta }(c+\varepsilon '). \end{aligned}$$

Therefore, by the comparison theorem for ODE,

$$\begin{aligned} -\dfrac{1}{1+\frac{\varepsilon '}{c}}\log \left( K_{1}+Ac\left( 1+\dfrac{\varepsilon '}{c}\right) \xi \right)<\theta (\xi ) <-\log \left( K_{1}+A(c+\varepsilon ')\xi \right) \end{aligned}$$

(23)

holds with some constant $K_{1}$. By $\tau =-\theta$, we get

$$\begin{aligned} \log \left( K_{1}+A(c+\varepsilon ')\xi \right)< \tau (\xi ) <\dfrac{1}{1+\frac{\varepsilon '}{c}}\log \left( K_{1}+A(c+\varepsilon ')\xi \right) , \end{aligned}$$

which means that there exists $|\xi _{-}|<+\infty$ such that $\tau \rightarrow -\infty$ as $\xi \rightarrow \xi _- +0$. In addition, we obtain $\xi _{-}=-K_{1}(Ac)^{-1}$. Therefore,

$$\begin{aligned} \tau (\xi ) \sim \log [Ac(\xi -\xi _{-})] \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0 \end{aligned}$$

holds. Moreover, it follows from (20) and (23) that

$$\begin{aligned} -\dfrac{c-\varepsilon '}{1+\frac{\varepsilon '}{c}}\log [K_{1}+A(c+\varepsilon ')\xi ]+\alpha<\dfrac{1}{\lambda (\theta )} <-(c+\varepsilon ')\log [K_{1}+A(c+\varepsilon ')\xi ]+\beta .\nonumber \\ \end{aligned}$$

(24)

Since $\psi =1/\lambda$ and both limits of $\alpha /\log [Ac(\xi -\xi _{-})]$ and $\beta /\log [Ac(\xi -\xi _{-})]$ go to 0 as $\xi \rightarrow \xi _{-}+0$, we see that

$$\begin{aligned} \psi (\xi ) \sim -c\log [Ac(\xi -\xi _{-})] \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0, \end{aligned}$$

which implies that the asymptotic form of $\psi$ in (5) holds. In addition, as $\xi \rightarrow \xi _-+0$, we obtain $\psi (\xi )\rightarrow +\infty$ and thus $\phi (\xi )\rightarrow 0$ holds by the dynamics on the Poincaré disk.

Since $\phi '=\psi$, integrating each side of (24), we have

$$\begin{aligned}&-\dfrac{c-\varepsilon '}{1+\frac{\varepsilon '}{c}} (\xi -\xi _{-}^{\varepsilon '})\log [A(c+\varepsilon ')(\xi -\xi _{-}^{\varepsilon '})]+K_2^{\varepsilon '}(\xi -\xi _{-}^{\varepsilon '})\\&\quad<\phi (\xi )-\phi (\xi _{-}^{\varepsilon '}) < -(c+\varepsilon ') (\xi -\xi _{-}^{\varepsilon '})\log [A(c+\varepsilon ')(\xi -\xi _{-}^{\varepsilon '})]+K_3^{\varepsilon '}(\xi -\xi _{-}^{\varepsilon '}) \end{aligned}$$

with constants $\xi _{-}^{\varepsilon '}=-\frac{K_1}{A(c+\varepsilon ')}$ and

$$\begin{aligned} K_{2}^{\varepsilon '}=\left\{ \dfrac{c-\varepsilon '}{1+\frac{\varepsilon '}{c}} -(c-\varepsilon ')\theta _0+\frac{1}{\lambda (\theta _0)}\right\} ,\quad K_3^{\varepsilon '}=\left\{ (c+\varepsilon ')-(c+\varepsilon ')\theta _0+\frac{1}{\lambda (\theta _0)}\right\} . \end{aligned}$$

Note that $\lim _{\varepsilon '\rightarrow 0}\phi (\xi _-^{\varepsilon '})=0$ since $\lim _{\varepsilon '\rightarrow 0}\xi _-^{\varepsilon '}= \xi _-$ holds. We also remark that both of $K_2^{\varepsilon '}$ and $K_3^{\varepsilon '}$ converge to the same value $B=c(1-\theta _0)+(\lambda (\theta _0))^{-1}$ when $\varepsilon '\rightarrow 0$. Thus, we obtain the asymptotic form of $\phi$ in (5):

$$\begin{aligned} \phi (\xi ) \sim -c(\xi -\xi _{-})\log [Ac(\xi -\xi _{-})] +B(\xi -\xi _{-}) \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0, \end{aligned}$$

with the constant B. Note that the constant A is positive. The proof of Theorem 1 is complete. $\square$

5 Discussion

In this section we give some comments on the results of the asymptotic forms. We also discuss some observations on the “bifurcation of traveling waves” due to the clarification of the $p=1$ case in (2).

In Sect. 2, we provided the existence of non-negative traveling waves at $p=1$ and clarified their asymptotic forms. In particular, our approach to the asymptotic form (5) is completely different from the previous ones [7,8,9,10]. It seems difficult to derive (5) by the asymptotic analysis presented in the previous studies.

The behavior of $\phi (\xi )$ obtained in the previous study [7] for $1<p\in {\mathbb {R}}$ is

$$\begin{aligned} \phi (\xi ) \sim C_{1}(\xi -\xi _{-})^{\frac{1}{p}},\quad \phi '(\xi ) \sim C_{2}(\xi -\xi _{-})^{-\frac{p-1}{p}} \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0 \end{aligned}$$

(25)

with constants $C_{j}>0$. Letting $p\rightarrow 1$ formally, we obtain

$$\begin{aligned} \phi (\xi ) \sim C_{1}(\xi -\xi _{-}), \quad \phi '(\xi ) \sim C_{2} \quad \mathrm{{as}} \quad \xi \rightarrow \xi _{-}+0. \end{aligned}$$

However, as shown in Fig. 1, they do not match the limits

$$\begin{aligned} \lim _{\xi \rightarrow \xi _{-}+0} \phi (\xi )=0, \quad \lim _{\xi \rightarrow \xi _{-}+0}\phi '(\xi )=+\infty \end{aligned}$$

derived from the corresponding equilibrium $(\phi , \psi )=(0, +\infty )$, which implies that we need much more detailed information of the behavior of $\phi$. This is the reason why the case $p=1$ cannot be treated in the previous studies [7, 9]. We remark that the asymptotic analysis developed in [7, 9] works only for the case that the equilibrium at infinity is hyperbolic.

In order to overcome such difficulties, we developed a new asymptotic analysis for the dynamics near the non-hyperbolic equilibrium in Sect. 4. The key idea in our approach is to estimate the final time scale $\theta =-\tau$ by the first scale $\xi$ with the special relation (19). This allows us to extract more information about the behavior of traveling waves, i.e., the dynamics of (16) near the non-hyperbolic equilibrium at infinity.

We emphasize that the asymptotic form of $\phi$ in (5) has two terms and corresponds to the dynamics near the non-hyperbolic equilibrium at infinity, which could not be obtained by the conventional asymptotic analysis. In the previous studies for the hyperbolic equilibrium at infinity, using the information of the linear term of the system around the equilibrium, only the main term of $\phi$ is obtained as in (25). Regarding the dynamics at infinity and the multi-term asymptotic form arising from Poincaré-type compactification, there are related studies [4, 11] which discuss the multi-term asymptotic expansions of the blow-up solutions for ordinary differential equations. However, these discussions assume that the equilibrium at infinity is hyperbolic, and are not expected to be directly applicable to our dynamical system (16) near the non-hyperbolic equilibrium $E_{2}$. Therefore, this paper presents an example that has the potential to extend the argument of [4, 11].

Since we now have the classification of the traveling waves in (2), we can combine the results of [9], which treats the case $0<p<1$, and those of [7], which treats the case $1<p\in {\mathbb {R}}$. Note that we offer Theorem 1 for $\delta =0$ and Theorem 2 for $\delta =1$. Here we consider the case $\delta =0$. The case $\delta =1$ can be discussed in a similar way. When $1<p\in {\mathbb {R}}$, Theorem 1 holds except for (5). Let $\phi _1$ be the traveling wave obtained here. Then $\phi _1$ has the asymptotic form given by (25) for $\xi \rightarrow \xi _-+0$ (see [7]). We call $\phi _1$ the type (i) traveling wave. Moreover, for $0<p<1$, in addition to Theorem 1 except for the asymptotic form (5), we have two types of traveling waves satisfying

$$\begin{aligned} \lim _{\xi \rightarrow \xi _{-}+0} \phi _2(\xi )=\lim _{\xi \rightarrow \xi _{+}-0}\phi _2(\xi )=\lim _{\xi \rightarrow \xi _{+}-0}\phi _2'(\xi )=0,\quad \lim _{\xi \rightarrow \xi _{-}+0} \phi _2'(\xi )=M \end{aligned}$$

and

$$\begin{aligned} \lim _{\xi \rightarrow \xi _{-}+0} \phi _3(\xi )=\lim _{\xi \rightarrow \xi _{+}-0}\phi _3(\xi )=0, \quad \lim _{\xi \rightarrow \xi _{+}-0}\phi _3'(\xi )=-M,\quad \lim _{\xi \rightarrow \xi _{-}+0} \phi _3'(\xi )=M. \end{aligned}$$

respectively with a positive constant M. Let $\phi _2$ and $\phi _3$ be these two types of traveling waves, and we call $\phi _2$ and $\phi _3$ type (ii) and (iii), respectively. Then, as mentioned in [9], the result for $p=1$ is expected to be the “middle case" between the cases $1<p\in {\mathbb {R}}$ and $0<p<1$, that is, traveling waves of type (ii) and (iii) appear when p is moved from $1<p\in {\mathbb {R}}$ to $0<p<1$ via $p=1$. For (i), it is pointed out in [7, 9] that the asymptotic form is (25) for each of $1<p\in {\mathbb {R}}$ and $0<p<1$. However, as can be seen from the asymptotic form of $\phi '(\xi )$, the limit forms for $1<p\in {\mathbb {R}}$ and $0<p<1$ are different. The asymptotic form of $\phi '(\xi )$ for $p=1$ shown in Sect. 2 reveals the whole picture of changes of the classifications for traveling waves depending on the parameter p of the spatial one-dimensional degenerate parabolic equation (2).

The results of this paper, combined with previous studies [7, 9], provide a complete understanding of the geometric structure of non-negative traveling waves of (2). When $p\in (1,+\infty )$ goes to $p=1$, the type (i) traveling wave is still type (i) but its asymptotic behavior near $\xi _{-}$ changes. Then, when $p=1$ becomes to $0<p<1$, new types (ii) and (iii) of traveling waves appear. Thus, we have a qualitative change, i.e., “bifurcation", of the behavior of traveling waves in terms of their classifications. Note that the problem of the stability of traveling waves should also be considered but it is out of scope of our present study. From the above discussion, this paper clarifies the structure of the non-negative traveling waves of the degenerate parabolic equation (2) with the parameter p including the critical value $p=1$ from a geometric viewpoint. It also gives an example of bifurcation of traveling waves, and we believe that this result provides a new perspective on the bifurcation theory for partial differential equations using the Poincaré-type compactification.

Appendices

Overview of the Poincaré Type Compactification

The Poincaré compactification is one of the compactifications of the original phase space (the embedding of ${\mathbb {R}}^{n}$ into the unit upper hemisphere of ${\mathbb {R}}^{n+1}$). In this appendix, we briefly introduce the Poincaré compactification. Here Section 2 of [8] are reproduced. Also, it should be noted that we refer [6] for more details. Let

$$\begin{aligned} X = P(\phi ,\psi ) \dfrac{\partial }{\partial \phi } + Q(\phi ,\psi ) \dfrac{\partial }{\partial \psi } \end{aligned}$$

be a polynomial vector field on ${\mathbb {R}}^{2}$, or in other words

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\phi } = P(\phi ,\psi ), \\ \dot{\psi } = Q(\phi ,\psi ), \end{array}\right. } \end{aligned}$$

where denotes d/dt, and P, Q are polynomials of arbitrary degree in the variables $\phi$ and $\psi$.

We consider ${\mathbb {R}}^{2}$ as the plane in ${\mathbb {R}}^{3}$ defined by $(y_{1},y_{2},y_{3})=(\phi ,\psi ,1)$. Then the sphere ${\mathbb {S}}^{2} = \{ y \in {\mathbb {R}}^{3} \, |\, y_{1}^{2} + y_{2}^{2}+y_{3}^{2}=1\}$ is said to be the Poincaré sphere. We divide the Poincaré sphere into

$$\begin{aligned} H_{+} = \{ y \in {\mathbb {S}}^{2}\,|\,y_{3}>0\}, \quad H_{-} = \{ y \in {\mathbb {S}}^{2}\,|\,y_{3}<0\} \end{aligned}$$

and

$$\begin{aligned} {\mathbb {S}}^{1} = \{y \in {\mathbb {S}}^{2}\, | \, y_{3}=0\}. \end{aligned}$$

Let us consider the embedding of vector field X from ${\mathbb {R}}^{2}$ to ${\mathbb {S}}^{2}$ given by

$$\begin{aligned} f^{+}:{\mathbb {R}}^{2} \rightarrow {\mathbb {S}}^{2}, \quad f^{-}:{\mathbb {R}}^{2} \rightarrow {\mathbb {S}}^{2}, \end{aligned}$$

where

$$\begin{aligned} f^{\pm }(\phi ,\psi ):= \pm \left( \dfrac{\phi }{\Delta (\phi ,\psi )},\dfrac{\psi }{\Delta (\phi ,\psi )},\dfrac{1}{\Delta (\phi ,\psi )} \right) \end{aligned}$$

with $\Delta (\phi ,\psi ) = \sqrt{\phi ^{2}+\psi ^{2}+1}$.

Then we have six local charts on ${\mathbb {S}}^{2}$ given by $U_{k} = \{y \in {\mathbb {S}}^{2} \, | \, y_{k}>0\}$, $V_{k} = \{y \in {\mathbb {S}}^{2} \, | \, y_{k}<0\}$ for $k=1,2,3$. Consider the local projection

$$\begin{aligned} g^{+}_{k}: U_{k} \rightarrow {\mathbb {R}}^{2}, \quad g^{-}_{k}: V_{k} \rightarrow {\mathbb {R}}^{2} \end{aligned}$$

defined as

$$\begin{aligned} g^{+}_{k}(y_{1},y_{2},y_{3}) = - g^{-}_{k}(y_{1},y_{2},y_{3}) = \left( \dfrac{y_{m}}{y_{k}},\dfrac{y_{n}}{y_{k}} \right) \end{aligned}$$

for $m<n$ and $m,n \not = k$. The projected vector fields are obtained as the vector fields on the planes

$$\begin{aligned} \overline{U}_{k} = \{y \in {\mathbb {R}}^{3} \, | \, y_{k} = 1\}, \quad \overline{V}_{k} = \{y \in {\mathbb {R}}^{3} \, | \, y_{k} = -1\} \end{aligned}$$

for each local chart $U_{k}$ and $V_{k}$. We denote by $(x,\lambda )$ the value of $g^{\pm }_{k}(y)$ for any k.

For instance, it follows that

$$\begin{aligned} (g^{+}_{2} \circ f^{+})(\phi ,\psi ) = \left( \dfrac{\phi }{\psi },\dfrac{1}{\psi }\right) = (x,\lambda ), \end{aligned}$$

therefore, we can obtain the dynamics on the local chart $\overline{U}_{2}$ by the change of variables $\phi = x/\lambda$ and $\psi = 1/\lambda$. The locations of the Poincaré sphere, $(\phi ,\psi )$-plane and $\overline{U}_{2}$ are expressed as Fig. 2. Throughout this paper, we follow the notations used here for the Poincaré compactification. It is sufficient to consider the dynamics on $H_{+}\cup {\mathbb {S}}^{1}$, which is called Poincaré disk.

Fig. 2

Locations of the Poincaré sphere and chart $\overline{U}_{2}$

Overview of Derivation of Asymptotic Behavior

In this appendix, we state the outline of the proof of (6), (7) and (8). In the following, we reproduce the proof given in [7,8,9,10].

First, we outline the derivation of (6) in Theorem 1. If the initial value is on the center manifold, the solution around $E_{0}$ on Poincaré disk has the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi (s)=\sqrt{\dfrac{1}{\dfrac{2\mu }{c}s-A_{0}}} =\left( \dfrac{2\mu }{c}s-A_{0} \right) ^{-\frac{1}{2}},\\ \psi (s)=-\dfrac{\mu }{c}\left( \dfrac{2\mu }{c}s-A_{0} \right) ^{-1}=-\dfrac{\mu }{2\mu s-cA_{0}}. \end{array}\right. } \end{aligned}$$

Since the initial value $\phi (0)$ is located on $\{\phi >0\}$, it holds that $A_{0}<0$. We then have

$$\begin{aligned} \dfrac{ds}{d\xi }=\phi ^{-1}=\left( \dfrac{2\mu }{c}s-A_{0} \right) ^{\frac{1}{2}}. \end{aligned}$$

Therefore, there exists a solution $s(\xi )$ such that the following holds:

$$\begin{aligned} s(\xi )=\dfrac{\mu }{2c}\xi ^{2}+ \dfrac{\mu }{c}K_{1}\xi +\dfrac{\mu }{2c}K_{1}^{2}+\dfrac{c}{2\mu }A_{0} \sim \dfrac{\mu }{2c}\xi ^{2} \quad \mathrm{{as}}\quad \xi \rightarrow +\infty \end{aligned}$$

with constants $K_{1}$. Therefore, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi (\xi )=\left( \dfrac{2\mu }{c}s-A_{0} \right) ^{-\frac{1}{2}} \sim \dfrac{c}{\mu }\xi ^{-1}, \\ \psi (\xi )\sim -\dfrac{\mu }{c}\cdot \left( \dfrac{\mu ^{2}}{c^{2}}\xi ^{2}\right) ^{-1}=-\dfrac{c}{\mu }\xi ^{-2}, \end{array}\right. } \quad \mathrm{{as}}\quad \xi \rightarrow +\infty . \end{aligned}$$

In addition, we can see that $\phi '\sim \psi$ as $\xi \rightarrow +\infty$ holds. Therefore, we can derive (6).

Second, we outline the derivation of (7) in Theorem 2. Then, there are three cases to consider:

• (i) Let us consider the case that $D>0$, namely, the matrix $J_{1}$ has the real distinct eigenvalues

  $$\begin{aligned} \omega _{1}=\dfrac{-\mu c+\sqrt{D}}{2},\quad \omega _{2}=\dfrac{-\mu c-\sqrt{D}}{2}. \end{aligned}$$

  The eigenvectors corresponding to each eigenvalue are

  $$\begin{aligned} \textbf{v}_{1}=\left( \begin{array}{cc} 1 \\ \omega _{1} \end{array} \right) ,\quad \textbf{v}_{2}=\left( \begin{array}{cc} 1 \\ \omega _{2} \end{array} \right) . \end{aligned}$$

  Therefore, the solution around the equilibrium $E_{1}$ is

  $$\begin{aligned} \phi (\xi ) \sim B_{1}e^{\omega _{1}\xi }+B_{2}e^{\omega _{2}\xi }+\mu ^{-1} \end{aligned}$$

  with any constants $B_{1}$ and $B_{2}$.

• (ii) Consider the case that $D=0$, namely, the matrix $J_{1}$ has a multiple real eigenvalue $\omega =-2^{-1}\mu c$. The eigenvector $\textbf{v}_{1}$ and the generalized eigenvector corresponding to the eigenvalue $\textbf{v}_{2}$ are

  $$\begin{aligned} \textbf{v}_{1}=\left( \begin{array}{cc} 1 \\ -\dfrac{\mu c}{2} \end{array} \right) ,\quad \textbf{v}_{2}=\left( \begin{array}{cc} \alpha \\ 1-\dfrac{\mu c}{2}\alpha \end{array} \right) \end{aligned}$$

  with $\alpha$ is arbitrary constant. Therefore, the solution around the equilibrium $E_{\delta }$ is

  $$\begin{aligned} \phi (\xi ) \sim (B_{3}\xi +B_{4})e^{\omega \xi }+\mu ^{-1}. \end{aligned}$$

• (iii) Consider the case that $D<0$, namely, the matrix $J_{1}$ has the complex eigenvalues $\omega =\rho \pm i\nu =-2^{-1}\mu c\pm i\dfrac{1}{2}\sqrt{|D|}$. The eigenvectors corresponding to each eigenvalue are

  $$\begin{aligned} \textbf{v}=\left( \begin{array}{cc} 1 \\ -\frac{\mu c}{2} \end{array} \right) \pm i\left( \begin{array}{cc} 0 \\ \frac{1}{2}\sqrt{|D|} \end{array} \right) . \end{aligned}$$

  The function $\phi (\xi )$ and $\psi (\xi )$ are expressed as following:

  $$\begin{aligned}\left( \begin{array}{cc} \phi (\xi ) -\mu ^{-1}\\ \psi (\xi ) \end{array} \right) =z(\xi )\left( \begin{array}{cc} 0 \\ \frac{1}{2}\sqrt{|D|} \end{array} \right) +w(\xi )\left( \begin{array}{cc} 1 \\ -\frac{c}{2} \end{array} \right) , \end{aligned}$$

  where

  $$\begin{aligned} \left( \begin{array}{cc} z(\xi ) \\ w(\xi ) \end{array} \right)&=e^{\rho \xi }\left( \begin{array}{cc} \cos \nu \xi & -\sin \nu \xi \\ \sin \nu \xi & \cos \nu \xi \end{array} \right) \left( \begin{array}{cc} z(0) \\ w(0) \end{array} \right) . \end{aligned}$$

  Therefore, the solution $\phi (\xi )$ around the equilibrium $E_{\delta }$ is

  $$\begin{aligned} \phi (\xi ) = e^{-\frac{\mu c}{2}\xi } \left( z(0)\sin \frac{\sqrt{|D|}}{2}\xi +w(0)\cos \frac{\sqrt{|D|}}{2}\xi \right) +\mu ^{-1}. \end{aligned}$$

Thus, we can derive (7).

Finally, we outline the derivation of (8) in Theorem 2. We set $w(s)=\phi (s)^{-1}>0$. From (14), we have

$$\begin{aligned} w'(s)\sim -\dfrac{1}{c}+\dfrac{1}{c^{3}}(\mu c^{2}+1)w^{-1}=A+Bw^{-1}, \end{aligned}$$

where $A=-c^{-1}<0$ and $B=c^{-3}(\mu c^{2}+1)>0$. These are consistent with the results obtained in [10] when $\mu =1$. Since our interest is the dynamics of $\phi (s)$ near 0, we can suppose that w(s) is sufficiently large so that $AB^{-1}w+1<0$. Therefore, the solution of the above equation satisfies the following:

$$\begin{aligned} -(1+Aw/B)e^{-\left( \frac{A}{B}w+1\right) }= -AB^{-1} e^{-\frac{A^{2}}{B}s-\frac{A^{2}C_{1}+B}{B}}. \end{aligned}$$

Here $C_{1}$ is a constant. By using $w=\phi ^{-1}$ and the Lambert W function, we obtain

$$\begin{aligned} \phi (s)=[-A^{-1}B\{W(E(s))+1\} ]^{-1},\quad E(s)=-AB^{-1} e^{-\frac{A^{2}}{B}s-\frac{A^{2}C_{1}+B}{B}}. \end{aligned}$$

We consequently have

$$\begin{aligned} \dfrac{ds}{d\xi } =\phi ^{-1} =-\dfrac{B}{A} \{W(E(s))+1\}. \end{aligned}$$

Now we shall prove

$$\begin{aligned} \xi (s) \rightarrow -\infty \quad \text{ as } \quad s \rightarrow - \infty . \end{aligned}$$

Its proof is given in [10] and is used properties of the Lambert W function. We represent $\xi$ as a function of $\phi$. Using $d\xi /ds=\phi$, we can obtain

$$\begin{aligned} \xi +K&=\int \phi (s) \, ds = \int \phi \dfrac{ds}{d\phi } \,d\phi \\&= \int \phi \left( \dfrac{1}{c}\phi ^{2}-\dfrac{1}{c^{3}}(\mu c^{2}+1) \phi ^{3}\right) ^{-1} \,d\phi \\&=c^{3} \int \left[ \dfrac{1}{c^{2}}\dfrac{1}{\phi }+\dfrac{1}{c^{2}}(\mu c^{2}+1)\dfrac{1}{c^{2}-(\mu c^{2}+1)\phi } \right] \, d\phi \\&=c\log |\phi |-c\log |(\mu c^{2}+1)\phi -c^{2}|\\&=c\log \left| \dfrac{\phi }{(\mu c^{2}+1)\phi -c^{2}} \right| \end{aligned}$$

with a constant K. Then the constant K is given by

$$\begin{aligned} C_{3}=c\log \left| \dfrac{\phi _{0}}{(\mu c^{2}+1)\phi _{0}-c^{2}} \right| , \end{aligned}$$

where $\phi (0)=\phi _{0}$. Note that we can conclude that $K<0$. Next, we will represent $\phi$ as a function of $\xi$. As mentioned above, we obtain

$$\begin{aligned} \xi +c\log \left| \dfrac{\phi _{0}}{(\mu c^{2}+1)\phi _{0}-c^{2}} \right| =c\log \left| \dfrac{\phi }{(\mu c^{2}+1)\phi -c^{2}} \right| . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \phi (\xi )=\dfrac{Mc^{2}e^{\frac{1}{c}\xi }}{M(\mu c^{2}+1)e^{\frac{1}{c}\xi }-1}, \quad M=- \left| \dfrac{\phi _{0}}{(\mu c^{2}+1)\phi _{0}-c^{2}} \right| , \end{aligned}$$

where $M<0$ is the constant that depends on the initial state $\phi _{0}$. Thus, we can derive (8).