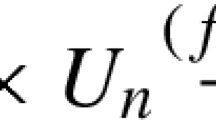Pro-Nilfactors of the Space of Arithmetic Progressions in Topological Dynamical Systems

Abstract

For a topological dynamical system (X, T), $l\in \mathbb {N}$ and $x\in X$, let $N_l(X)$ and $L_x^l(X)$ be the orbit closures of the diagonal point $(x,\ldots ,x)$ (l times) under the actions $\mathscr {G}_{l}$ and $\tau _l$ respectively, where $\mathscr {G}_{l}$ is generated by $T\times \ldots \times T$ (l times) and $\tau _l=T\times \ldots \times T^l$. In this paper, we show that for a minimal system (X, T) and $d,l\in \mathbb {N}$, the maximal d-step pro-nilfactor of $(N_l(X),\mathscr {G}_{l})$ is $(N_l(X_d),\mathscr {G}_{l})$, where $X_d$ is the d-step pronilfactor of (X, T). Meanwhile, when (X, T) is a minimal nilsystem, we also calculate the pro-nilfactors of the system $(L_x^l(X),\tau _l)$ for almost every x w.r.t. the Haar measure. In particular, there exists a minimal 2-step nilsystem (Y, T) and a countable subset $\Omega$ of Y such that for every $y\in Y\backslash \Omega$ the maximal equicontinuous factor of $(L_y^2(Y),\tau _2)$ is not $(L_{\pi _1(y)}^2(Y_{1}),\tau _2)$, where $Y_1$ is the maximal equicontinuous factor of (Y, T) and $\pi _1:Y\rightarrow Y_1$ is the factor map.

1 Introduction

1.1 Background

By a topological dynamical system (system for short) , we mean a pair (X, T), where X is a compact metric space with a metric $\rho$, and $T:X\rightarrow X$ is a homeomorphism.

For a minimal system (X, T), $l\in \mathbb {N}$ and $x\in X$, the orbit closures of $(x,\ldots ,x)$ (l times) under the actions $\mathscr {G}_l=\langle \sigma _l,\tau _l\rangle$ and $\tau _l$ are denoted by $N_l(X,T,x)$ and $L_x^l(X)$ respectively, where

$$\begin{aligned} \tau _l=\tau _l(T)=T\times \ldots \times T^l, \quad \mathrm {and} \quad \sigma _l=\sigma _l(T)=T\times \ldots \times T\; (l \; \mathrm {times}). \end{aligned}$$

Since (X, T) is minimal, it is easy to see that $N_l(X,T, x)$ is independent of x, which will be denoted by $N_l(X,T)$ or $N_l(X)$. We call $N_l(X)$ and $L_x^l(X)$ the space of arithmetic progressions of length l and the space of simple arithmetic progressions of length l for x respectively. A basic result proved by Glasner [5] is that $N_l(X)$ is minimal under the $\mathscr {G}_l$ action.

Arithmetic progressions in topological dynamical systems relate to the pointwise convergence of multiple ergodic averages. We refer to [9] for more details.

In the recent years, the study of the nilsystems and inverse limits of this kind of dynamics has drawn much interest, since it relates to many dynamical properties and has important applications in number theory. We refer to [7] and the references therein for a systematic treatment on the subject.

In a pioneer work, Host Kra and Maass [8] introduced the notion of regionally proximal relation of order d for a system (X, T), denoted by $\mathbf {RP}^{[d]}$. For $d\in \mathbb {N}$, we say that a minimal system (X, T) is a d-step pro-nilsystem if $\mathbf {RP}^{[d]}=\Delta$ and this is equivalent for (X, T) being an inverse limit of d-step nilsystems (see [8, Theorem 2.8]). For a minimal distal system (X, T), it was proved that $\mathbf {RP}^{[d]}$ is an equivalence relation and $X/\mathbf {RP}^{[d]}$ is the maximal d-step pro-nilfactor [8]. Later, Shao and Ye [16] showed that in fact for any minimal system, $\mathbf {RP}^{[d]}$ is an equivalence relation and $\mathbf {RP}^{[d]}$ has the so-called lifting property. Moreover, $\mathbf {RP}^{[\infty ]}=\bigcap _{d=1}^{\infty }\mathbf {RP}^{[d]}$ can be defined and it is also an equivalence relation for any minimal system [3].

Let (X, T) be a minimal system. For $l\in \mathbb {N}$, the maximal equicontinuous factor (1-step pro-nilfactor) of $(N_l(X),\mathscr {G}_l)$ plays an important role in [6, 13]. In this paper, we would like to study the pro-nilfactors of $(N_l(X),\mathscr {G}_l)$ and $(L_x(X),\tau _l)$ respectively. In particular, for the maximal d-step pro-nilfactor $X_d$ of X, we want to know whether the maximal d-step pro-nilfactor of the space of arithmetic progressions of X and the space of arithmetic progressions of $X_d$ coincide.

In [6], the authors showed that for any $d,l\in \mathbb {N}$, the maximal d-step pro-nilfactors of $(N_l(X),\mathscr {G}_l)$ and the one of $(N_l(X_\infty ),\mathscr {G}_l)$ coincide. Therefore to study the pro-nilfactors of $(N_l(X),\mathscr {G}_l)$, we can restrict to the case that X is an $\infty$-step pro-nilsystem, which is an inverse limit of minimal nilsystems [3]. Since the inverse limit is easy to handle, we need only to focus on nilsystems.

1.2 The Space of Arithmetic Progressions and Pro-Nilfactors

Following the ideas in [7, Chapter 14], we can view the space of arithmetic progressions of a minimal nilsystem as a nilmanifold. Thus it suffices to compute the pro-nilfactors of a minimal s-step nilsystem $(Z=L/\Gamma ,T_1,\ldots ,T_k)$. The similar question was considered in [15] and it was shown that the maximal d-step pro-nilfactor of Z has the form $L/(L_{d+1}\Gamma )$ for $d=1,\ldots , s$, where $L_{i}$ is the $i^{\mathrm {th}}$-step commutator subgroup of L, i.e., $L_1=L$ and $L_{i+1}=[L,L_{i}]$ for $i\ge 1$.

From this, we can prove:

Theorem A

Let $s\ge 2$ be an integer and let $(X=G/\Gamma ,T)$ be a minimal s-step nilsystem. Assume that G is spanned by $G^0$ and the element t of G defining the transformation T, where $G^0$ is the connected component of the unit element of G. For $d=1,\ldots ,s$, let $X_d=G/(G_{d+1}\Gamma )$. Then for every $l\in \mathbb {N}$, the maximal d-step pro-nilfactor of $(N_l(X),\mathscr {G}_{l})$ is $(N_l(X_d),\mathscr {G}_{l})$.

Thus, combining the previous result [6, Theorem 5.6] we can show:

Theorem B

Let (X, T) be a minimal system and $d\in \mathbb {N}$. Then for every $l\in \mathbb {N}$, the maximal d-step pro-nilfactor of $(N_l(X),\mathscr {G}_{l})$ is $(N_l(X_d),\mathscr {G}_{l})$, where $X_d=X/\mathbf {RP}^{[d]}$.

1.3 The Space of Simple Arithmetic Progressions of Nilsystems and Pro-Nilfactors

Up to now, all of the conclusions are expected. In the process of studying the pro-nilfactors of the space of simple arithmetic progressions of nilsystems, we find a surprising result: there exists a minimal 2-step nilsystem (Y, T) and a countable subset $\Omega$ of Y such that for every $y\in Y\backslash \Omega$ the maximal equicontinuous factor of $(\overline{\mathscr {O}_{T\times T^2}(y,y)},T\times T^2)$ is not $(\overline{\mathscr {O}_{T\times T^2}(\pi (y),\pi (y))},T\times T^2)$, where $\pi :Y\rightarrow Y/\mathbf {RP}^{[1]}$ is the factor map.

Indeed, for a minimal s-step nilsystem $(X=G/\Gamma ,T)$ we can calculate the pro-nilfactors of the space of simple arithmetic progressions for $m_X$-a.e. $x\in X$, where $m_X$ is the uniquely ergodic measure of (X, T). (See [7, Chapter 12, Section 2], for exmaple, that any minimal nilsystem is uniquely ergodic.)

Before stating our result, we need define two subgroups of $G^{\mathbb {Z}_+}$ (see also Sect. 2.4). Define

$$\begin{aligned} HP(G)=\{ (gg_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots g_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) })_{n\in \mathbb {Z}_{+}}: g\in G,\; g_i\in G_i,\; i=1,\ldots ,s\} \end{aligned}$$

which is called the Hall-Petresco group, and

$$\begin{aligned} HP_e(G)=\{\phi \in HP(G):\phi (0)=1_G\}, \end{aligned}$$

where $1_G$ is the unit element of G.

The groups HP(G) and $HP_e(G)$ play an important role in the study of arithmetic progressions in nilsystems. We have:

Theorem C

Let $s\ge 2$ be an integer and let $(X=G/\Gamma ,T)$ be a minimal s-step nilsystem. Assume that G is spanned by $G^0$ and the element t of G defining the transformation T, where $G^0$ is the connected component of the unit element of G. For $m_X$-a.e. x and $d=1,\ldots ,s$, the maximal d-step pro-nilfactor of $(L_x^l(X),\tau _l)$ is conjugate to the system

$$\begin{aligned} (HP_e^{(l)}(G)/\big (HP_e^{(l)}(G)_{d+1}\cdot (HP_e^{(l)}(G)\cap \Gamma ^l)\big ),\; \tau _{l,x}) \end{aligned}$$

for some nilrotation $\tau _{l,x}$, where $HP_e^{(l)}(G)=\{(\phi (n))_{1\le n\le l}:\phi \in HP_e(G)\}$ and $HP_e^{(l)}(G)_k$ is the $k^{\mathrm {th}}$-step commutator subgroup of $HP_e^{(l)}(G)$ for $k=1,\ldots ,s$. Moreover, if $G^0$ is simply connected, then $HP_e^{(l)}(G)_k$ is generated by

$$\begin{aligned} \{(g^{n^j})_{1\le n\le l}: g\in G_{j},\;j=k,\ldots ,s \}. \end{aligned}$$

The paper is organized as follows. In Sect. 2, the basic notions used in the paper are introduced. In Sect. 3, we give a proof of Theorem A and by using Theorem A, we prove Theorem B. In the final section, we show the conclusions in Sect. 1.3.

2 Preliminaries

In this section we gather definitions and preliminary results that will be necessary later on. Let $\mathbb {Z}_+$ ($\mathbb {N}$, $\mathbb {Z}$, respectively) be the set of all non-negative integers (positive integers, integers, respectively).

2.1 Topological Dynamical Systems

A transformation of a compact metric space X is a homeomorphism of X to itself. A topological dynamical system (system for short) is a pair (X, T), where X is a compact metric space and T is a transformation of X. For $x\in X,\mathscr {O}_T(x)=\{T^nx: n\in \mathbb {Z}\}$ denotes the orbit of x. A system (X, T) is called minimal if every point has a dense orbit in X.

A homomorphism of systems (X, T) and (Y, T) is a continuous onto map $\pi :X\rightarrow Y$ which intertwines the actions; one says that (Y, T) is a factor of (X, T) and that (X, T) is an extension of (Y, T). One also refers to $\pi$ as a factor map or an extension and one uses the notation $\pi : (X,T) \rightarrow (Y,T)$. The systems are said to be conjugate if $\pi$ is a bijection. An extension $\pi$ is determined by the corresponding closed invariant equivalence relation

$$\begin{aligned} R_\pi =\{(x,x')\in X\times X:\pi (x)=\pi (x')\}. \end{aligned}$$

2.2 Regional Proximality of Higher Order

For $\vec {n} = (n_1,\ldots , n_d)\in \mathbb {Z}^d$ and $\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _d)\in \{0,1\}^d$, we define

$$\begin{aligned} \vec {n}\cdot \varepsilon = \sum _{i=1}^d n_i\varepsilon _i . \end{aligned}$$

Definition 2.1

Let (X, T) be a system and $d\in \mathbb {N}$. The regionally proximal relation of order d is the relation $\mathbf{RP} ^{[d]}$ (or $\mathbf {RP}^{[d]}(X)$ in case of ambiguity) defined by: $(x,y)\in \mathbf{RP} ^{[d]}$ if and only if for any $\delta >0$, there exist $x',y'\in X$ and $\vec {n}\in \mathbb {N}^d$ such that: $\rho (x,x')<\delta ,\rho (y,y')<\delta$ and

$$\begin{aligned} \rho ( T^{\vec {n}\cdot \varepsilon } x', T^{\vec {n}\cdot \varepsilon } y')<\delta ,\quad \forall \;\varepsilon \in \{0,1\}^d\backslash \{ \vec {0}\}. \end{aligned}$$

A minimal system is called a d-step pro-nilsystem if its regionally proximal relation of order d is trivial.

Theorem 2.2

[16, Theorem 3.3] For any minimal system and $d\in \mathbb {N}$, the regionally proximal relation of order d is an equivalence relation.

The regionally proximal relation of order d allows to construct the maximal d-step pro-nilfactor of a minimal system. That is, any factor of d-step pro-nilsystem factorizes through this system.

Theorem 2.3

[16, Theorem 3.8] Let $\pi :(X,T)\rightarrow (Y,T)$ be a factor map of minimal systems and $d\in \mathbb {N}$. Then,

• (1) $(\pi \times \pi ) \mathbf {RP}^{[d]}(X)=\mathbf {RP}^{[d]}(Y)$.

• (2) (Y, T) is a d-step pro-nilsystem if and only if $\mathbf {RP}^{[d]}(X)\subset R_\pi$.

In particular, the quotient of X under $\mathbf {RP}^{[d]}(X)$ is the maximal d-step pro-nilfactor of X.

Remark 2.4

When $d=1$, $\mathbf {RP}^{[1]}$ is nothing but the classical regionally proximal relation. For a minimal system (X, T), we call it equicontinuous instead of a 1-step pro-nilsystem if its regionally proximal relation is trivial and call $X/\mathbf {RP}^{[1]}$ the maximal equicontinuous factor instead of the maximal 1-step pro-nilfactor.

It follows from Theorem 2.3 that for any minimal system,

$$\begin{aligned} \mathbf {RP}^{[\infty ]}=\bigcap _{d\ge 1}\mathbf {RP}^{[d]} \end{aligned}$$

is a closed invariant equivalence relation.

Now we formulate the definition of $\infty$-step pro-nilsystems.

Definition 2.5

A minimal system is an $\infty$-step pro-nilsystem, if the equivalence relation $\mathbf {RP}^{[\infty ]}$ is trivial, i.e., coincides with the diagonal.

2.3 Nilpotent Groups, Nilmanifolds and Nilsystems

Let G be a group and denote its unit element by $1_G$. For $g,h\in G$, we write $[g,h]=ghg^{-1}h^{-1}$ for the commutator of g and h, we write [A, B] for the subgroup spanned by $\{[a,b]:a\in A,b\in B\}$. The commutator subgroups $G_j,j\ge 1$, are defined inductively by setting $G_1=G$ and $G_{j+1}=[G_j,G]$. Let $k\ge 1$ be an integer. We say that G is k-step nilpotent if $G_{k+1}$ is the trivial subgroup.

Let G be a k-step nilpotent Lie group and $\Gamma$ a discrete cocompact subgroup of G. The compact manifold $X=G/\Gamma$ is called a k-step nilmanifold. The group G acts on X by left translations and we write this action as $(g,x)\mapsto gx$. Let $t\in G$ and T be the transformation $x\mapsto t x$ of X. Then (X, T) is called a k-step nilsystem.

We also make use of inverse limits of nilsystems and so we recall the definition of an inverse limit of systems (restricting ourselves to the case of sequential inverse limits). If $(X_i,T_i)_{i\in \mathbb {N}}$ are systems with $\text {diam}(X_i)\le 1$ and $\phi _i:X_{i+1}\rightarrow X_i$ are factor maps, the inverse limit of the systems is defined to be the compact subset of $\prod _{i\in \mathbb {N}}X_i$ given by $\{(x_i)_{i\in \mathbb {N}}:\phi _i(x_{i+1})=x_i,i\in \mathbb {N}\}$, which is denoted by $\lim \limits _{\longleftarrow }\{ X_i\}_{i\in \mathbb {N}}$. It is a compact metric space endowed with the distance $\rho (x,y)=\sum _{i\in \mathbb {N}}1/ 2^i \rho _i(x_i,y_i)$. We note that the maps $\{T_i\}$ induce a transformation T on the inverse limit.

The following structure theorems characterize inverse limits of nilsystems.

Theorem 2.6

(Host-Kra-Maass). [8, Theorem 1.2] Let $d\ge 2$ be an integer. A minimal system is a d-step pro-nilsystem if and only if it is an inverse limit of minimal d-step nilsystems.

Theorem 2.7

[3, Theorem 3.6] A minimal system is an $\infty$-step pro-nilsystem if and only if it is an inverse limit of minimal nilsystems.

2.4 Hall-Petresco Groups

Let G be an s-step nilpotent group. A geometric progression in $G^{\mathbb {Z}_+}$ is defined by the following form

$$\begin{aligned} (gg_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots g_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) })_{n\in \mathbb {Z}_{+}}, \end{aligned}$$

where $g\in G$ and $g_i\in G_i$ for $i=1,\ldots ,s$. The collection of all such progressions is the Hall-Petresco group HP(G) for G (see [7, Chapter 15, Section 1] that HP(G) is a group). We also define the following group

$$\begin{aligned} HP_e(G)=\{\phi \in HP(G):\phi (0)=1_G\}. \end{aligned}$$

An observation is that every element $\phi \in HP_e(G)$ has the form

$$\begin{aligned} \phi (n)=g_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots g_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) },\quad n\in \mathbb {Z}_+, \end{aligned}$$

where $g_i\in G_i$ for $i=1,\ldots ,s$.

3 Arithmetic Progressions In Topological Dynamical Systems

In this section, we will study the space of arithmetic progressions of a minimal nilsystem. As an application, we give a proof of Theorem A. Among other things, we can show Theorem B.

3.1 Nilsystems

We start by recalling some basic results in nilsystems. For more details and proofs, see [1, 7, 14]. If G is a nilpotent Lie group, let $G^0$ denote the connected component of its unit element $1_G$. In the sequel, $s\ge 2$ is an integer and $(X=G/\Gamma ,T_1,\ldots ,T_k)$ is a minimal s-step nilsystem with k commuting transformations. That is, there exist $t_1,\ldots ,t_k \in G$ defining the transformations $T_1,\ldots ,T_k$: $T_i:g\Gamma \rightarrow t_i g\Gamma$ such that $T_iT_j=T_jT_i$ for $1\le i<j\le k$.

If $(X,T_1,\ldots ,T_k)$ is minimal, let $G'$ be the subgroup of G spanned by $G^0$ and $t_1,\ldots ,t_k$ and let $\Gamma '=\Gamma \cap G'$, then we have that $G=G'\Gamma$. Thus the system $(X,T_1,\ldots ,T_k)$ is conjugate to $(X',T_1',\ldots ,T_k')$, where $X'=G'/\Gamma '$ and $T_i'$ is the translation by $t_i$ on $X'$ for $i=1,\ldots ,k$. Therefore, without loss of generality, we can restrict to the case that G is spanned by $G^0$ and $t_1,\ldots ,t_k$. We can also assume that $G^0$ is simply connected (see for example [1] or [12] for the case that $G=G^0$ and [11] for the general case). This in turns implies that the commutator subgroups $G_i,i=2,\ldots ,s$ are connected and included in $G^0$. Moreover, $G^0$ is divisible, i.e., for any $g\in G^0$ and $d\in \mathbb {N}$, there is some $h\in G^0$ with $h^d=g$ (see for example [7, Chapter 10, Corollary 9]).

The following theorem characterizes the pro-nilfactors of minimal nilsystems.

Theorem 3.1

[15, Theorem 1.2] Let $s\ge 2$ be an integer and let $(X=G/\Gamma ,T_1,\ldots ,T_k)$ be a minimal s-step nilsystem. Assume that G is spanned by $G^0$ and the elements $t_1,\ldots ,t_k$ of G defining the commuting transformations $T_1,\ldots ,T_k$. For $d=1,\ldots ,s$, if $X_d$ is the maximal factor of order d of X, then $X_d$ has the form $G/(G_{d+1}\Gamma )$, endowed with the translations by the projections of $t_1,\ldots ,t_k$ on $G/G_{d+1}$.

3.2 The Space of Arithmetic Progressions of Nilsystems

Let $(X=G/\Gamma ,T)$ be a minimal s-step nilsystem. For $d=1,\ldots ,s$, let $HP(G)_d$ be the collection of the element with the following form

$$\begin{aligned} \big (gg_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots g_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) }\big )_{n\in \mathbb {Z}_+}, \end{aligned}$$

where $g,g_1,\ldots ,g_d\in G_d,\; g_i\in G_i,i=d+1,\ldots ,s$ and $\left( {\begin{array}{c}n\\ i\end{array}}\right) =0$ if $n<i$.

It is clear that $HP(G)_1$ is the Hall-Petresco group HP(G) for G and

$$\begin{aligned} HP(G)_d=G_d^{\mathbb {Z}_+}\cap HP(G), \end{aligned}$$

(1)

which implies that every $HP(G)_d$ is a group. In [7, Chapter 15, Corollary 1,2], it was shown that HP(G) is a nilpotent Lie group and its discrete cocompact subgroup is $HP(G)\cap \Gamma ^{\mathbb {Z}_+}=\widetilde{\Gamma }$. Write

$$\begin{aligned} HP(X)=HP(G)/\widetilde{\Gamma }. \end{aligned}$$

Define $t^*,t^{\Delta }\in G^{\mathbb {Z}_+}$ as

$$\begin{aligned} t^*= 1_G\times t\times t^2\times \ldots ,\; \mathrm {and}\quad t^{\Delta }= t\times t\times t\times \ldots . \end{aligned}$$

and let $\tau ,\sigma$ be the translations by $t^*$ and $t^{\Delta }$ respectively. Let $\mathscr {G}$ be the group generated by $\sigma$ and $\tau$. The nilmanifold HP(X) is invariant under the $\mathscr {G}$ action as the elements $t^*$ and $t^{\Delta }$ both belong to HP(G). Moreover, in [7, Chapter 15, Theorem 5], it was shown that the nilsystem $(HP(X),\mathscr {G})$ is minimal. That is, for any $x\in X$, one has

$$\begin{aligned} \overline{\mathscr {O}_{\mathscr {G}}(x)}=HP(X). \end{aligned}$$

(2)

We first study the pro-nilfactors of the nilsystem $(HP(X),\mathscr {G})$. To do this, we need some intermediate lemmas.

Lemma 3.2

Let H be a normal subgroup of G. For $g,h\in G$, if $gh\in H$, then $g^nh^n\in H$ for all $n\in \mathbb {Z}_+$.

Proof

For $n\in \mathbb {Z}_+$, write $w_n=g^nh^n$. In particular, $w_0=1_G,w_1=gh$.

For positive integer n, as

$$\begin{aligned} w_n=g^nh^n=gw_{n-1}h=gh(h^{-1}w_{n-1}h), \end{aligned}$$

and H is normal in G, we deduce inductively that $w_n\in H$. $\square$

Proposition 3.3

$HP(G)_d$ is the $d^{\mathrm {th}}$-step commutator subgroup of HP(G) for $d=1,\ldots ,s$.

Proof

For $d=1,\ldots ,s$, denote by $\widetilde{HP}(G)_d$ the $d^{\mathrm {th}}$-step commutator subgroup of HP(G). In particular, $\widetilde{HP}(G)_1=HP(G)$. By (1), the inclusion $\widetilde{HP}(G)_d\subset HP(G)_d$ is trivial.

To prove the converse, we proceed by induction on the degree s of nilpotency. When $s =1$, $G_2$ is trivial and there is nothing to prove. Assume that $s \ge 2$, that the result holds for any $(s-1)$-step nilmanifold, and that G is s-step nilpotent. Write $H = G/G_s$ and let $p: G \rightarrow H$ denote the associated quotient map. Then H is an $(s-1)$-step nilpotent Lie group. We need the following claims.

Claim 1: $\widetilde{HP}(G)_d\cdot HP(G)_s= HP(G)_d$ for $d=1,\ldots ,s$.

Proof of Claim 1

$\widetilde{HP}(G)_d$ and $HP(G)_s$ are obviously subgroups of $HP(G)_d$, and therefore so is $\widetilde{HP}(G)_d\cdot HP(G)_s$.

We next show the converse. Let $\phi =(\phi (n))_{n\in \mathbb {Z}_+}\in HP(G)_d=G_d^{\mathbb {Z}_+}\cap HP(G)$, then $p\circ \phi =(p\circ \phi (n))_{n\in \mathbb {Z}_+}$ lies in $H_d^{\mathbb {Z}_+}\cap HP(H)=HP(H)_d$. Thus by the induction hypothesis, $p\circ \phi$ also belongs to $\widetilde{HP}(H)_d$. It follows that there exist $\psi \in \widetilde{HP}(G)_d$ and $\theta \in G_s^{\mathbb {Z}_+}$ such that $\phi =\psi \theta$. Since HP(G) is a group, $\theta \in HP(G)$. By (1), we get that $\theta \in HP(G)_s$.

This shows Claim 1. $\square$

Claim 2: For any $g\in G_d$ and $m\in \{1,\ldots ,d\}$, the sequence whose terms are $g^{\left( {\begin{array}{c}n-1\\ m\end{array}}\right) }$ belongs to $HP(G)_{d}$.

Proof of Claim 2

We show this claim by induction on m.

When $m=1$. For $g\in G_d$, by the definition of the group $HP(G)_d$, the sequence whose terms are $g^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }$ and the constant sequence $g^{-1}$ both belong to $HP(G)_{d}$, and thus the sequence with terms of form $g^{\left( {\begin{array}{c}n-1\\ 1\end{array}}\right) }=g^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\cdot g^{-1}$ belongs to $HP(G)_d$.

Assume that $m\in \{2,\ldots ,d\}$, that the sequence whose terms are $h^{\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) }$ belongs to $HP(G)_{d}$ for any $h\in G_d$. Let $g\in G_d$, notice that $g^{\left( {\begin{array}{c}n-1\\ m\end{array}}\right) }=g^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }\cdot (g^{-1})^{\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) }$, and by the definition of the group $HP(G)_d$, the sequence whose terms are $g^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to $HP(G)_{d}$ and by the induction hypothesis the sequence whose terms are $(g^{-1})^{\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) }$ belongs to $HP(G)_d$, and thus the sequence with terms of the form $g^{\left( {\begin{array}{c}n-1\\ m\end{array}}\right) }$ belongs to $HP(G)_d$.

This shows Claim 2. $\square$

Since $G_s$ is abelian, for $m=0,1,\ldots ,s$, the set

$$\begin{aligned} H_m=\{a\in G_s:(a^{\left( {\begin{array}{c}n\\ m\end{array}}\right) })_{n\in \mathbb {Z}_+}\in \widetilde{HP}(G)_{s}\} \end{aligned}$$

is a subgroup of $G_s$.

Claim 3: $H_m=G_s$ for $m=0,1,\ldots ,s$.

Proof of Claim 3

When $m<s$, it suffices to show that for any $b\in G_{s-1}$ and $c\in G$ , the sequence whose terms are $[b,c]^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to $\widetilde{HP}(G)_{s}$. Let $\beta =(b^{\left( {\begin{array}{c}n\\ m\end{array}}\right) })_{n\in \mathbb {Z}_+}$ and $\gamma$ be the constant sequence c, then $\beta \in HP(G)_{s-1}$ and $\gamma \in HP(G)$. By Claim 1 for $d=s-1$, there exist $\psi \in \widetilde{HP}(G)_{s-1}$ and $\theta \in HP(G)_s$ such that $\beta =\psi \theta$, and thus $[\psi ,\gamma ]\in \widetilde{HP}(G)_{s}$. As $\theta \in G_s^{\mathbb {Z}_+}$, we get that

$$\begin{aligned} {[}\beta ,\gamma ](n)=[\beta (n),\gamma (n)]= [\psi (n)\theta (n),\gamma (n)]=[\psi (n),\gamma (n)]=[\psi ,\gamma ](n) \end{aligned}$$

for any $n\in \mathbb {Z}_+$, which implies $[\beta ,\gamma ]=[\psi ,\gamma ]\in \widetilde{HP}(G)_{s}$ and the sequence with terms of the form $[b^{\left( {\begin{array}{c}n\\ m\end{array}}\right) },c]$ belongs to $\widetilde{HP}(G)_{s}$. As G is s-step nilpotent, the commutator map $(x,y)\mapsto [x,y]$ taking $G_{s-1}\times G$ to $G_s$ is a homomorphism in each coordinate. Thus $[b^{\left( {\begin{array}{c}n\\ m\end{array}}\right) },c]=[b,c]^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$, and the statement follows.

Assume now that $m=s$. Since $s\ge 2$, the group $G_s$ is connected and so is divisible. Thus it suffices to show that for $a \in G_s$, we have $a^s \in H_s$ , and thus for all $b\in G_{s-1}$ and $c \in G$, the sequence whose terms are $[b,c]^{s\left( {\begin{array}{c}n\\ s\end{array}}\right) }$ belongs to $\widetilde{HP}(G)_{s}$. By Claim 2, the sequence whose terms are $b^{\left( {\begin{array}{c}n-1\\ s-1\end{array}}\right) }$ belongs to $HP(G)_{s-1}$, and the sequence whose terms are $c^n$ belongs to HP(G). By a similar argument for the case $m<s$, we can get that the sequence with terms of the form $[b^{\left( {\begin{array}{c}n-1\\ s-1\end{array}}\right) },c^n]$ belongs to $\widetilde{HP}(G)_s$. Notice that $[b,c]^{s\left( {\begin{array}{c}n\\ s\end{array}}\right) }=[b^{\left( {\begin{array}{c}n-1\\ s-1\end{array}}\right) },c^n]$, thus the statement follows.

This shows Claim 3. $\square$

From Claim 3, as $\widetilde{HP}(G)_s$ is a group, $(a_0a_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots a_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) })_{n\in \mathbb {Z}_+}\in \widetilde{HP}(G)_s$ if $a_0,\ldots ,a_s\in H_s=G_s$. Thus we get that $\widetilde{HP}(G)_s= HP(G)_s$. Combining Claim 1, we deduce that $HP(G)_d$ is the $d^{\mathrm {th}}$-step commutator subgroup of HP(G) for $d=1,\ldots ,s$. $\square$

Lemma 3.4

$(G_{d}\Gamma )^{\mathbb {Z}_+}\cap HP(G)=HP(G)_{d}\cdot \widetilde{\Gamma }$ for $d=1,\ldots ,s$.

Proof

Recall that $\widetilde{\Gamma }=HP(G)\cap \Gamma ^{\mathbb {Z}_+}$. Notice that $HP(G)_{d}$ and $\widetilde{\Gamma }$ are obviously subgroups of $(G_{d}\Gamma )^{\mathbb {Z}_+}\cap HP(G)$, and therefore so is $HP(G)_{d}\cdot \widetilde{\Gamma }$.

We next prove the converse. Let $\phi =(\phi (n))_{n\in \mathbb {Z}_+}\in (G_{d}\Gamma )^{\mathbb {Z}_+}\cap HP(G)$, then by the definition of the group HP(G) there exist $g\in G$ and $g_m\in G_m,m=1,\ldots ,s$ such that for $n\in \mathbb {Z}_+$

$$\begin{aligned} \phi (n)= gg_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }\ldots g_s^{\left( {\begin{array}{c}n\\ s\end{array}}\right) }. \end{aligned}$$

As $\phi \in (G_d\Gamma )^{\mathbb {Z}_+}$, we deduce that $g,g_1,\ldots ,g_s\in G_d\Gamma$ inductively. It suffices to show that the sequence whose terms are $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ and the constant sequence g all belong to $HP(G)_{d}\cdot \widetilde{\Gamma }$. First, as $g\in G_d\Gamma$, there exist $h\in G_d$ and $\gamma \in \Gamma$ such that $g=h\gamma$. By the definition of the group $HP(G)_d$, we get that the constant sequence h belongs to $HP(G)_{d}$ and the constant sequence $\gamma$ belongs to $\widetilde{\Gamma }$, as was to be shown.

If $m\ge d$, since $g_m\in G_m$, we get that the sequence whose terms are $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to $HP(G)_{d}$, and thus belongs to $HP(G)_{d}\cdot \widetilde{\Gamma }$.

If $1\le m\le d-1$, as $g_m\in G_d\Gamma$, there exist $h_m\in G_d$ and $\gamma _m\in \Gamma$ such that $g_m=h_m\gamma _m$. Recall that $g_m\in G_m$, we get $\gamma _m=h_m^{-1}g_m\in G_m$ and thus the sequence whose terms are $\gamma _m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to HP(G).

We next claim that the sequence whose terms are $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }(\gamma _m^{-1})^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to $HP(G)_d$.

To prove the claim, notice that the sequence whose terms are $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }(\gamma _m^{-1})^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to HP(G), it suffices to show that $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }(\gamma _m^{-1})^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }\in G_d$ for all $n\in \mathbb {Z}_+$. As $g_m\gamma _m^{-1}=h_m\in G_d$, by Lemma 3.2 we have $g_m^k\gamma _m^{-k}\in G_d$ for all . In particularly, $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }(\gamma _m^{-1})^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }\in G_d$ for all $n\in \mathbb {Z}_+$, and thus the claim follows. From this claim we deduce that the sequence whose terms are $g_m^{\left( {\begin{array}{c}n\\ m\end{array}}\right) }$ belongs to $HP(G)_{d}\cdot \widetilde{\Gamma }$.

This completes the proof. $\square$

Lemma 3.5

The group HP(G) is spanned by $(HP(G))^0$ and the elements $t^*,t^{\Delta }$.

Proof

We first show that the group $HP(G)_2$ is included in $(HP(G))^0$. Indeed, for every $n\in \mathbb {Z}_+$ the projection $\pi _n:HP(G)_2\rightarrow G_2,(\varphi (n))_{n\in \mathbb {Z}_+}\mapsto \varphi (n)$ is surjective and open, and $G_2$ is included in $G^0$ and hence connected, we get that the group $HP(G)_2$ is connected and thus it is included in $(HP(G))^0$.

It is easy to see that any constant sequence is spanned by $(HP(G))^0$ and the element $t^{\Delta }$.

For $g\in G$, let $\phi _g=(\phi _g(n))_{n\in \mathbb {Z}_+}\in G^{\mathbb {Z}_+}$ such that $\phi _g(n)=g^n$, then $\phi _g\in HP(G)$. We claim that there exist $\psi \in (HP(G))^0$ and $k\in \mathbb {Z}$ such that $\phi _g =\psi \cdot (t^*)^{k}$. As G is spanned by $G^0$ and t, there exist $h\in G^0$ and $k\in \mathbb {Z}$ such that $g=ht^k$. Since $G^0$ is normal in G, by Lemma 3.2 we get that $\psi =\phi _g \cdot (t^*)^{-k}\in (G^0)^{\mathbb {Z}_+}$. As HP(G) is a group and $t^*\in HP(G)$, $\psi \in HP(G)$. There exists some $\varphi \in HP(G)_2$ such that $\psi =\phi _h \varphi$. As $\phi _h\in HP(G^0)\subset (HP(G))^0$, we deduce that $\psi \in (HP(G))^0$ as was to be shown.

Recall that the group HP(G) is spanned by the constant sequence, the sequence whose terms are $g^n$, where $g\in G$ and $HP(G)_2$, thus the lemma follows. $\square$

Now we calculate the pro-nilfactors of the nilsystem in (2) that

Theorem 3.6

Let $(X=G/\Gamma ,T)$ be a minimal s-step nilsystem. Assume that G is spanned by $G^0$ and the element t of G defining the transformation T. For $d=1,\ldots ,s$, let $X_d=G/(G_{d+1}\Gamma )$, then the maximal d-step pro-nilfactor of $(HP(X),\mathscr {G})$ is $(HP(X_d),\mathscr {G})$.

Proof

Let $X_d=G/(G_{d+1}\Gamma )$ and $p:X\rightarrow X_d$ be the quotient map, and let $t'=p(t)$. Then the transformation induced by T on $X_d$ is the translation by $t'$, which also denoted by T. There exists a natural quotient map $p^*:X^{\mathbb {Z}_+}\rightarrow X_d^{\mathbb {Z}_+}$ by $(x(n))_{n\in \mathbb {Z}_+} \mapsto (p(x(n)))_{n\in \mathbb {Z}_+}$. Moreover $p^*$ induces a factor map: $p^*:(HP(X),\mathscr {G})\rightarrow (HP(X_d),\mathscr {G})$.

To show the statement, it is sufficient to show¹

$$\begin{aligned} \mathbf {RP}^{[d]}(HP(X))=R_{p^*}. \end{aligned}$$

As $(HP(X_d),\mathscr {G})$ is a minimal d-step nilsystem, by Theorem 2.3 we have

$$\begin{aligned} \mathbf {RP}^{[d]}(HP(X))\subset R_{p^*}. \end{aligned}$$

We next show the inverse inclusion. Let $\mathbf {x},\mathbf {y}\in HP(X)$ with $p^{*}(\mathbf {x})=p^{*}( \mathbf {y})$. Recall that HP(X) is the nilmanifold $HP(G)/\widetilde{\Gamma }$, where $\widetilde{\Gamma }=HP(G)\cap \Gamma ^{\mathbb {Z}_+}$, then there exists some $\phi \in HP(G)$ with $\mathbf {y}=\phi \mathbf {x}$, which implies $\phi \in (G_{d+1}\Gamma )^{\mathbb {Z}_+}$. By Lemma 3.4 we have

$$\begin{aligned} \phi \in (G_{d+1}\Gamma )^{\mathbb {Z}_+}\cap HP(G)=HP(G)_{d+1}\cdot \widetilde{\Gamma }. \end{aligned}$$

On the other hand, by Lemma 3.5 and Theorem 3.1, the maximal d-step pro-nilfactor of HP(X) is

$$\begin{aligned} HP(G)/(HP(G)_{d+1}\cdot \widetilde{\Gamma }), \end{aligned}$$

which meaning $(\mathbf {x},\phi \mathbf {x})\in \mathbf {RP}^{[d]}(HP(X))$, and so $(\mathbf {x},\mathbf {y})\in \mathbf {RP}^{[d]}(HP(X))$.

We conclude that the maximal d-step pro-nilfactor of $(HP(X),\mathscr {G})$ is $(HP(X_d),\mathscr {G})$. $\square$

3.3 Proof of Theorem A

Now we are able to give a proof of one of our main results.

Proof of Theorem A

Let $X_d=G/(G_{d+1}\Gamma )$ and $p:X\rightarrow X_d$ be the quotient map, and let $t'=p(t)$. Then the transformation induced by T on $X_d$ is the translation by $t'$, which also denoted by T.

When $l=1$, the result is trivial, as the system $(N_1(X),\mathscr {G}_1)$ is conjugate to the system (X, T). For $l\in \mathbb {N}$, notice that the projection $p_l:X^{\mathbb {Z}_+}\rightarrow X^{l}:(x(n))_{n\in \mathbb {Z}_+}\mapsto (x(n))_{0\le n\le l}$ induces a factor map

$$\begin{aligned} p_l: (HP(X),\mathscr {G}) \rightarrow (N_{l+1}(X),\mathscr {G}_{l+1}). \end{aligned}$$

By Theorem 3.6, the maximal d-step pro-nilfactor of HP(X) is $HP(X_d)$, thus by Theorem 2.3 the maximal d-step pro-nilfactor of $N_{l+1}(X)$ is $p_l(HP(X_d))$ which equals $N_{l+1}(X_d)$.

This completes the proof. $\square$

3.4 Proof of Theorem B

In this subsection, we will show Theorem B. Proving it, we need some intermediate lemmas. We start from the following simple observation.

Lemma 3.7

Let (X, T) be an inverse limit of a sequence of minimal systems $\{(X_i,T)\}_{i\in \mathbb {N}}$. Then for every $l\in \mathbb {N}$, $(N_l(X),\mathscr {G}_{l})$ is an inverse limit of the sequence $\{(N_l(X_i),\mathscr {G}_{l})\}_{i\in \mathbb {N}}$.

Lemma 3.8

[15, Lemma 5.4] Let (X, T) be an inverse limit of a sequence of minimal systems $\{(X_i,T)\}_{i\in \mathbb {N}}$. For $i,d\in \mathbb {N}$, let $Z_{i,d}$ be the maximal d-step pro-nilfactor of $X_i$. Then the maximal d-step pro-nilfactor of X is an inverse limit of the sequence $\{(Z_{i,d},T)\}_{i\in \mathbb {N}}$.

Lemma 3.9

[15, Lemma 5.6] Let (X, T) be a minimal system and $d\in \mathbb {N}$. Let $R\subset X\times X$ be an equivalence relation of X with $R\subset \mathbf {RP}^{[d]}$, then the maximal d-step pro-nilfactors of $Y=X/R$ and X coincide.

Lemma 3.10

[3, Theorem 3.8] Let (X, T) be a minimal system. If $\mathbf {RP}^{[d]}=\mathbf {RP}^{[d+1]}$ for some $d\in \mathbb {N}$, then $\mathbf {RP}^{[n]}=\mathbf {RP}^{[d]}$ for all $n>d$.

Theorem 3.11

[6, Theorem 5.7] Let (X, T) be a minimal system and $d\in \mathbb {N}$. Then for $l\in \mathbb {N}$, the maximal d-step pro-nilfactors of $N_l(X)$ and $N_l(X_\infty )$ coincide, where $X_\infty = X/\mathbf {RP}^{[\infty ]}$.

Now we are able to show Theorem B.

Proof of Theorem B

Let $X_d=X/\mathbf {RP}^{[d]}$ for $d\in \mathbb {N}\cup \{\infty \}$. It follows from Theorem 3.11 that the maximal d-step pro-nilfactors of $N_l(X)$ and $N_l(X_\infty )$ coincide.

It suffices to show that the maximal d-step pro-nilfactor of $N_l(X_\infty )$ is $N_l(X_d)$.

If $\mathbf {RP}^{[d]}=\mathbf {RP}^{[d+1]}$, then $\mathbf {RP}^{[d]}=\mathbf {RP}^{[\infty ]}$ by Lemma 3.10. On this moment, $X_\infty$ is equal to $X_d$ and $N_l(X_\infty )$ is a d-step pro-nilsystem.

If $\mathbf {RP}^{[d]}\ne \mathbf {RP}^{[d+1]}$. By Theorem 2.7, there exists a sequence of minimal nilsystems $\{ (Y_i ,T)\}_{i\in \mathbb {N}}$ such that $X_\infty =\lim \limits _{\longleftarrow }\{Y_i\}_{i\in \mathbb {N}}$. Without loss of generality, we may assume that the nilpotency class of $Y_i$ is not less than d for every $i\in \mathbb {N}$. Let $X_d$ and $Y_{i,d}$ be the maximal d-step pro-nilfactors of X and $Y_i$ respectively. By Lemma 3.9, $X_d$ is also the maximal d-step pro-nilfactor of $X_\infty$ and thus $X_d$ is an inverse limit of the sequence $\{Y_{i,d}\}_{i\in \mathbb {N}}$ by Lemma 3.8. As $Y_i$ is a minimal nilsystem, the maximal d-step pro-nilfactor of $N_l(Y_i)$ is $N_l(Y_{i,d})$ by Theorem A. Note that $N_l(X_\infty )$ is an inverse limit of the sequence $\{N_l(Y_i)\}_{i\in \mathbb {N}}$ by Lemma 3.7, we deduce that the maximal d-step pro-nilfactor of $N_l(X_\infty )$ is an inverse limit of the sequence $\{N_l(Y_{i,d})\}_{i\in \mathbb {N}}$ by Lemma 3.8, which is equal to $N_l(X_d)$.

We conclude that the maximal d-step pro-nilfactor of $(N_l(X),\mathscr {G}_{l})$ is $(N_l(X_d),\mathscr {G}_{l})$. $\square$

4 Simple Arithmetic Progressions In Nilsystems

In the last part of this paper, we first give the example which is mentioned in the introduction. That is,

Example 4.1

There exists a minimal 2-step nilsystem (Y, T) and a countable subset $\Omega$ of Y such that for every $y\in Y\backslash \Omega$ the maximal equicontinuous factor of $(\overline{\mathscr {O}_{T\times T^2}(y,y)},T\times T^2)$ is not $(\overline{\mathscr {O}_{T\times T^2}(\pi (y),\pi (y))},T\times T^2)$, where $\pi :Y\rightarrow Y/\mathbf {RP}^{[1]}$ is the factor map.

Let $G=\mathbb {Z}\times \mathbb {T}\times \mathbb {T}$, with the multiplication given by

$$\begin{aligned} (k,x,y)*(k',x',y')=(k+k',x+x',y+y'+2kx'). \end{aligned}$$

Then G is a Lie group. Its commutator subgroup $G_2$ is $\{0\}\times \{0\}\times \mathbb {T}$ and G is 2-step nilpotent. The subgroup $\Gamma =\mathbb {Z}\times \{0\}\times \{0\}$ is discrete and cocompact. Let Y denote the nilmanifold $G/\Gamma$ and let $Z=G/(G_2\Gamma )$. Let $\alpha$ be irrational, $t=(1,\alpha ,\alpha )$ and $T : Y\rightarrow Y$ be the translation by t. Then (Y, T) is a 2-step nilsystem. We can also view the nilsystem (Y, T) as $T:\mathbb {T}^2\rightarrow \mathbb {T}^2,(x,y)\mapsto (x+\alpha ,y+2x+\alpha )$, and $(Z,T_Z)$ as $T_Z:\mathbb {T}\rightarrow \mathbb {T},x \mapsto x+\alpha$.

Since $\alpha$ is irrational, the rotation $(Z,T_Z)$ is minimal and (Y, T) is minimal too. By Theorem 3.1, $(Z,T_Z)$ is the maximal equicontinuous factor of (Y, T). Let $\pi$ be the factor map, i.e., $\pi :\mathbb {T}^2\rightarrow \mathbb {T},(x,y)\mapsto x$. For $(x,y)\in \mathbb {T}^2$, $\pi (x,y)=x$ and

$$\begin{aligned} \overline{\mathscr {O}_{T_Z\times T_Z^2}(x,x)}=(x,x)+\overline{\{(n\alpha ,2n\alpha ):n\in \mathbb {Z}\}} =\{(x+z,x+2z):z\in \mathbb {T}\}. \end{aligned}$$

Thus the system $(\overline{\mathscr {O}_{T_Z\times T_Z^2}(x,x)},T_Z\times T_Z^2)$ is conjugate to the system $(Z,T_Z)$.

Claim: For $(a,b)\in \mathbb {T}^2$, the maximal equicontinuous factor of $(\overline{\mathscr {O}_{T\times T^2}(a,b,a,b)},T\times T^2)$ is conjugate to the system $(\overline{\mathscr {O}_{R_{2a}}(0,0)},R_{2a})$, where $R_{c}:\mathbb {T}^2\rightarrow \mathbb {T}^2,(x,y)\mapsto (x+\alpha ,y+c)$ for $c\in \mathbb {T}$. In particular, if $\alpha ,a$ are rationally independent, the system $(\overline{\mathscr {O}_{R_{2a}}(0,0)},R_{2a})$ is not conjugate to the system $(Z,T_Z)$.

To show the claim, we start from the following simple observation.

Lemma 4.2

Let (X, T) and (Y, S) be minimal systems. If there exists a continuous onto map $h:X\rightarrow Y$ and $x\in X$ such that $h(T^nx)=S^n(h(x))$ for all $n\in \mathbb {Z}$, then h induces a factor map between systems (X, T) and (Y, S).

Now we are in position to show the claim.

Proof of Claim

For $\beta \in \mathbb {T}$, let $S_{\beta }:\mathbb {T}^2\rightarrow \mathbb {T}^2$ be defined by

$$\begin{aligned} S_{\beta }(x,y)= (x+\alpha ,y+2x+\alpha +\beta ). \end{aligned}$$

When $\beta =0$, $S_0=T$. The system $(\mathbb {T}^2, S_\beta )$ is minimal (see for example [4, Lemma 1.25]).

Let $U_{\beta }:\mathbb {T}^3\rightarrow \mathbb {T}^3$ be defined by

$$\begin{aligned} U_{\beta }(x,y,z)=(x+\alpha ,y+2x+\alpha +\beta ,z+2\beta ). \end{aligned}$$

Step 1: A special case.

Let $h:\mathbb {T}^{4}\rightarrow \mathbb {T}^{3}$ be defined by

$$\begin{aligned} h(x,y,z,w) =(x,y,4y-w). \end{aligned}$$

Note that

$$\begin{aligned} (S_{\beta }\times S_{\beta }^2)^n(0,0,0,0)=(n\alpha ,n^2\alpha +n\beta ,2n\alpha ,4n^2\alpha +2n\beta ) \end{aligned}$$

and

$$\begin{aligned} h\big ((S_{\beta }\times S_{\beta }^2)^n(0,0,0,0)\big )&=(n\alpha ,n^2\alpha +n\beta ,2n\beta ) \\&=U_{\beta }^n(0,0,0)\\&=U_{\beta }^n\big (h(0,0,0,0)\big ), \end{aligned}$$

thus by Lemma 4.2, h induces a factor map:

$$\begin{aligned} h:(\overline{\mathscr {O}_{S_{\beta }\times S_{\beta }^2}(0,0,0,0)},S_{\beta }\times S_{\beta }^2)\rightarrow (\overline{\mathscr {O}_{U_{\beta }}(0,0,0)},U_{\beta }). \end{aligned}$$

For any $(x_1,x_2,x_3,x_4)\in \overline{\mathscr {O}_{S_{\beta }\times S_{\beta }^2}(0,0,0,0)}$, we have $x_3=2x_1$. It follows that h is a bijection and thus h is a conjugation.

Write $L=\overline{\mathscr {O}_{U_{\beta }}(0,0,0)}$. Notice that for $(x,y_1,z),(x,y_2,z)\in L$ with $y_1\ne y_2$, $\big ((x,y_1,z),(x,y_2,z)\big )\in \mathbf {RP}^{[1]}(L,U_\beta )$, we deduce that the maximal equicontinuous factors of systems $(L,U_{\beta })$ and $(\overline{\mathscr {O}_{R_{\beta }}(0,0)},R_{\beta })$ coincide. As the system $(\overline{\mathscr {O}_{R_{\beta }}(0,0)},R_{\beta })$ is equicontinuous, it is also the maximal equicontinuous factor of $(L,U_{\beta })$.

Finally, the maximal equicontinuous factor of $(\overline{\mathscr {O}_{S_{\beta }\times S_{\beta }^2}(0,0,0,0)},S_{\beta }\times S_{\beta }^2)$ is conjugate to the system $(\overline{\mathscr {O}_{R_{\beta }}(0,0)},R_{\beta })$.

Step 2: The general case.

Fix $(a,b)\in \mathbb {T}^2$. Let $g:\mathbb {T}^4\rightarrow \mathbb {T}^4$ be defined by

$$\begin{aligned} g(x,y,z,w)=(x-a,y-b,z-a,w-b). \end{aligned}$$

Note that

$$\begin{aligned} (T\times T^2)^n(a,b,a,b)=(a,b,a,b)+ (n\alpha ,n^2\alpha +2na,2n\alpha ,4n^2\alpha +4na) \end{aligned}$$

and

$$\begin{aligned} g\big ((T\times T^2)^n(a,b,a,b)\big )&=(n\alpha ,n^2\alpha +2na,2n\alpha ,4n^2\alpha +4na) \\&=(S_{2a}\times S_{2a}^2)^n(0,0,0,0)\\&=(S_{2a}\times S_{2a}^2)^n(g(a,b,a,b)), \end{aligned}$$

thus by Lemma 4.2, g induces a conjugation:

$$\begin{aligned} g:(\overline{\mathscr {O}_{T\times T^2}(a,b,a,b)},T\times T^2) \rightarrow (\overline{\mathscr {O}_{S_{2a}\times S_{2a}^2}(0,0,0,0)},S_{2a}\times S_{2a}^2). \end{aligned}$$

Therefore, by Step 1 the maximal equicontinuous factor of $(\overline{\mathscr {O}_{T\times T^2}(a,b,a,b)},T\times T^2)$ is conjugate to the system $(\overline{\mathscr {O}_{R_{2a}}(0,0)},R_{2a})$.

This completes the proof. $\square$

4.1 Proof of Theorem C

Before proving Theorem C, we need some lemmas.

Lemma 4.3

[10, Section 3.4] For $k_1,\ldots ,k_l\in \mathbb {N}$, let $g_1,\ldots ,g_l$ be elements of G with $g_j\in G_{k_j}$, and let $p_1,\ldots ,p_l:\mathbb {Z}^r\rightarrow \mathbb {Z}$ be polynomials with $\deg p_j\le k_j$ for $j=1,\ldots ,l$. Fix a linear ordering on the set $\mathbb {Z}_+^r$. Then for every $(l_1,\ldots ,l_r)\in \mathbb {Z}_+^r$, there exists $z_{l_1,\ldots ,l_r}\in G_{l_1+\ldots +l_r}$ such that

$$\begin{aligned} \prod _{j=1}^l g_{j}^{p_j(n_1,\ldots ,n_r)}=\prod _{I}z_{l_1,\ldots ,l_r}^{\left( {\begin{array}{c}n_1\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n_r\\ l_r\end{array}}\right) } \end{aligned}$$

(3)

for all $(n_1,\ldots ,n_r)\in \mathbb {Z}_+^r$, where $I=\{0\le l_1\le n_1\}\times \ldots \times \{0\le l_r\le n_r\}$ and the factors in the product on the right-hand side of (3) are multiplied in accordance with the ordering induced on I from $\mathbb {Z}_+^r$ .

Lemma 4.4

[7, Chapter 1, Lemma 4] Let G be an s-step nilpotent group. If $2i+j>s$, then for every $y\in G_j$ the map from $G_i$ to $G_{i+j}$ given by $x\mapsto [y,x]$ is a group homomorphism. In particular, for any $x_1,\ldots ,x_i\in G,y\in G_{s-i}$ and $n_1,\ldots ,n_i,n_{i+1}\in \mathbb {Z}$,

$$\begin{aligned} {[}\ldots [[x_1^{n_1},x_2^{n_2}],\ldots ,x_{i}^{n_i}] ,y^{n_{i+1}}] =[\ldots [[x_1,x_2],\ldots ,x_i], y]^{n_1n_2\cdots n_in_{i+1}}. \end{aligned}$$

Definition 4.5

Let G be an s-step nilpotent group. For $d=1,\ldots ,s$, define $A_d\subset G^{\mathbb {Z}_+}$ as the group generated by

$$\begin{aligned} \{( g^{n^k})_{n\in \mathbb {Z}_+}:g\in G_k,\;k=d,\ldots ,s\}. \end{aligned}$$

Proposition 4.6

Let G be an s-step nilpotent group and assume that $G_d$ is divisible for every $d=2,\ldots ,s$. Then the $d^{\mathrm {th}}$-step commutator subgroup of $A_1$ is $A_d$ for $d=2,\ldots ,s$.

Proof

For $d=2,\ldots ,s$, let $\widetilde{A}_d$ be the $d^{\mathrm {th}}$-step commutator subgroup of $A_1$. To show the statement, we need the following claims. Let $d\ge 2$.

Claim 1: For any $l_1,\ldots ,l_d\in \mathbb {N}$ and $z\in G_{l_1+\ldots +l_d}$, there exist $w_d,\ldots ,w_{l_1+\ldots +l_d}\in G_{l_1+\ldots +l_d}$ such that for all $n\in \mathbb {N}$,

$$\begin{aligned} z^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) } =\prod _{j=d}^{l_1+\ldots +l_d}w_j^{n^j}. \end{aligned}$$

In particular, $(z^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) })_{n\in \mathbb {Z}_+}\in A_{d}$.

Proof of Claim 1

Fix $l_1,\ldots ,l_d\in \mathbb {N}$ and let $l=l_1+\ldots +l_d,z\in G_{l}$. Notice $l\ge d\ge 2$, then by the assumption $G_{l}$ is divisible, and thus there exists some $w\in G_{l}$ such that $w^{l_1 !\cdots l_d!}=z$. Write $l_1 !\cdots l_d!\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) =n^l+a_{l-1}n^{l-1}+\ldots +a_dn^d$, where $a_{l-1},\ldots ,a_d\in \mathbb {Z}$. Then

$$\begin{aligned} {z}^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) }= w^{l_1 !\cdots l_d!\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) }= w^{n^l+a_{l-1}n^{l-1}+\ldots +a_dn^d} =w_l^{n^l}w_{l-1}^{n^{l-1}}\cdots w_d^{n^d}, \end{aligned}$$

where $w_i=w^{a_i}\in G_{l}$ for $i=d,\ldots ,l-1$ and $w_l=w$, as was to be shown.

We next show that $(z^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) })_{n\in \mathbb {Z}_+}\in A_{d}$. By the definition of the group $A_d$, $(w_j^{n^j})_{n\in \mathbb {Z}_+}\in A_d$ for every $j=d,\ldots ,l$ and thus the statement follows. $\square$

Claim 2: Let $\phi _1,\phi _2,\ldots ,\phi _d\in A_1$, then for any $(n_1,n_2,\ldots ,n_d)\in \mathbb {N}^d$ one has

$$\begin{aligned} {[}\ldots [\phi _1(n_1),\phi _2(n_2)],\ldots ,\phi _d(n_d)] =\prod _{I}z_{l_1,\ldots ,l_d}^{\left( {\begin{array}{c}n_1\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n_d\\ l_d\end{array}}\right) }, \end{aligned}$$

where $z_{l_1,\ldots ,l_d}\in G_{l_1+\ldots +l_d}$ and $I=\{(l_1,\ldots ,l_d)\in \mathbb {N}^d:l_1+\ldots +l_d\le s\}$.

In particular, $[\ldots [\phi _1,\phi _2],\ldots ,\phi _d]\in A_d.$

Proof of Claim 2

Let $\phi _1,\phi _2,\ldots ,\phi _d\in A_1$. It follows from Lemma 4.3 that

$$\begin{aligned} \Phi (n_1,n_2,\ldots ,n_d)= [\ldots [\phi _1(n_1),\phi _2(n_2)],\ldots ,\phi _d(n_d)] =\prod _{I}z_{l_1,\ldots ,l_d}^{\left( {\begin{array}{c}n_1\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n_d\\ l_d\end{array}}\right) }, \end{aligned}$$

where $z_{l_1,\ldots ,l_d}\in G_{l_1+\ldots +l_d}$ and $I=\{(l_1,\ldots ,l_d)\in \mathbb {Z}_+^d:l_1+\ldots +l_d\le s\}$.

We first show that $z_{l_1,\ldots ,l_d}=1_G$ if $l_i=0$ for some $i\in \{1,\ldots ,d\}$. Without loss of generality, assume that $l_1=0$. Notice that $\phi _1(0)=1_G$ and thus

$$\begin{aligned} 1_G= [\ldots [\phi _1(0),\phi _2(n_2)],\ldots \phi _d(n_d)] \end{aligned}$$

for all $n_2,\ldots ,n_d\in \mathbb {Z}_+$.

On the other hand, we have

$$\begin{aligned} \begin{array}{ll} 1_G &{} =\Phi (0,\ldots ,0,0)=z_{0,\ldots ,0}\\ &{} =\Phi (0,\ldots ,0,1)=z_{0,\ldots ,0}z_{0,\ldots ,0,1}\\ &{} =\Phi (0,\ldots ,0,2)=z_{0,\ldots ,0}z_{0,\ldots ,0,1}^2z_{0,\ldots ,0,2}\\ &{}\ldots \ldots \end{array} \end{aligned}$$

which implies that $z_{0,l_2,\ldots ,l_d}=1_G$ for every $(0,l_2,\ldots ,l_d)\in I$, as was to be shown.

Thus by Claim 1, we get that $\Phi \in A_d$. $\square$

It follows from Claim 2 that $\widetilde{A}_d\subset A_d$ for $d=2,\ldots ,s$.

Claim 3: For $k\ge d$ and $g\in G_k$, one has $(g^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$.

Proof of Claim 3

We first show this claim for $k=s$ and $2\le d\le s$. Let $g\in G_s$ and let $g_1,\ldots ,g_{d-1}\in G,g_d\in G_{s+1-d}$ such that $g=[\ldots [g_1,g_2],\ldots ,g_d]$. As $(g_i^n)_{n\in \mathbb {Z}_+}\in A_1$ for $i=1,\ldots ,d$ and $g^{n^d}=[\ldots [g_1^n,g_2^n],\ldots , g_d^n]$ for any $n\in \mathbb {Z}_+$, by Lemma 4.4 we have $(g^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$.

We will prove this claim by the decreasing induction for d. When $d=s$, it follows by the argument above for the case $k=s$ and $2\le d\le s$.

Let $d<s$ and assume that this statement is true for all $j=d+1,\ldots ,s$, i.e.,

(*) for any $j\ge d+1,(z^{n^j})_{n\in \mathbb {Z}_+}\in \widetilde{A}_j$ for $k\ge j$ and $z\in G_k$.

Now for d, we will show that $(g^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$ for $k\ge d$ and $g\in G_k$ inductively on k. It follows by the argument above for the case $k=s$ and $2\le d\le s$ that $(g^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$ for $g\in G_s$. Let $d\le k<s$ and assume that

(**) $(g^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$ for any $j\ge k+1$ and $g\in G_j$.

Let $h\in G_k$ and let $h_1,\ldots ,h_{d-1}\in G,h_d\in G_{k+1-d}$ such that $h=[\ldots [h_1,h_2],\ldots , h_d]$. Let $\varphi _i=(h_i^n)_{n\in \mathbb {Z}_+}$ for $i=1,\ldots ,d$, then $\varphi _i\in A_1$ and $[\ldots [\varphi _1,\varphi _2],\ldots ,\varphi _d]\in \widetilde{A}_d.$

By Claim 2, for any $(n_1,n_2,\ldots ,n_d)\in \mathbb {N}^d$,

$$\begin{aligned} {[}\ldots [\varphi _1(n_1),\varphi _2(n_2)],\ldots ,\varphi _d(n_d)] =\prod _{I}z_{l_1,\ldots ,l_d}^{\left( {\begin{array}{c}n_1\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n_d\\ l_d\end{array}}\right) }, \end{aligned}$$

where $z_{l_1,\ldots ,l_d}\in G_{l_1+\ldots +l_d}$ and $I=\{(l_1,\ldots ,l_d)\in \mathbb {N}^d:l_1+\ldots +l_d\le s\}$.

By taking $n_1=\ldots =n_d=n$, we have

$$\begin{aligned} {[}\ldots [\varphi _1(n),\varphi _2(n)],\ldots ,\varphi _d(n)]= \prod _{I}{z_{l_1,\ldots ,l_d}}^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) }. \end{aligned}$$

In particular, $z_{1,\ldots ,1}=h$.

Fix $(l_1,\ldots ,l_d)\in \mathbb {N}^d$ with $d+1\le l\le s$, where $l=l_1+\ldots +l_d$. By Claim 1, there exist $w_d,\ldots ,w_{l}\in G_{l}\subset G_{d+1}$ such that for all $n\in \mathbb {N}$

$$\begin{aligned} z_{l_1,\ldots ,l_d}^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) } =\prod _{j=d}^{l}w_j^{n^j}. \end{aligned}$$

Therefore by the induction hypothesis (*),

$$\begin{aligned} (w_l^{n^l})_{n\in \mathbb {Z}_+}\in \widetilde{A}_l,\; (w_{l-1}^{n^{l-1}})_{n\in \mathbb {Z}_+}\in \widetilde{A}_{l-1},\;\ldots , \;(w_{d+1}^{n^{d+1}})_{n\in \mathbb {Z}_+}\in \widetilde{A}_{d+1}, \end{aligned}$$

and by (**), $(w_d^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{A}_d$. Notice that $\widetilde{A}_d$ is a group and $\widetilde{A}_l\subset \ldots \subset \widetilde{A}_d$, thus

$$\begin{aligned} ({z_{l_1,\ldots ,l_d}}^{\left( {\begin{array}{c}n\\ l_1\end{array}}\right) \ldots \left( {\begin{array}{c}n\\ l_d\end{array}}\right) })_{n\in \mathbb {Z}_+} =(w_l^{n^l})_{n\in \mathbb {Z}_+} \cdots (w_d^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{ A}_d. \end{aligned}$$

From this we get that

and thus $(h^{n^d})_{n\in \mathbb {Z}_+}\in \widetilde{ A}_d$, as was to be shown.

This completes the proof. $\square$

Recall that $A_d$ is generated by

$$\begin{aligned} \{( g^{n^k})_{n\in \mathbb {Z}_+}:g\in G_k,\; k=d,\ldots ,s\}, \end{aligned}$$

thus by Claim 3, $A_d\subset \widetilde{A}_d$.

We conclude that $A_d$ is the $d^{\mathrm {th}}$-step commutator subgroup of $A_1$ for $d=2,\ldots ,s$. $\square$

Theorem 4.7

[7, Chapter 15, Theorem 7] Let $(X=G/\Gamma ,T)$ be a minimal s-step nilsystem. For $x\in X$, set

$$\begin{aligned} HP_x(X)=\{\phi \in HP(X):\phi (0)=x\}. \end{aligned}$$

Then for $m_X$-almost every $x\in X$, the nilsystem $(HP_x(X),\tau )$ is minimal.

Now we are able to show Theorem C.

Proof of Theorem C

By Theorem 4.7, there is a full-measure subset $\Omega$ of X such that $(HP_x(X),\tau )$ is minimal for every $x\in \Omega$. Recall that HP(G) is a nilpotent Lie group, it follows that $HP_e(G)$ is also a nilpotent Lie group. Write

$$\begin{aligned} L(X)=HP_e(G)/\big (HP_e(G)\cap \Gamma ^{\mathbb {Z}_+} \big ). \end{aligned}$$

For $x\in X$, let $g\in G$ be a lift of x and let $t_x=g^{-1}tg$. Define $t_x^*,g^{\Delta }\in G^{\mathbb {Z}_+}$ as

$$\begin{aligned} t_x^*= 1_G\times t_x\times t_x^2\times \ldots ,\; \mathrm {and}\quad g^{\Delta }= g\times g\times g\times \ldots . \end{aligned}$$

and let $\tau _x,\sigma _g$ be the translations by $t_x^*$ and $g^{\Delta }$ respectively. Note that $\sigma _g$ is a transformation of $X^{\mathbb {Z}_+}$ and $\tau _x$ is a transformation of L(X) as $t_x^*\in HP_e(G)$.

Claim 1: For any $x\in X$, $\sigma _g$ induces a conjugation: $\sigma _g:(L(X),\tau _x)\rightarrow (HP_x(X),\tau )$.

Proof of Claim 1

Recall that $t_x=g^{-1}tg$, then $g\cdot t_x^n=t^n\cdot g$ for all $n\in \mathbb {Z}$, which implies that $\sigma _g \tau _x \phi =\tau \sigma _g \phi$ for any $\phi \in X^{\mathbb {Z}_+}$, and thus $\sigma _g$ induces a factor map: $\sigma _g:(L(X),\tau _x)\rightarrow (HP_x(X),\tau )$. Note that $g^{\Delta }HP_e(G)=\{\phi \in HP(G):\phi (0)=g\}$, and thus $g^{\Delta }$ is a homeomorphism of L(X) and $HP_x(X)$. This shows that $\sigma _g:(L(X),\tau _x)\rightarrow (HP_x(X),\tau )$ is a conjugation. $\square$

Claim 2: $HP_e(G)$ is generated by $\big (HP_e(G)\big )^0$ and $\tau _x$.

Proof of Claim 2

Note $t_x t^{-1}=g^{-1}tgt^{-1}\in G^0$ and thus G is spanned by $G^0$ and $t_x$.

We first show that the group $HP_e(G)_2$ is included in $(HP_e(G))^0$. Indeed, for every $n\in \mathbb {Z}_+$ the projection $\pi _n:HP_e(G)_2\rightarrow G_2,(\varphi (n))_{n\in \mathbb {Z}_+}\mapsto \varphi (n)$ is surjective and open, and $G_2$ is included in $G^0$ and hence connected, we get that the group $HP_e(G)_2$ is connected and thus it is included in $(HP_e(G))^0$.

For $g\in G$, let $\phi _g=(\phi _g(n))_{n\in \mathbb {Z}_+}\in G^{\mathbb {Z}_+}$ such that $\phi _g(n)=g^n$, then $\phi _g\in HP_e(G)$. We claim that there exist $\psi \in (HP(G)_e)^0$ and $k\in \mathbb {Z}$ such that $\phi _g =\psi \cdot (t_x^*)^{k}$. As G is spanned by $G^0$ and $t_x$, there exist $h\in G^0$ and $k\in \mathbb {Z}$ such that $g=ht_x^k$. Since $G^0$ is normal in G, by Lemma 3.2 we get $\psi =\phi _g \cdot (t_x^*)^{-k}\in (G^0)^{\mathbb {Z}_+}$. As $HP_e(G)$ is a group and $t_x^*\in HP_e(G)$, $\psi \in HP_e(G)$. There exists some $\varphi \in HP_e(G)_2$ such that $\psi =\phi _h \varphi$. As $\phi _h\in HP_e(G^0)\subset (HP_e(G))^0$, we deduce that $\psi \in (HP_e(G))^0$ as was to be shown.

Recall the group $HP_e(G)$ is spanned by $\phi _g$ for $g\in G$ and $HP_e(G)_2$, thus the claim follows. $\square$

By Claim 1, $(HP_x(X),\tau )$ is conjugate to the system $(L(X),\tau _x)$. It follows form Theorem 3.1 and Claim 2 that the maximal d-step pro-nilfactor of $(L(X),\tau _x)$ is

$$\begin{aligned} (HP_e(G)/\big (HP_e(G)_{d+1} \cdot (HP_e(G)\cap \Gamma ^{\mathbb {Z}_+}) \big ),\tau _x). \end{aligned}$$

We next compute the commutator subgroups of $HP_e(G)$. To do this, we assume that $G^0$ is simply connected.

Claim 3: The $d^{\mathrm {th}}$-step commutator subgroup of $HP_e(G)$ is generated by

$$\begin{aligned} \{( g^{n^k})_{n\in \mathbb {Z}_+}:g\in G_k,\; k=d,\ldots ,s\}, \end{aligned}$$

for $d=1,\ldots ,s$.

Proof of Claim 3

As $G^0$ is simply connected, $G_i$ is divisible for every $i=2,\ldots ,s$. Thus by Proposition 4.6, it suffices to show $HP_e(G)=A_1$. Recall that $A_1$ is generated by

$$\begin{aligned} \{( g^{n^k})_{n\in \mathbb {Z}_+}:g\in G_k,\;k=1,\ldots ,s\}. \end{aligned}$$

For $d\ge 2$ and $g\in G_d$, there is some $h\in G_d$ such that $h^{d!}=g$. Write $d!\left( {\begin{array}{c}n\\ d\end{array}}\right) =n^d+a_{d-1}n^{d-1}+\ldots +a_1n$, where $a_{d-1},\ldots ,a_1\in \mathbb {Z}$. Then

$$\begin{aligned} g^{ \left( {\begin{array}{c}n\\ d\end{array}}\right) } h^{d!\left( {\begin{array}{c}n\\ d\end{array}}\right) }= h^{n^d+a_{d-1}n^{d-1}+\ldots +a_1n} =h_d^{n^d}h_{d-1}^{n^{d-1}}\cdots h_1^{n}, \end{aligned}$$

where $h_i=h^{a_i}\in G_d,i=1,\ldots ,d-1$ and $h_d=h$. By the definition of $A_1$, we have $(h_i^{n^i})_{n\in \mathbb {Z}_+}\in A_1$ for every $i=1,\ldots ,d$. This shows that $HP_e(G)\subset A_1$.

On the other hand, for $d\in \mathbb {N}$ there exist $b_0,b_1,\ldots ,b_d\in \mathbb {Z}$ such that $n^d=b_d\left( {\begin{array}{c}n\\ d\end{array}}\right) +\ldots +b_1\left( {\begin{array}{c}n\\ 1\end{array}}\right) +b_0$. Let $n=0$, we get $b_0=0$. Then for $z\in G_d$,

$$\begin{aligned} z^{n^d}=z^{b_d\left( {\begin{array}{c}n\\ d\end{array}}\right) +\ldots +b_1\left( {\begin{array}{c}n\\ 1\end{array}}\right) }=z_d^{\left( {\begin{array}{c}n\\ d\end{array}}\right) }\cdots z_1^{\left( {\begin{array}{c}n\\ 1\end{array}}\right) }, \end{aligned}$$

where $z_i=z^{b_i}\in G_d$ for $i=1,\ldots ,d$. By the definition of $HP_e(G)$, we have $(z_i^{\left( {\begin{array}{c}n\\ i\end{array}}\right) })_{n\in \mathbb {Z}_+}\in HP_e(G)$ for every $i=1,\ldots ,d$. This shows that $A_1\subset HP_e(G)$.

From this, we deduce that $A_1=HP_e(G)$. $\square$

For $l\in \mathbb {N}$, let $p_l$ be the projection $p_l:X^{\mathbb {Z}_+}\rightarrow X^{l}:(x(n))_{n\in \mathbb {Z}_+}\mapsto (x(n))_{1\le n\le l}$. For any $n\in \mathbb {Z}$, we have $p_l(\tau ^nx^{\Delta })=\tau _l^n x^l$, where $x^{\Delta }\in X^{\mathbb {Z}_+}$ is the constant sequence x for $x\in X$. Fix $x\in \Omega$. Notice that $x^{\Delta }\in HP_x(X)$ and the system $(HP_x(X),\tau )$ is minimal, it follows from Lemma 4.2 that $p_l$ induces a factor map $p_l: (HP_x(X),\tau ) \rightarrow (L_x^l(X),\tau _{l}).$ Moreover, there is a commutative diagram:

where $\tau _{l,x},\sigma _{l,g}$ are translations by $t_x\times t_x^2\times \ldots \times t_x^l$ and $g\times \ldots \times g$ (l times) respectively.

Let $HP_e^{(l)}(G)=p_l(HP_e(G))=\{(\phi (n))_{1\le n\le l}:\phi \in HP_e(G)\}$, where $p_l$ is the projection $p_l:G^{\mathbb {Z}_+}\rightarrow G^{l}:(\phi (n))_{n\in \mathbb {Z}_+} \mapsto (\phi (n))_{1\le n\le l}$, then $HP_e^{(l)}(G)$ is a nilpotent Lie group and its discrete subgroup is $HP_e^{(l)}(G)\cap \Gamma ^l=\widetilde{\Gamma }^{(l)}$. Moreover, for $d=1,\ldots ,s$ the $d^{\mathrm {th}}$-step commutator subgroup $HP_e^{(l)}(G)_d$ of $HP_e^{(l)}(G)$ is $p_l(HP_e(G)_d)$ which is generated by

$$\begin{aligned} \{( g^{n^k})_{1\le n\le l}:g\in G_k,\;k=d,\ldots ,s\}. \end{aligned}$$

Clearly, we can view $L_{e_X}^l(X)$ as the nilmanifold $HP_e^{(l)}(G)/\widetilde{\Gamma }^{(l)}$, and thus the maximal d-step pro-nilfactor of $(L_x^l(X),\tau _l)$ is conjugate to the system

$$\begin{aligned} \Big (HP_e^{(l)}(G)/\big (HP_e^{(l)}(G)_{d+1}\cdot \widetilde{\Gamma }^{(l)}\big ), \; \tau _{l,x}\Big ). \end{aligned}$$

This completes the proof. $\square$