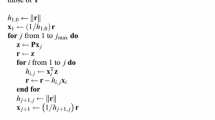Abstract
We develop validated numerical methods for the computation of Floquet multipliers of equilibria and periodic solutions of delay differential equations, as well as impulsive delay differential equations. Using our methods, one can rigorously count the number of Floquet multipliers outside a closed disc centered at zero or the number of multipliers contained in a compact set bounded away from zero. We consider systems with a single delay where the period is at most equal to the delay, and the latter two are commensurate. We first represent the monodromy operator (period map) as an operator acting on a product of sequence spaces that represent the Chebyshev coefficients of the state-space vectors. Truncation of the number of modes yields the numerical method, and by carefully bounding the truncation error in addition to some other technical operator norms, this leads to the method being suitable to computer-assisted proofs of Floquet multiplier location. We demonstrate the computer-assisted proofs on two example problems. We also test our discretization scheme in floating point arithmetic on a gamut of randomly-generated high-dimensional examples with both periodic and constant coefficients to inspect the precision of the spectral radius estimation of the monodromy operator (i.e. stability/instability check for periodic systems) for increasing numbers of Chebyshev modes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Linearized growth and decay rates near steady states and invariant manifolds play a central role in the analysis of dynamical systems. When these manifolds have simple descriptions such as fixed points or periodic orbits, the computation of these growth rates is equivalent to an eigenvalue problem. For delay differential equations (or more generally, retarded functional differential equations), several authors have proposed solutions to the “delay eigenvalue problem”. For autonomous linear equations, these include methods based on discretization of the associated infinitesimal generator [3, 4, 18, 33] and the solution operator [15]. In the scope of equations with periodic coefficients, there are several results concerning discretization and characteristic matrices [15, 16, 26, 29, 30].
Discretization schemes can provide strong convergence properties, but these still may not be able to provide mathematical proof concerning one or more approximate eigenvalues. For example, the spectral accuracy of the infinitesimal generator method with Chebyshev collocation [5] guarantees that each eigenvalue of the delay differential equation (DDE) is well-approximated by some eigenvalue of the discretized problem. Such convergence results exist also for methods based on the solution operator [16] and they can be summarized by the statement: every eigenvalue of the DDE is the limit of some eigenvalue of the discretized problem. However, one is often interested in a situation dual to this. That is, one wants to know when one or more eigenvalues of the discretized problem are close (or have the same relative location in the complex plane) as a pairing of eigenvalues of the DDE.
There has been progress recently on methods that can automatically prove (with the assistance of a computer and interval arithmetic) results concerning the location of eigenvalues of DDEs based on the eigenvalues of some discretization. We highlight the 2017 paper by Miyajima [23] on verified error bounds for particular eigenvalues, and the 2020 paper by Lessard and Mireles James [21] on validation of generalized Morse indices. These papers both concern autonomous problems, so one motivation of the present paper is to build on the results of Lessard and Mireles James to accomodate DDEs with periodic coefficients. Since we get a numerical discretization scheme for the monodromy operator (i.e. the period map) for free out of our analysis, we simultaneously get an alternative to the method of Gilsinn and Potra [16] for the computation of Floquet multipliers (the linearized stability-determining quantities) of DDEs with periodic coefficients.
In the case of autonmous DDEs, if the explicit location of an eigenvalue is required to high accuracy then there are several ways this can be accomplished [7, 21, 23]. Of mention is that in this case, the eigenvalues are precisely the zeroes \(\lambda \) of the characteristic equation \(\det (\Delta (\lambda ))=0\), where \(\Delta (\lambda )\) is the characteristic matrix of the DDE. The characteristic equation is transcedental in \(\lambda \), but the result is still a scalar (complex) zero-finding problem (\(\Delta (\lambda )\) is a \(d\times d\) matrix with d equal to the dimension of the DDE), so a given eigenvalue can be verified to a provable level of accuracy using the radii polynomial method; see Theorem 2.2 of [21] for a direct application of the method to the present situation. While characteristic matrices for periodic DDEs can be constructed [26, 30] and the eigenvalues of these matrices are related to the Floquet multipliers, a discretization step must still be performed. Even if the characteristic matrix is explicitly available, such as when the delay is a multiple of the period [32], the computation of the matrix generally requires at least computing the Cauchy matrix of a time-periodic ordinary differential equation and computing weighted integrals involving this and the periodic coefficients. We have been unable to find publications concerning error estimates between the approximate eigenvalues of discretized characteristic matrices for periodic DDEs and the Floquet multipliers. As such, another goal of the present paper is to devise a strategy to validate the location of specific Floquet multipliers of DDEs with periodic coefficients.
Some physical systems are characterized by smooth evolution in addition to brief bursts of activity. This might be due to exogenous forcing or it might be an intrinsic property of the system. If these bursts of activity incur relatively large distrubances to the state and do not occur too frequently, it can be beneficial to model them as discontinuities. One mathematical formalism for such a construction is impulsive dynamical systems, which include impulsive differential equations [2, 20, 25], impulsive evolution equations [13] and impulsive functional differential equations [8, 28]. One of the simplest classes of impulsive dynamical system is one in which these discontinuities (hereafter called impulses) occur at fixed times. Even for more complicated classes of problems where impulses are triggered according to mixed spatio-temporal relations, the case of fixed (in time) impulses is still relevant since linear systems of this type arise linearization at bounded or periodic trajectories [2]. When the sequence of impulses has periodic structure and this is compatible with the continuous dynamics, the result is a periodic system. The Floquet theory has been developed for linear periodic impulsive retarded functional differential equations [10] and characteristic equations/matrices for special cases of periodic linear impulsive DDE [17, 27] have been developed, but at present there is no rigorous numerical method to compute Floquet multipliers for a general class of such equations. Our approach in this paper will simultaneously address the approximation of Floquet multipliers for impulsive delay differential equations by way of a Chebyshev spectral method, computer-assisted proof of Floquet multiplier location, and computer-assisted proof of the count of the number of unstable Floquet multipliers (or generally, the number of Floquet multipliers having absolute value greater than some prescribed value). Formally, the most broad class of systems for which our numerical method applies is systems of the form

for (sufficiently regular) real matrix-valued functions A(t) and B(t), real matrices \(C_1\) and \(C_2\), and natural numbers p (period) and q (delay). Necessary background on these systems appears in Sect. 2. More generally, we can treat systems with commensurate period and delay by way of a time scaling.
With the previous paragraph in mind, we will state and prove all results in the context of periodic impulsive delay differential equations. This class of equations includes delay differential equations with periodic coefficients by taking \(C_1=C_2=0\) in the displayed equation above, so our results can be applied to those equations as well. Finally, although this is an extreme level of reduction, the results also apply to ordinary and impulsive differential equations without delays. To give the reader a taste of the kinds of results that can be proven using our validated numerics framework, we still state two theorems that are consequences of results that appear in (and are proven in) Sect. 8.
Theorem
Let \(\beta =0.1\), \(\rho =1\), \(K=1\), \( d_1=0.02\), \(d_2=0.03\) in the following time-delay predator-prey model with impulsive harvesting
The equilibrium \((K,0)=(1,0)\) enjoys the following properties for any \(r>0\):
-
its unstable manifold is one-dimensional if \(h=0.060\) and \(\tau \in \{1,2,3\}\);
-
it is locally asymptotically stable if \(h=0.075\) and \(\tau \in \{1,2,3\}\);
-
its unstable manifold is one-dimensional for all \(h\in [0,0.060]\) if \(\tau =1\);
-
with \(\tau =1\), one of its Floquet multipliers crosses the unit circle at some \(h\in [0.065,0.066]\), and over this entire range of h there is exactly one eigenvalue whose absolute value is greater than 0.8.
Theorem
Consider the following two-dimensional delay equation modeled on the normal form of the Hopf bifurcation:
For \(\tau \in {\mathbb {N}}\), there is a nontrivial (i.e. nonzero) branch of periodic solutions parameterized by \(\beta \). At parameter \(\beta =\frac{3}{2}\) and \(\tau =1\), the unstable manifold of this periodic solution is at least two-dimensional.
1.1 Overview of the paper
The scope of this paper is fairly broad. It is therefore expected that many readers will only be interested in the numerical method and its applications to stability. Others, however, will want to see all the technical details concerning computer-assisted proofs. The difficulty is that the theory is intrinsically tied to the numerical method and its machine implementation. To ensure a sufficiently wide range of researchers are able to appreciate the content, we will overview the paper here with these points in mind.
The core of the numerical method is derived in Sects. 3 and 4 with the help of the background from Sect. 2. The first, Sect. 3, concerns an explicit representation of the monodromy operator. In Sect. 4.1 we review Chebyshev expansion and convolution, and in Sect. 4.2 we represent the monodromy operator on a sequence space by way of correspondence with Chebyshev series. The representation of the operator is on an infinite-dimensional space, and the explicit numerical method is obtained by projecting to a finite-dimensional subspace by mode truncation and projection. These mechanisms are described at the beginning of Sect. 4.3, in Sect. 4.4 and in Remark 6.3.1. The last remark involves some technical machinery, and a simplified implementation that would function only in the case of equal period p and delay q could be obtained by following Remark 6.1.1 from Sect. 6.1 instead. Once these details are ironed out, implementing the method for general period and delay amounts to simple matrix algebra and this is covered in Sect. 7.2, where some convergence guarantees are also discussed. Several examples featuring the double arithmetic implementation are provided in Sect. 9 to show how the implementation scales with respect to the dimension of the problem and the order of the method.
Concerning the rigorous numerics, we prove a few necessary results concerning Floquet theory in Sect. 2. Section 3 is devoted to an abstract functional-analytic representation of the monodromy operator. In Sect. 4 we transition from the abstract representation to a concrete representation of the monodromy operator in terms of Chebyshev series and establishes the basis for computer-assisted proof of eigenvalue location. Section 5 contains several auxiliary bounds of linear maps and operators that are needed later. Section 6 contains proofs of (computable) upper bounds for various abstract operators that are needed for computer-assisted proofs of eigenvalue location. We discuss MATLAB implementation in Sect. 7, while Sect. 8 is devoted to examples of computer-assisted proof.
We wrap up the paper with a conclusion in Sect. 10.
2 Preliminaries
In this section we will state relevant background concerning impulsive delay differential equations and Floquet multipliers. We will state some basic assumptions that will be needed throughout the paper, and we will prove results concerning the regularity of the eigenfunctions that will be needed later.
2.1 Impulsive delay differential equations
In this paper, a nonlinear periodic impulsive delay differential equation will consist of of a delay differential equation together with a discrete-time update rule:
The periodicity comes from the assumption that there exists some \(n>0\) and \(T>0\) such that \(t_{k+n}=t_k+T\) for all integers k, while also \(g(k+n,\cdot ,\cdot )=g(k,\cdot ,\cdot )\) and \(f(t+T,\cdot ,\cdot )=f(t,\cdot ,\cdot )\). Equation (2) should be interpreted as
where \(x(t^-)\) denotes the limit from the left at time t. Systems with multiple and time-varying delays can also be considered. More generally, impulsive retarded functional differential equations can be considered without periodicity assumptions. We refer the reader to [1, 2, 25, 28] for background on impulsive differential equations. In future we will refer to (1)–(2) simply as a nonlinear IDDE, and will drop the reference to periodicity. In what follows we will assume that f is \(C^1\) in its second and third variables and continuous from the right and bounded in its first, while g is \(C^1\) in its second and third variables.
The following definitions are adapted from [8]. A solution (unconditional on any initial data) \(x:{\mathbb {R}}\rightarrow {\mathbb {R}}^d\) of (1)–(2) is a function that is continuous from the right, possesses limits on the left, and satisfies both equations (1) and (2), with the derivative being interpreted as a right-hand derivative. These solutions are continuous from the right at times \(t_k\) with finite limits on the left. Any natural phase space for (1)–(2) with a vector space structure must therefore contain functions that have many discontinuities. To see why, observe that at each time \(t_k\), the solution in \({\mathbb {R}}^d\) will have a discontinuity, so the solution history \(\theta \mapsto x_t(\theta )\) for \(x_t:[-\tau ,0]\rightarrow {\mathbb {R}}^d\) and defined by \(x_t(\theta )=x(t+\theta )\) will have a discontinuity at the lagged argument \(\theta \) whenever \(t+\theta =t_k\). This observation leads naturally to the choice of phase space
These are the right-continuous regulated functions. We will often write it simply as \(\mathcal {RCR}\) when there is no ambiguity. When equipped with the supremum norm \(||\phi ||=\sup _{\theta \in [-\tau ,0]}|\phi (\theta )|\) for \(|\cdot |\) some norm on \({\mathbb {R}}^d\), \(\mathcal {RCR}\) becomes a Banach space. One can then define a solution satisfying the initial condition \(x_s=\phi \) for some \((s,\phi )\in {\mathbb {R}}\times \mathcal {RCR}\) to be a function \(x:[s-\tau ,s+\beta )\rightarrow {\mathbb {R}}^d\) such that \(x|_{(s,s+\beta )}\) satisfies (1)–(2) and \(x_s=\phi \). Under the conditions described above, such a solution is guaranteed to exist and be unique for any \((s,\phi )\in {\mathbb {R}}\times \mathcal {RCR}\), and defined on a maximal interval of existence. Following this, an IDDE generates a (nonlinear) two-parameter semigroup on \(\mathcal {RCR}\) through the solution map in the usual way.
It is typical for nonlinear IDDE to possess no fixed points, and these will typically not be robust under perturbations of the vector field f and jump map g. This can be seen by observing that the problem of finding zeroes of the map \(F:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d\times {\mathbb {R}}^d\) defined by \(F(x)=(f(x),g(x))\) is generally overdetermined. However, a generic periodic solution (of period jT for \(j\in {\mathbb {N}}\)) is robust under small T-periodic perturbations (this is a fairly direct consequence of Theorem 5.1.1 from [10], the Floquet theory and the implicit function theorem) of f and g, so in this regard periodic solutions are the simplest structurally stable invariant sets one can study in IDDE.
2.2 Monodromy operator and Floquet multipliers
The local stability of a periodic solution \(\gamma \) is determined by the trivial solution \(y=0\) of the linearization
If \(\gamma \) has period jT for some \(j\in {\mathbb {N}}\), then (4)–(5) has period \({\tilde{T}}=jT\).
Let \(t\mapsto y(t,s,\phi )\) denote the unique solution of (4)–(5) satisfying the initial condition \(y_s(\cdot ,s,\phi )=\phi \). Each (eventually compact) linear operator \(M_t:\mathcal {RCR}\rightarrow \mathcal {RCR}\) defined by
is called a monodromy operator. The spectrum of each monodromy operator is identical, so by convention we will usually refer to \(M:=M_0\) as the monodromy operator. \(\gamma \) is locally asymptotically stable if all eigenvalues of M are in the open ball \(B_1(0)=\{z\in {\mathbb {C}} : |z|<1\}\). When some eigenvalues have unit modulus but all others have modulus less than one, the stability of \(\gamma \) depends on some more algebraic properties (eg. whether the restriction of M to the direct sum of generalized eigenspaces associated to the eigenvalues of unit modulus has a diagonalizable representation) and dynamical properties (i.e. the flow on its centre manifold). If any eigenvalue has modulus greater than one, \(\gamma \) is unstable. The eigenvalues of M are called Floquet multipliers.
The computation of Floquet multipliers is important for several reasons. Apart from verifying stability or instability of a periodic solution, the number of Floquet multipliers outside of the disc \(\overline{B_1(0)}\) together with the dimension of their generalized eigenspaces dictates the dimension of the unstable manifold of \(\gamma \). The classification of a bifurcation in a parameter-dependent system depends on the structure of the centre fibre bundle in additional to higher-order normal form data, all of which depends on the Floquet multipliers on the unit circle and their associated eigenfunctions. For these reasons, we will now dispense with the explicit dependence on \(\gamma \) and consider the more general linear periodic impulsive delay differential equation
We will refer to such a system as a linear periodic IDDE (impulsive delay differential equation). The periodicity here means that there exists \(T>0\) and \(n>0\) such that \(A(t+T)=A(t)\), \(B(t+T)=B(t)\), \(C_1(k+n)=C_1(k)\), \(C_2(k+n)=C_2(k)\), and \(t_{k+n}=t_k+T\).
2.3 Eigenfunctions are densely nonsmooth
Our approach to rigorous computation of Floquet multipliers will be based in part on a suitable representation of the eigenfunctions of the monodromy operator as infinite series with good convergence properties. Unfortunately, the problem of computing the Floquet multipliers for the fully general periodic system (7)–(8) seems not very amenable to this approach, even if we assume A and B are analytic. The following proposition and its associated proof should demonstrate the main problem.
Proposition 2.3.1
Let \(\phi \) be an eigenfunction of the monodromy operator M associated to the scalar impulsive delay differential equation
for \(\alpha \ne 0\), \(\beta \ne -1\) and \(\tau \in {\mathbb {R}}{\setminus }{\mathbb {Q}}\) irrational. Let \((a,b)\subset [-\tau ,0]\). There exists \(q>0\) such that \(\phi |_{(a,b)}\) is at most q times differentiable.
Proof
\(t\mapsto y(t;0,\phi )\) is a solution that can be represented in the form \(e^{t\lambda }p(t)\) for p periodic with period one and differentiable from the right. Substituting this ansatz into the IDDE and simplifying, it follows that p is a 1-periodic solution of
We first prove that p is discontinuous at each integer \(k\in {\mathbb {Z}}\). Suppose not, then we must have \(p(k)=0\) since \(\beta \ne -1\). p is therefore a 1-periodic solution of the DDE
with \(p(0)=0\). The phase space of the above DDE decomposes \({\mathcal {C}}={\mathcal {C}}([-\tau ,0],{\mathbb {R}})\) as
where S, N and U are the stable, centre and unstable subspaces respectively, while R generates those solutions that have superexponential decay: \(\psi \in R\) if and only if
Consequently, any periodic solution must be generated by an element of the centre subspace and is therefore of the form
for some \(\omega >0\). Since p must be 1-periodic, we get \(\omega =2\pi \). The condition \(p(0)=0\) implies \(p(t)=c\sin (2\pi t)\) for a constant c, with \(c\ne 0\) because \(\phi \) is an eigenfunction. Substituting this ansatz into the delay differential equation, performing some algebraic simplifications and recalling that \(\alpha \ne 0\), we can derive the equation
From the linear independence of sine and cosine, \(\tau \) must be rational, which contradicts our assumption of \(\tau \) being irrational. We conclude that p must be discontinuous at the integers.
Next, we prove that if p is infinitely many-times differentiable at some \(t\in {\mathbb {R}}\), then \(t-k\tau \notin {\mathbb {Z}}\) for all integers \(k\ge 0\). We prove this by strong induction on k. We already know that p is discontinuous on the integers, so we must have \(t\notin {\mathbb {Z}}\) for p to be differentiable at t. Suppose now that p is infinitely many-times differentiable and that \(t-j\tau \notin {\mathbb {Z}}\) for \(j=0,\dots ,k\) for some \(k\ge 0\). We have
If p is indeed infinitely many-times differentiable at t, then the right-hand side must be continuous at t. A straightforward inductive proof shows that each of \(p^{(k)}\) and \(p^{(k)}(t-\tau )\) can be written as a finite linear combination of the terms \(p(t-j\tau )\) for \(j=0,\dots ,k+1\), and in particular the right-hand side of (9) written in terms of these has a nonzero coefficient on \(p(t-(k+1)\tau )\). By the strong induction hypothesis, \(t-j\tau \notin {\mathbb {Z}}\) for \(j=0,\dots ,k\). If the right-hand side of (9) is indeed continuous at t, then we must also have \(t-(k+1)\tau \notin {\mathbb {Z}}\). This completes the inductive proof, and it follows that \(t-j\tau \notin {\mathbb {Z}}\) for all \(j\ge 0\).
Finally, let \((a,b)\subset [-\tau ,0]\). The restriction \(\phi |_{(a,b)}\) is \(C^\infty \) if and only if \(p|_{(a,b)}\) is also \(C^\infty \). Consider the sequences
where \([x]_1=x-\lfloor x\rfloor \). \(c_n\) is dense in [0, 1], from which it follows that there exist integers \(k,j\ge 0\) such that \(p_k\in (a+j,b+j)\). Define \(c=k\tau -j\in (a,b)\). From previous analysis, p is not infinitely many-times differentiable at c since \(c-k\tau =-j\in {\mathbb {Z}}\). \(\square \)
When the delay and the period are non-commensurate, it should be expected that the eigenfunctions of a linear periodic IDDE will have a lower order of smoothness in any subinterval of their domain. In particular, the set of points where an eigenfunction fails to be infinitely many times differentiable is dense in in its domain.
2.4 Regularity of the eigenfunctions under commensurate delay and period
With the observations of the previous section in mind, we will need to make the following additional assumption on the structure of (7)–(8) in order to have a chance of eigenfunctions with appropriate series representations. The following definition will be used fairly often.
Definition 2.4.1
Let X be a complex Banach space and let \((a_k,b_k)\) be a (finite, infinite or bi-infinite) sequence of nondegenerate open intervals with \(b_k=a_{k+1}\). A function \(f:I\subset {\mathbb {R}}\rightarrow X\) (possibly real-valued) for an interval I is piecewise-analytic with respect to \((a_k,b_k)\) if:
-
f is continuous from the right and locally bounded,
-
for each k, there exists an open neighbourhood \(U_k\) of \([a_k,b_k]\) in \({\mathbb {C}}\) such that \(f|_{(a_k,b_k)\cap I} = {\tilde{f}}_k|_{(a_k,b_k)\cap I}\) for some analytic function \({\tilde{f}}_k:U_k\rightarrow X\).
Given such a function f, the sequence \({\tilde{f}}_k\) will denote the analytic extensions from \((a_k,b_k)\).
Assumption 0
The following conditions are satisfied.
-
A0.1
The sequence \(t_k\) satisfies \(t_{k+1}=t_k+T\) and, additionally, \(C_1(k)\) and \(C_2(k)\) are constant.
-
A0.2
There exist \(p,q\in {\mathbb {N}}\) such that \(qT - p\tau =0\).
-
A0.3
The T-periodic functions \(t\mapsto A(t)\) and \(t\mapsto B(t)\) are piecewise-analytic with respect to the open intervals \(I_k:=\displaystyle \left( t_0 + \frac{kT}{p},t_0+\frac{(k+1)T}{p}\right) \) for \(k\in {\mathbb {Z}}\).
We refer to the above as Assumption 0 because we will shortly perform a change of variables that will make its characterization a bit nicer. Under this assumption, we make the change of variables
for s a new rescaled time. Defining \(z(s)=y(t(s))\) and observing that \(\frac{\tau }{q}=\frac{T}{p}\), we get the IDDE
Observe that the matrix-valued functions \(s\mapsto {\tilde{A}}(s) = \frac{T}{p}A(t_0+\frac{T}{p}s)\) and \(s\mapsto {\tilde{B}}(s) = \frac{T}{p}B(t_0+\frac{T}{p}s)\) are now periodic functions with period p and are analytic on the intervals \((k,k+1)\) for \(k\in {\mathbb {Z}}\), while the restriction to each such interval is the itself the restriction of some analytic function. Dropping the tildes and relabeling the variables, we can therefore consider without loss of generality IDDEs of the form
with \(p,q\in {\mathbb {N}}\) and p-periodic functions A and B that are piecewise-analytic with respect to the open intervals \((k,k+1)\) for \(k\in {\mathbb {Z}}\).
Remark 2.4.1
If the linear system (7)–(8) is actually the linearization (4)–(5) at a periodic solution from a nonlinear periodic IDDE such as (1)–(2), the piecewise-analytic condition of A0.3 will be satisfied provided f is analytic, \(\gamma \) is piecewise-analytic with respect to the intervals \(I_k\), and both A0.1 and A0.2 are satisfied. The piecewise-analyticity of periodic solutions \(\gamma \) w.r.t. these intervals is a technical detail, but it can be proven with similar arguments as those used in proving Proposition 2.4.1. For our examples, however, we will be taking \(\gamma \) to be a constant solution or an explicitly computable periodic solution, so this detail is unimportant.
The following result will be of fundamental importance once we move onto the representation of eigenfunctions. It states that the eigenfunctions of (10)–(11) with A and B piecewise-analytic with respect to \((k,k+1)\) are also piecewise-analytic with respect to the same intervals.
Proposition 2.4.1
Suppose the matrix-valued functions A and B in (10)–(11) are p-periodic and piecewise-analytic with respect to \((k,k+1)\) for \(k\in {\mathbb {Z}}\). Every eigenfunction of the monodromy operator M with nonzero eigenvalue is piecewise-analytic with respect to the same intervals.
Proof
From the Floquet theory of IDDE [11], \(\phi \) is an eigenfunction of M with eigenvalue \(\mu \ne 0\) if and only if there exists a p-periodic function \(z:{\mathbb {R}}\rightarrow {\mathbb {C}}^d\) and \(\lambda \in {\mathbb {C}}\) such that \(y(t,0,\phi )=e^{\lambda t}z(t)\) is a solution of (10)–(11), and \(\mu =e^{\lambda p}\). In particular, \(\phi (\theta )=e^{\lambda \theta }z(\theta )\). It follows that z is a complex-valued p-periodic solution of the IDDE
Define the translates \(z_i(t)=z(t-i)\) for \(i=0,1,\dots ,q-1\) and let \([j]_p\) denote the remainder of j modulo p—that is, \([j]_p\in [0,\dots ,p-1)\) is the unique integer such that \(j = [j]_p+rp\) for some \(r\in {\mathbb {Z}}\). It suffices to prove that the \(z_i\) are piecewise-analytic with respect to \((k,k+1)\), and then to establish the analogous analytic continuation. By construction, \((z_1,\dots ,z_{q-1})\) is a p-periodic solution of
Since each of \(t\mapsto A(t-i)\) and \(t\mapsto B(t-i)\) is piecewise-analytic with respect to \((k,k+1)\) for \(k\in {\mathbb {Z}}\), each \(z_i\) is also piecewise-analytic w.r.t these intervals since it can be identified with the solution of a Cauchy problem of a linear system of ordinary differential equations with analytic coefficients on each interval \([k,k+1]\). It follows that z is piecewise-analytic with respect to the same intervals. \(\square \)
The following proposition strengthens the analyticity of the solution by assuming a more precise form of the domain of analytic extensions \({\tilde{A}}_k\) and \({\tilde{B}}_k\) of \(A|_{(k,k+1)}\) and \(B|_{(k,k+1)}\). Its proof is a consequence of the monodromy theorem of complex analysis, which states sufficient conditions under which analytic continuation can be accomplished. The proof is omitted.
Proposition 2.4.2
Let \(E_\nu \) denote the Bernstein \(\nu \)-ellipse in \({\mathbb {C}}\); for background see [31]. Let \(s_k(\omega )=k+\frac{1}{2}(s+1)\) and suppose \({\tilde{A}}_k\circ s_k\) and \({\tilde{B}}_k\circ s_k\) are analytic on \(E_\nu \). Then every eigenfunction \(\phi \) of M has \({\tilde{\phi }}_k\circ s_k:E_\nu \rightarrow {\mathbb {C}}^d\) analytic.
With these propositions in mind, the following definition and corollary are appropriate.
Definition 2.4.2
The space of piecewise-analytic functions \(\phi :[-q,0]\rightarrow {\mathbb {C}}^d\) with respect to \((k,k+1)\) for \(k\in {\mathbb {Z}}\) will be denoted \({\mathcal {P}}([-q,0],{\mathbb {C}}^d)\). When no confusion arises, we will write it simply as \({\mathcal {P}}\).
Corollary 2.4.1
Let \({\tilde{M}}:{\mathcal {P}}\rightarrow \mathcal {RCR}\) denote the restriction of M to \({\mathcal {P}}\). Then \(\sigma ({\tilde{M}})\subseteq \sigma (M)\) and if \(M\phi =\lambda \phi \) for \(\lambda \ne 0\), then \(\phi \in {\mathcal {P}}\). Moreover, \({\tilde{M}}\) has range in \({\mathcal {P}}\).
Proof
The properties of the spectrum are straightforward given Proposition 2.4.1. Given a piecewise-analytic initial condition \(\phi \), the solution y(t) of (10)–(11) with \(y_0=\phi \) is determined, on each interval \([k,k+1)\) with \(0\le k <\min \{p,q\}\), is the solution of an ordinary differential equation (with analytic coefficients) via the method of steps. The resulting solution is therefore piecewise-analytic at least on \([0,\min \{p,q\})\). Successively stepping forward, \(y:[0,p]\rightarrow {\mathbb {C}}^d\) is piecewise-analytic with respect to \([k,k+1)\), from which it follows that \({\tilde{M}}\) has range in \({\mathcal {P}}\). \(\square \)
Note that \({\mathcal {P}}\) is not complete (and hence not a Banach space) with respect to the supremum norm inherited from \(\mathcal {RCR}\), but \({\tilde{M}}\) is still compact. In future, we will drop the tildes and identify M with the restricted operator \({\tilde{M}}\).
There is a natural isomorphism between \({\mathcal {P}}\) and a particular product space; see Fig. 1 for a visual aid. This isomorphism will be useful later, and since we are currently discussing M and the structure of \({\mathcal {P}}\), it is worth defining it now.
Top: a typical element of \({\mathcal {P}}([-2,0],{\mathbb {R}})\). Hollow circles denote left limits, while filled circles denote function value at the discontinuity. Bottom: the corresponding element of \({\mathcal {S}}={\mathbb {R}}\times {\mathcal {A}}^2\) under the isomorphism m in order from left to right
Proposition 2.4.3
Introduce the spaces
Let \(j:{\mathcal {A}}_0\rightarrow {\mathcal {A}}\) be the restriction map: \(j(f)=f|_{[-1,0)}\). Let \(\pi _x:[-1,0)\rightarrow [-1+x,x)\) be the translation defined by \(\pi _x(y)=x+y\). The following are true.
-
When \({\mathcal {A}}_0\) and \({\mathcal {A}}\) are equipped with the supremum norm, j is an isometric isomorphism.
-
The function \(m:{\mathcal {P}}\rightarrow {\mathbb {C}}^d\times {\mathcal {A}}^q\) defined by
$$\begin{aligned} m(\phi ) = (\phi (0),\phi |_{[-1,0)},\phi |_{[-2,-1)}\circ \pi _{-1},\dots ,\phi |_{[-q,0)}\circ \pi _{1-q}) \end{aligned}$$is an isomorphism.
Definition 2.4.3
The space \({\mathcal {S}}={\mathbb {C}}^d\times {\mathcal {A}}^q\) will be referred to as the space of piecewise-analytic segments of length q.
Corollary 2.4.2
The map \(M^{\mathcal {S}}:{\mathcal {S}}\rightarrow {\mathcal {S}}\) with \(M^{S} = m\circ M\circ m^{-1}\) is well-defined and \(\sigma (M){\setminus }\{0\}=\sigma (M^{{\mathcal {S}}}){\setminus }\{0\}\).
Corollary 2.4.3
Let \(E_\nu \) denote the Bernstein \(\nu \)-ellipse in \({\mathbb {C}}\) and denote \(s_k(\omega )=k+\frac{1}{2}(s+1)\). Suppose \({\tilde{A}}_k\circ s_k\) and \({\tilde{B}}_k\circ s_k\) are analytic on \(E_\nu \). Define \(\theta :[-1,0]\rightarrow [-1,1]\) by \(\theta (s)=\frac{1}{2}(s-1)\). Let \(\phi =(\phi (0),\phi _0,\dots ,\phi _{1-p})\in \sigma (M^{\mathcal {S}})\). Then, \(\phi _j\circ \theta :[-1,1]\rightarrow {\mathbb {C}}^d\) has an analytic continuation to \(E_\nu \) for \(j=0,\dots ,1-p\).
\(M^{\mathcal {S}}:{\mathcal {S}}\rightarrow {\mathcal {S}}\) is the representation of M on the space of piecewise-analytic segments of length q. As we will see, it is very natural to work with the space of piecewise-analytic segments as opposed to the full space \({\mathcal {P}}\) when attempting to represent the monodromy operator.
3 Segment decomposition and representation of the monodromy operator
Following the analysis of Sect. 2.4 on the regularity of eigenfunctions, we will from this point on restrict our attention to linear systems
with the following assumptions: The linear system (12)–(13) satisfies:
-
A1.1
\(p\le q\) (but see later Sect. 7.2).
-
A1.2
A and B are p-periodic and piecewise-analytic with respect to the intervals \((k,k+1)\) for \(k\in {\mathbb {Z}}\).
For the purposes of developing a numerical method with guaranteed convergence, assumption A1.1 is not too strong (see Sect. 7.2). Given Proposition 2.4.1, we know that the eigenfunctions associated to the monodromy operator M of this linear system are in \({\mathcal {P}}\)—that is, piecewise-analytic with respect to the intervals \((k,k+1)\). The identification of M with the operator on piecewise-analytic segments of length q, \(M^{\mathcal {S}}:{\mathcal {S}}\rightarrow {\mathcal {S}}\), is designed to reflect this. Our goal in this section will be to represent \(M^{\mathcal {S}}\) in terms of concrete integral operators.
Remark 3.0.1
In the following four sections, we will be defining some linear operators E and W that will be used to represent \(M^{\mathcal {S}}\). The definitions of these operators depend on the relationship between p and q. This should not cause confusion.
3.1 Intuition and diagrams: the example of \(p=1\), \(q=2\)
For arbitrary natural numbers \(p\le q\), the representation of \(M^{\mathcal {S}}\) ends up being fairly cumbersome and does not provide good intuition. To simplify the exposition we will derive the representation for one of the simplest cases—the pair \((p,q)=(1,2)\)—before presenting the construction in full generality.
It is best to begin with \(M:{\mathcal {P}}\rightarrow {\mathcal {P}}\) and then to construct \(M^{\mathcal {S}}\) using the isomorphism. When \(p=2\), the monodromy operator is a map \(M:{\mathcal {P}}([-2,0],{\mathbb {C}}^d)\rightarrow {\mathcal {P}}([-2,0],{\mathbb {C}}^d)\). Formally,
where \(t\mapsto y(t,\phi )\) is the solution of the IDDE (12)–(13) satisfying the initial condition \(y_0(\cdot ,\phi )=\phi \). For \(t\in [0,1]\), we can write
We can write this in a slightly more suggestive fashion. Define for \(\theta \in [-1,0)\) the functions
Also define \(y_1(0)=y(1)\). See Fig. 2 for a schematic diagram.
After translating onto the interval \([-1,0)\), the functions \(\phi |_{[-2,-1)}\) (red solid curve) and \(\phi |_{[-1,0)}\) (blue dashed curve) together with \(\phi (0)\) (magenta dot) are sufficient to specify the analytic initial condition \(\phi \). Up to translation, \(M^{\mathcal {S}}\) acts on this data by \(M^{\mathcal {S}}:(\text{ magenta } \text{ dot, } \text{ blue } \text{ curve, } \text{ red } \text{ curve})\mapsto (\text{ black } \text{ dot, } \text{ magenta } \text{ curve, } \text{ blue } \text{ curve}).\) Curves are for illustrative purposes only (e.g. the red solid curve one does not appear to represent an analytic function since it has a pole approaching the right endpoint) (Color figure online)
Performing a few changes of variables, we can write \(y_1\) as follows:
where \(A_1(s)=A(1+s)\), \(B_1(s)=B(1+s)\), and \(L_1[f](\theta )=\int _{-1}^\theta A_1(s)f(s)ds\) and \(L_2[f](\theta )=\int _{-1}^\theta B_1(s)f(s)ds\) are defined for \(\theta \in [-1,0)\). Note that \(L_1\) and \(L_2\) define bounded linear operators on \({\mathcal {A}}\) and also on \({\mathcal {A}}_0\). From (14)–(15), it is clear that each of \(y_1\) and \(y_1(0)\) can be expressed implicitly in terms of \(y_1\) and \(\phi _{-1}\). This will be helpful later.
We can now very suggestively write \(M\phi \) as follows:
From here, we can make use of the isomorphism \(m:{\mathcal {P}}\rightarrow {\mathcal {S}}={\mathbb {C}}^d\times {\mathcal {A}}^2\) so that we may instead work with the piecewise-analytic segments of length 2. To do this, we first write
where we have abused notation and identified \(\phi \in {\mathcal {P}}\) with \((\phi (0),\phi _0,\phi _{-1})\in {\mathcal {S}}\). By definition of the monodromy operator, \(y_1=e_2^\intercal M^{\mathcal {S}}(\phi )\) where \(e_2^\intercal \) denotes projection onto the second factor. From our previous derivation, it follows that \(M^{\mathcal {S}}(\phi )\) satisfies the implicit equation
This can be further factored as the sum of two linear maps: \(E:{\mathcal {S}}\rightarrow {\mathcal {S}}\) that only involves the initial condition, and the other one \(W:{\mathcal {S}}\rightarrow {\mathcal {S}}\) taking \(M^{\mathcal {S}}(\phi )\) as its input.
In this sense, we can think of E as the explicit part of the monodromy operator, and W as the implicit part. If \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is an isomorphism, we can write
Indeed, it turns out that \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is an isomorphism and the inverse \((I-W)^{-1}\) is bounded. We will not prove this now, since we will prove a more general result in the following section.
3.2 Segment representation of monodromy operator: the case \(p<q\)
First, identify \(\phi \in {\mathcal {P}}\) with \((\phi (0),\phi _{0},\dots ,\phi _{1-q})\in {\mathcal {S}}\) through the isomorphism m. Let \(t\mapsto y(t)\) denote the solution of (12)–(13) satisfying the initial condition \(y_0(\cdot )=\phi \). Define a finite sequence in \({\mathcal {A}}\) as follows:
By definition, we can reconstruct y from the sequence \(z_k\) for \(t\in [-q,p)\) via
so, we may identify \(y|_{[-q,p)}\) with this sequence. For \(t\in [k-1,k)\) for \(k=1,\dots ,p\), the function y satisfies the integral equation
We can make use of the sequence z and a change of variables to write this equivalently in the form
Remark that for \(1\ne k \le p\), we have
because \(k-1\notin p{\mathbb {Z}}\), so y is continuous at \(t=k-1\). This justifies the use of the left limit above. Since \(p<q\), each of the terms \(z_{k-q}\) in (16) can be replaced with \(\phi _{k-q}\). The result is
Also, y(p) is given as follows:
Once again, \(z_{p-q}=\phi _{p-q}\). Similarly, \(p<q\) implies \(z(p-q)=\phi _{p-q+1}(-1)\). We can therefore equivalently express (18) as
In the space \({\mathcal {S}}={\mathbb {C}}^d\times {\mathcal {A}}^q\) we have the representation
of the action of the monodromy operator on the element \(\phi \).
Let us define some linear maps to make the expressions (17) and (19) a bit more compact. Define for \(k=1,\dots ,p\) the maps \(E_k:{\mathcal {S}}\rightarrow {\mathcal {A}}\), \(E_p^0:{\mathcal {S}}\rightarrow {\mathbb {C}}^d\), \(W_k:{\mathcal {S}}\rightarrow {\mathcal {A}}\), \(W_p^0:{\mathcal {S}}\rightarrow {\mathbb {C}}^d\) as follows. For \(f=(f(0),f_0,\dots ,f_{1-q})\in {\mathcal {S}}\),
Remark 3.2.1
Observe that if \(k=p=1\) then \(W_k[f](\theta )\) is defined by the first line of (23), so it is of no consequence that \(f=(f(0),f_0)\) does not contain the element \(f_{k-p-1}=f_{-1}\) needed to define the second line. We have also taken the liberty to define \(E_p^0\) when \(q=p\) at this time as well; the main difference is that when \(p=q\), we have \(z(p-q)=z(0)=\phi (0)\) and the latter can not not be identified with \(\phi _{p-q+1}(-1)=\phi _1(-1)\) since this is not part of the initial condition vector \((\phi (0),\phi _0,\dots ,\phi _{1-q})\).
Remark 3.2.2
\(E_p^0[f]\) and \(W_p^0[f]\) can be written more succinctly as
where \({\mathbf {f}}\) is one of \(f_{p-q+1}(-1)\) or f(0), depending on whether or not \(p=q\).
With these maps defined, we can write
for \(k=1,\dots ,p\). In view of (20), it makes sense to define a pair of operators \(E:{\mathcal {S}}\rightarrow {\mathcal {S}}\) and \(W:{\mathcal {S}}\rightarrow {\mathcal {S}}\) as follows:
where there are \(q-p\) zeroes at the end of Wf. Finally, using (20), (25) and (26), we can write the monodromy operator on the piecewise-analytic segments of length q in the explicit-implicit form
We will now characterize the invertibility of the bounded linear operator \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) with the goal of providing a more explicit representation of \(M^{\mathcal {S}}\). The main result is Theorem 3.2.1. It is preceded by three short lemmas, the first of which is straightforward and will not be proven.
Lemma 3.2.1
Denote \(X=\{\phi :[-1,0)\rightarrow {\mathbb {C}}^d \text{ continuous, } \text{ such } \text{ that } \lim _{t\rightarrow 0^-}\phi (t) \text{ exists }\},\) and let \(\tilde{{\mathcal {S}}}={\mathbb {C}}^d\times X^q\). The operator \(W:{\mathcal {S}}\rightarrow {\mathcal {S}}\) is the restriction of \({\tilde{W}}:\tilde{{\mathcal {S}}}\rightarrow \tilde{{\mathcal {S}}}\) to \({\mathcal {S}}\), with
where each of \(W_k\) and \(W_p^0\) are defined as in (23) and (24). \(\tilde{{\mathcal {S}}}\) is a Banach space with norm \(||(f(0),f_0,\dots ,f_{1-q})||_{\tilde{{\mathcal {S}}}}=\max \{|f(0)|,||f_{0}||,\dots ,||f_{1-q}||,\}\) and \(||\cdot ||\) either denotes some norm on \({\mathbb {C}}^d\) or the induced supremum norm.
Lemma 3.2.2
\((I-{\tilde{W}}):\tilde{{\mathcal {S}}}\rightarrow \tilde{{\mathcal {S}}}\) is injective. Also, \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is injective.
Proof
Let \(f\in \tilde{{\mathcal {S}}}\) and suppose \((I-{\tilde{W}})f=0\). Since the trailing \(q-p\) elements of \({\tilde{W}}(f)\) are zero, It follows that \((f_{-p},\dots ,f_{1-q})=0.\) We will prove now that \(f_{-p+k}=0\) for \(k=0,\dots ,p\) by way of induction. The base case already proven, suppose \(f_{-p+k}=0\) for some \(k\in \{0,\dots ,p\}\). Then, \(h=f_{-p+k+1}\) satisfies
for \(\theta \in [-1,0)\). By Gronwall’s inequality, \(h\equiv 0\). By induction, we have \(f_0=f_{-1}=\cdots =f_{1-p}=0\). Since \(f(0)=W_p^0[(f(0),0,\dots ,0)]=0\), we conclude that \(f=0\), so \((I-{\tilde{W}})\) is injective. The same argument proves that \((I-W)\) is injective. \(\square \)
Lemma 3.2.3
\((I-{\tilde{W}}):\tilde{{\mathcal {S}}}\rightarrow \tilde{{\mathcal {S}}}\) is surjective. Also, \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is surjective.
Proof
Let \(\psi \in \tilde{{\mathcal {S}}}\). We will construct \(f\in \tilde{{\mathcal {S}}}\) such that \((I-{\tilde{W}})f=\psi \). To begin, set \((f_{-p},\dots ,f_{1-q})=(\psi _{-p},\dots ,\psi _{1-q})\). Next, given \(f_{-p+k}\) for \(k\in \{0,\dots ,p-1\}\), let \(h=f_{-p+k+1}\in X\) denote the solution of the Volterra integral equation
A straightforward inductive argument demonstrates that each of \(f_{-p+1},\dots ,f_{0}\) exists, is unique and is an element of X. Finally, set \(f(0) = W_p^0[(0,f_0,\dots ,f_{1-q})]-\psi (0)\). By construction, \((I-{\tilde{W}})f=\psi \). If \(\psi \in {\mathcal {S}}\), a small modification of this proof shows that \(h\in {\mathcal {A}}\) and, consequently, \(f\in {\mathcal {S}}\), thereby proving \((I-W)\) is surjective. \(\square \)
Theorem 3.2.1
With E and W defined by (26), \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is an isomorphism, \((I-W)^{-1}\) is bounded, and \(M^{\mathcal {S}}=(I-W)^{-1}E\). We refer to E as the explicit part and W the implicit part of \(M^{\mathcal {S}}\).
Proof
By Lemmas 3.2.2 and 3.2.3, \((I-{\tilde{W}}):\tilde{{\mathcal {S}}}\rightarrow \tilde{{\mathcal {S}}}\) is a bijection. \((I-{\tilde{W}})\) is clearly bounded, and as \(\tilde{{\mathcal {S}}}\) is a Banach space the bounded inverse theorem guarantees \((I-{\tilde{W}})^{-1}\) exists and is bounded. Similarly, \((I-W)^{-1}\) exists, and by Lemma 3.2.1, W is the restriction of \({\tilde{W}}\), from which it follows that \((I-W)^{-1}\) is also bounded. Solving for \(M^{\mathcal {S}}\) in (27), the theorem is proven. \(\square \)
3.3 Segment representation of monodromy operator: the boundary case \(p=q\)
First suppose \(p=q=1\); we will deal with the other case later. With the same notation as the previous section, we have \(M^{{\mathcal {S}}}(\phi )=(y(1),z_1)\) with
We can perform an analogous decomposition. With the same definitions of \(E_1\), \(E_1^0\), \(W_1\) and \(W_1^0\) from (21)–(24), we can write \(M^{\mathcal {S}}(\phi )=E(\phi )+W(M^{\mathcal {S}}\phi )\) with
Theorem 3.2.1 then holds verbatim with the appropriate definitions of E and W. The proof is omitted.
Theorem 3.3.1
With E and W defined by (30), \((I-W):{\mathcal {S}}\rightarrow {\mathcal {S}}\) is an isomorphism, \((I-W)^{-1}\) is bounded, and \(M^{\mathcal {S}}=(I-W)^{-1}E\). We refer to E as the explicit part and W the implicit part of \(M^{\mathcal {S}}\).
Remark 3.3.1
If \(p=q\ne 1\), the changes in the definition of the operators E and W are not dramatic. We get instead
4 Chebyshev series and validated numerics framework for the monodromy operator
In Sect. 3 we represented the monodromy operator on the space \({\mathcal {S}}\) of piecewise-analytic segments of length q in terms of integral operators that we referred to as the explicit and implicit part(s) of \(M^{\mathcal {S}}\). The next step is to replace the abstract space \({\mathcal {S}}\) with a concrete space that is more amenable to numerical computation and determine how \(M^{\mathcal {S}}\) acts on this space.
4.1 Banach spaces of infinite sequences and Chebyshev series
Let \(||\cdot ||\) be a norm on \({\mathbb {C}}^d\). Let \(\nu >1\). For a sequence \(a=\{a_n:n\in {\mathbb {N}}\}\subset {\mathbb {C}}^d\), define a weighted norm \(||\cdot ||_\nu \) by
We then define the space \(\ell _\nu ^1\) by
Equipped with the norm \(||\cdot ||_\nu \), \(\ell _\nu ^1\) is a Banach space. Next, define \(X_\nu ={\mathbb {C}}^d\times (\ell _\nu ^1)^q\) and let it be equipped with the norm \(||\cdot ||\) defined by
Then, \((X_\nu ,||\cdot ||)\) is a Banach space. Define also
where \(||A||_\nu =\sum _{n\ge 0}||A||\nu ^n\) and the norm inside the summation is the operator norm on \({\mathbb {C}}^{d\times d}\) induced by \(||\cdot ||\). Finally, to the space \(B(X_\nu )\) of bounded linear operators on \(X_\nu \), we let \(||\cdot ||_{B(X_\nu )}\) denote the induced operator norm.
The following result will be helpful later; its proof is simple and omitted.
Proposition 4.1.1
For \(x\in \ell _\nu ^1\) and \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\), define the sequence \(\{(Y*x)_n\}_{n\ge 0}\) by
Then \(Y*x\in \ell ^1_\nu \) and \(||Y*x||_\nu \le \left( 2||Y||_\nu -||Y_0||\right) \left( 2||x||_\nu -||x_0||\right) \le 4||Y||_\nu ||x||_\nu \).
The following lemma and corollary follow from Propositions 2.4.1, 2.4.2, Corollary 2.4.2, and the linear scaling \(\theta \in [-1,0]\rightarrow [-1,1]\) via \(\theta = \frac{1}{2}\left( \omega -1\right) .\) The proof is simple and omitted.
Lemma 4.1.1
Let \(\nu >1\). For \(g_j=\{g_{j,n}\}_{n\ge 0}\), denote \({\mathcal {E}}_\nu (x,g_0,\dots ,g_{1-q})=(x,f_0,\dots ,f_{1-q})\) with
and \(T_n\) the nth Chebyshev polynomial of the first kind. This expression induces a well-defined, bounded linear map \({\mathcal {E}}_\nu :X_\nu \rightarrow {\mathcal {S}}\). This map is one-to-one onto its range, and so denoting \({\mathcal {S}}_\nu ={\mathcal {E}}(X_\nu )\), the map \({\mathcal {E}}_\nu :X_\nu \rightarrow {\mathcal {S}}_\nu \) is an isomorphism.
Corollary 4.1.1
There exists some \(\nu ^*>1\) such that if \(\phi \) is an eigenvector of \(M^{\mathcal {S}}\) with nonzero eigenvalue, then \(\phi \in {\mathcal {S}}_\nu \) for all \(\nu \in (1,\nu ^*)\). More precisely, let \(\theta (\omega )=\frac{1}{2}(\omega -1)\) and write \(\omega \mapsto Y_k(\theta (\omega ))\) for \(Y\in \{A,B\}\) as a Chebyshev series
for matrix sequences \(\{Y_{k,n}\}_{n\ge 0}\subset {\mathbb {R}}^{d\times d}\), where \(Y_k(s):=Y(k+s)\) for \(s\in [-1,0]\). Then
Remark 4.1.1
Under Assumption A1.2, the Chebyshev series of \(A_k\) have coefficients in \(\ell _\nu ^1({\mathbb {R}}^{d\times d})\) for some \(\nu =\nu _k^A>1\) for each k, and those of \(B_k\) are in \(\ell _\nu ^1({\mathbb {R}}^{d\times d})\) for some \(\nu =\nu _k^B>1\). By the periodicity Assumption A.1, we have \(\nu ^*=\min \{\nu _0^A,\dots ,\nu _{p-1}^A,\nu _0^B,\dots ,\nu _{p-1}^B\}\).
From the above lemma and corollary, it makes sense to consider the (formal) linear operator \(M^\nu :X_\nu \rightarrow X_\nu \) defined by
If \(M^{\mathcal {S}}({\mathcal {S}}_\nu )\subseteq {\mathcal {S}}_\nu \), this expression is well-defined and, in particular, we will immediately have from Corollaries 2.4.2, 2.4.3 and Corollary 4.1.1 the spectral equivalence \(\sigma (M^\nu ){\setminus }\{0\}=\sigma (M^{{\mathcal {S}}}){\setminus }\{0\}\). Since \(M^\nu \) is an operator on sequence spaces, it is amenable to approximation, truncation and other constructs. In the following section we will show that this operator is indeed well-defined.
4.2 Representation of \(M^\nu \) on Chebyshev series in \(X_\nu \) coefficients
To represent \(M^\nu \) on the space \(X_\nu \), we will need to settle on a convention for the Chebyshev series coefficients of the matrix-valued functions \(A_k\) and \(B_k\) needed to define the explicit and implicit parts of \(M^{\mathcal {S}}\)—for example, in equations (21)–(24). A brief reminder: \(A_k(\theta )=A(k+\theta )\) and \(B_k(\theta )=B(k+\theta )\). Recall that by Assumption 1, A and B are piecewise-analytic with respect to \((k,k+1)\) for the integers k. This means for each integer k there exists \({\tilde{A}}_k:U_k^A\rightarrow {\mathbb {C}}^{d\times d}\) and \({\tilde{B}}_k:U_k^B\rightarrow {\mathbb {C}}^{d\times d}\) analytic such that \(A_k={\tilde{A}}_k|_{[-1,0]}\) and \(B_k={\tilde{B}}_k|_{[-1,0]}\), for some open neighbourhoods \(U_k^A\) and \(U_k^B\) of \([-1,0]\). For \(\omega \in [-1,1]\), define
We will write our (uniformly convergent) Chebyshev series for \({\hat{A}}_k\) and \({\hat{B}}_k\) as follows:
By construction, the entries of the matrix sequences \(\{{\hat{A}}_{k,n}\}_{n\ge 0}\) and \(\{{\hat{B}}_{k,n}\}_{n\ge 0}\) are elements of \(\ell _\nu ^1({\mathbb {C}}^{d\times d})\) for any \(\nu \in (1,\nu ^*)\), where \(\nu ^*\) is the constant guaranteed by Corollary 4.1.1 (or more concretely from Remark 4.1.1). Similarly, if \({\hat{f}}_k(\omega ) = f_k\left( \frac{1}{2}(\omega -1)\right) \) for \(f_k:[-1,0]\rightarrow {\mathbb {C}}^d\) and some \(k\in \{1-q,\dots ,-1,0\}\), we will write
Remark 4.2.1
From this point onward, unless explicitly stated, it will be assumed that \(\nu \in (1,\nu ^*)\).
Recall that if \(u_k(t) = u_{k,0} + 2\sum _{n\ge 1}u_{k,n}T_n(t)\) for \(k=1,2\) are two Chebyshev series such that the product \(u_1(t)u_2(t)\) is well-defined (i.e. \(u_1\) is a \(a\times b\) matrix and \(u_2\) is a \(b\times c\) matrix), then their product has the Chebyshev series
with \(u_{k,-m}=u_{k,m}\). These can therefore be written in terms of the convolution:
where here the interpretation is we are identifying \(u_k\) with its sequence of Chebyshev cofficients. Using this property and the fact that \(T_0=1\), the equations
in addition to \(T_n(-1)=(-1)^n\), we can derive formulas for the action of the explicit and implicit parts of \(M^\nu \) in the space \(X^\nu \), as follows. Let \(f=(f(0),f_0,\dots ,f_{1-q})\in {\mathcal {S}}_\nu \), so we can write each \({\hat{f}}_k\) as in (32). This also ensures that \(f = {\mathcal {E}}_\nu (f(0),\{{\hat{f}}_{0,n}\}_{n\ge 0},\dots ,\{{\hat{f}}_{1-q,n}\}_{n\ge 0})\). Then, for \(k\ne 1\),
where \(\theta = \frac{1}{2}(\omega -1)\). When \(k=1\), we need to add f(0) to the right-hand side of the above. Since \(f(0)=f(0)T_0(\omega )\), the modification is straightforward. The induced map \({\hat{E}}_k:X_\nu \rightarrow \ell ^1_\nu \) obtained by applying \({\mathcal {E}}_\nu ^{-1}\) to the above is then given in indexed form as follows:
for \({\hat{f}} = (f(0),\{{\hat{f}}_{0,k}\}_{k\ge 0},\dots ,\{{\hat{f}}_{1-q,k}\}_{k\ge 0})\in X_\nu \). Notice that we have incorporated the inclusion of \(f(0)T_0(\omega )\) when \(k=1\) by way of the indicator function: \(\mathbb {1}_{0}(t)=1\) if and only if \(t=0\), otherwise it is zero. Making use of Proposition 4.1.1, we see that \({\hat{E}}_k\) is well-defined as a map \({\hat{E}}_k:X_\nu \rightarrow \ell _\nu ^1\).
We can perform a similar derivation for the map \(E_p^0:{\mathcal {S}}\rightarrow {\mathbb {C}}^d\). Since \(E_p^0[f]=(I+C_1)E_p[f](0) + C_2{\mathbf {f}}\)—see Remark 3.2.2—the observation that \(\theta =0\) precisely when \(\omega =1\) gives
for the (well-defined) linear map \({\hat{E}}_p^0:X_\nu \rightarrow {\mathbb {C}}^d\). Note that we have used the identities \(T_n(-1)=(-1)^n\) and \(T_n(1)=1\).
The differences between the implicit parts \(W_k\) and \(W_p^0\) and the explicit parts \(E_k\) and \(E_p^0\) are mostly symbolic (the main difference being the appearance of \(f_{k-p-1}(0^-)\) rather than f(0), the former which is easily managed at the Chebyshev level), and the derivation of the induced maps \({\hat{W}}_k:X_\nu \rightarrow \ell ^1_\nu \) and \({\hat{W}}_p^0:X_\nu \rightarrow {\mathbb {C}}^d\) are nearly identical. They are well-defined and can be expressed as
Next, we need to form the implicit and explicit part functions acting on \(X_\nu \). This is accomplished by replacing each of the relevant maps \(E_k\), \(E_p^0\), \(W_k\) and \(W_p^0\) on \({\mathcal {S}}\) with their associated “hat” counterparts on \(X_\nu \). To spell this out explicitly, it is best to separate the two relevant cases.
4.2.1 \(p<q\)
Define \({\hat{E}}:X_\nu \rightarrow X_\nu \) and \({\hat{W}}:X_\nu \rightarrow X_\nu \) by
where there are \(q-p\) zeroes at the end of \({\hat{W}}{\hat{f}}\). Then \((I-{\hat{W}}):X_\nu \rightarrow X_\nu \) is invertible and \(M^\nu =(I-{\hat{W}})^{-1}{\hat{E}}\) is the representation of the restriction of \(M^{\mathcal {S}}\) to \({\mathcal {S}}_\nu \) in the space \(X_\nu \).
4.2.2 \(p=q\)
If \(p=q=1\), define \({\hat{E}}:X_\nu \rightarrow X_\nu \) and \({\hat{W}}:X_\nu \rightarrow X_\nu \) by
\((I-{\hat{W}}):X_\nu \rightarrow X_\nu \) is invertible and \(M^\nu =(I-{\hat{W}})^{-1}{\hat{E}}\) is the representation of the restriction of \(M^{\mathcal {S}}\) to \({\mathcal {S}}_\nu \) in the space \(X_\nu \).
Remark 4.2.2
If \(p=q\ne 1\), Remark 3.3.1 extends analogously to the operator \({\hat{E}}\) and \({\hat{W}}\).
4.3 The validated numerics setup
At this stage we will drop all of the hats and identify the maps \(E_k\), \(W_k\), \(E_p^0\) and \(W_p^0\) with their representations on \(X_\nu \). The same thing will be done with the matrix-valued functions \(A_k\) and \(B_k\). Moreover, we will identify each of \(A_k\) and \(B_k\) with their associated sequence of Chebyshev coefficients. This should not provide too much confusion. Finally, we will drop the superscripts of \(\nu \) on M.
In view of applications, we should always keep in mind that not all Chebyshev modes of \(A_k\) and \(B_k\) might be known, and they may be subject to error. This could be the case if, for example, they are the matrices associated to a linearization at a periodic solution, the latter which is obtained by a computer-assisted proof. Additionally, any computations that are done on a computer and make use of specific Chebyshev modes will need to take into account some truncation even if the coefficients of every mode are available analytically. To this end, given a matrix sequence \(Y\in \ell _\nu ^1({\mathbb {R}}^{d\times d})\), define the \(N_1\)-mode truncation \(Y^{N_1}\) as follows:
Then, define \(M_{N_1}:X_\nu \rightarrow X_\nu \) to be the operator \(M^\nu \) as defined in Sect. 4.2, except that \(A_k\) and \(B_k\) for \(k=1,\dots ,p\) are replaced with the \(N_1\)-mode truncations \(A_k^{N_1}\) and \(B_k^{N_1}\).
The next level of approximation comes from the need to represent \(M_{N_1}\) as a finite matrix operator. As we will see, the specific way this is done will depend somewhat on the relationship between p and q. In the simplest case (\(p=q=1\)), we will truncate the domain and range of each of the implicit and explicit parts at some prescribed number \(N_2\) of modes, and use these to define a mode-truncated version of \(M_{N_1}\) that can be represented by a matrix up to an appropriate embedding. In all cases, the symbol \(M_{N_1,N_2}\) will be used to refer to the truncation and this operator will always be compact (or eventually compact).
To state some technical requirements concerning the truncated operator \(M_{N_1,N_2}\), we will need to specify two subspaces of \(X_\nu \). Define
\(X_\nu \) can be expressed as the internal direct sum \(X_\nu =X_\nu ^{N_2}\oplus X_\nu ^\infty \) for any \(N_2\ge 0\).
Our objective is to use information concerning the eigenvalues of \(M_{N_1,N_2}\) to infer properties of the eigenvalues of \(M:X_\nu \rightarrow X_\nu \), the representation of the monodromy operator on \(X_\nu \). With a view toward stability and so-called generalized Morse indices, we adapt a result attributed to Lessard and Mireles-James [21]. The main idea is captured by the following lemma.
Lemma 4.3.1
(Generalized Morse index validation) Let \(r>0\) and let \(M_{N_1,N_2}\) be a bounded operator on \(X_\nu \) with with the following properties.
-
\(M_{N_1,N_2}\) has only finitely many eigenvalues in the complement of the closed disc \(D_r\) in the \({\mathbb {C}}\).
-
\(M_{N_1,N_2}\) has no eigenvalues on the circle of radius r in \({\mathbb {C}}\).
-
Each of \(X_\nu ^{N_2}\) and \(X_\nu ^\infty \) are invariant subspaces of \(M_{N_1,N_2}\): that is, \(M_{N_1,N_2}(X_\nu ^{N_2})\subseteq X_\nu ^{N_2}\) and \(M_{N_1,N_2}(X_\nu ^\infty )\subseteq X_\nu ^\infty \).
Suppose there are positive constants \(c_1,c_2\) and \(c_3\) such that
and \(c_1c_2c_3<1\). Then, \(M_{N_1,N_2}\) and M have the same number of eigenvalues in the complement of the open ball of radius r.
Proof
By construction, \(M_{N_1,N_2}\) has only finitely many non-zero eigenvalues in the complement of \(D_r\). Since the monodromy operator is eventually compact, the representation \(M\in B(X_\nu )\) has only finitely-many eigenvalues in the complement of \(D_r\). Consider the straight-line homotopy
Since \(H:[0,1]\rightarrow B(X_\nu )\) is continuous, M and \(M_{N_1,N_2}\) can only have a different number of eigenvalues in the complement of \(D_r\) if there is some \(s\in [0,1]\) and \(\theta \in [0,2\pi ]\) such that \(re^{i\theta }\) is an eigenvalue of H(s). This follows by the continuity of a finite eigensystem of a continuous family of bounded linear operators [19]. It suffices to show \(H(s)-re^{i\theta }I\) is boundedly invertible for all \(s\in [0,1]\) and \(\theta \in [0,2\pi ]\).
Define \(N(\theta )=M_{N_1,N_2}-re^{i\theta }I\). From the assumptions of the lemma, \(N(\theta )\) satisfies the estimate \(||N(\theta )^{-1}||_{B(X_\nu )}\le c_1\).
Next, observe that
From the previous result, it remains to show that the term in curly braces boundedly is invertible. To accomplish this, observe that
from which it follows that \(||M_{N_1,N_2}-M||_{B(X_\nu )}\le c_2c_3\). Thus, \(||sN(\theta )^{-1}(M_{N_1,N_2}-M)||_{B(X_\nu )}\le c_1c_2c_3<1\), so by the Neumann series theorem, the term in the curly braces is invertible. It follows that \(H(s)-re^{i\theta }I\) is invertible with inverse satisfying
This would complete the proof if we were only interested in the eigenvalues in the complement of the closed disc of radius r. To extend to the complement of the open ball of radius r, observe that the inequality \(||sN(\theta )^{-1}(M_{N_1,N_2}-M)||_{B(X_\nu )}\le c_1c_2c_3<1\) is strict, implying that the conclusion is robust with respect to the radius. \(\square \)
The previous lemma exploits the fact that each of M and (by assumption) \(M_{N_1,N_2}\) have only finitely many eigenvalues in the complement of \(D_r\) for any finite \(r>0\). However, this is not the only set in which the number of eigenvalues of M must be finite. In fact, this is true for any set—open or closed—that is bounded away from zero, since M is compact (or eventually compact). If the goal is to validate a specific eigenvalue of \(M_{N_1,N_2}\) rather than a generalized Morse index, one can accomplish this using a very similar setup.
Lemma 4.3.2
(Compact eigenvalue validation) Let \(U\subset {\mathbb {C}}\) be compact, bounded away from zero, path-connected and have a continuous boundary. Let \(M_{N_1,N_2}\) be a bounded operator on \(X_\nu \) with with the following properties.
-
\(M_{N_1,N_2}\) has only finitely many eigenvalues in U.
-
\(M_{N_1,N_2}\) has no eigenvalues on the boundary of U (denoted \(\partial U\)).
-
Each of \(X_\nu ^{N_2}\) and \(X_\nu ^\infty \) are invariant subspaces of \(M_{N_1,N_2}\).
Suppose there are positive constants \(c_1,c_2\) and \(c_3\) such that
and \(c_1c_2c_3<1\). Then, \(M_{N_1,N_2}\) and M have the same number of eigenvalues in U.
Proof
By assumption, \(M_{N_1,N_2}\) has only finitely-many eigenvalues in U, and the same is true of M due to compactness (or eventual compactness) and the assumption U is bounded away from zero. Let \(z:[0,1]\rightarrow \partial U\) be a parameterization of the boundary. If H is denotes the straight-line homotopy (40), to prove the theorem it suffices to show that \(H(s)-z(t)I\) is boundedly invertible for all \((s,t)\in [0,1]\times [0,1]\), for then no eigenvalue of H(s) crosses the boundary \(\partial U\) and the continuity of a finite eigensystem of a family of bounded linear operators implies that M and \(M_{N_1,N_2}\) must have the same number of eigenvalues inside U.
Define \(N(t)=M_{N_1,N_2}-z(t)I\). By assumption, \(||N(t)^{-1}||_{B(X_\nu )}\le c_1\). Also,
It remains to show that the term in the curly braces is boundedly invertible. By the same argument as in the proof of Lemma 4.3.1, we know that \(||M_{N_1,N_2}-M||\le c_2c_3\), so \(||sN(t)^{-1}(M_{N_1,N_2}-M)||_{B(X_\nu )}\le c_1c_2c_3<1\) for all \((s,t)\in [0,1]^2\). It follows that the term in curly braces is boundedly invertible. This completes the proof. \(\square \)
4.3.1 Interpretation of the bounds \(c_1\), \(c_2\) and \(c_3\)
\(c_1\) is an upper bound for \(\sup _{z\in \partial U}||(M_{N_1,N_2}-zI)^{-1}||_{B(X_\nu )}\). If \(M_{N_1,N_2}\rightarrow M\) as \((N_1,N_2)\rightarrow \infty \), it can be interpreted as an asymptotic proxy for the distance between the spectrum of M and the boundary of the set U, whatever this happens to be. \(c_3\) is a proxy for numerical defect: if \(\Delta M:=M_{N_1,N_2}-M\) satisfies \(||\Delta M||_{B(X_\nu )}=\epsilon \), then
As for \(c_2\), it is a technical bound on the inverse \((I-W)^{-1}\) and does not lend itself to interpretation relative to the discretization \(M_{N_1,N_2}\). The only connection it has is that we always have the estimate
so \(c_2\) contributes to the upper bound of the discretization error \(||\Delta M||_{B(X_\nu )}\).
4.3.2 Candidates sets for compact eigenvalue validation
There are two fairly natural candidates for compact sets on which one might want to validate eigenvalues. The most obvious is simply a closed ball \(D_r(\lambda ):=\overline{B_r(\lambda )}\) centered at an approximate eigenvalue \(\lambda \) with radius \(r\in (0,|\lambda |)\). We have \(b(\cdot ,\lambda ,r):[0,2\pi ]\rightarrow \partial D_r(\lambda )\) defined by
is a continuous parameterization of the boundary. An alternative to such a closed ball is the following.
Definition 4.3.1
(Radial sector) Let \(\lambda \in {\mathbb {C}}\). The radial sector centered at \(\lambda \) with width \(r\in (0,|\lambda |)\) and sweep \(\omega \in (0,\pi )\) is the set
We will refer to such a set without qualification as being a radial sector centered at \(\lambda \).
A radial sector is simply a translated rectangle in polar coordinates, parameterized by its half-width and half-length. Having two parameters (width and sweep, versus only a radius) allows for a finer level of control. Additionally, as we will see later (see Remark 6.1.2), the tail bounds (i.e. on \(B(X_\nu ^\infty )\)) for \(c_1\) are generally tighter for a radial sector (of width r) than they are for a closed ball (of radius r) centered at a given \(\lambda \). Also, though the associated boundary parameterization is only piecewise continuous, it is smooth on each piece and this poses no problem for the \(c_1\) bound computation; see Sect. 7.1. The function \(z(\cdot ,\lambda ,r,\omega ):[0,4]\rightarrow \partial R_\lambda (r,\omega )\) given by
is a parameterization of the boundary. For the purposes of later validation and enclosure, the following proposition concerning inclusions of balls inside radial sectors as well as inclusion characterizations of two radial sectors will be of use. Its proof is a straightforward geometry exercise.
Proposition 4.3.1
The ball \(B_r(x)\) with \(r<|x|\) satisfies \(B_r(x)\subset R_x\left( r,2\arcsin \left( \frac{r}{2|x|}\right) \right) \). Also, we have \(R_{\lambda _1}(r_1,\omega )\subseteq R_{\lambda _2}(r_2,\omega _2)\) if and only if the following are satisfied:
4.4 Infinite matrix representation of implicit and explicit part maps
Each of the maps \(E_k\), \(W_k\), \(E_p^0\) and \(W_p^0\) with their representations on \(X_\nu \) are linear with respect to two pieces of datum: the input \(f=(f(0),f_0,\dots ,f_{1-q})\) and a convolution term \({\mathbf {X}}_k*f_m\), where \({\mathbf {X}}_k\) is one of \({\hat{A}}_k\) or \({\hat{B}}_k\), and \(m\in \{0,\dots ,1-q\}\) is some index. It will be beneficial later to have these maps split into those parts that are linear in f and those that are linear in \({\mathbf {X}}_k*f_m\). One can verify by inspection that the following representations are valid:
where \(H_1\) and \(H_2\) are infinite matrices defined inductively by
and the remaining terms are
Note that in (49), the final (rightmost) displayed column has index nth, the final (bottom) displayed row is index nth as well, and similarly in (50) the final displayed entry has index nth entry, where indexing is from zero so that the first rows and columns have index zero.
For convenience, we will write \(H_1\) as the sum
where \((H_1^0x)_0=(H_1x)_0\) and \((H_1^0x)_j=0\) for \(j>0\) (i.e. \(H_1^0\) is the first row of \(H_1\) continuously embedded as an operator on \(\ell _\nu ^1\)), T is Toeplitz and D is a diagonal operator defined as follows:
where the \(\frac{1}{4n}\) occurs at the (n, n) diagonal index (again with zero-indexing).
We conclude this section with an observation concerning an elementwise product operation. First, concerning the maps \(H_2\) and S. Each of these commute with \(d\times d\) matrix multiplication in the following sense. If \(M\in {\mathbb {C}}^{d\times d}\), \(h\in \ell _\nu ^1\) and we define \((M\odot h)_n=Mh_n\) to be the “elementwise (block) product”, then
Next, if \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\) and \(h\in \ell _\nu ^1\), we have the following identity concerning “associativity” of the elementwise product with convolution:
provided we overload the notation and define \((M\odot Y)_n=MY_n\).
5 A dictionary of norm bounds
In the sections that follow, we will be computing formulas for the \(c_2\) and \(c_3\) bounds of Lemma 4.3.1. Especially once we consider the case \(1<p<q\) for the period and delay, the individual linear maps that we need to bound (in norm) to get tight estimates for \(c_2\) and \(c_3\) become quite numerous and the analysis can at times be technical. To facilitate the presentation of later proofs, in this section we will list and prove a collection of norm bounds for such maps. However, as some bounds are used very frequently and it is easier to locate them from a table, we place these bounds (and their proofs) in “Appendix A”.
There are some common elements between the computation of the bounds, so at this stage we introduce some additional notation. For \(N>0\), define \(\pi ^N:\ell _\nu ^1\rightarrow \ell _\nu ^1\) by \([\pi ^Nh]_n=h_n\) if \(n\le N\), and zero otherwise. Then, define \(\pi _N^\infty :\ell _\nu ^1\rightarrow \ell _\nu ^1\) to be the complementary projector \(\pi _N^\infty h = h - \pi ^Nh\). For \(h\in \ell _\nu ^1\), the decomposition \(h=h^N+h^\infty \) will always mean \(h^N=\pi ^N h\) and \(h^\infty =\pi _N^\infty h\). Analogously, if \(\phi \in X_\nu \) and \(N\ge 0\), we will write \(\phi =\phi ^N + \phi ^\infty \) for \(\phi ^N\in X_\nu ^N\) and \(\phi ^\infty \in X_\nu ^\infty \). Also, because \(\ell _\nu ^1\) admits the internal direct sum \(\ell _\nu ^1=\pi ^{N}(\ell _\nu ^1)\oplus \pi ^\infty _{N}(\ell _\nu ^1)\) and \(h=h^N+h^\infty \) satisfies \(||h||_\nu = ||h^N||_\nu + ||h^\infty ||_\nu \), any linear operator \(L:\ell _\nu ^1\rightarrow \ell _\nu ^1\) satisfies
where the suprema are taken over \(h^N\in \pi ^N(\ell _\nu ^1)\) and \(h^\infty \in \pi ^\infty _N(\ell _\nu ^1)\). Similarly, for \(L_0:\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) we have
Analogous bounds hold for a linear operator \({\mathcal {L}}:X_\nu \rightarrow X_\nu \). First, write
We can decompose by linearity over the direct sum:
for \(j=1-q,\dots ,0\). Then each \(L_j:X_\nu \rightarrow \ell _\nu ^1\) satisfies
where \(L_j(x(0),0)\equiv L_j(x(0),0,\dots ,0)\), and \(L_j(0,x_k)\equiv L_j(0,\dots ,x_k,\dots )\) has zeros except at the k index. It then follows by definition of the norm on \(X_\nu \) that
Conversely, if the right-hand side of (60) is finite then \({\mathcal {L}}\) is bounded.
In the following sections we will be playing somewhat fast and loose with the notation involving our convolutions. The primary abuse of notation will be as follows. If \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\) and \(L\in B(\ell _\nu ^1)\), we define the operator \(Y*L\in B(\ell _\nu ^1)\) by \(h\mapsto Y*L(h):=Y*(Lh)\). For example, often L will be a projection operator (although there are exceptions). Finally, the following equivalent norm on \(\ell _\nu ^1({\mathbb {C}}^{d\times d})\) will be beneficial later. For \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\), define \(||Y||_\omega = 2||Y||_\nu -||Y_0||\). This implies the convenient formula \(||(Y*h)||_\nu \le 2||Y||_\omega ||h||_\nu \) whenever \(h\in \ell ^1_\nu \); see Proposition 4.1.1.
A brief warning before we proceed. The symbol I will always denote an the identity operator, though on which space it acts will sometimes be left implicit by context. When we wish to make the domain X explicit, we will write \(I_X\).
5.1 The operators Q and \({\widetilde{Q}}\)
Many of the bounds of this section will involve the following pair of linear operators. They appear frequently in the “block operator” representation of implicit part operators. Let \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\) and \(N_2,N_1\in {\mathbb {N}}\).
Whenever these symbols appear, \(N_1\) and \(N_2\) will always be fixed a priori so they can be used without ambiguity. We will sometimes also write \({\widetilde{Q}}^{-1}(Y^{N_1})\) whenever we want to make the dependence on \(N_1\) explicit.
Remark 5.1.1
It is a simple consequence of Theorem 3.2.1 that \({\widetilde{Q}}^{-1}(Y)\) exists and is bounded.
Lemma 5.1.1
\(||{\widetilde{Q}}^{-1}(Y)||_{B(\ell _\nu ^1)}\le \max \{||{\widetilde{Q}}^{-1}(Y)\pi ^{N_2}||_{B(\ell _\nu ^1)},1\}\).
Proof
By construction, \(\widetilde{Q}^{-1}\) acts as the identity on \(\pi _{N_2}^\infty (\ell _\nu ^1)\). The inequality then follows from (58). \(\square \)
Lemma 5.1.2
\(\pi ^{N_2}{\widetilde{Q}}^{-1}(Y)=\pi ^{N_2}{\widetilde{Q}}^{-1}(Y)\pi ^{N_2}\) and \(\pi _{N_2}^\infty {\widetilde{Q}}^{-1}(Y)=\pi _{N_2}^\infty \).
Proof
Set \({\widetilde{Q}}^{-1}={\widetilde{Q}}^{-1}(Y)\). If \({\widetilde{Q}}^{-1}x=y\) then \(x=y-\pi ^{N_2}H_1Y^{N_1}*\pi ^{N_2}y\) and \(x^{N_2}=y^{N_2}-\pi ^{N_2}H_1Y^{N_1}*y^{N_2}\). But then
which coincides with \(\pi ^{N_2}{\widetilde{Q}}^{-1}\pi ^{N_2}x\). The other statement is proven by similar arguments. \(\square \)
Lemma 5.1.3
Let \(N_2,N_1\ge 0\) and given \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\), let \(Y^{N_1}=(Y_0,\dots ,Y_{N_1}\) and \(Y^\infty =Y-Y^{N_1}\). Denote \(Q=Q(Y)\) and \({\widetilde{Q}}^{-1}={\widetilde{Q}}^{-1}(Y)\). The linear operators \(I_{\ell _\nu ^1}-{\widetilde{Q}}^{-1}Q\) and \(I_{\ell _\nu ^1}-Q{\widetilde{Q}}^{-1}\) can be written as follows:
Proof
Keeping track of the projection operators, recalling that each of \(\pi ^{N_2}(\ell _\nu ^1)\) and \(\pi _{N_2}^\infty (\ell _\nu ^1)\) is invariant under \(\widetilde{Q}^{-1}\) and the latter acts as the identity on \(\pi _{N_2}^\infty (\ell _\nu ^1)\), we can equivalent write
Similarly, one can verify
\(\square \)
5.2 A general-purpose finite computation norm estimate
For a given linear operator \(L:X_\nu \rightarrow X_\nu \), it is often useful to work with a “block decomposition”,
The following lemma facilitates the computation of the norm of such an operator. When \(\ker L = X_\nu ^\infty \), the bound of the lemma reduces to a tight, finite computation.
Lemma 5.2.1
Denote \(X_\nu (0)={{\,\mathrm{span}\,}}\{(e_j,0,\dots ,0):j=1,\dots ,d\}\subset X_\nu \) and \(\pi (0):X_\nu \rightarrow X_\nu (0)\) the projection onto \(X_\nu (0)\). Let \(L:X_\nu \rightarrow X_\nu \) be a bounded operator being expressible in the form \(L = T + U + V\) with the following specifications:
-
T has range in \(X_\nu (0)\) and there exists T(0) and \(T_{m,j}\in {\mathbb {C}}^{d\times d}\) for \(m=1-q,\dots ,0\) and \(j\in {\mathbb {N}}\) such that
$$\begin{aligned} (Th)(0) = T(0)h(0) + \sum _{m=1-q}^0 \sum _{j=0}^\infty T_{m,j}h_{m,j}, \end{aligned}$$ -
\(\ker (U)={{\,\mathrm{im}\,}}(I_{X_\nu }-\pi (0))\), U has range in \({{\,\mathrm{im}\,}}(I_{X_\nu }-\pi (0))\), and there exist \(U_{m}\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\) for \(m=1-q,\dots ,0\) such that \((Uh)_{m,j} = U_{m,j}h(0)\),
-
\(\ker (V)=X_\nu (0)\), V has range in \({{\,\mathrm{im}\,}}(I_{X_\nu }-\pi (0))\), and there exist \((V_{m,k})_{j,n}\in {\mathbb {C}}^{d\times d}\) with \(m,k\in \{1-q,\dots ,0\}\) and \(j,n\in {\mathbb {N}}\) such that
$$\begin{aligned} (Vh)_{m,j} = \sum _{k=1-q}^0\sum _{n=0}^\infty (V_{m,k})_{j,n}h_{k,n}. \end{aligned}$$
Then \(||L||_{B(X_\nu )}\le \max \{{\mathcal {T}},\mathcal {U+V}\},\) where
Proof
By definition of the norm on \(X_\nu \), we have
Making use of the decomposition \(L=T+U+V\), the contribution from ||(Lh)(0)|| comes solely from T. We bound this term first. First, observe that by definition of \({\mathcal {T}}_m\) we have \(||T_{m,j}||\le \nu ^j{\mathcal {T}}_m\) for all \(j\ge 0\). Then
Next, since \((Lh)_m = (Uh)_m + (Vh)_m\) for \(m=1-q,\dots ,0\), we will bound \(||(Lh)_m||_\nu \) using the triangle inequality. Clearly \(||(Uh)_m||_\nu \le ||U_m||_\nu \). As for the V terms, first observe that by definition of \({\mathcal {V}}_{m,k}\),
for all \(n\ge 0\). Then
where in the third line we make use of Fubini’s theorem. Combining the previous two estimates, it follows that \(||(Lh)_m||_\nu \le ||U_m||_\nu + \sum _k{\mathcal {V}}_{m,k}\). Taking the maximum over m and applying (62), we obtain the bound \(||L||_{B(X_\nu )}\le \max \{{\mathcal {T}},\mathcal {U+V}\}\). \(\square \)
5.3 Finite convolutions and the operator \(H_1\)
Let \({\mathbf {L}}\) be a \(d\times (N_2+1)\times d(N_2+1)\) matrix, and define \(L:\ell _\nu ^1\rightarrow \ell _\nu ^1\) by
where \({\mathbf {L}}_{n,k}\) denotes the \(d\times d\) block with row-column index (n, k) with indexing from zero (that is, \(n=0\) corresponds to the first row). We write \(L=i\circ {\mathbf {L}}\).
We are will later need to bound operators of the form \(\pi _{N_2}^\infty H_1(Y^{N_1}*L)\) in norm. To accomplish this, we first make two observations.
-
1.
The image of \(Y^{N_1}*L\) is finite-dimensional and equal to \(\pi ^{N_1+N_2}(\ell _\nu ^1)\).
-
2.
The kernel of \(\pi _{N_2}^\infty H_1\) is equal (for \(N_2\ge 1\)) to \(\pi ^{N_2-1}(\ell _\nu ^1)\).
To proceed, we will therefore represent \((Y^{N_1}*L)\) as an infinite matrix with a finite nonzero block and multiply it with a matrix representation of \(\pi ^\infty _{N_2}H_1\) on the left. Let \(\zeta ^{N_2-1}\) be the matrix associated to the linear map
\(\xi ^{N_2-1}\) is a \(d(N_1+N_2+1)\times d(N_1+N_2+1)\) diagonal matrix. Define
where \((Y^{N_1}*{\mathbf {L}})\) is the \(d(N_1+N_2+1)\times d(N_2+1)\) matrix defined row-wise
For \(h\in \ell _\nu ^1\), we have by definition of convolution and L that
where \({\mathbf {h}}_n=h_n\) for \(n\le N_2\) and zero otherwise. From this, we conclude that for \(h\in \ell _\nu ^1\),
where \(\psi _{N}:\pi ^{N}(\ell _\nu ^1)\rightarrow {\mathbb {C}}^{d(N+1)}\) is the isomorphism defined by \((\psi _N h)_{1+nd:(n+1)d}=h_n\). Formally,
Taking into account Lemma 5.2.1 and that the first \(N_2-1\) (block) rows of \({\mathbf {G}}(Y^{N_1},L)\) are zero, this proves the following proposition.
Proposition 5.3.1
Let \({\mathbf {L}}\) be a \(d(N_2+1)\times d(N_2+1)\) matrix, and \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\). Define \({\mathbf {G}}(Y^{N_1},i\circ {\mathbf {L}})\) according to (63). Then,
6 Truncated monodromy operator and tight formulas for \(c_2\), \(c_3\) and \(||(M_{N_1,N_2}-zI)^{-1}||_{B(X_\nu ^\infty )}\) bounds
In this section we will compute tight bounds \(c_2\), \(c_3\) and \(||(M_{N_1,N_2}-zI)^{-1}||_{B(X_\nu ^\infty )}\) from Lemma 4.3.1 for the cases \(p=q=1\), \(1=p<q\) and \(1\ne p<q\). It is beneficial both for clarity of presentation and also for some slight mathematical differences to consider these cases separately. As for the \(c_1\) bound, in all cases it involves a computation of a finite matrix norm and will be done on a computer. This will be elaborated upon in Sect. 7.1.
For a fixed \(Y\in \ell _\nu ^1({\mathbb {C}}^{d\times d})\), let \(\mathbf {{\widetilde{Q}}}^{-1}(Y)\) be the \(d(N_2+1)\times d(N_2+1)\) block matrix such that
where \(\mathbf {{\widetilde{Q}}}^{-1}_{j,k}(Y)\) denotes the row j, column k block of dimension \(d\times d\), with zero-indexing (that is, row one corresponds to \(j=0\) and column one corresponds to \(k=0\)). Let \(\mathbf {DT}\) denote the \(d(N_2+1)\times d(N_2+2)\) block matrix
that is, \(\mathbf {DT}\) is the nontrivial finite-dimensional block of \(\pi ^{N_2}DT\). Let \({\mathbf {H}}_1^0\) denote the \(d\times d(N_2+2)\) matrix
that is, \({\mathbf {H}}_1^0\) is a domain truncation of the finite-dimensional block of \(H_1^0\). For \(k=0,\dots ,N_1\), let \(Z_k^{N_1,N_2}\) denote the \(d(N_2+2)\times d(2N_1+1)\) block Toeplitz matrix and \({\mathbf {S}}(Y^{N_1})\) denote the \(d(2N_1+1)\times d\) matrix
where the first nonzero block in \(Z_k^{N_1,N_2}\) has row index \(N_2-N_1+1+k\) (and consequently the last nonzero block column has index \(N_1-k\)). Let \(\mathbf {{\widetilde{Q}}}^{-1}_j(Y)\) and \(\mathbf {DT}_j\) denote the jth (d-dimensional block) row of \(\mathbf {{\widetilde{Q}}}^{-1}(Y)\) and \(\mathbf {DT}\), and also let \(\mathbf {DT}_{j,k}\) denote the row j, column k block of \(\mathbf {DT}\). With a slight abuse of notation, we define \(\mathbf {{\widetilde{Q}}}^{-1}_{j,k}=0\) whenever the indices (j, k) are out of range: that is, \(j>N_2\) or \(k>N_2\) (recall we index from zero).
6.1 Bounds in the case \(p=q=1\)
Let \(N_2>0\) be given. Making use of the identifications from Sect. 4.4, we can write E and \((I-W)\) as block matrix operators acting on \({\mathbb {C}}^d\times \ell _\nu ^1\) as follows. If \(h=(h(0),\phi )\),
Next, let \(N_1\ge 0\). We can write \(E_{N_1,N_2}\) and \(I-W_{N_1,N_2}\) using this same notation:
where this time we have suppressed the input h. From here it follows that
We have included the explicit domains on the identity operators for clarity. We can now express the truncated monodromy operator \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\) in block operator form:
Remark 6.1.1
When we want to use the computer to calculate eigenvalues of our impulsive delay differential equation, we implement the matrix representation of the restriction of the linear operator \(M_{N_1,N_2}\) to the finite-dimensional vector space \(X_\nu ^{N_2}\).
Lemma 6.1.1
(Truncated monodromy operator, \(p=q=1\)) Define \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\). Suppose \(\phi \) is an eigenvector of \(M_{N_1,N_2}\) with eigenvalue \(\lambda \). If \(\lambda \ne 0\) then with \(\phi =\phi ^{N_2}+\phi ^\infty \), we have \(\phi ^\infty =0\). Also, each of \(X_\nu ^\infty \) and \(X_\nu ^{N_2}\) is an invariant subspace for \(M_{N_1,N_2}\) and for \(r>0\) we have
If \(\lambda \in {\mathbb {C}}\), \(0<r<|\lambda |\) and \(0<\omega < \pi \), then for \(U\in \{D_r(\lambda ),R_\lambda (r,\omega )\}\),
Proof
The assertions concerning the eigenvalues, eigenvectors and invariant subspaces follow directly from the definition of \(E_{N_1,N_2}\) and \((I-W_{N_1,N_2})^{-1}\). As for the bound, we have \(M_{N_1,N_2}\phi ^\infty = 0\), which implies \((M_{N_1,N_2}-re^{i\theta })^{-1}\phi ^\infty = \frac{1}{r}e^{-i\theta }\phi ^\infty \) and subsequently, \(||(M_{N_1,N_2}-re^{i\theta })^{-1}\phi ^\infty ||_{X_\nu }\le \frac{1}{r}||\phi ^\infty ||_{X_\nu }.\) For the proof concerning the closed ball \(D_r(\lambda )\), observe that \((M_{N_1,N_2}-(\lambda +re^{it})I)^{-1}\phi ^\infty = (\lambda +re^{it})^{-1}\phi ^\infty \) for \(t\in [0,2\pi ]\), so that
which attains its maximum when \(t=-\arg \lambda \), resulting in the bound claimed in the lemma. As for the radial sector, we have
for the parameterization in (44). Taking norms and suprema for \(t\in [0,4]\), the upper bound stated in the lemma is attained for \(t\in [0,1]\). \(\square \)
Remark 6.1.2
For fixed \(\lambda \in {\mathbb {C}}\) and \(r\in (0,|\lambda |)\), the coarse bound for \(\sup _{z\in \partial U}||(M_{N_1,N_2}-zI)^{-1}||_{B(X_\nu ^\infty )}\) is attained at a single point in the boundary parameterization for a closed ball \(D_\lambda (r)\), whereas it is attained on a continuum for a given radial sector \(R_\lambda (r,\cdot )\). In this sense, \(\sup _{z\in \partial U}||(M_{N_1,N_2}-zI)^{-1}||_{B(X_\nu ^\infty )}\) can be more conservatively bounded on a radial sector (of a given width) than it can for a closed ball (of radius equal to the prior width).
This lemma gives preliminary justification for why \(M_{N_1,N_2}\) is a reasonable choice for a truncated monodromy operator. It also guarantees that the nonzero eigenvalues of the truncation can in principle be computed from the finite (and generally nontrivial) part of \(M_{N_1,N_2}\) . The following theorems gives computable bounds \(c_2\) and \(c_3\).
Theorem 6.1.1
(\(c_2\) bound, \(p=q=1\)) Let \(N_2>N_1\ge 0\). Denote \(A_1^{N_1}=(A_{1,0},\dots ,A_{1,N_1},0,\dots )\) and \(A_1^\infty = A_1-A_1^{N_1}\). Define
and introduce the quantities
Suppose \(\rho :=\max \{ \rho _1,\rho (0)\}<1\). Then, with
the operator \(I-W\) satisfies \(||(I-W)^{-1}||_{B(X_\nu )}\le c_2\).
Proof
Define the operator \(\Lambda =I-(I-W_{N_1,N_2})^{-1}(I-W)\). By construction,
so if we can estimate the norm of \(\Lambda \) and prove that this is less than one, a Neumann series argument will give a constructive bound for \(c_2\), since the norm \(||(I_{\ell _\nu ^1}-W_{N_1,N_2})^{-1}||_{B(\ell _\nu ^1)}\) can be approximated (or rigorously enclosed) on a computer: in particular, it is bounded above by \(\max \{1,||(I-W_{N_1,N_2})^{-1}\pi ^{N_2}||_{B(X_\nu ^{N_2})}\}\).
Moving on to the estimation of the operator norm of \(\Lambda \), a careful multiplication shows
with the upper right block given by
By definition of the norm on \(X_\nu ={\mathbb {C}}^d\times \ell _\nu ^1\), it follows that
We will estimate these two norms separately. For brevity, write \({\widetilde{Q}} = {\widetilde{Q}}(A_1^{N_1})\) and \(Q = Q(A_1)\). First, we use Lemma 5.1.3 to write
We will now bound this linear operator using (58) to consider the maximum of the contribution from the body \(\pi ^{N_2}(\ell _\nu ^1)\) and tail \(\pi _{N_2}^\infty (\ell _\nu ^1)\). Using Propositions 4.1.1, 5.3.1 and rows 3, 4, and 8 of Table A, we can get the bound
Similarly, using Proposition 4.1.1 and rows 3, 4, 8, 12 and 14 of Table A, we get
Taking into account (58), it follows that \(||I_{\ell _\nu ^1}-{\widetilde{Q}}^{-1}Q||_{B(\ell _\nu ^1)}\le \rho _1\).
Next, we deal with \(\Lambda _{12}\). We begin by splitting \(\pi ^{N_2}({\widetilde{Q}}^{-1}Q-I_{\ell _\nu ^1})\) into two separate terms:
With this decomposition, we can write \(-\Lambda _{12}\) as follows:
This decomposition has the effect of separating the terms that are asymptotically \(O(||A_1^\infty ||_\omega )\) from everything else. After distributing through the \(I+C_1\) matrix term using the elementwise product operand \(\odot \), we use Proposition 4.1.1, rows 1, 2, 3, 4 and 15 and (59) to obtain the bound
Combining the previous estimates, we conclude \(||\Lambda ||_{B(\ell _\nu ^1)}\le \max \{\rho _1,\rho (0)\}=\rho \). By Neumann series, \(||(I-\Lambda )^{-1}||_{B(\ell _\nu ^1)}\le \frac{1}{1-\rho }\), which combined with the discussion at the beginning completes the proof. \(\square \)
Remark 6.1.3
The matrix \(\mathbf {{\widetilde{Q}}}^{-1}(A_1^{N_1})\) can be identified with the nontrivial, finite block of
and is computed explicitly in our numerical scheme. As such, any finite computations involving this can be accomplished on a computer.
Theorem 6.1.2
(\(c_3\) bound, \(p=q=1\)) Let \(N_2>1\) and \(N_1>0\), and let \(K_0\), \(A_1^{N_1}\) and \(A_1^\infty \) be defined as in Theorem 6.1.1. Denote \(B_1^{N_1}=(B_{1,0},\dots ,B_{1,N_1},0,\dots )\) and \(B_1^\infty =B_1-B_1^{N_1}\). Let \({\mathbf {M}}\) be the \(d(N_2+1)\times d(N_2+1)\) matrix such that for all \(h\in \pi ^{N_2}(\ell _\nu ^1)\),
where \(\psi \) the isomorphism defined by in (64). Introduce the quantities
Then, with
we have the estimate \(||(I-W)M_{N_1,N_2}-E||_{B(X_\nu )}\le c_3\).
Proof
Define \({\overline{\Lambda }}=(I-W)M_{N_1,N_2}-E\). Using (65)–(69) one can write \({\overline{\Lambda }}\) in the form
with the more complicated terms being given by
Like in the proof of the previous theorem, we can bound \(||{\overline{\Lambda }}||_{B(\ell _\nu ^1)}\) via
where the norms are norms on appropriate spaces of linear maps. It therefore suffices to compute the individual norm bounds. Starting with \({\overline{\Lambda }}_{21}\), we can write
This we bound using Propositions 4.1.1, 5.3.1 and rows 3 and 9 of Table A to get
Next, we write down \({\overline{\Lambda }}_{22}\) with more structure. We have
We can bound the individual terms with Propositions 4.1.1, 5.3.1, Lemma 5.2.1 and rows 3, 4, 13 and 14 of Table A. Additionally taking into account the tail-body split inequality (58), we get
Combining the two previous estimates, we have \(||{\overline{\Lambda }}_{21}||+||{\overline{\Lambda }}_{22}||\le \kappa _1\). Next we bound \((I+C_1){\overline{\Lambda }}_{11}\). Using Proposition 4.1.1 and rows 1 and 9 of Table A, We have
To handle \((I+C_1){\overline{\Lambda }}_{12}\), we use Propositions 4.1.1, 5.3.1, Lemma 5.2.1, rows 1 and 2 of Table A and inequality (59) to get
It follows that \(||(I+C_1){\overline{\Lambda }}_{11}|| + ||(I+C_1){\overline{\Lambda }}_{12}||\le \kappa (0)\). Combining these with the previous inequality (76) for \(||{\overline{\Lambda }}||_{B(\ell _\nu ^1)}\), we get \(||{\overline{\Lambda }}||_{B(\ell _\nu ^1)}\le c_3\) as claimed.
Remark 6.1.4
\({\mathbf {M}}\) coincides with the nontrivial \(d(N_2+1)\times d(N_2+1)\) block of \(M_{N_1,N_2}^{22}\) from (70). \(\square \)
6.2 Bounds in the case \(1=p<q\)
The implicit part W has a particular structure, which in turn induces a structure on \((I-W)\). From (38) and the representations of Sect. 4.4, we can interpret it as being the following block operator acting on \(X_\nu \). For \(\phi =(\phi (0),\phi _0,\dots ,\phi _{1-q})\),
where the identity operators I are on the implied spaces: for instance, the first one is on \({\mathbb {C}}^d\) and the others are on \(\ell _\nu ^1\). If we take a direct \((N_1,N_2)\)-mode truncation of W (in the same way we did for \(p=q=1\)), we obtain
We can similarly express the explicit part E as a block operator acting on \(X_\nu \). We have
We can now truncate the sequence \(B_1\) to \(N_1\) modes, while for the second level of truncation we will do something a bit different. We define
Remark 6.2.1
When we want to use the computer to calculate eigenvalues of our impulsive delay differential equation, we implement the matrix representation of the restriction of the linear operator \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\) to the finite-dimensional vector space \(X_\nu ^{N_2}\).
Remark 6.2.2
It might be tempting to replace the identity maps \(I_{\ell _\nu ^1}\) in the lower diagonal part of E with projections \(\pi ^{N_2}\) in the expression for \(E_{N_1,N_2}\). The reason we do not is because if we do, the analogous diagonal terms of \(E-E_{N_1,N_2}\) become projections \(\pi _{N_2}^\infty \), which have norm 1 for all \(N_2>0\). This would eliminate our ability to control the bound \(c_3\) by taking more modes, which is undesirable for computer-assisted proofs. It would also imply \(M_{N_1,N_2}\) does not converge to M as a bounded operator on \(X_\nu \) as we increase the number of modes, which is completely wrong if we want to think of \(M_{N_1,N_2}\) as an approximation of M.
Lemma 6.2.1
(Truncated monodromy operator, \(1=p<q\)) Define \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\). Suppose \(\phi \) is an eigenvector of \(M_{N_1,N_2}\) with eigenvalue \(\lambda \). If \(\lambda \ne 0\) then with \(\phi =\phi ^{N_2}+\phi ^\infty \), we have \(\phi ^\infty =0\). Also, each of \(X_\nu ^\infty \) and \(X_\nu ^{N_2}\) is an invariant subspace for \(M_{N_1,N_2}\) and for \(r>0\) we have
unless \(r=1\), in which case \(||(M_{N_1,N_2}-re^{i\theta })^{-1}||_{B(X_\nu ^\infty )}\le 1\). If \(\lambda \in {\mathbb {C}}\), \(0<r<|\lambda |\) and \(0<\omega < \pi \), then for \(U\in \{D_r(\lambda ),R_\lambda (r,\omega )\}\),
Proof
The assertions concerning the eigenvalues, eigenvectors and invariant subspaces follow directly from the definition of \(E_{N_1,N_2}\) and \((I-W_{N_1,N_2})^{-1}\). As for the bound, one can verify directly that if \(\phi ^\infty \) and \(h^\infty \) satisfy \((M_{N_1,N_2}-re^{i\theta })\phi ^\infty =h^\infty \), then
Thus, if \(||h^\infty ||_{X_\nu }\le 1\), then \(||\phi _0^\infty ||_\nu \le \frac{1}{r}\) and by a quick inductive proof, one can check that
unless \(r=1\), in which case \(||\phi _k^\infty ||_\nu \le 1\). To complete the proof, observe that w is strictly decreasing and therefore reaches its maximum at index \(k=1-q\). The argument for the radial sector and closed ball are similar and omitted. \(\square \)
Theorem 6.2.1
(\(c_2\) bound, \(1=p<q\)) Let \(N_2>N_1\ge 0\). With \(\rho \) as defined in Theorem 6.1.1, the operator \(I-W\) satisfies \(||(I-W)^{-1}||_{B(X_\nu )}\le c_2\) with
Proof
Define \(\Omega =I-(I-W_{N_1,N_2})^{-1}(I-W)\). Then
where empty entries are zero (of appropriate spaces of linear maps) and \({\mathbf {0}}=\text{ diag }(0,\dots ,0)\) is the zero operator on \((\ell _\nu ^1)^{q-1}\). The nontrivial part of \(\Omega \) coincides precisely with \(\Lambda \) from the proof of Theorem 6.1.1. To show that \(||(I-W_{N_1N_2})^{-1}||_{B(X_\nu )}=\max \{1,||(I-W_{N_1,N_2})^{-1}||_{B(X_\nu ^{N_2})}\}\), observe that \((I-W_{N_1,N_2})^{-1}\) is still the identity operator when restricted to \(X_\nu ^\infty \). \(\square \)
Theorem 6.2.2
(\(c_3\) bound, \(1=p<q\)) Let \(N_2\ge N_1>0\) and let \(\kappa _1\) and \(\kappa (0)\) be defined as as defined in Theorem 6.1.2. Then, with
we have the estimate \(||(I-W)M_{N_1,N_2}-E||_{B(X_\nu )}\le c_3\).
Proof
Let \({\overline{\Omega }}=(I-W)(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}-E\). Making use of the previous expressions for \(I-W\), \((I-W_{N_1,N_2})^{-1}\), E and \(E_{N_1,N_2}\), we find that in block operator form,
with zeroes representing the zero maps in the appropriate spaces, and
where the \({\overline{\Lambda }}_{ij}\) are the same as those appearing in the proof of Theorem 6.1.2. The conclusion then follows by the same estimates as in the proof of the aforementioned, together with the bound for the norm of \(C_2S^*\pi _{N_2}^\infty \) being supplied by row 7 of Table A. \(\square \)
6.3 Bounds in the case \(1<p<q\)
In this final subsection we will compute the bounds \(c_2\) and \(c_3\) in the final case, where \(1<p<q\). This case will be a fair bit more involved than the previous ones and the bounds are significantly more complicated. Like in the last section, we write \(I-W\) using (38) and the representations of Sect. 4.4. Making use of the short form \(L\phi _j:=(L\phi )_j\) and \(L\phi (0):=(L\phi )(0)\) for a linear operator \(L:X_\nu \rightarrow X_\nu \),
where we denote \(Q_j=Q(A_j)\) and \({\widetilde{Q}}_j={\widetilde{Q}}(A_j)\). Similarly, we can write down the explicit part operator E and define the truncation \(E_{N_1,N_2}\).
Note that here we are using the short form \(L\phi _j:=(L\phi )_j\) and \(L\phi (0):=(L\phi )(0)\) for \(L\in \{E,E_{N_1,N_2}\}\).
Remark 6.3.1
When we want to use the computer to calculate eigenvalues of our impulsive delay differential equation, we implement the matrix representation of the restriction of the linear operator \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\) to the finite-dimensional vector space \(X_\nu ^{N_2}\).
Lemma 6.3.1
(Truncated monodromy operator, \(1<p<q\)) Define \(M_{N_1,N_2}=(I-W_{N_1,N_2})^{-1}E_{N_1,N_2}\). Suppose \(\phi \) is an eigenvector of \(M_{N_1,N_2}\) with eigenvalue \(\lambda \). If \(\lambda \ne 0\) then with \(\phi =\phi ^{N_2}+\phi ^\infty \), we have \(\phi ^\infty =0\). Also, each of \(X_\nu ^\infty \) and \(X_\nu ^{N_2}\) is an invariant subspace for \(M_{N_1,N_2}\) and for \(r>0\) we have
unless \(r=1\), in which case \(||(M_{N_1,N_2}-re^{i\theta })^{-1}||_{B(X_\nu ^\infty )}\le 1\). If \(\lambda \in {\mathbb {C}}\), \(0<r<|\lambda |\) and \(0<\omega < \pi \), then for \(U\in \{D_r(\lambda ),R_\lambda (r,\omega )\}\),
Proof
The assertions concerning the eigenvalues, eigenvectors and invariant subspaces follow directly from the definition of \(E_{N_1,N_2}\) and \((I-W_{N_1,N_2})\). Indeed, it is easy to verify that each of \(X_\nu ^{N_2}\) and \(X_\nu ^\infty \) are invariant subspaces for \(I-W_{N_1,N_2}\) and its inverse. As for the bound, one can verify directly that if \(\phi ^\infty \) and \(h^\infty \) satisfy \((M_{N_1,N_2}-re^{i\theta })\phi ^\infty =h^\infty \), then
If \(||h^\infty ||_{X_\nu }\le 1\) then \(||\phi _k^\infty ||_\nu \le \frac{1}{r}\) for \(1-p\le k\le 0\), and for \(1-q\le k\le -p\), we have
If \(r=1\) we get \(||\phi _k^\infty ||_\nu \le 1\) for \(k=1-q,\dots ,0\). Otherwise, observe that \(||\phi _k^\infty ||_\nu \le x_k\), where
with \(x_0=\cdots =x_{1-p}=r^{-1}\). It is easy to verify by induction that this sequence is nonincreasing and therefore reaches its maximum at \(k=1-q\). Also, since the initial conditions \(x_0,\dots ,x_{1-p}\) are equal, we have \(x_{k+jp}=x_k\) for integers \(j\le 0\) and \(k\in \{1-p,\dots ,0\}\). Consequently,
Since \(j^*=1-\lfloor q/p\rfloor \) is the most negative integer such that \(k+j^*p\ge 1-q\) for some \(k\in \{1-p,\dots ,0\}\), we conclude \(||\phi ^\infty ||_\nu \le \max \{1/r,w(j^*)\}\). The proof for the radial sector and closed ball are similar. \(\square \)
Lemma 6.3.2
Let \(N_1,N_2>0\) and suppose \((I-W_{N_1,N_2})^{-1}(I-W)f=\phi \) for some \(f,\phi \in X_\nu \). Denote \(Q_j=Q(A_j)\) and \({\widetilde{Q}}_j={\widetilde{Q}}(A_j)\). Then \(\phi _k=f_k\) for \(1-q\le k\le -p\) and
where product denotes composition from right to left (bottom to top index), the empty product is defined to be the identity and the empty sum to be zero.
Proof
The assertion that \(\phi _k=f_k\) for \(1-q\le k\le -p\) is clear. We next prove the formula for \(\phi _{n-p}\) for \(n=1,\dots ,p\). The definition of \(\phi \) and f is equivalent to having
We prove this by induction. Starting with \(n=1\), using (79)–(80) with the above equation implies \(Q_1f_{1-p}={\widetilde{Q}}_1\phi _{1-p}\) and consequently, \(\phi _{1-p}={\widetilde{Q}}_1^{-1}Q_1f_{1-p}\). This is consistent with (83). Taking an inductive step, if \(n\ge 1\) we can again use the above equation together with the explicit expressions (79)–(80) to get
Solving for \(\phi _{n+1-p}\), we have
which is precisely (83) at index \(n+1\). To get Eq. (84) for \(\phi (0)\) one uses the same strategy, except we have left the result implicit. \(\square \)
Lemma 6.3.3
Let \(N_1,N_2>0\) and suppose \((I-W)(I-W_{N_1,N_2})^{-1}f=\phi \) for some \(f,\phi \in X_\nu \). Denote \(Q_j=Q(A_j)\) and \({\widetilde{Q}}_j={\widetilde{Q}}(A_j)\). Then \(\phi _k=f_k\) for \(1-q\le k\le -p\) and
where product denotes composition from right to left (bottom to top index), the empty product is defined to be the identity and the empty sum to be zero.
Proof
The proof here is similar to the one for Lemma 6.3.2, so we will provide only an outline. Set \(z=(I-W_{N_1,N_2})^{-1}f\). Then \(z_k=f_k\) for \(1-q\le k\le -p\), and using (80) one can prove by induction that
Next, one computes \(\phi =(I-W)(I-W_{N_1,N_2})^{-1}f = (I-W)z\) using (79) and the above expressions. The result is \(\phi _k=f_k\) for \(1-q\le k\le -p\) and (85) for \(n=1,\dots ,p\), while
We obtain (86) by substituting \(z_0\) and \(z_{-1}\) into the above, but we will point out one subtlety. Since \(\pi _{N_2}^\infty {\widetilde{Q}}_n^{-1}\pi ^\infty _{N_2}\)—see Lemma 5.1.2—we have
since all terms in the summation except for the \(p-1\) term contain a \({\mathbf {e}}_0\) on the extreme left, which maps into \(\pi ^{N_2}(\ell _\nu ^1)\), while for the \(p-1\) term the product collapses to the trivial product (identity). \(\square \)
Theorem 6.3.1
(\(c_2\) bound, \(1<p<q\)) Let \(N_2>N_1\ge 0\). For \(m=1,\dots ,p\), define \(A_m^{N_1}=(A_{m,0},\dots ,A_{m,N_1},0,\dots )\), \(A_m^\infty =A_m-A_m^{N_1}\),
With \(\rho :=\max \{\rho (0),\rho _1,\dots ,\rho _p\}\), the operator \(I-W\) satisfies \(||(I-W)^{-1}||_{B(X_\nu )}\le c_2\) with
Proof
Define \(\Lambda =I-(I-W_{N_1,N_2})^{-1}(I-W)\). Let \(h\in X_\nu \) satisfy \(||h||_{X_\nu }\le 1\). By Lemma 6.3.2, we have \((\Lambda h)_k=0\) for \(1-q\le k\le -p\), while for \(n=1,\dots ,p\),
We separately majorize in norm for \(h\in X_\nu ^{N_2}\) and \(h\in X_\nu ^\infty \). From Lemma 5.1.3, we can decompose as follows:
Bounding each of \((I-{\widetilde{Q}}_n^{-1}Q_n)\pi ^{N_2}\) and \((I-{\widetilde{Q}}_n^{-1}Q_n)\pi _{N_2}^\infty \) can be accomplished in the same way as in the proof of Theorem 6.1.1; see (72) and (73). We have \(||{\widetilde{Q}}_n^{-1}{\mathbf {e}}_0||\le K_{0,n}^0\) by row 9 of the table, while row 11 gives the estimate \(||S\pi ^{N_2}{\widetilde{Q}}_j^{-1}{\mathbf {e}}_0||\le K_{0,j}^{S,0}\). As for the remaining terms, row 3, 5, 6, 10 and 12 give
Combining the previous estimates, we apply (60) to get \(||(\Lambda h)_{n-p}||_\nu \le \rho _n\).
Also using Lemma 6.3.2, writing \((\Lambda h)(0)=(I+C)({\overline{\Lambda }} h)(0)\), we have
We can bound this term in norm using much the same estimates as before. The only differences are that we will need to use (56) to commute \((I+C_1)\) through the operator \(H_2\), while a bound for
can be constructed by observing that the quantity being bounded symbolically coincides (except for a single projector, which does not effect the norm) with \((I+C_1)\Lambda _{12}\) from the proof of Theorem 6.1.1, so (74) can be re-used. In total, we get
We then get \(||\Lambda h(0)||\le \rho (0)\) and taking into account (60), we conclude \(||\Lambda ||_{B(X_\nu )}\le \rho \). The rest of the proof is nearly identical to the proof of Theorem 6.1.1. Verifying that
is clear by definition of \(W_{N_1,N_2}\). \(\square \)
Theorem 6.3.2
(\(c_3\) bound, \(1<p<q\)) Let \(N_2>N_1\ge 0\). For \(j=1,\dots ,p\), define \(A_m^{N_1}=(A_{m,0},\dots ,A_{m,N_1},0,\dots )\), \(A_m^\infty =A_m-A_m^{N_1}\), \(B_m^{N_1}=(B_{m,0},\dots ,B_{m,N_1},0,\dots )\) and \(B_m^\infty =B_m-B_m^{N_1}\). Let \({\mathbf {M}}^{(m)}\) be the \(d(N_2+1)\times d(N_2+1)\) matrix such that for all \(h\in \pi ^{N_2}(\ell _\nu ^1)\),
where \(\psi \) the isomorphism defined by in (64). Also for \(m=1,\dots ,p\) define the quantities
Then, with
we have the estimate \(||(I-W)M_{N_1,N_2}-E||_{B(X_\nu )}\le c_3\).
Proof
Define \(\Omega =(I-W)M_{N_1,N_2}-E\). Let \(h\in X_\nu \) satisfy \(||h||_{X_\nu }\le 1\) and denote \(\phi =Eh\) and \({\tilde{\phi }} = E_{N_1,N_2}h\). Making use of Lemma 6.3.3, we have for \(h\in X_\nu \), \(n=1,\dots ,p\) and \(1-q\le m\le -p\),
To derive a bound for \(||\Omega ||_{B(X_\nu )}\), we will need to separately bound the terms above. First, the easy one: by definition of E and \(E_{N_1,N_2}\) we have \({\tilde{\phi }}_m - \phi _m=0\) for \(1-q\le m\le -p\). Next, observe that \((E_{N_1,N_2}\pi _{N_2}^\infty h)_{k-p}=0\) for \(k=1,\dots ,p\). As such, all of the “product” terms vanish for arguments \(h\in X_\nu ^\infty \) as they are terminated (at the right) by a \({\tilde{\phi }}_{k-p}\). This will simplify the application of the direct sum operator norm inequality (60) for \(B(X_\nu )\). We will therefore bound each of the above for \(h\in X_\nu ^\infty \) first.
Let \(h^\infty \in X_\nu ^\infty \). Replacing h with \(h^\infty \) in the above expressions, we get
Row 2 and 7 of Table A and Proposition 4.1.1 can be used to bound the second quantity with geometric decay in \(N_2\). As for the first, we use row 13 and 14 to handle the body \(B_n^{N_1}\) of the sequence \(B_n\), with row 3 and Proposition 4.1.1 to handle the tail \(B_n^\infty \). All together, we get
Now we let \(h^{N_2}\in X_\nu ^{N_2}\). Replacing h with \(h^{N_2}\) in the first set of equations, we will work piece by piece. Making use of (81) and (82),
These terms all appear in the expression for \({\overline{\Lambda }}_{22}\) from the proof of Theorem 6.1.2 (modulo some projections that do not alter the norms), so we can bound them using the same methods. Namely, we use Propositions 4.1.1, 5.3.1, Lemma 5.2.1 and rows 3, 4, 13 and 14 of Table A (and some algebra) to get
Next, recalling the argument from the proof of Theorem 6.1.2 (see the \({\overline{\Lambda }}_{21}\) term), we can make the estimate
For the summation-product part, recall that the \(S{\widetilde{Q}}_j^{-1}{\mathbf {e}}_0\) terms in the products can ban be bounded individually using row 11, with \(||S{\widetilde{Q}}_j^{-1}{\mathbf {e}}_0||_{L({\mathbb {C}}^d,\ell _\nu ^1)}\le K_{0,j}^{S,0}\). As for the “external” terms of the form \(S\pi ^{N_2}{\widetilde{Q}}_k^{-1}{\tilde{\phi }}_{k-p}\), since we have replaced h with \(h^{N_2}\), these are given by
We can bound these using a combination row 3 and 10 of the table and Proposition 4.1.1. We get
Next, expanding \({\tilde{\phi }}_{k-p}\) in \({\widetilde{Q}}_k^{-1}{\tilde{\phi }}_{k-p}\) we can get the estimate
using row 3 and 9 of Table A and Proposition 4.1.1. By combining (91), (92), (93), (94) and the inline estimates, we can finally get the bound
Taking the maximum of the above with (89), the result is \(||(\Omega h)_{n-p}||_\nu \le \kappa _n\).
To get a bound for \(||\Omega h(0)||\), we will also need to compute and bound \({\tilde{\phi }}(0)-\phi (0)\). This is straightforward: as we have already obtained a bound for \(h^\infty \), we let \(h^{N_2}\in X_\nu ^{N_2}\) so that
The last thing we need to do is deal with the \(H_2(A_p*I_{\ell _\nu ^1} - A_p^{N_1}*\pi ^{N_2})\) terms, multiplied on the right by \({\widetilde{Q}}_p^{-1}{\tilde{\phi }}_0\) or \({\widetilde{Q}}_p^{-1}{\mathbf {e}}_0\). However, since the latter two have range in \(\pi ^{N_2}(\ell _\nu ^1)\) (recall we already have a bound for the case \(h\in X_\nu ^\infty \), see (90)), this can be equivalently written (for placeholder \(z\in {\mathbb {C}}^d\)) as
The map \(H_2(A_p*I_{\ell _\nu ^1} - A_p^{N_1}*\pi ^{N_2})\) can without loss of generality be replaced with \(H_2(A_p^\infty *\pi ^{N_2})\), which gives the bound
Combining the previous estimates again, we finally get the bound
Applying (60) to take the maximum of the above with (90) we get the bound \(||(\Omega h)(0)||\le \kappa (0)\). Finally, applying (60) again but this time to \(\Omega :X_\nu \rightarrow X_\nu \), we get \(||\Omega ||_{B(X_\nu )}\le \max \{\kappa (0),\kappa _1,\dots ,\kappa _p\}\). \(\square \)
7 MATLAB implementation
To accompany this publication we have implemented the numerical discretization of the monodromy operator in MATLAB. It can be found at the author’s GitHub [9]. The implementation can handle arbitrary period p and delay q, provided these are integers. Rigorous enclosures of the \(c_2\) and \(c_3\) bounds is accomplished with the INTLAB library [24], although at present we have only implemented the case \(1=p\le q\). In the same way, \(c_1\) bound computation for generalized Morse index and radial sector validation are implemented and handled with INTLAB. The code is general-purpose, taking as input the matrix-valued functions A(t) and B(t) appropriately pre-processed, impulse matrices \(C_1\) and \(C_2\) and various other user-specified data. The code can be found at [9]. INTLAB is required for rigorous proof, but is not required for monodromy operator discretization, so the latter is suitable for eigenvalue (Floquet multiplier) estimation. The validation code can also be run with floating point arithmetic, but in this mode the output should not be considered rigorous (especially the \(c_1\) bound code). At time of writing there are several parts of the code that could be vectorized (specifically some functions that implement block-matrix convolutions), leading to performance improvement.
7.1 Computation of \(c_1\) bounds
For generalized Morse index validation, the \(c_1\) bound must satisfy
where \(c_1^\dagger =\sup _{\theta \in [0,2\pi ]}||(M_{N_1,N_2}-re^{i\theta }I)^{-1}||_{B(X_\nu ^\infty )}\) can be bounded using an explicit formula (Lemmas 6.1.1, 6.2.1 and 6.3.1). Since the eigenvalues of \(M_{N_1,N_2}\) come in complex-conjugate pairs, it is enough to perform the former bound over \(\theta \in [0,\pi ]\). The strategy is therefore to fix a mesh size m, partition \([0,\pi ]\) according to
and compute
where \(c_1^\dagger \) is replaced by an appropriate upper bound. The supremums are done using interval arithmetic (INTLAB). If \(c_1c_2c_3\ge 1\), one should refine the mesh (to reduce the over-estimation due to interval arithmetic and subsequently decrease \(c_1\)), increase the number of modes (to push \(c_3\) closer to zero and decrease the error \(||M-M_{N_1,N_2}||_{B(X_\nu )}\)) or work with \(\nu \) if such flexibility is afforded by the given problem. It may also be necessary to change the value of the radius r.
The situation is similar for validation in a closed ball. The \(c_1\) bound must satisfy
where \(c_1^\dagger =\sup _{\theta \in [0,2\pi ]}||(M_{N_1,N_2}-(\lambda + re^{i\theta })I)^{-1}||_{B(X_\nu ^\infty )}\). There is no symmetry that can be exploited here, so we must partition the entire interval \([0,2\pi ]\). With m mesh points, we compute
using interval arithmetic. The conditioning guidelines are the same as for generalized Morse index validation.
For radial sector validation, the \(c_1\) bound must satisfy
for the radial sector parameterization z from (44), where \(c_1^\dagger =\sup _{t\in [0,r]}||(M_{N_1,N_2}-z(t;\lambda ,r,\omega )I)^{-1}||_{B(X_\nu ^\infty )}\) can once again be bounded using an explicit formula (Lemmas 6.1.1, 6.2.1 and 6.3.1). By choosing mesh sizes \(m_k\) and partitioning the intervals \([k,k+1]\) for \(k=0,1,2,3\) according to
one can then compute
where \(c_1^\dagger \) is replaced by an appropriate upper bound and all suprema are calculated using interval arithmetic (INTLAB). Conditioning guidelines are the same as the previous case, except that generally it might also be necessary to change the value of the width r or sweep \(\omega \) of the radial sector.
Remark 7.1.1
In all cases, an appropriate bound for \(c_1^\dagger \) is available from one of Lemmas 6.1.1, 6.2.1 or Lemma 6.3.1.
7.1.1 Mesh generation
In our implementation of the \(c_1\) bound we have allowed two options for the mesh. The first is a uniform grid, and the second one is a pre-specified mesh. A script is included to generate a (nonuniform) mesh in one of two ways. The first, which is generally very slow, involves first computing
at a specified number of equally-spaced points throughout the domain \(\text{ dom }(z)\) of the parameterization for \(\partial U\) (for U the set to validated) with floating point arithmetic (for speed). A mesh \(0=s_1<\cdots <s_m=\max (\text{ dom }(z))\) for specified m is then computed so that
is (nearly) equal for \(i=1,\dots ,m\). A much faster way is to instead take \(\{\sigma _1,\dots ,\sigma _N\}=\sigma (M_{N_1,N_2})\) the eigenvalues of \(M_{N_1,N_2}\) and compute
at a specified number of equally-spaced points throughout the domain \(\text{ dom }(z)\), and then generate the mesh in such a way that
is (nearly) equal for \(i=1,\dots ,m\)
7.2 Handling arbitrary period and delay in the absence of validation
Our basic implementation of the discretized monodromy operator is built on the premise that the the period p and delay q are coprime and \(p\le q\). In this section we explain how the implementation handles the other cases. If p and q are not coprime but \(p\le q\), one can interpret the monodromy operator M as being a product:
with \(U(t_1,t_0)\) denoting the solution operator from time \(t_0\) to time \(t_1\) for (12)–(13). Each of \(U(k,k-1)\) for \(k=1,\dots ,p\) can be discretized using our scheme, since these operators can, themselves, be interpreted as the monodromy operator for a system of the type (12)–(13) except with period \(p_0=1\) and delay q. This is not optimal, and implementing the discretization from the ground up treating arbitrary \(p\le q\) would improve efficiency by reducing the amount of large matrix multiplications.
Depending on the relationship between p and q and the regularity of the matrix-valued functions A(t) and B(t), one might be able to write M using fewer than p factors. Suppose \(p\le q\) have a common factor m. Then \(p=jm\) for some \(j\ge 0\), and we can write
Provided the matrix-valued functions A(t) and B(t) are piecewise-analytic with respect to the intervals \((km,(k+1)m)\) for \(k\in {\mathbb {Z}}\), we can apply our discretization scheme by interpreting each factor as the monodromy operator of a system of the type (12)–(13) with period \(p_0=m\) and delay q. After an appropriate time rescaling (since the new period m divides q) we can rescale the period to 1. However, since this is problem-specific, we do not implement it directly in our MATLAB code and instead implement the worst-case fallback option outlined in the previous paragraph.
Suppose now that \(p>q\): that is, the period is greater than the delay. We can write \(p=jq+k\) for some positive integer j and a remainder \(k\in \{0,\dots ,q-1\}\). We can then write the monodromy operator M as
In the same way as last time, we can interpret \(U(mq,(m-1)q)\) as being a monodromy operator for a system of the type (12)–(13) except with period and delay both equal to q, while U(p, jq) can be interpreted as a monodromy operator for a system of the same type, except with period equal to \(p_0=k\) and delay equal to q. This is handled automatically in our MATLAB implementation, where each of the \(M(mq,(m-1)q)\) operators are discretized using the worst-case product fallback approach from the first paragraph.
At a theoretical level, the discretization \(M_{N_1,N_2}\) resulting from this construction converges to M (although with a generally worse rate) in \(B(X_\nu )\) just as it does for the coprime cases \(p\le q\); namely, the convergence is achieved as \(N_1,N_2\rightarrow \infty \) provided \(N_2-N_1\rightarrow \infty \). This can be proven by careful analysis of the bounds \(c_2\) and \(c_3\). Namely, \(c_2\) is uniformly bounded and \(c_3\) is \(O(1/(N_2-N_1))\). One can then apply the error bound (42). However, the validated numerics of Sect. 4.3 no longer apply. The proof of the main lemma and theorem in the latter section explicitly uses the decomposition of M in terms of a single implicit and explicit part operator, and if \(p>q\) or they are not coprime it is generally necessary to split M into several such operators. We briefly demonstrate the problem at the end of Sect. 10. While the result can indeed be generalized to the case \(p>q\) or non-coprime p and q, the estimation of the analogous bounds (such as \(c_2\) and \(c_3\)) quickly become rather involved. Thus, while these cases could be handled using our validated numerics setup, we do not do so at this time.
7.3 Optimizations for some special scalar problems
Some additional preprocessing can improve the speed of computer-assisted proofs if \(q=kp\) for a natural number k and the impulsive delay differential equation is scalar. First recall [10] that \(\mu \) is a Floquet multiplier if and only if to \(\lambda :=p^{-1}\log \mu \) there is associated a nontrivial complex-valued p-periodic function \(\phi (t)\) such that \(t\mapsto \phi (t)e^{t\lambda }\) is a solution of (10)–(11). One can then check directly that \(\phi \) is a periodic solution of
However, since \(q=kp\) for p the period of \(\phi \), the above is equivalent to
Let \({\overline{A}}=p^{-1}\int _0^p A(t)dt\) and \({\overline{B}}=p^{-1}\int _0^t {\overline{B}}(t)dt.\) If \(\phi \) is scalar, \(\phi \) is periodic with period p and nontrivial if and only if
as can be verified by solving the ordinary impulsive differential equation and imposing the equality \(\phi (0)=\phi (p)\). However, this is the exact same equation one obtains upon substituting the ansatz \(y(t)=\phi (t)e^{t\lambda }\) into
and imposing periodicity of \(\phi \). The above impulsive DDE and (10)–(11) therefore have the same Floquet multipliers, so in the computation of the bounds \(c_1\), \(c_2\) and \(c_3\), it is sufficient to replace the inputs A and B with rigorous interval enclosures of the mean over the entire interval [0, p]. The tail terms can also be rolled into this rigorous enclosure of the means, so that in the bound computations one can take them to be zero.
8 Examples and applications: rigorous numerics
The following sections demonstrate the strengths (and weaknesses) of our numerical monodromy operator discretization scheme and the rigorous numerics approach to eigenvalue validation. The models of the first two sections (Sects. 8.1, 8.2) are motivated in part by existing mathematical models or well-known equations. In the first of these sections we exploit the robustness of INTLAB to prove results that are uniform with respect to model parameters. In particular, we prove some robust stability and bifurcation enclosure results. Section 8.3 demonstrates the importance of eigenvalue validation by way of a family of simple examples.
In all proofs of this section, the periodic coefficients of our delay equations will be entire. By Corollary 4.1.1, we can therefore use any \(\nu >1\) in proofs that we want. For the most part we will use \(\nu =1.17\), but when we need to take \(N_2\) very large as we do in the proof of Theorem 8.2.1, it will be necessary to use a smaller \(\nu \) to balance the interval arithmetic.
Remark 8.0.1
All references to computing time in the computer-assisted proofs were as performed on a Windows 10 machine with an AMD Ryzen 5 1500X processor and 16gb of memory in MATLAB R2019b with INTLAB v12 unless otherwise stated. The times are for the entire runtime of the proof (e.g. they include interval arithmetic computations of \(M_{N_1,N_2}\)), not just the \(c_1\), \(c_2\) and \(c_3\) bound calculation. Times were done using the tic/toc MATLAB function. These times are not necessarily optimal. Different choices of modes \((N_1,N_2)\) and weight (\(\nu \)) can have a significant impact on computing time while still yielding correct proofs. The computation times include negligible overhead associated to the computation of the mesh (generated using the “fast” method from Sect. 7.1.1) for the \(c_1\) bound. The number of points in this mesh has a significant impact on computation time, and this number is generally different for each proof. See the associated MATLAB code [9] for documentation.
8.1 Time-delay predator-prey model with impulsive harvesting
The following predator-prey system is modeled off of one considered in [22]:
The difference between the above system and one cited is that instead of impulsive harvesting of prey (x), we consider impulsive harvesting of the mature predator (y). Predator age structure is taken into account, but the juvenile dynamics do not have an influence on the remaining population classes and have been neglected here. One may consult [22] for details.
There is a predator-free equilibrium, \((x^*,y^*)=(K,0)\). The linearization at this equilibrium is
This system is upper triangular and it is easy to verify that its stability (and, consequently, the dimension of the unstable manifold of \((x^*,y^*)\)) is entirely determined by the following scalar equation:
Making use of this observation, our numerical implementation of the discretized monodromy operator and implementations of the \(c_1\), \(c_2\) and \(c_3\) bounds, we can prove the following.
Theorem 8.1.1
(Pointwise stability) Suppose \(\tau \in \{1,2,3\}\). With the parameters \(\beta =0.1\), \(\rho =1\), \(K=1\), \(d_1=0.02\) and \(d_2=0.03\), the predator-free equilibrium \((x^*,y^*)=(K,0)\) of (95)–(97) is:
-
unstable if \(h=0.060\) with a one-dimensional unstable manifold,
-
locally asymptotically stable if \(h=0.075\).
Proof
(Outline) For each choice of \(\tau \) and h, we compute the interval enclosures of the discretized monodromy operator \({\mathbb {M}}\) (with a suitable number of nonconstant Chebyshev modes) with INTLAB. We then compute \(c_2\) and \(c_3\) bounds, as well as the \(c_1\) bound for Morse index validation. Following this, we count the eigenvalues of the interval matrix \({\mathbb {M}}\) with absolute value at least one. We do this using the radii polynomial approach from [6]. This count then gives the number of Floquet multipliers of (98)–(99) with absolute value greater than (and, by robustness, greater than or equal to) one. By previous observations, these results carry over to the linearization of the full system (95)–(97) at the predator-free equilibrium. \(\square \)
The results of the computer-assisted proof are tabulated in Table 1 and the approximate spectrum for \(h=0.060\) and \(\tau =3\) is plotted in Fig. 3.
We can also prove the following “robust instability” result for the system with \(\tau =1\). The results of the computer-assisted proof can be found in Table 1.
Theorem 8.1.2
(Robust instability) Suppose \(\tau =1\). With the parameters \(\beta =0.1\), \(\rho =1\), \(K=1\), \(d_1=0.02\) and \(d_2=0.03\), the predator-free equilibrium \((x^*,y^*)=(K,0)\) of (95)–(97) is unstable with a one-dimensional unstable manifold for all \(h\in [0,0.060]\).
Proof
(Outline) Let \(M_{N_1,N_2}(h)\) denote discretized the monodromy operator of (98)–(99) for harvesting parameter h (and all others fixed as in the theorem), and let M(h) be the (undiscretized) monodromy operator. We compute an interval enclosure \({\mathbb {M}}\) of the discretized monodromy operator with \(N_2=40\) nonconstant Chebyshev modes and interval parameters \(h_0=[0,0.050]\) and \(h_1=[0.050,0.060]\). Consequently, for each \(h\in h_0\), we have \(M_{0,N_2}(h)\in {\mathbb {M}}(h_0)\) and for each \(h\in h_1\), \(M_{0,N_2}(h)\in {\mathbb {M}}(h_1)\). We therefore compute upper estimates for the \(c_1\), \(c_2\) and \(c_3\) bounds for the interval matrices \({\mathbb {M}}(h_0)\) and \({\mathbb {M}}(h_1)\) using INTLAB, for Morse index validation (i.e. radius \(r=1\)). If \(c_1c_2c_3<1\), then M(h) and \(M_{0,N_2}(h)\) have the same number of eigenvalues in the complement \(B_1(0)\) for all \(h\in [0,0.060]\). By Theorem 8.1.1, we already know this number of eigenvalues is exactly one. The supplied MATLAB code completes all these calculations. \(\square \)
Left: Approximate spectrum of monodromy operator for the linearized predator-prey model (98)–(99) with parameters from Theorem 8.1.1, \(\tau =3\) and \(h=0.060\), with a unit circle for scale and visual instability reference. Right: zoomed in portion of the region in the dashed box showing the unstable Floquet multiplier (black dot)
Finally, we can accurately enclose the possible bifurcation that is identified by Theorem 8.1.1. Doing this requires:
-
selection of an interval \({\mathbf {h}}\) in which the bifurcation is contained,
-
validation of a generalized Morse index (of an appropriate radius \(r<1\)) uniformly over \({\mathbf {h}}\),
-
validation of a radial sector (of appropriate radius and sweep), uniformly over \({\mathbf {h}}\),
-
two sets of rigorous interval eigenvalue enclosures, one for each endpoint of \({\mathbf {h}}\),
-
two additional Morse index validations (at radius \(r=1\)) at the endpoints of \({\mathbf {h}}\).
The computer-assisted proof took 1155 s (19 min, 15 s) to complete. The following theorem summarizes the result, and we outline the proof in a similar manner to the previous one. Figure 4 provides a visual depiction of the combined validation structure and output of the code, while Table 2 provides the \(c_1\), \(c_2\) and \(c_3\) bounds for each step.
Theorem 8.1.3
(Bifurcation) Suppose \(\tau =1\). Let \({\mathbf {h}}=[0.065,0.066]\). With \(\beta =0.1\), \(\rho =1\), \(K=1\), \(d_1=0.02\) and \(d_2=0.03\), the predator-free equilibrium \((x^*,y^*)=(K,0)\) of (95)–(97) enjoys the following properties.
-
For all \(h\in {\mathbf {h}}\), it has a single Floquet multiplier \(\lambda (h)\) that satisfies \(|\lambda (h)|\ge 0.8\), and all other multipliers are strictly contained in the interior of the ball \(B_{0.8}(0)\subset {\mathbb {C}}\).
-
\(\lambda (h)\in R_{\lambda ^*}(r,\omega )\) with \(\lambda ^*=1\), \(r=5\times 10^{-3}\) and \(\omega =2.5\times 10^{-3}\) for all \(h\in {\mathbf {h}}\).
-
\(|\lambda (0.066)|<1<|\lambda (0.065)|\). That is, \(\lambda (h)\) crosses the unit circle at some \(h\in {\mathbf {h}}\).
Visual depiction of the content of Theorem 8.1.3 generated by the computer-assisted proof. Left: the Morse index at radius 0.8 is validated and is represented by the solid black circle. The dashed blue circle has radius 1 and is provided for comparison. At the extreme right are two eigenvalues (one for \(h=0.065\) and another for \(h=0.066\)) and the radial sector \(R_{\lambda ^*}(r,\omega )\) that are too small to resolve at this level of magnification. Right: zoomed in portion of a region within the dotted black square. The radial sector appears as a solid black curve, and the individual eigenvalues (red dots, \(h=0.065\) on the right and \(h=0.066\) on the left) can be resolved. Note that the exact location of the eigenvalues is only known up to inclusion within this radial sector and the ordering \(|\lambda (0.066)|<1<|\lambda (0.065)|\) (Color figure online)
Proof
(Outline) Similar to the previous proof, we let \(M_{N_1,N_2}(h)\) denote the discretized the monodromy operator of (98)–(99) for harvesting parameter h (and all others fixed as in the theorem), and M(h) the (undiscretized) monodromy operator. We compute an interval enclosure We compute an interval enclosure \({\mathbb {M}}\) of the discretized monodromy operator with \(N_2=150\) nonconstant Chebyshev modes and interval parameter \({\mathbf {h}}\). As such, for each \(h\in {\mathbf {h}}\) we have \(M_{0,N_2}(h)\in {\mathbb {M}}\). We therefore compute upper estimates for the \(c_2\) and \(c_3\) bounds for the interval matrix \({\mathbb {M}}\). Next, we compute \(c_1\) bounds for two validation structures:
-
1.
the ball \(B_{0.8}(0)\), for generalized Morse index validation at radius 0.8,
-
2.
the radial sector \(R_{\lambda ^*}(r,\omega )\) with \(\lambda ^*=1\), \(r=5\times 10^{-3}\) and \(\omega =2.5\times 10^{-3}\), for compact eigenvalue validation.
If \(c_1c_2c_3<1\) for the Morse index structure, we can conclude that for all \(h\in {\mathbf {h}}\), the number of eigenvalues of M(h) and \(M_{N_2,0}(h)\) in the complement of \(B_{0.8}(0)\) are constant and equal. If \(c_1c_2c_3<1\) for the radial sector structure, the number of eigenvalues of M(h) and \(M_{N_2,0}(h)\) in \(R_{\lambda ^*}(r,\omega )\) is constant and equal for all \(h\in {\mathbf {h}}\). This proves the first two points. For the final point, we need to compute \({\mathbb {M}}(0.065)\) and \({\mathbb {M}}(0.066)\), validate their eigenvalues and ensure that the eigenvalues with absolute value greater than 0.8 have rigorous enclosures contained in \(R_{\lambda ^*}(r,\omega )\) and satisfy \(|\lambda (0.066)|<1<|\lambda (0.065)|\). To ensure that this ordering is correct for the exact eigenvalues, we need to validate the Morse index at radius 1 for \(h=0.065\) and also at \(h=0.066\). Verifying rigorously that the eigenvalues (of the discretized operator) are contained within \(R_{\lambda ^*}(r,\omega )\) is accomplished with Proposition 4.3.1 and the radii polynomial approach for enclosure of eigenvalues of interval matrices from [6]. The supplied MATLAB code completes all these calculations, and we use \(\nu =1.17\) to complete the proof. As a final remark, the \(c_2\) and \(c_3\) bounds for \({\mathbb {M}}\) can be used for all validation proofs since they are by definition over-estimates for the associated \(c_2\) and \(c_3\) bounds for the interval matrices \(M_{0,N)2}(0.065)\) and \(M_{0,N_2}(0.066)\). \(\square \)
The bifurcation proven in Theorem 8.1.3 corresponds to a transcritical bifurcation of periodic solutions. There is some \(h^*\in [0.065,0,066]\) at which a nontrivial periodic solution of (95)–(97) collapses onto the equilibrium solution (K, 0). Its distance to (K, 0) is \(O(|h-h^*|)\) and it is locally asymptotically stable when \(h<h^*\). For visualization, we have provided in Fig. 5 a numerical integration of the system at the parameters where this solution is stable.
8.2 Hopf bifurcation “normal form” with symmetry-breaking delays
Consider the following planar delay differential equation with real parameter \(\beta \) and integer delay \(\tau \in {\mathbb {N}}\):
The system (100)–(101) is qualitatively similar to the normal form of the Hopf bifurcation for ODEs with angular velocity \(\pi \), except we have inserted two delays \(\tau >0\) into the nonlinear terms. The solutions of the traditional Hopf normal form are invariant under rotation about zero, but this is not the case for the system above.
\((x,y)=(0,0)\) is an equilibrium solution and as \(\beta \) crosses through zero, a supercritical Hopf bifurcation occurs. The bifurcating periodic solution is explicitly available: for given parameter \(\beta >0\) it is precisely
This follows almost immediately from the observation that \(x^*(t-\tau )=(-1)^\tau x^*(t)\) and \(y^*(t-\tau )=(-1)^\tau y^*(t)\). We are interested in the stability and possible bifurcations that can occur on this branch of periodic orbits. After some algebraic simplifications and use of trigonometric identities, one can show that the linearization at \((x^*,y^*)\) is
for \(z\in {\mathbb {R}}^2\). Note that even though the original periodic solution has period two, we can see that the linearization has period one. If we let \(U(t,s):C([-\tau ,0],{\mathbb {R}}^2)\rightarrow C([-\tau ,0],{\mathbb {R}}^2)\) denote the associated solution operator, the monodromy operator \(M:=U(2,0)\) can be factored: if we define \({\tilde{M}}:=U(1,0)\), then
due to the periodicity of the coefficients. By the spectral mapping theorem, the eigenvalues of M are the squares of the eigenvalues of \({\tilde{M}}\). Thus, to investigate the stability of \((x^*,y^*)\) it suffices to work with the monodromy operator for (102) interpreted as a periodic system with period \(p=1\) and delay \(q=\tau \), rather than period two. Also, recall that since \((x^*,y^*)\) is a periodic solution of an autonomous delay differential equation, \(\mu =1\) will always be a Floquet multiplier [14, Section XIV.2, Proposition 2.6], so we will always have \(\sqrt{\mu }\in \pm 1\) as an eigenvalue of \({\tilde{M}}\). Stability of \((x^*,y^*)\) is determined by the remaining Floquet multipliers. Namely, orbital asymptotic stability with asymptotic phase (i.e. asymptotic stability modulo phase difference) occurs if all other multipliers have modulus less than one, and instability occurs if there is a multiplier with modulus greater than one.
Left: numerical simulation of the system (95)–(97) at the parameters \(\tau =1\), \(\beta =0.1\), \(\rho =1\), \(K=1\), \(d_1=0.02\), \(d_2=0.03\), \(r=0.7\) and \(h=0.06\) from the constant initial condition \((x_0,y_0)=(1,0.01)\) for \(t\in [0,2000)\). The equilibrium \((x,y)=(1,0)\) is unstable by Theorem 8.1.2. The x component is the top curve (black) and y is the blue curve (bottom). The discontinuities occurring at the integers make the y curve difficult to resolve (note the varying “thickness” of the curve with respect to t). Top right: x component windowed to \(t\in [1995,2000)\). Bottom right: y component with the same windowing. At this resolution the converged periodic solution (of period 1) is easily discernible
Since each of \(\cos (2\pi t)\) and \(\sin (2\pi t)\) (the nontrivial time-varying coefficients in (102)) can be generated as solutions of the two-dimensional linear ODE
we can:
-
get the terms of the truncated Chebyshev series of \(\cos (\pi (s-1))\) and \(\sin (\pi (s-1))\) with rigorous interval enclosures (for a partiaular level of discretization) using monodromy operator discretization on (104);
-
obtain bounds for the absolute error in the truncated coefficients using the discretization error \(c_2c_3\);
-
bound the tails using the discretization error.
This information is then used to obtain interval enclosures of the truncated Chebyhev series of the matrices in (102) (after transforming the time domain from \(t\in [-1,0]\) to \(s\in [-1,1]\)) and bounds on the tails. Using our rigorous numerical method, we can prove then prove the following theorem.
Theorem 8.2.1
Let \(\tau =1\). The unstable manifold of the nontrivial periodic solution \((x^*(t),y^*(t))\) of the two-dimensional Hopf-like normal form (100)–(101) at parameter \(\beta =\frac{3}{2}\) is at least two-dimensional.
Proof
(Outline) We validated the radial sector \(R_{\lambda ^*}(r,\omega )\) with
The validation was done at \(N_1=65\), \(N_2=1000\) and \(\nu =1.04\). We used the radii polynomial method and Proposition 4.3.1 to prove that \({\tilde{M}}_{N_1,N_2}\) has exactly one eigenvalue within this radial sector. As the non-real eigenvalues of the monodromy operator come in complex-conjugate pairs and \(R_{\lambda ^*}(r,\omega )\) does not intersect the real axis, we conclude that there is also a conjugate eigenvalue. By Lemma 4.3.2, the (undiscretized, true) monodromy operator \({\tilde{M}}\) has a pair of complex-conjugate eigenvalues contained in the union of \(R_{\lambda ^*}(r,\omega )\) and its reflection over the real axis. This sector is strictly outside of the unit disc in the complex plane, so the eigenvalues have absolute value greater than one. From our observations above concerning the spectral mapping theorem and the relationship between the eigenvalues of M and \({\tilde{M}}\), we conclude the unstable manifold of the periodic solution \((x^*(t),y^*(t))\) is at least two-dimensional. See Fig. 6 for the validation structure and approximate eigenvalues. \(\square \)
The black dots are the eigenvalues of the finite (matrix) part of the operator \({\tilde{M}}_{N_1,N_2}\). Observe that \(-1\) is a (numerical) eigenvalue, which is consistent with the discussion following (103). The radial sector \(R_{\lambda ^*}(r,\omega )\) from the proof of Theorem 8.2.1 appears in blue. The unit circle is provided for relative scale, and is delineated by a black dashed curve. The gap between the radial sector and the unit circle is very small and difficult to resolve in the figure: in the radial direction the length of the gap is bounded below by \(3.4\times 10^{-3}\)
The attractor of the planar system (100)–(101) at \(\tau =1\) and \(\beta =\frac{3}{2}\). Computed by forward integration in ddde23 for \(t\in [0,2000]\) and truncated to [1000, 2000]. The delayed variable \(y(t-2)\) is included to realize the embedding of the two-dimensional manifold (equivalent to a torus) in three-dimensional space
The proof is computationally expensive. Based on some heuristics, we would expect an unparallelized version of the proof to take approximately 23 days to complete on our machine. Almost all of this time is due to the lengthy \(c_1\) bound calculation. To speed up the computation for the proof, we distributed the load over our primary machine and a laptop running an Intel Core i7 5950HQ with 32GB of memory. Each machine then ran five simultaneous instances of MATLAB, and each instance was tasked with 1/10 of the load associated to the \(c_1\) bound. The script at [9] includes a parameter that controls which section of the proof is to be completed, and it was this script that was simultaneously run on the ten MATLAB instances. Doing the proof this way, it took a bit over two days to complete. The results are found in Table 3.
This theorem provides strong evidence for the existence of an invariant torus, since the two unstable Floquet multipliers would need to have crossed through the unit circle between \(\beta =0\) and \(\beta =\frac{3}{2}\). The likely scenario is that this would have occured at a Neimark-Sacker bifurcation. Numerical integration of the delay differential equations does indeed reveal an attracting, invariant torus: see Fig. 7.
8.3 Spurious flower petals
This final example demonstrates the importance of validated numerics. It also provides some aesthetically pleasing figures. Consider the following piecewise-constant delay equation:
where \(\tau \) is a nonnegative integer and \(c\in {\mathbb {R}}\). It is worth mentioning that this equation is notoriously difficult to integrate to high precision.
Proposition 8.3.1
For any nonnegative integer delay \(\tau \) and \(c\in {\mathbb {R}}\), the only nonzero Floquet multiplier of (105) is \(\mu =1\).
Proof
Let \(x(t)=\phi (t)e^{t\lambda }\) be a Floquet eigensolution—that is, \(\lambda \in {\mathbb {C}}\) and \(\phi \) complex-valued with period 2. Let \(V(\lambda )=\left[ \begin{array}{cc}0&{}-ce^{-\lambda \tau }\\ ce^{-\lambda \tau }&{}0\end{array}\right] \). Then
Case 1: \(\tau \) is even. Then \(\phi (t-\tau )=\phi (t)\) since \(\phi \) is periodic with period 2. Then
One can verify that the matrices \(-\lambda I + V(\lambda )\) and \(-\lambda I-V(\lambda )\) commute, from which it follows that the solution \(\phi (t)\) of the above differential equation satisfies
Since \(\phi \) is nontrivial, we must have \(\lambda =0\). Therefore \(\mu =e^0=1\) is the only nonzero Floquet multiplier.
Case 2: \(\tau \) is odd. Define \(\phi _0(t)=\phi (t)\) and \(\phi _1(t)=\phi (t-1)\). Since \(\phi \) is periodic with period 2, we have \(\phi _0(t-\tau )=\phi _1(t)\) and \(\phi _1(t-\tau )=\phi _0(t)\). The pair \((\phi _0,\phi _1)\) therefore satisfies the ODE
The matrices \(M_1=-\lambda I_{4\times 4} + \text{ diag}^\perp (V(\lambda ),-V(\lambda ))\) and \(M_2=-\lambda I_{4\times 4} - \text{ diag}^\perp (V(\lambda ),-V(\lambda ))\) commute, where \(\text{ diag}^\perp (A,B)=\left[ \begin{array}{cc}0&{}\quad A\\ B&{}\quad 0\end{array}\right] \). It follows that \(\mathbf {\phi }(t)=(\phi _0(t),\phi _1(t))\) satisfies
As \(\phi \) is nontrivial, we must have \(\lambda =0\). Therefore \(\mu =e^0=1\) is the only nonzero Floquet multiplier. \(\square \)
Even though \(\mu =1\) is the only Floquet multiplier, the discretized operator \(M_{N_1,N_2}\) has some rather interesting flower petal-shaped numerical eigenvalue patterns that are present for seemingly arbitrarily high level of modes \(N_2\) (note: \(N_1=0\) for this problem). The latter is a common element of the spurious eigenvalue phenomenon [12]. We provide plots of the eigenvalues of \(M_{N_1,N_2}\) in Fig. 8 for \(c=10\), \(\tau =3,5,7\) and various values of \(N_2\). We should also emphasize that neither the radii polynomial method [6] nor verifyeig (applied to validation of distinct eigenvalues) from INTLAB [24] are able to verify any of the eigenvalues of the associated matrices \(M_{N_1,N_2}\), so even if we were able to numerically verify \(c_1c_2c_3<1\) for for the closed circle with radius \(r=0.99\) (which seems bounded away from the all of the discretized spectra), we would be unable to prove using a computer that there is an eigenvalue with absolute value greater than 0.99.
Eigenvalues in the complex plane (horizontal axis real, vertical axis imaginary) of the discretized monodromy operator \(M_{N_1,N_2}\) as computed by eig in MATLAB for the two-dimensional system (105) with \(c=10\). Since the periodic coefficient \((-1)^{\lfloor t \rfloor }\) is piecewise-constant, \(N_1=0\). Plots are provided for \(\tau =3,5,7\) and \(N_2=50,200,400\). Though the figures are not reported here, we did the same calculation with \(N_2=1000\) and the same “flower petal” patterns were present
Another interesting observation is that the diameter of the “flower” portion of the eigenvalue pattern seems to be proportional to the parameter c. We do not provide figures demonstrating this scaling but refer the reader to the MATLAB code [9] where they may adjust the parameters \(\tau \), c and \(N_2\) as desired. Even with \(c=10^{-2}\), none of the eigenvalues (treated as distinct, as opposed to clusters) can be validated with the radii polynomial method or verifyeig.
9 Examples with floating point arithmetic
It is worthwhile doing some large-scale tests of our numerical method for monodromy operator discretization of impulsive delay differential equations in floating point arithmetic. In particular, we are interested in how fast our implementation is for larger systems.
9.1 Methodology: examples with periodic coefficients
We generated six systems of the form (10)–(11) for each dimension \(d=10,50\). The delays were \(q\in \{1,2,3\}\) and the periods \(p\in \{1,2\}\), so that each combination of delay and period is seen at each dimension. The systems were constructed as follows.
-
1
The matrices A(t) and B(t) were designed at the Chebyshev level. After transformation to the \(s\in [-1,1]\), suppose we write truncated Chebyshev series for the restriction of one of A(t) or B(t) to an integer-length interval \(t\in [n,n+1]\) as
$$\begin{aligned} S_0 + 2\sum _{k=1}^{N_1}S_kT_k(s) \end{aligned}$$for \(d\times d\) matrices \(S_k\) and \(T_k\) the kth Chebyshev polynomial. The entries of \(S_k\) are drawn from the uniform distribution on \(2^{-k}[-1,1]\) to simulate analytic coefficients with geometric decay rate 2. We took \(N_1=50\) so that all remaining terms of this (presumably) analytic function would have norm bounded above by \(9\times 10^{-16}\). The coefficients are then rescaled by a random number drawn from uniform [0, 1].
-
2
The \(C_1\) matrices was designed to induce contraction (or at least non-expansion). We first generate a random matrix D by sampling entries from the uniform distribution on \([-1,1]\). We then take k to be sampled from the uniform [0, 1] and define
$$\begin{aligned} C_1=\frac{k}{||D||}D-I_{d\times d}. \end{aligned}$$By construction, \(||I+C_1||=k\le 1\), so the effect of the impulse due to \(C_1\) is nonexpansive (contractive if \(k<1\)).
-
3
The \(C_2\) matrices was taken to be a (relatively) small and random. Their entries were drawn from the normal distribution with mean \(\mu =0\) and variance \(\sigma ^2=10^{-1}\), truncated to the interval \([-10^{-1},10^{-1}]\).
9.2 Methodology: examples with piecewise-constant coefficients
With constant coefficient systems it makes sense to look at lower-mode discretizations (since we do not need to take into account the standing hypothesis \(N_2>N_1\)). This also gives us more flexibility (in terms of computer memory) to look at systems of higher dimension. We look this time at systems of dimension \(d=10,50\) and also 100. Our design methodology is identical to the periodic coefficients case except that we take \(N_1=0\) so that our Chebyshev series for A(t) and B(t) have zero nonconstant modes (i.e. A(t) and B(t) are piecewise constant).
9.3 Results
Remark 9.3.1
All references to computing time were as performed on a Windows 10 machine with an AMD Ryzen 5 1500X processor and 16gb of memory in MATLAB R2019b. All operations were completed in 64-bit floating point arithmetic. Times were done using the tic/toc MATLAB function. While this is relatively accurate for long computations, short computations are subject to jitter and the actual computation time might be shorter.
Before we begin presenting the results, we should briefly mention that due to how we have designed the matrices A(t), B(t), \(C_1\) and \(C_2\), it is expected that higher-dimensional problems we study will be unstable (in the sense of Lyapunov stability) and therefore have larger spectral radii \(\sigma (M_{N_1,N_2})\). Intuitively, this is because since these have been generated randomly there is greater potential for multilayered feedback mechanisms to overwhelm the contraction generated by \(I+C_1\).
The time needed to compute \(M_{N_1,N_2}\) in floating point arithmetic for each tuple of dimension, period, delay and number of modes \((d,p,q,N_2)\) is stated in Tables 4 and 5 for the systems with periodic coefficients. The systems with constant coefficients have the results stated in Tables 6, reftablespsfp50c and 8. The spectral radius of \(M_{N_1,N_2}\) for each tuple is also stated, so that one can compare the predicted spectral radius (and inferred stability) as the order (i.e. number of modes) increases. We should emphasize that the part of \(M_{N_1,N_2}\) that lives in memory (i.e. the finite part) is a \(qd(N_2+1)\times qd(N_2+1)\) matrix. The construction of each such matrix requires storing other large matrices in memory and multiplying them. In those instances where we were unable to complete the calculation because we ran out of memory, the associated entry in the table is flagged “OOM” (Out Of Memory).
From the point of view of spectral radius approximation, we see that computing more than \(N_2=50\) nonconstant modes does not improve precision. For example, comparing the results for the systems with periodic coefficients, the estimations of \(\sigma (M_{N_1,N_2})\) agree to \(10^{-13}\) precision for each problem (i.e. fixed p and q). Thus, at least insofar as stability verification is concerned, there is no reason to use more than \(N_2=50\) nonconstant modes. The same trend is present for the systems with piecewise-constant coefficients. Going further, comparing from \(N_2=10\) to \(N_2=50\) modes, we see that the spectral radius calculations agree to \(10^{-8}\) for all problems of dimension \(d=10,50\), and to \(10^{-4}\) for the 100-dimensional problems.
10 Conclusions
We have developed a numerical method for the discretization of the monodromy operator associated for impulsive delay differetial equations with periodic coefficients. The method is able to accomodate systems where the period and delay are commensurate: that is, their ratio is a rational number. The numerical scheme is based Chebyshev collocation: we identify concrete linear operators that act on Chebyshev series coefficients that represent sufficiently smooth initial conditions to the impulsive delay differential equation. We also represent the periodic coefficients in the Chebyshev polynomial basis (with matrix coefficients). Truncating the number of modes at the level of the inputs (initial conditions) and at the level of the periodic coefficients yields a numerical method.
An advantage of our framework is that it is amenable to computer-assisted proofs concerning the location of Floquet multipliers based on the discretized monodromy operator. In Sect. 6 we proved explicit and computable formulas for quantities \(c_1\), \(c_2\) and \(c_3\) such that if \(c_1c_2c_3<1\), the location of the Floquet multipliers of the impulsive DDE relative to a specified validation structure has the same location as analogous eigenvalues of the discretized monodromy operator. These structures include specific compact sets in the complex plane that are bounded away from the origin (e.g. radial sector validation) and complements of closed discs centered at zero (i.e. generalized Morse index validation).
We implemented our numerical scheme for arbitrary integer period p and delay q in MATLAB. We also implemented the bounds \(c_1\), \(c_2\) and \(c_3\) for the cases \(p=q=1\) and \(1=p<q\). We demonstrated the computer-assisted proof techniques on two problems. The first was a scalar problem motivated by a model from mathematical ecology. For this problem we first proved binary stability/instability results by validating a Morse index at radius 1. We then proved some robust stability and bifurcation enclosure results. The second example was a two-dimensional nonlinear system modeled off of the Hopf bifurcation normal form. We linearized about a periodic solution and verified using our method that at a particular parameter value, the unstable manifold of this periodic solution is two-dimensional.
We tested our numerical implementation in floating point arithmetic on several problems. The implementation is fast for problems of moderate (\(\le 50\)) dimension and a reasonable number (\(N_2 \le 50\)) of modes provided p and q are fairly small. For the test problem of calculating the spectral radius of the monodromy operator, there was not a significant difference in relative accuracy when the number of modes \(N_2\) was dramatically increased (i.e. from 50 to 100 or from 100 to 200), so fewer modes (e.g. 10 to 50) may be perfectly suitable for situations where validated numerics are not needed. As should be expected, the computing time and memory requirements become steep as the (rescaled, relative to period) delay q increases. Some of the matrices needed to compute \(M_{N_1,N_2}\) are sparse, so memory could be saved with a sparse matrix implementation at the cost of speed. Moreover, our implementation for arbitrary period and delay outlined in Sect. 7.2 has some inefficiencies and could certainly be improved.
It should be emphasized that the extra dimensions (of which there are \((q-1)(N_2+1)\)) in the discretization due to the delay q are only present because of our stated goal of developing not only a rigorous numerical method, but also techniques for computer-assisted proof of Floquet multiplier location. Indeed, the extra dimensions are necessary to ensure that all eigenfunctions can be represented as uniformly convergent Chebyshev series with coefficients in \(X_\nu \). However, if one were to expand the solutions in terms of other basis functions and the form of convergence was taken to be more coarse (e.g. \(L^2\) convergence), a faster numerical method could be developed that does not suffer from this drawback. However, such a method would likely not be as well-suited to computer-assisted proof of eigenvalue location and proving its convergence might be difficult.
We have claimed that our approach to computer-assisted proof could be extended to the case where the period is greater than the delay: \(p>q\). We elaborate on this briefly now by way of an example. Suppose that \(p=2\) and \(q=1\). Let \(M_1=(I-W_1)^{-1}E_1\) denote the operator that sends an initial condition at time \(t=0\) to its value at time \(t=1\) after flowing along the dynamical system (10)–(11). Similarly, Let \(M_2=(I-W_2)E_2\) be the operator that an initial condition from time \(t=1\) forward to time \(t=2\). Then \(M=M_2M_1\) is the monodromy operator. If \({\tilde{E}}_1\), \({\tilde{W}}_1\), \({\tilde{E}}_2\) and \({\tilde{W}}_2\) are approximations of \(E_1\), \(W_1\), \(E_2\) and \(W_2\), then one may be interested in adapting Lemma 4.3.1 to the operator M and its “approximation” \({\tilde{M}}={\tilde{M}}_2{\tilde{M}}_1\), with \({\tilde{M}}_2=(I-{\tilde{W}}_2)^{-1}{\tilde{E}}_2\) and \({\tilde{M}}_1=(I-{\tilde{W}}_1)^{-1}{\tilde{E}}_1\). Observe that
The norm of \({\tilde{M}}_1\) can (presumably) be obtained precisely using a computer. Each of \((I-{\tilde{W}}_2)^{-1}\) and \((I-W_2){\tilde{M}}_2 - E_2\) are formally analogous to operators that are bounded above by \(c_2\) and \(c_3\) in our present proof of Lemma 4.3.1. The latter lemma can technically be applied as stated to obtain a bound on the norm of \({\tilde{M}}_1-M_1\). As for \(E_2\), its norm can in principle be estimated by writing
computing a bound for the norm of \({\tilde{E}}_2\) on a computer, and deriving a computable bound for the norm of the error \(E_2-{\tilde{E}}_2\) by careful inspection. In summary, there should be an explicit computable bound for the norm of \({\tilde{M}}-M\) and its computation will involve similar estimates to those involved in the statement of Lemma 4.3.1, so we would expect many of the bounds from Sect. 6 to be be applicable. The rest of the proof could be carried out essentially verbatim. The above argument can be extended to general commensurate period-delay pairs.
References
Akhmet, M: Principles of discontinuous dynamical systems. Springer, New York, New York, NY (2010)
Bainov, D., Simeonov, P.: Impulsive Differential Equations: Periodic Solutions and Applications. Chapman and Hall/CRC, (1993)
Breda, D.: Computing the characteristic roots for delay differential equations. IMA Journal of Numerical Analysis 24(1), 1–19 (2004)
Breda D, Maset S, Vermiglio R (2005) Characteristic roots of delay differential. SIAM J. Sci. Comput 27(22), 482–495
Breda, D., Maset, S., Vermiglio, R.: Pseudospectral approximation of eigenvalues of derivative operators with non-local boundary conditions. Appl. Numer. Math., 56:318–331 (2006)
Castelli, R., Lessard, J.-P.: A method to rigorously enclose eigenpairs of complex interval matrices. In: Conference Applications of Mathematics 2013 in Honor of the 70th Birthday of Karel Segeth. Institute of Mathematics AS CR, Prague 2013, pp. 1–11 (2013)
Cepeda-Gomez R, Michiels W (2015) Special cases in using the matrix Lambert W function for the stability analysis of high-order linear systems with time delay. IFAC-PapersOnLine 28(12), 7–12
Church, K.: Invariant Manifold Theory for Impulsive Functional Differential Equations with Applications. Ph.D. thesis, University of Waterloo (2019)
Church, K.E.M.: Codes to accompany Eigenvalues and delay differential equations: periodic coefficients, impulses and rigorous numerics (2020). https://github.com/kemchurch/IFDE_spectral_methods/tree/master/JDDE-2020
Church KEM, Liu X (2018) Smooth centre manifolds for impulsive delay differential equations. J. Differ. Equ. 265(4), 1696–1759
Church KEM, Liu X (2019) Computation of centre manifolds and some codimension-one bifurcations for impulsive delay differential equations. J. Differ. Equ. 267(6), 3852–3921
Dawkins PT, Dunbar SR, Douglass RW (1998) The origin and nature of spurious eigenvalues in the spectral Tau method. J. Comput. Phys. 147(2), 441–462
Diamond P (1990) Impulsive evolution equations and population models. In: Vincent TL, Mees AI, Jennings LS (eds) Dynamics of Complex Interconnected Biological Systems. Birkhäuser, Boston, pp. 175–203
Diekmann O, Verduyn Lunel SM, van Gils SA, Walther H-O (1995) Delay Equations: Functional-, Complex-, and Nonlinear Analysis, Applied Mathematical Sciences. Springer, New York
Engelborghs, K.: DDE-BIFTOOL: A Matlab Package for Bifurcation Analysis of Delay Differential Equations. Technical report (2000)
Gilsinn DE, Potra FA (2006) Integral operators and delay differential equations. J. Integr. Equ. Appl. 18(3), 297–336
Ivanov, I.L., Slyn’Ko, V.I.: A stability criterion for autonomous linear time-lagged systems subject to periodic impulsive force. International Applied Mechanics 49(6), 732–742 (2013)
Jarlebring E, Meerbergen K, Michiels W (2010) A Krylov method for the delay eigenvalue problem. SIAM J. Sci. Comput. 32(6), 3278–3300
Kato T (1995) Perturbation Theory for Linear Operators Classics in Mathematics, vol. 132. Springer, Berlin
Lakshmikantham, V., Bainov, D.D., Simeonov, P.S.: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Lessard, JP, Mireles James JD (2019) A functional analytic approach to validated numerics for eigenvalues of delay equations. J. Comput. Dyn., 7, 123
Meng X, Jiao J, Chen L (2008) The dynamics of an age structured predator-prey model with disturbing pulse and time delays. Nonlinear Anal. Real World Appl. 9(2), 547–561
Miyajima S (2017) Verified solutions of delay eigenvalue problems. Appl. Math. Comput. 303, 211–225
Rump SM (1999) INTLAB—INTerval LABoratory. In: Tibor C (ed) Developments in Reliable Computing. Kluwer Academic Publishers, Dordrecht, pp 77–104
Samoilenko AM, Perestyuk NA (1995) Impulsive Differential Equations, World Scientific Series on Nonlinear Science Series A. World Scientific, Singapore
Sieber J, Szalai RR (2011) Characteristic matrices for linear periodic delay differential equations. SIAM J. Appl. Dyn. Syst. 10(1), 129–147
Slynko VI, Tunç C, Erdur S (2020) Sufficient conditions of interval stability of a class of linear impulsive systems with a delay. J. Comput. Syst. Sci. Int. 59(1), 88–18
Stamova I (2009) Stability Analysis of Impulsive Functional Differential Equations. De Gruyter, Berlin
Szalai, R.: Knut: A Continuation and Bifurcation Software for Delay-differential Equations
Szalai R, Stépán G, John Hogan S (2006) Continuation of bifurcations in periodic delay–differential equations using characteristic matrices. SIAM J. Sci. Comput. 28(4), 1301–1317
Trefethen LN (2013) Approximation Theory and Approximation Practice. Society for Industrial and Applied Mathematics, Philadelphia
Verduyn Lunel, S.M.: Small solutions and completeness for linear functional differential equations. In: Oscillations and Dynamics in Delay Equations, Contemporary Mathematics, vol. 129. AMS, Providence, pp. 127–152 (1992)
Zhen W, Michiels W (2012) Reliably computing all characteristic roots of delay differential equations in a given right half plane using a spectral method. J. Comput. Appl. Math. 236(9), 2499–2514
Acknowledgements
The author thanks Jean-Philippe Lessard for some helpful technical discussions. Kevin E. M. Church acknowledges the support of NSERC (Natural Sciences and Engineering Research Council of Canada) through the NSERC Postdoctoral Fellowships Program.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Table of useful norm bounds
Table of useful norm bounds
The two linear operators expressed in Lemma 5.1.3 appear often in estimates concerning the \(c_2\) and \(c_3\) bound, and they are often accompanied by a projection operator. Several other auxiliary operator norms are also required. Here, we list such operators and upper bounds on their norms (in the appropriate spaces of linear maps) in the form of a table. We then prove each bound directly. In what follows, we always have \(\nu >1\), \(U,Y\in \ell _\nu ^1({\mathbb {C}}^d)\) and \(N_2>N_1\ge 0\). Also, let \({\mathbf {Q}}^{-1}(Y)\), \(\mathbf {DT}\), \({\mathbf {H}}_1^0\), \(Z_k^{N_1,N_2}\) and \(S(Y^{N_1})\) be defined as at the beginning of Sect. 6.
Row | Linear map \(F:X\rightarrow Y\) | Bound for \(||F||_{L(X,Y)}\) |
|---|---|---|
1 | \(H_2:\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(\displaystyle 2+\left( \frac{1}{\nu }-\nu \right) \tanh ^{-1}\left( \frac{1}{\nu }\right) \equiv g(\nu )\) |
2 | \(H_2(Y*\pi _{N_2}^\infty ):\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(\displaystyle \frac{2}{\nu ^{N_2+1}}\left( ||Y^{N_1}||_\nu + \left( 1+\frac{1}{\nu ^{N_2+1}}\right) ||Y^\infty ||_\nu \right) \) |
3 | \(H_1:\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\displaystyle \frac{1}{2}+\frac{\nu }{4}\) |
4 | \(\pi _{N_2}^\infty H_1:\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\displaystyle \frac{\nu +\nu ^{-1}}{4(N_2+1)}\) |
5 | \(S:\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(\max \{1,2\nu ^{-1}\}\) |
6 | \(S\pi ^\infty _{N_2}:\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(2\nu ^{-(N_2+1)}\) |
7 | \(S^*\pi _{N_2}^\infty :\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \( 2\nu ^{-(N_2+1)}\) |
8 | \({\widetilde{Q}}^{-1}(Y^{N_1})\pi ^{N_2}:\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\displaystyle \max _{k=0,\dots ,N_2}\frac{1}{\nu ^k}\sum _{j=0}^{N_2}||\mathbf {{\widetilde{Q}}}^{-1}_{j,k}(Y^{N_1})||\nu ^j\) |
9 | \({\widetilde{Q}}^{-1}(Y^{N_1}){\mathbf {e}}_0:{\mathbb {C}}^d\rightarrow \ell _\nu ^1\) | \(\displaystyle \sum _{j=0}^{N_2}||\mathbf {{\widetilde{Q}}}^{-1}_{j,0}(Y^{N_1})||\nu ^j\) |
10 | \(S{\widetilde{Q}}^{-1}(Y^{N_1})\pi ^{N_2}:\ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(\displaystyle \max _{k=0,\dots ,N_2}\frac{1}{\nu ^k}\left( ||\mathbf {{\widetilde{Q}}}^{-1}_{0,k}(Y^{N_1})|| + 2\sum _{n=1}^{N_2}||\mathbf {{\widetilde{Q}}}^{-1}_{n,k}(Y^{N_1})||\right) \) |
11 | \(S{\widetilde{Q}}^{-1}(Y^{N_1}){\mathbf {e}}_0:{\mathbb {C}}^d\rightarrow {\mathbb {C}}^d\) | \(\displaystyle ||\mathbf {{\widetilde{Q}}}^{-1}_{0,0}(Y^{N_1})|| + 2\sum _{j=1}^{N_2}||\mathbf {{\widetilde{Q}}}^{-1}_{j,0}(Y^{N_1})||\) |
12 | \({\widetilde{Q}}^{-1}(Y^{N_1})\pi ^{N_2}H_1(U^{N_1}*\pi _{N_2}^\infty ):\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\begin{array}{lll} &{}\displaystyle \max _{k=0,\dots ,N_1}\frac{1}{\nu ^{N_2+1+k}}\sum _{j=0}^{N_2} (\frac{||U^{N_1}||_\omega }{(N_2+1-N_1)^2-1}||\mathbf {{\widetilde{Q}}}^{-1}_{j,0}||\\ &{}\quad + ||\mathbf {{\widetilde{Q}}}^{-1}_{j}\mathbf {DT}Z_k^{N_1,N_2}{\mathbf {S}}(U^{N_1})||)\nu ^j \end{array}\) |
13 | \(\pi ^{N_2}H_1(Y^{N_1}*\pi _{N_2}^\infty ):\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\begin{array}{lll} &{}\displaystyle \max _{k=0,\dots ,N_1}\frac{1}{\nu ^{N_2+1+k}}\sum _{j=0}^{N_2} (\frac{||U^{N_1}||_\omega }{(N_2+1-N_1)^2-1}\mathbb {1}_0(j) \\ &{}\quad + ||\mathbf {DT}_jZ_k^{N_1,N_2}{\mathbf {S}}(U^{N_1})||)\nu ^j \end{array} \) |
14 | \(\pi _{N_2}^\infty H_1(Y^{N_1}*\pi _{N_2}^\infty ):\ell _\nu ^1\rightarrow \ell _\nu ^1\) | \(\displaystyle \frac{1}{4(N_2+1)}\left( \left( \nu +\frac{2}{\nu } + \frac{1}{\nu ^3}\right) ||Y^{N_1}||_\nu - \left( \frac{1}{\nu }+\frac{1}{\nu ^3}\right) ||Y^{N_1}_0||\right) \) |
15 | \(H_2(\pi ^{N_2}{\widetilde{Q}}^{-1}(Y^{N_1})H_1(U_1^{N_1}*\pi _{N_2}^\infty )): \ell _\nu ^1\rightarrow {\mathbb {C}}^d\) | \(\begin{array}{lll} &{}\displaystyle {\mathbf {m}}_0 + \sum _{k=2}^{N_2}\frac{(-1)^k+1}{k^2-1}{\mathbf {m}}_k, \\ &{}\displaystyle {\mathbf {m}}_k = \max _{j=0,\dots ,N_1}\frac{1}{\nu ^{N_2+1+j}}(\frac{||U^{N_1}||_\omega }{(N_2+1-N_1)^2-1}||\widetilde{{\mathbf {Q}}}_{k,0}^{-1}||\\ &{}\quad + ||\mathbf {\widetilde{ Q}}^{-1}_k\mathbf {DT}{\tilde{Z}}_j^{N_1,N_2}{\mathbf {S}}(U^{N_1})|| ) \end{array}\) |
1.1 Proofs of the bounds from the table in Appendix A
This subsection will be structured with proofs being completed by row. The row number will be stated and a proof will immediately follow.
1.1.1 Proof of Row 1
Let \(h\in \ell _\nu ^1\) satisfy \(||h||_\nu \le 1\). Then
1.1.2 Proof of Row 2
Let \(h\in \ell _\nu ^1\) satisfy \(||h||_\nu \le 1\). Then with \(h^\infty = \pi _{N_2}^\infty h\),
Conversely, one can check that \(||H_2(Y^{N_1}*h^\infty )||\le \frac{2}{\nu ^{N_2+1}}||Y^{N_1}||_\nu \) by a similar argument.
1.1.3 Proof of Row 3
1.1.4 Proof or Row 4
Let \(h\in \ell _\nu ^1\) satisfy \(||h||_\nu \le 1\).
1.1.5 Proof of Row 5
Write \(h\in \ell _\nu ^1\) with \(||h||_\nu = 1\) as \(h = h^0 + h^\infty \), where \(h^0=(h_0,0,\dots )\). Set \(\lambda =||h^0||\). Then \(||h^\infty ||_\nu = 1-\lambda \) and
1.1.6 Proof of Row 6/7
The proof for \(S^*\) is essentially identical.
1.1.7 Proof of Row 8
We will apply Lemma 5.2.1 to the operator \(L:X_\nu \rightarrow X_\nu \) for \(X_\nu ={\mathbb {C}}^d\times \ell _\nu ^1\), with \(Lh = (0,{\widetilde{Q}}^{-1}\pi ^{N_2} h_0)\). By construction,
for \(0\le j\le N_2\) and is zero for all other indices. In that notation L consists of only a V-type operator. Then \(||L||_{B(X_\nu )}\) is bounded above by
and we obtain the bound for \(||\widetilde{Q}^{-1}\pi ^{N_2}||_{B(\ell _\nu ^1)}\) by restriction.
1.1.8 Proof of Row 9
Let \(z\in {\mathbb {C}}^d\). Then
The proof is then similar to the one for Row 8. Apply Lemma 5.2.1 to the linear operator \(L:X_\nu \rightarrow X_\nu \) with \(Lh = ({\widetilde{Q}}^{-1}{\mathbf {e}}_0h(0),0)\). In the notation of the lemma, L consists of only a U-type operator.
1.1.9 Proof of Row 10/11
Apply Lemma 5.2.1 to \(L:X_\nu \rightarrow X_\nu \) with \(Lh=(S{\widetilde{Q}}^{-1}\pi ^{N_2}h_0,0)\). In the notation of the lemma, L consists of only a T-type operator and \(T(0)=0\). The result for row 10 then follows by definition of \({\mathbf {Q}}^{-1}\). The proof for row 11 is similar and omitted.
1.1.10 Proof of Row 12/13
Since \({\widetilde{Q}}^{-1}\pi ^{N_2}=\pi ^{N_2}{\widetilde{Q}}^{-1}\pi ^{N_2}\) (Lemma 5.1.2), we can really think of \({\widetilde{Q}}^{-1}\pi ^{N_2}\) as being the infinite block diagonal matrix \({\widetilde{Q}}^{-1}\pi ^{N_2} = \text{ diag }(\mathbf {{\widetilde{Q}}^{-1}},0^\infty )\), where \(0^\infty \) represents the infinite zero block. To represent the operator-valued convolution \((U^{N_1}*\pi _{N_2}^\infty )\), we write
where convolution acts “column-wise” and the first nonzero column is at index \(N_2+1\). Lemma 5.2.1 implies the bound
where we have abused notation and allowed the row-column indices for \(\widetilde{{\mathbf {Q}}}^{-1}\) to run greater than \(N_2\) by treating the associated blocks as zero. It is our job to make this expression more explicit. First, observe that since only the (block) rows \(0,\dots ,N_2\) of \(\widetilde{{\mathbf {Q}}}^{-1}\) can be nonzero, we need only explicitly compute the rows \(0,\dots ,N_2\) of the product \((H_1^0+DT)(U^{N_1}*\pi _{N_2}^\infty )\).
We first concentrate on \(H_1^0(U^{N_1}*\pi _{N_2}^\infty )\). \(H_1^0\) has only one nontrivial row (the zero row), and for computations later the only observation we need to make is that if \(N_2>N_1\), then we have the bound
This follows because \((U^{N_1}*\pi _{N_2}^\infty )_k=0\) for \(k\le N_2\), while the first nonzero entry for \(k\ge N_2+1\) occurs at index \(N_2+1-N_1\). The calculation is then straightforward given the definition of \(H_1^0\). Denote \({\mathbf {N}}=N_2+1-N_1\) for later.
Next we deal with \(DT(U^{N_1}*\pi _{N_2}^\infty )\). Restricting to the block “rows” \(0,\dots ,N_2\) of the infinite matrix DT, only the “columns” \(0,\dots ,N_2+1\) are nonzero. Thus, we need only explicitly compute those columns of \(U^{N_1}*\pi _{N_2}^\infty \) that are nonzero at or above row index \(N_2+1\). The final column index where this is satisfied is \(N_2+1+N_1\), and one can verify that the first \(N_2+1\) rows correspond precisely to \({\tilde{Z}}_k^{N_1,N_2}{\mathbf {S}}(U^{N_1})\) for \(N_2+1\le k\le N_2+1+N_1\). Finally, we already know that \((U^{N_1}*\pi _{N_2}^\infty )_k=0\) for \(0\le k\le N_2\).
We now combine all of the previous discussion. Our bound becomes
The proof for row 13 follows by formally replacing \(\widetilde{Q}^{-1}\) with the identity.
1.1.11 Proof of Row 14
Denote \(e^k\in L({\mathbb {C}}^d,\ell _\nu ^1)\) the map defined by \((e^k z)_n = \delta _{k,n}z\) for \(\delta \) the Kronecker delta. The operator \(\pi _{N_2}^\infty H_1(A_1^{N_1}*\pi _{N_2}^\infty )\) satisfies for \(\pi _{N_2}^\infty H_1(A_1^{N_1}*\pi _{N_2}^\infty )e^k=0\) for \(k\le N_2\), while for \(k\ge N_2+1,\)
for \(j\ge N_2+1\), while it is identically zero for \(j\le N_2\) because of the projection \(\pi _{N_2}^\infty \) on the left. We can therefore set \(c_{j,k}=0\) without loss of generality whenever \(0\le j,k\le N_2\). Since we can write \(\ell _\nu ^1\ni h=\sum _{k\ge 0}e^k h_k\), we have the expression
Next we apply Lemma 5.2.1.
1.1.12 Proof of Row 15
To complete this proof, we determine bounds for \((\pi ^{N_2}{\widetilde{Q}}^{-1}(Y^{N_1})H_1(U^{N_1}*\pi _{N_2}^\infty ))_j\), \(k=0,\dots ,N_2\). An application of the triangle inequality will then supply the bound for row 15. However, since \(\pi ^{N_2}{\widetilde{Q}}^{-1}(Y^{N_1})=\pi ^{N_2}{\widetilde{Q}}^{-1}(Y^{N_1})\pi ^{N_2}\), much of the work has already been done in the proof of row 12/13. Indeed, for fixed \(k\in \{0,\dots ,N_2\}\), this calculation shows that
Note, the roles of j and k are reversed relative to the previous proof.
Rights and permissions
About this article
Cite this article
Church, K.E.M. Eigenvalues and delay differential equations: periodic coefficients, impulses and rigorous numerics. J Dyn Diff Equat 33, 2173–2252 (2021). https://doi.org/10.1007/s10884-020-09900-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-020-09900-0