On Co-Circular Central Configurations in the Four and Five Body-Problems for Homogeneous Force Law

Abstract

We study the central configurations (cc for short) for four masses arranged on a common circle (called co-circular cc) in two different situations, namely with no mass inside and later adding a fifth mass at the center of the circle. In the former, we focus the kite shape configurations by proving the existence of a one-parameter family of cc which goes from the kite containing an equilateral triangle up to the square shape. After, by putting a fifth mass at the center, we feature the planar cc of five bodies as a tensor of corange two see, “Albouy and Chenciner (Invent Math 131:151–184, 1998)” and we prove that cc is stacked see, “Hampton (Nonlinearity 18:2299–2304, 2005b)” in a such way that the center of mass of the four bodies should be the center of the circle. We emphasize that our approach includes not only the Newtonian force law, but the homogeneous ones with exponent $a\le -1$.

1 Introduction

It is known that, in the Newtonian $N$-body problem, the simplest possible motions are those whose configurations are invariant up to rotation and scaling, and where each body describes a Keplerian orbit. Only few special configurations of particles are allowed in these motions, the so called central configurations [16]. More precisely, let $\mathbb{E }$ be a finite dimensional vector space, $\mathbf{q}_1,\ldots ,\mathbf{q}_n\in \mathbb{E }, m_1,\ldots ,m_n$ be $n$ positives numbers, $a$ be a negative real number, $M=\sum m_i$ be the total mass and $\mathbf{q}_G=\frac{1}{M}\sum m_i\mathbf{q}_i$ be the center of mass of these particles.

Definition 1

A configuration $\mathbf{q}=(\mathbf{q}_1, \ldots , \mathbf{q}_N)\in \mathbb{E }^{N}$ is a central configuration for the masses $m_1,\ldots ,m_n$ if there exists a constant $\lambda \in \mathbb{R }$ such that

$$\begin{aligned} \lambda (\mathbf{q}_i - \mathbf{q}_G) = \sum \limits _{j\ne i} m_j \Vert \mathbf{q}_i - \mathbf{q}_j \Vert ^{2a} (\mathbf{q}_i - \mathbf{q}_j), \end{aligned}$$

(1.1)

for all $i=1\dots ,n$. When $a=-3/2$ we have the Newtonian case and when $a=-1$ the vortex case.

Many questions have arisen about the set of central configurations, denoted cc for short. So far, the main conjecture, still open, is the Chazy–Wintner–Smale conjecture: given $N$-positive masses $m_1,\ldots , m_N$ interacting by the Newtonian potential, the set of equivalence classes of central configurations is finite. In the case $N=3$, the central configurations were completely classified by Euler [9] and Lagrange [14]: for any choice of three positive masses there are only five distinct affine equivalence classes, two equilateral configurations and three collinear configurations. For $N=4$, the conjecture was proved first in the case of equal masses by Albouy in [1, 2], and in the general case by Hampton and Moeckel in [13] with a proof based on symbolic and exact integer computations which were carried out by computer. For $N=5$ recent progress can be found in [7] and [12].

Another type of question is proving the existence of central configurations with a given geometric shape. In this direction, there are many works, e.g., [8, 10, 11, 15]. Our present paper is also included in this list. In fact, we propose to study central configurations of four masses on a circle in two distinct situations, namely, without and with a fifth mass located at the center of the circle, regardless of the negative value of the exponent $a\in (-\infty ,-1]$.

We remark that in [8], the authors have considered the problem to describe all co-circular central configuration of the four body-problem. They carried out a thorough study of this type of cc, including our result, in which only the Newtonian case was considered. However, we emphasize that the present work deals with central configurations for homogeneous force laws. At this point it is important to justify why we take the exponent $a$ varying in the range $(-\infty ,-1]$. Indeed, new phenomena can arise when considering other force laws that are not inversely proportional to the square of the distance as for example, a flat homographic solution of the three body-problem with force proportional to the cube of distance $(a=-2)$ that is not planar and which appear in the §374 bis of [16]. Also, the number of planar cc of four equal masses which depends on the value of the exponent $a$: for $a=-1/2$ and for a certain value $a^*\in (-3/2,-1)$ one has two planar cc, namely, the square and the equilateral triangle with a mass at the barycenter while for the Newtonian force law where $a=-3/2$, we have one more cc, the isosceles triangle with a mass on the axis of symmetry. In [2], Simó and Albouy conjectured that there is a unique central configuration of four equal mass with a given axis of symmetry and no other symmetry, for any $a$ in some interval containing the exponent $-3/2$.

We are going to proceed as follows: in Sect. 4, we put four points on a common circle by imposing that they form a central configuration and we deduce some geometric properties. In the Sect. 5, we write the equations defining the kite-shape central configurations. After that, by setting the exponent $a=-1$ (vortex problem) in Sect. 5.1, we succeed in solving that system of equations explicitly. We obtain a one-parameter family of central configurations which goes from the kite with three masses at the vertices of an equilateral triangle (which is a central configuration of the restricted $3+1$ body-problem) up to the square with equal masses. In Sect. 5.2, for homogeneous force laws with $a<-1$, we prove the existence of that same parameterized family of cc, but in an implicit and global way. Finally in Sect. 6, we consider configurations of four masses on a common circle with a fifth mass located at its geometric center. By applying the results of Sect. 4, we shown that the central configurations with that shape are stacked so that the four bodies on the circle form a co-circular central configuration whose center of mass coincides with the center of the circle. In particular, if we take $a=-3/2$ (the Newtonian case) then, by [10], we have that the unique central configuration of this five body-problem is the square with four equal masses at the corners and an arbitrary mass at the center. Here, we decided to apply the tensorial approach presented in [3] aiming to introduce a new way of studying central configurations in the planar five body-problem. Hampton’s paper [11] has motivated us to work with this tool.

2 General Aspects

If we set $s_{ij}= \Vert \mathbf{q}_i - \mathbf{q}_j \Vert ^2$ and replace $\mathbf{q}_G$ by its expression, the Eq. (1.1) becomes

$$\begin{aligned} \sum \limits _{j\ne i} m_j S_{ij} \big (\mathbf{q}_i - \mathbf{q}_j \big ) =0, \end{aligned}$$

(2.1)

where $S_{ij} = -s_{ij}^a + \lambda /M$. The constant $\lambda$ corresponds to the Lagrange multiplier in the variational point of view and one can show that it is positive for any central configuration as defined above in (1).

We will work with the tensorial viewpoint in a attempt to obtain an alternative description for central configurations of the planar five body-problem. This will be important later in Sect. 6. Further details of the tensorial approach are found in [3, 4]. For brevity, we will state only the main properties of central configurations that arise from this approach and that will be used in the proof of our results.

In this context, a relative configuration of $n$ points, up to rigid movements, in general position in a vector space $\mathbb{E }$ of dimension $d$ will be a positive tensor $\beta \in \mathcal{D }\vee \mathcal{D }$ of range $d$ where $\mathcal{D }=\mathbb{R }^n/\langle (1,\ldots ,1)\rangle$. If $\mathbf{q}_i=(q_{i1},\,q_{i2},\ldots ,\,q_{id})$ then we write $\beta$ as

$$\begin{aligned} \beta =\text{ X }_1\otimes \text{ X }_1 + \text{ X }_2\otimes \text{ X }_2 +\cdots +\text{ X }_d\otimes \text{ X }_d \end{aligned}$$

where $\text{ X }_j=(q_{1j},\ldots ,q_{nj})\in \mathcal{D }$ is the class of vector whose coordinates are the $n$ projections of the configuration on the $j$ axis in the space $\mathbb{E }$, and the set $\{\text{ X }_1,\ldots ,\text{ X }_d\}$ is linearly independent in $\mathcal{D }$.

It is not difficult to see that $\beta$ admits the following decomposition

$$\begin{aligned} \beta =-\frac{1}{2}\sum \limits _{i<j}s_{ij}(\mathbf{e}_i\otimes \mathbf{e}_j+\mathbf{e}_j\otimes \mathbf{e}_i) \end{aligned}$$

(2.2)

where $\mathbf{e}_i$ is the class of the canonical vector $\mathbf{e}_i=(0,\ldots ,1,\ldots ,0)$ of $\mathbb{R }^n$. The tensor $\beta$ is interpreted as a positive symmetric bilinear form of range $d$ on the dual space $\mathcal{D }^*=\{\mathbf{x}\in \mathbb{R }^n/\sum x_i=0\}$ and as such, it has a matrix representation as follows

$$\begin{aligned} \beta =-\frac{1}{2}\left( \begin{array}{llll} 0 &{} s_{12} &{} \cdots &{} s_{1n} \\ s_{12} &{} 0 &{} \cdots &{} s_{2n} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ s_{1n} &{} s_{2n} &{} \cdots &{} 0 \end{array}\right) . \end{aligned}$$

This representation takes into account the identification

$$\begin{aligned} \text{ Bil }(\mathcal{D }^*)=\text{ Bil }(\mathbb{R }^n)/\big \{(x_i+y_j)_{n\times n}\big \} \end{aligned}$$

The set of positive symmetric bilinear forms of range d on $\mathcal{D }^*$ is a differentiable manifold and it will be denoted here by $(\mathcal{D }\vee \mathcal{D })_{+,d}$. Details of this geometric model are explained in either [5] or [15].

Now let $\Phi (s)=\frac{\lambda }{M}s-\frac{1}{a+1}s^{a+1}$ be a primitive of the function $\varphi (s)=-s_{ij}^a+\frac{\lambda }{M}$ and consider the function $g:(\mathcal{D }\vee \mathcal{D })_{+,d}\rightarrow \mathbb{R }$ defined by the rule

$$\begin{aligned} g(\beta )=\sum \limits _{i<j} m_im_j\Phi (s_{ij}). \end{aligned}$$

As stated in [3], we give the definition of relative central configuration

Definition 2

A relative central configuration of dimension $d$ for the masses $m_1,\ldots ,m_n$ is a positive tensor $\beta \in (\mathcal{D }\vee \mathcal{D })_{+,d}$ such that

$$\begin{aligned} \beta \circ dg(\beta )=0\in \mathcal{D }\otimes \mathcal{D }^*\end{aligned}$$

(2.3)

where the symbol $\circ$ denotes the contraction of tensors.

The connection between the tensorial Eq. (2.3) and the usual definition of cc becomes clear when we see (2.1) as a product of matrices $\mathbf{X}\cdot A=0$ where $\mathbf{X}$ is a $d\times n$ configuration matrix whose columns are the position vectors $\mathbf{q}_i$ and $A$ is the $n\times n$ matrix with entries:

$$\begin{aligned} A_{ij}=m_iS_{ij}\quad (i\ne j)\qquad A_{jj}=-\sum \limits _{i\ne j}A_{ij}. \end{aligned}$$

Multiplying on the left $\mathbf{X}\cdot A=0$ by $\mathbf{X}^t$ and using that the columns of $A$ are in $\mathcal{D }^*$, we obtain the matrix form of Eq. (2.3). See [3] for details.

By calling the differential $dg(\beta )=\alpha$ we have that

$$\begin{aligned} \alpha =\sum \limits _{i<j}\frac{\partial g}{\partial s_{ij}}ds_{ij} = \sum \limits _{i<j}m_im_j\varphi (s_{ij})\xi _{ij}\otimes \xi _{ij} \end{aligned}$$

(2.4)

where $\xi _{ij}=\mathbf{e}_i- \mathbf{e}_j\in \mathcal{D }^*.$

At this point, some remarks should be placed

Remark 1

The tensor $\alpha$ is a symmetric bilinear form on the quotient space $\mathcal{D }$ and if we denote its range by $r$ then, the Eq. (2.3) gives us an important estimative

$$\begin{aligned} d+r\le n-1. \end{aligned}$$

Sometimes we call the range of $\alpha$ as the co-range of $\beta$.

Remark 2

The set $\left\{ \xi _{ij}\otimes \xi _{ij}\right\} _{1\le i<j\le n}$ is a basis of the linear space $\mathcal{D }^*\vee \mathcal{D }^*$ and so, $\alpha =0$ if, and only if, $\varphi (s_{ij})=0$ for all pair $(i,j)$, that is,

$$\begin{aligned} s_{ij}=s_0=\left( \frac{\lambda }{M}\right) ^{1/a}. \end{aligned}$$

The configuration of $n$ points in which the mutual distances $s_{ij}$ are all equal has dimension $n-1$ and generalizes Lagrange (equilateral triangle) for three bodies and Lehmann-Filhès (regular tetrahedron) for four bodies. This central configuration will be denoted by

$$\begin{aligned} \beta _0=-\frac{s_0}{2}\sum \limits _{i<j}\big (\mathbf{e}_i\otimes \mathbf{e}_j+\mathbf{e}_j\otimes \mathbf{e}_i \big ). \end{aligned}$$

Remark 3

In [3], Albouy proved that a relative central configuration must satisfy the radial minimization estimate

$$\begin{aligned} \langle \beta _0,\alpha \rangle <0. \end{aligned}$$

(2.5)

3 Dziobek’s Configurations

Let $\beta$ be a relative central configuration of the $n$ body-problem.

Definition 3

We call $\beta$ a Dziobek configuration if it has corange one.

Thus, taking into account that $\alpha =dg(\beta )$ is a symmetric tensor and has range one, the relative configuration $\beta$ is a Dziobek configuration if, and only if, there is a real number $\eta \ne 0$ and a non null vector $\Delta \in \mathcal{D }^*$ such that

$$\begin{aligned} \alpha =\eta \Delta \otimes \Delta . \end{aligned}$$

By following [3], this identity and the radial minimization estimate in (2.5) imply that $\eta <0$ and we can take it as being $\eta =-1$ to normalize the vector $\Delta$ up to multiples.

After some computations in the tensorial notation (see [3]), one sees that the definition (3) can be rewritten by saying that a relative central configuration $\beta$ for the masses $m_1,\ldots ,m_n$ is Dziobek iff there exists a non-null vector $\Delta \in \mathbb{R }^n$ such that

$$\begin{aligned}&\sum \limits _{k\ne i}s_{ik}\Delta _k=\sum \limits _{k\ne j}s_{jk}\Delta _k,\end{aligned}$$

(3.1)

$$\begin{aligned}&\sum \limits _{k=1}^n \triangle _k =0, \end{aligned}$$

(3.2)

$$\begin{aligned}&-s_{ij}^a +\frac{\lambda }{M}=\frac{\triangle _i}{m_i}\frac{\triangle _j}{m_j}, \qquad 1 \le i < j\le n. \end{aligned}$$

(3.3)

The range of a Dziobek configuration satisfies¹ $\text{ rg }(\beta )\le n-2$. It is proved in [4], that if $\beta$ is a central configuration of dimension exactly $n-2$, then $\beta$ is a Dziobek configuration. Moreover, the vector $\Delta$ in Eqs. (3.1) and (3.2) is unique, up to a factor, and the normalization of $\eta$ makes it unique up to orientation. The uniqueness implies that the $\Delta$’s coordinates are proportional to the oriented areas (or volumes) of the simplex of $n-1$ vertices. For example, $|\Delta _1|$ is proportional to the area (or volume) of the simplex given by the vertices $(q_2,\ldots ,q_n)$, and so on.

Remark 4

In terms of the Dziobek approach, it is clear that the set of variables $\{\ldots ,\Delta _j,\ldots ,$ $s_{ij},\ldots \}$ solves the system (3.1)–(3.3) with multiplier $\lambda$ if and only if, for any $c\in \mathbb{R }^+$, the set $(\ldots ,\sqrt{c}\Delta _j,\ldots ,c^{1/a} s_{ij},\ldots )$ also solves the same system with multiplier $c \lambda$. So, fixing the multiplier $\lambda$ corresponds to choosing a unique central configuration in the class of homothety. In what follows, we will take $\lambda =1$ with the aim to eliminate the invariance by homotheties and we will normalize the total mass by taking $M=1$.

4 Central Configurations for Four Bodies on a Circle

In this section, we will consider a central configuration of four bodies with the masses $m_1,\, m_2,\, m_3$ and $m_4$ arranged on a common circle and derive some geometric properties, which will be important later. In this case, we have four non collinear points in the plane that makes the configuration to have dimension exactly two and puts us in position to apply the Dziobek approach [Eqs. (3.1)–(3.3)]. An interesting question raised by Albouy and cited in [10] asks: to characterize all the four-body central configurations which lie on a common circle. In the next section, we will go exactly on this direction, aiming to get a complete description about a particular symmetric central configuration of four bodies on a common circle for any gravitational potential, not only for the Newtonian one.

We proceed as follows: by supposing that the points $\mathbf{q}_1,\ldots , \mathbf{q}_4$ satisfy the Eqs. (3.1)–(3.3), which is a system of ten equations, ten variables and four parameters, we impose the configuration to be co-circular. This is equivalent to making $t_i=\displaystyle \sum \nolimits _{k\ne i}s_{ik}\Delta _k=0$ for all $i$ (it is not difficult to prove this fact) and so, we get another equation while one of the masses becomes dependent variable. Initially, we take $m_4$ in order to be this new variable so that we must solve a system of 11 equations, 11 variables $(s_{12},s_{13},\ldots ,s_{34},\Delta _1,\ldots ,\Delta _4,m_4)$ and three parameters $(m_1,\,m_2,\,m_3).$

$$\begin{aligned}&t_i= \sum \limits _{k\ne i}s_{ik}\Delta _k=0, \qquad i=1,\ldots ,4\end{aligned}$$

(4.1)

$$\begin{aligned}&\sum \limits _{j=1}^4 \triangle _j =0, \end{aligned}$$

(4.2)

$$\begin{aligned}&-s_{ij}^a + 1 = \frac{\triangle _i\triangle _j}{m_im_j}, \qquad 1\le i < j \le 4, \end{aligned}$$

(4.3)

which correspond to the equations defining the central configurations of the co-circular four body-problem with multiplier $\lambda =1.$

A very intuitive result about co-circular central configurations of four points states the following

Lemma 1

Let $(\mathbf{q}_1,\ldots , \mathbf{q}_4)$ be a co-circular central configuration of the four body-problem whose diagonals of the polygon are the segments $[\mathbf{q}_1\mathbf{q}_2]$ and $[\mathbf{q}_3\mathbf{q}_4]$. Let $R$ be the radius of the circle. Then

• (a) the center of the circle is in the interior of the convex hull of the four co-circular points.

• (b) at least one of the sides must be greater than $\sqrt{2}R$.

Proof

Any co-circular configuration is strictly convex and we can label the four points so that the following distribution of signals holds

$$\begin{aligned} \Delta _3,\Delta _4<0<\Delta _1,\Delta _2. \end{aligned}$$

(4.4)

Also, $\Delta _1,\Delta _2,\Delta _3$ and $\Delta _4$ correspond to the oriented areas of the triangles (234), (431), (124) and (321), respectively.

The configuration is assumed to be central, so that, by the Eq. (4.3) and inequalities (4.4) one has

$$\begin{aligned} \varphi (s_{13}),\,\varphi (s_{23}),\,\varphi (s_{24}),\,\varphi (s_{14})<0<\varphi (s_{12}),\,\varphi (s_{34}) \end{aligned}$$

and since $\varphi (s)=-s^a+1$ is a increasing function one has

$$\begin{aligned} s_{13},\,s_{23},\,s_{24},\,s_{14}<1<s_{12},\,s_{34}. \end{aligned}$$

(4.5)

In order to prove item (a), we suppose that the center of the circle is not in the interior of the convex hull of the four points. Then, without loss of generality, we can apply a rotation on the configuration so that

$$\begin{aligned} q_1=(R,0)\qquad \text{ and } \quad q_i=(x_i,y_i) \end{aligned}$$

where $y_i\ge 0$ and $-R\le x_i<R, \forall i=2,3,4.$ Let’s write the determinants $\Delta _i$ as

$$\begin{aligned} \Delta _2=\left| \begin{array}{lll}1 &{} 1 &{} 1 \\ x_4 &{} x_3 &{} R \\ y_4 &{} y_3 &{} 0\end{array} \right| \quad \Delta _3=\left| \begin{array}{lll}1 &{} 1 &{} 1 \\ R &{} x_2 &{} x_4 \\ 0 &{} y_2 &{} y_4\end{array} \right| \quad \Delta _4=\left| \begin{array}{lll}1 &{} 1 &{} 1 \\ x_3 &{} x_2 &{} R \\ y_3 &{} y_2 &{} 0\end{array} \right| . \end{aligned}$$

Once $\Delta _2>0$, we have that

$$\begin{aligned} y_4(R-x_3)>y_3(R-x_4), \end{aligned}$$

and since both sides are non negative, we have

$$\begin{aligned} y_4^2(R-x_3)^2>y_3^2(R-x_4)^2. \end{aligned}$$

For all $i=1,\ldots ,4$ we have satisfied the equations $y_i^2=R^2-x_i^2$. After replacing $y_i$ and canceling the terms $R-x_i$, we get

$$\begin{aligned} (R+x_4)(R-x_3)>(R+x_3)(R-x_4) \end{aligned}$$

which leads us to

$$\begin{aligned} \frac{R+x_4}{R-x_4}>\frac{R+x_3}{R-x_3}\quad \Rightarrow \quad x_4>x_3. \end{aligned}$$

Likewise, the inequalities $\Delta _3<0$ and $\Delta _4<0$ show that

$$\begin{aligned} -R\le x_3< x_2<x_4<x_1=R \end{aligned}$$

from where it follows that

$$\begin{aligned} 0<s_{14}<s_{12}<s_{13}\le 4R^2. \end{aligned}$$

But, $s_{12}<s_{13}$ contradicts (4.5) and the configuration could not be central. Thus, for a co-circular central configuration, the center of the circle is in the interior of the convex hull.

The proof of item (b) is as follows. The sides of the polygon $(\mathbf{q}_1,\ldots , \mathbf{q}_4)$ are the bases of isosceles triangles whose equal sides correspond to the radius $R$. By assertion a, the respective angles $\alpha _{ij}$ of each triangle are in the interval $(0,\pi )$ and their sum is worth $2\pi$. Note that $\alpha _{ij}$ satisfy (see Fig. 1)

$$\begin{aligned} \sin \frac{\alpha _{ij}}{2} = \frac{r_{ij}}{2R},\qquad \left( r_{ij}=\Vert \mathbf{q}_i-\mathbf{q}_j\Vert \right) . \end{aligned}$$

If all of the lengths $r_{ij}<\sqrt{2}R$, then

$$\begin{aligned} 0<\sin \frac{\alpha _{ij}}{2}<\frac{\sqrt{2}}{2}\quad \Rightarrow \quad 0<\alpha _{ij}<\frac{\pi }{2}. \end{aligned}$$

In this case, the sum of all angles would be less than $2\pi$ which is a contradiction. The assertion (b) is proved. $\square$

Fig. 1

Proof of Lemma 1

Remark 5

A consequence of the above lemma (item b), is that in a co-circular central configuration of four bodies, we should have

$$\begin{aligned} \varphi (R^2)<\varphi (2R^2)<\varphi (s_{ij})<0 \end{aligned}$$

(4.6)

for some pair of indices.

5 Co-Circular Kite Central Configurations

From now on, we will consider kite-shape central configurations which are not a square. According to the main result in [6], for any value of $a<0$, this type of symmetry is characterized by the constraints

$$\begin{aligned} \Delta _3< \Delta _4< 0 <\Delta _1=\Delta _2, \end{aligned}$$

(5.1)

or equivalently, by $m_1=m_2$ and $m_3 < m_4$.

Let four co-circular points $(\mathbf{q}_1,\, \mathbf{q}_2,\, \mathbf{q}_3,\, \mathbf{q}_4)$ form a kite configuration where the segments $[\mathbf{q}_1\mathbf{q}_2]$ and $[\mathbf{q}_3\mathbf{q}_4]$ are the diagonals. Let $s_{13}=s_{23}=x,\, s_{14}=s_{24}=y,\, s_{34}=d$ and $s_{12}=l$ be the square of the mutual distances (see Fig. 2).

Fig. 2

Kite-shape configuration

The Eqs. (4.1) and (4.2) become

$$\begin{aligned}&t_1 = l\Delta _2 + x\Delta _3 + y\Delta _4 =0 \end{aligned}$$

(5.2)

$$\begin{aligned}&t_2 = l\Delta _1 + x\Delta _3 + y\Delta _4 =0 \end{aligned}$$

(5.3)

$$\begin{aligned}&t_3 = 2x\Delta _1 + d\Delta _4 =0 \end{aligned}$$

(5.4)

$$\begin{aligned}&t_4 = 2y\Delta _1 + d\Delta _3 =0 \end{aligned}$$

(5.5)

$$\begin{aligned}&2\Delta _1+\Delta _3+\Delta _4=0. \end{aligned}$$

(5.6)

By adding $t_3$ and $t_4$, we have that $d=x+y$. From $t_3=0$ and $t_4=0$, we isolate $\Delta _3$ and $\Delta _4$ to insert them into $t_1=0$. So, we obtain

$$\begin{aligned} d l= 4\,x\,y. \end{aligned}$$

(5.7)

Moreover, $\Delta _3<\Delta _4<0$ implies that $x<y$.

It’s easy to verify that the Eqs. (5.3)–(5.6) are equivalent to the system

$$\begin{aligned} d&= x+y \end{aligned}$$

(5.8)

$$\begin{aligned} d l&= 4xy \end{aligned}$$

(5.9)

$$\begin{aligned} \frac{\Delta _3}{\Delta _1}&= -\frac{l}{2x} \end{aligned}$$

(5.10)

$$\begin{aligned} \frac{\Delta _4}{\Delta _1}&= -\frac{l}{2y} \end{aligned}$$

(5.11)

Note that $d\ (d-l)=(x-y)^2>0$, so $d>l$ as shown in Fig. 2.

Now, we consider the increasing function $\varphi \!:\mathbb{R }_+\rightarrow \mathbb{R }$ given by

$$\begin{aligned} \varphi (s)=1-s^a\qquad (a\le -1) \end{aligned}$$

and remember that a Dziobek configuration $(s_{12},\ldots ,s_{34},\Delta _1,\ldots ,\Delta _4)$ is central, if and only if,

$$\begin{aligned} m_im_j\varphi (s_{ij})=\Delta _i\Delta _j\quad \text{ for } \text{ any } i,j. \end{aligned}$$

By imposing that the kite configuration be central and making $m_1=m_2$, we obtain the following relations

$$\begin{aligned} \varphi (l)&= \frac{\Delta _1^2}{m_1^2} \end{aligned}$$

(5.12)

$$\begin{aligned} \varphi (x)&= \frac{\Delta _1\Delta _3}{m_1m_3} \end{aligned}$$

(5.13)

$$\begin{aligned} \varphi (y)&= \frac{\Delta _1\Delta _4}{m_1m_4} \end{aligned}$$

(5.14)

$$\begin{aligned} \varphi (d)&= \frac{\Delta _3\Delta _4}{m_3m_4}. \end{aligned}$$

(5.15)

Remark 6

According to the signs of the $\Delta _i$’s in (5.1), the Eqs. (5.12)–(5.15) together with the monotonicity of $\varphi$ provide the inequalities

$$\begin{aligned} \varphi (x)<\varphi (y)<0<\varphi (l)<\varphi (d), \end{aligned}$$

and consequently,

$$\begin{aligned} 0<x<y<s_0<l<d, \end{aligned}$$

(5.16)

where $s_0=1$ is the unique root of $\varphi$.

Once the variables $\Delta _i$ can not assume the value zero, we can make the ratios between the Eqs. (5.12)–(5.15) and we apply the relations (5.8)–(5.11) to simplify them. Thus, we obtain

$$\begin{aligned} \frac{\varphi (x)}{\varphi (l)}&= -\frac{m_1}{m_3}\frac{l}{2x} \\ \frac{\varphi (y)}{\varphi (l)}&= -\frac{m_1}{m_4}\frac{l}{2y} \\ \frac{\varphi (x)}{\varphi (y)}&= \frac{m_4}{m_3}\frac{y}{x} \\ \frac{\varphi (d)}{\varphi (l)}&= \frac{m_1^2}{m_3m_4}\frac{l}{d}. \end{aligned}$$

The above system suggests the introduction of the function $f\!:\mathbb{R }_+\rightarrow \mathbb{R },\, f(s)=s \varphi (s)$ whose derivative is $f^\prime (s)=1-(1+a)s^a\ge 1$ for $a\le -1$. After defining the relative masses $m_3^\prime =m_3/m_1$ and $m_4^\prime =m_4/m_1$ we get

$$\begin{aligned} 2m_3^\prime f(x)+f(l)&= 0 \end{aligned}$$

(5.17)

$$\begin{aligned} 2m_4^\prime f(y)+f(l)&= 0 \end{aligned}$$

(5.18)

$$\begin{aligned} m_3^\prime f(x)-m_4^\prime f(y)&= 0 \end{aligned}$$

(5.19)

$$\begin{aligned} m_3^\prime m_4^\prime f(d)-f(l)&= 0 \end{aligned}$$

(5.20)

where one sees that the Eqs. (5.17)–(5.19) are linearly dependent. By substituting $f(l)=m_3^\prime m_4^\prime f(d)$ into (5.17) and combining it with (5.18) by eliminating $m_4^\prime$, we arrive to the following system

$$\begin{aligned}&4f(x)f(y)-f(l)f(d)=0 \end{aligned}$$

(5.21)

$$\begin{aligned}&m_3^\prime f(x)-m_4^\prime f(y)=0 \end{aligned}$$

(5.22)

$$\begin{aligned}&m_3^\prime m_4^\prime f(d)-f(l)=0, \end{aligned}$$

(5.23)

which, together with (5.8) and (5.9), define the kite-shape central configurations on a circle.

Remark 7

By (5.16) and (5.23) and since $f$ is increasing, we have that the product $m_3^\prime m_4^\prime <1$. By the same argument, we should have that $\displaystyle \frac{m_3^\prime }{m_4^\prime }<1$ from (5.22). In what follows, let’s insert two new parameters $p=m_3^\prime m_4^\prime$ and $q=\displaystyle \frac{m_3^\prime }{m_4^\prime }$, where both of them are in the open interval $(0,1)$.

5.1 Applications to the Vortex Problem, i.e., $a=-1$

In this case, the solution of (5.21)–(5.23) can be obtained explicitly. In fact, if $a=-1$, the function $f$ assumes the form $f(s)=s-1$ and the system (5.21)–(5.23) becomes

$$\begin{aligned}&3x^2+2xy+3y^2-3x-3y=0 \end{aligned}$$

(5.24)

$$\begin{aligned}&q x-q-y+1=0 \end{aligned}$$

(5.25)

$$\begin{aligned}&px^2+2(p-2)xy+py^2+(1-p) x+(1-p)y=0. \end{aligned}$$

(5.26)

Now, in order to find the common solutions of (5.24)–(5.26), we calculate the resultant of the two polynomials (5.24) and (5.26) with respect to the variable $y$. We obtain

$$\begin{aligned} Res = 4x^2\ \left[ 4(3-p)^2x^2-4(3-p)(4-p)x+3(4-p)\right] . \end{aligned}$$

The positive zeroes of $Res$

$$\begin{aligned} x^{\prime }=\frac{4-p-\sqrt{(1-p)(4-p)}}{2(3-p)}\quad \text{ and }\quad x^{\prime \prime }=\frac{4-p+\sqrt{(1-p)(4-p)}}{2(3-p)}, \end{aligned}$$

correspond to the values of $x$ for which the above system has a solution. By symmetry, the other solution of (5.24) and (5.26) is the pair $(x^{\prime \prime },\,x^{\prime })$. As $x<y$ we should take $x=xx^{\prime }$ and $y=x^{\prime \prime }$. By inserting these expressions into (5.25), we get

$$\begin{aligned} q=\frac{2-p-\sqrt{(1-p)(4-p)}}{2-p+\sqrt{(1-p)(4-p)}}. \end{aligned}$$

Thus, we have the complete solution of the system (5.21)–(5.23) parameterized by $p\in (0,1)$

$$\begin{aligned} x&= \frac{4-p-\sqrt{(1-p)(4-p)}}{2(3-p)} \end{aligned}$$

(5.27)

$$\begin{aligned} y&= \frac{4-p+\sqrt{(1-p)(4-p)}}{2(3-p)} \end{aligned}$$

(5.28)

$$\begin{aligned} d&= \frac{4-p}{3-p}, \qquad l=\frac{3}{3-p} \end{aligned}$$

(5.29)

$$\begin{aligned} m_3^\prime&= \sqrt{pq}=2-p-\sqrt{(1-p)(4-p)},\\ m_4^\prime&= \sqrt{\frac{p}{q}}=2-p+\sqrt{(1-p)(4-p)},\\ M&= 1 \quad \Rightarrow \quad \frac{1}{m_1}=2+m_3^\prime +m_4^\prime =2(3-p) \end{aligned}$$

$$\begin{aligned}&\Rightarrow \quad m_1=\frac{1}{2(3-p)} \end{aligned}$$

(5.30)

$$\begin{aligned} m_3&= \frac{2-p-\sqrt{(1-p)(4-p)}}{2(3-p)} \end{aligned}$$

(5.31)

$$\begin{aligned} m_4&= \frac{2-p+\sqrt{(1-p)(4-p)}}{2(3-p)} \end{aligned}$$

(5.32)

In Fig. 3 we present the evolution of the co-circular kites in the vortex problem according the parameter $p\in [0, 1]$.

Fig. 3

Evolution of the co-circular kites in the vortex problem according the parameter $p \in [0,1]$

This way, we have proved the following result

Theorem 2

In the vortex four body-problem, there is a unique one-parameter family of kite shape co-circular central configurations described by the expressions (5.27)–(5.32).

Remark 8

The Newtonian case, i.e., $a=-3/2$, is not so friendly, for it produces polynomials of very higher degrees. Nevertheless, this case will be considered below.

5.2 Applications to Homogeneous Force Law

Here, we consider $m_3^\prime$ and $m_4^\prime$ as variables to be obtained from (5.22)–(5.23) and we work with the system

$$\begin{aligned}&4f(x)f(y)-f(l)f(d)=0\end{aligned}$$

(5.33)

$$\begin{aligned}&d=x+y \end{aligned}$$

(5.34)

$$\begin{aligned}&l=\frac{4xy}{x+y} \end{aligned}$$

(5.35)

where $f(s)=s-s^{a+1}$ with $a<-1$. Note that the equation

$$\begin{aligned} F(x,y)=4f(x)f(y)-f\left( \frac{4xy}{x+y}\right) f(x+y)=0 \end{aligned}$$

(5.36)

is symmetric with respect to $x$ and $y$ which means that the trace of the zero level curve of $F$ is symmetric about the line $y=x$.

The domain of equation $F=0$ will be given by the restrictions in (5.16). There, we have that $0<x<y<1$, but by symmetry, we will leave $(x,y)\in [0,1]\times [0,1]$. Easily, one verifies three trivial solutions of $F(x,y)=0$ which are

$$\begin{aligned} A=(1/3,1), \quad B=\left( \left( \frac{2}{1+2^a}\right) ^{1/a},\,\left( \frac{2}{1+2^a}\right) ^{1/a}\right) \quad C=(1,1/3) \end{aligned}$$

The point $B$ corresponds to the square configuration and the points $A$ and $C$ represent the kite with an equilateral triangle.

The three points $A, B$ and $C$ lie in the square $\left[ 1/3,1\right] \times \left[ 1/3,1\right]$. For $0<x<1/3$ we have that $l=\frac{4xy}{x+y}<1$ for any $y\in [0,1]$. This would give us $f(l)<0$ and the configuration would not be central according to (5.12). Likewise, we will disregard the range $0<y<1/3$.

Once that $1\le \displaystyle \frac{4xy}{x+y}$, we will take the region (see Fig. 4)

$$\begin{aligned} \Omega =\left\{ (x,y)\in \left[ \frac{1}{3},\,1\right] \times \left[ \frac{1}{3},\,1\right] / x+y\le 4xy\right\} \end{aligned}$$

as the domain of $F$ and we will show that $F(x,y)=0$ defines a decreasing curve in $\Omega$ passing through the points $A, B$ and $C$, regardless of the value of the exponent $a<-1.$

Fig. 4

Region $\Omega$: the branch of hyperbola is the graph of $4xy-x-y=0 \,\,(l=1)$

Proposition 1

For any $x\in [1/3,1]$ there exists a unique $y\in [1/3,1]$ such that $F(x,y)=0$.

Proof

Remember that $f^\prime (s)\ge 1,\; \forall s>0$ and that $f(x)\le 0$ and $f(d),\,f(l)\ge 0$ on $\Omega$. The partial derivative of $F$ with respect to $y$ is

$$\begin{aligned} \frac{\partial F}{\partial y}= 4f^\prime (y)f(x)-f^\prime (l)f(x+y)\frac{4x^2}{d^2}-f(l)f^\prime (d), \end{aligned}$$

and then

$$\begin{aligned} \frac{\partial F}{\partial y} \le 4f(x)-f(d)\frac{4x^2}{d^2}-f(l)\le 0, \end{aligned}$$

so $\displaystyle \partial _y F=0$, if and only if,

$$\begin{aligned} f(x)=f(d)=f(l)=0\quad \Leftrightarrow \quad x=d=l=1 \end{aligned}$$

which is impossible. Thus, we have that $\displaystyle \partial _yF$ is a strictly negative continuous function on $\Omega$.

Given $x^*\in (1/3,1)$, let $y^*\in (1/3,1)$ be the unique ordinate such that $(x^*,y^*)$ is on the curve $l=1$. We have the following behavior of the function $h(y)=F(x^*,y)$ on the segment of the vertical line $x=x^*$ which goes from the curve $l=1$ up to the horizontal line $y=1$:

• $h^\prime (y)=\partial _yF(x^*,y)<0$, i.e., $h$ is a strictly decreasing function

• $h(y^*)=F(x^*,y^*) = 4f(x^*)f(y^*)>0$

• $h(1)=F(x^*,1) = -f(x^*+1)f\left( \displaystyle \frac{4x^*}{x^*+1}\right) <0$.

By the continuity of $F$ on the region $\Omega$, we have that there is $y=\xi (x^*)\in (y^*,1)$ such that $F(x^*,\,\xi (x^*))=0$. The monotonicity of $h$ guarantees the uniqueness. $\square$

Naturally, the graph of the function $\xi \!:[1/3,1]\rightarrow [1/3,1]$ passes through the points $A, B$ and $C$ and since

$$\begin{aligned} \frac{\partial F}{\partial y}(x,\xi (x))\ne 0 \end{aligned}$$

for all $x\in [1/3,1]$, the Implicit Function Theorem ensures that $\xi$ is differentiable. Furthermore, its derivative

$$\begin{aligned} \xi ^\prime (x)=-\left( \frac{\partial F}{\partial y}\right) ^{-1}\frac{\partial F}{\partial x} \end{aligned}$$

is negative and this lead us to conclude the following theorem.

Theorem 3

For any value of the exponent $a<-1$, there is a unique one-parameter family of kite shape co-circular central configurations of the four body-problem implicitly described by the Eq. (5.36) which goes from the kite with an equilateral triangle up to the square.

Remark 9

The Eqs. (5.22) and (5.23) give the following expressions for $q$ and $p$

$$\begin{aligned} q(x)=\frac{f(\xi (x))}{f(x)},\qquad p(x)=\frac{f(l(x))}{f(x+\xi (x))} \end{aligned}$$

which are defined for $x\in [1/3,1]$.

In Fig. 5, we describe the behavior of $\xi$ for the Newtonian case.

Fig. 5

The concave curve is the graph of $\xi$ for $a=-3/2$. The points $A$ and $C$ are the extreme points on this curve. The point $B$ is its intersection with the bisectrix $y=x$

Remark 10

In the Ref. [8], the Newtonian case is considered and all the co-circular central configurations are determined. Using mutual distances as coordinates, it is shown that the set of co-circular central configurations with positive masses is a two-dimensional surface parameterized by two of the exterior side-lengths. Two symmetric families, the kite and isosceles trapezoid, are investigated extensively.

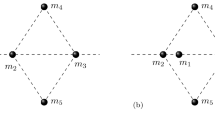
6 Co-Circular Central Configurations of Four Bodies with a Fifth Mass at the Center

In this section, we consider a configuration of five bodies with the following shape: four masses $m_1,\,m_2,\,m_3,\,m_4$ lying on a common circle and a fifth body with mass $m$ at the center of that circle (see Fig. 6). We will refer to this type of configuration as a co-circular (4,1)-configuration. By following A. Chenciner (see [10]), we raise the question: what are the co-circular (4,1)-central configurations? Again, let $M$ be the total mass of the system and whenever a tilde accent is used in the notation, we will be referring to the co-circular four-body configuration, e.g, ${\tilde{M}}=M-m$ and ${\tilde{\beta }}$ is the relative configuration of the four co-circular masses on the circle.

Fig. 6

Co-circular $(4,1)$-configuration

We will apply the tensorial approach presented in Sect. 2. In this context, the tensor $\beta$ has range $2$ and by Remark 1, the differential $\alpha =dg(\beta )$ must have $\text{ rg }\,\alpha \le 2$. This allows us to write

$$\begin{aligned} \alpha =a Z_1\otimes Z_1+b Z_2\otimes Z_2,\qquad Z_1,\;Z_2\in \mathcal{D }^*\end{aligned}$$

where either $a<0$ or $b<0$ by virtue of radial minimization (Remark 3). Without loss of generality, suppose that $a<0$ and consider the vector $Z_1$ factoring by $a=-\left( \sqrt{|a|}\right) ^2$, so that

$$\begin{aligned} \alpha = -Z_1\otimes Z_1+b\ Z_2\otimes Z_2 \end{aligned}$$

The two vectors $Z_1$ and $Z_2$ are assumed to be linearly independent. By supposing that $\beta$ is a relative central configuration—what will be done from now on—by Definition 2, we must have that

$$\begin{aligned} \beta \circ \alpha =-(\beta \circ Z_1)\otimes Z_1+b\ (\beta \circ Z_2)\otimes Z_2=0 \end{aligned}$$

i.e., the contractions $Z_1\circ \beta$ and $Z_2\circ \beta$ should be zero in $\mathcal{D }$.

Lemma 4

$b\ne 0$.

Proof

In fact, if $\alpha = -Z\otimes Z$ for some $Z=(z_0,\,z_1,\,z_2,\,z_3,\,z_4)\in \mathcal{D }^*$, then

$$\begin{aligned} \alpha _{ij}=m_im_j\varphi (s_{ij})=z_iz_j. \end{aligned}$$

(6.1)

By assuming that $z_0\ne 0$, we would have for any $j=1,\ldots ,4$,

$$\begin{aligned} \frac{z_j}{m_j} = \varphi (R^2)\frac{m}{z_0} = k\; \text{(constant) } \end{aligned}$$

so that, for $i\ne 0\ne j$

$$\begin{aligned} \varphi (s_{ij}) = \frac{z_iz_j}{m_im_j}= k^2\quad \Rightarrow \quad s_{ij}=\text{ constant } \end{aligned}$$

and this would imply that the four-body configuration $(q_1,\ldots ,q_4)$ is spatial, which is a contradiction. So, we must have $z_0=0$ and $\varphi (R^2)=0$

$$\begin{aligned} R^{2a}=\frac{\lambda }{M}\quad \Rightarrow \quad \varphi (s_{ij})=-s_{ij}^a+\rho ^a.\quad (\rho =R^2) \end{aligned}$$

On the other hand, the nullity of the contraction $Z\circ \beta$ gives us that

$$\begin{aligned} \sum \limits _{j\ne 0,i} s_{ij}z_j=-2z_0R^2=0,\quad \forall i=1,\ldots ,4. \end{aligned}$$

This system together with the Eq. (6.1) for $i\ne 0\ne j$ show that the four bodies $(\mathbf{q}_1,\ldots ,\mathbf{q}_4)$ form a co-circular central configuration (see Sect. 4). By Lemma 1, one of the sides of the polygon must be greater than $\sqrt{2}R$ and so, one of the mutual distances $s_{13},\,s_{14},\,s_{23},\,s_{24}$ must be greater than $2\rho .$ This implies that

$$\begin{aligned} \varphi (s_{ij})>0 \end{aligned}$$

for some pair $(i,j)$ which corresponds to some side of the polygon. This is absurd, since according to estimates in the proof of Lemma 1, convex central configurations of the four-body problem must have $\varphi (s_{ij})<0$ for all external sides.

This way, we have shown that $b$ is not zero. $\square$

By Lemma 4, we can write

$$\begin{aligned} \alpha =-Z_1\otimes Z_1+\sigma Z_2\otimes Z_2, \end{aligned}$$

(6.2)

where $\sigma =\pm 1$ and the vectors $Z_1,Z_2\in \mathcal{D }^*$ are linearly independent.

In order to characterize the co-circular $(4,1)$-central configurations, we will need a further constraint on the vectors $Z_j$. By writing

$$\begin{aligned} Z_1=(\xi ,\ldots )\quad \text{ and } \quad Z_2=(\eta ,\ldots ), \end{aligned}$$

we have:

Lemma 5

If $\sigma =1$ then $|\xi |\ne |\eta |$.

Proof

Firstly, $\xi$ and $\eta$ can not be simultaneously null, for in this case, we would have

$$\begin{aligned} {\tilde{\beta }}\circ {\tilde{Z}}_1= {\tilde{\beta }}\circ {\tilde{Z}}_2=0 \end{aligned}$$

That is, the two linearly independent vectors ${\tilde{Z}}_1$ and ${\tilde{Z}}_2$ would be in a 1D vector space, namely, $\ker \{{\tilde{\beta }}\}$.

Suppose that $\eta =\pm \xi$. By equating the coordinates of $\alpha$ in (2.4) and (6.2) and considering the hypothesis $\sigma =1$, we have

$$\begin{aligned} mm_i\varphi (R^2) = \xi \ Z_{1i}-\eta \ Z_{2i} = \xi \big (Z_{1i}\mp Z_{2i}\big ), \end{aligned}$$

for all $i=1,\ldots ,4.$ This provides that the vector $Z_1\mp Z_2$ has all its coordinates either non-negative or non-positive. But this vector is in the hyperplane $\mathcal{D }^*$, so $Z_1=\pm Z_2$ and they are linearly dependent which is an absurd. Thus, if $\sigma =1$ then $\xi$ and $\eta$ must have different absolute values. $\square$

Lemma 6

There exists $\Delta \in \mathcal{D }^*$ whose first coordinate is zero and such that

$$\begin{aligned} \alpha =-\Delta \otimes \Delta +\sigma Z\otimes Z \end{aligned}$$

(6.3)

Proof

Let $\alpha$ be as written in (6.2). If $\sigma =-1$, take $a,b\in \mathbb{R }$ given by

$$\begin{aligned} a=\frac{-\eta }{\sqrt{\xi ^2+\eta ^2}}\quad \text{ and }\quad b=\frac{\xi }{\sqrt{\xi ^2+\eta ^2}} \end{aligned}$$

so that $a^2+b^2=1$ and the vector

$$\begin{aligned} \Delta =a Z_1+b Z_2=\big (0,\,\Delta _1,\,\Delta _2,\,\Delta _3,\,\Delta _4 \big ) \end{aligned}$$

has its first coordinate being zero. By defining

$$\begin{aligned} Z=-b Z_1+a Z_2 \end{aligned}$$

it is easy to see that

$$\begin{aligned} \Delta \otimes \Delta +Z\otimes Z = Z_1\otimes Z_1 + Z_2\otimes Z_2 = -\alpha \end{aligned}$$

as stated. Now, if $\sigma =1$ take $a,b\in \mathbb{R }$ as

$$\begin{aligned} a=\frac{-\eta }{\sqrt{|\xi ^2-\eta ^2|}}\quad \text{ and } \quad b=\frac{\xi }{\sqrt{|\xi ^2-\eta ^2|}}. \end{aligned}$$

By Lemma 5, these expressions are well defined and the vector

$$\begin{aligned} \Delta =a Z_1+b Z_2=\big (0,\,\Delta _1,\,\Delta _2,\,\Delta _3,\,\Delta _4 \big ), \end{aligned}$$

has its first coordinate null. By defining

$$\begin{aligned} Z=b Z_1+a Z_2 \end{aligned}$$

one has that

$$\begin{aligned} \Delta \otimes \Delta -Z\otimes Z = (a^2-b^2) \left( Z_1\otimes Z_1 - Z_2\otimes Z_2\right) =-(a^2-b^2)\alpha . \end{aligned}$$

It only remains to demonstrate that $a^2-b^2=1$ to prove the lemma.

Supposing by absurd that $a^2-b^2=-1$, i.e., $\alpha =\Delta \otimes \Delta -Z\otimes Z.$ In coordinates, this produces the relations

$$\begin{aligned} m_im_j\varphi (s_{ij}) = -\Delta _i\Delta _j + Z_iZ_j. \end{aligned}$$

For $j=0$, we have that $s_{0i}=R^2$ and $\Delta _0=0$, so

$$\begin{aligned} m_im\varphi \left( R^2\right) =Z_0Z_i, \quad \forall i\ne 0. \end{aligned}$$

By remembering that $Z_0$ is not zero, we see that

$$\begin{aligned} \frac{Z_i}{m_i}=\frac{m\varphi \left( R^2\right) }{Z_0}=k \end{aligned}$$

is constant for all $i=1,\ldots ,4$. Thus

$$\begin{aligned} Z=k\big (m-M,\,m_1,\,m_2,\,m_3,\,m_4 \big ) \end{aligned}$$

and for $1\le i<j\le 4$,

$$\begin{aligned} m_im_j\varphi (s_{ij}) = -\Delta _i\Delta _j + k^2m_im_j. \end{aligned}$$

Once the vector ${\tilde{\Delta }}=(\Delta _1,\,\Delta _2,\,\Delta _3,\,\Delta _4)\in \mathcal{D }^*_4$ is in $\ker \{{\tilde{\beta }}\}$, it is the unique vector, up to a scalar factor, such that

$$\begin{aligned} \sum \limits _{i=1}^4\Delta _i=0\quad \text{ and } \quad \sum \limits _{i=1}^4\Delta _i\mathbf{q}_i=0. \end{aligned}$$

Furthermore, a co-circular configuration of four bodies is convex and the previously adopted labeling gives us $\Delta _3,\,\Delta _4<0<\Delta _1,\,\Delta _2$. The equation

$$\begin{aligned} \frac{\Delta _i\Delta _j}{m_im_j} = k^2-\varphi (s_{ij}) \end{aligned}$$

and the distribution of the $\Delta _i$’s signs imply that

$$\begin{aligned} \varphi (s_{12}),\,\varphi (s_{34})< k^2 < \varphi (s_{13}),\,\varphi (s_{14}),\,\varphi (s_{23}),\,\varphi (s_{24}). \end{aligned}$$

Once $\varphi$ is increasing, both diagonals are smaller than any external side of the co-circular polygon and this is geometrically impossible. $\square$

The next theorem is the tensorial characterization of the co-circular $(4,1)$-central configurations.

Theorem 7

Let $\beta$ be a relative co-circular $(4,1)$-central configuration of the five body-problem. Then the tensor $\alpha =dg(\beta )$ admits the following parametrization

$$\begin{aligned} \alpha =-\Delta \otimes \Delta -\gamma \Gamma \otimes \Gamma \end{aligned}$$

where

• $\Delta _0=0$ and ${\tilde{\Delta }}=(\Delta _1,\ldots ,\Delta _4)\in \mathcal{D }_4^*$ is a Dziobek cc of the co-circular 4 body–problem.

• $\Gamma =(M-m,\,-m_1,\,-m_2,-m_3,\,-m_4)$

• $\gamma =-\frac{m}{M-m}\varphi (R^2)>0.$

Proof

By the Lemma 6, there are vectors $\Delta ,\,Z\in \mathcal{D }^*_5$ such that $\Delta _0=0$ and

$$\begin{aligned} \alpha =-\Delta \otimes \Delta +\sigma Z\otimes Z. \end{aligned}$$

Choose $\Delta _1>0$ and $Z_0>0.$ Introducing coordinates, the tensor equation becomes

$$\begin{aligned} m_im_j\varphi (s_{ij})=\Delta _i\Delta _j-\sigma Z_iZ_j. \end{aligned}$$

By taking $j=0$ and $i\ne 0$, we get

$$\begin{aligned} -\sigma Z_0Z_i=mm_i\varphi (R^2), \end{aligned}$$

(6.4)

whose summation gives us

$$\begin{aligned} \sigma Z_0^2&= \sum \limits _{i=1}^4Z_0Z_i=\sum \limits _{i=1}^4mm_i\varphi (R^2) = m(M-m)\varphi (R^2)\nonumber \\&\Rightarrow \quad Z_0^2 = \sigma m(M-m)\varphi (R^2)>0. \end{aligned}$$

(6.5)

On the other hand, all $Z_i$ coordinates must be non zero and their quotients by the respective masses $m_i$ are constants because of (6.4). Thus

$$\begin{aligned} \frac{Z_i}{m_i}&= -\sigma \frac{m\varphi (R^2)}{Z_0} = -\frac{Z_0}{M-m}\\ Z&= \frac{Z_0}{M-m} \big (M-m,\,-m_1,\,-m_2,\,-m_3,\,-m_4\big ). \end{aligned}$$

By defining

$$\begin{aligned} \Gamma =\big (M-m,\,-m_1,\,-m_2,\,-m_3,\,-m_4 \big )\quad \text{ and } \quad \gamma =\frac{Z_0^2}{(M-m)^2} \end{aligned}$$

we arrive to the expression

$$\begin{aligned} \alpha =-\Delta \otimes \Delta +\sigma \cdot \gamma \cdot \Gamma \otimes \Gamma . \end{aligned}$$

The Eq. (6.5) allows us to write the expression for $\gamma$ in another way

$$\begin{aligned} \gamma = \sigma \frac{m}{M-m}\varphi (R^2). \end{aligned}$$

(6.6)

If $1\le i<j\le 4$, then

$$\begin{aligned}&m_im_j\varphi (s_{ij}) = \Delta _i\Delta _j -\sigma \gamma m_im_j\\&m_im_j\left( \sigma \gamma +\varphi (s_{ij})\right) = \Delta _i\Delta _j\\&m_im_j{\tilde{\varphi }}(s_{ij}) = \Delta _i\Delta _j \end{aligned}$$

where we have made ${\tilde{\varphi }}(s)=\sigma \gamma +\frac{\lambda }{M}-s^a$.

However

$$\begin{aligned} \sigma \gamma +\frac{\lambda }{M}=\frac{m}{M-m}\varphi (R^2)+\frac{\lambda }{M} = \frac{m}{M-m}\left( \frac{\lambda }{M}-R^{2a}\right) +\frac{\lambda }{M} =\frac{\lambda -mR^{2a}}{M-m}. \end{aligned}$$

We define

$$\begin{aligned} {\tilde{\lambda }}=\lambda -mR^{2a} \end{aligned}$$

to obtain the function

$$\begin{aligned} {\tilde{\varphi }}(s)=\frac{{\tilde{\lambda }}}{M-m}-s^a \end{aligned}$$

and it follows that the four bodies lying on the circle must satisfy the equations

$$\begin{aligned} m_im_j{\tilde{\varphi }}(s_{ij}) = \Delta _i\Delta _j, \quad \sum \limits _{i=1}^4\Delta _i=0, \quad \sum \limits _{i=1}^4\Delta _i\mathbf{q}_i=0. \end{aligned}$$

We claim that ${\tilde{\lambda }}>0$. In fact, if ${\tilde{\lambda }}\le 0$ then we would have all the ${\tilde{\varphi }}(s_{ij})$ to be negative, which does not hold, since at least two of $\Delta _i^{\prime }s$ have the same sign. Thus $(\mathbf{q}_1,\ldots ,\mathbf{q}_4)$ is a co-circular Dziobek configuration associated to the multiplier ${\tilde{\lambda }}.$

By Remark (5), we have that

$$\begin{aligned} 0>{\tilde{\varphi }}(R^2) = \frac{\lambda -mR^{2a}}{M-m}-R^{2a} = \frac{M}{M-m}\, \left( \frac{\lambda }{M}-R^{2a}\right) =\frac{M}{M-m}\varphi (R^{2}). \end{aligned}$$

On the other hand, the expression (6.6) and the positiveness of $\gamma$ imply that

$$\begin{aligned} \sigma =-1. \end{aligned}$$

$\square$

Remark 11

In the above proof, we saw that the co-circular $(4,1)$-central configurations are, in fact, stacked central configurations as defined in [11].

Corollary 1

In a co-circular $(4,1)$-central configuration, the radius of the circle $R$ must satisfy

$$\begin{aligned} \frac{\lambda }{M}<R^{2a}<\frac{\lambda }{m}. \end{aligned}$$

Indeed, this follows from the two estimates

$$\begin{aligned} \varphi (R^2)<0\quad \text{ and } \quad 0<{\tilde{\lambda }}. \end{aligned}$$

Corollary 2

In a co-circular $(4,1)$-central configuration, the center of mass for the four co-circular particles is located at the center of the circle.

Proof

In fact, both vectors $\Delta$ and $\Gamma$ are in $\ker \{\beta \}$. As a quadratic form on the hyperplane $\mathcal{D }^*$, the tensor $\beta$ has another representation by the matrix

$$\begin{aligned} \beta =\left( \begin{array}{lllll} \ddots &{} &{} \vdots \\ &{} \langle \mathbf{q}_i,\mathbf{q}_j\rangle &{} \\ \vdots &{} &{} \ddots \end{array}\right) _{0\le i,j\le 4}. \end{aligned}$$

By using the relations $M-m=\sum _{i=1}^4 m_i$ and $\beta \circ \Gamma =0$ in $\mathcal{D }$, we get

$$\begin{aligned} \left\langle \mathbf{q}_0,\,\sum \limits _{j=1}^4(\mathbf{q}_0-\mathbf{q}_j)m_j \right\rangle = \left\langle \mathbf{q}_i,\,\sum \limits _{j=1}^4(\mathbf{q}_0-\mathbf{q}_j)m_j\right\rangle \end{aligned}$$

for all $i=1,\ldots ,4$, that is,

$$\begin{aligned} \left\langle \mathbf{q}_0-\mathbf{q}_i,\,\sum \limits _{j=1}^4(\mathbf{q}_0-\mathbf{q}_j)m_j \right\rangle = 0. \end{aligned}$$

Thus, the vector $\displaystyle \sum _{j=1}^4(\mathbf{q}_0-\mathbf{q}_j)m_j$ is orthogonal to its components and so, it must be zero. By extracting $\mathbf{q}_0$ from this expression, we get

$$\begin{aligned} \mathbf{q}_0=\frac{1}{M-m}\sum \limits _{i=1}^4m_i\mathbf{q}_i. \end{aligned}$$

$\square$

Consider the Newtonian five-body problem, i.e., $a=-3/2$. Once the four bodies on the circle form a co-circular central configuration whose center of mass is located at the center  of the circle, the configuration $(\mathbf{q}_1,\ldots ,\mathbf{q}_4)$ is a square and the masses $m_1,\ldots ,m_4$ are all equal, as proved by Hampton in [10].

This allows partially to answer the question raised at the beginning of this section

Corollary 3

For $a=-3/2$, the only co-circular $(4,1)$-central configuration is the square with four equal masses on the circle and an arbitrary mass located at the center.

We finish with a few words about the question posed by Chenciner in the co-circular four-body problem (see [10]). We think that the condition of fixing the center of mass at the center of the circle is a condition of symmetry as well as the condition of equal masses in [1], for example. Despite the result published in [10], we propose to search for a general method to prove that the co-circular central configurations for four bodies having its center of mass located at the center of the circle present some kind of symmetry, for any homogeneous force law, i.e., for any $a\le -1$.

7 Conclusions

In this work, we intended to draw attention on two aspects in the research of central configurations. First of all, the generality of some results that apply to the Newtonian case and which can work for any homogeneous force law, as for example, questions dealing with symmetry. We consider the Chenciner’s question about co-circular central configurations as a problem of this type and therefore, the Hampton’s result in [10] may be true for any homogeneous force law. For instance, we saw here a partial generalization of the result found in [8] about kites. In effect, we could show the existence of a family of co-circular kite central configurations in the four body-problem, regardless of the value of the exponent $a$ in the interval $(-\infty ,-1]$.

The other aspect is the application of the tensorial approach to model the central configurations. In here, we succeed to describe all co-circular (4,1)-central configurations in a first application of these techniques to the study of central configurations of the planar five body-problem.