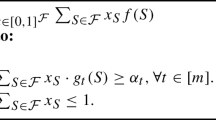Group fairness in non-monotone submodular maximization

Abstract

Maximizing a submodular function has a wide range of applications in machine learning and data mining. One such application is data summarization whose goal is to select a small set of representative and diverse data items from a large dataset. However, data items might have sensitive attributes such as race or gender, in this setting, it is important to design fairness-aware algorithms to mitigate potential algorithmic bias that may cause over- or under- representation of particular groups. Motivated by that, we propose and study the classic non-monotone submodular maximization problem subject to novel group fairness constraints. Our goal is to select a set of items that maximizes a non-monotone submodular function, while ensuring that the number of selected items from each group is proportionate to its size, to the extent specified by the decision maker. We develop the first constant-factor approximation algorithms for this problem. We also extend the basic model to incorporate an additional global size constraint on the total number of selected items.

1 Introduction

Submodular function refers to a broad class of functions which satisfy the natural diminishing returns property: adding an additional item to a larger existing subset is less beneficial. A wide range of machine learning and AI problems, including exemplar-based clustering (Dueck and Frey 2007), feature selection (Das and Kempe 2008), active learning (Golovin and Krause 2011), influence maximization in social networks (Tang and Yuan 2020), recommender system (El-Arini and Guestrin 2011), and diverse data summarization (Sipos et al. 2012), can be formulated as a submodular maximization problem. This problem, whose goal is to select a set of items to maximize a submodular function, and its variants (Gu et al. 2022; Shi et al. 2021) have been extensively studied in the literature subject to various constraints, including cardinality, matroid, or knapsack-type restrictions.

We notice that in practise, items or individuals are often associated with different groups based on various attributes, such as gender, race, age, religion, or other factors. Existing algorithms might exhibit bias if left unchecked, for example, some of the groups might be over- or under-represented in the final selected subset. Therefore, it becomes increasingly important to design fairness-aware algorithms to mitigate such issues. Towards this end, we propose and study the classic non-monotone submodular maximization problem subject to novel group fairness constraints. Our goal is to select a balanced set of items that maximizes a non-monotone submodular function, such that the ratio of selected items from each group to its size is within a desired range, as determined by the decision maker. Non-monotone submodular maximization has multiple compelling applications, such as feature selection (Das and Kempe 2008), profit maximization (Tang and Yuan 2021), maximum cut (Gotovos et al. 2015) and data summarization (Mirzasoleiman et al. 2016). Formally, we consider a set V of items (e.g., datapoints) which are partitioned into m groups: $V_1, V_2, \cdots , V_m$ such that items from the same group share same attributes (e.g., gender). We say that a set $S\subseteq V$ of items is $(\alpha ,\beta )$-fair if for all groups $i \in [m]$, it holds that $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i| \le \lfloor \beta |V_i|\rfloor$. Using our model, it allows for the decision maker to specify the desired level of fairness by setting appropriate values of $\alpha$ and $\beta$. Specifically, setting $\alpha =\beta$ leads to the highest level of fairness in that the number of selected items is strictly proportional to its group size; if we set $\alpha =0$ and $\beta =1$, there are no fairness constraints. Our goal is to find such a $(\alpha ,\beta )$-fair subset of items that maximizes a submodular objective function. Our definition of fairness, which balances solutions with respect to sensitive attributes, has gained widespread acceptance in the academic community, as demonstrated by its frequent use in previous studies (Celis et al. 2018b; El Halabi et al. 2020; Chierichetti et al. 2019). There are several other notations of fairness that can be captured by our formulation such as the $80\%$-rule (Biddle 2017), statistical parity (Dwork et al. 2012) and proportional representation (Monroe 1995).

1.1 Our contributions

• Our study breaks new ground by examining the classic (non-monotone) submodular maximization problem under $(\alpha ,\beta )$-fairness constraints. Our model offers flexibility in capturing varying degrees of fairness as desired by the decision maker, by adjusting the values of $\alpha$ and $\beta$.

• We develop the first constant-factor approximation algorithm for this problem. We observe that the parameter $\alpha$ is closely linked to the complexity of solving the $(\alpha ,\beta )$-fair non-monotone submodular maximization problem. In particular, when $\alpha \le 1/2$, we design a $\frac{\gamma }{2}$-approximation algorithm and when $\alpha > 1/2$, we develop a $\frac{\gamma }{3}$-approximation algorithm, where $\gamma$ is the approximation ratio of the current best algorithm for matroid-constrained submodular maximization. We also extend the basic model to incorporate an additional global size constraint on the total number of selected items. We provide approximation algorithms that have a constant-factor approximation ratio for this extended model.

1.2 Additional related works

In recent years, there has been a growing awareness of the importance of fair and unbiased decision-making systems. This has led to an increased interest in the development of fair algorithms in a wide range of applications, including influence maximization (Tsang et al. 2019), classification (Zafar et al. 2017), voting (Celis et al. 2018b), bandit learning (Joseph et al. 2016), and data summarization (Celis et al. 2018a). Depending on the specific context and the type of bias that one is trying to mitigate, existing studies adopt different metrics of fairness. This can lead to different optimization problems and different fair algorithms that are tailored to the specific requirements of the application. Our notation of fairness is general enough to capture many existing notations such as the $80\%$-rule (Biddle 2017), statistical parity (Dwork et al. 2012) and proportional representation (Monroe 1995). Unlike most of existing studies on fair submodular maximization (Celis et al. 2018b) whose objective is to maximize a monotone submodular function, (El Halabi et al. 2020) develop fair algorithms in the context of streaming non-monotone submodular maximization. Their proposed notation of fairness is more general than ours, leading to a more challenging optimization problem which does not admit any constant-factor approximation algorithms. Tang et al. (2023), Tang and Yuan (2023) aim to develop randomized algorithms that satisfy average fairness constraints. Very recently, Tang and Yuan (2022) extend the studies of fair algorithms to a more complicated adaptive setting and they propose a new metric of fairness called group equality.

2 Preliminaries and problem statement

We consider a set V of n items. There is a non-negative submodular utility function $f: 2^V\rightarrow {\mathbb {R}}_+$. Denote by $f(e\mid S)$ the marginal utility of $e\in V$ on top of $S\subseteq V$, i.e., $f(e\mid S)=f(\{e\}\cup S)-f(S)$. We say a function $f: 2^V\rightarrow {\mathbb {R}}_+$ is submodular if for any two sets $X, Y\subseteq V$ such that $X\subseteq Y$ and any item $e \in V\setminus Y$,

$$\begin{aligned}f(e\mid Y) \le f(e\mid X).\end{aligned}$$

Assume V is partitioned into m disjoint groups: $V_1, V_2,\cdots , V_m$. We assume that there is a given lower and upper bound on the fraction of items of each group that must be contained in a feasible solution. These two bounds, namely $\alpha$ and $\beta$, represent group fairness constraints. The problem of $(\alpha , \beta )$-fair submodular maximization problem (labelled as ${\textbf {P.0}}$) can be written as follows.

One can adjust the degree of group fairness in a feasible solution through choosing appropriate values of $\alpha$ and $\beta$. I.e., strict group fairness is achieved at $\alpha =\beta$ in which case every feasible solution must contain the same $\alpha$ fraction of items from each group; if we set $\alpha =0$ and $\beta =1$, then there is no group fairness constraints. We next present the hardness result of this problem.

Lemma 1

Problem ${\textbf {P.0}}$ is NP-hard.

Proof

We prove this through reduction to the classic cardinality constrained submodular maximization problem which we define below.

Definition 1

The input of cardinality constrained submodular maximization problem is a group of items U, a submodular function $h: 2^U\rightarrow {\mathbb {R}}_+$, and a cardinality constraint b; we aim to select a group of items $S\subseteq U$ such that h(S) is maximized and $|S|\le b$.

We next show a reduction from cardinality constrained submodular maximization problem to ${\textbf {P.0}}$. Consider any given instance of cardinality constrained submodular maximization problem, we construct a corresponding instance of ${\textbf {P.0}}$ as follows: Let $V=U$, $f=h$, assume there is only one group, i.e., $V=V_1$, and let $\alpha =0$, $\beta =b/|U|$. It is easy to verify that these two instances are equivalent. This finishes the proof of the reduction. $\Box$

3 Non-monotone submodular maximization with group fairness

Warm-up: Monotone Utility Function If f is monotone and submodular, we can easily confirm that ${\textbf {P.0}}$ can be simplified to ${\textbf {P.1}}$ by removing the lower bound constraints. This is because in this case, increasing the size of a solution by adding more items will not decrease its utility. As a result, the lower bound constraints in ${\textbf {P.0}}$, which state that $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i|$ for all $i \in [m]$, can always be met by adding sufficient items to the solution.

Since f is a monotone submodular function, ${\textbf {P.1}}$ is a well-known problem of maximizing a monotone submodular function subject to matroid constraints¹. This problem has a $(1-1/e)$-approximation algorithm.

We then proceed to develop approximation algorithms for non-monotone functions. We will examine two scenarios, specifically when $\alpha \le 1/2$ and when $\alpha > 1/2$.

3.1 The case when $\alpha \le 1/2$

In the scenario where $\alpha \le 1/2$, we use the solution of ${\textbf {P.1}}$ as a building block to construct our algorithm. First, it is easy to verify that ${\textbf {P.1}}$ is a relaxed version of ${\textbf {P.0}}$ with lower bound constraints $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i|$ in ${\textbf {P.0}}$ being removed. Because f is a submodular function, ${\textbf {P.1}}$ is a classic problem of maximizing a (non-monotone) submodular function subject to matroid constraints. There exist effective solutions for ${\textbf {P.1}}$. Now we are ready to present the design of our algorithm as below.

• 1. Apply the state-of-the-art algorithm ${\mathcal {A}}$ for matroid constrained submodular maximization to solve ${\textbf {P.1}}$ and obtain a solution $A^{P.1}$.

• 2. Note that $A^{P.1}$ is not necessarily a feasible solution to ${\textbf {P.0}}$ because it might violate the lower bound constraints $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i|$ for some groups. To make it feasible, we add additional items to $A^{P.1}$. Specifically, for each group $i\in [m]$ such that $|A^{P.1} \cap V_i|< \lfloor \alpha |V_i|\rfloor$, our algorithm selects a backup set $B_i$ of size $\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|$, by randomly sampling $\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|$ items from $V_i\setminus A^{P.1}$. Define $B_i=\emptyset$ if $|A^{P.1} \cap V_i|\ge \lfloor \alpha |V_i|\rfloor$.

• 3. At the end, add $\cup _{i\in [m]}B_i$ to $A^{P.1}$ to build the final solution $A^{approx}$, i.e., $A^{approx}= A^{P.1}\cup (\cup _{i\in [m]}B_i)$.

The pseudocode of this approximation algorithm is given as Algorithm 1. Observe that $A^{P.1}$ is a feasible solution to ${\textbf {P.1}}$, hence, $A^{P.1}$ satisfies upper bound constraints of ${\textbf {P.1}}$ and hence ${\textbf {P.0}}$, i.e., $|S \cap V_i| \le \lfloor \beta |V_i|\rfloor , \forall i \in [m]$. According to the construction of $B_i$, it is easy to verify that adding $\cup _{i\in [m]}B_i$ to $A^{P.1}$ does not violate the upper bound constraints because $\cup _{i\in [m]}B_i$ are only supplemented to those groups which do not satisfy the lower bound constraints of ${\textbf {P.0}}$, i.e., $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i|$. Moreover, adding $\cup _{i\in [m]}B_i$ to $A^{P.1}$ makes it satisfy lower bound constraints of ${\textbf {P.0}}$. Hence, $A^{approx}$ is a feasible solution to ${\textbf {P.0}}$.

Lemma 2

$A^{approx}$ is a feasible solution to ${\textbf {P.0}}$.

3.1.1 Performance analysis

We next analyze the performance of Algorithm 1. We first introduce a useful lemma from Buchbinder et al. (2014).

Lemma 3

If f is submodular and S is a random subset of V, such that each item in V is contained in S with probability at most p, then ${\mathbb {E}}_S[f(S)] \ge (1-p)f(\emptyset )$.

The next lemma states that if $A^{P.1}$ is a $\gamma$-approximate solution of ${\textbf {P.1}}$, then $f(A^{P.1})$ is at least $\gamma$ fraction of the optimal solution of ${\textbf {P.0}}$.

Lemma 4

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint. Let OPT denote the optimal solution of ${\textbf {P.0}}$, we have $f(A^{P.1})\ge \gamma f(OPT)$.

Proof

Because ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint, we have $f(A^{P.1})\ge \gamma f(O^{P.1})$ where $O^{P.1}$ denotes the optimal solution of ${\textbf {P.1}}$. Moreover, because ${\textbf {P.1}}$ is a relaxed version of ${\textbf {P.0}}$, we have $f(O^{P.1})\ge f(OPT)$. Hence, $f(A^{P.1})\ge \gamma f(OPT)$. $\Box$

We next show that augmenting $A^{P.1}$ with items from the random set $\cup _{i\in [m]}B_i$ reduces its utility by a factor of at most 1/2 in expectation. Here the expectation is taken over the distribution of $\cup _{i\in [m]}B_i$.

Lemma 5

Suppose $\alpha \le 1/2$, we have ${\mathbb {E}}_{A^{approx}}[f(A^{approx})]\ge \frac{1}{2}f(A^{P.1})$ where $A^{approx}= A^{P.1}\cup (\cup _{i\in [m]}B_i)$.

Proof

Recall that $B_i= \emptyset$ for all $i\in [m]$ such that $|A^{P.1} \cap V_i|\ge \lfloor \alpha |V_i|\rfloor$, hence, adding those $B_i$ to $A^{P.1}$ does not affect its utility. In the rest of the proof we focus on those $B_i$ with

$$\begin{aligned} |A^{P.1} \cap V_i|< \lfloor \alpha |V_i|\rfloor . \end{aligned}$$

(1)

Recall that for every $i\in [m]$ such that $|A^{P.1} \cap V_i|< \lfloor \alpha |V_i|\rfloor$, $B_i$ is a random set of size $\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|$ that is sampled from $V_i\setminus A^{P.1}$. It follows that each item in $V_i\setminus A^{P.1}$ is contained in $B_i$ with probability at most

$$\begin{aligned} \frac{\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|}{|V_i\setminus A^{P.1}|}. \end{aligned}$$

(2)

We next give an upper bound of (2). First,

$$\begin{aligned} \lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|\le \lfloor \alpha |V_i|\rfloor \le |V_i|/2, \end{aligned}$$

(3)

where the second inequality is by the assumption that $\alpha \le 1/2$. Moreover,

$$\begin{aligned}{} & {} |V_i\setminus A^{P.1}|=|V_i|- |A^{P.1} \cap V_i|=(\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|)+ (|V_i|-\lfloor \alpha |V_i|\rfloor ) \nonumber \\\end{aligned}$$

(4)

$$\begin{aligned}{} & {} \ge (\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|)+|V_i|/2, \end{aligned}$$

(5)

where the inequality is by the assumption that $\alpha \le 1/2$.

Hence,

$$\begin{aligned} (15) \le \frac{\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|}{ (\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|)+|V_i|/2}\le \frac{|V_i|/2}{|V_i|/2+|V_i|/2}=1/2, \end{aligned}$$

(6)

where the first inequality is by (5); the second inequality is by (3) and the assumption that $\lfloor \alpha |V_i|\rfloor -|A^{P.1} \cap V_i|>0$ (listed in (1)). That is, the probability that each item in $V_i\setminus A^{P.1}$ is contained in $B_i$ is at most 1/2. It follows that the probability that each item in $V \setminus A^{P.1}$ is contained in $\cup _{i\in [m]}B_i$ is at most 1/2. Moreover, Lemma 3 states that if f is submodular and S is a random subset of V, such that each item in V appears in S with probability at most p, then ${\mathbb {E}}_A[f(A)] \ge (1-p)f(\emptyset )$. With the above discussion and the observation that $f(A^{P.1}\cup \cdot )$ is submodular, it holds that ${\mathbb {E}}_{A^{approx}}[f(A^{approx})]={\mathbb {E}}_{\cup _{i\in [m]}B_i}[f(A^{P.1}\cup (\cup _{i\in [m]}B_i))]\ge (1-\frac{1}{2})f(A^{P.1}\cup \emptyset )=\frac{1}{2}f(A^{P.1})$. $\Box$

Our main theorem as below follows from Lemma 4 and Lemma 5.

Theorem 1

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint and $\alpha \le 1/2$, we have ${\mathbb {E}}_{A^{approx}}[f(A^{approx})]\ge \frac{\gamma }{2}f(OPT)$.

One option of ${\mathcal {A}}$ is the continuous double greedy algorithm proposed in Feldman et al. (2011) which gives a $1/e-o(1)$-approximation solution, that is, $\gamma \ge 1/e-o(1)$. This, together with Theorem 1, implies that ${\mathbb {E}}_{A^{approx}}[f(A^{approx})]\ge \frac{1/e-o(1)}{2}f(OPT)$.

3.2 The case when $\alpha > 1/2$

We next consider the case when $\alpha > 1/2$. We first introduce a new utility function $g: 2^V\rightarrow {\mathbb {R}}_+$ as below:

$$\begin{aligned} g(\cdot ) = f(V\setminus \cdot ). \end{aligned}$$

(7)

We first present a well-known result, which states that submodular functions maintain their submodularity property when taking their complement.

Lemma 6

If f is submodular, then g must be submodular.

With utility function g, we present a new optimization problem ${\textbf {P.2}}$ as below:

${\textbf {P.2}}$ is a flipped version of the original problem ${\textbf {P.0}}$ in the sense that if there is a $\gamma$-approximate solution $A^{P.2}$ to ${\textbf {P.2}}$, it can be easily verified that $V\setminus A^{P.2}$ is a $\gamma$-approximate solution to ${\textbf {P.0}}$. As a result, we will focus on solving ${\textbf {P.2}}$ for the rest of this section.

To solve ${\textbf {P.2}}$, we introduce another problem (labeled as ${\textbf {P.3}}$) as follows:

${\textbf {P.3}}$ is relaxed version of ${\textbf {P.2}}$ with lower bound constraints $|V_i|-\lfloor \beta |V_i|\rfloor \le |S \cap V_i|$ in ${\textbf {P.2}}$ being removed. Because g is a submodular function, ${\textbf {P.3}}$ is a classic problem of maximizing a submodular function subject to matroid constraints. Now we are ready to present the design of our algorithm.

• 1. Apply the state-of-the-art algorithm ${\mathcal {A}}$ for matroid constrained submodular maximization to solve ${\textbf {P.3}}$ and obtain a solution $A^{P.3}$.

• 2. Note that $A^{P.3}$ is not necessarily a feasible solution to ${\textbf {P.2}}$ because it might violate the lower bound constraints $|V_i|-\lfloor \beta |V_i|\rfloor \le |S \cap V_i|$ for some groups. We add additional items to $A^{P.3}$ to make it feasible. Specifically, for each group $i\in [m]$ such that $|A^{P.3} \cap V_i|< |V_i|-\lfloor \beta |V_i|\rfloor$, our algorithm selects a backup set $B_i$ of size $|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|$, by randomly sampling $|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|$ items from $V_i\setminus A^{P.3}$. Define $B_i=\emptyset$ if $|A^{P.1} \cap V_i|\ge |V_i|-\lfloor \beta |V_i|\rfloor$.

• 3. Add $\cup _{i\in [m]}B_i$ to $A^{P.3}$ to build $A^{approx}$, i.e., $A^{approx}= A^{P.3}\cup (\cup _{i\in [m]}B_i)$. Return $V\setminus A^{approx}$ as the final solution.

The pseudocode of this approximation algorithm is given as Algorithm 2. Observe that $A^{P.3}$ satisfies upper bound constraints of ${\textbf {P.3}}$ and hence ${\textbf {P.2}}$ because $A^{P.3}$ is a feasible solution to ${\textbf {P.3}}$. According to the construction of $B_i$, adding $\cup _{i\in [m]}B_i$ to $A^{P.1}$ does not violate the upper bound constraints because $\cup _{i\in [m]}B_i$ are added to meet the lower bound constraints of ${\textbf {P.2}}$ if necessary. Moreover, adding $\cup _{i\in [m]}B_i$ to $A^{P.3}$ makes it satisfy lower bound constraints of ${\textbf {P.2}}$. Hence, $A^{approx}$ is a feasible solution to ${\textbf {P.2}}$.

Lemma 7

$A^{approx}$ is a feasible solution to ${\textbf {P.2}}$.

3.2.1 Performance analysis

We first introduce a technical lemma which states that if $A^{P.3}$ is a $\gamma$-approximate solution of ${\textbf {P.3}}$, then $f(A^{P.3})$ is at least $\gamma$ fraction of the optimal solution of ${\textbf {P.2}}$. This lemma follows from the observation that ${\textbf {P.3}}$ is a relaxation of ${\textbf {P.2}}$ .

Lemma 8

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint. Let $O^{P.2}$ denote the optimal solution of ${\textbf {P.2}}$, it holds that $g(A^{P.3})\ge \gamma g(O^{P.2})$.

We next show that augmenting $A^{P.3}$ with items from $\cup _{i\in [m]}B_i$ reduces its utility by a factor of at most 2/3 in expectation.

Lemma 9

Suppose $\alpha > 1/2$, ${\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{1}{3}g(A^{P.3})$ where $A^{approx}= A^{P.3}\cup (\cup _{i\in [m]}B_i)$.

Proof

Recall that $B_i= \emptyset$ for all $i\in [m]$ such that $|A^{P.3} \cap V_i|\ge |V_i|-\lfloor \beta |V_i|\rfloor$, hence, adding those $B_i$ to $A^{P.3}$ does not affect its utility. Therefore, we focus on those groups $i\in [m]$ with $|A^{P.3} \cap V_i|< |V_i|-\lfloor \beta |V_i|\rfloor$ in the rest of the proof. Let $M=\{i\mid |A^{P.3} \cap V_i|< |V_i|-\lfloor \beta |V_i|\rfloor \}$ denote the set containing the indexes of all such groups and we assume $M\ne \emptyset$ to avoid trivial cases. We next show that it is safe to assume $\min _{i\in M}|V_i|>1$ without loss of generality, i.e., the smallest group in M contains at least two items. To prove this, we consider two cases, depending on the value of $\beta$. If $\beta =1$, then $|A^{P.3} \cap V_i|< |V_i|-\lfloor \beta |V_i|\rfloor$ does not hold for any group i such that $|V_i|=1$, that is, $\min _{i\in M}|V_i|>1$. If $\beta <1$, then according to the group fairness constraints listed in ${\textbf {P.0}}$, we are not allowed to select any items from those groups with $|V_i|=1$. Hence, removing all groups with size one from consideration does not affect the quality of the optimal solution.

With the assumption that $\min _{i\in M}|V_i|>1$, we are now in position to prove this lemma. Recall that for every $i\in M$, $B_i$ is a random set of size $|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|$ that is sampled from $V_i\setminus A^{P.3}$. It follows that each item in $V_i\setminus A^{P.3}$ appears in $B_i$ with probability at most

$$\begin{aligned} \frac{|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|}{|V_i\setminus A^{P.3}|}. \end{aligned}$$

(8)

We next give an upper bound of (8). Because we assume $\alpha > 1/2$, we have $\beta \ge \alpha >1/2$. This, together with the assumption that $\min _{i\in M}|V_i|>1$, implies that for all $i\in M$,

$$\begin{aligned} |V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i| \le |V_i|-\lfloor \beta |V_i|\rfloor \le 2|V_i|/3. \end{aligned}$$

(9)

Moreover,

$$\begin{aligned}{} & {} |V_i\setminus A^{P.3}|=|V_i|-|A^{P.3} \cap V_i|\end{aligned}$$

(10)

$$\begin{aligned}{} & {} =(|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|)+(|V_i|-(|V_i|-\lfloor \beta |V_i|\rfloor )) \end{aligned}$$

(11)

$$\begin{aligned}{} & {} = (|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|)+\lfloor \beta |V_i|\rfloor \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \ge (|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|)+|V_i|/3, \end{aligned}$$

(13)

where the inequality is by the observation that $\beta >1/2$. It follows that

$$\begin{aligned} (8)\le \frac{|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|}{(|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|)+|V_i|/3}\le \frac{2|V_i|/3}{2|V_i|/3+|V_i|/3}=2/3, \end{aligned}$$

(14)

where the first inequality is by (13) and the second inequality is by (9) and the assumption that $|V_i|-\lfloor \beta |V_i|\rfloor -|A^{P.3} \cap V_i|>0$. That is, each item in $V_i\setminus A^{P.3}$ appears in $B_i$ with probability at most 2/3. Lemma 3 and the observation that $g(A^{P.3}\cup \cdot )$ is submodular imply that ${\mathbb {E}}_{A^{approx}}[g(A^{approx})]={\mathbb {E}}_{\cup _{i\in [m]}B_i}[g(A^{P.3}\cup (\cup _{i\in [m]}B_i))]\ge (1-\frac{2}{3})g(A^{P.3}\cup \emptyset )= \frac{1}{3}g(A^{P.3})$. $\Box$

Lemmas 8 and 9 together imply that

$$\begin{aligned}{\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{1}{3}g(A^{P.3})\ge \frac{\gamma }{3}g(O^{P.2}).\end{aligned}$$

By the definition of function g, we have

$$\begin{aligned}{\mathbb {E}}_{A^{approx}}[f(V\setminus A^{approx})]={\mathbb {E}}_{A^{approx}}[g(A^{approx})] \ge \frac{\gamma }{3}g(O^{P.2})=\frac{\gamma }{3}f(OPT)\end{aligned}$$

where the last equality is by the observation that ${\textbf {P.2}}$ and ${\textbf {P.0}}$ share the same value of the optimal solution. Hence, the following main theorem holds.

Theorem 2

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint and $\alpha > 1/2$, we have ${\mathbb {E}}_{A^{approx}}[f(V\setminus A^{approx})]\ge \frac{\gamma }{3}f(OPT)$.

If we adopt the continuous double greedy algorithm (Feldman et al. 2011) as ${\mathcal {A}}$ to compute $A^{P.3}$, it gives a $1/e-o(1)$-approximation solution, that is, $\gamma \ge 1/e-o(1)$. This, together with Theorem 2, implies that ${\mathbb {E}}_{A^{approx}}[f(V\setminus A^{approx})]\ge \frac{1/e-o(1)}{3}f(OPT)$.

4 Extension: incorporating global cardinality constraint

In this section, we extend ${\textbf {P.0}}$ to incorporate a global cardinality constraint. A formal definition of this problem is listed in ${\textbf {P.A}}$. Our objective is to find a best S subject to a group fairness constraint $(\alpha ,\beta )$ and an additional cardinality constraint c.

4.1 The case when $\alpha \le 1/2$

We first consider the case when $\alpha \le 1/2$. We introduce a new optimization problem ${\textbf {P.B}}$ as follows:

It is easy to verify that ${\textbf {P.B}}$ is a relaxation of ${\textbf {P.A}}$ in the sense that every feasible solution to ${\textbf {P.A}}$ is also a feasible solution to ${\textbf {P.B}}$. Hence, we have the following lemma.

Lemma 10

Let OPT denote the optimal solution of ${\textbf {P.A}}$ and $O^{P.B}$ denote the optimal solution of ${\textbf {P.B}}$, we have $f(O^{P.B})\ge f(OPT)$.

It has been shown that the constraints in ${\textbf {P.B}}$ gives rise to a matroid (El Halabi et al. 2020). This, together with the assumption that f is a submodular function, implies that ${\textbf {P.B}}$ is a classic problem of maximizing a submodular function subject to matroid constraints. Now we are ready to present the design of our algorithm.

• 1. Apply the state-of-the-art algorithm ${\mathcal {A}}$ for matroid constrained submodular maximization to solve ${\textbf {P.B}}$ and obtain a solution $A^{P.B}$.

• 2. Note that $A^{P.B}$ is not necessarily a feasible solution to ${\textbf {P.A}}$ because it might violate the lower bound constraints $\lfloor \alpha |V_i|\rfloor \le |S \cap V_i|$ for some groups. To make it feasible, we add additional items to $A^{P.B}$. Specifically, for each group $i\in [m]$ such that $|A^{P.B} \cap V_i|< \lfloor \alpha |V_i|\rfloor$, our algorithm selects a backup set $B_i$ of size $\lfloor \alpha |V_i|\rfloor -|A^{P.B} \cap V_i|$, by randomly sampling $\lfloor \alpha |V_i|\rfloor -|A^{P.B} \cap V_i|$ items from $V_i\setminus A^{P.B}$. Define $B_i=\emptyset$ if $|A^{P.1} \cap V_i|\ge \lfloor \alpha |V_i|\rfloor$.

• 3. At the end, add $\cup _{i\in [m]}B_i$ to $A^{P.B}$ to build the final solution $A^{approx}$, i.e., $A^{approx}= A^{P.B}\cup (\cup _{i\in [m]}B_i)$.

The pseudocode of this approximation algorithm is given as Algorithm 3. Observe that $A^{P.B}$ satisfies the group-wise upper bound constraints of ${\textbf {P.A}}$ because $A^{P.B}$ meets the first set of constraints in ${\textbf {P.B}}$. According to the construction of $B_i$, adding $\cup _{i\in [m]}B_i$ to $A^{P.B}$ does not violate the group-wise upper bound constraints of ${\textbf {P.A}}$ because $\cup _{i\in [m]}B_i$ are added to meet the lower bound constraints of ${\textbf {P.A}}$ if necessary. Moreover, adding $\cup _{i\in [m]}B_i$ to $A^{P.B}$ does not violate the global cardinality constraint of ${\textbf {P.A}}$ because $A^{P.B}$ meets the second set of constraints in ${\textbf {P.B}}$. At last, it is easy to verify that adding $\cup _{i\in [m]}B_i$ to $A^{P.B}$ makes it satisfy the lower bound constraints of ${\textbf {P.A}}$. Hence, $A^{approx}$ is a feasible solution to ${\textbf {P.A}}$.

Lemma 11

$A^{approx}$ is a feasible solution to ${\textbf {P.A}}$.

Following the same proof of Theorem 1, we have the following theorem.

Theorem 3

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint and $\alpha \le 1/2$, we have ${\mathbb {E}}_{A^{approx}}[f(A^{approx})]\ge \frac{\gamma }{2}f(OPT)$.

4.2 The case when $\alpha > 1/2$

We next consider the case when $\alpha > 1/2$. Recall that $g(\cdot ) = f(V\setminus \cdot )$. We first present a flipped formation of ${\textbf {P.A}}$ as below:

Suppose there is a $\gamma$-approximate solution $A^{P.C}$ to ${\textbf {P.C}}$, it is easy to verify that $V\setminus A^{P.C}$ is a $\gamma$-approximate solution to ${\textbf {P.A}}$. We focus on solving ${\textbf {P.C}}$ in the rest of this section. We first introduce a new optimization problem (labeled as ${\textbf {P.D}}$) as follows:

${\textbf {P.D}}$ is relaxed version of ${\textbf {P.C}}$ with both group-wise lower bound constraints $|V_i|-\lfloor \beta |V_i|\rfloor \le |S \cap V_i|$ and global lower bound constraints $|S|\ge n-c$ in ${\textbf {P.C}}$ being removed. Hence, we have the following lemma.

Lemma 12

Let $O^{P.C}$ denote the optimal solution of ${\textbf {P.C}}$ and $O^{P.D}$ denote the optimal solution of ${\textbf {P.D}}$, we have $g(O^{P.D})\ge g(O^{P.C})$.

Recall that if f is submodular, g must be submodular (by Lemma 6). Hence, ${\textbf {P.D}}$ is a classic problem of maximizing a submodular function subject to matroid constraints. We next present the design of our algorithm.

• 1. Apply the state-of-the-art algorithm ${\mathcal {A}}$ for matroid constrained submodular maximization to solve ${\textbf {P.D}}$ and obtain a solution $A^{P.D}$.

• 2. Note that $A^{P.D}$ is not necessarily a feasible solution to ${\textbf {P.C}}$ because it might violate the group-wise or the global lower bound constraints of ${\textbf {P.C}}$. We add additional items to $A^{P.D}$ to make it feasible. Specifically, for each group $i\in [m]$, our algorithm selects a backup set $B_i$ of size $|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|$, by randomly sampling $|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|$ items from $V_i\setminus A^{P.D}$. Define $B_i=\emptyset$ if $|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|=0$.

• 3. Add $\cup _{i\in [m]}B_i$ to $A^{P.D}$ to build $A^{approx}$, i.e., $A^{approx}= A^{P.D}\cup (\cup _{i\in [m]}B_i)$. Return $V\setminus A^{approx}$ as the final solution.

The pseudocode of this approximation algorithm is given as Algorithm 4. Observe that adding $\cup _{i\in [m]}B_i$ to $A^{P.D}$ ensures that each group contributes exactly $|V_i|-\lfloor \alpha |V_i|\rfloor$ number of items to the solution. Because $n-c\le \sum _{i\in [m]}(|V_i|-\lfloor \alpha |V_i|\rfloor )$ (otherwise ${\textbf {P.C}}$ does not have a feasible solution), $A^{P.D}\cup (\cup _{i\in [m]}B_i)$ must satisfy all constraints in ${\textbf {P.C}}$. Hence, we have the following lemma.

Lemma 13

$A^{approx}$ is a feasible solution to ${\textbf {P.C}}$.

We next analyze the performance of $A^{approx}$. The following lemma states that adding $\cup _{i\in [m]}B_i$ to $A^{P.D}$ reduces its utility by a factor of at most 2/3 in expectation.

Lemma 14

Suppose $\alpha > 1/2$, we have ${\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{1}{3}g(A^{P.D})$.

Proof

Observe that $B_i= \emptyset$ for all $i\in [m]$ such that $|A^{P.D} \cap V_i|= |V_i|-\lfloor \alpha |V_i|\rfloor$, hence, adding those $B_i$ to $A^{P.D}$ does not affect its utility. Therefore, we focus on those groups $i\in [m]$ with $|A^{P.D} \cap V_i|< |V_i|-\lfloor \alpha |V_i|\rfloor$ in the rest of the proof. Let $Z=\{i\in [m]\mid |A^{P.D} \cap V_i|< |V_i|-\lfloor \alpha |V_i|\rfloor \}$ denote the set containing the indexes all such groups. We assume $Z\ne \emptyset$ to avoid trivial cases. We next show that it is safe to assume $\min _{i\in Z}|V_i|>1$ without loss of generality, i.e., the smallest group in Z contains at least two items. To prove this, we consider two cases, depending on the value of $\alpha$. If $\alpha =1$, then $|A^{P.D} \cap V_i|< |V_i|-\lfloor \alpha |V_i|\rfloor$ does not hold for any group i such that $|V_i|=1$. Hence, $\min _{i\in Z}|V_i|>1$. If $\alpha <1$, then according to the group fairness constraints listed in ${\textbf {P.A}}$, we are not allowed to select any items from those groups with $|V_i|=1$. Hence, removing all groups with size one from consideration does not affect the quality of the optimal solution.

With the assumption that $\min _{i\in Z}|V_i|>1$, we are now ready to prove this lemma. Recall that for every $i\in Z$, $B_i$ is a random set of size $|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|$ that is sampled from $V_i\setminus A^{P.D}$. It follows each item in $V_i\setminus A^{P.D}$ appears in $B_i$ with probability at most

$$\begin{aligned} \frac{|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|}{|V_i\setminus A^{P.D}|}. \end{aligned}$$

(15)

We next give an upper bound of (15). Because we assume $\alpha > 1/2$ and $\min _{i\in Z}|V_i|>1$, it holds that for all $i\in M$,

$$\begin{aligned} |V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i| \le |V_i|-\lfloor \alpha |V_i|\rfloor \le 2|V_i|/3. \end{aligned}$$

(16)

Moreover,

$$\begin{aligned}{} & {} |V_i\setminus A^{P.D}|= |V_i|-|A^{P.D} \cap V_i| \end{aligned}$$

(17)

$$\begin{aligned}{} & {} =(|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|)+(|V_i|-(|V_i|-\lfloor \alpha |V_i|\rfloor )) \end{aligned}$$

(18)

$$\begin{aligned}{} & {} = (|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|)+\lfloor \alpha |V_i|\rfloor \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \ge (|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|)+|V_i|/3, \end{aligned}$$

(20)

where the inequality is by the assumptions that $\alpha >1/2$ and $|V_i|>1$. It follows that

$$\begin{aligned} (15)\le \frac{|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|}{(|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|)+|V_i|/3}\le \frac{2|V_i|/3}{2|V_i|/3+|V_i|/3}=2/3, \end{aligned}$$

(21)

where the first inequality is by (20) and the second inequality is by (16) and the assumption that $|V_i|-\lfloor \alpha |V_i|\rfloor -|A^{P.D} \cap V_i|>0$. That is, each item in $V_i\setminus A^{P.D}$ appears in $B_i$ with probability at most 2/3. Lemma 3 and the observation that $g(A^{P.D}\cup \cdot )$ is submodular imply that ${\mathbb {E}}_{A^{approx}}[g(A^{approx})]={\mathbb {E}}_{\cup _{i\in [m]}B_i}[g(A^{P.D}\cup (\cup _{i\in [m]}B_i))]\ge (1-\frac{2}{3})g(A^{P.D}\cup \emptyset )=\frac{1}{3}g(A^{P.D})$. $\Box$

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint, we have

$$\begin{aligned} {\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{1}{3}g(A^{P.D})\ge \frac{\gamma }{3}g(O^{P.D}) \end{aligned}$$

where the first inequality is by Lemma 14. This, together with $g(O^{P.D})\ge g(O^{P.C})$ (as proved in Lemma 12), implies that ${\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{\gamma }{3}g(O^{P.C})$. By the definition of function g, we have

$$\begin{aligned}{\mathbb {E}}_{A^{approx}}[f(V\setminus A^{approx})] = {\mathbb {E}}_{A^{approx}}[g(A^{approx})]\ge \frac{\gamma }{3}g(O^{P.C})=\frac{\gamma }{3}f(OPT)\end{aligned}$$

where the last equality is by the observation that ${\textbf {P.A}}$ and ${\textbf {P.C}}$ share the same value of the optimal solution. Hence, the following main theorem holds.

Theorem 4

Suppose ${\mathcal {A}}$ is a $\gamma$-approximate algorithm for non-monotone submodular maximization subject to a matroid constraint and $\alpha > 1/2$, we have ${\mathbb {E}}_{A^{approx}}[f(V\setminus A^{approx})]\ge \frac{\gamma }{3}f(OPT)$.

5 Conclusion

This paper presents a comprehensive investigation of the non-monotone submodular maximization problem under group fairness constraints. Our main contribution is the development of several constant-factor approximation algorithms for this problem. In the future, we plan to expand our research to explore alternative fairness metrics.