Minimizing total weighted late work on a single-machine with non-availability intervals

Abstract

We explore the problem of scheduling n jobs on a single machine in which there are m fixed machine non-availability intervals. The target is to seek out a feasible solution that minimizes total weighted late work. Three variants of the problem are investigated. The first is the preemptive version, the second is the resumable version, and the third is the non-resumable version. For the first one, we present an $O((m+n) \log n)$-time algorithm to solve it. For the second one, we develop an exact dynamic programming algorithm and a fully polynomial time approximation scheme. For the third one, we first demonstrate that it is strongly $\mathcal{NP}\mathcal{}$-hard for the case where all jobs have the unit weight and common due date, and then we develop a pseudo-polynomial time algorithm for the unit weight case where the number of non-availability intervals is fixed, finally we propose a pseudo-polynomial time algorithm for the case where there is only one non-availability interval.

1 Introduction

For most theoretical research and practical applications of production scheduling models studied in the literature, it is presumed that the machines are continuously available throughout the whole scheduling horizon (Pinedo 2016). Nevertheless, machine non-availability intervals (MNAIs) are very common in the modern manufacturing and service systems. One reason of this situation is due to the machine breakdowns or preventive maintenance operations (Palmer 2012). Another reason may be due to the occurrence of fixed jobs in modern industrial software (Scharbrodt et al. 1999). Because of its theoretical importance as well as broad applications, scheduling models with MNAIs have attracted great savor over the last thirty years. Two main types of scheduling models with MNAIs are distinguished (Strusevich and Rustogi 2017). Under the fixed scenario, a MNAI takes place in a given interval, i.e., its starting time and finishing time are both given parameters. Under the flexible scenario, a MNAI must start before a given deadline. In this study, we explore a scheduling problem with one or more fixed MNAIs to minimize total weighted late work (TWLW) on a single machine.

1.1 Problem definition

Formally, the jobs of set ${\mathcal {J}}=\{J_1, J_2, \ldots , J_n\}$ are to be performed on a single machine. The n jobs in ${\mathcal {J}}$ are released at time zero. For each job $J_j \in {\mathcal {J}}$, it can be marked by a processing time $p_j$, a weight $w_j$ indicating its importance, and a due date $d_j$. At most one job is executed by the machine at a time and there are m fixed MNAIs ${\mathcal {I}}_k = [A_k, B_k]$, $k = 1, 2, \ldots , m$, during which the machine cannot deal with any job, where $A_1 \le B_1< A_2 \le B_2< \cdots <A_m \le B_m$. Let $\triangle _i=B_i-A_i$ ($i=1, 2, \ldots , m$) be the length of the i-th MNAI. Symmetrically, we define $m+1$ availability intervals ${\mathcal {R}}_i = [B_{i-1}, A_i]$, $i= 1, 2, \ldots , m+1$, where $B_0=0$ and $A_{m+1}=+\infty$. Moreover, let $\nabla _i=A_i-B_{i-1}$ ($i=1, 2, \ldots , m+1$) be the length of the i-th availability interval.

As introduced by Lee (1996), we study two patterns relating to the processing of a job that is interrupted by a MNAI. Under the resumable pattern, once the processing of a job is interrupted by some MNAI, it is resumed when the machine next becomes available. In this pattern, the total duration of the job interrupted by one or more MNAIs is still equal to its actual processing time. Under the non-resumable pattern, once the processing of a job is interrupted by some MNAI, it is restarted from scratch when the machine next becomes available. Moreover, we also study the pattern where job preemption is allowed. Under the preemptive pattern, the processing of the job may be interrupted at any time and resumed later at any latter time.

For a given feasible schedule, let $S_j$, $C_j$ and $Y_j$ indicate the starting time, completion time and late work of job $J_j$, $j=1, 2, \ldots , n$, respectively. Here, the late work $Y_j$ is defined as the amount of work executed on $J_j$ after its due date $d_j$. If $Y_j=0$, $J_j$ is referred to be early; if $0< Y_j< p_j$, $J_j$ is referred to be partially early; and if $Y_j=p_j$, $J_j$ is referred to be late. Moreover, a job is referred to be non-late if it is either early or partially early. In all problems under discussion, the target is to seek out a feasible schedule so that TWLW is minimized.

Extending the standard 3-field scheduling scheme, the resulting problems for minimizing TWLW under the resumable pattern, non-resumable pattern and preemptive pattern are denoted by $1 | h(m), res| \sum w_j Y_j$, $1 | h(m), n-res| \sum w_j Y_j$ and $1 | h(m), pmtn| \sum w_j Y_j$, respectively. To simplify the notations, let $V_r^{*}$, $V_{nr}^{*}$ and $V_p^{*}$ indicate the optimal objective values for the problems $1 | h(m), res| \sum w_j Y_j$, $1 | h(m), n-res| \sum w_j Y_j$ and $1 | h(m), pmtn| \sum w_j Y_j$, respectively. Evidently, we have $V_p^{*} \le V_r^{*} \le V_{nr}^{*}$.

Note that for a given job $J_j \in {\mathcal {J}}$, if the due date $d_j$ of $J_j$ belongs to certain MNAI ${\mathcal {I}}_k$, i.e., $A_k < d_j \le B_k$, then we can simply set $d_j:= A_k$. Henceforth, we assume that each due date $d_j$ belongs to some availability interval ${\mathcal {R}}_k$, i.e., $B_{k-1} < d_j \le A_k$. To simplify the presentation, we assume that the jobs in ${\mathcal {J}}$ are numbered in the order satisfying

$$\begin{aligned} d_1 \le d_2 \le \cdots \le d_n, \mathrm {and} ~ w_j \ge w_{j+1} ~ \mathrm {if} ~ d_j=d_{j+1}, j=1, 2, \ldots , n-1. \end{aligned}$$

(1)

In addition, write ${\mathcal {J}}_j=\{J_1, J_2, \ldots , J_j\}$ for $j=1, 2, \ldots , n$.

1.2 Literature review

The scheduling model introduced in this study belongs to the categorization of late work scheduling and the categorization of MNAI scheduling. Models related to these two aspects are very plentiful and extensive, we mainly review the related work from the perspective of computational complexity in the context of single-machine environment.

The research on late work scheduling was originated by Blazewicz (1984), who solved the parallel-machine problem $P|r_j, pmtn|\sum w_j Y_j$ by exploiting the linear programming technique. Potts and Van Wassenhove (1991) demonstrated that the single-machine problem $1||\sum Y_j$ is ordinary $\mathcal{NP}\mathcal{}$-hard and gave a pseudo-polynomial time (PPT) algorithm to solve it. They also proposed a simple $O(n \log n)$-time algorithm for $1| pmtn|\sum Y_j$. A polynomial time approximation scheme (PTAS) and two fully polynomial time approximation schemes (FPTASs) are later developed by Potts and Van Wassenhove (1992) for $1||\sum Y_j$. Hariri et al. (1995) presented an $O(n \log n)$-time algorithm for $1|pmtn|\sum w_jY_j$ and a PPT algorithm for $1||\sum w_j Y_j$. In contrast to their PPT algorithm, Kovalyov et al. (1994) established another PPT algorithm for $1||\sum w_j Y_j$, which is converted into an FPTAS. Chen et al. (2019) addressed a late work scheduling problem with deadlines. They demonstrated that $1|{\bar{d}}_j|\sum Y_j$ is strongly $\mathcal{NP}\mathcal{}$-hard and $1|d_j=d, {\bar{d}}_j|\sum w_jY_j$ is ordinary $\mathcal{NP}\mathcal{}$-hard. They also developed a PPT algorithm and an FPTAS for the latter problem. Mosheiov et al. (2021) examined a late work scheduling model with generalized due dates (GDD) or assignable due dates (ADD), where GDD means that the k-th smallest due-date is always designated to the k-th completed job in the schedule, and ADD means that each due date can be assigned to any job. They showed that the shortest processing time (SPT) rule solves $1|GDD|\sum Y_j$, and demonstrated that $1|GDD|\sum w_j Y_j$ and $1|ADD|\sum Y_j$ are both $\mathcal{NP}\mathcal{}$-hard. In recent years, a number of studies have been undertaken to explore the late work scheduling with multi-agents or multi-objectives, see Li and Yuan (2020), Chen and Li (2021), Chen et al. (2021), He et al. (2021), Zhang (2021), etc. Reviews of late work scheduling and its various applications can be discovered in Leung (2004), Shioura et al. (2018) and Sterna (2011; 2021).

The research on MNAI scheduling was initiated by Schmidt (1988), who addressed a parallel-machine scheduling problem with multiple MNAIs and deadlines. He constructed a polynomial time algorithm to determine the feasibility of the preemptive problem. In regard to the basic problem $1 | h(1), n-res| \sum C_j$, Adiri et al. (1989) and Lee and Liman (1992) demonstrated that it is ordinary $\mathcal{NP}\mathcal{}$-hard; Lee and Liman (1992) revealed that the worst-case bound of the SPT rule is 9/7; Sadfi et al. (2005) provided a 20/17-approximation algorithm, which is modified version of the SPT rule; He et al. (2006) designed a PTAS. In regard to the weighted problem $1 | h(1), n-res| \sum w_jC_j$, Kacem (2008) designed a 2-approximation algorithm; Kacem et al. (2008) proposed a branch-and-bound, a mixed integer programming, and a dynamic programming method to solve it; Kacem and Mahjoub (2009) presented an FPTAS based on the technique of interval partitioning; Kellerer and Strusevich (2010) devised a simple 4-approximation algorithm and an FPTAS by adopting the method developed for the symmetric quadratic knapsack problem. In regard to $1 | h(1), n-res| D_{\max }$, Yuan et al. (2008) provided a PPT algorithm and a PTAS; Kacem (2009) proposed a 3/2-approximation algorithm and an FPTAS; Kacem et al. (2016) further presented an improved FPTAS. Kacem et al. (2015) designed a PTAS to solve $1 | h(m), n-res| \max \sum w_j{\overline{U}}_j$ when m is fixed, and demonstrated that $1 | h(1), n-res, d_j=d| \max \sum {\overline{U}}_j$ does not admit an FPTAS, where ${\overline{U}}_j=1$ if $C_j \le d_j$ and ${\overline{U}}_j=0$ otherwise. Lee (1996) showed that the algorithm developed for $1 | | \gamma$ can be easily revised to solve the counterpart problem $1 | h(m), res| \gamma$, where $\gamma \in \{ C_{\max }, L_{\max }, \sum C_j, \sum U_j\}$. He also demonstrated that $1 | h(m), n-res| C_{\max }$ is strongly $\mathcal{NP}\mathcal{}$-hard. Wang et al. (2005) demonstrated that $1 | h(m), res| \sum w_jC_j$ is strongly $\mathcal{NP}\mathcal{}$-hard. In regard to $1 | h(1), res| \sum w_jC_j$, Lee (1996) demonstrated that it is ordinary $\mathcal{NP}\mathcal{}$-hard and presented a PPT algorithm; Wang et al. (2005) created a 2-approximation algorithm; Kellerer and Strusevich (2010) provided an FPTAS. Kacem et al. (2015) proposed a PPT algorithm and an FPTAS for $1 | h(m), res| \max \sum w_j{\overline{U}}_j$. Recent developments of MNAI scheduling models were examined, among many others, by Kacem and Kellerer (2018), Bülbül et al. (2019), Shabtay (2022), Mor and Shapira (2022), etc. For more practical applications as well as detailed results on this topic, it is referred to the reviews given by Lee (1996), Schmidt (2000), Ma et al. (2010) and Strusevich and Rustogi (2017).

As far as we are aware, there are only two studies probing the MNAI scheduling with late work criterion. Specifically, Yin et al. (2016) analyzed a late work scheduling problem with a MNAI. They first designed an $O(n \log n)$-time algorithm for $1 | h(1), pmtn| \sum Y_j$, then they proposed two PPT algorithms and an FPTAS for the revised problem $1 | h(1), n-res| \sum Y_j+p_{\max }$, where $p_{\max }=\max \{p_j, 1 \le j \le n\}$. Mosheiov et al. (2021) investigated a GDD scheduling problem with a MNAI to minimize total late work, i.e. $1 | GDD, h(1), n-res| \sum Y_j$. They indicated that the problem is $\mathcal{NP}\mathcal{}$-hard and devised a PPT algorithm to solve it.

1.3 Motivation and contributions

The motivation and contributions of this study are as follows. First, we discuss the more realistic and intricate scheduling model with the criterion of minimizing TWLW in the context of multiple MNAIs. Second, we make certain of the the computational complexity issue of the model under three different scenarios. Third, the preemptive problem $1 | h(m), pmtn| \sum w_j Y_j$ and the resumable problem $1 | h(m), res| \sum w_j Y_j$ under consideration generalize the problem $1 | pmtn| \sum w_j Y_j$ studied in Hariri et al. (1995) and the problem $1 | | \sum w_j Y_j$ studied in Kovalyov et al. (1994) by allowing arbitrary weights and multiple MNAIs, respectively. Fourth, the non-resumable problem $1 | h(1), non-res| \sum w_j Y_j$ under consideration generalizes the problem $1 | h(1), n-res| \sum Y_j$ studied in Yin et al. (2016) by allowing arbitrary weights.

The remainder of this study is structured as follows. In Sect. 2, an $O((m+n) \log n)$-time algorithm is first designed for $1 | h(m), pmtn| \sum w_j Y_j$, then a numerical example is presented. In Sect. 3, an $O(mn^2 \sum _{j=1}^n p_j)$-time algorithm and an FPTAS are developed for $1 | h(m), res| \sum w_j Y_j$. In Sect. 4, $1 | h(m), d_j=d, n-res| \sum Y_j$ is first demonstrated to be strongly NP-hard; then a PPT algorithm is provided for $1 | h(m), n-res| \sum Y_j$ when the number of MNAIs is fixed; finally a PPT algorithm is constructed for $1 | h(1), non-res| \sum w_j Y_j$. In Sect. 5, some remarks are summarized and several ideas are listed for future research.

2 The preemptive problem $1 | h(m), pmtn| \sum w_j Y_j$

We address the preemptive pattern, in which the processing of a job can be interrupted by another job at any time or by a MNAI and resumed later at any time. By generalizing the algorithm developed by Hariri et al. (1995) for $1 | pmtn| \sum w_j Y_j$, an $O((m+n) \log n)$-time algorithm is designed to solve the counterpart problem $1 | h(m), pmtn| \sum w_j Y_j$. To specify a solution, it is sufficient to search a schedule of the processing of each job’s early work. Write ${\mathcal {D}}=\{d_j: J_j \in {\mathcal {J}}\}$ and $D_0=0$. Let $D_1< D_2< \cdots < D_h$ be the ordered sequence of the distinct due dates $d_j$ of the n jobs, where $h=|{\mathcal {D}}|$. Moreover, for each $1 \le k \le h$, let ${\mathcal {R}}_{i_k}$ be the availability interval that $D_k$ belongs to, i.e., $B_{i_k-1}<D_k \le A_{i_k}$. Recall that the n jobs are numbered according to (1).

Algorithm 1.

Step 1. :

Set $r:=h$, $\tau :=D_r$, $q:=i_r$ and ${\mathcal {S}}:={\mathcal {J}}$.

Step 2. :

Set ${\mathcal {A}}_{\tau }:=\{J_j: J_j \in {\mathcal {S}}, d_j \ge \tau \}$ and calculate $k:=\arg \max \{w_j: J_j \in {\mathcal {A}}_{\tau }\}$. If $D_{r-1} \in {\mathcal {R}}_{q}$, set $l:=\min \{p_k, \tau -D_{r-1}\}$, go to Step 3; otherwise, set $l:=\min \{p_k, \tau -B_{q-1}\}$, go to Step 4.

Step 3. :

Assign l units of work of $J_k$ to the time interval $[\tau -l, \tau ]$, then do:

• (3.1) If $p_k>\tau -D_{r-1}$, set $p_k:=p_k-l$, $\tau :=\tau -l$ and $r:=r-1$.

• (3.2) If $p_k=\tau -D_{r-1}$, set $p_k:=0$, $\tau :=\tau -l$, $r:=r-1$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

• (3.3) If $p_k<\tau -D_{r-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_k\} \ne \emptyset$, set $p_k:=0$, $\tau :=\tau -l$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

• (3.4) If $p_k<\tau -D_{r-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_k\} = \emptyset$, set $p_k:=0$, $\tau :=D_{r-1}$, $r:=r-1$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

Step 4. :

Assign l units of work of $J_k$ to the time interval $[\tau -l, \tau ]$, then do:

• (4.1) If $p_k>\tau -B_{q-1}$, set $p_k:=p_k-l$, $\tau :=A_{q-1}$ and $q:=q-1$.

• (4.2) If $p_k=\tau -B_{q-1}$, set $p_k:=0$, $\tau :=A_{q-1}$, $q:=q-1$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

• (4.3) If $p_k<\tau -B_{q-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_k\} \ne \emptyset$, set $p_k:=0$, $\tau :=\tau -l$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

• (4.4) If $p_k<\tau -B_{q-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_k\} = \emptyset$, set $p_k:=0$, $\tau :=D_{r-1}$, $q:=i_{r-1}$, $r:=r-1$ and ${\mathcal {S}}:={\mathcal {S}} {\setminus } \{J_k\}$.

Step 5. :

If ${\mathcal {S}}=\emptyset$ or $\tau =0$ or $r=0$, calculate TWLW by $V_p^{*}=\sum _{J_j \in {\mathcal {S}}} w_j p_j$ and stop; otherwise, go to Step 2.

To facilitate the explanation, a small numerical instance is used to display the implementation of Algorithm 1 for $1 | h(m), pmtn| \sum w_j Y_j$.

Example 2.1

Consider an instance of $1 | h(m), pmtn| \sum w_j Y_j$ in which it contains seven jobs and two MNAIs ${\mathcal {I}}_1 = [A_1, B_1]=[6, 7]$ and ${\mathcal {I}}_2 =[A_2, B_2]=[11, 13]$, where job parameters are given in Table 1.

Table 1 The job data of the instance

Table 2 The due date and availability interval of Example 2.1

Before proceeding with the execution of Algorithm 1, we note that ${\mathcal {D}}=\{3, 5, 9, 16, 17\}$, which contains five distinct due dates, i.e., $h=|{\mathcal {D}}|=5$, see Table 2 for their representative availability interval, where ${\mathcal {R}}_1=[0, 6]$, ${\mathcal {R}}_2=[7, 11]$, ${\mathcal {R}}_3=[13, +\infty )$, and define $D_0=0$.

Initially, we have $r=h=5$, $\tau =D_5=17$, $q=i_5=3$ and ${\mathcal {S}}=\{J_1, J_2, J_3, J_4, J_5, J_6, J_7\}$.

At the iteration $j=1$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{17}=\{J_7\}$, job $J_7$ is selected. Since $D_{r-1}=D_4=16 \in {\mathcal {R}}_{q}={\mathcal {R}}_3$, we have $l=\min \{p_7, \tau -D_{r-1}\}=\min \{3, 17-16\}=1$, schedule $l=1$ units of work of $J_7$ in the interval $[\tau -l, \tau ]=[16, 17]$. Since $p_7=3>1=\tau -D_{r-1}$, Algorithm 1 executes Step 3.1, we have $p_7=2$, $\tau =16$ and $r=4$.

At the iteration $j=2$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{16}=\{J_6, J_7\}$, job $J_6$ is selected as $w_6=4>1=w_7$. Since $D_{r-1}=D_3=9 \notin {\mathcal {R}}_{q}={\mathcal {R}}_3$, we have $l=\min \{p_6, \tau -B_{q-1}\}=\min \{2, 16-13\}=2$, schedule $l=2$ units of processing of $J_6$ in the interval $[\tau -l, \tau ]=[14, 16]$. Since $p_6=2<3=\tau -B_{q-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_6\} \ne \emptyset$, Algorithm 1 executes Step 4.3, we have $p_6=0$, $\tau =14$ and ${\mathcal {S}}=\{J_1, J_2, J_3, J_4, J_5, J_7\}$.

At the iteration $j=3$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{14}=\{J_7\}$, job $J_7$ is selected. Since $D_{r-1}=D_3=9\notin {\mathcal {R}}_{q}={\mathcal {R}}_3$, we have $l=\min \{p_7, \tau -B_{q-1}\}=\min \{2, 14-13\}=1$, schedule $l=1$ units of work of $J_6$ in the interval $[\tau -l, \tau ]=[13, 14]$. Since $p_7=2>1=\tau -B_{q-1}$, Algorithm 1 executes Step 4.1, we have $p_7=1$, $\tau =A_{q-1}=11$ and $q=2$.

At the iteration $j=4$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{11}=\{J_7\}$, job $J_7$ is selected. Since $D_{r-1}=D_3=9 \in {\mathcal {R}}_{q}={\mathcal {R}}_2$, we have $l=\min \{p_7, \tau -D_{r-1}\}=\min \{1, 11-9\}=1$, schedule $l=1$ units of work of $J_7$ in the interval $[\tau -l, \tau ]=[10, 11]$. Since $p_7=1<2=\tau -D_{r-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_7\} = \emptyset$, Algorithm 1 executes Step 3.4, we have $p_7=0$, $\tau =D_{r-1}=9$, $r=3$ and ${\mathcal {S}}= \{J_1, J_2, J_3, J_4, J_5\}$.

At the iteration $j=5$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{9}=\{J_4, J_5\}$, job $J_4$ is selected as $w_4=5>1=w_5$. Since $D_{r-1}=D_2=5 \notin {\mathcal {R}}_{q}={\mathcal {R}}_2$, we have $l=\min \{p_4, \tau -B_{q-1}\}=\min \{1, 9-7\}=1$, schedule $l=1$ units of work of $J_4$ in the interval $[\tau -l, \tau ]=[8, 9]$. Since $p_4=1<2=\tau -B_{q-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_4\} \ne \emptyset$, Algorithm 1 executes Step 4.3, we have $p_4=0$, $\tau =8$ and ${\mathcal {S}}= \{J_1, J_2, J_3, J_5\}$.

At the iteration $j=6$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{8}=\{J_5\}$, job $J_5$ is selected. Since $D_{r-1}=D_2=5 \notin {\mathcal {R}}_{q}={\mathcal {R}}_2$, we have $l=\min \{p_5, \tau -B_{q-1}\}=\min \{4, 8-7\}=1$, schedule $l=1$ units of work of $J_5$ in the interval $[\tau -l, \tau ]=[7, 8]$. Since $p_5=4>1=\tau -B_{q-1}$, Algorithm 1 executes Step 4.1, we have $p_5=3$, $\tau =A_{q-1}=6$ and $q=1$.

At the iteration $j=7$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{6}=\{J_5\}$, job $J_5$ is selected. Since $D_{r-1}=D_2=5 \in {\mathcal {R}}_{q}={\mathcal {R}}_1$, we have $l=\min \{p_5, \tau -D_{r-1}\}=\min \{3, 6-5\}=1$, schedule $l=1$ units of work of $J_5$ in the interval $[\tau -l, \tau ]=[5, 6]$. Since $p_5=3>1=\tau -D_{r-1}$, Algorithm 1 executes Step 3.1, we have $p_5=2$, $\tau =5$ and $r=2$.

At the iteration $j=8$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{5}=\{J_3, J_5\}$, job $J_3$ is selected as $w_3=3>1=w_5$. Since $D_{r-1}=D_1=3 \in {\mathcal {R}}_{q}={\mathcal {R}}_1$, we have $l=\min \{p_3, \tau -D_{r-1}\}=\min \{2, 5-3\}=2$, schedule $l=2$ units of work of $J_3$ in the interval $[\tau -l, \tau ]=[3, 5]$. Since $p_3=2=\tau -D_{r-1}$, Algorithm 1 executes Step 3.2, we have $p_3=0$, $\tau =3$, $r=1$ and ${\mathcal {S}}= \{J_1, J_2, J_5\}$.

At the iteration $j=9$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{3}=\{J_1, J_2, J_5\}$, job $J_1$ is selected as $w_1=4>2=w_2>w_5=1$. Since $D_{r-1}=D_0 \in {\mathcal {R}}_{q}={\mathcal {R}}_1$, we have $l=\min \{p_1, \tau -D_{r-1}\}=\min \{2, 3-0\}=2$, schedule $l=2$ units of work of $J_1$ in the interval $[\tau -l, \tau ]=[1, 3]$. Since $p_1=2<\tau -D_{r-1}$ and ${\mathcal {A}}_{\tau } {\setminus } \{J_1\} \ne \emptyset$, Algorithm 1 executes Step 3.3, we have $p_1=0$, $\tau =1$ and ${\mathcal {S}}=\{J_2, J_5\}$.

At the iteration $j=10$, we have ${\mathcal {A}}_{\tau }={\mathcal {A}}_{1}=\{J_2, J_5\}$, job $J_2$ is selected as $w_2=2>1=w_5$. Since $D_{r-1}=D_0 \in {\mathcal {R}}_{q}={\mathcal {R}}_1$, we have $l=\min \{p_2, \tau -D_{r-1}\}=\min \{3, 1-0\}=1$, schedule $l=1$ units of work of $J_2$ in the interval $[\tau -l, \tau ]=[0, 1]$. Since $p_2=3>1=\tau -D_{r-1}$, Algorithm 1 executes Step 3.1, we have $p_2=2$, $\tau =0$ and $r=0$.

Because $\tau =0$ and $r=0$, Algorithm 1 stops and the objective value is

$$\begin{aligned} V_p^{*}=\sum _{J_j \in {\mathcal {S}}} w_j p_j=w_2 p_2+w_5 p_5=2 \times 2+1 \times 2=6, \end{aligned}$$

see Fig. 1 for the corresponding schedule delivered by Algorithm 1.

Fig. 1

An optimal schedule of $1 | h(m), pmtn| \sum w_j Y_j$

Lemma 2.2

Algorithm 1 solves $1 | h(m), pmtn| \sum w_j Y_j$.

Proof

Let $\sigma ^{*}$ and $\sigma$ be an optimal schedule for $1 | h(m), pmtn| \sum w_j Y_j$ and the schedule delivered by Algorithm 1, respectively. As in Hariri et al. (1995), we can assume that in $\sigma ^{*}$, any work performed before time $D_h$ is early and the number of preemptions is finite.

If $\sigma$ is identical with $\sigma ^{*}$ in the interval $[0, D_h]$, the lemma holds immediately. Otherwise, let $\tau$ be selected as small as possible so that $\sigma ^{*}$ and $\sigma$ are identical in the time interval $[\tau , D_h]$. From the execution of Algorithm 1 and the definition of $\tau$, it follows that the machine cannot be idle just before $\tau$ in $\sigma$. Hence, assume that job $J_k$ is performed in the interval $[\mu , \tau ]$ and not performed just before time $\mu$ in $\sigma$. Two cases need to be addressed.

Case 1: The machine is idle in the interval $[\nu , \tau ]$ and is not idle just before time $\nu$ in $\sigma ^{*}$. Let $\rho =\max \{\mu , \nu \}$. In this case, another schedule $\sigma '$ can be gained from $\sigma ^{*}$ by shifting $\tau -\rho$ units of work of $J_k$ to the interval $[\rho , \tau ]$. Clearly, $\sigma '$ is also an optimal schedule.

Case 2: Job $J_r$ ($r \ne k$) is performed in the interval $[\nu , \tau ]$ and not performed just before time $\nu$ in $\sigma$. Let $\rho =\max \{\mu , \nu \}$. In this case, another schedule $\sigma '$ can be gained from $\sigma ^{*}$ by swapping $\tau -\rho$ units of work of $J_r$ performed in $[\rho , \tau ]$ with $\tau -\rho$ units of work of $J_k$. From the execution of Algorithm 1, it follows that $J_k \in {\mathcal {A}}_{\tau }$, $J_r \in {\mathcal {A}}_{\tau }$, and $w_k \ge w_r$. Moreover, if $w_k = w_r$, then $d_k \ge d_r$. Clearly, $\sigma '$ is also an optimal schedule since this swap does not increase the objective value.

In both cases, $\sigma '$ is an optimal schedule and it is identical with $\sigma$ in the interval $[\rho , D_h]$ with $\rho <\tau$. Continuing this process, we come up with an optimal schedule $\sigma$ from $\sigma ^{*}$ after a finite number of alterations. $\square$

Lemma 2.3

Algorithm 1 can be executed in $O((m+n) \log n)$ time.

Proof

Note that in the execution of Algorithm 1, a preemption arises only when less than $p_k$ units of work of $J_k$ are processed in Step 3 and/or Step 4. This happens either when $\tau -p_k<D_{r-1} <\tau \le D_r$ for certain k, or when $\tau -p_k< B_{q-1}< \tau \le A_q$, or when $\tau < p_k$. Thus, there are at most $m+h$ preemptions, which implies that Steps 2-4 are implemented at most $n+m+h$ times. By utilizing the data structure, we index the jobs in ${\mathcal {A}}_{\tau }$ in nondecreasing order of their weights, and each operation of insert and delete can be done in $O(\log n)$ time, thus each iteration of Step 2 takes at most $O(\log n)$ time. Each iteration of Step 3 and Step 4 requires constant time. Since $h \le n$, Algorithm 1 can be executed in $O((m+n) \log n)$ time. $\square$

In view of Lemma 2.2 and Lemma 2.3, we state the main result of this section.

Theorem 2.4

Algorithm 1 can solve $1 | h(m), pmtn| \sum w_j Y_j$ in $O((m+n) \log n)$ time.

3 The resumable problem $1 | h(m), res| \sum w_j Y_j$

We address the resumable pattern, in which the processing of a job can only be interrupted by the MNAIs and it has to be resumed when the machine next becomes available. $1 | h(m), res| \sum w_j Y_j$ is $\mathcal{NP}\mathcal{}$-hard as its counterpart un-weighted problem $1 || \sum Y_j$ without MNAI is $\mathcal{NP}\mathcal{}$-hard (Potts and Van Wassenhove 1991). By exploiting the dynamic programming (DP) method, we first design a PPT algorithm for $1 | h(m), res| \sum w_j Y_j$, then we convert it into an FPTAS. Due to the fact that the TWLW criterion is regular, we only focus on those solutions in which all jobs in ${\mathcal {J}}$ are performed contiguously (but it may be interrupted by the MNAI) without any inserted idle times.

Let $s \in {\mathcal {R}}_1 \cup {\mathcal {R}}_2 \cup \cdots \cup {\mathcal {R}}_{m+1}$. For a given job J with processing time p, due date d and starting time s, we use $\Phi (s, p)$ and $\Psi (s, p, d)$ to denote its completion time and late work, respectively. Recall that the processing of a job cannot be interrupted by another job, but it may be interrupted by one MNAI or multiple MNAIs. Moreover, we use ${\mathcal {R}}_{\kappa (s)}$ to denote the availability interval that s belongs to, i.e., $B_{\kappa (s)-1} \le s \le A_{\kappa (s)}$. Clearly, the index $\kappa (s)$ for a given s can be computed in $O(\log m)$ time. Recall that $\triangle _i=B_i-A_i$ and $\nabla _i=A_i-B_{i-1}$ for $i=1, 2, \ldots , m$. Then the values $\Phi (s, p)$ and $\Psi (s, p, d)$ can be computed in O(m) time as follows:

$$\begin{aligned} \Phi (s, p) =\left\{ \begin{array}{ll} s+p &{} \hbox {if}~ p \le \upsilon \\ s+p+\triangle _{\kappa (s)} &{} \hbox {if}~ \upsilon< p \le \upsilon +\nabla _{\kappa (s)+1} \\ s+p+\triangle _{\kappa (s)}+\triangle _{\kappa (s)+1} &{} \hbox {if}~ \upsilon +\nabla _{\kappa (s)+1}< p \le \upsilon +\nabla _{\kappa (s)+1} +\nabla _{\kappa (s)+2} \\ ~~~~\vdots \\ s+p+\sum _{h=\kappa (s)}^{m-1} \triangle _h &{} \hbox {if}~ \upsilon +\sum _{h=\kappa (s)+1}^{m-2} \nabla _h < p \le \upsilon +\sum _{h=\kappa (s)+1}^{m-1}\nabla _h\\ s+p+\sum _{h=\kappa (s)}^m \triangle _h &{} \hbox {if}~ p> \upsilon +\sum _{h=\kappa (s)+1}^{m-1} \nabla _h \end{array} \right. \nonumber \\ \end{aligned}$$

(2)

and

$$\begin{aligned} \Psi (s, p, d)=\left\{ \begin{array}{ll} 0 &{} \hbox {if}~ \Phi (s, p) \le d \\ s+p-d+\sum _{h=\kappa (s)}^{\kappa (d)-1} \triangle _h &{} \hbox {if}~ s< d < \Phi (s, p) \\ p &{} \hbox {if}~ d \le s \end{array} \right. \end{aligned}$$

(3)

where $\upsilon =A_{\kappa (s)}-s$.

3.1 A DP algorithm

Since the late jobs can be arbitrarily performed after all non-late jobs, we can describe an optimal solution by a permutation of non-late jobs. For a given permutation $\pi$, a non-late job $J_j$ is referred to be deferred (with respect to its index specified by (1)) in $\pi$, if it is performed after a non-late job $J_k$ with $k > j$.

The following lemma is very crucial for the design of our DP algorithm. We omit the details of its proof as it can be proved in the same spirit of the lemma established in Hariri et al. (1995) for $1 || \sum w_j Y_j$.

Lemma 3.1

There exists an optimal permutation for $1 | h(m), res| \sum w_j Y_j$ in which (i) the non-late jobs having the same due date are performed in the order of their indices, and (ii) for every early job $J_k$, at most one deferred job $J_r$ with $r < k$ is performed after $J_k$.

In view of Lemma 3.1, by exploiting the method introduced in Kovalyov et al. (1994) and Hariri et al. (1995), an exact DP approach is proposed to search an optimal permutation for $1 | h(m), res| \sum w_j Y_j$. We scan the jobs in their natural order defined by (1). For each job $J_j$ under consideration, it can either be claimed non-late or late. In the former scenario, $J_j$ is either performed in its natural order or deferred. By Lemma 3.1, if $J_j$ is a deferred job and it is performed just after the non-late job $J_t$ such that $t>j$, those non-late jobs within the set $\{J_{j+1}, J_{j+2}, \ldots , J_t\}$ should be performed in their natural order.

Recall that ${\mathcal {J}}_j=\{J_1, J_2, \ldots , J_j\}$. For each $j=1, 2, \ldots , n$, let ${\mathcal {H}}_j$ represent the set of all partial permutations that satisfy the key properties stated in Lemma 3.1 for ${\mathcal {J}}_j$. Each permutation $\sigma _{j} \in {\mathcal {H}}_j$ can be marked by a unique state (r, t, l), where the first variable r denotes that $J_r$ is deferred in $\sigma _{j}$ if $r>0$, the second variable t indicates the sum of the processing times of the non-late jobs in ${\mathcal {J}}_j {\setminus } \{J_r\}$, and the last variable l stands for the TWLW of the jobs in ${\mathcal {J}}_j {\setminus } \{J_r\}$. By Lemma 3.1, we know that (i) if $r=0$, then there exists no deferred job, and (ii) if $1 \le r \le j$, then $J_r$ is a deferred job and it will be performed after one of jobs in ${\mathcal {J}} {\setminus } {\mathcal {J}}_j$.

Let ${\mathcal {Q}}_j$ include all possible states defined by the partial permutations in ${\mathcal {H}}_j$. It is initialized by setting ${\mathcal {Q}}_0=\{(0, 0, 0)\}$, and for each $j=1, 2, \ldots , n$, the state set ${\mathcal {Q}}_j$ can be constructed from ${\mathcal {Q}}_{j-1}$ progressively. With respect to a given state $(r, t, l) \in {\mathcal {Q}}_{j}$, let $\sigma _j \in {\mathcal {H}}_j$ be a permutation corresponding to the state (r, t, l). Also, let $\sigma _{j-1}$ be the permutation of ${\mathcal {J}}_{j-1}$ that is gained from $\sigma _{j}$ by removing job $J_j$. Evidently, we have $\sigma _{j-1} \in {\mathcal {H}}_{j-1}$. Let $(r', t', l') \in {\mathcal {Q}}_{j-1}$ be the unique state corresponding to $\sigma _{j-1}$. In view of Lemma 3.1 and the above discussion, we have to distinguish the following four scenarios.

Scenario 1: $J_j$ is performed as late in $\sigma _{j}$. In this scenario, we have $(r, t, l)=(r', t', l'+w_j p_j)$.

Scenario 2: $J_j$ is deferred in $\sigma _j$. In this scenario, we have $(r, t, l)=(j, r', l')$. This is feasible only when $r'=0$ and $\Phi (0,t')<d_j$.

Scenario 3: $J_j$ performed as non-late and the deferred job $J_{r'}$ (if $r'>0$) is not performed just after $J_j$ in $\sigma _j$. In this scenario, we have $(r, t, l)=(r', t'+p_j, l'+w_j\Psi (\Phi (0,t'), p_j, d_j))$ . This is feasible only when either $r'>0$ and $\Phi (0,t'+p_j)<d_{r'}$, or $r'=0$ and $\Phi (0, t')<d_j$.

Scenario 4: $J_j$ is performed as early and the deferred job $J_{r'}$ ($1 \le r' <j$) is performed just after $J_j$ in $\sigma _j$. In this scenario, we have $(r, t, l)=(0, t+p_j+p_{r'}, l'+w_{r'}\Psi (\Phi (0,t'+p_j), p_{r'}, d_{r'}))$. This is feasible only when $r'>0$ and $\Phi (0,t'+p_j)< d_{r'}$.

For the target of reducing the state space of the DP, the following dominant property can be easily observed.

Lemma 3.2

Given two states (r, t, l) and $(r, t', l')$ in ${\mathcal {Q}}_j$ satisfying $t \le t'$ and $l \le l'$, the latter state can be deleted from ${{\mathcal {Q}}}_j$.

In fact, in the generation of ${\mathcal {Q}}_j$, a weaker dominant setting than the result in Lemma 3.2 is utilized. More precisely, if there are multiple states in ${\mathcal {Q}}_j$ having the same r and t values, only the state having the smallest l value is preserved.

Summarizing the above discussion, the following DP algorithm is constructed to solve $1 | h(m), res| \sum w_j Y_j$.

Algorithm 2.

Step 1. :

Set ${\mathcal {Q}}_0=\{(0, 0, 0)\}$ and ${{\mathcal {Q}}}_j:=\emptyset$ for $j=1, 2, \ldots , n$.

Step 2. :

For $j=1, 2, \ldots , n$, construct ${\mathcal {Q}}_j$ from ${\mathcal {Q}}_{j-1}$ as follows:

Step 2.1. :

For each state $(r, t, l) \in {\mathcal {Q}}_{j-1}$, do:

• (2.1.1) Set ${\mathcal {Q}}_j:={\mathcal {Q}}_j \cup \{(r, t, l+w_j p_j)\}$;

• (2.1.2) If $r=0$ and $\Phi (0,t)<d_j$, set ${\mathcal {Q}}_j := {\mathcal {Q}}_j \cup \{(j, t, l)\}$;

• (2.1.3) If either [$r>0$ and $\Phi (0, t+p_j)<d_r$] or [$r=0$ and $\Phi (0, t)<d_j$], set ${\mathcal {Q}}_j := {\mathcal {Q}}_j \cup \{(r, t+p_j, l+w_j\Psi (\Phi (0,t), p_j, d_j))\}$;

• (2.1.4) If $r>0$ and $\Phi (0,t+p_j)< d_r$, set ${\mathcal {Q}}_j := {\mathcal {Q}}_j \cup \{(0, t+p_j+p_r, l+w_r\Psi (\Phi (0,t+p_j), p_r, d_r))\}$.

Step 2.2. :

Among all states in ${\mathcal {Q}}_j$ having the same r and t values, reserve only one state having the smallest l value.

Step 3. :

Set $V_r^{*}=\min \{l: (0, t, l) \in {\mathcal {Q}}_n\}$ and disclose the corresponding optimal permutation by the backtracking method.

Theorem 3.3

Algorithm 2 can solve $1 | h(m), res| \sum w_j Y_j$ in $O(mn^2 \sum _{j=1}^n p_j)$ time.

Proof

By Lemma 3.1, Lemma 3.2 and the general DP principle, Algorithm 2 clearly solves $1 |h(m), res| \sum w_j Y_j$. In Step 1, it needs linear time. In the j-th iteration of Step 2, for every state $(r, t, l) \in {\mathcal {Q}}_{j-1}$, we create at most three states in ${\mathcal {Q}}_j$ in Step 2.1, where every such state can be created in O(m) time; and at most $O(n \sum _{j=1}^n p_j)$ different states (r, t, l) in ${\mathcal {Q}}_j$ are preserved after Step 2.2. Step 3 can be executed in $O(\sum _{j=1}^n p_j)$ time. Since there are n iterations, Algorithm 2 can be executed in $O(m n^2 \sum _{j=1}^n p_j)$ time. $\square$

3.2 An FPTAS

We will propose an FPTAS by applying the technique of interval partitioning to the DP algorithm designed in Sect. 3.1.

We start with presenting an procedure to solve the auxiliary problem $1 | h(m), res| \max w_j Y_j$. Let $c \in {\mathcal {R}}_1 \cup {\mathcal {R}}_2 \cup \cdots \cup {\mathcal {R}}_{m+1}$. For a given job J with processing time p, due date d and completion time c, we use $\Upsilon (c, p)$ and $\Omega (c, p, d)$ to denote its starting time and late work, respectively. Similar to the computation of $\Phi (s, p)$ and $\Psi (s, p, d)$ given by (2) and (3), the values $\Upsilon (c, p)$ and $\Omega (c, p, d)$ can also be calculated in O(m) time. Note that $\Phi (\Upsilon (c, p), p)=c$ and $\Psi (\Upsilon (c, p), p, d)=\Omega (c, p, d)$. The following algorithm is similar to that of Lawler (1973) designed for $1|prec|f_{\max }$, where $f_{\max }(\cdot )$ is a nondecreasing function.

Algorithm 3.

Step 1. :

Set $k:=n$, ${\mathcal {J}}_U:={\mathcal {J}}$, $c:=\Phi (0, \sum _{j=1}^n p_j)$, $f:=0$.

Step 2. :

If $k \ge 1$, select the job $J_{i^{*}}$ from ${\mathcal {J}}_U$ with the smallest weighted late work, i.e., $w_{i^{*}}\Omega (c, p_{i^{*}}, d_{i^{*}})=\min \{w_j\Omega (c, p_j, d_j): J_j \in {\mathcal {J}}_U\}$, appoint job $J_{i^{*}}$ to the k-th position, i.e., $J_{[k]}:=J_{i^{*}}$, set $k:=k-1$, ${\mathcal {J}}_U:={\mathcal {J}}_U {\setminus } \{J_{i^{*}}\}$, $c:=\Upsilon (c, p_{i^{*}})$, $f:=\max \{f, w_{i^{*}}\Omega (c, p_{i^{*}}, d_{i^{*}})\}$, then go to Step 2; otherwise, go to Step 3.

Step 3. :

Deliver the optimal maximum weighted late work f and the job permutation $J_{[1]} \rightarrow J_{[2]} \rightarrow \cdots \rightarrow J_{[n]}$.

Theorem 3.4

Algorithm 3 can solve $1 | h(m), res| \max w_j Y_j$ in $O(m n^2)$ time.

Proof

Let $\pi ^{*}$ and $\pi$ be be an optimal permutation for $1 | h(m), res| \max w_j Y_j$ and the permutation delivered by Algorithm 3, respectively. If $\pi ^{*}=\pi$, the result holds immediately. Otherwise, we assume that $\pi$ is selected so that the index u is as small as possible, in which u is the maximum index satisfying that $J_{\pi _{[l]}} \ne J_{\pi ^{*}_{[l]}}$. This means that $J_{\pi ^{*}_{[i]}} = J_{\pi _{[i]}}$ for $i=u+1, u+2, \ldots , n$. Hence, the set of the first u jobs in $\pi$ and $\pi ^{*}$ are identical. Write $c=\Phi (0, \sum _{j=1}^u p_{\pi _{[j]}})=\Phi (0, \sum _{j=1}^u p_{\pi ^{*}_{[j]}})$. We can get another schedule $\pi '$ from $\pi ^{*}$ by shifting job $J_{\pi _{[u]}}$ to the u-th position. From the selection of job $J_{\pi _{[u]}}$ in Algorithm 3 and the regularity of the objective function, the maximum weighted late work of $\pi '$ is not more than that of $\pi ^{*}$. This disproves the selection of $\pi ^{*}$. Thus, $\pi$ is also an optimal permutation.

Because there are n iterations, and each selection of the job in Step 2 takes O(mn) time, Algorithm 3 can be executed in $O(m n^2)$ time. $\square$

Let $V_{\max }^{*}$ be the minimum objective value of $1 | h(m), res| \max w_j Y_j$. Clearly, we have

$$\begin{aligned} V_{\max }^{*} \le V_r^{*} \le n V_{\max }^{*}. \end{aligned}$$

(4)

Let $\epsilon >0$ be any given arbitrary number. To construct an FPTAS for $1 | h(m), res| \sum w_j Y_j$, we remove some special states created by Algorithm 2.

Algorithm 4.

Step 0. :

Set $z= \lceil \frac{n^2}{\epsilon } \rceil$ and $\delta =\frac{\epsilon V_{\max }^{*}}{n}$. Partition the interval $[0, n V_{\max }^{*}]$ into z subintervals ${\mathcal {K}}_i$ such that ${\mathcal {K}}_i=[(i-1) \delta , i \delta )$ for $1 \le i \le z-1$, and $I_{z}=[(z-1) \delta , n V_{\max }^{*}]$.

Step 1. :

Set $\widehat{{\mathcal {Q}}}_0=\{(0, 0, 0)\}$ and $\widehat{{\mathcal {Q}}}_j:=\emptyset$ for $j=1, 2, \ldots , n$.

Step 2. :

For $j=1, 2, \ldots , n$, construct $\widehat{{\mathcal {Q}}}_j$ from $\widehat{{\mathcal {Q}}}_{j-1}$.

Step 2.1. :

Implement the identical action as Step 2.1 of Algorithm 2.

Step 2.2. :

Among all states (r, t, l) in $\widehat{{\mathcal {Q}}}_j$ having the same r value and the value of the third variable l falling into the same subinterval ${\mathcal {K}}_i$, reserve only one state having the smallest t value.

Step 3. :

Set ${\hat{V}}_r=\min \{l: (0, t, l) \in \widehat{{\mathcal {Q}}}_n\}$ and disclose the corresponding approximate solution by the backtracking method.

Lemma 3.5

For each state $(r, t, l) \in {\mathcal {Q}}_j$, Algorithm 4 finds a state $(r, {\hat{t}}, {\hat{l}}) \in \widehat{{\mathcal {Q}}}_j$ with ${\hat{t}} \le t$ and ${\hat{l}} \le l+j \delta$.

Proof

We demonstrate the lemma by induction on $j=1,2, \ldots , n$. For $j=1$, we have ${\mathcal {Q}}_1=\widehat{{\mathcal {Q}}}_1=\{(0, 0, w_1 p_1), (1, 0, 0), (0, p_1, w_1\Psi (0, p_1, d_1)\}$. Therefore, the lemma holds for $j=1$.

Inductively, we assume that the lemma holds up to iteration $j-1$. Consider an arbitrary state $(r, t, l) \in {\mathcal {Q}}_j$. Algorithm 2 creates this state into ${\mathcal {Q}}_j$ when $J_j$ is added to some feasible state $(r', t', l') \in {\mathcal {Q}}_{j-1}$ for the first $j-1$ jobs. Based on the induction assumption, there is a state $(r', {\hat{t}}', {\hat{l}}') \in \widehat{{\mathcal {Q}}}_{j-1}$ with

$$\begin{aligned} {\hat{t}}' \le t' \end{aligned}$$

(5)

and

$$\begin{aligned} {\hat{l}}' \le l'+(j-1) \delta . \end{aligned}$$

(6)

From the definition of $\Phi (0, \cdot )$ and (5), we have

$$\begin{aligned} \Phi (0, {\hat{t}}') \le \Phi (0, t'). \end{aligned}$$

(7)

In the following, we demonstrate that the lemma holds for four different cases.

Case 1: $(r, t, l)=(r', t', l'+w_j p_j)$. This corresponds to the case where $J_j$ is performed as late. Since $(r', {\hat{t}}', {\hat{l}}') \in \widehat{{\mathcal {Q}}}_{j-1}$, Algorithm 4 creates the state $(r', {\hat{t}}', {\hat{l}}'+w_j p_j)$ in Step 2.1-(1). Due to the deletion operation in Step 2.2 and (5)-(6), there must exist a state $(r', {\hat{t}}, {\hat{l}}) \in \widehat{{\mathcal {Q}}}_j$ with

$$\begin{aligned} {\hat{t}} \le {\hat{t}}' \le t'=t \end{aligned}$$

(8)

and

$$\begin{aligned} {\hat{l}} \le {\hat{l}}'+w_j p_j+\delta \le l'+w_j p_j+j\delta =l+j\delta , \end{aligned}$$

(9)

The lemma holds for iteration j in the first case since $r=r'$.

Case 2: $(r, t, l)=(j, t', l')$. This corresponds to the case where $J_j$ is deferred, $k'=0$ and $\Phi (0, t')<d_j$. Since $(r', {\hat{t}}', {\hat{l}}') \in \widehat{{\mathcal {Q}}}_{j-1}$, Algorithm 4 creats the state $(j, {\hat{t}}', {\hat{l}}')$ in Step 2.1-(2). Due to the deletion operation in Step 2.2 and (5)-(6), there must exist a state $(j, {\hat{t}}, {\hat{l}}) \in \widehat{{\mathcal {Q}}}_j$ with

$$\begin{aligned} {\hat{t}} \le {\hat{t}}' \le t'=t \end{aligned}$$

(10)

and

$$\begin{aligned} {\hat{l}} \le {\hat{l}}'+\delta \le l'+j \delta =l+j\delta , \end{aligned}$$

(11)

The lemma holds for iteration j in the second case since $r=j$.

Case 3: $(r, t, l)=(r', t'+p_j, l'+w_j\Psi (\Phi (0,t'), p_j, d_j))$. This corresponds to the case where $J_j$ is performed as non-late and the deferred job $J_r$ (if $r > 0$) is not performed just after $J_j$. Since $(r', {\hat{t}}', {\hat{l}}') \in \widehat{{\mathcal {Q}}}_{j-1}$ and ${\hat{t}}' \le t'$, Algorithm 4 creates the state $(r', {\hat{t}}'+p_j, {\hat{l}}'+w_j \Psi (\Phi (0,{\hat{t}}'), p_j, d_j))$ in Step 2.1-(3). Due to the deletion operation in Step 2.2, there must exist a state $(k', {\hat{t}}, {\hat{l}}) \in \widehat{{\mathcal {Q}}}_j$ with

$$\begin{aligned} {\hat{t}} \le {\hat{t}}'+p_j \le t'+p_j=t \end{aligned}$$

(12)

and

$$\begin{aligned} {\hat{l}} \le {\hat{l}}'+w_j \Psi (\Phi (0,{\hat{t}}'), p_j, d_j)+\delta \le l'+w_j \Psi (\Phi (0,t'), p_j, d_j)+j\delta =l+j\delta ,\nonumber \\ \end{aligned}$$

(13)

where the inequalities (12)-(13) follow from (5)-(7) and $\Psi (\cdot , p_j, d_j)$ is a nondecreasing function. The lemma holds for iteration j in the third case since $r=r'$.

Case 4: $(r, t, l)=(0, t'+p_j+p_{k'}, l'+w_{k'} \Psi (\Phi (0,t'+p_j), p_{k'}, d_{k'}))$. This corresponds to the case where $J_j$ is performed as early and the deferred job $J_{r'}$ is performed just after $J_j$. It happens only when $r' >0$ and $\Phi (0, t'+p_j)<d_{r'}$. Since $(r', {\hat{t}}', {\hat{l}}') \in \widehat{{\mathcal {Q}}}_{j-1}$ and ${\hat{t}}' \le t'$, Algorithm 4 creates the state $(0, {\hat{t}}'+p_j+p_{r'}, {\hat{l}}'+w_{r'} \Psi (\Phi (0,{\hat{t}}'+p_j), p_{r'}, d_{r'}))$ in Step 2.1-(4). Due to the deletion operation in Step 2.2, there must exist a state $(0, {\hat{t}}, {\hat{l}}) \in \widehat{{\mathcal {Q}}}_j$ with

$$\begin{aligned} {\hat{t}} \le {\hat{t}}'+p_j+p_{k'} \le t'+p_j+p_{k'}=t \end{aligned}$$

(14)

and

$$\begin{aligned}&{\hat{l}} \le {\hat{l}}'+w_{k'} \Psi (\Phi (0,{\hat{t}}'+p_j), p_{k'}, d_{k'})+\delta \le l'+w_{k'} \Psi (\Phi (0,t'+p_j),\nonumber \\&\quad p_{k'}, d_{k'})+j\delta =l+j\delta , \end{aligned}$$

(15)

where the inequalities (14)-(15) follow from (5)-(7) and $\Psi (\cdot , p_{k'}, d_{k'})$ is a nondecreasing function. The lemma holds for iteration j in the fourth case since $r=0$. $\square$

Theorem 3.6

Given an arbitrary number $\epsilon >0$, Algorithm 4 is an FPTAS with running time $O(\frac{mn^4}{\epsilon })$ for $1 | h(m), res| \sum w_j Y_j$.

Proof

By Theorem 3.3, Algorithm 2 finds a state $(0, t^{*}, l^{*})$ in ${\mathcal {Q}}_n$, which defines an optimal solution to $1 | h(m), res| \sum w_j Y_j$. By Lemma 3.5, Algorithm 4 finds a state $(0, {\hat{t}}^{*}, {\hat{l}}^{*})$ in $\widehat{{\mathcal {L}}}_n$ with

$$\begin{aligned} {\hat{l}}^{*} \le l^{*}+n \delta =l^{*}+\epsilon V_{\max }^{*}=(1+\epsilon )V_{r}^{*}. \end{aligned}$$

(16)

By Theorem 3.4, the value $V_{\max }^{*}$ can be computed in $O(m n^2)$ time. In Step 0, it needs $O(n^2/\epsilon )$ time for partition. In Step 1, it needs linear time. Based on the deletion operation in Step 2.2, at most $O(n^3/\epsilon )$ different states $({\hat{r}}, {\hat{t}}, {\hat{l}})$ are kept in $\widehat{{\mathcal {Q}}}_j$. Furthermore, for every state in $\widehat{{\mathcal {Q}}}_{j-1}$, we create at most three states in $\widehat{{\mathcal {Q}}}_j$, where every such state can be created in O(m) time. Since there are n iterations, Algorithm 4 can be executed in $O(\frac{mn^4}{\epsilon })$ time. $\square$

Next, we study the special case where all jobs have the same processing time, i.e., $p_j=p$ for $j=1, 2, \ldots , n$. For each $j=1, 2, \ldots , n$, set $C_{[j]}=\Phi (0, jp)$, which can be computed by (2) in O(mn) time. As the TWLW criterion is regular, it can be observed that there exists an optimal permutation $\pi$ for $1 | h(m), res, p_j=p| \sum w_j Y_j$ in which the completion time of j-th job in $\pi$ is exactly $C_{[j]}$, $j=1, 2, \ldots , n$. Then if job $J_k$ $(k=1, 2, \ldots , n)$ is the j-th job in $\pi$, then its weighted late work is $C_{kj}=w_k \min \{ \max \{ C_{[j]}-d_k, 0\}, p_k\}$. Clearly, this problem reduces to the linear assignment problem, which can be solved in $O(n^3)$ time (Schrijver 2003). Hence, the following remark holds.

Remark 3.7

Problem $1 | h(m), res, p_j=p| \sum w_j Y_j$ can be solved in $O(nm+n^3)$ time.

4 The non-resumable problem $1 | h(m), n-res| \sum w_j Y_j$

We address the non-resumable scenario, in which if the processing of a job is interrupted by some MNAI, it has to be restarted from scratch when the machine next becomes available. A feasible solution for $1 | h(m), n-res| \sum w_j Y_j$ can be marked by (i) a partition of ${\mathcal {J}}$ into $m+1$ subsets ${\mathcal {S}}_k$, $k=1, 2, \ldots , m+1$, where ${\mathcal {S}}_k$ denotes the set of jobs performed within the k-th availability interval ${\mathcal {R}}_k$; and (ii) a processing sequence of the jobs in ${\mathcal {S}}_k$. The following property can be easily proved.

Lemma 4.1

There exists an optimal solution for $1 | h(m), n-res| \sum w_j Y_j$ in which all late jobs are performed after all non-late jobs in an arbitrary order.

It is well known that $1||\sum Y_j$ is ordinary $\mathcal{NP}\mathcal{}$-hard. Next, we show that when m is arbitrary, $1 | h(m), n-res| \sum w_j Y_j$ is strongly $\mathcal{NP}\mathcal{}$-hard even if $w_j=1$ and $d_j=d$ for all $1 \le j \le n$. The following decision version (referred to as $\hbox {DV}_1$) of the strongly $\mathcal NP$-hard problem $1 | h(m), n-res| C_{\max }$ (Lee 1996) is used for the reduction.

${\textbf {DV}}_1$: Given a job set ${\mathcal {J}}'=\{J'_1, J'_2, \ldots , J'_{n'}\}$ and $m'$ fixed MNAIs ${\mathcal {I}}'_k=[A_k, B_k]$, $k=1, 2, \ldots , m'$, each job $J'_j$ is associated with a processing time $p'_j$, does there exist a schedule with makespan not exceeding a given threshold value Q.

Theorem 4.2

When m is arbitrary, $1 | h(m), n-res| \sum w_j Y_j$ is strongly NP-hard even if $w_j=1$ and $d_j=d$ for $1 \le j \le n$.

Proof

Given an instance of $\hbox {DV}_1$, the decision instance (referred to as $\hbox {DV}_2$) of $1 | h(m), n-res| \sum w_j Y_j$ is established as follows: a set ${\mathcal {J}}=\{J_1, J_2, \ldots , J_n\}$ of $n=n'$ jobs with $p_j=p'_j$, $w_j=1$, $d_j=Q$ for $1 \le j \le n$, and $m=m'$ MNAIs ${\mathcal {I}}_k={\mathcal {I}}'_k$ for $1 \le k \le m$, does there exist a schedule with TWLW not exceeding zero.

Clearly, $\hbox {DV}_1$ has a solution if and only if $\hbox {DV}_2$ has a solution. $\square$

4.1 $1 | h(m), n-res| \sum Y_j$

We assume that the number m of MNAIs is fixed and all jobs have the unit weight. By Lemma 4.1, we know that the jobs assigned to ${\mathcal {S}}_k$ ($k=1, 2, \ldots , m$) should be non-late and all late jobs should be performed after all non-late jobs in ${\mathcal {S}}_{m+1}$ in arbitrary order. The following key property can be demonstrated by the simple job interchange logic.

Lemma 4.3

There exists an optimal solution for $1 | h(m), n-res| \sum Y_j$ in which the non-late jobs assigned to each availability interval are performed in the order of their indices.

In view of Lemma 4.1 and Lemma 4.3, we design a PPT approach to solve $1 | h(m), n-res| \sum Y_j$. Let $F_j(t_1, t_2, \ldots , t_{m+1})$ denote the minimum objective value of the partial solution for ${\mathcal {J}}_j$, in which the sum of processing times of the non-late jobs in ${\mathcal {R}}_k$ is $t_k$, $k=1, 2, \ldots , m+1$. In the j-th iteration, $J_j$ is either performed as a non-late job in some ${\mathcal {R}}_k$, $k=1, 2, \ldots , m+1$, or performed as a late job.

Algorithm 5.

Step 1. :

Set $F_0(t_1, t_2, \ldots , t_{m+1})=0$ for $t_1=t_2=\cdots =t_{m+1}=0$, and $F_0(t_1, t_2, \ldots , t_{m+1})=+\infty$ otherwise. Set $j:=1$.

Step 2. :

For each $t_k=0, 1, \ldots , \min \{\sum _{l=1}^j p_l, \nabla _k\}$ ($k=1, 2, \ldots , m+1$) such that $\sum _{k=1}^{m+1} t_k \le \sum _{l=1}^j p_l$, compute the following recursive formula:

$$\begin{aligned}&F_j(t_1, t_2, \ldots , t_{m+1})\\&\quad =\min \left\{ \begin{array}{ll} F_{j-1}(t_1, t_2, \ldots , t_{m+1})+p_j \\ F_{j-1}(t_1-p_j, t_2, \ldots , t_{m+1})+\max \{t_1-d_j, 0\} \\ \hbox {if}~ 0 \le t_1-p_j<d_j \\ F_{j-1}(t_1, t_2-p_j, \ldots , t_{m+1})+\max \{B_1+t_2-d_j, 0\} \\ \hbox {if}~ 0 \le B_1+t_2-p_j<d_j \\ ~~~~~~~~~~~~~~\vdots &{} ~\\ F_{j-1}(t_1, \ldots , t_m-p_j, t_{m+1})+\max \{B_{m-1}+t_m-d_j, 0\} \\ \hbox {if}~ 0 \le B_{m-1}+t_m-p_j<d_j \\ F_{j-1}(t_1, \ldots , t_m, t_{m+1}-p_j)+\max \{B_m+t_{m+1}-d_j, 0\} \\ \hbox {if}~ 0 \le B_m+t_{m+1}-p_j <d_j \end{array} \right. \end{aligned}$$

Step 3. :

If $j < n$, set $j: = j + 1$, go to Step 2; else go to Step 4.

Step 4. :

Define

$$\begin{aligned} V_{nr}^{*}\!=\!\min \{F_n(t_1, t_2, \ldots , t_{m+1}): t_k\!=\!0, 1, \ldots , \min \{\sum _{l=1}^n p_l, \nabla _k\}, k\!=\!1, 2, \ldots , m\!+\!1\} \end{aligned}$$

and disclose the corresponding optimal solution by the backtracking method.

Theorem 4.4

Algorithm 5 can solve $1 | h(m), n-res| \sum Y_j$ in $O(m n T^{m} \sum _{j=1}^n p_j)$ time, where $T=\max \{\nabla _i: 1 \le i \le m\}$, which is pseudo-polynomial for fixed m.

Proof

The reason that Algorithm 5 solves $1 | h(m), n-res| \sum Y_j$ follows from Lemma 4.1 and the general DP principle. In the j-th iteration, $t_k \le \nabla _k \le T$ for $1 \le k \le m$, where $T=\max \{\nabla _i: 1 \le i \le m\}$, and $t_{m+1} \le \sum _{l=1}^j p_l \le \sum _{l=1}^n p_l$. Therefore, the number of different states $(t_1, t_2, \ldots , t_{m+1})$ is bounded by $O(T^{m} \sum _{j=1}^n p_j)$. Clearly, every value $F_j(t_1, t_2, \ldots , t_{m+1})$ can be calculated in O(m) time. Since there are n iterations, Algorithm 5 can be executed in $O(m n T^{m} \sum _{j=1}^n p_j)$ time. $\square$

4.2 $1 | h(1), n-res| \sum w_j Y_j$

We focus on the case where there is only one MNAI, referred to as ${\mathcal {I}}=[A, B]$. Recall that ${\mathcal {S}}_1$ and ${\mathcal {S}}_2$ denote the set of jobs performed during ${\mathcal {R}}_1$ and ${\mathcal {R}}_2$, respectively. Before proceeding with the discussion of $1 | h(1), n-res| \sum w_j Y_j$, we introduce some additional notations. Let ${\mathcal {S}}_2^{N}$ and ${\mathcal {S}}_2^{L}$ denote the set of non-late and late jobs in ${\mathcal {S}}_2$, respectively. Given a set ${\mathcal {S}}_2^{N}$, define $\chi =\arg \min \{j: J_j \in {\mathcal {S}}_{2}^{N}\}$, and define $\chi =n+1$ if ${\mathcal {S}}_{2}^{N}=\emptyset$. Moreover, define ${\mathcal {S}}_{1}^{1}={\mathcal {S}}_{1} \cap {\mathcal {J}}_{\chi }$ and ${\mathcal {S}}_{1}^{2}={\mathcal {S}}_{1} {\setminus } {\mathcal {S}}_{1}^{1}$.

Lemma 4.5

There exists an optimal solution for $1 | h(1), n-res| \sum w_j Y_j$ in which the following properties hold:

• (1) all jobs in ${\mathcal {S}}_1$ are non-late;

• (2) all jobs in ${\mathcal {S}}_2^{N}$ are performed before all jobs in ${\mathcal {S}}_2^{L}$;

• (3) all jobs in ${\mathcal {S}}_{1}^{2}$ are performed after all jobs in ${\mathcal {S}}_1^{1}$ in an arbitrary order;

• (4) for ${\mathcal {X}} \in \{{\mathcal {S}}_1^{1}, {\mathcal {S}}_2^{N}\}$, the jobs in ${\mathcal {X}}$ having the same due date are performed in the order of their indices, and with regard to every early job $J_k \in {\mathcal {X}}$, at most one deferred job $J_r \in {\mathcal {X}}$ with $r < k$ is performed after job $J_k$.

Proof

Properties (1) and (2) follow directly from the result of Lemma 4.1.

If ${\mathcal {S}}_{2}^{N} = \emptyset$, then ${\mathcal {S}}_{1}^{2}= \emptyset$, so property (3) follows. Therefore, assume that ${\mathcal {S}}_{2}^{N} \ne \emptyset$. From the definition of $\chi$, we have $d_j \ge d_{\chi }>C_{\chi }-p_{\chi } \ge B \ge A \ge C_j$ for each job $J_j \in {\mathcal {S}}_{1}^{2}$. Hence, all jobs in ${\mathcal {S}}_{1}^{2}$ are early and they can be performed after all jobs in ${\mathcal {S}}_1^{1}$ in an arbitrary order. This complete the proof of property (3).

By applying the result of Lemma 3.1 to the set ${\mathcal {X}}$, property (4) follows immediately. $\square$

Clearly, the set of possible candidates for the non-late job in ${\mathcal {S}}_2^{N}$ is

$$\begin{aligned} {\mathcal {M}}=\{J_j: J_j \in \mathcal {{\mathcal {J}}}, d_j>B\} \cup \{J_{n+1}\}, \end{aligned}$$

(17)

where $J_{n+1}$ is an artificial job with $p_{n+1}=0$, $w_{n+1}=0$ and $d_{n+1}=d_n+1$.

Note that for each job $J_j \in {\mathcal {M}}$, if it starts its processing at time B, it is either an early or partially early job. In order to construct a PPT algorithm for $1 | h(1), n-res| \sum w_j Y_j$, we partition the original problem into a set of r auxiliary subproblems, where $r=|{\mathcal {M}}|$ is the number of jobs in $\mathcal {{\mathcal {M}}}$. For each $J_h \in {\mathcal {M}}$, our h-auxiliary problem (referred to as ${\mathcal {P}}_h$) is a restricted version of $1 | h(1), n-res| \sum w_j Y_j$, where $J_h$ is restricted to be assigned to ${\mathcal {S}}_2^{N}$ and it has the smallest index in ${\mathcal {S}}_2^{N}$. For $h=n+1$, the h-auxiliary problem ${\mathcal {P}}_h$ is such that all non-late jobs are assigned to ${\mathcal {S}}_1$.

Recall that $V_{nr}^{*}$ denote the optimal objective value for $1 | h(m), n-res| \sum w_j Y_j$. Let $V_{nr}^{*}(h)$ be the optimal objective value for ${\mathcal {P}}_h$. Then, we have

$$\begin{aligned} V_{nr}^{*}=\min \{V_{nr}^{*}(h): h \in {\mathcal {M}}\}. \end{aligned}$$

(18)

Next, we show how we can solve each of ${\mathcal {P}}_h$ with $J_h \in {\mathcal {M}}$ via the DP method in PPT.

Consider an h-auxiliary problem ${\mathcal {P}}_h$ with $J_h \in {\mathcal {M}}$. For each $j=1, 2, \ldots , n$, let ${\mathcal {H}}_j(h)$ represent the set of all partial solutions of ${\mathcal {P}}_h$ that satisfy the key properties stated in Lemma 4.5 for ${\mathcal {J}}_j$. Each solution $\sigma _{j} \in {\mathcal {H}}_j(h)$ can be marked by a unique state $(r, t_1, t_2, l)$, where the first variable r denotes that $J_r$ is deferred if $r > 0$ in $\sigma _{j}$, for $i \in \{1, 2\}$, the variable $t_i$ represents the sum of processing times of the non-late jobs in ${\mathcal {S}}_i {\setminus } \{J_r\}$, and the last variable l indicates the TWLW of the jobs in ${\mathcal {J}}_j {\setminus } \{J_r\}$ in $\sigma _j$. Moreover, let ${\mathcal {Q}}_j(h)$ include all possible states defined by the partial solutions in ${\mathcal {H}}_j(h)$. By Lemma 4.5, the following remark can be observed.

Remark 4.6

Let $(r, t_1, t_2, l)$ be a given state in ${\mathcal {Q}}_j(h)$. If $r=0$, then no job is deferred in regard to $J_j$. If $j<h$ and $1 \le r \le j$, then $J_r$ is a deferred job and it will be performed just after some non-late job $J_k$ such that $j+1 \le k \le h-1$. If $j \ge h$ and $h \le r \le j$, then $J_r$ is a deferred job and it will be performed just after some non-late job $J_k$ such that $j+1 \le k \le n$.

It is initialized by setting ${\mathcal {Q}}_0(h)=\{(0, 0, 0, 0)\}$, and for each $j=1, 2, \ldots , n$, the state set ${\mathcal {Q}}_j(h)$ can be constructed from ${\mathcal {Q}}_{j-1}(h)$ progressively. With respect to each given state $(r, t_1, t_2, l) \in {\mathcal {Q}}_{j}(h)$, let $\sigma _j \in {\mathcal {H}}_j(h)$ be a solution corresponding to the state $(r, t_1, t_2, l)$. Also, let $\sigma _{j-1}$ be the solution of ${\mathcal {J}}_{j-1}$ that is gained from $\sigma _{j}$ by removing $J_j$. Evidently, we have $\sigma _{j-1} \in Q_{j-1}(h)$. Let $(r', t'_1, t'_2, l') \in {\mathcal {Q}}_{j-1}(h)$ be the unique state corresponding to $\sigma _{j-1}$. In view of Lemma 4.5 and Remark 4.6, we have to distinguish the following different scenarios.

Scenario 1: $j < h$. In this scenario, $t_2=t'_2=0$ and $J_j$ must be either a non-late job in ${\mathcal {S}}_1^1$ or a late job in ${\mathcal {S}}_2^{L}$ in $\sigma _{j}$. Four subcases are further investigated as follows:

Scenario 1.1: $J_j$ is performed as late in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_2^L$ and $(r, t_1, t_2, l)=(r', t'_1, 0, l'+w_j p_j)$.

Scenario 1.2: $J_j$ is deferred in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_1^1$ and $(r, t_1, t_2, l)=(j, t'_1, 0, l')$. This is feasible only when $r'=0$, $t'_1<d_j$ and $t'_1+p_j<A$.

Scenario 1.3: $J_j$ is performed as non-late and the deferred job $J_{r'}$ (if any) is not performed just after $J_j$ in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_1^1$ and $(r, t_1, t_2, l)=(r', t'_1+p_j, 0, l'+w_j \max \{0, t'_1+p_j-d_j\})$. This is feasible only when either $r'>0$, $t'_1+p_j<d_{r'}$ and $t'_1+p_j+p_{r'}<A$, or $r'=0$, $t'_1<d_j$ and $t'_1+p_j \le A$.

Scenario 1.4: $J_j$ is performed as early and the deferred job $J_{r'}$ ($1 \le r' <j$) is performed just after $J_j$ in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_1^1$ and $(r, t_1, t_2, l)=(0, t'_1+p_j+p_{r'}, 0, l'+w_{r'} \max \{0, t'_1+p_j+p_{r'}-d_{r'} \})$. This is feasible only when $r'>0$, $t'_1+p_j< d_{r'}$ and $t'_1+p_j+p_{r'} \le A$.

Scenario 2: $j = h$. In this scenario, $r'=0$, $t'_2=0$ and $J_h$ must be a non-late job in ${\mathcal {S}}_2^N$ in $\sigma _{j}$. Two subcases are further investigated as follows:

Scenario 2.1: $J_h$ is deferred in $\sigma _j$. In this scenario, we have $(r, t_1, t_2, l)=(j, t'_1, 0, l')$.

Scenario 2.2: $J_h$ is not deferred in $\sigma _j$. In this scenario, it is the first performed job after time B, so we have $(r, t_1, t_2, l)=(0, t'_1, p_h, l'+w_h \max \{0, B+p_h-d_h\})$.

Scenario 3: $j > h$. In this scenario, $J_j$ must be either a non-late job in ${\mathcal {S}}_1^2 \cup {\mathcal {S}}_2^{N}$ or a late job in ${\mathcal {S}}_2^{L}$ in $\sigma _{j}$. Five subcases are further investigated as follows.

Scenario 3.1: $J_j$ is performed as late in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_2^L$ and $(r, t_1, t_2, l)=(r', t'_1, t'_2, l'+w_j p_j)$.

Scenario 3.2: $J_j$ is is performed as early before time A in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_1^2$ and $(r, t_1, t_2, l)=(r', t'_1+p_j, t'_2, l')$. This is feasible only when $t'_1+p_j \le A$.

Scenario 3.3: $J_j$ is deferred in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_2^N$ and $(r, t_1, t_2, l)=(j, t'_1, t'_2, l')$. This is feasible only when $r'=0$ and $B+t'_2<d_j$.

Scenario 3.4: $J_j$ is performed as non-late and the deferred job $J_{r'}$ (if any) is not performed just after $J_j$ in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_2^{N}$ and $(r, t_1, t_2, l)=(r', t'_1, t'_2+p_j, l'+w_j \max \{0, B+t'_2+p_j-d_j\})$. This is feasible only when either $r' \ge h$ and $B+t'_2+p_j<d_{r'}$, or $r'=0$ and $B+t'_2<d_j$.

Scenario 3.5: $J_j$ is performed as early and the deferred job $J_{r'}$ ($h \le r' <j$) is performed just after $J_j$ in $\sigma _j$. In this scenario, we have $J_j \in {\mathcal {S}}_2^{N}$ and $(r, t_1, t_2, l)=(0, t'_1, t'_2+p_j+p_{r'}, l'+w_{r'} \max \{0, B+t'_2+p_j+p_{r'}-d_{r'} \})$. This is feasible only when $r' \ge h$ and $B+t'_2+p_j< d_{r'}$.

For the target of reducing the state space of the DP, the following dominant property can be easily observed.

Lemma 4.7

Given two states $(r, t_1, t_2, l)$ and $(r, t'_1, t'_2, l')$ in ${\mathcal {Q}}_j(h)$ satisfying $t_1 \le t'_1$, $t_2 \le t'_2$ and $l \le l'$, the latter state can be deleted from ${{\mathcal {Q}}}_j(h)$.

Summarizing the above discussion, the following DP algorithm is constructed to solve ${\mathcal {P}}_h$.

Algorithm 6.

Step 1. :

Set ${\mathcal {Q}}_0(h)=\{(0, 0, 0, 0)\}$ and ${{\mathcal {Q}}}_j(h):=\emptyset$ for $j=1, 2, \ldots , n$.

Step 2. :

For $j=1, 2, \ldots , n$, construct ${\mathcal {Q}}_j(h)$ from ${\mathcal {Q}}_{j-1}(h)$ as follows:

Step 2.1. :

If $j<h$, go to Step 2.2; if $j=h$, go to Step 2.3; if $j>h$, go to Step 2.4.

Step 2.2. :

For each $(r, t_1, t_2, l) \in {\mathcal {Q}}_{j-1}(h)$, do:

• (2.2.1) Set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(r, t_1, t_2, l+w_j p_j)\}$;

• (2.2.2) If $r=0$, $t_1<d_j$ and $t_1+p_j<A$, set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(j, t_1, t_2, l)\}$;

• (2.2.3) If either [$r>0$, $t_1+p_j<d_r$ and $t_1+p_j+p_{r}<A$] or [$r=0$, $t_1<d_j$ and $t_1+p_j \le A$], set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(r, t_1+p_j, t_2, l+w_j \max \{0, t_1+p_j-d_j\})\}$;

• (2.2.4) If $r>0$, $t_1+p_j< d_{r}$ and $t_1+p_j+p_{r} \le A$, set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(0, t_1+p_j+p_r, t_2, l+w_r\max \{0, t_1+p_j+p_r-d_r\})\}$.

Step 2.3. :

Set ${\mathcal {Q}}_{h-1}(h):=\{(0, t_1, 0, l): (0, t_1, 0, l) \in {\mathcal {Q}}_{h-1}(h)\}$. For each $(r, t_1, t_2, l) \in {\mathcal {Q}}_{h-1}(h)$, do:

• (2.3.1) Set ${\mathcal {Q}}_h(h):= {\mathcal {Q}}_h(h) \cup \{(h, t_1, t_2, l)\}$;

• (2.3.2) Set ${\mathcal {Q}}_h(h):= {\mathcal {Q}}_h(h) \cup \{(0, t_1, t_2+p_h, l+w_h \max \{0, B+p_h-d_h\})\}$.

Step 2.4. :

For each $(r, t_1, t_2, l) \in {\mathcal {Q}}_{j-1}(h)$, do:

• (2.4.1) Set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(r, t_1, t_2, l+w_j p_j)\}$;

• (2.4.2) If $t_1+p_j \le A$, set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(r, t_1+p_j, t_2, l)\}$;

• (2.4.3) If $r=0$ and $B+t_2<d_j$, set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(j, t_1, t_2, l)\}$;

• (2.4.4) If either [$r \ge h$ and $B+t_2+p_j<d_r$] or [$r=0$ and $B+t_2<d_j$], set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(r, t_1, t_2+p_j, l+w_j \max \{0, B+t_2+p_j-d_j\})\}$;

• (2.4.5) If $r \ge h$ and $B+t_2+p_j< d_r$, set ${\mathcal {Q}}_j(h):= {\mathcal {Q}}_j(h) \cup \{(0, t_1, t_2+p_j+p_r, l+w_r \max \{0, B+t_2+p_j+p_r-d_r\})\}$.

Step 2.5. :

Among all states in ${\mathcal {Q}}_j(h)$ having the same k and $t_i$ values ($i=1, 2$), reserve only one state which has the smallest l value.

Step 3. :

Set $V_{nr}^{*}(h)=\min \{l: (0, t_1, t_2, l) \in {\mathcal {Q}}_n(h)\}$ and disclose the corresponding optimal solution for ${\mathcal {P}}_h$ by the backtracking method.

Remark 4.8

In the n-iteration of Algorithm 6, all states $(r, t_1, t_2, l)$ in ${\mathcal {Q}}_n(h)$ with $r \ne 0$ can be deleted from ${\mathcal {Q}}_n(h)$.

Theorem 4.9

Algorithm 6 can solve ${\mathcal {P}}_h$ in $O(n^2 A \sum _{j=1}^n p_j)$ time.

Proof

The reason that Algorithm 6 solves ${\mathcal {P}}_h$ follows from the above discussion and the general DP principle. In Step 1, it needs linear time. In Step 2, for every state $(r, t_1, t_2, l) \in {\mathcal {Q}}_j(h)$, we create at most three, two and four states in Step 2.2, Step 2.3 and Step 2.4, respectively, where every such state can be created in constant time. Due to $r \le j \le n$, $t_1 \le A$, $t_2 \le \sum _{l=1}^{j} p_l$ and the deletion rule in Step 2.5, the number of different states in ${\mathcal {Q}}_j(h)$ is bounded by $O(n A \sum _{l=1}^j p_l)$. In Step 3, it needs at most $O(A \sum _{j=1}^n p_j)$ time to find the optimal objective value. Since there are n iterations, Algorithm 6 can be executed in $O(n^2 A \sum _{j=1}^n p_j)$ time. $\square$

To facilitate the explanation, a small numerical instance provided in Appendix is used to demonstrate the implementation of Algorithm 6 for ${\mathcal {P}}_h$.

For the purpose of solving $1 | h(1), n-res| \sum w_j Y_j$, we need to solve separately each of the h-auxiliary problems, and choose the best of these r solution values. Hence, the following theorem holds.

Theorem 4.10

$1 | h(1), n-res| \sum w_j Y_j$ is solvable in $O(n^3 A \sum _{j=1}^n p_j)$ time, which is pseudo-polynomial.

Remark 4.11

Unless ${\mathcal {P}}=\mathcal{NP}\mathcal{}$, the PPT algorithm designed for $1 | h(1), n-res| \sum w_j Y_j$ cannot be converted into an FPTAS, since Yin et al. (2016) demonstrated that $1 | h(1), n-res| \sum Y_j$ has no polynomial $(1+\rho )$-approximation algorithm with $\rho < +\infty$.

5 Conclusions

We analyze the problem of scheduling n independent jobs on a single machine in which there are m fixed machine non-availability intervals. The purpose is to seek out a feasible solution that minimizes total weighted late work. Three variants of the problem are investigated.The main results are listed as follows:

• For $1 | h(m), pmtn| \sum w_j Y_j$, we design an $O((m+n) \log n)$-time algorithm to solve it.

• For $1 | h(m), res| \sum w_j Y_j$, we develop an $O(mn^2 \sum _{j=1}^n p_j)$-time DP approach and an FPTAS with running time $O(\frac{mn^4}{\epsilon })$ to solve it.

• For $1 | h(m), n-res| \sum Y_j$, we demonstrate that it is strongly $\mathcal{NP}\mathcal{}$-hard even for the common due date case, and devise a PPT algorithm for fixed m.

• For $1 | h(1), non-res| \sum w_j Y_j$, we develop an $O(n^3 A \sum _{j=1}^n p_j)$-time DP approach to solve it.

For future research, several interesting topics can be suggested. First, one can continue to study $1 | h(m), non-res| \sum w_j Y_j$ for the case where $m \ge 2$ is fixed and determine its exact computational complexity. Second, one can design effective heuristic or meta-heuristic algorithms to solve these $\mathcal{NP}\mathcal{}$-hard problems. Third, one may also study the general MNAI scheduling problem that involves multi-agents and/or resource dependent processing times.

Appendix

Consider an instance of $1 | h(1), n-res| \sum w_j Y_j$ in which it contains six jobs and one MNAI ${\mathcal {I}} = [7, 9]$, where job parameters is given in Table 3.

Table 3 The job data of the instance

By Eq. (17), the set of possible candidate jobs in $\mathcal {{\mathcal {S}}}_2^N$ is ${\mathcal {M}}=\{J_4, J_5, J_6, J_7\}$. We illustrate the execution of Algorithm 6 by choosing $J_4$ as the candidate job in ${\mathcal {S}}_2^N$ having the smallest index and solve ${\mathcal {P}}_4$ as follows:

Step 1. Set ${\mathcal {Q}}_0(4)=\{(0, 0, 0, 0)\}$ and ${{\mathcal {Q}}}_j(4)=\emptyset$ for $j=1, 2, \ldots , 6$.

Step 2. For $j=1<4$, $J_1$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_1(4)=\{(0, 0, 0, 2), (0, 2, 0, 0), (1, 0, 0, 0)\}$, see Table 4 for the creation procedure.

Table 4 Creation of ${\mathcal {Q}}_1(4)$ from ${\mathcal {Q}}_0(4)$

For $j=2<4$, $J_2$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_2(4)=\{(0, 0, 0, 8), (2, 0, 0, 2), (0, 3, 0, 2), (1, 0, 0, 6), (0, 2, 0, 6), (2, 2, 0, 0), (0, 5, 0, 2)\}$, see Table 5 for the creation procedure.

Table 5 Creation of ${\mathcal {Q}}_2(4)$ from ${\mathcal {Q}}_1(4)$

For $j\!=\!3\!<\!4$, $J_3$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_3(4)=\{(0, 0, 0, 20), (0, 2, 0, 18), (0, 3, 0, 14), (0, 4, 0, 8), (0, 5, 0, 14), (0, 6, 0, 6), (0, 7, 0, 5), (1, 0, 0, 18), (2, 0, 0, 14), (2, 2, 0, 12), (3, 0, 0, 8), (3, 2, 0, 6)\}$, see Table 6 for the creation procedure.

Table 6 Creation of ${\mathcal {Q}}_3(4)$ from ${\mathcal {Q}}_2(4)$

For $j=4$, $J_4$ falls into Case 2. Algorithm 6 executes Step 2.3, we obtain ${\mathcal {Q}}_4(4)=\{(0, 0, 3, 20), (0, 2, 3, 18), (0, 3, 3, 14), (0, 4, 3, 8), (0, 5, 3, 14), (0, 6, 3, 6), (0, 7, 3, 5), (4, 0, 0, 20), (4, 2, 0, 18), (4, 3, 0, 14), (4, 4, 0, 8), (4, 5, 0, 14), (4, 6, 0, 6), (4, 7, 0, 5)\}$, see Table 7 for the creation procedure.

Table 7 Creation of ${\mathcal {Q}}_4(4)$ from ${\mathcal {Q}}_3(4)$

For $j=5>4$, $J_5$ falls into Case 3. Algorithm 6 executes Step 2.4 and Step 2.5, we obtain ${\mathcal {Q}}_5(4)=\{(0, 0, 3, 32), (0, 0, 7, 26), (0, 2, 3, 30), (0, 2, 7, 24), (0, 3, 3, 26), (0, 3, 7, 20), (0, 4, 3, 20)$, $(0, 4, 7, 14), (0, 5, 3, 26), (0, 5, 7, 20), (0, 6, 3, 18), (0, 6, 7, 12), (0, 7, 3, 14), (0, 7, 7, 11), (4, 0, 0, 32)$, $(4, 2, 0, 30), (4, 3, 0, 26), (4, 4, 0, 20), (4, 5, 0, 26), (4, 6, 0, 18), (4, 7, 0, 14), (5, 0, 3, 20), (5, 2, 3, 18)$, $(5, 3, 3, 14), (5, 4, 3, 8), (5, 5, 3, 14), (5, 6, 3, 6), (5, 7, 3, 5)\}$, see Table 8 for the creation procedure, where the underlined state $(k, t_1, t_2, l)^{x}$ is dominated by the corresponding state ${(r, t_1, t_2, l)}^{(x)}$.

Table 8 Creation of ${\mathcal {Q}}_5(4)$ from ${\mathcal {Q}}_4(4)$

For $j=6>4$, $J_6$ falls into Case 3. Algorithm 6 executes Step 2.4 and Step 2.5, we obtain ${\mathcal {Q}}_6(4)=\{(0, 0, 3, 44), (0, 0, 5, 32), (0, 0, 7, 38), (0, 2, 3, 32), (0, 2, 5, 30), (0, 2, 7, 26), (0, 3, 3, 38)$, $(0, 3, 5, 26), (0, 3, 7, 32), (0, 4, 3, 30), (0, 4, 5, 20), (0, 4, 7, 24), (0, 5, 3, 26), (0, 5, 7, 20), (0, 5, 5, 26)$, $(0, 6, 3, 20), (0, 6, 5, 18), (0, 6, 7, 14), (0, 7, 3, 26), (0, 7, 5, 14), (0, 7, 7, 20) \}$, see Table 9 for the creation procedure, where those state $(r, t_1, t_2, l) \in {\mathcal {Q}}_6(4)$ with $r > 0$ are deleted (by Remark 4.8).

Table 9 Creation of ${\mathcal {Q}}_6(4)$ from ${\mathcal {Q}}_5(4)$

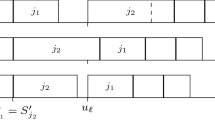
Step 3. $V_{nr}^{*}(4)=\min \{l: (0, t_1, t_2, l)\} \in {\mathcal {Q}}_6(4)\}=14$, the states (0, 6, 7, 14) and (0, 7, 5, 14) both correspond to the optimal value 14 for ${\mathcal {P}}_4$, see Figs. 2 and 3 for their corresponding optimal schedules, where the late jobs in ${\mathcal {S}}_2^L$ are omitted.

Fig. 2

The schedule corresponding to the state (0, 6, 7, 14) of ${\mathcal {P}}_4$

Fig. 3

The schedule corresponding to the state (0, 7, 5, 14) of ${\mathcal {P}}_4$