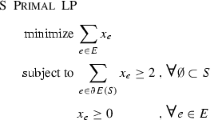Heuristics for the network design problem with connectivity requirements

Abstract

We consider the NP-complete problem of finding a spanning $k$-tree of minimum weight in a complete weighted graph. This problem has a number of applications in designing reliable backbone telecommunication networks. We propose effective algorithms based on a greedy strategy and several variable neighborhood search metaheuristics. We also develop an integer linear programming model for calculating a lower bound. Preliminary numerical experiments using random and real-word data sets are reported to show the effectiveness of our approach. In addition, we compare our approach with known metaheuristics.

1 Introduction

Nowadays, due to a significant increase in scales and complexity of telecommunication infrastructures, one of the most important problems is designing telecommunication networks of minimal costs with a given level of network reliability (Thai and Pardalos 2011; Pardalos and Thai 2011; Dinh et al. 2012). Traditionally, this problem is considered in two variants. The first one, when a network topology is not specified and it is computed in the process of solving the problem (Haidine 2013; Elshqeirat et al. 2013; Dengiza et al. 2010; Johnston et al. 2013). The second one, when the network topology is given (Konak and Smith 2011; Khandekara et al. 2013; Simonetti et al. 2011; Alvarez-Mirandaa et al. 2013; Bansal et al. 2013). In the second variant, connectivity requirements of a network are a kind of surrogate for reliability (Magnanti and Raghavan 2005). Researches in this field have led to the appearance of the concept of isolated failure immune (IFI) networks (Farley 1981) in the 80s of the last century. Such networks remain connected even in the presence of a large number of failures. Specifically, IFI networks work with three types of failures (Farley 1981; Candia and Bravo 2002):

• $[i,j]$ and $[p,q]$ are two line isolated failures if $[i,j]$ and $[p,q]$ are not incident to a common node;

• $i$ and $j$ are two node isolated failures if $i$ and $j$ are not connected;

• a line failure $[i,j]$ and a node failure $p$ are isolated if $[i,j]$ is not incident to $p$ or to a node connected to $p$.

A set of failures is isolated if failures in the set are pairwise isolated. The network is IFI if it remains connected as long as network failures are isolated. In Farley (1981) it is proved that 2-trees are minimal (with respect to edge inclusion) IFI networks. Many problems of designing IFI networks can be formulated as a Minimum Spanning k-Tree Problem (MSkT), which generalizes the classical problem, the Minimum Spanning Tree Problem (MST) (Prim 1957).

The mathematical formulation of the MSkT problem is as follows. We are given a complete weighted undirected graph $G=(V,E)$, where $V$ refers to a set of nodes (telecommunication stations) and $E$ refers to a set of edges among $n=|V|$ nodes (possible links). The expense of each edge $[i,j]$ between vertices $i$ and $j$ is quantified as a nonnegative value $w(i,j)$. We are given a positive integer constant $k$. Let $T(G)$ be the set of all spanning $k$-trees in the graph $G$, where a spanning $k$-tree is a $k$-tree that contains all vertices and some edges of the graph $G$. Let $w(T)$ be the weight of edges of the spanning $k$-tree $T\in T(G)$. It is required to find the spanning $k$-tree $T^*$ of minimum weight in the complete weighted graph $G$, that is $T^*=\arg \min _{T\in T(G)}\{w(T)\}.$

In Bern (1987), Cai and Maffray (1992) it is proved that the MSkT problem when $k\ge 2$ is NP-complete. In Bern (1987) it is proved that the cardinality of the set of feasible solutions of the MSkT problem equals to $n!(n+k-1)!/k!$. Thus, the time complexity of an exhaustive search is $O(n^{2n}/k^k)$. Also in Bern (1987) there has been proposed a nonpolynomial exact algorithm based on dynamic programming, which has a significantly lower complexity $O(n^{k+1}3^{n})$ than the exhaustive search. In Bern (1987) there has been proved inapproximability of the MS2T problem (i.e. where $k=2$). In Beck and Candia (1993), Beck et al. (1993), Candia and Bravo (2002), Beltran and Skorin-Kapov (1993), Cai (1996), Beck and Candia (2000), Wald and Colbourn (1983) there have been proposed effective heuristics and metaheuristics for solving the MS2T. Although the MS2T is well studied, nevertheless, there is little attention given in the literature to the development of algorithms for solving the MSkT, where $k>2$. The main purpose of this work is to develop effective heuristics and metaheuristics for solving the MSkT problem (i.e. where $k\ge 2$) on a complete weighted graph.

The plan of this paper is as follows. In Sect. 2, we give the definition of a $k$-tree and several of its basic properties. In Sect. 3, we propose heuristics that use a greedy strategy. In Sect. 4, we propose variable neighborhood search metaheuristics. In Sect. 5, we present an integer linear program for computing a lower bound for the MSkT. In Sect. 6, we present results of computational experiments. In Sect. 7 we summarize our findings and discuss directions for further research.

2 Definition and basic properties of $k$-trees

Here is a well-known definition of a $k$-tree.

Definition

(Rose 1974) A $k$-tree is a member of a class of undirected graphs defined recursively as follows: a complete graph with $k$ vertices is a $k$-tree; if $T$ is a $k$-tree with $n$ vertices, then a new $k$-tree with $n+1$ vertices is formed by creating a new vertex $v$ and adding edges between $v$ and every vertex of an existing $k$-clique (clique with $k$ vertices) in $T$.

The class of $k$-trees was introduced in the 70s of the last century by D. Rose. Besides using trees in the networks design, wide interest in the study of such graphs is caused by the fact that some NP-hard combinatorial problems are solvable in polynomial time when they are restricted to $k$-trees. Today there are polynomial time algorithms for solving some classical problems of graph theory on $k$-trees for example, maximum clique problem, minimum dominating set problem, Steiner tree problem, etc (Garey and Johnson 1976). Polynomial time algorithms for many location problems on $k$-trees are also known: simple location problem (Granot and Skorin-Kapov 1994), $p$-median and $p$-center problems (Shi 2008), etc.

If $T$ is a $k$-tree with $n$ vertices, then

• 1. All maximal cliques in $T$ have size equals to $k$;

• 2. The size of a minimal separator (disconnecting set) in $T$ equals to $k$;

• 3. The number of edges of the $k$-tree $T$ equals to $nk-\frac{k(k+1)}{2}$;

• 4. The number of $(k+1)$-cliques in $T$ equals to $n-k$;

• 5. The number of $k$-cliques in $T$ equals to $(n-k)k+1$;

• 6. For all nonadjacent vertices $i,j\in V$, there exist exactly $k$ vertex-disjoint paths.

The recursive definition of $k$-trees implies that they have the perfect elimination order property (Golumbic 1980). That is, for a $k$-tree $T$ with $n$ vertices, there exists an ordering of the set $V$, say $v_1,v_2,\ldots ,v_j,...,v_n$, such that in the node-induced subgraph $V\setminus \{v_j:j=1,2,\ldots ,i-1\}$, where $i\ge 1$, nodes adjacent to $v_i$ form a $k$-clique. A detailed study of $k$-trees properties is presented, for example, in Golumbic (1980), Rose (1970).

3 Heuristics based on greedy strategy

In this section, we propose greedy algorithms, which compute a feasible approximate solution for the MSkT. These algorithms will be used both for solving the MSkT problem and for computing a starting solution in metaheuristics.

3.1 Algorithm Greedy

We propose the algorithm Greedy which uses the idea of the well-known Prim’s algorithm for the MST problem (Prim 1957). Let $W_i=(V^\prime _i,E^\prime _i)$ be a complete graph with $i$ nodes. Let $T_i=(V_i,E_i)$ be a $k$-tree with $i$ nodes and $K(T_i)$ is a set of all $k$-cliques in $T_i$.

Proposition 1

The time complexity of the algorithm Greedy is $O(n^3 k)$.

Proof

At step 1 for finding the cheapest edge in graph $G$ one needs $O(|E|)$ operations. Step 2 can be implemented in $O((k-1)\cdot n)$ operations because $O(n)$ operations are necessary to compute the new vertex $m^*\in V\setminus V^\prime _i$ at every iteration of step 2, and the number of such iterations at step 2 equals to $k-1$. At every iteration of step 3 one needs $O((n-k)^2\cdot k)$ operations because there are $(n-k)\cdot k$ cliques of the size $k$ in the $k$-tree $T_i$, and the number of all possible variants of the new vertex $m^*\in V\setminus V_i$ at each iteration of step 3 does not exceed $n-k$. As far as the number of iterations performed at step 3 is $n-k-1$, then at step 3 one requires $O((n-k)^3\cdot k)$ operations. Based on this, the time complexity of the algorithm Greedy is $O(n^3 k)$. $\square$

Despite the fact that the idea of the algorithm Greedy is simple and natural, this heuristic computes approximate solutions of good quality (see Sect. 6.1). Note that, the Greedy is a modification of the known heuristic proposed by Beck and Candia (2000). The basic difference between our algorithm and the known heuristic is in the method of computing the “starting” clique. In our algorithm it is computed in order to minimize the weight of edges in $W_i$ and in Beck and Candia’s heuristic it is chosen randomly. Figure 1 shows the ways of constructing solutions for the MSkT problem by the Greedy heuristic.

Fig. 1

Construction of the solutions by the Greedy heuristic for: a MS2T; b MS3T

3.2 Neighborhoods

Let $C_T$ be a set of all cliques of a size $k+1$ in a $k$-tree $T$. The neighborhood $N_l^L(T)$ of the solution $T$ is a set of spanning $k$-trees that differ from $T$ by exactly $l$ cliques of a size $k+1$, that is $N_l^L(T)=\{T^\prime :|C_{T^\prime }\setminus C_T|=l\}$. The element $T^\prime$ of the neighborhood $N_l^L(T)$ can be built from $T$ by $l$-fold repetition of the operations: delete $k$ edges connecting some simplicial vertex $j^\prime$ ($k$-leaf) with vertices of some $k$-clique $K$ and then add $k$ new edges connecting the vertex $j^\prime$ with another $k$-clique $K^\prime$, where $K^\prime \ne K$. The cardinality of the neighborhood $N_l^L$ does not exceed $O(n^{l+1}k^l)$ because the number of all possible connections of a $k$-leaf with other $k$-cliques is at most $nk$ and the number of $k$-leaves does not exceed $n$. Figure 2 shows elements of the neighborhoods $N_l^L(T)$ for $2$-tree and $3$-tree.

Fig. 2

Elements of the neighborhoods $N_l^L(T)$ with $l=1,2,3$ for $2$-tree and $3$-tree

It is quite obvious that the search within the neighborhood $N_l^L$ for large values of $l$ is not justified from the computational point of view, despite the fact that it very often leads to really good approximate solutions. This drawback of $N_l^L$ can be eliminated by using the Kernighan–Lin neighborhood $\mathcal {K}_l^L$, which includes the neighborhood $N_1^L$ and is part of $N_l^L$. Its main idea is to find the best solution in $N_l^L$ by using a greedy procedure. The Kernighan–Lin neighborhood of $T$ is defined by the following steps:

• Step 0 Let $T_0=T$.

• Step 1 Find the solution $T^\prime$ in $N_1^L(T_0)$ of minimal weight. Let $T_0=T^\prime$.

• Step 2 Repeat step 1 $l$ times such that we do not consider vertices that have already been used in the previous iterations.

Obviously, $O(l n^{2}k)$ operations are required for computing the neighborhood $\mathcal {K}_l^L$ because $O(n^{2}k)$ operations are required to build the neighborhood $N_1^L$, and $\mathcal {K}_l^L$ contains $l$ such neighborhoods.

3.3 Modifications of the Greedy heuristic

We propose several modifications of the Greedy, aimed at improving its accuracy.

The first modification Greedy $^1$ is to combine the heuristic Greedy with a local descent algorithm. In this modification at every iteration $i=k+2,\ldots ,n$ the deterministic steepest local descent with the neighborhood $N_1^L$ will be applied to improve the computed solution $T_{i+1}$. If the local descent algorithm is able to find a lower-cost solution, then solution $T_{i+1}$ is replaced by the new computed solution, otherwise the solution $T_{i+1}$ does not change. The time complexity of this modification is also $O(n^3 k)$ because the local descent with $N_1^L$ requires no more than $O(n^2k)$ operations at every iteration of step 3.

The second modification Greedy $^2$ is as follows. We sort edges from $G$ in increasing order based on their weights and select the first $n$ edges. For every selected edge $[x,y]$ we construct a spanning $k$-tree using the Greedy heuristic, where we select the edge $[x,y]$ at step 1. A solution of this algorithm is a spanning $k$-tree of minimum weight over all computed $k$-trees. The time complexity of this modification is $O(n^4 k)$ because the number of constructed $k$-trees by this algorithm equals to $n$.

The third modification Greedy $^3$ combines ideas of two previous modifications. In the algorithm for every selected edge we construct a spanning $k$-tree using the Greedy $^1$ algorithm. Then we find a spanning $k$-tree of minimum weight over all computed $k$-trees. Essentially, the computational complexity of this modification is also $O(n^4 k)$.

4 Variable neighborhood search metaheuristics

The variable neighborhood search metaheuristic was proposed by Hansen et al. (2010). This approach uses several neighborhoods and changes them systematically that allows to escape from local optima and find better and better solutions.

4.1 Basic scheme of variable neighborhood search

The variable neighborhood search algorithm can be implemented in many ways, such as deterministic (VND), probabilistic (RVNS) or mixed (VNS). In this paper, we will focus on the mixed scheme because it combines strengths of both schemes.

There are two phases in the VNS: the shaking phase, thanks to which the algorithm escapes from local optima, and the local search phase, where the iterative improvement is carried out from solutions generated at the shaking phase. Denote by $N_t^S, t=1,2,\ldots ,t_{m}$ neighborhoods used at the shaking phase and let $N_l^L, l=1,2,\ldots ,l_{m}$ be neighborhoods used at the local search phase. Let $I_{m}$ be a maximal number of iterations at every $t$.

As the starting solution, we will use the solution found by the Greedy $^3$ because of its high accuracy and small computational time costs (see Sect. 6.1).

4.2 Neighborhoods

Denote by $S=\{1,2,\ldots ,i,\ldots ,j,\ldots ,n\}$ a sequence of vertices of a spanning $k$-tree, where the vertices are ordered in accordance with the perfect order elimination property (see Sect. 2). Note that for any $k$-tree we can compute the sequence of vertices $S$ in linear time (Golumbic 1980). Obviously, from some sequence $S$ we can construct a spanning $k$-tree by the following modification of the Greedy algorithm. In this modification at the iteration $i$ of step 3 we include the vertex with number $i$ from the sequence $S$ and the set of edges $\{[i,j]:j\in K^*\}$ of minimal weight. Naturally, the time complexity of this modification is $O(n^2k)$. Let $S^{(t)}$ be a set of sequences obtained from the sequence $S$ by sequential permutation of $t$ pairs of its elements. For example, the set $S^\prime =\{\underline{1},6,3,2,\underline{4},5\}$ is obtained from $S=\{\underline{4},6,3,2,\underline{1},5\}$ by permutation of the one pair of vertices and hence $S^\prime \in S^{(1)}$.

The neighborhood $N_t^S(T)$ of the solution $T$ is a set of spanning $k$-trees constructed from sequences belonging to the set $S^{(t)}$, where $S$ is the sequence of vertices corresponding to the $k$-tree $T$. Naturally, the cardinality of the neighborhood $N_t^S$ is at most $O(n^{2t})$. Note that the idea of using such a neighborhood was partially used in Candia and Bravo (2002), Beltran and Skorin-Kapov (1993).

4.3 Modifications of the basic scheme

Denote by VNS$(t_{m},l_{m}, I_{m})$ the algorithm VNS with the maximum neighborhoods $N_{t_{m}}^S$ and $N_{l_{m}}^L$ and the maximum number of iterations $I_{m}$, performed for every $t$.

Proposition 2

The time complexity of the algorithm VNS$(t_{m},l_{m}, I_{m})$ does not exceed $O(t_{m} I_{m} n^{l_{m}+1} k^{l_{m}})$.

Proof

The sequence $S^\prime$ is chosen randomly from the set $S^{(t)}$ that requires no more than $O(t_{m})$ operations. Computing a solution $T^\prime$ from $S^\prime$ requires $O(n^2k)$ time and a number of repetitions of this step equals to $t_{m} I_{m}$. Hence, step 1.1 of the VNS requires $O(t_{m} I_{m} n^2k)$ operations. Step 1.2 requires $O(t_{m} I_{m} n^{l_{m}+1} k^{l_{m}})$ operations because the cardinality of $N_l^L$ does not exceed $O(n^{l_{m}+1} k^{l_{m}})$, and a number of repetitions of step 1.2 equals to $t_{m} I_{m}$. Hence, the time complexity of the algorithm VNS$(t_{m},l_{m}, I_{m})$ does not exceed $O(t_{m} I_{m} n^{l_{m}+1} k^{l_{m}})$. $\square$

Next, we propose several modifications of the VNS algorithm.

The first modification VNS$^1(t_{m},l_{m}, I_{m})$ of the VNS consists in changing the way of choosing a solution from $N_t^S$ at step 1.1 (shaking phase). In this modification, the new solution is not selected from $N_t^S$ at random, but by analogy with the simulated annealing approach we select the solution, or with lower costs then record, or with larger costs then record, but with a probability depending on its costs. Based on this, step 1.1 of the VNS$^1$ is as follows:

Step 1.1 Select $T$ at random from the neighborhood $N_t^S(T^*)$. If $w(T)<w(T^*)$, then let $T^\prime =T$, else let $T^\prime =T$ with the probability $e^{-\frac{\Delta w\cdot \gamma }{\lambda }}$, where $\Delta w=\frac{w(T)-w(T^*)}{w(T^*)}$ and $\gamma =1,2,...$ is a sensitivity coefficient of the probability from the solution’s costs. If $T^\prime$ is selected, then go to step 1.2, else repeat step 1.1.

This method of selecting solutions from the neighborhood $N_t^S(T^*)$ has the following meaning. The smaller the costs of the solution are, the more likely its choice is. The longer the algorithm can not improve the record, the lower the costs of the solution $T$ affect the probability of its selecting. The time complexity of the algorithm VNS$^1$ equals to the complexity of the VNS because this modification requires $O(1)$ repetitions of step 1.1, while the solution $T^\prime$ is not selected. The numerical experiments showed that the algorithm achieves the highest accuracy when $\gamma \in [4,7]$. Based on this, we assume that the value $\gamma$ equals to 5.

The second modification VNS$^2(t_{m},l_{m}, I_{m})$ of the basic scheme consists in using the Kernighan–Lin neighborhood at the local search phase. The time complexity of this algorithm is $O(t_{m} I_{m} l_{m} n^{2}k)$ because the cardinality of $\mathcal {K}_{l_{m}}^L$ equals to $O(l_{m} n^{2}k)$.

The third modification VNS$^3(t_{m},l_{m}, I_{m})$ contains ideas of the previous two modifications. The time complexity of the third modification also equals to $O(t_{m} I_{m} l_{m} n^{2}k)$.

5 Lower bound for the MSkT problem

We present an integer linear programming (ILP) model for calculating the lower bound of the MSkT problem. This model is based on well-known properties of a $k$-tree which are partially given in statement 1. We have the vertex set $V=1,2,\ldots ,n$. For any $i,j\in V, i<j$ the boolean variable $x_{ij}$ is defined, where $x_{ij}=1$ if the edge $[i,j]$ is included in the solution, and $x_{ij}=0$ otherwise. The ILP model for the lower bound is as follows:

$$\begin{aligned} F_{LB}=\min _{x}\left\{ \sum _{i,j\in V: \ i<j}w(i,j)x_{ij}\right\} \end{aligned}$$

(1)

subject to

$$\begin{aligned}&\sum _{i,j\in V: \ i<j}x_{ij}= n k-\frac{k(k+1)}{2},\end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j\in V: \ i<j}x_{ij}+\sum _{j\in V: \ i>j}x_{ji}\ge k; \qquad (\forall i\in V), \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i,j\in S: \ i<j}x_{ij}\le |S| k-\frac{k(k+1)}{2}; \qquad (\forall S\subseteq V, |S|\ge k), \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{i\in S, j\in V\setminus S: \ i<j}x_{ij}+\sum _{i\in S, j\in V\setminus S: \ i>j}x_{ji} \ge \frac{k(k+1)}{2}; \qquad (\forall S\subseteq V, |S|\ge k),\quad \quad \end{aligned}$$

(5)

$$\begin{aligned}&x_{ij}\in \{0,1\}, \ i<j, \ i,j\in V. \end{aligned}$$

(6)

Constraint (2) fixes the total number of edges to $n k-k(k+1)/2$. Constraints (3) say that every vertex of a $k$-tree must be connected by at least $k$ vertices. Constraints (4) say that a number of edges in a subgraph induced by a set of vertices $S, |S|\ge k$ does not exceed the number of edges in a $k$-tree with $|S|$ vertices. Constraints (5) say that a set of vertices $S,|S|\ge k$ of some subgraph in a $k$-tree is connected with other vertices of a $k$-tree by at least $k(k+1)/2$ edges. Note that this ILP model partially uses the idea of computing a lower bound for the MS2T problem (where $k=2$) (Beltran and Skorin-Kapov 1993), and the idea of computing a lower bound for the minimum spanning $2$-connected graph problem (Grotschel and Monma 1992).

Obviously, this ILP problem has an exponential number of constraints and it is difficult to handle directly. We propose the algorithm LB for computing the lower bound which has a significantly lower time complexity than the model (1)–(6). The algorithm LB uses an idea of a sequential inclusion of constraints (4) and (5) for some $S\subseteq V$ in the model (1)–(3), (6). At every step of this algorithm we consider a relaxation of problem (1)–(6), and its objective function is also a lower bound for the MSkT problem.

Constraints (7) say that a subgraph of a $k$-tree which is induced by a vertex $i\in V$ and vertices adjacent to $i$ is also a $k$-tree (Rose 1970). Obviously, constraints (7) are a special case of constraints (4). Constraints (8) say that when we remove $q,q <k$ vertices that belong to a minimal separator $Q$ in a $k$-tree, vertices of every subgraph $Y\in C_Q,|Y|\ge k$ will be connected with other vertices by at least $(k-q)(k-q+1)/2$ edges (Rose 1970).

Evidently, the number of separators of a size $<k$ in the graph $T2$ is at most $n^{k-1}$, and the cardinality of the set $C_Q$ does not exceed $nk$. Hence, a number of constraints added to the ILP model at every iteration does not exceed $n^k$. The numerical experiments indicated that for problems MS2T and MS3T of dimension $|V|=20$ at every iteration the average number of added constraints was 17 and 26, respectively, and the average number of iterations was 6 and 8, respectively, when maximal number $I_{m}$ was 15.

6 Experimental results

The numerical experiments were performed to compare the effectiveness of the proposed algorithms with known metaheuristics. By efficiency of an algorithm we understand its running time and accuracy. All algorithms were implemented in “MATLAB R2011a” . To calculate the lower bound of the MSkT we used “IBM ILOG CPLEX Optimization Studio 12.2” (solving the ILP by the branch and bound algorithm). Calculations have been performed on a PC with the processor “Intel Core i7 2.6 GHz”. The study of the efficiency of the algorithms was performed on two classes of instances:

• instances where weights of edges are Euclidean distances (class Euclidean);

• instances where weights of edges are generated at random with uniform distribution (class Uniform).

We also tested the algorithms on a real-world data of the European backbone IP-network provided by the “TeleGeography” consultancy (http://www.telegeography.com). Denote by $\bar{t}$ an average running time of an algorithm, sec.; $\bar{\varepsilon }$ – an average relative error of an algorithm, %; $\sigma$ – standard deviation of the relative error. Note that, the value $\varepsilon$ is computed by the formula $\varepsilon =(w_{alg}-w_{LB})/w_{LB}\cdot 100\,\%$, where $w_{alg}$ is the weight of a spanning $k$-tree constructed by the algorithm, and $w_{LB}$ is the lower bound computed by the algorithm LB.

Table 1 presents the time complexity of the proposed algorithms.

Table 1 The time complexity of the proposed algorithms

6.1 Analysis of the algorithms based on the greedy strategy

Figure 3 shows the results of the computational experiments to analyze the efficiency of the algorithm Greedy and its modifications. The experiments were conducted on sets of instances, where every set includes 20 instances of the same dimension.

Fig. 3

The average relative errors of the algorithms based on the greedy strategy

On the Uniform class the algorithm Greedy $^3$ showed the best results in terms of accuracy, and values of its average error were less than 2.2 and 2.9 % for the problems MS2T and MS3T, respectively. For the problems MS2T and MS3T the algorithm Greedy showed the worst results in terms of accuracy. Furthermore, there was a significant increase of its relative error by increasing dimension of the problem.

On the Euclidean class errors of the greedy algorithms were much lower than on the Uniform class, that takes place, apparently, due to the triangle inequality at the matrices of distances. Despite this, Greedy showed the worst results and Greedy $^3$ showed the best results in terms of accuracy.

6.2 Analysis of the variable neighborhood search algorithms

Figure 4 illustrates the results of the experiments to analyze the efficiency of the variable neighborhood search algorithms.

Fig. 4

The average relative error of the variable neighborhood search algorithms

On all sets of instances for Uniform and Euclidean classes errors of the algorithm VNS and all its modifications were less than 2 % that indicates high accuracy of such metaheuristics. The error in most cases was because it is not calculated with respect to an optimum but with respect to the lower bound, which is often less than the optimum. The algorithm VNS $^1$ showed the best results in terms of accuracy but its running time for instances of dimension $|V|=100$ was about 30 min. The algorithm VNS $^2$, which uses the Kernighan–Lin neighborhood on the local search phase, showed the worst results in terms of accuracy. It is interesting to note that the VNS $^3$, which uses Kernighan–Lin neighborhood and implements the idea of the simulated annealing approach, showed significantly better results in comparison with the algorithm VNS $^2$. Its running time for instances of dimension $|V|=100$ does not exceed 150 s.

6.3 Comparison of the effectiveness of the proposed algorithms

This section presents the results of the experiments to analyze the proposed algorithms in comparison with known metaheuristics: Tabu Search (Beltran and Skorin-Kapov 1993), SA (Simulated Annealing) (Candia and Bravo 2002) and GA (Genetic Algorithm) (Ghashghai and Rardin 2002). The efficiency was evaluated on random and real-word data sets.

Table 2 Comparison of the efficiency of the proposed algorithms

Table 3 Comparison of the efficiency of the proposed algorithms

Tables 2 and 3 present results of the experiments to analyze the effectiveness of the algorithms on the random data set. The experiments show that the algorithm VNS $^1$ demonstrated the smallest error, which on the Uniform class was less than 0.25 %. Note that this algorithm significantly outperformed all known metaheuristics in terms of accuracy. The algorithms Greedy $^3$, SA and GA showed almost the same results in terms of accuracy, surpassing each other on different instances. The Greedy $^3$ is insignificantly worse than the Tabu Search.

Table 4 demonstrates the results on the real-world data provided by “TeleGeography” consultancy. The data includes information about 25 hub-level nodes of the European backbone IP-network and the matrix of shortest distances between the nodes.

Table 4 Comparison of the proposed algorithms on the real-world data

On the real data the metaheuristic VNS $^1$ demonstrates the best results in terms of accuracy. The algorithm VNS $^3$ outperformed all known metaheuristics. Figure 5 shows the solution of the MS2T problem with the real-world data built by the algorithm VNS $^1$. Note that this solution is very similar to the existing structure of the IP-network but at the same time there are some differences. The differences are largely due to unaccounted conditions in the MSkT problem, such as probability of link failure, probability of node failure, bandwidth restrictions, etc.

Fig. 5

The solution of the MS2T with the real-world data built by the algorithm VNS $^1$

7 Concluding remarks

In this paper we have considered the minimal spanning $k$-tree problem in a complete weighted graph. We have proposed algorithms based on the greedy strategy and the variable neighborhood search metaheuristics.

We have conducted numerical experiments to analyze the effectiveness of the proposed algorithms on random and real-word data sets. The experiments showed that VNS $^1$ outperformed metaheuristics Tabu Search, SA and GA and all other algorithms proposed in this paper. The average error of this algorithm on random instances does not exceed 0.25 % and the running time for instances of dimension $|V|=100$ does not exceed 35 min. The algorithm VNS $^3$, which uses Kernighan–Lin neighborhood on the local search phase and partially implements the idea of the simulated annealing approach showed almost the same accuracy with the known metaheuristics. The running time of the algorithm VNS $^3$ for solving the problem of dimension $|V|=100$ does not exceed 125 s. The results indicate prospects of use the algorithm for solving problems of large and extra large dimensions, while the algorithm VNS $^1$, due to its high time complexity, is advised to be applied for solving problems of small and medium dimensions.

Importantly, the numerical experiments on the real-world data showed that the MSkT problem in its pure form is interesting from more theoretical than practical point of view because its mathematical model does not take into account many conditions that are critical in designing real-world communication networks: probability of link failure, probability of node failure, bandwidth restrictions, etc. Based on this, as a direction of the further research, it seems appropriate to study modifications of the MSkT problem which take into account conditions listed above. This direction seems to be promising for the following reasons. First, many real-world communication networks are partial $3$-trees (i.e. connected spanning subgraphs of a $3$-tree) (Granot and Skorin-Kapov 1994). Second, reliability of $k$-trees, due to their connectivity properties, outperforms reliability of many well-known topologies, for instance, tree topology, ring topology, etc (Candia and Bravo 2002). Third, the problem of calculating a network reliability measure, which is NP-complete on arbitrary graphs, is solvable in polynomial time on $k$-trees (for fixed $k$) (Granot and Skorin-Kapov 1994).