Introduction

Presently the clusters obtained by the adiabatic free expansion of different gases are a unique tool not only for fundamental researches but also for various technical applications, such as a generation of optical harmonics and X-rays by intense laser pulses action, a processing of materials by gas cluster ion beams, etc. [1,2,3]. In all cases, the cluster size is one of the key parameters, which must be determined. The complexity of cluster formation processes in non-equilibrium conditions of supersonic flow does not allow to fully solve the problem analytically. The known models of cluster formation are approved only for certain gases and allow performing numerical simulation of flows with condensation in restricted conditions.

For the characterization of gas flows with clusters, O. Hagena introduced the scaling law based on the principle of “corresponding jets” [4,5,6,7]. The dimensionless condensation scaling parameter Г* is a function of the gas parameters in the source (stagnation pressure P 0 and temperature T 0), the shape of the nozzle (as the equivalent nozzle diameter d eq ) and a gas specific constant k [4, 8, 9]. In most general form the parameter Г* can be expressed as follows:

$$\varGamma^{*} = k(P_{0} /mbar)(d_{eq} /\mu m)^{q} (T_{0} /K)^{sq - i} ,$$
(1)

where q, i and s is the gas-specific parameters, that depend on symmetry of the expansion (spherical from axially symmetric source flow or planar from linear source flow). The specific constant k depends on respective gas [6] and has been calculated for noble and some of molecular gases [10, 11]. The concept of equivalent nozzles [4, 5] allows one to compare the condensing flows after nozzles with different geometry. For a sonic (flat) nozzles equivalent diameter d eq is equal to the throat diameter d*. For the conical nozzles equivalent diameter given as:

$$d_{eq} = c(\gamma )d_{*} /\tan \alpha ,$$
(2)

Here α is the half angle of the diverging section, c is constant depends on γ (the ratio of specific heats) and symmetry of the flow. For axisymmetric expansion usually c(γ) = 0.736, 0.866 and 0.986 for monoatomic (γ = 5/3), diatomic (γ = 7/5) and triatomic (γ = 9/7) gases, respectively [1]. Different relationship for parameter c has been proposed in [8]:

$$c = 0.5(f + 1)^{ - (f + 1)/4} A^{f/2} ,$$
(3)

where A is the constant from [12], and for axisymmetric flows A = 3.83. The empirical parameter q (0 < q < 1) also depends on respective gas and can be determine from experiments [7]. By analysing the experimental results, it was found that q = 0.85 for Ar [7], and q = 0.6 for CO2 [13]. Generally the parameters i and s are defined by the flow symmetry and the ratio of specific heats γ:

$$i = \gamma /(\gamma - 1),\quad s = (2 - \beta (\gamma - 1))/2\beta (\gamma - 1),$$
(4)

where β = 2 for axisymmetric and β = 1 for linear source expansion. For axially symmetric flows considering all possible degree of freedom s = 0.25, 0.75 and 1.25 for γ = 5/3, 7/5 and 9/7, respectively [4]. But at room-level temperatures only some of degrees of freedom are active during free jet expansion. Therefore for axially symmetric flows more correct s = (f – 2)/4, where f is the numbers of a thermally active degree of freedom [8, 9]. It should be noted that the numerical values of the gas-specific constants have been approved only for finite number of molecular gases.

Starting from Hagena, dependence for the mean cluster size N has the following general form:

$$N = b\left( {\frac{\varGamma ^{*}}{1000}} \right)^{a} ,$$
(5)

The parameters a and b are commonly defined by the generalization of the experimental data. It was registered what the numerical values of the parameters a and b are distinguished significantly not only for different gases but for various ranges of Г* also. Even for argon with simplest monoatomic structure and well-known basic properties, there are sufficient discrepancies between the results obtained by different authors at the equals Г* (see Conclusions section). The widest divergence of experimental data is noted when using conical nozzles of different geometry and measuring large clusters for Г* > 103. As a result, the mean cluster size N is given usually as a function of stagnation pressure \(N \propto P_{0}^{a}\), and numerical value of the degree a varies from 2.35 to 1.0 [7, 14, 15].

At present, there are a lot of different experimental methods for determination of mean gas clusters sizes, which can be divided into conditionally direct measurements and indirect or scattering techniques. Each experimental method has both certain advantages and some restrictions or disadvantages. For direct measurements, which include all mass spectrometric methods [13, 16, 17], mass spectra of cluster ions are registered directly. It is known that the true neutral cluster size distribution can be severely distorted by the effects of the ionization induce cluster fragmentation, mass discrimination during transportation and detection of the heavy ion. Therefore, for reconstruction of the true cluster sizes the different correction procedures are used based on fragmentation data [16]. However, the fragmentation of the clusters upon their ionization has been studied in detail only for a limited number of gases. Numerous scattering methods of gas cluster size determination may be divided into the scattering of cluster beam itself (e.g. on a buffer gas) and scattering of the external flow on the cluster beam: crossed molecular beam [14, 18], laser light scattering (Rayleigh or Raman spectroscopy) [15, 19,20,21,22,23], X-ray photoelectron spectroscopy (XPS) [9, 24], high-energy electron diffraction [25, 26], IR spectroscopy [27, 28], etc. Methods of cluster beam scattering on a buffer gas caused by elastic scattering (beam attenuation [29], broadening of cluster beam [30]), or by pickup techniques (the variations of the average beam velocity [31,32,33], etc.), are based on destruction of the cluster beam, which is not always acceptable. All other scattering methods belong mainly to non-destructive techniques. Unfortunately, each tested gas requires the creation of a special model correlating the scattering cross section of this gas and the true cluster sizes. Typically, these models contain empirical constants, determination of which requires complicated calibration procedures. Furthermore, the scattering cross-section depends not only on the size but also on the structure and phase state of clusters. Due to the small absolute values of scattering cross-sections, such methods are mainly used to measure the sizes of large clusters. The widely used method of Rayleigh scattering does not allow determining the absolute cluster sizes alone because the intensity of scattered signal depends not only on cluster sizes but on their density as well. Therefore, to determine the absolute size of clusters a combination of different optical methods is often used: Raman and Rayleigh scattering [34], Rayleigh scattering and interferometry [21, 35, 36], Rayleigh scattering and absorption spectroscopy [37]. Another approach is based on Rayleigh scattering data that are scaled by other experimental results [15, 19] or numerical simulation [21]. Most of the experimental methods use Campargue`s type molecular beam scheme, consisting of a skimmer and a collimator with differential pumping. In order to minimize the skimmer disturbance, the skimmer entrance is usually located at a long distance from the nozzle in the far flow field at terminal cluster sizes. At the same time, the measurements by the laser scattering methods require the high density of clusters. So such measurements are carried out directly in a free jet near the nozzle exit. Obviously, due to the small absolute values of cross sections and local density of clusters, all experimental methods require using the complex high-sensitive equipment.

Previously [38] the possibility of mean gas clusters size determination by measuring the cross-section intensity profile of the cluster beam behind the skimmer has been shown. In Basic Approaches section of this paper a detailed description of the fundamental principles of this experimental method is provided. Experimental conditions and data processing procedure are given in Experimental Details and Data Reduction sections, respectively. In Results and Discussions section the results of measurement of cross-section the cluster beams generated from supersonic jets of various gases (CO2, Ar, N2, and C2H4) are shown and discusses. The results obtained for the mean cluster size are verified by comparison with estimates for empirical relationships and data from other authors’ works using the scaling parameter Г*.

Basic Approaches

The fundamental principles of this method are illustrated in Fig. 1. It is known that in the absence of the influence of the background gas, in the far field of an axially symmetric supersonic jet the radial flow streamlines occur from a virtual point source [4]. In the case of flow from a conical nozzle, including flow with condensation, radial expansion occurs in the small solid angle defined by the cone angle of the nozzle and the boundary layer on its wall [39]. The cluster beam is separated from the free jet through a skimmer with minimal disturbing effect on the supersonic flow. Changing from continuum to free-molecular expansion may occur upstream (Knudsen number on skimmer Kn sk ≥ 1) or downstream (Kn sk < 1) from the skimmer entrance. The solution of the Boltzmann equation in the hypersonic approximation shows that under conditions of collisionless expansion the flow of gas along the symmetry axis can be described as an anisotropic distribution function [40]:

$$f(v,x) = n(x)\left( {\frac{m}{2\pi k}} \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} T_{ \Downarrow }^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \exp \left( { - \frac{{m(v_{ \Downarrow } - U)^{2} }}{{2kT_{ \Downarrow } }}} \right)T_{ \bot }^{ - 1} \exp \left( { - \frac{{mv_{ \bot }^{2} }}{{2kT_{ \bot } }}} \right),$$
(6)

where U is the hydrodynamic flow velocity, m is the mass of particles, k is the Boltzmann’s constant, v is the thermal velocity, T ‖ and T ⊥ are the parallel and the perpendicular temperatures. At a long distance downstream from the skimmer (distance skimmer-detector L sk-det/d sk ≫ 1) gas density along the axis of the molecular beam changes as following [41]:

$$n_{\det } \approx n_{sk} \left( {1 - \exp ( - S_{ \bot sk}^{2} {{(\phi } \mathord{\left/ {\vphantom {{(\phi } 2}} \right. \kern-0pt} 2})^{2} )} \right)\frac{{d_{sk}^{2} }}{{L_{sk - \det }^{2} }},$$
(7)

where n sk is the density at skimmer entrance, S ⊥sk—speed ratio at the skimmer entrance, φ is the skimmer angle defined by radial line from the virtual source to the skimmer orifice lip, d sk is the skimmer diameter. Particle density n(x) is decreasing along the axis due to beam widening (increasing in diameter) and is characterized by transverse speed ratio S ⊥:

$$S_{ \bot } = \left( {\frac{{mU^{2} }}{{2kT_{ \bot } }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} .$$
(8)

Measurement of transverse density profile of particles in a molecular beam allows determining the translational temperature T⊥ and, accordingly, speeding ratio S⊥ [42]. As a result, given the radial flow at the skimmer entrance, at a distance L sk-det downstream from the skimmer entrance the diameter of molecular beam d beam is the sum of geometric beam width Θ, defined by the angle φ and broadening of molecular beam Δ occurring due to thermal spreading of particles:

$$d_{beam} = \varTheta + 2\Delta \approx \phi (L_{s - sk} + L_{sk - \det } ) + {\raise0.7ex\hbox{${2L_{sk - \det } }$} \!\mathord{\left/ {\vphantom {{2L_{sk - \det } } {S_{ \bot } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${S_{ \bot } }$}}$$
(9)

where L s-sk is the distance from the point source to the skimmer.

Fig. 1
figure 1

Schematic diagram of considered method 1—conical nozzle, 2—virtual point source, 3—supersonic jet, 4—skimmer, 5—intensity gauge

Full size image

It is known that in a molecular beam of particles with different mass (mA > mB) the Mach-number focusing effect is observed. During the formation of the beam in the far field of a hypersonic continuous flow (focusing parameter ζ = (S ⊥ θ)2 ≪ 1) the enrichment factor ξ on the beam axis is [41]:

$$\xi \approx {\raise0.7ex\hbox{${S_{ \bot A}^{2} }$} \!\mathord{\left/ {\vphantom {{S_{ \bot A}^{2} } {S_{ \bot B}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${S_{ \bot B}^{2} }$}} \approx {\raise0.7ex\hbox{${m_{A} }$} \!\mathord{\left/ {\vphantom {{m_{A} } {m_{B} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m_{B} }$}}.$$
(10)

In a molecular beam generated from a supersonic jet of condensable gases both monomers and clusters with a broad continuous size distribution (and respectively, weight) are present. Generally, at the entrance of the skimmer, the mass condensate fraction does not exceed 30% [43]. In conditions of free molecular expansion monomers and clusters form independent transverse distributions, which are characterized by the corresponding broadening and speed ratios: Δ mono  ≈ 1/S ⊥mono for monomers, Δ clust  ≈ 1/S ⊥clust for clusters with the mean size N. The monomers are spreading in a larger solid angle than the clusters and, as a result, at a larger distance behind the skimmer (L sk-det /d sk  ≫ 1) the percentage of clusters on the beam axis increases significantly compared to the skimmer entrance. It is known that with the increase of the stagnation pressure the distribution of cluster size becomes bimodal with one peak near the peak monomer and a second in large clusters (e.g., see Fig. 10b in Ref. 43, or Fig. 8 in Ref. 8). This leads to distinct distributions of the monomer and cluster components on the transverse intensity profile (see Fig. 3 below). Clusters of different sizes form a single distribution: in the axial region clusters of larger sizes are concentrated, and closer to the periphery the cluster sizes decrease. In addition, as in the beam of monomers, transverse profile of the clusters is described by a Gaussian distribution [32]. As well as the FWHM (the full width at half maximum) of a cross-section of monomers is determined by the translational temperature, the FWHM of the cluster cross-section is determined by the mean cluster size. The bigger the mean cluster size, the smaller the spreading angle, therefore the transversal cross-section of the cluster distribution is smaller. The assumption that where is no slip between clusters and monomers (that means the translational equilibrium between monomers and clusters) defines a simple relationship between speed ratios: \(S_{ \bot clust} = S_{ \bot mono} \sqrt N\). Thus, measurement of the broadening of the transverse profile of the monomer and cluster components of the beam at a fixed distance downstream behind the skimmer allows determining the mean cluster size N as follows:

$$N = \left( {{\raise0.7ex\hbox{${\Delta_{mono} }$} \!\mathord{\left/ {\vphantom {{\Delta_{mono} } {\Delta_{clust} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\Delta_{clust} }$}}} \right)^{2} = \left( {{\raise0.7ex\hbox{${S_{ \bot clust} }$} \!\mathord{\left/ {\vphantom {{S_{ \bot clust} } {S_{ \bot mono} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${S_{ \bot mono} }$}}} \right)^{2}.$$
(11)

Experimental Details

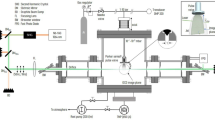
The experiments were performed on an experimental setup, the detailed description of which is given elsewhere [44]. Only the part of the experimental equipment is described here briefly and shown in Fig. 2. The setup consists of three differential pumping vacuum chambers: source chamber SC, buffer chamber BC, and measurement chamber MC. In this work the partition wall between the BC and MC chambers was removed. The gas source was mounted on a linear manipulator that allowed changing the distance between the nozzle and the skimmer. The measurements were carried out with pure gases Ar, N2, CO2, C2H4, expanding from conical nozzles of different geometrical dimensions. Actual nozzles dimensions used in the present experiments are given in Table 1. The clusters sizes were regulated by variation the stagnation pressure. The stagnation pressure P 0 was varied in the range from 3.0 × 104 to 6 × 105 Pa, the temperature of stagnation T 0 was equivalent to the room temperature (i.e., T 0 = 293 K). The beam was formed from the supersonic jet by skimmer with an inlet diameter of 0.44 mm. During the experiments, the distance from the nozzle to the skimmer was 50 mm. The background pressure in the SC chamber was 10−1–1 Pa depending on the stagnation pressure. Under such conditions, the barrel structure with the X-shaped configuration of oblique shock waves was formed instead of the typical Mach disk (e.g., see Fig. 2 in [43]). All basic measurements were performed for the location of the skimmer inside the barrel in a so-called silent zone. The background pressure in the MC chamber did not exceed 2 × 10−4 Pa, which ensured the passage of the particle beam from the skimmer to the detector without scattering on the background gas.

Fig. 2
figure 2

Scheme of measurements of the cluster beam cross-sections

Full size image
Table 1 Dimensions of the conical nozzles used in the present work
Full size table

The intensity of the cluster beam was determined by measuring the excess pressure arising during stagnation of the beam in the sensor of a small volume. A commercially available vacuum gauge (Granville-Philips model 356 Micro-Ion Plus) was used as a sensor. To measure the transverse profile the sensor is moved perpendicular to the axis of the beam at the distance of 6 inches using linear manipulator. The pressure in the sensor and the transverse coordinate were recorded using the ADC. To ensure spatial resolution of measurements a slit aperture with a width of 1.2 mm was set at the input of the sensor perpendicular to the direction of travel. The distance from the entrance of the skimmer to the aperture of the sensor (path length of the beam) was 326 mm.

Data Reduction

During the experiment, relations between the pressure in the sensor and the transverse coordinates of the sensor were measured. Sensor pressure P det is the sum of the background pressure in the chamber P bg and excess pressure P beam generated by the beam particles, stagnated inside the sensor. The background pressure in the MC chamber was monitored by a vacuum gauge, similar to the intensity sensor, located on the side wall of the chamber. However, due to the asymmetric location of the beam and turbomolecular pumps there can be significant variations in the local background pressure in different areas of the chamber. Therefore, for correct determination of P bg at a small distance from the beam axis a screen was installed, blocking the direct molecular beam (see Fig. 2). The pressure recorded for the movement of the intensity sensor behind the screen was assumed as the background pressure P bg , and the true pressure created by the beam was defined as P beam  = P det  − P bg .

Incoming into the sensor flux J in consisting of clusters and monomers with a density of n clust and n mono , respectively, can be defined as follows:

$$J_{in} = I_{total} A_{in} = (I_{clust} + I_{mono} )A_{in} = (n_{clust} N + n_{mono} )A_{in} U,$$
(12)

where I total is the total (mass) beam intensity, I clust and I mono are intensities of cluster and monomer components of flow, A in is the inlet area. The particles of a beam inflowing into the sensor are stagnated by colliding with the walls inside the sensor. The number of such collisions is defined as follows: \(\omega = {\raise0.7ex\hbox{${v\tau }$} \!\mathord{\left/ {\vphantom {{v\tau } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}\), where τ is the time constant of the sensor, v is the mean particle velocity, D is the characteristic dimension of the sensor. For free molecular flow of particles the time constant τ for sensor of volume V is determined as follows: \(\tau = {\raise0.7ex\hbox{${4V}$} \!\mathord{\left/ {\vphantom {{4V} {vA}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${vA}$}}\), where v is the mean monomer velocity corresponding to the sensor walls temperature T det: \(v = \sqrt {\frac{{8kT_{\det } }}{\pi m}}\). For V ≈ 15 cm3, A ≈ 0.1 cm2 and T det  ≈ 300 K the time constant of the sensor is τ ≈ 10 ms, so the number of particle collisions with the walls of the sensor is ω » 10. Under these conditions, all clusters falling in the sensor are fragmentized, and the gas flux J out coming out of the sensor consists of monomers which have acquired the temperature of the walls of the sensor T det:

$$J_{out} = I_{out} A_{out} = \frac{1}{4}n_{beam} vA_{out} ,$$
(13)

where n beam is the equilibrium density of the gas in the sensor, A out is the discharge area. For the background pressure P bg  ~ 10−4 Pa and typical pressure inside the sensor P det  ~ 10−3–10−2 Pa at the entrance of the sensor the mode of free molecular flow is activated, in which the inflowing and the outflowing stream of particles do not interact. Excessive pressure P beam , generated by the beam inside the sensor is the result of equilibrium of in- and outflowing fluxes. Assuming that the incoming and the outgoing streams pass through the same area (A in  = A out ), total (mass) intensity of beam cluster I total is defined as follows:

$$I_{total} = \frac{1}{4}\frac{{P_{beam} v}}{{kT_{\det } }} = \frac{{P_{beam} }}{{\sqrt {2\pi mkT_{\det } } }}.$$
(14)

A typical transverse intensity profile of the cluster beam is shown in Fig. 3. It is possible to allocate lower broad profile corresponding to the intensity distribution of the monomers, and the near-axial peak corresponding to the intensity distribution of clusters. Each of these profiles is well described by a separate Gaussian distribution with the maximum at the axis of symmetry of the beam. In Fig. 3 the geometrical width of the beam Θ is also marked, the value of which is determined by the geometry of the measurement system as follows (see Fig. 1):

Fig. 3
figure 3

Experimental cross-section fitted by Gaussian distributions. Nozzle no. 2. Ar. P 0 = 90 kPa

Full size image
$$\varTheta = 2(L_{s - sk} + L_{sk - \det } )tg({\raise0.7ex\hbox{$\phi $} \!\mathord{\left/ {\vphantom {\phi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}).$$
(15)

For a cluster beam, a virtual point source is located inside a conical nozzle in the region of formation of nuclei of condensation [39]. Determination of the exact position of the virtual source is a difficult task, so in this work for define the absolute value of Θ we have used the following empirical approach. At high stagnation pressures, and hence for large cluster sizes the cluster speed ratio is large, S ⊥clust  ≫ 1. Accordingly, at the finite path length, the broadening of the cross-section of the cluster component is small, Δ clust  ≪ Θ. Figure 4a shows the normalized cross-sections of the cluster beam, measured at high stagnation pressures. When P 0 > 300 kPa, the intensity profiles within the measurement error coincide. FWHM of the profile defines the geometric width of the beam Θ, which in these conditions is 2.9 mm. Similarly, it is possible to determine Θ for other geometric conditions: the skimmer diameter, the distances between the nozzle and the skimmer and between the skimmer and the detector.

Fig. 4
figure 4

Main measured experimental parameters of Ar cluster beam. Nozzle no. 1. a Definition of the geometrical width of the cluster beam. b Broadenings of the monomer and cluster components versus stagnation pressure

Full size image

Thus, to calculate the mean cluster size the following algorithm was used: the transverse intensity profile measured in the experiment was fitted by Gaussian distributions for cluster and monomer components of the beam. Broadening of monomer Δ mono and cluster Δ clust beam components was determined as the HWHM after subtracting the geometric half-width Θ/2:

$$\Delta_{clust} = \sqrt {2\ln 2} \sigma_{clust} - {\raise0.7ex\hbox{$\varTheta $} \!\mathord{\left/ {\vphantom {\varTheta 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\quad \Delta_{mono} = \sqrt {2\ln 2} \sigma_{mono} - {\raise0.7ex\hbox{$\varTheta $} \!\mathord{\left/ {\vphantom {\varTheta 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},$$
(16)

where σ clust and σ mono are standard deviations for a corresponding Gaussian distribution. The broadenings of the monomer and cluster components of the beam as a function of stagnation pressure are shown in Fig. 4b. Finally, the mean cluster size N for this regime was calculated using the Eq. (11).

Results and Discussions

A typical set of cross-sections measured at different stagnation pressures in the beam of weakly condensable N2 is shown in Fig. 5. Profiles of total intensity are shown in Fig. 5a, profiles with normalization to unity at the maximum of the signal are shown in Fig. 5b. With growing stagnation pressure the beam intensity increases in proportion to P 0. The FWHM with increasing P 0 from 30 to 40 kPa increases, then changes weakly. Estimates show that for a given geometry of a conical nozzle at the maximum values of P 0, the scaling parameter Г* < 1500, which corresponds to the initial stage of condensation. Under these conditions, the intensity of cluster flow is less than the intensity of the monomers. Therefore, despite the presence of small clusters in the beam, the transverse profile remains a smooth curve and can be fitted with a single Gaussian distribution. With increasing stagnation pressure, the background pressure in the SC chamber increases, which leads to the reduction in the size of the jet. At P 0 = 200 kPa the inlet skimmer can be found in the region of X-shaped shock wave; when P 0 = 300 kPa, in the region with high local gas density and small speed ratio. This leads to a sharp (more than an order of magnitude) growth of total beam intensity and simultaneous broadening of the beam.

Fig. 5
figure 5

Experimental cross-sections of N2 cluster beam at the different stagnation pressure. Nozzle no. 2. a Total intensity, b intensity normalized at the maximum of the signal

Full size image

Figure 6 shows the typical cross-sections of intensity, measured in easily condensable CO2. Total intensity profiles of the cluster beam are shown in Fig. 6a. In Fig. 6b the same profiles are normalized to unity at the maximum of the monomer components. For P 0 = 30 kPa at the initial stage of condensation, the cross-section has a smooth wide transverse profile. With increasing pressure P 0 the mean cluster size increases, with clusters concentrated on the axis of the beam in accordance with the Eq. (10) due to the effect of Mach focus. Starting with P 0 = 40 kPa, the intensity of the cluster flow begins to exceed the flow rate of monomers along axis beam. As a result, the beam profile has a characteristic non-monotonic form and is described by two Gaussian distributions with maxima on the beam axis. The cluster and the monomer components of the beam could be easily split. With the increase of the stagnation pressure the intensity of the monomer and the cluster component increase as well, but at different rates. This leads to a change in the ratio of monomers and clusters. For these conditions, if P0 increases from 40 to 200 kPa, the cluster percentage on the beam axis increases from 31 to 93. The release of the condensation heat in the gas flow leads to the gradual broadening of the profile of the monomers.

Fig. 6
figure 6

Experimental cross-sections of CO2 cluster beam at different stagnation pressure. Nozzle no. 2. a Total intensity, b intensity normalized at maximum of monomer component

Full size image

For P 0 = 300 kPa the inlet of the skimmer is in front of the X-shaped shockwave. Primarily, this leads to strong scattering of the monomer stream. As a result, the intensity and the speed ratio of the monomers are decreasing; the profile of the monomers is dramatically broadening. The clusters practically do not scatter, so the total beam intensity is not reduced, the cluster percentage is increased to 99. For P 0 = 350 kPa the inlet of the skimmer is in the region of shockwaves. When passing through a shockwave the clusters partially evaporate, their mean size decreases, which leads to the broadening of the cluster profile, the almost 5 times fall of the total beam intensity and decreasing of cluster percentage to 92. For P 0 = 400 kPa the beam is formed from the region behind the shock waves, which leads to an almost complete evaporation of the cluster and 50 times decrease of I total .

Figure 7 shows the obtained experimental dependences of total intensity on the axis of the cluster beam I total and the speed ratio of monomers for different gases S ⊥mono , defined in terms of the broadening of monomer profile ∆ mono depending on the stagnation pressure for nozzle no. 1. Experimental data S ⊥mono were obtained according to Eq. (9) as follows: S ⊥mono  = L sk-det /2∆ mono . The same figure also shows the corresponding calculated values obtained using numerical simulation. The calculated values of the mass condensate fraction for these regimes are shown in Fig. 8. The simulation of the gas flow behind the conical nozzle was performed in the frames of parabolized Navier–Stokes equations. The process of homogenous condensation in the supersonic jet was described using a Dillmann and Meier model [45]. Total intensity on the axis of the cluster beam was calculated using expressions proposed in [46]. Detailed description of the used numerical model is given in [43, 47].

Fig. 7
figure 7

Total intensity of cluster beam I total (a) and speed ratio S ⊥mono (b) versus stagnation pressure for different gases. Nozzle no. 1. Experimental results—solid symbols, simulation data—open symbols

Full size image
Fig. 8
figure 8

Simulation mass condensate fraction in different gases versus stagnation pressure. Nozzle no. 1

Full size image

In most cases, the obtained experimental values of the total beam intensity are in good agreement with numerical simulation. Usually, the absolute values of the measured intensity are smaller than the calculated ones, probably due to the skimmer interaction and scattering of the beam on the background behind the skimmer. These processes are not taken into account in the used numerical model. In N2 jet the portion of the condensate is small even for the maximum P 0, so condensation has no significant influence on the intensity profile of the beam. Under these conditions, the N2 beam intensity increases linearly with the stagnation pressure. The speed ratio S ⊥mono for a variation of stagnation pressure changes very poorly. When P 0 = 400 kPa the aforementioned effect of X-shaped shock-waves is appear, leading to the inhibition of gas flow and a corresponding sharp drop of the S ⊥mono value.

As expected, in the same conditions the condensation in CO2 starts much earlier in terms of pressure. Massive condensation (Г* > 103, N > 102) in CO2 jet begins at P 0 > 40 kPa, in Ar jet at P 0 > 70 kPa. Since then, the intensity of the beam cluster component begins to exceed the intensity of the monomer component, resulting in the appearance of the central peak in the transverse profile (see Fig. 6 for CO2 in this paper and Fig. 2 in [38] for Ar). Under conditions of mass condensation, the increase of stagnation pressure from 30 to 100 kPa leads to a sharp (more than 2 orders of magnitude) increase of the total beam intensity and mass condensate fraction q. For P 0 > 100 kPa the flow is entering the stage of developed condensation, in which the beam intensity slowly increases, and mass condensate fraction is gradually approaching the limit value. The conservative nature of the condensate mass fraction is caused by thermodynamic and kinetic limitations of non-equilibrium condensation under free jet expansion [43]. The release of condensation heat into the jet leads to a gradual decrease of S ⊥mono (see Fig. 7b). In Ar and CO2 jets the influence of boundary shockwaves manifests itself at P 0 ≥ 500 kPa. Primarily, this leads to scattering of the monomer flow and to the rapid decrease of speed ratio. Then, with P 0 = 600 kPa, evaporation of clusters during the passage through a shockwave starts, which leads to decrease in the total beam intensity, mass condensate fraction and speed ratio. Compare to nozzle no. 2, nozzle no. 1 has a smaller throat diameter d*, so provides a lower gas consumption. This leads to a bigger size of the supersonic jet and to evaporation of clusters started at a higher pressure P 0.

Apart from the widely used test gases Ar, N2 and CO2, measurements were also performed for expansion of pure ethylene C2H4. Condensation of ethylene in a supersonic jet is studied poorly, constants of condensation are unknown. Cross-sections of the total intensity registered in different gases under the same conditions are shown in Fig. 9. Since ionization intensity sensor was used, difference of the cross sections for ionization of molecules was taken into account when making the comparison. Maximum total intensity was registered in the beam of Ar, and maximum percentage of the cluster in the beam of CO2. In these conditions, the ethylene forms the smallest clusters; the total intensity of the cluster beam of C2H4 is close to the beam intensity of the weakly condensable N2.

Fig. 9
figure 9

Cross section of cluster beam intensity in different gases at the same conditions. Nozzle no. 1, P 0 = 200 kPa: a total intensity, b intensity normalized at the maximum of the monomer component

Full size image

Mean cluster sizes N, obtained from the experimental measurements of the transverse beam profile in different gases and two nozzles depending on the stagnation pressure are shown in Fig. 10. As was mentioned earlier, expansion condensation of CO2 starts earlier at the pressure P 0 than that of Ar. Therefore, with the same stagnation pressure, the mean size of clusters in CO2 is more than in Ar. Condensation in C2H4 is much delayed, pressure-wise. nozzle no. 1 has a smaller equivalent diameter than nozzle no. 2, so the mean cluster sizes for nozzle no. 2 are found systematically higher. For both nozzles, clusters were not registered in the whole range of variation of the pressure P 0 in a jet of N2.

Fig. 10
figure 10

Experimental mean cluster size N versus P 0 for different gases and different nozzles

Full size image

Due to monoatomic structure and well-known basic properties, argon has been used most frequently as a test gas in cluster beam experiments. Figure 11 shows data of other authors on mean size of the Ar clusters depending on the scaling parameter of Hagena Г*. For Ar from Eq. (4) parameters s = 0.25, i = 2.5, k = 1650 [10] and q = 0.85 [7], which finally lead to well-known equation:

Fig. 11
figure 11

Mean cluster size N for Ar versus Hagena’s parameter Г*. Compare with experimental results from other authors

Full size image
$$\varGamma^{*} = 1650(P_{0} /mbar)(d_{eq} /\mu m)^{0.85} (T_{0} /K)^{ - 2.29} .$$
(17)

These results are obtained by different experimental methods: by retarding potential method [13], by time-of-flight mass spectrometer [16], by cross beam scattering [14], by electron diffraction [25, 26], by scattering on buffer gas [30,31,32], by Rayleigh scattering [15, 19]. In the experiments both conical nozzles with different geometrical parameters (solid symbols) and sonic nozzles (blank symbols) were used. The lines denote dependencies obtained by known empirical equations, which had been recommended by O. Hagena [7]:

$$N = 33\left( {\frac{\varGamma ^{*}}{1000}} \right)^{2.35} \quad for\,\varGamma ^{*} > 1000,$$
(18)

and U. Buck [14]:

$$N = 38.4\left( {\frac{\varGamma ^{*}}{1000}} \right)^{1.64} \quad for \, 350 \le \varGamma ^{*} \le 1800\,{\text{and }}N = \exp (a_{0} + a_{1} (\ln \varGamma ^{*})^{0,8} ),\, \, for\,\varGamma ^{*} > 1800,$$
(19)

where a 0 = −12.83 and a 1 = 3.51. It can be noted that for fixed values of parameter Г* there is a considerable discrepancy between experimental results obtained not only by various methods, but the same technique by different authors. These disagreements can be explained by several factors: by errors of various methods of measurement, by significant differences in the geometry of nozzles used, by the early mentioned incomplete consideration of geometrical parameters of conical nozzles in the scaling parameter Г*. Results of measurements of the mean size of Ar clusters obtained with different nozzles in our experiment are also shown in Fig. 11. It can be seen that the obtained mean sizes of clusters are in general in satisfactory agreement with the results obtained by other experimental methods and estimations by the empirical dependencies.

Earlier [13] for generalization of experimental data for CO2 it has been proposed parameter q = 0.6. In [9] taking into account the thermodynamic parameters of the gas (the density of the solid at the expected cluster temperature and the sublimation enthalpy per atom at 0 K) for scaling parameter Г* it has been proposed gas-specific constant k = 5.58 × 105. But authors consider molecule CO2 as a system having 5 thermally active degrees of freedom only. It was therefore proposed s = 0.75 and in result Г* ~ (T 0)−3.05. Because at a room-level temperature some of the vibration degrees of freedom are also accessible, more correct to used the ratio of specific heats γ = 1.3 [48]. So from Eq. (4) s = 1.67, i = 4.33, and in finally for generalization of CO2 experimental data we recommend the next fitted equation:

$$\varGamma ^{*} = 2.3*10^{7} (P_{0} /mbar)(d_{eq} /\mu m)^{0.6} (T_{0} /K)^{ - 3.63} .$$
(20)

Figure 12 shows the obtained mean cluster sizes for CO2 depending on the Г* parameter for two nozzles. The same figure also shows results by other authors, measured by different methods: by retarding potential method [13], by Rayleigh and Raman scattering [34], by electron diffraction [26, 49], by photoelectron spectroscopy using synchrotron radiation (XPS) [9]. The solid line is denoting dependency from Eq. (18). It can be seen that by using Eq. (20) the experimental data of different authors and our results are generalized well not only among themselves but also with the data for Ar. It should be noted that the use of constants from [9] does not allow generalizing the data for different gases.

Fig. 12
figure 12

Mean cluster size N for CO2 versus Hagena’s parameter Г*. Compare with experimental results from other authors

Full size image

Conclusions

The experimental method for determination of the mean size of gas clusters based on measurement of the transverse intensity profile of cluster beam and comparing of the broadening of the cluster and the monomer components of the beam at a fixed distance behind the skimmer is described. Since the supersonic jet provides a high intensity of the cluster beam, this method does not require usage of complex and highly sensitive equipment. It can be used to determine the mean size of the clusters formed in free jets of any pure gases without the creation of special models or determination of additional empirical constants. The described method allows determining the sizes of small and medium clusters (N ~ 50–2000 molecule per clusters). The minimum size of clusters that can be determined by this method is governed by the equality of the intensities of the cluster and the monomer components in the transition of the flow into the mass condensation mode (Г* ≥ 1500). To determine the size of large clusters it is necessary to perform measurements on a large path length. Additionally, it is necessary to provide the flight of the beam particles from the skimmer to the sensor without their scattering on a background gas.

It is shown that the described method provides correct results for the formation of the cluster beam without any influence of the background gas in the expansion chamber, in the silent zone. The interaction of the cluster beam with the barrel shockwaves leads to a distortion of recorded intensity profile: slowdown of monomers and decrease of the cluster sizes as a result of their evaporation.

Possibilities of the method and reliability of its results were verified in the study of cluster formation in free jets of Ar, CO2, N2 and C2H4 expanding from different conical nozzles. The measured values of total intensity on the beam axis I total and speed relationship of monomers S ⊥mono were compared with the calculated (predicted) values obtained by the numerical simulation of the flow in free jets of Ar, CO2 and N2. The comparison showed good agreement of experimental results and calculated data. The average sizes of clusters determined by this method are in the range of from 70 to 1500 molecules per cluster for CO2, from 60 to 1000 molecules per cluster for Ar, from 70 to 1100 molecules per cluster for C2H4. The average sizes of clusters measured in the jets of Ar and CO2 are generalized according to the scaling parameter Г* and compared with the results obtained by other authors using different experimental methods, and estimations of the known empirical dependencies. Such comparison showed satisfactory agreement.