1 Introduction

Artificial neuron models can be helpful to explore working mechanism for biological neurons by taming the firing patterns and discovering its energy characteristic. The improved and proposed neuron models by applying mathematical and physical theories, which have potential practical implications for understanding brain working patterns and constructing brain-like networks. In 1952, Hodgkin and Huxley [1] proposed the first Hodgkin-Huxley (HH) neuron model by capturing and analyzing the experimental data about membrane potential series from squid axon. Neural networks consisting of HH neurons have been used to clarify the mechanisms of neural diseases [2, 3] and the stability of collective behaviors in networks [4, 5]. The setting of complex parameters of HH neurons is not conducive to the study of a single aspect of the electrical activity of neurons. In 1961, FitzHugh [6] designed a simple FitzHugh-Nagumo (FHN) model based on biological features for HH model, the FHN model composes two ordinary differential equations, and a variety of firing patterns can be induced by adjusting the amplitude or frequency of external periodic stimulus. In 1984, Hindmarsh and Rose [7] obtained the 3D Hindmarsh-Rose (HR) neuron model by voltage clamp experiments in snail nerve cells. The HR model neglects ion channel effects and is able to mimic the irregular firing behavior produced by mollusk neurons. Subsequently, many different types of neuron models have been proposed. For example, the Morris-Lecar neuron model [8,9,10], the Chay neuron model [11, 12], the memristive HR model [13], and the memristive FHN model [14].

For the these neuron models, due to the simple structure of the FHN model, the equivalent circuit is easy to achieve, and the rich firing behaviors and other characteristics can be explored by changing the external stimulus. Functional neuron models have been obtained by introducing different electronic components with special functions into simple FHN neural circuits. For instance, in Refs. [15, 16], a photosensitive neuron model is proposed by connecting a photocell into different branches of a simple neural circuit. An auditory neuron model [17] is proposed by connecting a neural circuit to a piezoelectric ceramic into. Xu et al. [18] designed a thermosensitive neuron by applying a thermistor to replace resistor of different branches in the FHN neural circuit. In Ref. [19], an ideal Josephson junction and a magnetic flux-affected memristor are in parallel connected into a FHN neural circuit for estimating the effect of external magnetic field. Yang et al. [20] developed a physical neuron for estimating electric field disturbance by connecting a charge-relative memeristor into a simple circuit. An improved photosensitive memristive neural circuit [21] is introduced by in parallel connecting a memristor into photosensitive neural circuit.

Neurons can be excited to show a rich dynamic behavior, such as resting state, spiking firing, bursting firing, chaotic firing and mixed firing. For memristive neurons, appearance of multistability supports coexistence of multiple firing patterns. The process of electrical activity requires a supply of energy. The Hamilton energy function for a neuron in oscillator form can be obtained by applying the Helmholtz’s theorem [22], and the energy function can also be mapped from the field energy for its equivalent neural circuit. In Refs. [23, 24], the energy correlation with firing modes of neuron model was discussed. Energy feedback control of dynamic for neuron model is investigated in Refs. [25,26,27]. Energy for a memristor coupled neurons model is calculated in Ref. [28]. For two or more neurons, energy propagation and exchange target to possible energy balance, so that the coupled neurons can be tamed in synchronous firing patterns. For example, energy balance [29,30,31,32,33] between neurons and energy balance in the neural networks [34] are explored. According to in Ref. [35], the exact Hamilton energy function is the most suitable Lyapunov function for this system. For further guidance, approach of Hamilton energy functions for some chaotic systems are presented in Refs. [36,37,38]. Energy flow is used to control the growth of synaptic [39] and synchronization between neurons [40, 41], in this way, adaptive regulation mechanism in parameter and energy shift for neurons are clarified. The recent work in Ref. [42] claimed that four main firing modes in the Hindmarsh-Rose neuron are relative to four energy levels approached by calculating the average energy under different firing modes. Mathematical neuron models seldom provide exact energy functions rather than generic Lyapunov functions. When specific electric components are used to connect nonlinear circuits for developing potential neural circuits [43,44,45,46], and the field energy kept in capacitor, inductor and memristors can be classified as capacitive and inductive forms. Ideal Josephson junction can discern external magnetic field but it seldom saves energy at all. Based on these memristive neurons, diverse electromagneitc induction [47,48,49,50,51], uniform and non-uniform electromagnetic radaition [52,53,54,55] can be discerned by measuring the pattern stability and wave propagation in the memristive networks. Furthermore, field coupling between memristive neurons throws light on knowing self-organization of neural networks without synaptic connections [56,57,58,59]. For a neural network, heterogeneity [60] can be formed by accumulating energy for finite neurons, and defect area [61] is obtained when reduction energy of finite neurons in the network.

The shape deformation of neurons is irregular due to their flexible structures and energy absorption from external stimuli. It is interesting to investigate energy diffusion phenomenon when the shape deformation of neuron occurs under noise disturbance and non-uniform stimuli. When energy function is available, energy distribution and energy balance between neurons present some clues to explore the wave propagation and self-organization in the functional neural network clustered with functional neurons. In this work, a regular network composed of temperature-light sensitive neurons is designed, energy function is defined and adaptive law is presented to control parameter shift for keeping local energy balance, which supports emergence of gradient energy distribution for emitting wave fronts. This study presents some guidance for exploring and understanding the transition of collective behaviors in a neural network controlled by energy flow.

2 Model and scheme

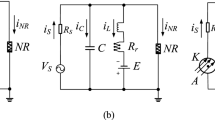
A temperature-light sensitive neural circuit is designed by connecting a phototube and a thermistor in a simple nonlinear circuit. This neuron can perceive external light and changes of temperature, and its the relation between electric components is displayed in Fig. 1.

Fig. 1
figure 1

Schematic diagram for a thermal neural circuit driven by photocurrent. A and K denote the anode and cathode of the phototube. RT is thermistor, R and RN are linear and nonlinear resistors, E, L and C represent constant voltage source, induction coil and capacitor, respectively

Full size image

According to the Kirchhoff's law, the circuit variables for Fig. 1 can be controlled under the criterion

$$\left\{ \begin{gathered} C\frac{dV}{{dt}} = \frac{{V_{s} - V}}{{R_{T} }} - i_{L} - i_{N} ; \hfill \\ L\frac{{di_{L} }}{dt} = V - Ri_{L} + E; \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(1)

where the current through the nonlinear resistor RN in Fig. 1 can be estimated by

$$i_{N} = - \frac{1}{\rho }(V - \frac{1}{3}\frac{{V^{3} }}{{V_{0}^{2} }});{\kern 1pt} {\kern 1pt}$$
(2)

where ρ and V0 represent the normalized parameters, and the variant voltage Vs for the phototube is considered with periodic form

$$V_{s} = B_{0} + A_{0} \cos (f_{0} t);{\kern 1pt} {\kern 1pt}$$
(3)

where B0 is a constant and A0 and f0 represent the amplitude and angular frequency of the periodic voltage source. The resistance across thermistor can be estimated by

$$R_{T} = R_{\infty } e^{{\frac{{B^{\prime}}}{T}}} ,B^{\prime} = \frac{q}{K};{\kern 1pt}$$
(4)

where q is the activation energy, T denotes the temperature, K represents the Boltzmann constant, and R∞ is a constant corresponding to the thermistor resistivity at an infinitely high temperature T (T→∞). The physical parameters and variables for Eqs. (1– 4) are replaced with dimensionless forms as follows

$$\left\{ \begin{array}{l} x = \frac{V}{{V_{0} }},y = \frac{{\rho i_{L} }}{{V_{0} }},\tau = \frac{t}{\rho C},a = \frac{E}{{V_{0} }},b = \frac{R}{\rho },c = \frac{{\rho^{2} C}}{L},f = \rho Cf_{0} ; \hfill \\ T^{\prime} = \frac{T}{{T_{0} }},\xi (T^{\prime}) = \frac{\rho }{{R_{T} }} = \xi e^{{ - \frac{1}{{T^{\prime}}}}} ,B(T^{\prime}) = \frac{{\rho B_{0} }}{{R_{T} V_{0} }} = Be^{{ - \frac{1}{{T^{\prime}}}}} ,A(T^{\prime}) = \frac{{\rho A_{0} }}{{R_{T} V_{0} }} = Ae^{{ - \frac{1}{{T^{\prime}}}}} ; \hfill \\ \end{array} \right.{\kern 1pt} {\kern 1pt}$$
(5)

where T0 is the reference temperature and it is selected a value as the material constant B′ (=q/K). Therefore, the neuron model controlled by photocurrent and temperature can be described by

$$\left\{ \begin{array}{l} \frac{dx}{{d\tau }} = x(1 - \xi (T^{\prime})) - \frac{1}{3}x^{3} - y + B(T^{\prime}) + A(T^{\prime})\cos (f\tau ); \hfill \\ \frac{dy}{{d\tau }} = c(x - by + a); \hfill \\ \end{array} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt}$$
(6)

Furthermore, the physical field energy in the neural circuit in Fig. 1 is calculated by

$$W = \frac{1}{2}CV^{2} + \frac{1}{2}Li_{L}^{2} ;$$
(7)

By applying the scale transformation in Eq. (5), the dimensionless Hamilton energy function is mapped from Eq.(7), it presents

$$H = \frac{W}{{CV_{0}^{2} }} = \frac{1}{2}x^{2} + \frac{1}{2c}y^{2} ;$$
(8)

From Eq. (8), the Hamilton energy function of an isolated neuron mainly depends on the variables (x, y) and parameters c. To theoretically approach of the Hamilton energy function for the neuron, the Helmholtz’s theorem requires a vector form for the neuron models in Eq. (6) as follows

$$\begin{aligned}\left(\frac{\displaystyle\frac{dx}{d\tau}}{\displaystyle\frac{dy}{d\tau}}\right)&=\begin{pmatrix}x(1-\xi(T))-\frac13x^3-y+B(T)+A(T)\;\cos\;(f\tau)\\c(x\;+\;a\;-\;by)\end{pmatrix}=F_c+F_d\\&=\begin{pmatrix}-\;y\\cx\end{pmatrix}+\begin{pmatrix}x(1-\xi(T^{\prime}))-\frac{1}{3}x^3+B(T^{\prime})+A(T^{\prime})\cos(f\tau)\\c(a\;-\;by)\end{pmatrix}\\&=\begin{pmatrix}0&-c\\c&0\end{pmatrix}\begin{pmatrix}x\\\frac {y}{c}\end{pmatrix}+\begin{pmatrix}(1-\xi(T^{\prime}))-\frac{1}{3}x^2+\frac{B(T^{\prime})+A(T^{\prime})\cos(f\tau)}x\;&0\\0&c^2(\frac {a}{y}-b)\end{pmatrix}\begin{pmatrix}x\\\frac {y}{c}\end{pmatrix};\end{aligned}$$
(9)

The Helmholtz theorem defines that the Hamilton energy function H meets the following criterion

$$\nabla H^{{\text{T}}} F_{c} = 0\;;\nabla H^{{\text{T}}} F_{d} = \dot{H} = \frac{dH}{{d\tau }};$$
(10)

A sole Hamilton energy function can be exact solution for formula as follows

$$0 = \nabla H^{{\text{T}}} F_{c} = ( - y)\frac{\partial H}{{\partial x}} + cx\frac{\partial H}{{\partial y}};$$
(11)

The superscript T indicates transpose operation of matrices for the gradient energy. As a result, a solution for Eq.(11) can be obtained to match the Hamilton energy function presented in Eq. (8).

When the neurons are activated by applying with different external stimuli, energy diversity between neurons can be generate. The connected channels will open and transmit energy for keeping energy balance. In presence of resistive coupling between these neurons, a regular network on a square array can be described by

$$\left\{ \begin{array}{l} \frac{{dx_{ij} }}{d\tau } = x_{ij} (1 - \xi (T^{\prime})) - \frac{1}{3}x_{ij}^{3} - y_{ij} + B(T^{\prime}) + A(T^{\prime})\cos (f\tau ) + G_{ij} ; \hfill \\ \frac{{dy_{ij} }}{d\tau } = c(x_{ij} - by_{ij} + a)\;; \hfill \\ G_{ij} = k(x_{i + 1,j} + x_{i - 1,j} + x_{i,j + 1} + x_{i,j - 1} - 4x_{ij} )\;; \hfill \\ \end{array} \right.{\kern 1pt}$$
(12)

where the subscripts (i, j) mean the node position and Gij denotes adjacent regulation on the node (i, j) in the regular network, k is the coupling intensity for electric synaptic connection. For an isotropic network, all nodes have the same parameters setting, while a gradient distribution of temperature may induce spatial diversity and homogeneity in the network.

3 Results and discussion

In this section, the numerical solutions for a single functional neuron and coupled neurons regular network are obtained on the MATLAB platform by applying the fourth-order Runge-Kutta algorithm with time step h=0.01. The bifurcation diagrams for the single neuron by changing one parameter are shown in Fig. 2.

Fig. 2
figure 2

Bifurcation diagram for a neuron with different parameters setting. For a ξ=0.175, B=0.6, A=0.9; b T′=5.5, B=0.6, A=0.9; c T′=5.5, ξ=0.175, A=0.9; d ξ=0.175, T′=5.5, B=0.6. Other parameters are chosen as a=0.7, b=0.8, c=0.1, f=1, and initial value is set as (0.1, 0.3). xpeak denotes peak values of membrane potential x

Full size image

The results in Fig. 2 show that photocurrent can excite the neuron to show periodic and chaotic firing patterns by adjusting parameter values including forcing signal and temperature. Furthermore, Fig. 3 plotted the largest Lyapunov exponent (LLE) with different parameters.

Fig. 3
figure 3

Distribution of LLE for a neuron with different parameters. For a ξ=0.175, B=0.6, A=0.9; b T′=5.5, B=0.6, A=0.9; c T′=5.5, ξ=0.175, A=0.9; d ξ=0.175, T′=5.5, B=0.6. Other parameters are fixed at a=0.7, b=0.8, c=0.1, f=1, and initial value is set as (0.1, 0.3)

Full size image

From Fig. 3, LLE greater than zero means occurrence of chaotic state, while LLE less than zero predicts appearance of periodic patterns. In fact, bursting and spiking firing patterns are periodic modes, furthermore, the sampled time series for membrane potential and Hamilton energy by changing frequency f are shown in Fig. 4.

Fig. 4
figure 4

Evolution of membrane potential and Hamilton energy with different angular frequencies f. For a f=0.02; b f=0.2; c f=0.7079. Setting parameters a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, T′=5.5, A=0.9, and initial value is set as (0.1, 0.3). <H> denotes the average value of Hamilton energy

Full size image

Fig. 4 illustrates that the neuron occurs three kinds of firing modes by adjusting the frequency, and the neuron has higher mean value of Hamilton energy with bursting and spiking firing patterns, while it has lower mean value of Hamilton energy with chaotic modes. To investigate collective dynamical behaviors for neural networks presented in Eq. (12), the firing patterns in networks under different coupling intensities k are calculated, the results are displayed in Fig. 5 for the network composed of 120*120 neurons by applying no-flux boundary condition. For simplicity, all nodes start from the random values within 0~1.

Fig. 5
figure 5

Developed patterns in the network at 1000 time units. For a k=0.08; b k=0.085; c k=0.088; d k=0.09. Parameters fixed at a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, T′=1.53, f=1, A=0.1, and initial values are selected as random within (0, 1). Snapshots are plotted in color scale

Full size image

From Fig. 5, it is demonstrated that spiral wave segments can coexist with target wave in local area of the network during adjusting coupling intensity. With the further increase of coupling intensity, the target waves will be broken to develop a spiral wave close to the border of the network. The energy diffusion and energy distribution in the network with different coupling intensities k are shown in Fig. 6.

Fig. 6
figure 6

Distribution of energy values in the network at 1000 time units. For a k=0.08; b k=0.085; c k=0.088; d k=0.09. Setting a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, T′=1.53, f=1, A=0.1, and initial values are selected as random within (0, 1). Snapshots are plotted in color scale

Full size image

Similar to results in Fig. 5, random diffusion of energy will form the coexistence of target waves and spiral waves, when the coupling intensity continues to increase, the coexistence of travelling waves will evolve into a single spiral wave. To dicern the collective behaviors response of neural network under noisy excitation, the dynamic equations of the coupled functional neural network are expressed by

$$\left\{\begin{array}{l}\begin{aligned}\frac{dx_{ij}}{d\tau}&=x_{ij}(1-\xi(T^{\prime}))-\frac13x_{ij}^3-y_{ij}+B(T^{\prime})+A(T^{\prime})\cos(f\tau)\\&+k(x_{i+1,j}+x_{i-1,j}+x_{i,j+1}+x_{i,j-1}-4x_{ij});\end{aligned}\\\frac{dy_{ij}}{d\tau}=c(x_{ij}-by_{ij}+a)+\zeta(\tau);\end{array}\right.$$
(13)

where ζ(τ) denotes the Gaussian white noise with zero average. The statistical relation is <ζ(τ)>=0, <ζ(τ)ζ(τ′)>=2Dδ(τ-τ′), here D means noise intensity and D=exp(−1/T′) accounts for temperature-dependent noisy disturbance. The noise is imposed on the network in two ways. When noisy disturbance is applied on different regions, the energy injection from external stimuli breaks the energy balance and induces parameter diversity in the network. In the first case, the noise is applied on the center of the network, and the size of the region is selected as N/2−10≤i, j≤N/2−10. In the second case, the noise is added on the boundary region of the network, and the size of the region is fixed as 1≤i≤10, 1≤j≤N. Firstly, the case that noise is imposed on the center of the network is investigated. The firing patterns in networks in presence of different noise intensities are displayed in Fig. 7.

Fig. 7
figure 7

Developed patterns in the network under noise at 3000 time units. For a T′=3; b T′=4; c T′=5; d T′=6. Setting a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, and initial values are selected as random within (0, 1). Snapshots are plotted in color scale

Full size image

It is confirmed that the stable and perfect target wave can be formed in the network with the decrease of noise intensity D (temperatures T′ increase). Indeed, noise is applied on the center area, which captures external energy for further spatial diffusion, and wave can be propagated in the network. Furthermore, the energy propagation in the network is analyzed by changing noise intensity carefully, and the energy patterns are plotted in Fig. 8 for showing the energy distribution under synaptic coupling.

Fig. 8
figure 8

Energy propagation in neural network under noise at 3000 time units. For a T′=3; b T′=4; c T′=5; d T′=6. Parameters are chosen as a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, and initial values are selected as random within (0, 1). Snapshots are plotted in color scale

Full size image

The results in Fig. 8 show that energy diffusion in the network formed stable and perfect target waves by applying noise on center region of network. It is interesting to investigate the case when the noise is added on the boundary region of the network, and the firing patterns of the network by adjusting noise intensity are displayed in Fig. 9.

Fig. 9
figure 9

Developed patterns in the network under noise at 3000 time units. For a T′=1.3; b T′=1.6; c T′=1.8; d T′=2.1. Parameters are chosen as a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, and initial values are selected as random within (0, 1). Snapshots are plotted in color scale.

Full size image

It is demonstrated from Fig. 9 that the modes in the network are transferred from a heterogeneity state to a stable traveling wave when noisy excitation is applied on the boundary region of the network. This result indicates that noisy excitation on the boundary of the network can be effective to induce similar plane wave with further increasing the temperature in the network. Fig. 10 show that energy propagation in the network during the wave propagation. It is found that the profile of energy levels has similar distribution of the membrane potential, that is, firing patterns are relative to the energy level in close way.

Fig. 10
figure 10

Energy propagation with noise intensity at 3000 time units. For a T′=1.3; b T′=1.6; c T′=1.8; d T′=2.1. Parameters are chosen as a=0.7, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, and initials are selected as random values within (0, 1)

Full size image

Similar to the results in Fig. 9, the stable traveling wave can be formed by applying noise on the boundary region of the network. Based on the adaptive property of biological neurons, a neural network with energy diversity controls parameter shifts is described as follows

$$\left\{\begin{array}{l} \begin{aligned}\frac{{dx_{ij} }}{d\tau } &= x_{ij} (1 - \xi (T^{\prime})) - \frac{1}{3}x_{ij}^{3} - y_{ij} + B(T^{\prime}) + A(T^{\prime})\cos (f\tau )\\&+ k(x_{i + 1,j} + x_{i - 1,j} + x_{i,j + 1} + x_{i,j - 1} - 4x_{ij} ); \end{aligned}\\\frac{{dy_{ij} }}{d\tau } = c(x_{ij} - by_{ij} + a_{ij} );\\\frac{{da_{ij} }}{d\tau } = g \cdot a_{ij} \cdot \theta (\Delta H_{ij} - \varepsilon ),m_{1} \le i \le n_{1} ,m_{2} \le j \le n_{2} ;\\\Delta H_{i} = \left| {4H_{ij} - H_{i + 1,j} - H_{i - 1,j} - H_{i,j + 1} - H_{i,j - 1} } \right|.{\kern 1pt}\end{array}\right.$$
(14)

where the superscripts and subscripts (i, j) mean the node position in the regular network, m and n represent the heterogeneity size or defect size. g denotes the gain for adjusting the internal parameter a. As presented in Eq. (6), the neuron model has several adjustable parameters including (a, b, c) and two parameters (A, B) are relative to temperature. The parameter a in Eqs. (6) and (14) accounts for the reverse voltage of the neural circuit and resting potential of one ion channel. In presence of energy diversity or external energy injection for electric stimuli, the excitable media suffers from depolarization and thus the reverse potential of ion channels can be switched. Therefore, Eq. (14) describes the adaptive growth of parameter a under energy flow. For extensive studies, readers can explore similar case for mode transition, pattern formation and energy shift when other adjustable intrinsic parameters (b, c) are regulated in similar adaptive law. The Heaviside function θ(*) is used to control the growth of parameter a. For finite neurons, higher energies occur in heterogeneous regions, while lower energies occur in defect regions. When m1=m2=N/2−10, n1=n2=N/2+10, the parameter a in the center of the network is increased from 0.1, and the parameter a for other areas remains 0.7. In this case, firing patterns in the network are shown in Fig. 11.

Fig. 11
figure 11

Developed patterns in the network. For a 1600 time units; b 2000 time units; c 2500 time units; d 3000 time units. Parameters are chosen as T′=1.53, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, ε=0.00001, g=0.001, and initial value for each node is set as random (0, 1)

Full size image

From Fig. 11, continuous target waves can be induced by applying the possible shift in the center of the network presenting in chaotic and/or periodic states. Heterogeneous regions will form target waves in the network within finite transient period. In this case, energy diffussion in the network is shown in Fig. 12.

Fig. 12
figure 12

Energy propagation with. For a 1600 time units; b 2000 time units; c 2500 time units; d 3000 time units. Parameters are chosen as T′=1.53, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, ε=0.00001, g=0.001, and initial value for each node is set as random (0, 1)

Full size image

It is confirmed that the propagation of target wave in the network is supported by energy diversity formed from center of the network. Furthermore, m1= m2=1, n1=10, n2=N, the parameter a on the boundary region of the network is increased from 0.1, and the parameter a for other areas remains 0.7. The firing patterns in the network in this case are shown in Fig. 13.

Fig. 13
figure 13

Developed patterns in the network. For a 1600 time units; b 2000 time units; c 2500 time units; d 3000 time unites. Parameters are chosen as T′=1.6, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, ε=0.00001, g=0.001, and initials are selected as random value within (0, 1)

Full size image

Similar to the case of the noise is applied on the boundary region of the network, stable and perfect traveling waves can be formed. The coexistence of traveling wave and spiral wave is formed within finite periods. The energy propagation in the network is shown in Fig. 14.

Fig. 14
figure 14

Energy propagation with. For a 1600 time unites; b 2000 time units; c 2500 time units; d 3000 time units. Parameters are chosen as T′=1.6, b=0.8, c=0.1, ξ=0.175, B=0.6, k=0.08, f=1, A=0.1, ε=0.00001, g=0.001, and initial value is set as random (0, 1)

Full size image

The results in Fig. 14 show that energy diversity exists on the boundary of the network, and parameter shift is induced to regulate energy diversity for reaching local energy balance and synchronization. The distribution of energy values is similar to the profile of membrane potential patterns because the firing patterns are relative to the energy levels of the neurons.

In a summary, connection of phototube and thermistor makes the photocurrent become dependent on the temperature. As a result, any changes of temperature will modify the excitability and mode selection is controlled completely. As a result, energy level is switched during the changes of temperature in a single neuron. When more neurons are clustered, synaptic coupling is helpful to decrease energy diversity and energy balance supports complete synchronization for developing homogeneous states in the network. Local noisy disturbance injects energy and breaks energy balance for developing wave fronts, which can diffuse the energy in the network. For fast approach of energy balance, one intrinsic controllable parameter shows adaptive growth under energy diversity until they reach stable energy balance and the growing parameter will keep a saturation value, which supports stable wave propagation and regular spatial patterns in the neural network.

4 Open problem

As is known, thermistors are divided into two types considering the its negative or positive signs for dR/dT. For negative temperature coefficient thermistor (NTCT) dR/dT<0 and its resistance is decreased by increasing the temperature. A positive temperature coefficient thermistor (PTCT) requires dR/dT>0, and the resistance is increased with temperature. When the thermistor in Fig. 1 is considered as a PTCT, the neural circuit described in Fig. 1 is the same as in Eq.(1). The channel current along RN in Fig. 1 can be estimated by Eq. (2) or other forms, and the time-varying voltage Vs across the phototube is considered as Eq. (3). The resistance across PTCT can be estimated by

$$R_{T} = R_{\infty } \exp ( - \frac{{B^{\prime}}}{T}),B^{\prime} = \frac{q}{K};{\kern 1pt}$$
(15)

R∞ measures the maximal resistance for the PTCT at T→0. Similar scale transformation for the physical variables and intrinsic parameters are updated with a group of dimensionless variables as follows

$$\left\{ \begin{gathered} x = \frac{V}{{V_{0} }},y = \frac{{\rho i_{L} }}{{V_{0} }},\tau = \frac{t}{\rho C},a = \frac{E}{{V_{0} }},b = \frac{R}{\rho },c = \frac{{\rho^{2} C}}{L},\xi (T^{\prime}) = \frac{\rho }{{R_{T} }} = \xi e^{{\frac{1}{{T^{\prime}}}}} ; \hfill \\ B(T^{\prime}) = \frac{{\rho B_{0} }}{{R_{T} V_{0} }} = Be^{{\frac{1}{{T^{\prime}}}}} ,f = \rho Cf_{0} ,A(T^{\prime}) = \frac{{\rho A_{0} }}{{R_{T} V_{0} }} = Ae^{{\frac{1}{{T^{\prime}}}}} ,T^{\prime} = \frac{T}{{T_{0} }}. \hfill \\ \end{gathered} \right.{\kern 1pt}$$
(16)

As a result, temperature-light sensitive neuron model can be updated as follows

$$\left\{ \begin{array}{l} \frac{dx}{{d\tau }} = x(1 - \xi (T^{\prime})) - \frac{1}{3}x^{3} - y + B(T^{\prime}) + A(T^{\prime})\cos (f\tau ); \hfill \\ \frac{dy}{{d\tau }} = c(x - by + a). \hfill \\ \end{array} \right.{\kern 1pt}$$
(17)

The field energy is mainly kept in two energy storage components including the capacitor and induction coil, the two kinds of neural circuits (and the equivalent neuron models) have the same energy function even the temperature changes have different impact on the mode transition and energy propagation in the neurons. This neuron model can be further used to explore the collective patterns and energy distribution in neural networks with gradient temperature distribution. Furthermore, memristive terms can also be introduced into Eq.(17), and the energy is shunted and shared in the memristive channel besides the capacitive and inductive components. When the functional neural network is excited by spatial stimuli, for example, gradient distribution in the illumination and temperature, all the neurons become non-identical, the self-organization and emergence of regularity in the networks can give possible clues to understand the regulation role of energy flow in the network. Besides the functional electric component as thermistor and piezoelectric ceramic, memristor is considered as important candidate for intelligent computation in AI design and adaptive control [62].

5 Conclusion

In this work, a temperature-light sensitive neuron is obtained by connecting a phototube and a thermistor into a simple capacitive-inductive circuit coupled with a nonlinear resistor. A regular network on square array is built to discern energy distribution during pattern formation and wave propagation under synaptic coupling. The heterogeneity and defect created accompanying with shift of the parameter a in a few neurons when noisy excitation is applied on local area of the network. Energy diffusion for center area and boundary area in the network are investigated, respectively. The result indicates that the energy diversity of different regions of the network will form stable and perfect target and traveling waves. Adaptive growth of one or more intrinsic parameters are helpful for decreasing energy diversity, and stable energy balance in the network is effective to induce continuous wave fronts and regular patterns can be developed in the network. As a result, external signals can be perceived and then signals are propagated in the network in effective way.