Effect of Joule heating and entropy generation on multi-slip condition of peristaltic flow of Casson nanofluid in an asymmetric channel

Abstract

In the present investigation, the effect of multi-slip condition on peristaltic flow through asymmetric channel with Joule heating effect is considered. We also considered the incompressible non-Newtonian Casson nanofluid model for blood, which is electrically conducting. Second law of thermodynamics is used to examine the entropy generation. Multi-slip condition is used at the boundary of the wall and the analysis is also restricted under the low Reynolds number and long wavelength assumption. The governing equations were transformed into a non-dimensional form by using suitable terms. The reduced non-dimensional highly nonlinear partial differential equations are solved by using the Homotopy Perturbation Sumudu transformation method (HPSTM). The influence of different physical parameters on dimensionless velocity, pressure gradient, temperature, concentration and nanoparticle is graphically presented. From the results, one can understand that the Joule heating effect controls the heat transfer in the system and as the magnetic parameter is increased, there will be decay in the velocity of fluid. The outcomes of the present investigation can be applicable in examining the chyme motion in the gastrointestinal tract and controlling the blood flow during surgery. Present study shows an excellent agreement with the previously available studies in the limiting case. 

1 Introduction

A continuous wave of contraction or expansion flowing through the channel or tube causes peristalsis. Pumping mechanism of peristalsis is involved in several biological organs in physiology and the mechanism of peristaltic transport has been exploited for industrial applications also. The phenomenon of peristaltic pumping was first initiated by Latham [1] in 1966. Shapiro et al. [2] and Jaffrin et al. [3] continued the research work on peristaltic flow. Makinde et al. [4] studied the effect of MHD peristaltic slip flow of Casson fluid and heat transfer in channel filled with a porous medium. Hayat et al. [5] examined simultaneous effects of slip and heat transfer on peristaltic flow. The effect of magnetic field in peristaltic transport of blood flow for couple stress and Eyring-Powell fluid model in a non-uniform channel using homotopy analysis method is studied by Asha et al. [6,7,8].

The entropy analysis is a method of determining the thermodynamic irreversibility of a flow stream. The quality of energy declines when entropy formation occurs. As a result, lowering the entropy generation can increase the systems performance. Entropy generation concept was first presented by Bejan [9]. Much energy-related equipment, such as modern refrigerating machines, electrical power generating machines from geothermal energy and surface heat, are subject to entropy formation. Irreversibility in system through different geometries is examined by many researchers. Rashidi et al. [10] studied the entropy generation analysis on the Magnetohydrodynamic blood flow in peristaltic wave motion. Furthermore, the work is extended by Asha et al. [11]. They investigated the effects of entropy analysis with nonlinear thermal radiation for magneto-micropolar fluid in a tapered channel. Whenever strong magnetic field is applied, Joule heating effect cannot be avoided. In most of the medical therapies, Joule heating controls the blood flow and reduces the body pain. Asha et al. [12] studied the effect of Joule heating with MHD in peristaltic blood flow. Study of entropy generation and Joule heating effects were helpful to design the thermofluidic micropumps for the purpose of diagnosis that was investigated by Ranjit et al. [13].

All the above investigations are carried out in the no-slip boundary conditions. In most of the situations, no-slip boundary conditions are inadequate. Specifically, non-Newtonian nanofluids show wall slip due to velocity and contraction. Fluids with slip boundary conditions find application in polymer technology such as internal cavities and polishing of heart valves. Navier [14] was the first to discuss the slip boundary condition, where at the boundary, the velocity is proportional to the shear stress. Investigation of slip effects on peristalsis was studied by Hayat et al. [15], Srinivas et al. [16] and Akbar et al. [17]. A pumping mechanism of peristalsis with multi-slip boundary constraints is so important that the authors were encouraged to look into the effect of multi-slip and Joule heating on the peristalsis mechanism of Casson nanofluid in an asymmetric channel. In the past few years, it is observed that the interest of using and developing the numerical and analytical techniques are increased. Such methods can help to overcome the non-linearity and complexity that appear in the non-Newtonian fluids. Mathematical model on peristaltic flow with non-Newtonian fluid requires highly non-linear partial differential equations. To obtain the exact solutions for such problems is difficult. In the present paper, we have used the Homotopy perturbation Sumudu transformation method (HPSTM) which is a combination of Homotopy perturbation method and Sumudu transformation method (STM). Weerakoon [18] investigated the application of Sumudu transform method by solving the linear partial differential equations, whereas Belagacem [19] and his team solved the integral equations using STM. Furthermore, investigator [20, 21] used STM for solving differential equations and they compare the obtained results with existing results. From previous investigation, it is observed that no work has been done using the HPSTM for solving non-linear PDE with boundary conditions. Thus, the present article shows the application of HPSTM for solving the PDE and compare the obtained results with existing results. Embedded parameters on velocity, pressure gradient, energy and nanoparticle concentration are shown graphically.

2 Mathematical analysis

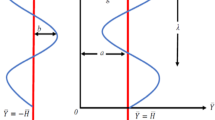
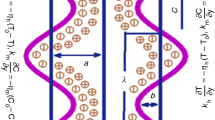
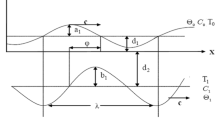
The propagation of peristaltic waves on the walls of a two-dimensional asymmetric channel of width $d_{1} + d_{2}$ have been considered and shown in Scheme 1. The variation in channel width as well as the amplitude and phase of the waves causes asymmetry in the channel. Casson nanofluid is placed into the channel. Due to propagation of the peristaltic, waves flow is generated. Peristaltic walls are given in mathematical form [4]:

$${H}_{1}={\widehat{d}}_{1}+{\widehat{a}}_{1}\mathrm{cos}\left[\frac{2\pi }{\lambda }(\widehat{\zeta }-c\widehat{t})\right],$$

(1)

$${H}_{2}=-{\widehat{d}}_{2}+{\widehat{b}}_{1}\mathrm{cos}\left[\frac{2\pi }{\lambda }(\widehat{\zeta }-c\widehat{t})+\widehat{\phi }\right].$$

(2)

In the above expression, $\hat{a}_{1} ,\hat{b}_{1} ,\hat{d}_{1} ,\hat{d}_{2}$ and $\hat{\phi }$ satisfies the condition.

$${\widehat{a}}_{1}{}^{2}+{\widehat{b}}_{1}{}^{2}+2{\widehat{a}}_{1}{\widehat{b}}_{1}\mathrm{cos}\ \widehat{\phi }\le {\left({\widehat{d}}_{1}+{\widehat{d}}_{2}\right)}^{2}.$$

(3)

The rheology of a Casson fluid is expressed as follows:

${\tau }_{ij}=\left({\mu }_{\beta }+\frac{{\rho }_{y}}{\sqrt{2\Pi }}\right)2{e}_{ij}$ when $\Pi \succ {\Pi }_{C},$

${\tau }_{ij}=\left({\mu }_{\beta }+\frac{{\rho }_{y}}{\sqrt{2{\Pi }_{C}}}\right)2{e}_{ij}$ when $\Pi \prec {\Pi }_{C},$where $\tau_{ij}$ is the stress tensor of the fluid with $(i,\,\,j)^{th}$ components, $\Pi = e_{ij}\ e_{ij} ,$ $e_{ij}$ is formation rate of $(i,\,\,j)^{th}$ component, $\rho_{y}$ is the yield stress of the fluid, $\mu_{\beta }$ is the dynamic plastic viscosity of the viscous fluid and $\Pi_{C}$ is the critical value of the product based on viscous fluid.

Vector form of the velocity field $V$ is given as follows:

Scheme 1

Schematic diagram of the channel

$$V=\left(\widehat{U}\left(\widehat{\zeta },\widehat{y},\widehat{t}\right),\widehat{V}\left(\widehat{\zeta },\widehat{y},\widehat{t}\right)\right)$$

where $\widehat{U}\left(\widehat{\zeta },\widehat{y},\widehat{t}\right)$ and $\widehat{V}\left(\widehat{\zeta },\widehat{y},\widehat{t}\right)$ are the velocity components.

The basic governing equations are defined as follows [10]:

$$\frac{\partial \widehat{u}}{\partial \widehat{\zeta }}+\frac{\partial \widehat{v}}{\partial \widehat{y}}=0,$$

(4)

$$\begin{array}{c}{\rho }_{f}\left(\frac{\partial \widehat{u}}{\partial \widehat{t}}+\widehat{u}\frac{\partial \widehat{u}}{\partial \widehat{\zeta }}+\widehat{v}\frac{\partial \widehat{u}}{\partial \widehat{y}}\right)=-\frac{\partial \widehat{p}}{\partial \widehat{\zeta }}+\mu \left(1+\frac{1}{{\beta }^{^{\prime}}}\right)\left(\frac{{\partial }^{2}\widehat{u}}{\partial {\widehat{\zeta }}^{2}}+\frac{{\partial }^{2}\widehat{u}}{\partial {\widehat{y}}^{2}}\right)+{\rho }_{f}g{\beta }_{T}(\widehat{T}-{\widehat{T}}_{0})\\ +{\rho }_{f}g{\beta }_{C}(\widehat{f}-{f}_{0}),\end{array}$$

(5)

$${\rho }_{f}\left(\frac{\partial \widehat{v}}{\partial \widehat{t}}+\widehat{u}\frac{\partial \widehat{v}}{\partial \widehat{\zeta }}+\widehat{v}\frac{\partial \widehat{v}}{\partial \widehat{y}}\right)=-\frac{\partial \widehat{p}}{\partial \widehat{\zeta }}+\mu \left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}\widehat{v}}{\partial {\widehat{y}}^{2}},$$

(6)

$$\begin{array}{l}\left(\rho c\right) _{f}\left(\frac{\partial \widehat{T}}{\partial \widehat{t}}+\widehat{u}\frac{\partial \widehat{T}}{\partial \widehat{\zeta }}+\widehat{v}\frac{\partial \widehat{T}}{\partial \widehat{y}}\right)={k}_{T}\left(\frac{{\partial }^{2}\widehat{T}}{\partial {\widehat{\zeta }}_{2}}+\frac{{\partial }^{2}\widehat{T}}{\partial {\widehat{y}}_{2}}\right)+{\left(\rho c\right)}_{p}{D}_{B}\left(\frac{\partial \widehat{f}}{\partial \widehat{\zeta }}\frac{\partial \widehat{T}}{\partial \widehat{\zeta }}+\frac{\partial \widehat{f}}{\partial \widehat{y}}\frac{\partial \widehat{T}}{\partial \widehat{y}}\right)\\ +\ {\left(\rho c\right) _{p}}\frac{{D}_{T}}{{T}_{m}}\left[{\left(\frac{\partial \widehat{T}}{\partial \widehat{\zeta }}\right)}^{2}+\left({\left(\frac{\partial \widehat{T}}{\partial \widehat{y}}\right)}^{2}\right)\right]+\Phi +\sigma {B}_{0}^{2}{\widehat{u}}^{2},\end{array}$$

(7)

$$\frac{\partial \widehat{f}}{\partial \widehat{t}}+\widehat{u}\frac{\partial \widehat{f}}{\partial \widehat{\zeta }}+\widehat{v}\frac{\partial \widehat{f}}{\partial \widehat{y}}={D}_{B}\left(\frac{{\partial }^{2}\widehat{f}}{\partial {\widehat{\zeta }}^{2}}+\frac{{\partial }^{2}\widehat{f}}{\partial {\widehat{y}}^{2}}\right)+\frac{{D}_{T}}{{T}_{m}}\left(\frac{{\partial }^{2}\widehat{T}}{\partial {\widehat{\zeta }}^{2}}+\frac{{\partial }^{2}\widehat{T}}{\partial {\widehat{y}}^{2}}\right).$$

(8)

where ${U^{\prime}}$ and $V^{\prime}$ are the velocity components along the $\hat{\zeta }$- and $\hat{y}$- direction respectively, $\rho_{f}$ is the fluid density, g is the gravitational acceleration, $\sigma$ is the electrical conductivity of the fluid, $B_{0}$ is the applied magnetic field, $k_{T}$ is the volume expansion coefficient, $\Phi$ is the constant heat addition/absorption, $\beta_{T}$ is the volumetric thermal expansion coefficient, $\rho c_{p}$ is the density of the particles, $T$ is the temperature of the fluid, $\hat{f}$ is the nanoparticle concentration, $D_{B}$ is the Brownian diffusion coefficient, $D_{T}$ is the thermophoretic diffusion coefficient and $T_{m}$ is the fluid mean temperature.

We introduce the transformation between the wave frame $\left( {\hat{\zeta },\hat{y}} \right)$ and laboratory frame $\left( {\zeta ,y} \right)$ in order to facilitate the analytical solutions $u$ and $v$ that are the velocity components in the wave frame $\left( {\hat{\zeta },\hat{y}} \right)$.

In order to make analytical solutions easier, introducing transformation between the wave frame and the laboratory frame.

$$\widehat{u}=u-c, \widehat{y}=\widehat{y}, \widehat{v}=v,\widehat{\zeta }=\widehat{\zeta }-c\widehat{t}.$$

(9)

Introducing non-dimensional variables,

$$\left.\begin{array}{c}\zeta =\frac{\widehat{\zeta }}{\lambda },y=\frac{\widehat{y}}{{\widehat{d}}_{1}},t=\frac{c\widehat{t}}{\lambda },v=\frac{\widehat{v}}{c},\delta =\frac{{\widehat{d}}_{1}}{\lambda },p=\frac{\widehat{p}{\widehat{d}}_{1}{}^{2}}{\mu c\lambda },u=\frac{\widehat{u}}{c},\widehat{d}=\frac{{\widehat{d}}_{2}}{{\widehat{d}}_{1}},\\ \widehat{a}=\frac{{\widehat{a}}_{1}}{{\widehat{d}}_{1}},\widehat{b}=\frac{{\widehat{b}}_{1}}{{\widehat{d}}_{1}},\alpha =\frac{{k}_{T}}{{(\rho c)}_{f}},\theta =\frac{\widehat{T}-{\widehat{T}}_{0}}{{\widehat{T}}_{1}-{\widehat{T}}_{0}},C=\frac{\widehat{f}-{\widehat{f}}_{0}}{{\widehat{f}}_{1}-{\widehat{f}}_{0}},Nt=\frac{{(\rho c)}_{p}{D}_{T}({\widehat{T}}_{1}-{\widehat{T}}_{0})}{{(\rho c)}_{f}\mu {T}_{m}},\\ Pr=\frac{{(\rho c)}_{f}\mu }{{K}_{T}},Gr=\frac{{\rho }_{f}g{\widehat{d}}_{1}{}^{2}({\widehat{T}}_{1}-{\widehat{T}}_{0}){\beta }_{T}}{c\mu },{Q}_{0}=\frac{\Phi {\widehat{d}}_{1}{}^{2}}{{(\rho c)}_{f}({\widehat{T}}_{1}-{\widehat{T}}_{0})},\\ Nb=\frac{{(\rho c)}_{p}{D}_{B}({\widehat{f}}_{1}-{\widehat{f}}_{0})}{{(\rho c)}_{f}\mu },Qr=\frac{{\rho }_{f}g{\widehat{d}}_{1}{}^{2}({\widehat{f}}_{1}-{\widehat{f}}_{0}){\beta }_{c}}{c\mu },J=\frac{\sigma {B}_{0}{}^{2}{\widehat{d}}_{1}{}^{2}{c}^{2}}{{k}_{f}\left({\widehat{T}}_{1}-{\widehat{T}}_{0}\right)},\\ Br=PrEc,Ec=\frac{{c}^{2}}{{\left(\rho c\right)}_{p}\left({\widehat{T}}_{1}-{\widehat{T}}_{0}\right)}.\end{array}\right\}$$

(10)

where $\delta$ is the dimensionless wave number and the stream function is taken as $\widehat{v}=-\delta \frac{\partial \psi }{\partial \zeta }, \widehat{u}=\frac{\partial \psi }{\partial y}$.

The non-dimensional governing equations are as follows:

$$0=\frac{\partial p}{\partial \zeta }+\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}u}{\partial {y}^{2}}+Gr\theta +QrC,$$

(11)

$$\frac{\partial p}{\partial y}=0,$$

(12)

$$\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{3}u}{\partial {y}^{3}}+Gr\frac{\partial \theta }{\partial y}+Qr\frac{\partial C}{\partial y}=0,$$

(13)

$$\frac{{\partial }^{2}\theta }{\partial {y}^{2}}+Nb\mathrm{Pr}\frac{\partial \theta }{\partial y}\frac{\partial C}{\partial y}+Nt\mathrm{Pr}{\left(\frac{\partial \theta }{\partial y}\right)}^{2}+{Q}_{0}\mathrm{Pr}+Br{M}^{2}{u}^{2}=0,$$

(14)

$$\frac{{\partial }^{2}C}{\partial {y}^{2}}+\frac{Nt}{Nb}\frac{{\partial }^{2}\theta }{\partial {y}^{2}}=0$$

(15)

where $Gr$ is Grashoff number, local nanoparticle Grashoff number $Qr$, Hartman number $M,$ $\beta$ Casson fluid parameter, volume flow rate $Q_{0}$, Brinkman number $Br,$ $Nt$ the thermophoresis parameter, $Nb$ is Brownian motion parameter, and $\Pr$ is the Prandtl number.

The corresponding dimensionless boundary conditions is as follows:

$$\psi =\frac{F}{2},\frac{\partial \psi }{\partial y}=-{\beta }_{1}\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}\psi }{\partial {y}^{2}}-1\; at\; {h}_{1}=1+a\ \mathrm{cos}\left(2\pi \zeta \right),$$

(16)

$$\psi =-\frac{F}{2},\frac{\partial \psi }{\partial y}={\beta }_{1}\left(1+\frac{1}{\beta }\right)\frac{{\partial }^{2}\psi }{\partial {y}^{2}}-1\; at\; {h}_{2}=-d-b\ \mathrm{cos}\left(2\pi \zeta +\phi \right),$$

(17)

$$\theta -\gamma \frac{\partial \theta }{\partial y}=1,\; at\; y={h}_{1},$$

(18)

$$C-{\gamma }_{1}\frac{\partial C}{\partial y}=1,\ at\ y={h}_{1},$$

(19)

$$\theta +\gamma \frac{\partial \theta }{\partial y}=0, at\ y={h}_{2},$$

(20)

$$C+{\gamma }_{1}\frac{\partial C}{\partial y}=0\; { at\; }y={h}_{2}.$$

(21)

Here, $\beta_{1}$, $\gamma$ and $\gamma_{1}$ represent the velocity slip parameter, thermal slip parameter and concentration slip parameter, respectively. The respective dimensionless time mean flows $\Theta$ and $F$ in the laboratory and wave frames are related through the following expression

$$F=\Theta -1-d.$$

3 Method of solution

The partial differential Eqs. (7) to (8) are solved by Homotopy Perturbation Sumudu transformation method (HPSTM), which is an analytical technique. It is used to calculate non-linear problem which comprises large and small physical parameters (convergent series is obtained after solving).

We get an approximate analytical solution by applying the HPSTM to the governing equations [22]. We get the following equation after applying the Sumudu transformation, inverse Sumudu transformation to the governing equations on both sides:

$$\begin{aligned}u(y)=&\frac{\frac{-\beta }{2}+b\beta +2{\beta }_{1}\left(\beta +1\right)b}{\beta +{\beta }_{1}\left(\beta +1\right)}\\&+\frac{\frac{-\beta }{2}-b\beta -2{\beta }_{1}\left(\beta +1\right)b}{{\beta }_{1}\left(\beta +1\right)-\beta }y+b\frac{{y}^{2}}{2}\\&-{s}^{-1}\left[\left(\frac{\beta }{\beta +1}\right){v}^{3}\left\{s\left[Gr\frac{\partial \theta }{\partial y}+Qr\frac{\partial C}{\partial y}\right]\right\}\right],\end{aligned}$$

(22)

$$\begin{aligned}\theta (y)=&-\frac{\gamma a}{\left(1-\gamma \right)}+by+{Q}_{0}\ \mathrm{Pr}\frac{{y}^{2}}{2}\\&-{s}^{-1}\left[{v}^{2}s\left[Nb\ \mathrm{Pr}\frac{\partial \theta }{\partial y}\frac{\partial C}{\partial y}+Nt\ \mathrm{Pr}\frac{{\partial }^{2}\theta }{\partial {y}^{2}}+Br{M}^{2}{u}^{2}\right]\right],\end{aligned}$$

(23)

$$C(y)=\frac{{\gamma }_{1}a}{\left(1-{\gamma }_{1}\right)}+by-{s}^{-1}\left[{u}^{2}\left\{s\left[\frac{Nt}{Nb}\frac{{\partial }^{2}\theta }{\partial {y}^{2}}\right]\right\}\right].$$

(24)

Applying HPM and using He’s polynomial [23], we compare the coefficients of like powers of $p$ to get the required series solution.

The volume flow rate is given by the following:

$$Q=\underset{{h}_{2}}{\overset{{h}_{1}}{\int }}\left(u+1\right)dy.$$

(25)

Integrating Eq. (20) and after manipulating, we get pressure gradient. The coefficient of heat transfer is given by [20], as follows:

$$\overline{Z }={\left({h}_{1}\right)}_{x}{\theta }_{y}.$$

(26)

4 Entropy generation

In the presence of the joule heating effect, the rate of entropy formation is given as follows:

$${S}_{G}=\frac{{k}_{f}}{{T}_{0}^{2}}{\left(\frac{\partial {T}^{^{\prime}}}{\partial {y}^{^{\prime}}}\right)}^{2}+\frac{{D}_{B}}{{C}_{0}}{\left(\frac{\partial {F}^{^{\prime}}}{\partial {y}^{^{\prime}}}\right)}^{2}+\frac{{D}_{B}}{{T}_{0}}\left(\frac{\partial {T}^{^{\prime}}}{\partial {y}^{^{\prime}}}\right)\left(\frac{\partial {C}^{^{\prime}}}{\partial {y}^{^{\prime}}}\right)+\frac{\sigma {B}_{0}^{2}{{u}^{^{\prime}}}^{2}}{{T}_{0}}.$$

(27)

Total entropy generation $N_{S}$ is given by as per Bejan [9], as follows:

$${N}_{S}={\left(\frac{\partial \theta }{\partial y}\right)}^{2}+\alpha {\left(\frac{\Lambda }{\Omega }\right)}^{2}{\left(\frac{\partial C}{\partial y}\right)}^{2}+\Gamma \left(\frac{\partial C}{\partial y}\right)\left(\frac{\partial \theta }{\partial y}\right)+\frac{J}{\Omega }u.$$

(28)

where $\Lambda$ is the temperature difference parameter, $\Omega$ is the concentration difference parameter, $\Gamma$ is the ratio of temperature to concentration parameters and $\alpha$ is defined as follows:

$$\Lambda =\frac{{\widehat{f}}_{1}-{\widehat{f}}_{0}}{{\widehat{f}}_{0}},$$

(29)

$$\Omega =\frac{{\widehat{T}}_{1}-{\widehat{T}}_{0}}{{\widehat{T}}_{0}},$$

(30)

$$\Gamma =\frac{{D}_{B}{T}_{0}{}^{^{\prime}}({\widehat{f}}_{1}-{\widehat{f}}_{0})}{{k}_{f}({\widehat{T}}_{1}-{\widehat{T}}_{0})},$$

(31)

$$\alpha =\frac{{D}_{B}{\widehat{f}}_{0}}{{k}_{f}}.$$

(32)

5 Discussion

We solved the nonlinear partial differential equations employing Homotopy Perturbation Sumudu transformation method (HPSTM). In this study, we utilised the symbolic software Mathematica. For velocity, pressure gradient, temperature, nanoparticle concentration is solved using Mathematica and plotted with Origin. The obtained results are compared with perturbation technique solved by Srinivas and Kothandapani [24] in the absence of Brownian motion and thermophoresis effects as shown in Table 1. It is found that there is greater improvement in the results obtained by the present method.

Table 1 Comparison of the numerical values of the heat transfer coefficient at the upper wall $Z = \left( {h_{1} } \right)_{x} \theta_{y}$ between the work of Srinivas and Kothandapani [24] and special case of present study when $We = 0$, $a = 0.5$, $b = 0.6$,$\phi = \frac{\pi }{4}$, $d = 1.5$, $\rho = 0.5$, $\Pr = 1.0$, $E = 3.0$ and $\beta = 0.0$ in absence of Brownian motion and thermophoresis effects

5.1 Velocity distribution

Figures 1, 2, 3, 4 show the influence of various parameters on velocity. We can observe the effects of local nanoparticle Grashoff number $Qr$, Hartman number $M,$ slip parameter $\beta_{1}$ and Casson fluid parameter $\beta$, respectively, on the velocity profile. As local nanoparticle Grashoff number $Qr$ increases, the velocity profile also increases. It is due to the fact that nanoparticle collision increases, as we increase $Qr$ in the system which leads to rise in velocity, which is shown in Fig. 1. Figure 2 shows the effect of the magnetic field parameter $M$ on velocity $u$. It is observed that velocity profile decreases as we enhance the values of $M$. When $M$ is applied in a transverse direction, it behaves as a hindering force on the fluid flow, causing velocity $u$ to decrease. Figure 3 shows the effect of slip parameter $\beta_{1}$ on velocity profile $u$. We can observe that velocity increases as slip parameter $\beta_{1}$ increases. This effect is helpful to determine the actual energy transfer between the channel and the fluid. Therefore, an increase in $\beta_{1}$ causes non-uniform velocity distribution inside the channel and resistance is reduced due to slip; hence, velocity increases. In Fig. 4, as the Casson fluid parameter $\beta$ increases, velocity profile increases.

Fig. 1

Variation of u on Qr when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, Br = 0.1, β₁= 1, Gr = 1, Q₀= 2, M = 0.1

Fig. 2

Variation of u on M when Nb = 0.1, Pr = 1, Nt =0.1, β = 0.5, Br = 0.1, β₁ = 1, Gr = 1, Q₀= 2, Qr = 1

Fig. 3

Variation of u on $\beta_{1}$ when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, Br = 0.1, Qr = 1, Gr = 1, Q₀= 2, M = 0.1

Fig. 4

Variation of $u$ on $\beta$ when Nb = 0.1, Pr = 1, Nt = 0.1, Qr = 0.1, Br = 0.1, β₁ = 0.5, Gr = 1, Q₀ = 2, M = 0.1

5.2 Pressure gradient

The effects of physical parameters such as Casson fluid parameter $\beta$, volume flow rate $Q$, Hartman number $M$, Brinkman number $Br$ and slip condition $\beta_{1}$ on pressure gradient for upper and lower wall are shown in Figs. 5, 6, 7, 8, 9. Similar effects can be observed for the physical parameter $\beta$_, $Q$ and $M$ that is pressure gradient decreases for these parameters. This fact is due to the inverse relation with viscosity of the fluid, which increases the motion of the fluid particles and velocity of the fluid increases, which reduces the pressure gradient in system. Pressure gradient increases as Brinkman number $Br$ and slip condition $\beta_{1}$ rise, which can be observed in Figs. 8, 9. 

Fig. 5

Variation of $\frac{\partial p}{{\partial \xi }}$ on $\beta$ when Nb = 0.1, Pr = 1, Nt = 0.1, Q = 0.1, γ = 0.1, γ₁ = 0.1, Br = 0.1, β₁ = 1, Gr = 0.1, Q₀ = 0.1, M = 0.1, d = 0.1, $\phi$ = 1.5, Qr = 0.5

Fig. 6

Variation of $\frac{\partial p}{{\partial \zeta }}$ on $Q$ when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, γ = 0.1, γ₁ = 0.1, Br = 0.1, β₁ = 1, Gr = 0.1, Q₀ = 0.1, M = 0.1, d = 0.1, $\phi$ = 1.5, Qr = 0.5

Fig. 7

Variation of $\frac{\partial p}{{\partial \zeta }}$ on M when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, Q = 0.1, γ = 0.1, γ₁ = 0.1, Br = 0.1, β₁ = 1, Gr = 0.1, Q₀ = 0.1, d = 0.1, $\phi$ = 1.5, Qr = 0.5

Fig. 8

Variation of $\frac{\partial p}{{\partial \zeta }}$ on $Br$ when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, Q = 0.1, γ = 0.1, γ₁ = 0.1, β₁ = 1, Gr = 0.1, Q₀ = 0.1, M = 0.1, d = 0.1, $\phi$ = 1.5, Qr = 0.5

Fig. 9

Variation of $\frac{\partial p}{{\partial \zeta }}$ on $\beta_{1}$ when Nb = 0.1, Pr = 1, Nt = 0.1, β = 0.5, Q = 0.1, γ = 0.1, γ₁ = 0.1, Br = 0.1, Gr = 0.1, Q₀ = 0.1, M = 0.1, d = 0.1, $\phi$ = 1.5, Qr = 0.5

5.3 Temperature profile

Through Figs. 10, 11, 12, 13, 14, we can observe the effect of Casson fluid parameter $\beta$, Prandtl number $\Pr$_, Hartman number $M$, thermal slip parameter $\gamma$ and Brinkman number $Br$, respectively, on $\;\theta$. Figure 10 represents that as Casson fluid parameter $\beta$ increases, temperature profile decreases. Physically, rising values of $\beta$ develop the viscous forces. These viscous forces have propensity to reduce the thermal boundary layers. Figure 11 shows the effect of Prandtl number $\Pr$ on temperature profile $\;\theta$. The prandtl number is inversely proportional to the thermal conductivity of the system, and higher Prandtl number has lesser thermal diffusivity; hence, weaker thermal conductivity reduced the temperature profile at the wall. Figure 12 shows the effect of Hartman number $M$ on temperature profile $\;\theta$. By enhancing magnetic parameter $M$, the temperature profile $\;\theta$ decreases. This is due to the fact that Lorentz force opposes the flow of fluid which produces more heat and there is an increase in temperature. From Fig. 13, we can observe that $\;\theta$ rises when thermal slip parameter $\gamma$ increases. The contact between wall and fluid increases, which enhances the heat transfer rate, and as a result, temperature raises consequently. Figure 14 indicates that the temperature $\;\theta$ rises as Brinkman number $Br$ increases. Brinkman number is actually caused by viscous dissipation which corresponds to the higher temperature diffusivity. It is reasonable to say that rise in temperature is produced by the stress-reversal process that develops with increasing $Br$.

Fig. 10

Variation of θ on $\beta$ when Nb = 0.1, Pr = 1, Nt = 1, γ = 0.1, Br = 0.1, β₁ = 1, Q₀ = 0.7, M = 0.1

Fig. 11

Variation of θ on $\Pr$ when Nb = 0.1, β = 0.5, γ = 0.1, Br = 0.1, β₁ = 1, Q₀ = 0.7, M = 0.1 

Fig. 12

Variation of $\;\theta$ on M when Nb = 0.1, Pr = 1, Nt = 1, β = 0.1, γ = 0.1, Br = 0.1, β₁ = 0.1, Q₀ = 0.7

Fig. 13

Variation of $\;\theta$ on $\gamma$ when Nb = 0.1, Pr = 1, Nt = 1, β = 0.1, Br = 0.1, β₁ = 0.1, Q₀ = 0.7, M = 0.1

Fig. 14

Variation of θ on Br when Nb = 0.1, Pr = 1, Nt = 1, β = 0.1, γ = 0.1, β₁ = 0.1, Q₀ = 0.7, M = 0.1

5.4 Nanoparticle concentration profile

Figures 15, 16, 17 are plotted to show the effects of concentration slip parameter $\gamma_{1}$, thermophoresis parameter $Nt$ and Brownian motion parameter $Nb$ on nanoparticle concentration $C$. Figure 15 shows the effect of concentration slip parameter $\gamma_{1}$, and it is noticed that concentration of nanoparticles decay as slip parameter $\gamma_{1}$ rises. Similar observation can be seen in case of thermophoresis parameter $Nt$. That is, as $Nt$ increases the concentration of nanoparticles decreases. The nanoparticles transfer from lower region to higher region during the transfer. A remarkable concentration distribution occurs, which results in the decrease of nanoparticle concentration in system, which can be observed in Fig. 16. Opposite behaviour can be seen in Brownian motion parameter $Nb$ in Fig. 17. For larger values of Brownian motion parameter $Nb$, collision of the nanoparticles in the system increases, which results in the increase of concentration of the nanoparticles.

Fig. 15

Variation of $\;C$ on $\gamma_{1}$ when Nb = 0.1, Pr = 1, Nt = 1.5, β = 0.1, γ = 0.1, Br = 0.2, β₁ = 0.1, Q₀ = 0.1, M = 0.5

Fig. 16

Variation of C on Nt when Nb = 0.1, Pr = 1, β = 0.1, γ = 0.1, γ₁ = 0.2, Br = 0.2, β₁ = 0.1, Q₀ = 0.1, M = 0.5

Fig. 17

Variation of C on $Nb$ when Pr = 1, Nt = 1.5, β = 0.1, γ = 0.2, Br = 0.2, β₁ = 0.1, Q₀ = 0.1, M = 0.5

5.5 Entropy generation

Figures 18, 19, 20 represent the effects of Joule heating parameter $J$_, temperature ratio parameter $\Lambda$ and thermal slip parameter $\gamma$ on entropy generation number $Ns$. We can observe that temperature ratio parameter $\Lambda$ and Joule heating parameter have the same effects on entropy generation number $Ns$, i.e., increasing the values of $\Lambda$ and $J$ causes more entropy generation, which is shown in Figs. 18, 19. Joule heating effects involve the electric field caused by the internal heating in the presence of potential gradient. Thus, increment of Joule heating parameter accelerates the entropy generation significantly. Figure 20 depicts the behaviour of slip parameter on entropy generation. It is observed that the rise in slip parameter at the wall diminishes the entropy generation in the system.

Fig. 18

Variation of $N_{S}$ on J when Nb = 0.1, Pr = 2, Nt = 0.1, Ω = 0.1, Γ = 0.1, γ = 0.1, γ₁ = 0.2, Br = 1, β₁ = 0.1, Q₀ = 0.1, M = 1, Gr = 1, Qr = 0.1, Λ = 0.3

Fig. 19

Variation of $N_{S}$ on $\Lambda$ when Nb = 0.1, Pr = 2, Nt = 0.1, J = 0.1, Ω = 0.1, Γ = 0.1, β = 0.1, γ = 0.1, γ₁ = 0.2, Br = 1, β₁ = 0.1, Q₀ = 0.1, M = 1, Gr = 1, Qr = 0.1

Fig. 20

Variation of $N_{S}$ on $\gamma$ when Nb = 0.1, Pr = 2, Nt = 0.1, J = 0.1, Ω = 0.1, Γ = 0.1, β = 0.1, γ₁ = 0.2, Br = 1, β₁ = 0.1, Q₀ = 0.1, M = 1, Gr = 1, Qr = 0.1, Λ = 0.3

6 Conclusions

In this article, we studied the effect of multi-slip condition on Peristaltic flow through asymmetric channel with Joule heating and entropy generation. The non-dimensional nonlinear equations are solved by the HPSTM. The main observations are summarised below:

• Behaviour of $\beta$ is similar on velocity, pressure gradient and temperature profiles.

• Similar behaviour can be observed on velocity, pressure gradient and temperature profiles on varying $M$.

• Opposite behaviour can be seen in $Nb$ and $Nt$ on nanoparticle concentration profile.

• Entropy generation presents increasing behaviour for $\Lambda$ and $J$.

• $\gamma$ decreases the entropy generation.