Abstract
A mathematical model is presented for the emergence of perceptual-cognitive-behavioral modes in psychophysical experiments in which participants are confronted with two alternatives. The model is based on the theory of self-organization and, in particular, the order parameter concept such that the emergence of a mode is conceptualized as an instability leading to the emergence of an appropriately defined order parameter. The order parameter model is merged with a second model that describes adaptation in terms of a system parameter dynamics. It is shown that the two-component model predicts hysteretic mode-mode transitions when control parameters are increased or decreased beyond critical values. The two-component model can account for both positive and negative hysteresis effects due to the interaction between order parameter and system parameter dynamics. Moreover, the model-based analysis reveals that response time curves look rather flat when response times are relatively decoupled from the mode-mode transition phenomenon. In general, response time curves exhibit a peaked close to the mode-mode transition point. In this context, the possibility is discussed that such peaked response time curves belong to the class of critical phenomena of self-organizing systems. In order to illustrate the relevance of peaked response time curves for future research and research reported in the past, results from a perceptual judgment experiment are reported, in which participants judged their ability to stand on a tilted slope for various angles of inclination. Response time curves were found that exhibited a peak around the mode-mode-transition points between “yes” and “no” responses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fundamental aspects of human perceptual and cognitive processes as well as human behavioral responses can be tested in laboratory settings in tasks that confront participants with two alternatives. Perception tasks of ambivalent figures [1], certain grasping tasks [2–6], problem-solving tasks featuring two different solution methods [7], stair-climbing tasks in which participants judge their own ability to perform the task and either reject or execute the required performance [8] exemplify problems studied in the literature to conduct research into this direction.
Let us introduce the notion of perceptual-cognitive-behavioral processes in general and how they can be understood from a self-organization perspective. Human activities may be broken down in different processes such as perception, cognition, and behavior. A given activity might be considered as the result of a sequential process that starts with the perception of a stimulus, proceeds with a cognitive evaluation of the perceived information, and is completed by a motor response depending on the outcome of the cognitive evaluation. For example, when a human actor catches a flying ball, we may say that the actor perceives the approaching ball, evaluates the situation at hand, and subsequently responds with an appropriate motor action [9]. However, human activities may not only be the result of such feed-forward sequences. For example, body movement may affect perception and cognition (embodied cognition). That is, there might be relevant feedback loops. Likewise, the human performance under consideration might not involve a cognitive component in the sense of a computational element. Action might be guided directly by perception (direct perception [10]). Consequently, in a first step, we introduce a perceptual-cognitive-behavioral process without any theoretical framework in mind (i.e., as a catch-all phrase). Accordingly, in what follows, we will refer to a perceptual-cognitive-behavioral process as a process that involves at least either perception, cognition, or behavior or involves more than one category. In doing so, we do not specifying whether these components are connected by feed-forward connections or exhibit feedback loops. Neither do we make a statement about the relevance of computational components. In contrast, in a second step, we specify the theoretical framework and assume that the theory of self-organization can be applied to the perceptual-cognitive-behavioral process underconsideration.
In this context, note that perceptual-cognitive-behavioral processes can be studied on various levels such as the cellular level, the neural level, the level of muscle activity, and the behavioral level. In general, such processes are associated with the emergence of certain neuro-biological patterns. In what follows, we assume that the processes from a phenomenological point of view and the physical, spatio-temporal patterns from a mechanistic modeling point of view arise due to self-organization [11–16]. In this context, a pattern exhibits order. The order emerges via bifurcations. The emergence of a pattern, in turn, is captured by the dynamics of certain amplitudes that have been called order parameters [17]. While the order parameter dynamics is a useful concept for the understanding of the self-organization of psychological processes [18–20], another concept is needed to account for the plasticity of the human brain in general and learning and adaptation in particular. This concept is the notion of system parameters that change, that is, the notion of a system parameter dynamics, see Table 1. We will show that a comprehensive understanding of hysteretic transitions between different modes of a given psychological process can be achieved by means of a combination of the two aforementioned concepts: the order parameter dynamics and the system parameter dynamics.
According to the order parameter concept [17], different modes of perceptual-cognitive-behavioral processes are associated with different physical, spatio-temporal patterns. Such patterns, in turn, can be described by a field variable q(x,t). In general, q has several components and corresponds to a vector-valued field variable. Likewise, x is a spatial coordinate in a N-dimensional space and represents a vector. Here, for clarity of presentation, we will consider q as a scalar variable and x is a coordinate in a one-dimensional space. Moreover, t is time. The spatio-temporal pattern q(x,t) can be expressed by means of a set of elementary spatio-temporal patterns (or physical modes) v k (x,t) that satisfy the task-related boundary conditions. The pattern decomposition reads
The variables ξ k are the amplitudes of the elementary patterns v k (x,t). The amplitudes ξ k depend on time t again. In (1) we have written out explicitly the first M terms given in terms of products of elementary patterns and amplitudes. The term denoted “other terms” involves additional terms that come with additional patterns and amplitudes. In principle, the set of patterns and amplitudes is infinite. If only one of the amplitudes ξ k is finite, say ξ j , whereas all other amplitudes ξ k are zero (i.e., ξ k =0 for k=1,…,j−1,j+1,…,M) and if in addition the term ”other terms” is negligibly small, then the pattern v j and the corresponding perceptual-cognitive-behavioral mode j can be observed. We may assume that an experiment is designed such that in the experiment M modes of a certain perceptual-cognitive-behavioral process can be observed. Without loss of generality, we can assign them to the first M patterns listed in the pattern decomposition (1). Then, the M amplitudes ξ 1,…,ξ M are the order parameters of the system. Note that this terminology strictly speaking only holds when a particular symmetry condition is satisfied as considered by Haken [18]. This symmetric case can be observed in non-equilibrium, inanimate systems such as fluid dynamical systems operating at the Rayleigh–Benard instability and exhibiting roll patterns [18]. Below we will consider the asymmetric case. In this case, we may refer to the amplitudes as “order parameter candidates” or “potential order parameters”. We will not dwell on this subtlety and simply refer to ξ k as order parameters or amplitudes. In particular, in tasks involving two alternative modes as described above, we may put M=2 and refer to ξ 1 and ξ 2 as the two order parameters or amplitudes of the task-related modes under consideration.
According to the theory of self-organizing systems, a pattern v k emerges via a bifurcation [14, 17, 18]. At that bifurcation point, the terms “other terms” can be eliminated by means of adiabatic elimination and the relevant dynamics is given by the order parameters ξ k only. In doing so, the system that in principle is described by an infinitely large set of patterns can adequately be described by means of a few patterns only involving a relatively small set of amplitudes. For a certain, general class of systems that operate far from thermal equilibrium (non-equilibrium systems), the evolution equations of ξ k can be determined explicitly. These evolution equations are the pattern formation and pattern recognition amplitude equations introduced by Haken [18], see Section 2. They have various applications both in the inanimate world and the life sciences [18, 22]. For example, they describe the emergence of roll patterns [18, 23] and rotating wave patterns [24] in fluid dynamical systems in Rayleigh–Benard convection. They have been used to describe oscillatory visual perception of ambivalent figures (e.g., Necker cube) [1] and behavioral switching between two alternative modes of grasping when the to-be-grasped objects increase in size [6, 25, 26]. They have been used to describe action-selection in the context of child development [25, 27] and to discuss the impact of priming on recognition times [28, 29]. In the field of artificial intelligence, they have been used as a pattern recognition algorithm mimicking associative-memory neural networks [18, 30–35]. They have also been applied to solve job assignment problems [36–39] and to model settlement dynamics [40].
In this context, note that the theory of dynamical systems allows us to make predictions about the behavior of dynamical systems in general and self-organizing systems in particular at bifurcation points. It can be shown that the emergence of a pattern v k via a bifurcation involves critical phenomena such a critical slowing down and critical fluctuations [17, 41–45]. In experimental studies, such critical phenomena have been found in the inanimate world and the life sciences. For example, critical phenomena have been observed during the emergence of roll patterns in fluid layers heated from below [46–48] and in optical systems in which so-called dissipative solitons emerge due to self-organization [49]. Likewise, they have been found in experiments on human motor coordination, in which participants switched between two distinct motor coordination modes [50–55]. In Section 3.3 it will be argued that such critical phenomena may give rise to peaked response time curves of participants performing in the aforementioned two-choice tasks.
As mentioned above and illustrated in Table 1, in addition to the concept of order parameters, there is another useful concept that is tailored to address the plasticity of the human brain. Although the phrase “order parameters” refers to “parameters”, order parameters are in fact time-dependent variables (amplitudes), see (1). They should be considered as variables that describe the state (or type of order) of a system and consequently belong to the class of state variables. The state variables and order parameters evolve in a certain way for fixed internal and external conditions of the systems or human agents under consideration. These conditions are typically described by parameters. In order to highlight the conceptual difference between those parameters and order parameter, we may refer to the former as “system parameters”. In summary, we may distinguish between order parameters and systems parameters or between state variables and system parameters [21]. The system parameters that are assumed to be time-independent in the first place may become time-dependent under certain circumstances, for example, during learning and adaptation. In this case, the distinction between state variables/order parameters, on the one hand, and system parameters, on the other, becomes less clear. However, one may consider the case in which system parameters evolve slowly relative to the state variables/order parameters [6, 30, 56]. Such a time-scale separation (see Appendix A) can then be exploited for classification purposes. In general, learning of neural networks via changes of synaptic weights [14] may be considered as a system parameter dynamics. Moreover, the concept of dynamical diseases [57–59] and the recently developed proposal of therapy success as a bifurcation [20, 60] that is, the notion that certain disease patterns emerge and disappear via bifurcations due to disease-related and therapy-related changes of system parameters, assumes that system parameters are (slowly evolving) time-dependent variables rather than fixed constants. In addition, the learning of new coordination patterns [13, 61], motor performance during prism adaptation [62, 63], and recently the adaptive interaction between humans and a virtual partner in dyadic rhythmic movement tasks [64] have been modeled using system parameter dynamics. In a similar vein, other phenomena such as attention [18, 30], priming [62, 63], and child development [25, 27] have been considered. In our context, the studies on visual perceptual oscillations [1], negative hysteresis [56, 65], and relapse due to medical non-adherence [66] are of particular interest. While a drift (change) of the values of system parameters in general affects the dynamics of state variables and order parameters, in these studies the idea has been entertained that the opposite can be true as well: a switch between order parameters (indicating a mode-mode transition of the ongoing perceptual-cognitive-behavioral process) may affect the evolution of system parameters.
In fact, the objective of the present effort is to study from a theoretical point of view the interplay between order parameter and system parameter dynamics and to discuss in this context hysteresis effects and response times. To this end, in Section 2 the model outlined in Fig. 1 will be developed. Accordingly to this model, a switch between order parameters ξ k reflecting a transition between alternative modes of a perceptual-cognitive-behavioral process may affect the evolution of certain system parameters L k . The relevant coupling parameters will be denoted by s k , see Section 2. Vice versa, a change in the values of the system parameters L k may affect the evolution of the order parameters ξ k and may even induce bifurcations corresponding to transitions between alternative perceptual-cognitive-behavioral modes. The relevant coupling parameters will be denoted by λ k , see Section 2. The coupling parameters λ k take also environmental impacts into account as captured by the parameter α. In doing so, the scheme described in Fig. 1 allows to discuss how environmental impacts are mediated by means of the interplay between order parameter dynamics and system parameter dynamics.
Outline of a generalized order parameter model for switches between alternative modes of perceptual-cognitive-behavioral processes. The generalized model is based on Haken’s synergetic order parameter model for non-equilibrium pattern formation and pattern recognition systems [14]. The model takes the interplay between order parameter dynamics and system parameter dynamics into account. Variables: ξ k order parameters, L k system parameters, α (experimentally accessible) control parameter reflecting properties of the environment, s k and λ k coupling parameters. See text for details. Mathematical details can be found in Section 2
In Section 3, the model outlined in Fig. 1 will be exploited to make predictions about response times. In this context, the response time reflects the time it takes for a physical, neuro-biological pattern to emerge that is associated to a certain mode of a perceptual-cognitive-behavioral process. This “build-up” time is assumed to be positively correlated to the decision-making times or reaction times observed in laboratory experiments. For the sake of simplicity, we will refer to these times as response times. We will demonstrate that the model sketched in Fig. 1 allows for two fundamental scenarios. Response times may exhibit little variations in the regions before and after transitions between perceptual-cognitive-behavioral modes. In this scenario, a relative flat response time curve can be found. In contrast, response times may increase monotonically if the transition point is approached gradually. In this second scenario, a peaked response time curve can be found. Furthermore, it will be shown that peaked response time curves may arise from the critical slowing down phenomenon reviewed above.
The main objective of the present study is to discuss the interplay between order parameter dynamics and system parameter dynamics based on theoretical considerations, to make predictions about transitions between perceptual-cognitive-behavioral modes and the shape of response time curves, and to point out a possible link between peaked response time curves and the phenomena of critical slowing down. In order to highlight the relevance of modeling peaked response time curves, in Section 3.4 we will also present results from an experimental study. In this study, participants were asked to judge their ability to stand on a tilted platform. In fact, it has been shown that participants are well aware of their limits of motor abilities in this task and consequently respond that they are able to stand on the slope for relatively small angles of inclination but would not be able to perform the task for relatively large angles of inclination. Yes-to-No and No-to-Yes transitions in the responses can be observed in ascending and descending conditions, respectively [67]. Moreover, response times increase when angles of inclination approach the critical angles at which the response switches. This experiment can be conducted with different sensory modalities such as vision and touch [67] and can be used to identify general principles of perception [67]. Moreover, it might be considered as a useful control experiment for studying the development of perception and action-selection during infancy. Several experiments targeting child development have been conducted in which infants and toddlers are put into a situation that requires to crawl or walk down a slope. From the circumstances under which children reject or comply to perform the required task researchers hope to get insights into child development. Therefore, the experiment is of interest both in its specific and broader context.
2 Order parameter equations of hysteretic perceptual-behavioral transitions in two choice tasks
2.1 Basic model
The order parameter equations for competing and mutually exclusive modes are described in detail in Ref. [18]. For the case of two modes described by two order parameters ξ 1(t) and ξ 2(t) the order parameter equations read [26]
with U 1,U 2,B,C>0. Note that we consider initial conditions ξ k (t=0)≥0 only, which implies that the order parameters remain positive for all times: ξ k (t)≥0 ∀ t≥0. The parameters U k describe the rate with which the order parameters ξ 1(t) and ξ 2(t) increase exponentially in time when both ξ 1 and ξ 2 are initially close to zero. Accordingly, they are referred to as exponential growth parameters. The parameters B,C are coupling constants that constitute a single effective coupling parameter, see below. Note that the parameters have the following units: [U k ]=Time−1, [B],[C]=Time−1[ξ]−2. Let us derive a simplified representation of the order parameter equations (2). To this end, we put τ=γ t, where γ is a time factor measured in a particular time unit (e.g., seconds). Then, from (2) we obtain
with λ k =U k /γ. The parameters λ k are dimensionless exponential growth parameters. Introducing the new variables \({\tilde \xi }_{k} = \sqrt {C/\gamma } \, \xi _{k}\), which correspond to dimensionless order parameters, from (3) we obtain
with g=1+B/C, which implies g>1. In what follows, we will drop the tilde. Then, the order parameter equations read
and exhibit three parameters λ 1, λ 2, and g. We will refer to them as system parameters. The parameters B and C occurring in the original equations (2) constitute the parameter g. The parameter g describes the strength of the inhibitory interaction between the two modes, that is, g describes the strength of the mode-mode competition. Taking an alternative point of view, we see that g is the weight of the mixed nonlinear terms \(\xi _{j} {\xi _{k}^{2}}\), whereas the cubic nonlinear terms \({\xi _{k}^{3}}\) exhibit weights equal to unity. The mixed nonlinear terms \(\xi _{j} {\xi _{k}^{2}}\) reflect cross-inhibition between the modes. In contrast, the cubic nonlinear terms \({\xi _{k}^{3}}\) account for the inhibition of a mode by itself (self-inhibition). Consequently, g measures the magnitude of cross-inhibition in units of the strength of the self-inhibition. In the limiting case g→1 the cross-inhibition has the same magnitude as the self-inhibition, whereas for g>1 cross-inhibition has a stronger impact than self-inhibition.
For fixed parameters and g>1 the model (5) is known to describe a winner-takes-all dynamics [18, 26]. Accordingly, for any initial condition ξ 1(t=0)>0, ξ 2(t=0)>0 the dynamical system (5) converges to either of two fixed points. The first fixed point corresponds to q=v 1 and exhibits an amplitude ξ 1 that is “on” and an amplitude ξ 2 that is “off”. More precisely, (5) exhibits a stationary solution such that
The second winner-takes-all fixed point describes the second mode with
The dynamical system (5) can be monostable or bistable [26]. In particular, there are critical conditions at which a stable fixed point becomes unstable. If the ratio λ 2/λ 1 is increased gradually starting with a small value λ 2/λ 1≈0 then the fixed point of the first mode q=v 1 becomes unstable at λ 2/λ 1=g. That is, we have
Otherwise, the fixed point q=v 1 is asymptotically stable. Likewise, if the ratio λ 1/λ 2 is increased gradually starting with a small value λ 1/λ 2≈0 then the fixed point of the second mode q=v 2 becomes unstable at λ 1/λ 2=g. That is, we have
Otherwise, the fixed point q=v 2 is asymptotically stable. (8) and (9) taken together imply that the dynamical system is bistable for
and monostable for λ 2/λ 1>g or λ 1/λ 2>g. Consequently, if a perceptual-behavioral system described by (5) is in the perceptual-behavioral mode v 1 (i.e., q=v 1) and λ 2/λ 1 is increased beyond the threshold λ 2/λ 1=g, then the mode v 1 becomes unstable and a transition v 1→v 2 occurs. Vice versa, if the perceptual-behavioral mode v 2 is “active” and λ 2/λ 1 is decreased gradually, then v 2 becomes unstable at λ 2/λ 1=1/g and a transition v 2→v 1 occurs. With respect to the ratio λ 2/λ 1 the switching between modes 1 and 2 exhibits positive hysteresis because the thresholds g and 1/g for the 1→2 and 2→1 transitions are different and g>1/g.
2.2 Positive and negative hysteresis
It has been shown that an order parameter model based on (5) combined with an appropriately defined adaptation dynamics can describe transitions between modes of perceptual-cognitive-behavioral processes that exhibit both positive and negative hysteresis [65]. However, the issue of response times has not yet been discussed in this context. Let us derive next a comprehensive model that can account for the two types of hysteresis effects (positive and negative) and in addition addresses response times. To this end, we will follow to a large extent [65]. However, we will simplify some relations such that response time predictions can be made on the basis of analytical considerations. Possible generalization involving numerical approaches will be discussed in Section 4.
Let α denote a control parameter. Typically, α is a property of the environment. In laboratory experiments, α is usually manipulated by the experimenter (e.g., acoustic parameters in speech perception [56] or object size in experiments on grasping [4, 5]). We distinguish between experimental trials in which α is either gradually increased (ascending condition) or decreased (descending condition). The critical values at which switches in perception and behavior can be observed are denoted by α c,1 for the descending case and α c,2 for the ascending case [6].
It is useful to define
as a signed measure for hysteresis size. For α c,1=α c,2, there is no hysteresis and we have Δα=0. For α c,2>α c,1 there is hysteresis of the ordinary type as can be found in physical system (e.g., magnetism). In particular, we have Δα>0 which is the reason why we will refer to this kind of hysteresis as positive hysteresis. In contrast, for α c,2<α c,1 there is an unconventional type of hysteresis as observed in certain decision-making and judgment experiments [4, 56, 65, 67]. In this case, we have Δα<0, which is the reason why we will refer to this effect as negative hysteresis, see Table 2. Note that in line with the literature positive hysteresis is considered as a static phenomenon [13], where the control parameter α is gradually increased or decreased and the state of the system under consideration is observed as a function of α. In contrast, negative hysteresis cannot be explained by a deterministic, dynamical model that involves a single control parameter [65]. It can be explained by assuming that in addition to a first control parameter α a second parameter is varied. If this second parameter could be controlled by the experimenter then the hysteresis would be a static phenomenon again. However, the psychophysics experiments in which negative hysteresis has been found did not feature a second parameter manipulated by the experimenter [4, 56, 65, 67]. The existence of a second parameter was conjectured from the observed phenomenon [56, 65]. Following this work, we assume that the second parameter varies in time during the performance of a participant in a negative hysteresis experiment (see below in this section). Therefore, the negative hysteresis effect may be considered as a phenomenon featuring a dynamic component. In this context, note that the classification in Table 2 ignores the existence of the postulated second parameter. According to the two-parameter hypothesis negative hysteresis should be considered as a round trip in a two-dimensional plane (see Section 3.2 and Fig. 5 below). The classification in Table 2 represent the point of view of an experimenter who typically collapses the (hypothesized) two-parametric space onto a single parameter space.
Next, let us introduce the mean critical value α m =(α c,1+α c,2)/2. Then, there is a useful mapping between α c,1, α c,2, on the one hand, and α m , Δα, on the other [65]:
In order to simplify the model proposed in [65], let us shift the control parameter axis α by the mean critical value α m . To this end, a control parameter relative to the mean critical value can be defined like
Note that in this shifted framework the critical control parameter values are given by α r e l,c,1=α c,1−α m =(α c,1−α c,2)/2 and α r e l,c,2=α c,2−α m =(α c,2−α c,1)/2 which implies
Furthermore, we have
That is, in the original non-shifted scale α c,2 is located by Δα/2 above or below the mean critical value α m , whereas α c,1 is by Δα/2 located below or above the mean critical value α m depending on the sign of Δα.
Following earlier work [26], the growth parameters λ 1 and λ 2 may be related by a linear approximation to the control parameter α. In line with this suggestion, we assume that the parameters λ k depend on α r e l by means of a linear approximation around α m like
In (16) the variables L 1 and L 2 are considered as system parameters — just as λ 1 and λ 2. Here, β is a scaling factor that scales variations in the control parameter α to variations in the growth parameters λ k . (16) describes how environmental properties (given in terms of α) and conditions on the system parameter level (in terms of L k ) affect the order parameter level, see Fig 1.
In order to make contact with experimental studies in which positive hysteresis has been found we put L 1=L 2=L 0, where L 0 is a constant. In this case, a detailed calculation shows that (see Appendix A)
In order to address experimental studies in which negative hysteresis has been observed, we consider the framework depicted in Fig. 1, in which there is an interplay between order parameter dynamics and system parameter dynamics that is mediated by changes in the environment. More precisely, when the same task is executed several times in a succession, then it is assumed that the system adapts to the task. Alternatively, we may say that there is a habituation with respect to the task. Mathematically speaking, we assume that the parameters L 1 and L 2 change due to the task activity reflecting the aforementioned adaptation or habituation process. Let n=1,…,M denote the M events in which in a laboratory experiment the task is executed consecutively in an ascending or descending condition. Then the system parameter dynamics for L 1 and L 2 can be described by an autoregressive model (AR) of order 1 as suggested in [65]. Note that higher-order AR models or nonlinear models could be used as well without changing qualitatively the overall model properties. Let X(n) denote a time-discrete variable. Then, in general, the AR-1 model for X(n) reads X(n+1)−s=a 1[X(n)−s]+𝜖, where s is the process mean value, a 1 is the first autoregressive coefficient, and 𝜖 corresponds to a white noise process with variance \(\sigma _{\epsilon }^{2}\) [68]. Accordingly, we put
Here, T denotes a time constant and corresponds to a real number (i.e., is not necessarily an integer) with T≥1. Equation (18) describes the system parameter dynamics that affects the order parameter dynamics, see Fig. 1. According to the AR-1 model, L k converges to the mean value s k in a monotonic fashion. If T is close to 1, then the decay is fast. In contrast, if T≫1, then the decay is slow. From T≥1, it follows that we have a 1∈[0,1]. It can be shown that in this case the deterministic system parameter dynamics L k converges in a monotonic fashion towards the mean value s k , e.g. [68].
In order to describe the aforementioned postulated adaptation or habituation effect, we need to link the mean values s k to the dynamics of the order parameters ξ j . In fact, it has been shown that the observation of negative hysteresis is consistent with a habituation effect modeled in terms of the interplay between order parameter and system parameter dynamics [65] as defined by
with h≥0. For h>0 there is a “penalty” or inhibition of the “active” mode (i.e., the mode that is “on”) in the sense that the mean s k and consequently the growth parameter λ k is decreased by h. Note that this “penalty” effect is independent of the environmental impact α because it affects the offset parameters L 1 and L 2 in (16). The parameter h measures the magnitude of the adaptation (or habituation) effect.
Note also that for h=0 the variables L 1 and L 2 converge to the stationary value L 0 such that after a transient period we have L 1=L 2=L 0. As a result there is no interplay between order parameter dynamics and system parameter dynamics. Therefore, the case h=0 corresponds to the positive hysteresis case mentioned above.
For sake of simplicity, we consider in what follows only the deterministic case in which the noise terms of the AR-1 processes can be neglected. In the deterministic case, the evolution of the two system parameters L 1 and L 2 can be captured by the evolution of a single, appropriately defined parameter. In order to see this, we introduce the variables ΔL and L m like
This implies that L m satisfies a deterministic AR-1 model of the form
The dynamics of L m exhibits a fixed point L m,s t =L 0−h/2 that is independent of the order parameter dynamics. Therefore, we assume that L m is at that fixed point value and put
for all n. In contrast, ΔL satisfies a deterministic AR-1 model that is affected by the order parameter dynamics like
with
The variable ΔL can be considered as a control parameter because it affects the parameters λ k (just as α, see also Fig. 1) and the parameters λ k determine the bifurcation point between the two alternatives. However, ΔL is not manipulated by the experiment. Rather it is adjusted by the perceptual-cognitive-behavioral machinery between consecutive task performances. In this sense, it is an auto-regulated or self-regulated variable and may be referred to as auto-regulated or self-regulated pseudo-control parameter [65]. A detailed calculation shows that (see Appendix A)
In particular, the hysteresis size is given by
Due to the h term in (26), it is possible that the dynamical model (5) exhibits negative hysteresis: α r e l,c,2<0 , α r e l,c,2>0, and Δα<0. Explicit examples will be given in Section 3.
2.3 Parameters g and h
As will be argued below, the parameters L 0 and β can be chosen based on theoretical considerations and Δα might reflect experimental data. When L 0, β, and Δα are given, then the question arises how to determine the remaining parameters g and h. In [65], a sophisticated procedure was developed to obtain g(Δα) and h(Δα) as smooth functions (i.e., continuously differentiable functions) of Δα. In what follows, we consider a simplified approach in which h(Δα) is given by a piecewise linear approximation of that aforementioned smooth function. This choice of h then implies that g satisfies a similar piecewise continuously differentiable function (that is however nonlinear with respect to Δα). In detail, for h(Δα) we use
From (27) it follows that the “habituation” effect is completely absent in the case of positive hysteresis. In contrast, in the case of negative hysteresis the parameter h increases linearly with the magnitude of the hysteresis size. In fact, the proportional factor has been chosen to be equal to unity such that h equals the size |Δα| of the hysteresis effect. Substituting (27) into (26), it follows that g satisfies
with
where we assume that the parameters β and L 0 are chosen such that y<1 for Δα>0 (we will return to this issue in Section 3.2). Note that g and h are continuous functions at Δα=0. In particular, for g(Δα) we have Δα>0∧Δα→0 ⇒y→0 ⇒g→1.
3 Response times as build-up times of emergent perceptual-cognitive-behavioral patterns
3.1 General considerations on the mode skeleton
Our focus is on two alternative perceptual-cognitive modes or two alternative behavioral patterns. As mentioned in the introduction, the perceptual-cognitive behavioral system in general is described by a field variable q(x,t). The mode skeleton in the case of two perceptual-cognitive-behavioral modes reads q(x,t)=ξ 1(t)v 1(x,t)+ξ 2(t)v 2(x,t). If q(x)=v 1(x) holds then the agent is in the perceptual-cognitive-behavioral mode k=1 and we have \(\xi _{1}=\sqrt {\lambda _{1}}>0 \ \wedge \ \xi _{2}=0\), see also (8). In contrast, if q(x)=v 2(x) holds then the agent is in the perceptual-cognitive-behavioral mode k=2 with \(\xi _{1}=0 \ \wedge \ \xi _{2}=\sqrt {\lambda _{2}}>0\), see also (9).
When considering a perceptual-cognitive-behavioral system as a self-organizing pattern formation system, then the field variable q(x,t) may converge towards a mode v k but q can only reach the fixed point represented by that mode v k in infinitely large times. More explicitly, the emergence of a mode v k is given in terms of the approach of the amplitude ξ k to a fixed point attractor of (5) and this approach takes an infinitely long amount of time because the strength of the attractive “force” of the fixed-point attractor becomes weaker and weaker in the vicinity of the attractor. Therefore, we define the emergence of a perceptual-cognitive-behavioral mode as the event when q is sufficiently close to one of the elementary modes v k [28]. If there is a time point t such that q(x,t)≈v 1 then the agent is in the perceptual-cognitive-behavioral mode k=1 and we say that ξ 1 is “on” and ξ 2 is “off”. Likewise, if there is a time point t such that q(x,t)≈v 2 then the agent is in the perceptual-cognitive-behavioral mode k=2 and we say that ξ 1 is “off” and ξ 2 is “on”. The time point t when either of the two events happen is considered as response time RT. We can quantify the notion of order parameters that are “on” and “off” in an approximate sense by introducing response thresholds. It is useful to scale these thresholds with respect to the growth parameters [28]. Accordingly, we put
where 𝜃 and η are percentage values (i.e., 𝜃,η∈[0,1]). Note that in (30) and (31) the expressions \(\theta \sqrt {\lambda _{k}}\) and \(\eta \sqrt {\lambda _{j}}\) are absolute thresholds, while 𝜃 and η are relative thresholds.
When there is a choice between two perceptual-cognitive modes or two behavioral patterns then the selection may be based on the winning mode or the losing mode or on both.
In what follows, we want to proceed an analytical approach (for considerations on numerical approaches see Section 4). In order to do so, we will consider the two scenarios in which perception, cognition, and behavior is based on either the winning or the losing mode but not on both. In the case of the winning mode scenario, the perceptual-cognitive-behavioral mode k is emerged when (30) is satisfied and the response time of that event is defined by
In the case of the losing mode scenario, the perceptual-cognitive-behavioral mode k is emerged when the alternative mode j has disappeared such that (31) is satisfied. The response time of this event is given by
3.2 Flat response time curves in pre- and post-transition regions
When the control parameter α is scaled beyond a critical value then the interaction between the two competing modes is essential and cannot be neglected. In contrast, when α is not too close to any critical value then the impact of one mode on the other might be relatively small. We consider the winning mode scenario and derive an analytical expression for response time RT under the idealization that the inhibitory interaction due to the losing mode is negligibly small when α is not too close to any critical value. Let k denote the index of the winning mode. Then, the evolution of the winning mode under the aforementioned approximation is given by
Let us assume that ξ k converges towards the stationary value \(\xi _{k,\text {st}}=\sqrt {\lambda _{k}}\) from ξ k =D ξ k,sts t with D∈[0,1] and D<𝜃. Then, the time to reach the threshold 𝜃 can be computed from (32) and (34). We obtain [28]
with
If Z is constant and λ k varies only to a small extent as a function of the control parameter α, then the response time RT is approximately constant except close to critical values of α when the perception or behavior switches from one mode to the alternative mode. As a result, the sequence of response times will be flat in the pre-transition and post-transition regions. Let us model this situation in more detail.
Let [λ min,λ max] denote the intervalFootnote 1 in which growth parameters λ 1 and λ 2 can be found. The range of this interval is
In line with the aforementioned considerations we assume that the range is small relative to L 0. We put
where w is a percentage value w∈[0,1]. For a perceptual-cognitive-behavioral system with a relatively small physiological range of growth parameters the parameter w is close to zero (e.g., w=0.01). From the linear approximation (16) it follows that (38) is satisfied if
If (39) holds then in turn it can also be shown that the auxiliary variable y as defined by (29) satisfies the condition y<1.
We conducted a set of simulations to illustrate the model prediction that the interplay between order parameter and system parameter dynamics based on a winning mode scenario can lead to transitions with positive and negative hysteresis and a flat response time curve in pre- and post-transition regions. Simulation of the order parameter dynamics ξ 1 and ξ 2 via (5) and system parameter dynamics via (18) were conducted. In the computer experiments, the system parameter dynamics and the environmental influences affected the order parameter dynamics via (16). The order parameter dynamics affected the system parameter dynamics via (19), see Fig. 1. The response was based on the winning mode scenario and RT was determined numerically using (32). The analytical value RT defined by (35) was calculated as well for comparison purposes with the numerical value.
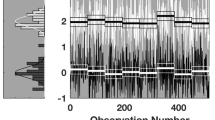
Figure 2 shows two representative trajectories of ξ 1(t) and ξ 2(t) computed from the order parameter equations (5) for fixed system parameters α, λ 1, and λ 2. In the simulation, the trajectories converged to their respective stationary values ξ 1,s t and ξ 2,s t . The trajectories shown in Fig. 2 are two trajectories from the first trial of several trials conducted in the aforementioned computer experiments. In fact, the control parameter α was increased in steps mimicking an ascending sequence of experimental conditions by the experimenter (e.g., change of object size in grasping-experiments). Subsequently, α was decreased reflecting a descending sequence of experimental conditions. For each α the model sketched in Fig. 1 was solved numerically.
Figure 3a shows λ 1 and λ 2 as function of α, while Fig. 3b shows the implicit dependency of L 1 and L 2 on α via ξ 1 and ξ 2. The parameters λ k changed as defined by (16): λ 1 decreased in the ascending condition, while λ 2 increased. Vice versa, λ 1 increased in the descending condition, while λ 2 decreased. Note that for the descending condition, the bottom panels in Fig. 3 should be read from right to left rather than from left to right. Since the computer experiments shown in Fig. 3 considered the case in which the system parameter dynamics was decoupled from the order parameter dynamics, L 1 and L 2 did not change. For each given α and the corresponding parameters λ k (α) and L k the trajectories ξ 1(t) and ξ 2(t) were computed numerically—just as it is shown in Fig. 2 for the very first trial. Figure 3c shows the stationary values ξ 1,s t and ξ 2,s t obtained from these simulations. Finally, Fig. 3d shows the responds times RT as obtained from the numerical simulation (symbols) and as predicted by (35). We found a good match between predicted and numerically obtained values. The numerically obtained values were slightly larger than the predicted values due to the inhibitory interaction between the modes. Importantly, Fig. 3d illustrates that the response times RT were approximately constant in the pre- and post-transition regions. That is, except for the transition point, the response times assumed more or less the same values. Figure 3 illustrates mode-mode transitions when α was increased gradually and subsequently decreased for the case of a system exhibiting positive hysteresis. In contrast, Fig. 4 demonstrates the negative hysteresis case — again for the flat response time curve.
Simulation results for hysteretic mode-mode transitions in the case of positive hysteresis and a flat response time curve in the pre- and post-transition regions. Panel a λ 1 (solid) and λ 2 (dashed). Panel b L 1 (solid) and L 2 (dashed). Both lines are on top of each other. Panel c ξ 1,s t (full circle) and ξ 2,s t (open diamonds). Panel d response times in a logarithmic scale as obtained numerically (symbols) and as defined by (35) (solid line). Parameters: g=1.0168, h=0, α={5,7,...,33}, 𝜃=0.95, D=0.60, w=0.10, L 0=0.7002, β=0.0023, T=5
Simulation results for hysteretic mode-mode transitions in the case of negative hysteresis and a response time curve that is flat in the pre- and post-transition regions. Panels as in Fig. 3. Parameters: g=1.0, h=0.0219, α={11,13,...,41}, 𝜃=0.95, D=0.60, w=0.10, L 0=0.7002, β=0.0022, T=5
The panels of Fig. 4 show the same quantities as the panels in Fig. 3. Figure 4a shows the growth parameters λ k for every trial with a given parameter α and with auto-regulated system parameters L k as shown in Fig. 4b. Figure 4b shows the implicit dependency of the system parameters L k on α via ξ k . The system parameters L k changes due to the dependency on ξ k and as a result of the mode-mode transitions. Figure 4c depicts again the order parameter values ξ 1,s t and ξ 2,s t , while Fig. 4d shows the responds times RT as obtained from the numerical simulation (symbols) and as predicted (solid line). As expected, the response time curve was found to be flat. Figure 5 illustrates the notion of a single effective auto-regulated pseudo control parameter ΔL as defined above. In experimental trials in which an external control parameter α is increased and subsequently decreased, the dynamical system actually makes a round trip in the parameter space spanned by α and ΔL [65].
3.3 Peaked response time curves
Here we consider the case when the losing mode determines the time point when a perceptual-cognitive mode has emerged, a behavioral response is initiated, or a behavioral pattern is being performed. That is, response time is based on the condition described by (31) and is defined explicitly by (33). In this context, using linear stability analysis, it can be shown that the order parameter ξ j of the losing mode decays to zero like [26]
where r denotes the Lyapunov exponent in the direction of ξ j . For r, we obtain
Here, λ k and λ j are the exponential growth rates of the winning and losing modes, respectively. When α approaches one of the critical parameters α c,1 or α c,2 then we have λ j /λ k =g, see (8) and (9). The Lyapunov exponent r goes to zero and it takes more and more time for perturbations to decay (“critical slowing down”). Let us assume ξ j (t) converges from \(\xi _{j}(t_{1})= E \, \sqrt {\lambda _{j}}\) to ξ j (t→∞)=0 with E∈[0,1] and E>η. Then, at a time point t 2>t 1 we have ξ j (t 2)=η. Then the response time RT defined by (33) for the linearized order parameter equation (40) is given by R T=t 2−t 1 and reads
When α→α c then r→0, which implies R T→∞. Note that due to the nonlinearities in the full order parameter equations defined by (5) the response time defined by (33) will be finite at α=α c,1 or α=α c,2 and will not go to infinity. However, since the linear “force” described by the right hand side of (30) becomes weaker and weaker in the limiting case α→α c , the response time RT of the full nonlinear model increases as a function of α for α→α c and will exhibit a peak at α=α c .
Just as in Section 3.2, we conducted a set of simulations to illustrate the effect of a vanishing Lyapunov exponent on the timing of recognition events and behavior. More precisely, we computed the evolution of the order parameters ξ 1 and ξ 2 from (5) and the evolution of the system parameters from (18). In these simulations, the system parameter dynamics and the environmental influences affected the order parameter dynamics via (16). The order parameter dynamics had an effect on the system parameter dynamics via (19). Response time calculations were based on the losing mode scenario and RT was determined numerically using (33). The analytical value RT defined by (42) was calculated as well for comparison purposes with the numerical values.
Figures 6 and 7 consider the positive and negative hysteresis cases, respectively. Figures 6a and 7a show the growth parameters λ k for every trial with a given parameter α. Figures 6b and 7b illustrate the implicit dependency of the system parameters L k on α via ξ k . While for the positive hysteresis case (Fig. 6b) the system parameters L k did not change, in the negative hysteresis case (Fig. 7b) they varied systematically as predicted above reflecting a “penalty” or inhibition of the “active” mode. Figures 6c and 7c report the order parameter values ξ 1,s t and ξ 2,s t . Figures 6d and 7d shows the responds times RT as obtained from the numerical simulation (symbols) and as predicted (solid line). As expected, the response times increased towards the transition points. The exact (i.e., numerically obtained) values were found to be larger than the predicted values. Note that the predicted value is derived by means of a linear stability analysis that assumes that the order parameter ξ k of the “active” mode is very close to its stationary values, while the order parameter ξ j of the mode that is “off” is very close to zero. These two conditions are only approximately satisfied. Due to the violation of these conditions, the exact (numerically obtained) response times (symbols) were larger than the response times predicted by the linear stability analysis. However, the linear stability analysis was still found to be useful in predicting at least qualitatively the increase of response times when the system approaches the transition point.
Simulation results for hysteretic mode-mode transitions in the case of positive hysteresis and a peaked response time curve. Panels as in Fig. 3. Parameters: g=1.0168, h=0, α={5,7,...,33}, η=0.10, E=0.20, w=0.10, L 0=0.7002, β=0.0023, T=5
Simulation results for hysteretic mode-mode transitions in the case of negative hysteresis and a peaked response time curve. Panels as in Fig. 3. Parameters: g=1.0, h=0.0219, α={11,13,...,41}, η=0.10, E=0.20, w=0.10, L 0=0.7002, β=0.0022, T=5
3.4 Experimental replication of the peaked response time curve observed by Fitzpatrick et al.
As mentioned in the introduction, a peaked response time curve was reported in the literature in an experiment in which participants were asked to judge whether they could stand on a tilted platform with a certain angle of inclination [67]. In order to highlight the relevance of modeling peaked response time curves, we conducted a similar experiment in order to replicate the response time curve. Note that the earlier study conducted by Fitzpatrick et al. examined various aspects of the judgment task. In contrast, we were only interested in illustrating the robustness of the phenomenon. That is, the objective was to show that with slightly different materials and a slightly different set of inclination angles the basic pattern of results, namely, the peaked response time curve, can be found as well.
3.4.1 Method
Participants
Ten University of Connecticut undergraduate students between the ages of 18 and 26 participated in the study, in partial fulfillment of a course requirement. Six participants were male and four were female. The experiment was conducted with the approval of the University of Connecticut Institutional Review Board.
Materials
A wooden dowel 121.92 cm in length and 1.59 cm in diameter was used for dynamic-touch trials. A felt blindfold was used on dynamic-touch trials to eliminate visual information, and on visual trials while the experimenters adjusted the slope of the surface. Participants wore circumaural headphones playing white noise to eliminate auditory information while the experimenters adjusted the slope. Beeping noises were also played through the headphones to signal the start of each trial. Participants indicated their responses by pressing a button on a Logitech wireless presentation remote. A PC running custom software written in Python controlled the audio and recorded participants’ responses and response times.
Apparatus
The apparatus consisted of a solid wooden 75.88 cm x 210.19 cm platform leaned on a heavy metal block. The slope of the platform was adjusted by sliding the block along the floor. For seven angles of inclination: 12∘, 17∘, 22∘, 27∘, 33∘, 39∘, and 45∘, the corresponding position of the block was determined and marked on the floor so it could be quickly recreated. The apparatus was strong and stable enough to support a person’s weight. A rubber mat was attached to the platform in order to increase friction.
Design and procedure
The participant’s task in this experiment was to determine whether a surface would support stable upright posture, defined as maintaining balance while standing with feet flat and parallel.
The participant perceived the slope either visually or haptically. In the haptic condition participants were allowed to touch the slope with the tip of the dowel. In both types of trials, participants stood with their heels 1 m away from the slope. They wore a blindfold and listened to white noise while the experimenters adjusted the slope of the surface. For haptic trials, the participants were instructed to hold the dowel touching the floor and the side of their foot during this time. An experimenter pressed a button on the PC to indicate that the slope was ready, pausing the white noise. After a random delay of 0.5–1.5 s, the participant heard a beep indicating the start of the trial. For visual trials, the participant lifted the blindfold at the sound of the beep; for haptic trials, the participant lifted the dowel and began exploring the slope.
The participants indicated their responses by pressing one of two buttons on the presentation remote, that a right button press indicated that the ramp could support upright posture, while a left button press indicated that it could not. Subsequently, participants returned their blindfold to their eyes (visual condition) or the dowel to the initial position (haptic condition). The experimenters then adjusted the angle of inclination of the slope for the next trial.
Response time was recorded beginning with the beep and ending when a button on the presentation remote was pressed. Participants were not asked to respond quickly; the instructions did not address the speed of the response in any way.
Seven angles of inclination were crossed with the two perceptual modalities for a total of 14 experimental conditions. Each condition was repeated three times for a total of 42 trials per participant. Haptic and visual trials were conducted in separate blocks. Half the participants began with the visual trials and half began with the haptic trials. Angle of inclination was randomized within each block.
At the end of each session, the participant’s maximum angle of inclination allowing upright posture was estimated. Beginning with the smallest angle, the participant attempted to stand on the platform. If the participant was able to achieve stable upright posture, the angle of inclination was increased. If the participant was not able to achieve stable upright posture within two attempts, the previous angle was recorded as the participant’s maximum possible angle of inclination. Note that in order to stand on the platform, participants were allowed to bend their bodies both at the hip and the ankle. This was different from the study by Fitzpatrick et al. [67], in which participants were only allowed to bend at the ankle. Our procedure more closely reflects real-world standing on inclined surfaces, and is also safer.
3.4.2 Results
Data were checked for outliers. In this step, data from one participant was excluded from any analyses because that participant dominated the results by taking more than three times the standard deviation longer than the mean response time for almost every trial. For each of the remaining nine participants, the proportion of “yes” responses and the mean response time was calculated for each of the 14 experimental conditions.
Figure 8 (top panel) shows the percentage of “yes” responses as function of the inclination angle for the visual and haptic conditions. The percentage of “yes” responses decayed more or less monotonically with increasing inclination angle. The pattern of responses were similar between the two perceptual modalities.
The perceived maximum possible angles of inclination, defined as the angle of inclination resulting in 50% yes responses, was estimated using linear interpolation. This was estimated to be 26.04∘ for visual perception and 27.75∘ for haptic perception. The maximum possible angle of inclination, averaged across participants, was 30.33∘.
For hypothesis testing purposes, the resulting proportions of “yes” responses were arcsine-transformed according to \(p^{\prime }=\arcsin \sqrt {p}\), where p is the proportion of “yes” responses. This transformation normalizes proportion data. A 2×7 (perceptual modality × angle of inclination) within-subjects ANOVA revealed no significant main effect of perceptual modality on proportion of “yes” responses, F(1,8)=1.47, p>.05. The main effect of angle of inclination on proportion of “yes” responses was significant, F(6,48)=29.42, p<.0001. The effect on proportion of “yes” responses of the interaction between angle of inclination and the perceptual modality was not significant, F(6,48)=0.83, p>.05.
Figure 8 (bottom panel) shows response times by inclination angle and condition. First of all, Fig. 8 (bottom panel) indicates consistently longer response times for haptic perception than for visual perception. Second, the graphs showed a more or less pronounced peaked. The maximum average response times occurred at 27∘ for both haptic and visual perception, closely matching the perceived maximum possible angles of inclination of 27.75∘ and 26.04∘, respectively.
A 2×7 (perceptual modality × angle of inclination) within-subjects ANOVA was performed on response times, finding a significant main effect of the perceptual modality, F(1,8)=25.32, p<.01 and marginally significant main effect of angle of inclination, F(6,48)=2.20, p=.059. The interaction between angle of inclination and perceptual modality was not significant, F(6,48)=0.55, p>.05.
4 Conclusions
Using a model-based approach, we investigated the interaction between self-organizing processes (related to perception, cognition, and behavior of humans) and learning and adaption processes (related to the plasticity of the human brain). Self-organizing processes were described by means of the evolution of order parameters. Learning and adaptation processes were described by postulating a system parameter dynamics, see Table 1. In particular, we developed the model sketched in Fig. 1 that involves different components such as the order parameter dynamics, system parameters dynamics, and the varying environmental influences. We showed that the model can describe switches between alternative perceptual-cognitive-behavioral modes in terms of bifurcations in an appropriately defined dynamical system. In particular, we showed that both positive and negative hysteresis is predicted to occur in such systems. Indeed, in particular, negative hysteresis has been observed experimentally in certain decision-making and judgment experiments [4, 56, 65, 67]. It is important to note that our model-based analysis reveals that negative hysteresis is a consequence of the interplay between order parameter dynamics and system parameter dynamics, where system parameters act as a pseudo-control parameters, see also Ref. [65]. In particular, as argued in a previous study [65], negative hysteresis cannot be explained by means of an order parameter model involving only a single externally manipulated control parameter. Since a deterministic, dynamical model that features a single parameter that is controlled by the experimenter cannot explain negative hysteresis, this also implies that the order parameter model (2) where λ 1 and λ 2 are certain functions of a control parameter α cannot be used to explain a negative hysteresis effect. An extended version of the order parameter model is required, which, for example, is given by the two-component model presented in Section 2 composed of order parameter dynamics and system parameter dynamics. In contrast, in the case of positive hysteresis the order parameter dynamics is sufficient to capture the hysteretic transition [26]. In this context, we would like to point out that the case of transitions that exhibit no hysteresis at all is included in the model as a special case for Δα=0. In this case, the order parameter dynamics model again is sufficient to describe the observed transitions between two alternative perceptual-cognitive-behavioral modes.
As such, the self-organization perspective of perceptual-cognitive-behavioral processes has its own conceptual stance. However, it is consistent to some extent with other theoretical concepts such as direct perception [10]. Let us illustrate this issue for the order parameter model described in Section 2. The model involves a control parameter α that has been related in the current study and earlier studies with physical properties of the environment. In the experimental study presented in Section 3.4, the parameter α has been associated with the angle of inclination of the floor. In previous studies on grasping transitions, α has been associated with relative object size defined as the length of an object in units of the hand span of the person intending to grasp the object [6, 25, 26]. Accordingly, cognitive processes (e.g., perceptual judgments) and behavioral responses (e.g., grasping) depend directly on physical quantities. Importantly, in the context of perceptual-cognitive-behavioral processes exhibiting negative hysteresis transitions, the processes at hand depend on the circumstances under which they takes place. In an ascending sequence, the control parameter α acts in a different way on the decision-making process than in a descending sequence. These circumstances are captured by the parameter dynamics. In summary, the modeling effort focusing on the interplay between order parameter dynamics and system parameter dynamics supports the notion of direct perception [10] and supports the hypothesis that direct perception can be mediated by the “occasion” under which it takes place [69, 70].
Response times were conceptualized as the times it takes for building-up the physical, neuro-biological patterns corresponding to the perceptual-cognitive-behavioral modes under consideration. We distinguished between two scenarios summarized in Table 3. If the criterion for a mode to be emerged is based on the emergence of the elementary pattern v k of that mode, that is, on the “winning mode” k, then the response time is determined by the growth parameter λ k of that mode. When systems parameters are changing such that the growth parameter λ k approaches its critical value at which the mode k becomes unstable and a transition to an alternative mode j occurs, then λ k does not necessarily vary in a dramatic ways. A relative small change in λ k can be sufficient. If so, the response time curve does not exhibit pronounced variations in the pre- and post-transition regions and is relatively flat, see Section 3. In contrast, if the criterion for a mode v k to be emerged is based on the disappearance of the alternative mode v j , that is, on the “losing mode”, then the response time is determined approximately by the Lyapunov exponent of the amplitude ξ j of the mode j. When approaching the transition point at which the mode k becomes unstable such that a transition from k to j is possible, the Lyapunov exponent goes to zero and consequently the response time increases. As a result, the response time curve exhibits a peak close to the transition point, see Section 3. Importantly, the model predicts that as such both types of response time curves can be observed under positive as well as negative hysteresis.
Within the framework of self-organization, response times are a direct consequence of the time scales on which spatio-temporal patterns evolves that describe perception, cognition, and behavior (see the Introduction for our initial hypothesis). More precisely, response times are determined by the characteristic time scales on which order parameters evolve. The reason for this is that perception, cognition, and behavior are considered as pattern formation processes in a physical system. Therefore, an appropriate metaphor for perceptual-cognitive-behavioral processes would be the Benard instability [18, 22]. The Benard instability is about roll patterns (convection rolls) emerging in fluid layers that are heated from below. The time scales on which the roll patterns emerge and in particular the phenomenon of critical slowing down has been studied by experimental work [46–48] and has been described mathematically by amplitude equations [18] of the kind used in Section 2. From a physicist’s point of view, there is no doubt that the amplitude (order parameter) equations determine the build-up of the roll patterns. Consequently, as long as there is an agreement among scientists working in psychology, biology, and related fields that the Benard instability is a valid and useful metaphor for the self-organization of perceptual-cognitive-behavioral processes, then it is clear that response times are explained by the theory of self-organization. Having said that, we would like to mention that in the literature this point of view has been questioned [71]. Although an in-depth analysis of the arguments developed in [71] is beyond the scope of the present study, a key step in the argumentation presented in [71] is that a self-organization process is associated with a search algorithm.
The notion of a search algorithm, however, is inconsistent with the aforementioned metaphor of the Benard instability. From a physicists point of view, the emergence of a roll pattern has little to do with a search algorithm. There is no entity (e.g., a homunculus) hidden somewhere inside the fluid layer searching for the correct solution. Therefore, it seems that the considerations in [71] are based on a metaphor (search algorithm implying the existence of a homunculus) that is not appropriate for self-organizing systemsFootnote 2. Having said that, a more comprehensive analysis of this issue should be carried out but is left for future work.
As opposed to the aforementioned notion of a search algorithm, self-organization processes described by order parameter dynamics and system parameter dynamics clearly evolve in time and the evolution can be described as a trajectory or “solution path” in the space of order parameter and system parameter variables. Focusing only on the order parameter dynamics such a trajectory in special cases satisfies a gradient dynamics. If so, then the trajectory descends in an appropriately defined potential and it may look as if the process would “search for” a potential minimum. For example, the order parameter equation (5) can be written as a gradient dynamics like
If λ 1 and λ 2 do not vary with time, then the trajectory ξ 1(t),ξ 2(t) describes a solution path that descends in the potential V towards a local potential minimum.
Within the statistical mechanics framework of neuronal interactions proposed by Ingber [72], response times are considered as the time it takes for appropriately defined trajectories to visit and pass along certain attractors corresponding to representations of memorized items [73]. These trajectories may be seen as counterparts to the trajectories of order parameter variables. For example, a generalized version of (5) for three order parameters ξ 1,ξ 2,ξ 3 has been used to describe the perception of letters E, F, and H [35]. For an initial letter that is incomplete but similar to the letters E and H, the perceptual process follows a trajectory in the three-dimensional order parameter space ξ 1,ξ 2,ξ 3 that is initially close to the attractors that represent the letters E and H. Eventually, the perceptual process converges to one of the two attractors (see Fig. 3 in [35] for a graphical illustration). Similar to Ingber’s proposal and in line with the definition of response times presented in Section 3, the time to perceive a letter would be given by the time it takes the trajectory to pass along the attractors in the order parameter space ξ 1,ξ 2,ξ 3 and to converge to the final attractor. Note that since Ingber’s approach is a statistical approach, response times are computed from averages over several possible solution paths. This statistical aspect is not addressed in Section 3. However, we will make below some comments on stochastic generalizations of the model discussed in Sections 2 and 3.
In Section 3 the two scenarios were worked out analytically. Numerical solutions were used for illustration purposes only. In general, the criterion that determines the time point at which a mode has emerged (e.g., a decision is made or a behavioral response is initiated or executed) can be based on complicated rules or mechanisms that go beyond the two scenarios listed in Table 3. In particular, we may imaging that both the “winning mode” has to be emerged and the “losing mode” must have been disappeared such that both threshold conditions (30) and (31) must be satisfied at the same time. Such a scenario and other more comprehensive situations may be studied using extensive simulations of the model sketched in Fig. 1. However, this is beyond the scope of the present effort and might be investigated in future work. Likewise, future efforts may extend the model developed above by taking aspects of perceptual-cognitive-behavioral processes into account that have not been considered so far. For example, when measuring a behavioral response (e.g., pressing a button) there might be a motor delay between the verbal response and the emergence of a neuro-biological pattern in a certain brain area that triggers the behavioral response. A famous model in this regard that roughly speaking involves a motor delay component in addition to some kind of decision-making component is the Wing-Kristofferson model for timing of repetitive movements [74].
We directed special attention to the scenario that involves peaked response time curves. On the one hand, we argued in Section 3.3 that peaked response time curves are consistent with a fundamental phenomenon of equilibrium and non-equilibrium phase transitions: the phenomenon of critical slowing down. One the other hand, we conducted a small-scaled experimental study to replicate a peaked response time curve reported earlier by Fitzpatrick et al. [67] and reported the results in Section 3.4. In particular, we found inverted U-shaped response time curves with peaks close to the transition points of “yes” and “no” responses. This is consistent with the response time graphs reported in the original study by Fitzpatrick et al. [67]. Following the protocol of the original study, in order to determine the response times of the participants inclination angles were presented in random sequences. Consequently, the hysteresis size and the type of hysteresis could not be determined in the experiment reported in Section 3.4. However, the hysteresis size and type was determined in the study by Fitzpatrick et al. [67] by means of an additional experiment. They found transitions with negative hysteresis. Taken our observations and the results of the previous study together,we are inclined to say that in the experiment on judging one’s ability to stand on tilted platforms the judgments are subjected to hysteretic transitions and feature peaked response time curves. That is, that participant behavior features one of the four cases addressed by the generalized order parameter model sketched in Fig. 1. Recall that as pointed out above negative hysteresis is consistent with an interplay between order parameter dynamics and systems parameter dynamics and peaked response times may arise due to critical slowing down. Therefore, according to the model sketched in Fig. 1, the underlying principles that lead to the observed negative hysteresis and the observed peaked response time curves in the Fitzpatrick et al. experiment are the interaction between order parameter and system parameter dynamics reflecting some kind of (short term) plasticity of the human brain and the critical slowing down phenomenon that classifies the observed transitions between behavior responses as non-equilibrium phase transitions of a self-organizing system.
Noise can affect various components of perceptual-cognitive-behavioral processes [9]. It might affect perception, neural information processing related to cognition, or motor responses executed on the muscular-skeletal level. Typically, noise leads to performance variability. That is, a task that is performed several times is not performed each time in exactly the same way. The model outlined in Sections 2 and 3 might be generalized to account for the impact of noise sources. For sake of brevity, we will address only two issues in this context: the definition of response times and implications for the observation of peaked response time curves related to critical slowing down. Due to the impact of noise on perceptual-cognitive-behavioral processes certain thresholds as defined in Section 3 may be reached at different time points when a task is repeated several times. In the literature of stochastic processes, these time points represent first passage times [75]. An ensemble of first passage times constitutes a distribution. Consequently, response times constitute a distribution function. However, for sake of clarity it is often preferred to report a single numerical value rather than a whole curve. In this context, the mean value of the first passage times, the so-called mean first passage time has been studied extensively in physics [75]. Importantly, the mean first passage time has also been applied in motor control problems described by order parameter equations [76]. Having identified the mean first passage time as a possible replacement for the response times defined in Section 3 when noise is taken into account, let us briefly address a implication of strong noise for the observation of peaked response time curves. In order to simplify the argument let us consider an extension of the model described in Sections 2 and 3 in line with the aforementioned Wing-Kristofferson model for timing of repetitive movements [74]. Accordingly, let us assume that the two-component model composed of order parameter dynamics and system parameter dynamics is not subjected to noise. However, there is a motor delay component subjected to strong motor noise. Let us assume that the deterministic two-component model yields a peaked response time curve with a peak that exceeds by Z time units the response times that can be observed far away from the bifurcation point. If the noise in the motor delay is strong relative to the effective peak size Z (i.e., standard deviation of the noise is comparable or much larger than Z) then it will be difficult to identify the peak. That is, based on a small sample of observations we will not be able to arrive at the conclusion that the response time curve exhibits a statistically significant peak. From these considerations it follows that when experimentally observed response times do not exhibit a “clear” peaked at a bifurcation point, then this does not necessarily rule out the peaked response times model proposed in Section 3.
The model developed in Section 2 is similar to a model discussed earlier by Lopresti-Goodman et al. [65] but also features some differences. In order to highlight the similarities and differences, we may refer to Fig. 1 again. The model presented here as well as the earlier model feature the same three components: order parameter dynamics, system parameter dynamics, and environmental influences. In particular, the evolution equations for the order parameter dynamics and systems parameter dynamics are identical across the two studies. In addition, the coupling parameters s k depend in the order parameters ξ k in the same way in both studies. However, the coupling parameters λ k have been treated differently in Section 2. Qualitatively, in both models λ k depend in the same way on the control parameter α (e.g., relative object size or angle of inclination). However, in the sections above we introduced a relative control parameter α r e l normalized with respect to mean critical control parameter values, whereas in the study by Lopresti-Goodman et al. the control parameter was used as it is. Moreover, in the sections above, we introduced a scaling parameter β that determines the extent to which variations in α r e l induce variations in λ k , see (16). In contrast, in the study by Lopresti-Goodman et al. such a proportionality factor was not considered (because it was not in line with the main objective of the Lopresti-Goodman et al. study). The normalization and the proportionality factor allowed us the make predictions about response times based on theoretical considerations. These predictions were confirmed in Section 3 by numerical solution methods. The question arises whether these modifications are necessary in order to predict flat and peaked response time curves. An answer to this question cannot be given at this stage. Extensive numerical work may be conducted to show that the original model can produce flat response time curves for an appropriate chosen set of model parameters and peaked response time curves for other sets of model parameters. If such parameter sets could be found, we would be inclined to say that the differences between the models suggested here and in the Lopresti-Goodman et al. study are not essential.
In the previous sections, perceptual-cognitive-behavioral processes that exhibit transitions between two alternatives were considered. These considerations may be generalized to take more than two alternative into account. In fact, the originally proposed order parameter equations by Haken [18] describe pattern recognition of an arbitrary number of patterns. Likewise, an order parameter model for four behavioral grasping modes featuring growth parameters that depend on two different control parameters was discussed in the context of infant development [25]. However, for human actors confronted with several alternatives to choose from, the Hick-Hyman law has been established in the literature [77, 78]. The law states that response times increases in a logarithmic function with the number of alternatives. The Hick-Hyman law is derived from an information theoretical perspective, where information refers to statistical information as defined by Shannon’s information theory. A detailed discussion about response times predicted by the order parameter model presented in Section 3 and the Hick-Hyman law goes beyond the scope of this paper. We will restrict our considerations only to two aspects.
First, the response times defined by (35) and (36) apply to the situation in which the alternative patterns (i.e., options for decision-making) do not interact with each other. Therefore, based on (35) and (36) we immediately arrive at (a somewhat trivial) prediction for a generalized order parameter model that involves more than two alternatives. If the alternatives to be considered in the task do not interact with each other, then the response time is predicted by (35) and (36) and does not depend on the number of alternatives. In particular, if there are several control parameters (or a single one) that induce bifurcations between the alternatives (i.e., make the actor to chose between different options), then ”sufficiently” far away from the bifurcation points the response times do not depend on the number of alternatives. Note that this prediction is not in conflict with the aforementioned Hick-Hyman law. From a dynamical systems perspective, the law focuses on the situation when the actor rapidly switches between alternatives. In this case, the dynamical system underlying the perceptual-cognitive-behavioral process at hand operates close to bifurcation points (see also Haken [18] for some comments supporting this assumption).
Second, if the order parameter dynamics defined in Section 2 operates close to bifurcation points, then response times in general depend on the interactions between the order parameters. It is not clear whether in this case analytical solutions can be derived because a detailed mathematical analysis of the coupled set of order parameter equations (5) for more than two order parameters is technically involved. Nevertheless the structure of the equations allows us to arrive at a scientific guess about the effect of the number of alternatives on the response times. Recall that as stated in Section 2.1 the mixed nonlinear terms \(\xi _{j} {\xi _{k}^{2}}\) describe the inhibitory interaction between two patterns j and k associated with the order parameters ξ j and ξ k . That is, the nonlinear mixed terms slow down the increase of the order parameters. In other words, they describe that the build-up of a pattern is inhibited by another pattern. In a generalized model featuring a number M of alternative patterns each pattern is affected by M−1 inhibitory impacts due to the competition between patterns. Therefore, if M increases the total inhibition may increase. In this scenario, response times increase with the number M of alternative patterns. In fact, in a special case, it is possible to determine an analytical solution that shows explicitly that response times predicted by the order parameter model increase monotonically as a function of M (see Appendix B). In this special case, the order parameter model yields predictions that are at least qualitatively consistent with the Hick-Hyman law. However, in general, the relationship between response times and the number of alternatives M under consideration depends on various details such as the initial conditions of the order parameters and the model parameters g and λ k . Therefore, in order to obtain a comprehensive picture about predicted response times and the number of alternative choices in a generalized order parameter model of the form (5) a more detailed analysis is need. In any case, response times and how response times depend on the number of alternatives (the question underlying the Hick-Hyman law) is approached in the current study from a dynamical system perspective, whereas in the literature the Hick-Hyman law is approached from a statistical, information theoretical perspective [73, 77, 78].
Figure 1 outlines a generalized order parameter model that involves two dynamical systems that interact with each other: the order parameter dynamics and the system parameter dynamics. In general and in particular for our understanding of negative hysteresis, there is a bi-directional interaction between the two dynamical systems. This implies that the generalized model features circular causality. A switch between order parameters may induce a change in the evolution of the system parameters. Changes in the values of the system parameter may induce bifurcations in the order parameter dynamical systems, that is, transitions between order parameters. On a phenomenological level this circular causality reflects that when perceptual-cognitive-behavioral processes change from one mode to another then this may affect or induce learning and adaptation and changes the neural connections of the human brain. The learning and adaptation processes in turn may affect the perceptual-cognitive-behavioral processes and even lead to changes between different modes of those processes. The generalized order parameter model belongs to a class of models, where circular causality plays an important role. In this context, short-term adaptation to visual stimuli has been modeled within the order-parameter/system-parameter dynamics framework outlined above and has been proposed to lead to oscillatory visual perception of ambivalent figures (e.g., Necker cube) [1] and temporary motion-induced blindness [79]. The concept of circular causality connecting order parameter dynamics and system parameter dynamics may has clinical applications as well. It has been proposed that the rituals of patients suffering from obsessive-compulsive disorders arise from the interaction of dynamic processes taking place on both the behavioral level and the neural level. More precisely, actions that are initiated by neural trigger stimuli self-inhibit these stimuli and at the same time excite the stimuli that trigger the appropriate follow-up actions [80, 81]. Likewise, disease emergence and treatment of bipolar disorder patients may be understood from an interplay between order parameter and system parameter dynamics. Accordingly, mood oscillations in bipolar disorder patients emerge when a clinically relevant control parameter exceeds a certain threshold. As a candidate for this clinically relevant control parameter a measure for the malfunctioning of the mood-regulatory cell signaling on synaptic cells has been considered [59]. It has been argued that if a bipolar disorder patient is treated with a drug therapy then the control parameter will decay below a particular threshold level (not necessarily identical with the first one) and the pathological mood swings will disappear. In this case, the amplitude of the mood swings is considered as an order parameter that satisfies an order parameter equation similar to (5), while the clinically relevant control parameter is regarded as a system parameter that evolves in time according to an appropriately defined system parameter equation [66]. Table 4 summarizes these studies. Table 4 also points out that in previous studies timing aspects have only been addressed with respect to the switching times of perceptual reversals (oscillations), whereas the efforts in Section 3 were concentrated on the discussion of response times.
In the context of clinical applications we would like to highlight again that the system parameter dynamics is tailored to describe processes related to the plasticity of the human brain. In this context a model for stroke rehabilitation has been proposed that includes among other components a behavioral component and an adaptation component capturing changes in the synaptic connections of the motor cortex [82]. Accordingly, training the limb affected by stroke results in reorganization of the motor cortex network exhibiting the stroke-induced brain lesion such that the motor control of the affected limb improves. Importantly, the training increases the chance that in voluntary (free choice) movements patients will use the affected limb again which will further improve the organization of the affected motor cortex area. In this scenario, a certain type of motor activity improves neural network connectivity. Due to the improved connectivity structure the beneficial motor activity is performed more frequently, which supports a sustained recovery process. The detailed mechanistic model proposed in [82] may be approximated from a top-down perspective using a model featuring a circular causality between order-parameter dynamics and system-parameter dynamics. The motor actions may be described in terms of an order parameter dynamics similar to (2), whereas the changes in the connectivity may be captured by a systems parameter dynamics.
Other models in the psychological literature that belong to this class of models featuring circular causality describe for example the interplay between perception and action as reviewed by Warren [15] or between the state of an agent and the state of the environment [83]. Roughly speaking, perceptual inputs may guide behavioral responses, in general, and motor actions, in particular. These behavioral responses may allow a human actor to experience different perceptual inputs. In doing so, perception and action affect each other in a circular way. The question arises to what extent insights obtained in such other studies focusing on psychological relevant instances of circular causality are helpful to improve our understanding of the interaction between order parameter and system parameter dynamics. Vice versa, it seems to be of interest to examine to what extent the issues discussed in the previous sections and the mathematical methodology used throughout this study can be helpful for other studies dealing with two interacting dynamical systems giving rise to circular causality.
Notes
In our study, growth parameters occur in the order parameter dynamics as a-priori unknown parameters as a result of the proposed top-down modeling approach. As such the growth parameters reflect functions of physical parameter that would occur in mechanistic, bottom-up modeling approaches. For example, for the amplitude equations governing the emergence of roll patterns due to a Benard instability the growth parameters can be expressed in terms of physical parameters from hydrodynamics [22]. In our context, it is assumed that the growth parameters depend both on physical quantities of the environment (e.g., inclination angle of a ramp or platform for standing upon), body-dimensions (body height, weight, etc) and parameters of the neural and muscular-skeletal system (e.g., synaptic weights). For a given subject and a given task these physical parameters may vary in a certain range which then implies that the growth parameters take on values from a certain interval.
In fact, the notion of a search algorithm is not useful for any physical system being self-organized or not. For example, let us consider a diffusion process. Let us assume a closed container fill with air. The container walls and the air molecules are at room temperature. Inside the container there is a bottle of perfume. The lid can be opened by remote control. Let us assume we open the lid. The perfume molecules diffuse out of the bottle and distribute themselves across the container. Eventually, the molecules are distributed uniformly in space and exhibit a Maxwell–Boltzmann velocity distribution. In doing so, the stationary distribution corresponds to a maximum entropy solution. Consequently, the perfume molecules effectively solve an optimization problem under constraints. That is, the molecules configure themselves such that the entropy is maximized under given isothermal boundary conditions and spatial boundaries given by the container walls. However, the molecules do not perform a search for the correct solution. The molecules simply satisfy a Boltzmann transport equation (a diffusion equation) and the time it takes to approach the stationary state will be determined by the diffusion constant (a parameter of the transport equation). This is another example of a time scale (here the relaxation time of the diffusion process) that is determined by the laws of physics and is not related to the performance of a search algorithm.
References
Ditzinger, T., Haken, H.: Oscillations in the perception of ambiguous patterns: a model based on synergetics. Biol. Cybern. 61, 279–287 (1989)
Newell, K.M., Scully, D.M., Tenenbaum, F., Hardiman, S.: Body scale the development of prehension. Dev. Psychobiol. 22, 1–13 (1989)
Newell, K.M., Scully, D.M., McDonald, P.V., Baillargeon, R.: Task constraints configuration, infant grip. Dev. Psychobiol. 22, 817–832 (1989)
Richardson, M.J., Marsh, K.L., Baron, R.M.: Judging and actualizing intrapersonal and interpersonal affordances. J. Exp. Psychol. - Hum. Percept. Perform 33, 845–859 (2007)
Lopresti-Goodman, S.M., Richardson, M., Baron, M.J., Carello, C., Marsh, K.L.: Task constraints on affordance boundaries. Mot. Control. 13, 69–83 (2009)
Lopresti-Goodman, S.M., Turvey, M.T., Frank, T.D.: Behavioral dynamics of the affordance “graspable”, attention perception. Psychophys. 73, 1948–1965 (2011)
Stephen, D.G., Isenhower, R.W., Dixon, J.A.: Dynamics of representational change: entropy, action, and cognition. J. Exp. Psychol. - Hum. Percept. Perform 35, 1811–1832 (2009)
Warren, W.H.: Perceiving affordances: visual guidance of stair climbing. J. Exp. Psychol. - Hum. Percept. Perform. 10, 683–703 (1984)
Faisal, A.A., Selen, L.P.J., Wolpert, D.M.: Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303 (2008)
Gibson, J.J.: The Ecological Approach to Visual Perception. Houghton-Mifflin, Boston (1979)
Turvey, M.T.: Coordination. Am. Psychol. 45, 938–953 (1990)
Beek, P.J., Peper, C.E., Stegeman, D.F.: Dynamical models of movement coordination. Hum. Mov. Sci. 14, 573–608 (1995)
Kelso, J.A.S.: Dynamic Patterns - The Self-Organization of Brain and Behavior. MIT Press, Cambridge (1995)
Haken, H.: Principles of Brain Functioning. Springer, Berlin (1996)
Warren, W.H.: The dynamics of perception and action. Psychol. Rev. 113, 358–389 (2006)
Araujo, D., Davids, K., Hristovski, R.: The ecological dynamics of decision-making in sport. Psychol. Sport Exerc. 7, 653–676 (2006)
Haken, H. Synergetics. An Introduction. Springer, Berlin (1977)
Haken, H.: Synergetic Computers and Cognition. Springer, Berlin (1991)
Tschacher, W., Dauwalder, J.P.: Situated cognition, ecological perception, and synergetics: a novel perspective for cognitive psychology? In: Tschacher, W., Dauwalder, J.P. (eds.) : Dynamics, Synergetics, Autonomous Agents, pp 83–104. World Scientific, Singapore (1999)
Schiepek, G., Strunk, G.: The identification of critical fluctuations and phase transitions in short term and coarse-grained time series: a method for real-time monitoring of human change processes. Biol. Cybern. 102, 197–207 (2010)
Saltzman, E.L., Munhall, K.G.: Skill acquisition and development: the roles of state-, parameter-, and graph-dynamics. J. Motor Behav. 24, 49–57 (1992)
Frank, T.D.: Multistable pattern formation systems: candidates for physical intelligence. Ecol. Psychol. 24, 220–240 (2012)
Bestehorn, M., Haken, H.: Associative memory of a dynamical system: an example of the convection instability. Z. Physik. B 82, 305–308 (1991)
Bestehorn, M., Friedrich, R., Haken, H.: Two-dimensional traveling wave patterns in nonequilibrium systems. Z. Physik B 75, 265–274 (1989)
Frank, T.D., van der Kamp, J., Savelsbergh, G.J.P.: On a multistable dynamic model of behavioral and perceptual infant development. Dev. Psychobiol. 52, 352–371 (2010)
Frank, T.D., Richardson, M.J., Lopresti-Goodman, S.M., Turvey, M.T.: Order parameter dynamics of body-scaled hysteresis and mode transitions in grasping behavior. J. Biol. Phys. 35, 127–147 (2009)
Frank, T.D.: Motor development during infancy: a nonlinear physics approach to emergence, multistability, and simulation. In: Columbus, A.M. (ed.) Advances in Psychology Research, vol. 83, Chap. 9, pp. 143–160. Nova Publ., New York (2011)
Frank, T.D.: On a multistable competitive network model in the case of an inhomogeneous growth rate spectrum with an application to priming. Phys. Lett. A 373, 4127–4133 (2009)
Frank, T.D.: Psycho-thermodynamics of priming, recognition latencies, retrieval-induced forgetting, priming-induced recognition failures and psychopathological perception. In: Hsu, N., Schütt, Z. (eds.) Psychology of Priming, Chap. 9, pp 175–204. Nova Publ., New York (2012)
Fuchs, A., Haken, H.: Pattern recognition and associative memory as dynamical processes in a synergetic system. II. Decomposition of complex scenes, simultaneous invariance with respect to translation, rotation, and scaling. Biol. Cybern. 60, 107–109 (1988)
Daffertshofer, A., Haken, H.: A new approach to recognition of deformed patterns. Pattern Recog. 27, 1697–1705 (1994)
Yudashkin, A.A.: Bifurcations of steady-state solutions in the synergetic neural network and control of pattern recognition. Auto Remote Control. 57, 1647–1653 (1996)
Bressloff, P.C., Roper, P.: Stochastic dynamics of the diffusive Haken model with subthreshold periodic forcing. Phys. Rev. E 58, 2282–2287 (1998)
Nakagawa, M.: A circularly connected synergetic neural network. IEICE Trans. Fund. Electr. Commu. Comput. Sci. E83A, 909–922 (2000)
Frank, T.D.: New perspectives on pattern recognition algorithm based on Haken’s synergetic computer network. In: Fournier, M.D. (ed.) Perspective on Pattern Recognition, Chap. 7, pp 153–172. Nova Publ., New York (2011)
Haken, H., Schanz, M., Starke, J.: Treatment of combinatorial optimization problems using selection equations with cost terms. Part I Physica. D 134, 227–241 (1999)
Starke, J., Schanz, M., Haken, H.: Treatment of combinatorial optimization problems using selection equations with cost terms. Part II Physica. D 134, 242–252 (1999)
Starke, J., Ellsaessar, C., Fukuda, T.: Self-organized control in cooperative robots using a pattern formation principle. Phys. Lett. A 375, 2094–2098 (2011)
Frank, T.D.: Multistable selection equations of pattern formation type in the case of inhomogeneous growth rates: with applications to two-dimensional assignment problems. Phys. Lett. A 375, 1465–1469 (2011)
Daffertshofer, A.: How do ensembles occupy space?. Eur. Phys. J. Spec. Top. 157, 79–91 (2008)
Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena. Oxford University Press, New York (1971)
Binnen, J.J., Dowrick, N.J., Fisher, A.J., Newman, M.E.J. The theory of critical phenomena. Oxford University Press, New York (1992)
Nicolis, G. Introduction to Nonlinear Sciences. Cambridge University Press. Cambridge (1995)
Nitzan, A., Ortoleva, P., Deutch, J., Ross, J.: Fluctuations and transitions at chemical instabilities: the analogy to phase transition. J. Chem. Phys. 61, 1056–1074 (1974)
Frank, T.D., Daffertshofer, A., Beek, P.J., Haken, H.: Impacts of noise on a field theoretical model of the human brain. Physica. D 127, 233–249 (1999)
Allain, C., Cummins, H.C., Lallemand, P.: Critical slowing down near the Rayleigh-Benard convection instability. Le J. de Phys. Lett. 24, L474–L477 (1978)
Wesfreid, J., Pomeau, Y., Dubois, M., Normand, C., Berge, P.: Critical effects in Rayleigh–Benard convection. Le J. de Phys. Lett. 7, 726–731 (1978)
Ecke, R.E., Haucke, H., Maeno, Y., Wheatley, J.C.: Critical dynamics at a Hopf bifurcation to oscillatory Rayleigh–Benard convection. Phys. Rev. A 33, 1870–1878 (1986)
Bakonyi, A., Michaelis, D., Peschel, U., Onishchukov, G., Lederer, F.: Dissipative solitons and their critical slowing down near a supercritical bifurcation. J. Opt. Soc. Am. B 19, 487–491 (2002)
Kelso, J.A.S., Scholz, J.P., Schöner, G.: Non-equilibrium phase transitions in coordinated biological motion: critical fluctuations. Phys. Lett. A 118, 279–284 (1986)
Schmidt, R.C., Carello, C., Turvey, M.T.: Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. J. Exp. Psychol. - Hum. Percept. Perform. 53, 247–257 (1990)
Scholz, J.P., Kelso, J.A.S., Schöner, G.S.: Non-equilibrium phase transitions in coordinated biological motion: critical slowing down and switching time, Phys. Lett. A 123, 390–394 (1987)
Wallenstein, G.V., Kelso, J.A.S., Bressler, S.L.: Phase transitions in spatiotemporal patterns of brain activity and behavior. Physica D 84, 626–634 (1995)
Wallenstein, G.V., Nash, A.J., Kelso, J.A.S.: Frequency and phase characteristics of slow cortical potentials preceding bimanual coordination, Electroenceph. Clin. Neurophysiol 94, 50–59 (1995)
Diedrich, F.J., Warren, W.H.: Why change gaits? Dynamics of the walk-run transition. J. Exp. Psychol. - Hum. Percept. Perform. 21, 183–202 (1995)
Tuller, B., Case, P., Ding, M., Kelso, J.A.S.: The nonlinear dynamics of speech recognition. J. Exp. Psychol. - Hum. Percept. Perform. 20, 3–16 (1994)
Mackey, M.C., Glass, L.: Oscillations and chaos in physiological control systems. Science 197, 287–289 (1977)
Glass, L., Mackey, M.C.: From Clocks to Chaos. Princeton University Press, Princeton (1988)
Frank, T.D.: A limit cycle model for cycling mood variations of bipolar disorder patients derived from cellular biochemical reaction equations. Commun. Nonlinear Sci. Numer. Simul. 18, 2107–2119 (2013)
Haken, H., Schiepek, G.: Synergetik der Psychologie. Hogrefe, Gottingen (2006). (in German)
Schöner, G. S., Kelso, J.A.S.: A synergetic theory of environmentally specified and learned patterns of movement coordination. I. Relative phase dynamics. II. Component oscillator dynamics. Biol. Cybern. 58, 71–89 (1988)
Frank, T.D., Blau, J.J.C., Turvey, M.T.: Nonlinear attractor dynamics in the fundamental and extended prism adaptation paradigm. Phys. Lett. A 373, 1022–1030 (2009)
Frank, T.D., Blau, J.J. C., Turvey, M. T.: Symmetry breaking analysis of prism adaptations’s latent aftereffect. Cogn. Sci. 36, 674–697 (2012)
Kelso, J.A.S., Dumas, G., Tognoli, E., de Guzman, G.C.: Bridging neural, behavioral and social coordination dynamics using the human dynamic clamp Program No. 667.20/III45.2013. Neuroscience Meeting Planner. San Diego, Society for Neuroscience (2013). Online
Lopresti-Goodman, S.M., Turvey, M.T., Frank, T.D.: Negative hysteresis in the behavioral dynamics of the affordance “graspable”. Atten. Percept. Psychophys. 75, 1075–1091 (2013)
Frank, T.D.: From systems biology to systems theory of bipolar disorder. In: Miranda, F. (ed.) Systems Theory: Perspectives, Applications and Developments, Chap. 2, pp 17–36. Nova Publ., New York (2014)
Fitzpatrick, P., Carello, C., Schmidt, R.C., Corey, D.: Haptic and visual perception of an affordance for upright posture. Ecol. Psychol. 6, 265–287 (1994)
Diggle, P.J.: Time Series, a Biostatistical Introduction. The Clarendon Press, Oxford (1990)
Turvey, M.T., Shaw, R.: The Primacy of Perceiving: An ecological reformulation of perception for understanding memory. In: Nilssen, L.G. (ed.) : Perspective on Memory Research: in Honor of Uppsala University’s 500th anniversary, Erlbaum, pp 167–222. Hillsdale, NJ (1979)
Shaw, R., Turvey, M.T., Mace, W.: Ecological Psychology: The consequence of a commitment to realism. In: Weimer, W., Palermo, D. (eds.) : Cognition and the Symbolic Processes II, Erlbaum , pp 159–226. Hildsdale, NJ (1982)
van Rooij, I.: Self-organization takes time too. Top. Cognit. Sci. 4, 63–71 (2012)
Ingber, L.: Statistical mechanics of neocortical interactions. Dynamics of synaptic information. Phys. Rev. A 28, 395–416 (1983)
Ingber, L.: Statistical mechanics of neocortical interactions: reaction time correlates of the g factor. Psycoloquy 10, article 068 (1999)
Wing, A.M., Kristofferson, A.B.: Response delays and the timing of discrete motor responses. Percept. Psychophys. 14, 5–12 (1973)
Risken, H.: The Fokker-Planck Equation – Methods of Solution and Applications. Springer, Berlin (1989)
Schöner, G.S., Haken, H., Kelso, J.A.S.: A stochastic theory of phase transitions in human hand movement. Biol. Cybern. 53, 247–257 (1986)
Hick, W.: On the rate of gain of information. Q. J. Experiment. Psychol. 4, 11–26 (1952)
Hyman, R.: Stimulus information as a determinant of reaction time. J. Experiment. Psychol. 45, 188–196 (1953)
Frank, T.D.: Multistable perception in schizophrenia: a model-based analysis via coarse-grained order parameter dynamics and a comment on the 4th law. Univ. J. Psychol. 2, 231–240 (2014)
Frank, T.D.: Secondary bifurcations in a Lotka-Volterra model for n competitors with applications to action selection and compulsive behaviors. Int. J. Bif. and Chaos 24, article 1450156 (2014)
Frank, T.D.: Action flow in obsessive-compulsive disorder rituals: a model based on extended synergetics and a comment on the 4th law. J. Adv. Phys. 5, 845–853 (2014)
Han, C.E., Arbib, M.A., Schweighofer, N.: Stroke rehabilitation reaches a threshold, PLoS. Comput. Biol. 4, article e1000133 (2008)
Beer, R.D.: Computational and dynamical languages for autonomous agents. In: Port, R.F., van Gelder, T. (eds.) Mind as Motion, pp 121–147. MIT Press, Cambridge (1995)
Acknowledgments
We are thankful to Professor Claudia Carello and Professor Michael Turvey for various discussions supporting the present study. Vitor L.S. Profeta was supported by Grant 0991/12-0 of the Coordination of Improvement of Higher Education Personnel (CAPES).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix: A: Derivation of (17b) and (25b)
Recall that α r e l,c,2 is the critical control parameter value at which the transition from mode 1 to mode 2 occurs when α is gradually increased (ascending condition). From (16) it follows that an increase in α implies that the ratio λ 2/λ 1 increases. The critical condition for the ratio λ 2/λ 1 is defined by (8). Substituting (16) into (8) and replacing α r e l by α r e l,c,2, we obtain
Solving for α r e l,c,2 yields (17a). By analogy, the critical value α r e l,c,1 can be determined. Recall that α r e l,c,1 denotes the critical control parameter value at which the transition from mode 2 to mode 1 occurs when α is decreases gradually (descending condition). The decrease of α implies an increase of the ratio λ 1/λ 2, see (16) again. The critical condition for the ratio λ 1/λ 2 is given by (9) Substitute (16) into (9) and replacing α r e l by α r e l,c,2, we obtain
Solving for α r e l,c,1 yields (17b). Note that (17a) and (17b) exemplify the two control parameter principles given by (14) and (15) that hold for any dynamical system that exhibits hysteresis. In particular, using (17a) and (17b) we see explicitly that
holds, which is (15). Consequently, we have α r e l,c,2=Δα/2 and α r e l,c,1=−Δα/2, as stated see (17b) again.
The critical control parameter values in the case of negative hysteresis can be determined by a similar argumentation. To this end, however, we need to assume that a time scale separation holds for the variables involved in the order parameter and system parameter model. The characteristic time scales are summarized in Table 5.
First of all, it is assumed that order parameters ξ k evolve quickly every time a perceptual process or behavioral response is required. The L k (n) system parameters evolve slowly relative to ξ k (t). However, they evolve quickly on the time scale of the repetitively performed judgment tasks or executed behavioral responses. That is, they are considered as fast evolving variables relative to changes of the control parameter α. Consequently, at the bifurcation point as defined by the critical control parameter values α c,1 and α c,2 the system parameters L k are in good approximation at their respective stationary values.
Let us determined the critical control parameter value α r e l,c,2 for transitions from mode 1 to mode 2 when α is increased (ascending condition) provided that mode “1” has been “on” or active in several previous behavioral responses. Increasing α implies that the ratio λ 2/λ 1 increases. In (16) we replace α r e l by α r e l,c,2 such that λ k =L k −β α r e l,c,2 For L k we use the corresponding stationary values s k : L 1=s 1 and L 2=s 2. That is, as mentioned above, we assume that at the transition point the system parameter dynamics is close to its fixed point. From (19) we obtain L 1=s 1=L 0−h and L 2=s 2=L 0. Substituting these results into (8), we obtain
Solving for α r e l,c,2 yields (25a). By analogy, (25b) can be derived.
Appendix : B: More than two alternatives for the special case of a set of almost indistinguishable stimuli
In the conclusions (Section 4), a generalized order parameter model involving more than two alternatives has been discussed and a heuristic argument has been developed that suggests that increasing the number of alternatives or choices will increase the response times predicted by that generalized model. This argument can be worked out in detail for a decision-making process in the special case when all order parameters evolve in exactly the same way for most of the time of the process. That is, we consider M alternatives or choices, where each alternative is described by an order parameter ξ k . Based on certain stimuli decisions have to be made (e.g., in an experiment on associative memory involving stimulus-response pairs the learned associations are tested by presenting the stimuli in an random order). The stimuli are assumed to be almost indistinguishable such that all ξ k assume that same values for most of the decision-making processes: ξ k (t)=z(t) for k=1,…,M. Note that in this context we also assume that λ k =λ holds for k=1,…,M. That is, all growth parameters are identical. Eventually, the order parameters ξ k will diverge (i.e., ξ k ≠ξ j for all k≠j) due to the impact of fluctuations and only one order parameter will ”survive” (winner-takes-all dynamics, see Section 2.1). In the following calculations, we do not account for this final phase and assume that the final phase does not qualitatively affect the relationship between the number of choices M and the response times.
For ξ k (t)=z(t)>0 we need to take the interaction terms \(g \xi _{k} {\xi _{j}^{2}}\) into consideration. That is, (34) has to be supplemented with M−1 interaction terms describing the inhibitory impacts of the other patterns or choices on the pattern (choice) of consideration. Since we have ξ k (t)=z(t) for all k it follows that all interaction terms have the same form and are equal to g z 3(t). Adding M−1 terms g z 3(t) to the right-hand side of (34) and using ξ k rather than z as variable (for sake of consistency with our presentation in Section 3), we obtain
with
Note that as long as ξ k (t)=z(t) for all k holds, the trajectories converge to an unstable saddle point with \(\xi _{k}=\sqrt {\lambda /G} \ \forall \ k\). Therefore, we assume that the trajectories ξ k converge from ξ k =ξ 0 at t=0 towards a value ξ k =ξ T at time T with ξ T >ξ 0 and \(\xi _{T}<\sqrt {\lambda /G}\). After that point the trajectories start to diverge and one of the trajectories will approach the finite value \(\xi _{k}=\sqrt {\lambda }>\sqrt {\lambda /G}\), while all others will converge to zero. Consequently, the response time RT exceeds the time point T: R T>T. The time T can be calculated just as in Section 2.1. We obtain
Note that for G=1 and \(\xi _{0}=D\sqrt {\lambda }\), \(\xi _{T}=\theta \sqrt {\lambda }\) we re-obtain (35). Importantly, the auxiliary parameter G increases with the number of choices M, see (49). Therefore, the question arises how does the time T depend on the factor G. Differentiating T with respect to G yields
with \(W=(\lambda -G{\xi _{0}^{2}})(\lambda -G{\xi _{T}^{2}})>0\). We see that the duration T contributing to the response time RT increases when G increases. This implies that T increases when the number M of choices increases. As mentioned above, this calculation is a crude estimate for the response time RT. The response time includes a final phase in which ξ j ≠ξ k holds. In fact, the assumption ξ k (t)=z(t) for t<T and ξ j ≠ξ k for t>T should be considered as a simplified two-phases scenario that is used to derive by analytical methods an estimate for the lower bound T of the response time RT. Nevertheless, this estimate suggests that the response time RT increases as a function of M. More detailed calculations (involving simulation studies) are needed to obtain an advanced understanding of this issue but are left to the future.
Rights and permissions
About this article
Cite this article
Frank, T.D., Profeta, V.L.S. & Harrison, H.S. Interplay between order-parameter and system parameter dynamics: considerations on perceptual-cognitive-behavioral mode-mode transitions exhibiting positive and negative hysteresis and on response times. J Biol Phys 41, 257–292 (2015). https://doi.org/10.1007/s10867-015-9378-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10867-015-9378-z