Spatio temporal interdependent calcium and buffer dynamics regulating DAG in a hepatocyte cell due to obesity

Abstract

Calcium ions (Ca²⁺) serve as a crucial signaling mechanism in almost all cells. The buffers are proteins that bind free Ca²⁺ to reduce the cell’s Ca²⁺ concentration. The most studies reported in the past on calcium signaling in various cells have considered the buffer concentration as constant in the cell. However, buffers also diffuse and their concentration varies dynamically in the cells. Almost no work has been reported on interdependent calcium and buffer dynamics in the cells. In the present study, a model is proposed for inter-dependent spatio-temporal dynamics of calcium and buffer by coupling reaction–diffusion equations of Ca²⁺ and buffer in a hepatocyte cell. Boundary and initial conditions are framed based on the physiological state of the cell. The effect of various parameters viz. inositol 1,4,5-triphosphate receptor (IP3R), diffusion coefficient, SERCA pump and ryanodine receptor (RyR) on spatio-temporal dynamics of calcium and buffer regulating diacylglycerol (DAG) in a normal and obese hepatocyte cell has been studied using finite element simulation. From the results, it is concluded that the dynamics of calcium and buffer impact each other significantly along the spatio-temporal dimensions, thereby affecting the regulation of all the processes including DAG in a hepatocyte cell. The proposed model is more realistic than the existing ones, as the interdependent system dynamics of calcium and buffer have different regulatory impacts as compared to the individual and independent dynamics of these signaling processes in a hepatocyte cell.

Introduction

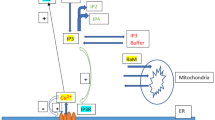
Many normal and pathological processes involve calcium ions. Elevations in cytoplasmic Ca²⁺ regulate a wide range of biological activities, including rapid processes, such as muscle contraction and neurosecretion as well as slower and more intricate ones like cell division, differentiation and apoptosis. IP₃, a second messenger produced by phospholipase C, most frequently causes the intracellular release of Ca²⁺, whereas the stimulation of plasma membrane store-operated channels cause Ca²⁺ to enter cells (Dupont et al. 2011). There is a need for an universal Ca²⁺ homeostasis system because calcium ions are essential not only for many cellular processes along the cell’s life cycle but they are also toxic to all phylogenetic phases (Gilabert 2001). A few of the mechanisms that regulate calcium concentration ($[C{a}^{2+}]$) at resting value include calcium inflow and efflux from the extracellular space, Ca²⁺ sequestration towards internal Ca²⁺ stores, Ca²⁺ release from internal Ca²⁺ stores and calcium buffering. Ca²⁺ buffers are among a small number of proteins that bind Ca²⁺ and have acidic side-chain residues. The two primary mechanisms that regulate Ca²⁺ persistence in the cytosol and subsequent Ca²⁺ mediated activities are Ca²⁺ elimination and Ca²⁺ diffusion (Gilabert 2001). Ca²⁺ efflux and sequestration together remove Ca²⁺ from the cytosol, whereas Ca²⁺ diffusion is predominantly regulated by Ca²⁺ buffering. The quick binding of Ca²⁺ to various cellular binding sites when they enter the cytoplasm is known as buffering of Ca²⁺. Only 1–5% of the Ca²⁺ that enter the cell are thought to remain in its free physiologically active state, making Ca²⁺ buffering an essential step in Ca²⁺ signaling. It is possible for mobile or immobile buffers to mediate Ca²⁺ buffering at the cytosol which will control the diffusion and confine the movement of free Ca²⁺ inside the cytoplasm. Immobile buffers are represented by molecules that are tethered to intracellular structures or molecules with a high molecular weight. Mobile buffers are compounds with small molecular weights usually less than 20–25 kDa. Ca²⁺ binding capability in mobile buffers is thought to be approximately one-tenth that of the cytosol. ATP is one of the most important transportable Ca²⁺ buffers. Around 2–3 mM of ATP are thought to be present in the cytosol from which 0.4 mM are in a free state. A powerful and extremely portable Ca²⁺ chelator is ATP. Within 10 to 50 nm of the Ca²⁺ entry site, more than 95% of the Ca²⁺ are quickly linked to the buffers. When such elevated $[C{a}^{2+}]$ domains occur, a mobile Ca²⁺ buffer will act to disperse them, whereas stationary Ca²⁺ buffers will act to prolong them. The Ca²⁺ binding proteins can be identified as soluble proteins in the cytosol, intraluminal proteins in organelles like the endoplasmic reticulum (ER) or intrinsic proteins in membranes like the plasma or organellar membranes. Physiological processes that rely on Ca²⁺ can be modulated by Ca²⁺ buffering changes that can impact signaling patterns. Phospholipase C (PLC) signaling channels become active when Ca²⁺ signaling is activated. An agonist activates a PLC type ( PLCγ or PLCβ) when it interacts with a cell surface receptor. This kind of PLC catalyzes the subsequent breakdown of phosphatidyl inositol bisphosphate (PIP2) into IP₃ and DAG. A brief rise in $[C{a}^{2+}]$ results from the release of Ca²⁺ from the IP₃-sensitive Ca²⁺ storage. The activation of a plasma membrane TRPC (T-cell receptor) channel by the second messenger DAG leads to the direct influx of Ca²⁺ into the cytosol. IP3R interacts with the DAG-activated TRPC to contribute to DAG-induced Ca²⁺ influx (Chakrabarti and Chakrabarti 2006).

Calcium signaling has been studied in various cells like neurons, oocytes, myocytes, astrocytes, pancreatic acinars, hepatocytes etc. by various researchers (Jha and Adlakha 2014; Jha et al. 2016; Panday and Pardasani 2013; Jagtap and Adlakha 2019; Kotwani and Adlakha 2017; Manhas and Anbazhagan 2021; Tewari 2012; Manhas and Pardasani 2014a, b; Singh and Adlakha 2019a, b, c). Kotwani et al. have attempted to study one-dimensional calcium concentration variation in fibroblast cells to study the influence of calcium transfer between different cellular compartments, involving excess buffers using the finite difference method (Kotwani and Adlakha 2017). A two-dimensional mathematical model for calcium distribution in fibroblast cells was also developed by them for an unsteady state case. The study was done for two cases of source geometry viz. point source and line source (Kotwani et al. 2014a, b; Kotwani et al. 2014a, b). Panday et al. formulated a model for Ca²⁺ distribution in oocytes involving Na⁺/Ca²⁺ exchanger (NCX) and advection of Ca²⁺ in the cell (Panday and Pardasani 2013). Naik et al. studied the calcium distribution involving voltage-gated calcium channels(VGCC), ryanodine receptors(RyR) and buffers in oocyte cells. They concluded that the increase of Ca²⁺ concentration due to RyR was higher than that of VGCC (Naik and Pardasani 2015). Amrita et al. observed the effects of NCX, source geometry, leak, SERCA pump etc. on Ca²⁺ oscillations in dendritic spines & neuron cells employing finite element approach (Jha and Adlakha 2014, 2015; Jha et al. 2016; Yripathi and Adlakha 2013). Pathak et al. devised a mathematical model of calcium distribution in cardiac myocyte cells involving pump, excess buffer and leaks (Pathak and Adlakha 2015). Manhas et al. studied calcium variation in pancreatic acinar cells describing the effect of mitochondria on Ca²⁺ signaling (Manhas and Pardasani 2014a, b; Manhas and Anbazhagan 2021; Manhas and Pardasani 2014a, b). Tewari et al. have developed a model for neuron cells expressing the impact of sodium pump on Ca²⁺ oscillation and calcium diffusion with excess buffer (Tewari 2012; Tewari and Pardasani 2012). Jagtap et al. studied calcium variation in a hepatocyte cell using finite volume method. They developed a steady-state one-dimensional mathematical formulation using the advection–diffusion equation for calcium and IP₃ (Jagtap and Adlakha 2019). They also solved the problem for calcium concentration fluctuation in two-dimensions using the finite volume method for the unsteady state situation (Jagtap and Adlakha 2018). Kumar et al. devised a mathematical model to obtain insight through the one-dimensional unsteady state intracellular calcium distribution in T cells. The model takes into account factors like source inflow, buffers, ryanodine receptors (RyRs) and diffusion coefficient (Kumar et al. 2017). Kothiya et al. provided a mathematical model to analyze the effect of Ca²⁺ signaling on the synthesis of ATP and IP₃ in fibroblast cells (Kothiya and Adlakha 2023). The results revealed that variations in source influxes, buffers and diffusion coefficient can alter the production and degradation of ATP and IP₃, resulting in anomalies in fibroblast cells that contribute to cancer, inflammation and wound healing such as cardiac fibroblast cell proliferation and migration (Kothiya and Adlakha 2022). Bhardwaj et al. employed a differential quadrature approach based on radial basis functions to study nonlinear spatio-temporal dynamics of Ca²⁺ in T cells involving the SERCA pump, RyR, source amplitude and buffers (Bhardwaj and Adlakha 2023). Singh et al. developed a mathematical model in one and three dimension for the study of nonlinear IP₃- dependent calcium dynamics in cardiac myocyte (Singh and Adlakha 2019a, b, c; Singh and Adlakha 2019a, b, c; Singh and Adlakha 2019a, b, c). The cytosolic calcium level was found to be potentially regulated by IP₃ signaling, source input of calcium, leak and maximum IP₃ production. Pawar et al. studied the interdependence of calcium and IP₃ using a two-way feedback model effecting the production of nitric oxide and the production and degradation of $\beta$-amyloid in neuron cells. A dopaminergic neuron cell’s dopamine control and dysregulation were also analyzed by developing a numerical model (Pawar and Raj Pardasani 2022; Pawar and Pardasani 2022a, b, c; Pawar and Pardasani 2023). Using the system of reaction–diffusion equations for calcium and $\beta$-amyloid, the dependency of calcium and $\beta$-amyloid in a neuron cell was investigated (Pawar and Pardasani 2022a, b, c). A reaction–diffusion equation system was employed to study the alterations in different factors such as buffer, RyR, SERCA pump, source inflow, etc. which contribute to the regulation and dysregulation of spatio-temporal calcium and NO dynamics in neuron cells (Pawar and Pardasani 2022a, b, c). Vaishali et al. investigated beta cell’s response to calcium and IP₃ dynamics in terms of secreting insulin (Vaishali and Adlakha 2023). Yogita et al. analyzed the effects of Ca²⁺ and IP₃ dynamics on glycogen phosphorylase regulation in hepatocyte cells (Jagtap and Adlakha 2023).

Neher et al. studied the buffer and calcium gradient in bovine chromaffin cells. It was concluded that 98–99% of the calcium which typically enter the cell is absorbed by the fast endogenous Ca²⁺ buffer, according to two independent estimates of its capacity (Neher and Augustine 1992). Smith et al. developed asymptotic approximations, including the excess buffer approximation, rapid buffer approximation and immobile buffer approximation to address the steady state problem of buffered diffusion of Ca²⁺ at a single source. In their investigation, they took into account the three-parameter regimes described by the dimensionless diffusion coefficients of Ca²⁺ and buffer with respect to one another and the rate of response (Smith et al. 1996; Smith 1996). Schwaller observed that the impact of a particular Ca²⁺ buffer on intracellular Ca²⁺ signals depends on a variety of variables including intracellular concentration, affinities for Ca²⁺ and other metal ions, the kinetics of Ca²⁺ binding and release in different cells (Schwaller 2019). Martin Falcke used reaction–diffusion equations and developed a mathematical model including calcium concentration, slow buffer, mobile buffer etc. and discovered that a fast buffer’s concentration profile around an open channel is more localized than a slow buffer’s (Falcke 2003). Nowycky et al. employed diffusion equations and showed that fixed and diffusible calcium buffers affect the spatial and temporal distribution of free Ca²⁺ after Ca²⁺ entrance through voltage-gated ion channels in chromaffin cells (Nowycky and Pinter 1993). Klingauf et al. discussed that the kinetic data from flash-photolysis experiments can be combined with Ca²⁺ data to explain a range of catecholamine secretion-related phenomena from chromaffin cells (Klingauf and Neher 1997). Naraghi et al. presented an explicit solution to a linear approximation of the combined reaction–diffusion problem that takes into consideration of any number of calcium buffers that can be produced naturally or introduced exogenously (Naraghi and Neher 1997). M.D. Stern developed a mathematical model and illustrated that when intracellular processes including the opening and closing of channels, induce rapid fluctuations in calcium fluxes, a buffer with rapid kinetics is required to stabilize the level of $[C{a}^{2+}]$ (Stern 1992). Agarwal et al. developed a model incorporating calcium binding buffers and the advection diffusion equation. The impacts on the calcium concentration level were discussed in relation to EGTA, BAPTA, Calmodulin and Troponine (Agarwal et al. 2021). Ahmed et al. investigated the process of Archidoris monteryensis neuron’s soma regulating calcium levels and buffers calcium transients at physiological levels. To minimize transient changes in free calcium, measured amounts of intracellular EGTA was used in an indirect technique to measure the cytoplasm’s ability to buffer calcium (Ahmed and Connor 1988). Prins et al. discussed the idea that the multifunctionality of organellar Ca²⁺ buffers which exhibit such diversity in their Ca²⁺ binding and reactions, is one feature that unites them. Protein folding, apoptosis control and Ca²⁺ release pathway modulation are just a few of the functions that Ca²⁺ buffering proteins perform in addition in acting as an inactive Ca²⁺ breakdown within intracellular organelles for eukaryotic cells (Prins and Michalak 2011). Faas et al. concluded that the calcium binding protein has one independent and four cooperative binding sites simultaneously, it was also found that calcium binding to calretinin in different cells was a phenomenon due to the reduction of free calcium following significant rise in calcium concentration caused by the release of calcium from DM-nitrophen (Faas et al. 2007). Foehring et al. identified cell break-in over steady state using fluorescent Ca²⁺ $\mu$ M fura-2 exogenous buffer stimulating with a single action potential and measured the Ca²⁺ transient from the proximal dendrite for dopamine neurons (Foehring et al. 2009). Gabso et al. showed the effect of cellular Ca²⁺-buffers on the intensity and diffusional spread of Ca²⁺-impulses in neurons. Mobile buffers aid in Ca²⁺ redistribution whereas fixed Ca²⁺ buffers tend to delay the signal and lower the measured Ca²⁺ diffusion coefficient (Gabso et al. 1997).

Dysregulation in calcium signaling results in various diseases like obesity, insulin resistance, diabetes etc. Obesity is characterized as a condition in which there is an accumulation of extra body fat that may have a negative impact on health. Obesity in the upper body is characterized by an intra-abdominal accumulation of adipose tissue, this is crucial for the emergence of hypertension, elevated plasma insulin levels, insulin resistance, type 2 diabetes and hyperlipidemia (Kopelman 2000). Excess lipid accumulation is a defining feature of obesity. The WHO BMI (kg/m²) standards are followed by the majority of definitions of obesity, though other definitions are sometimes used. If a person’s BMI is $\ge$ 30 kg/m², they are considered fat. Obesity can range from class 1 (30.0–34.9 kg/m²) to class 2 (35.0–39.9 kg/m²) and class 3 (above or equal to 40 kg/m²) (Montalto 2021). Obesity is a significant contributing factor to increased morbidity and death, especially for diabetes and cardiovascular disease (CVD), cancer and other chronic illnesses like osteoarthritis, liver and kidney disease, sleep apneaspa and depression (Pi-Sunyer 2002).

The survey of literature gives a fair idea that not much attention is given to mathematical modelling to study interdependent calcium and buffer dynamics for a hepatocyte cell. The studies reported above on calcium dynamics have been performed by taking buffer as a constant in their model. The studies on interdependent Ca²⁺ and IP₃, Ca²⁺ and NO, Ca²⁺ and dopamine etc. were reported by taking buffers as constant. But, the concentration of buffers is also dynamic. To obtain better insights, a model of the interdependent Ca²⁺ and buffer dynamics in a hepatocyte cell must be developed. In the present study, a novel two-way reaction–diffusion model for interdependent Ca²⁺ and buffer dynamics has been formulated. The reaction–diffusion equations of Ca²⁺ and buffer have been coupled through their interdependent fluxes. Also, the temporal DAG growth equation has been coupled in this work to analyze the impact of interdependent Ca²⁺ & buffer dynamics on DAG net growth in normal and obese hepatocyte cells. Further, numerical simulation has been performed using the finite element method and the Crank-Nicolson method.

Mathematical formulation

A mathematical model proposed by Smith and Caamal et al. (Smith et al. 1996; Lopez-Caamal et al. 2014) is modified in this study by incorporating IP3R, SERCA pump, RyR and calcium buffering fluxes. The following reaction–diffusion equation for calcium is used for the study

$$\frac{\partial [C{a}^{2+}]}{\partial t}={D}_{Ca}\frac{{\partial }^{2}[C{a}^{2+}]}{\partial {x}^{2}}+{J}_{IPR}+{J}_{RYR}-{J}_{SERCA}-{J}_{on}+{J}_{off}$$

(1)

Here $[C{a}^{2+}]$ represents calcium concentration in the cytosol, ${D}_{Ca}$ is the diffusion coefficient of calcium, ${J}_{IPR}$ is calcium influx through IP3R, ${J}_{RYR}$ is calcium influx through RyR, ${J}_{SERCA}$ is efflux of calcium from SERCA pumps, ${J}_{on}$ and ${J}_{off}$ represent Ca²⁺ buffering flux and it’s release from the buffers.

The various fluxes are modelled as,

$${J}_{IPR}=\frac{{K}_{IPR}{O}_{IPR}}{{V}_{c}}(CT-(1+{V}_{c})[C{a}^{2+}])$$

(2)

${K}_{IPR}$ represents receptor activity levels in the cytosol, $CT$ is total calcium content and ${V}_{c}$ is the proportion of cytosol to total cell volume & ${O}_{IPR}$ is given by (Wacquier et al. 2016),

$${O}_{IPR}=\frac{{q}_{26}}{{q}_{62}+{q}_{26}}D$$

(3)

Here ${O}_{IPR}$ represents the open probability of IP3R receptors in the cytosol. ${q}_{26}$ and ${q}_{62}$ are transition rate from C₂ to O₆ and transition rate from O₆ to C₂ respectively.

$$D=\frac{{q}_{42}({q}_{62}+{q}_{26})}{{q}_{42}{q}_{62}+{q}_{42}{q}_{26}+{q}_{24}{q}_{62}}$$

(4)

D represents the proportions of the IP3Rs in the cytosol, ${q}_{42}$ and ${q}_{24}$ are the transition rates between the modes park to drive and drive to park respectively.

$${J}_{RYR}=\frac{{V}_{RyR}{P}_{O}}{{V}_{e}}(CT-({V}_{e}+{V}_{c})[C{a}^{2+}])$$

(5)

Here ${P}_{O}$ is the rate of calcium efflux, ${V}_{e}$ is the ratio of ER volume to total cell volume and ${V}_{RyR}$ is rate of RyR (Naik and Pardasani 2015).

$${J}_{SERCA}={\lambda }_{SERCA}\frac{[C{a}^{2+}{]}^{2}}{[C{a}^{2+}{]}^{2}+{K}_{SERCA}^{2}}$$

(6)

Here the bulk cytosol’s maximal SERCA flux is ${\lambda }_{SERCA}$ and the cytosolic Ca²⁺ concentration of SERCA at half-maximal activation is ${K}_{SERCA}$ (Wagner et al. 2004).

$${J}_{on}={k}_{j}^{+}[C{a}^{2+}]b$$

(7)

$${J}_{off}={k}_{j}^{-}\frac{{b}_{tot}[C{a}^{2+}]}{K+[C{a}^{2+}]}$$

(8)

Here ${k}_{j}^{+}$ and ${k}_{j}^{-}$ represent the buffer association rate and buffer dissociation rate respectively (Lopez-Caamal et al. 2014; Smith et al. 1996).

Diffusion equation for buffer is given as (Lopez-Caamal et al. 2014),

$$\frac{\partial b}{\partial t}={D}_{b}\frac{{\partial }^{2}b}{\partial {x}^{2}}-{J}_{on}+{J}_{off}$$

(9)

where ${D}_{b}$ represents the diffusion coefficient of the buffer, $b$ is buffer concentration in the cytosol, ${J}_{on}$ and ${J}_{off}$ are given in Eqs. (7) and (8).

The following initial conditions are imposed based on the assumption that Ca²⁺ and buffer concentration at rest is 0.1 $\mu M$ and 0 $\mu M$ in the cell.

$$([C{a}^{2+}{]}_{t=0})=0.1\mu M$$

(10)

$$({b}_{t=0})=0\mu M$$

(11)

The following boundary conditions based on physical conditions are applied to obtain the solution.

$$li{m}_{x\to 0}-{D}_{Ca}\left(\frac{\partial [C{a}^{2+}]}{\partial x}\right)={\sigma }_{Ca},$$

(12)

where ${\sigma }_{Ca}$ represents source influx (Jagtap and Adlakha 2019).

$$li{m}_{x\to 15}([C{a}^{2+}])={C}_{\infty }=0.1\mu M,$$

(13)

$$li{m}_{x\to 0}{D}_{b}\left(\frac{\partial b}{\partial x}\right)=0,$$

(14)

$$li{m}_{x\to 15}(b)={b}_{\infty }=\frac{K{b}_{tot}}{K+{C}_{\infty }},$$

(15)

Here $K$=$\frac{{k}^{-}}{{k}^{+}}$ is dissociation constant of the buffer and total buffer concentration is ${b}_{tot}$ (Patil et al. 2022, Jagtap and Adlakha 2019).

The terms of the various fluxes given in Eqs. (6) and (7) are nonlinear, therefore linearized using the Taylor’s approximation method around the point where calcium and buffer concentration is 0.1 and 5 $\mu M$. The nonlinear terms in Taylor series approximation becomes negligible.

Rate of DAG net growth is calculated by (Siso-Nadal et al. 2009),

$$\frac{d[DAG]}{dt}={v}_{i}\frac{[C{a}^{2+}][PL{C}^{*}]}{{K}_{c}^{(1)}+[C{a}^{2+}]}-{b}_{d}[DAG],$$

(16)

Here $[DAG]$ represents DAG concentration in the cell, $[PL{C}^{*}]$ denotes the concentration of activated PLC $\beta$, the rate at which activated PLC can produce IP₃ at its maximal capacity is ${v}_{i}$ and $[C{a}^{2+}]$ at which this rate is halved is ${K}_{c}^{(1)}$.

The Eq. (1) can be rewritten after linearization as,

$$\frac{\partial u}{\partial t}={D}_{Ca}\frac{{\partial }^{2}u}{\partial {x}^{2}}-{A}_{1}u+{B}_{1} 0\le x\le 15, t\ge 0$$

(17)

where u represents $[C{a}^{2+}]$ and A₁ and B₁ are constants obtained after Taylor’s approximation method.

In a similar manner representing free buffer concentration as b, Eq. (9) can be rewritten as,

$$\frac{\partial b}{\partial t}={D}_{b}\frac{{\partial }^{2}b}{\partial {x}^{2}}-{A}_{2}b+{B}_{2} 0\le x\le 15, t\ge 0$$

(18)

where A₂ and B₂ are constants obtained after Taylor’s approximation method.

The numerical solution is obtained by the variational finite element method by dividing the cytosol of the hepatocyte cell into 80 elements. The variational functional of the problem (17) in discretized form is expressed by

$$\begin{array}{l}{I}^{(e)}=\frac{1}{2}{\int }_{{x}_{i}}^{{x}_{j}}\left[{{u}^{(e)\mathrm{^{\prime}}}}^{2}+\frac{1}{{D}_{Ca}}\frac{\partial {{u}^{(e)}}^{2}}{\partial t}+{A}_{1}{{u}^{(e)}}^{2}-2{B}_{1}{u}^{(e)}\right]-{\mu }^{(e)}\left(\frac{{\sigma }_{Ca}}{{D}_{Ca}}{u}_{(x=0)}^{(e)}\right)\end{array}$$

(19)

Here ${\mu }^{(e)}$ is one for the first element and zero for the remaining elements.

The elements are very small in size therefore for calcium concentration shape function is assigned as following linear variation,

$${u}^{(e)}={c}_{1}+{c}_{2}x$$

(20)

The Eq. (20) can be expressed as

$${u}^{(e)}={P}^{T}{C}^{(e)}$$

(21)

Here ${P}^{T}=\left[\begin{array}{ll}1& x\end{array}\right]$and

$${C}^{(e)}=\left[\begin{array}{l}{c}_{1}\\ {c}_{2}\end{array}\right]$$

Values of ${u}^{(e)}$ at nodes ${x}_{i}$ and ${x}_{j}$ are given by,

$${u}^{(e)}({x}_{i})={c}_{1}+{c}_{2}{x}_{i}$$

(22)

$${u}^{(e)}({x}_{j})={c}_{1}+{c}_{2}{x}_{j}$$

(23)

using above equations, it is obtained as,

$${\overline{u}}^{(e)}={P}^{(e)}{C}^{(e)}$$

(24)

Here ${P}^{(e)}=\left[\begin{array}{ll}1& {x}_{i}\\ 1& {x}_{j}\end{array}\right]$

& ${\overline{u}}^{(e)}=\left[\begin{array}{l}{u}_{i}\\ {u}_{j}\end{array}\right]$

From Eqs. (22)-(24),

$${u}^{(e)}={P}^{T}{R}^{(e)}{\overline{u}}^{(e)}$$

(25)

Here ${R}^{(e)}={{P}^{(e)}}^{-1}=\frac{1}{{x}_{j}-{x}_{i}}\left[\begin{array}{ll}{x}_{j}& -{x}_{i}\\ -1& 1\end{array}\right]$

$${I}^{(e)}={I}_{k}^{(e)}+{I}_{m}^{(e)}+{I}_{l}^{(e)}-{I}_{r}^{(e)}-{I}_{s}^{(e)}$$

Here

$$\begin{array}{c}{I}_{k}^{(e)}=\frac{1}{2}{\int }_{{x}_{i}}^{{x}_{j}}\left[\left({{P}_{x}}^{T}{R}^{(e)}{{\overline{u}}^{(e)}}^{2}\right)\right]dx\\ {I}_{m}^{(e)}=\frac{1}{2}{\int }_{{x}_{i}}^{{x}_{j}}\frac{1}{{D}_{Ca}}\frac{\partial }{\partial t}\left[\left({P}^{T}{R}^{(e)}{{\overline{u}}^{(e)}}^{2}\right)\right]dx\\ {I}_{l}^{(e)}=\frac{1}{2}{\int }_{{x}_{i}}^{{x}_{j}}{A}_{1}\left[\left({P}^{T}{R}^{(e)}{{\overline{u}}^{(e)}}^{2}\right)\right]dx\\ {I}_{r}^{(e)}={\int }_{{x}_{i}}^{{x}_{j}}{B}_{1}\left[\left({P}^{T}{R}^{(e)}{\overline{u}}^{(e)}\right)\right]dx\\ {I}_{s}^{(e)}={\mu }^{(e)}\left[\left(\frac{{\sigma }_{Ca}}{2{D}_{Ca}}{P}^{T}{R}^{(e)}{\overline{u}}_{(x=0)}^{(e)}\right)\right]\end{array}$$

Minimizing ${I}^{(e)}$ with respect to ${\overline{u}}^{(e)}$,

$$\frac{d{I}^{(e)}}{d{\overline{u}}^{(e)}}=0$$

that is,

$$\frac{d{I}^{(e)}}{d{\overline{u}}^{(e)}}=\frac{d{I}_{k}^{(e)}}{d{\overline{u}}^{(e)}}+\frac{d{I}_{m}^{(e)}}{d{\overline{u}}^{(e)}}+\frac{d{I}_{l}^{(e)}}{d{\overline{u}}^{(e)}}-\frac{d{I}_{r}^{(e)}}{d{\overline{u}}^{(e)}}-\frac{d{I}_{s}^{(e)}}{d{\overline{u}}^{(e)}}$$

which can be written as,

$$\frac{dI}{d{\overline{u}}^{(e)}}=\sum \nolimits_{e=1}^{80}{\overline{M}}^{(e)}\frac{d{I}^{(e)}}{d{\overline{u}}^{(e)}}({\overline{M}}^{(e)}{)}^{T}=0$$

where

$$\begin{array}{ccc}{\overline{M}}^{(e)}={\left[\begin{array}{ll}0& 0\\ .& .\\ 0& 0\\ 1& 0\\ 0& 1\\ 0& 0\\ .& .\\ 0& 0\end{array}\right]}_{81\times 2}& \begin{array}{l}{i}^{th}row\\ {j}^{th}row\end{array},& {\overline{u}}^{(e)}={\left[\begin{array}{l}{u}_{1}\\ {u}_{2}\\ {u}_{3}\\ {u}_{4}\\ .\\ .\\ {u}_{80}\\ {u}_{81}\\ \end{array}\right]}_{81\times 1}\end{array}$$

In a similar manner Eq. (18) is solved using linear elements leading again to an $81\times 81$ system.

This results in the set of linear algebraic equations,

$$[\overline{K}{]}_{(162\times 162)}\overline{U}+[\overline{N}{]}_{(162\times 162)}{\frac{\partial \overline{U}}{\partial t}}_{(162\times 1)}=[\overline{F}{]}_{(162\times 1)}$$

(26)

where $\overline{U}$ is given by $\left[\begin{array}{l}\overline{u}\\ \overline{B}\end{array}\right]$, system matrices are represented as $\overline{K}$ and $\overline{N}$ & $\overline{F}$ is characteristic vector. For solving the system Crank-Nicolson method is used and simulated using MATLAB program.

Table

The following physiological parameters are used for solving the formulated problem (26).

Results & discussion

Figure 1 displays calcium and free buffer concentration distribution with respect to space and time. Figure 1A shows spatial calcium concentration fluctuations. The figure displays that the concentration of calcium is highest near the source which decreases to reach equilibrium value on moving away from the source. Highest steady state concentration of calcium is close to $\approx$ 0.7 M$\mu$. Figure 1B shows the concentration of calcium variation with respect to time. Initially, the concentration of calcium increases sharply till 500 ms and then attains a steady state. Figure 1C shows free buffer concentration variation with respect to space. Free buffer binds with free calcium to form calcium-bound buffer because excessive amount of calcium is harmful to cells. Near the source, the concentration of calcium is highest therefore more amount of buffer is needed to reduce the concentration of calcium. Hence, the free buffer value is smallest near the source. Buffer diffuses to the calcium source whereas calcium diffuses toward the other end of the cell. Thus near the source influx of free calcium, it is observed that source influx dominates the buffering process while on the other end of the boundary, the buffering process dominates over calcium signals. Figure 1D shows free buffer concentration variation with respect to time. Initially, free buffer concentration increases gradually and smoothly till 500 ms and then attains steady state. The maximum steady state value of the buffer is observed to be 6.667 $\mu M$.

Fig. 1

Calcium and free buffer distribution with ${\sigma }_{Ca}=15$ $pA$, ${D}_{Ca}=200$ $\mu {m}^{2}se{c}^{-1}$ and ${D}_{b}=75$= $\mu {m}^{2}se{c}^{-1}$

Figure 2 displays calcium concentration distribution with respect to space and time for dynamic and constant buffer values. For the purpose of comparison, the constant buffer value is taken as the maximum steady state value i.e. 6.667 $\mu M$ as obtained in Fig. 1. Figure 2A shows spatial calcium concentration fluctuations for dynamic and constant buffer values. It displays that the concentration of calcium is highest near the source which decreases to reach equilibrium value on moving away from the source. It is observed from the Fig. 2A that dynamic buffer is dominated by constant buffer as seen in the plot because constant buffer drops calcium concentration drastically near the source while dynamic buffer gradually decreases calcium concentration and therefore, smoother curve is observed for dynamic buffer. Figure 2B shows concentration of calcium variation with respect to time for dynamic and constant buffer values. Initially, concentration of calcium increases sharply till 300 ms, in case of constant buffer value and then it attains steady state around 300 ms. But in the presence of dynamic buffer, calcium concentration increases sharply till 500 ms and attains steady state thereafter 500 ms. The case of constant buffer is an idealistic situation whereas the case of dynamic buffer represents more realistic situation. Slight oscillations are observed in the curves because of time gap between free calcium and buffers diffusing towards each other and the binding time required to form buffer bound calcium reducing free calcium and buffer concentration. It is observed from the Fig. 2 A and B that in the presence of dynamic buffer value, it almost uniformly reduces concentration of calcium in the entire domain whereas in the presence of constant buffer value, the concentration of calcium reduces drastically which is possible in an ideal case only. Difference of calcium concentration in the cytosol of the cell in the presence of dynamic and constant buffer value is $\approx$ 30%. The significant difference is observed in calcium concentration profile for idealistic and realistic scenario of buffer.

Fig. 2

Calcium dynamics for dynamic and constant buffer with ${\sigma }_{Ca}=15$ $pA$, ${D}_{Ca}=200$ $\mu {m}^{2}se{c}^{-1}$ at 500 ms

Figure 3 displays changes in calcium concentration for various calcium diffusion coefficient values with respect to time and space. Figure 3A is plotted for spatial variations in calcium concentration. It is observed that with increasing values of the diffusion coefficient of calcium, calcium concentration decreases. Calcium diffusion rises as the value of the diffusion coefficient rises, hence the concentration of calcium is inversely proportional to the diffusion coefficient. Near the source calcium concentration is highest and moving away from the source attains its equilibrium state. Figure 3B shows calcium concentration variation with respect to time. Initially, calcium concentration increases sharply till 300 ms and then attains a steady state. Slight oscillations are observed in the curves because of the time gap between free calcium and free buffers diffusing towards each other and the binding time required to form buffer-bound calcium reducing free calcium and free buffer concentration.

Fig. 3

Calcium dynamics for different values of calcium’s diffusion coefficient

Figure 4 shows a change in calcium concentration for various buffer’s diffusion coefficient values with respect to space and time. Figure 4A is plotted for variations in calcium concentration with respect to space. It is observed that with increasing values of the diffusion coefficient of buffer, calcium concentration decreases. Buffer diffusion increases with an increase in diffusion coefficient, which increases the formation of buffers that are calcium-bound. Near the source, calcium concentration is highest and moving away from the source attains its equilibrium state. Figure 4B shows calcium concentration variation with respect to time. Initially, calcium concentration increases sharply till 300 ms and then attains a steady state. Slight oscillations are observed in the curves because of the time gap between free calcium and free buffers diffusing towards each other and the binding time required to form buffer-bound calcium reducing free calcium and buffer concentration.

Fig. 4

Calcium dynamics for various levels of the buffer’s diffusion coefficient

Figure 5 shows variation in buffer concentration for different buffer’s diffusion coefficient values with respect to space and time. Figure 5A demonstrates spatial buffer concentration for various buffer diffusion coefficient values. It is seen from the figure that with increasing value of diffusion coefficient of buffer, buffer concentration in the cytosol of the cell increases as diffusion of buffer increases. At the source calcium concentration is highest, to reduce the concentration of calcium buffer concentration has increased at the source. Figure 5B shows buffer concentration for different values of the buffer’s diffusion coefficient with respect to time. Initially, buffer concentration increases gradually up to 30 ms then oscillates for some time around 30 ms to 350 ms (maximum time period) and attains a steady state. Oscillations remain for the maximum time period with increasing the buffer’s diffusion coefficient.

Fig. 5

Buffer dynamics for different diffusion coefficient values of the buffer

Figure 6 displays variations in calcium concentration for various levels of source influx with respect to space and time. Figure 6A is plotted for calcium concentration variation with respect to space. It has been found that calcium concentration rises with rising calcium source inflow values. Near the source calcium concentration is highest and on moving away from the source attains its equilibrium state. Figure 6B shows calcium concentration variation with respect to time. Initially, calcium concentration increases sharply till 400 ms and then reaches a steady state. The calcium concentration variation has the same behavior as seen in Fig. 1.

Fig. 6

Calcium dynamics for different values of source influx

Figure 7 displays variations in calcium concentration for various total buffer concentration values with respect to space and time. Figure 7A is plotted for calcium concentration variation with respect to space. Calcium concentration is seen to decrease with increasing total buffer concentration levels. With the increase in the total value of buffer, the quantity of calcium-bound buffer increases, hence calcium concentration decreases. Near the source calcium concentration is highest and moving away from the source attains its equilibrium state. Figure 7B shows calcium concentration variation with respect to time. Initially, calcium concentration increases sharply till 350 ms and then reaches a steady state. Behavior of calcium concentration variation is the same as seen in Fig. 1. Slight oscillations are observed with increasing value of source influx.

Fig. 7

Calcium dynamics for various values of b_tot

Figure 8 shows variations in buffer concentration at various total buffer concentration levels with respect to space and time. Figure 8A displays the fluctuation in buffer concentration with respect to space for various total buffer concentration values. The figure demonstrates that when the overall buffer concentration is at its maximum, the value of the buffer is highest. Additionally, at the source, the buffer reaches a fixed value in less time compared to the scenario where the total buffer concentration is low. Figure 8B shows variation in buffer concentration for different values of total buffer concentration with respect to time. It is seen that buffer starts from a fixed value of 0 $\mu M$ then initially decreases near the source and then increases with an increase in time.

Fig. 8

Buffer dynamics for various total buffer concentration values

Figure 9 demonstrates the fluctuation in calcium concentration along time and space for dissociation constants of different buffers which are EGTA, Triponin C and BAPTA. Figure 9A shows calcium concentration variation with respect to space. Upon comparison of calcium concentrations at the source, it is observed that the presence of an EGTA buffer results in the highest calcium concentration, surpassing the concentrations observed with Troponin C and BAPTA. The behavior of the calcium concentration is similar to Fig. 1A in the presence of EGTA buffer. Presence of Triponin C reduced the concentration at the source $\approx$ by 5% and the BAPTA buffer changed the behavior of the curve. Calcium concentration is highest at the source and decreases as one moves away from the source until it achieves a steady state when EGTA and Triponin C is present. Calcium concentration first rises in the presence of BAPTA buffer for a while before reaching a steady state. Figure 9B shows calcium concentration variation with respect to time. It is seen that in the presence of EGTA, initially, calcium concentration increases sharply and gradually till 350 ms and then attains a steady state. When Triponin C and BAPTA buffers are present steady state is attained in 30 ms. With respect to time, oscillations appear when Triponin C and BAPTA buffers are present.

Fig. 9

Calcium dynamics for different values of various buffer association rates

Figure 10 shows the spatial and temporal DAG net growth rate. Figure 10A shows spatial DAG net growth rate. From the Fig. 10A, it is seen that close to the source, DAG net growth rate is largest and moving away from the source, DAG net growth rate decreases to a certain fixed value. There is a change in the nonlinear behavior of the curve compared to that in Fig. 1A. Figure 10B shows DAG net growth rate with respect to time. It is seen from the curves that the net growth rate increases more gradually and smoothly compared to the temporal calcium profile in Fig. 1B.

Fig. 10

DAG concentration net growth

Figure 11 displays DAG net growth rate distribution with respect to space and time for dynamic and constant buffer values. Figure 11A shows spatial DAG net growth rate for dynamic and constant buffer values. It displays that the DAG net growth rate is highest near the source which decreases to reach equilibrium value on moving away from the source. It is observed from the Fig. 11A that dynamic buffering is dominated by constant buffering process as seen in the plot because constant buffer drops DAG net growth rate drastically near the source while dynamic buffer gradually decreases DAG net growth rate and therefore, smoother curve is observed for dynamic buffering process. Figure 11B shows DAG net growth rate with respect to time for dynamic and constant buffer values. DAG net growth rate increases gradually for both the cases dynamic and constant buffer values. It is observed from the Fig. 11A and B that in the presence of dynamic buffer value, it almost uniformly reduces DAG net growth rate in the entire domain whereas in the presence of constant buffer value, the DAG net growth rate reduces drastically which is possible in an ideal case only. Difference of DAG net growth rate in the cytosol of the cell in the presence of dynamic and constant buffer value is $\approx$ 30%. The significant difference is observed in DAG net growth rate for idealistic and realistic scenario of buffer.

Fig. 11

DAG net growth rate for dynamic and constant buffer with ${\sigma }_{Ca}=15$ $pA$, ${D}_{Ca}=200$ $\mu {m}^{2}se{c}^{-1}$

Figure 12 displays a difference of calcium concentration variation from obese hepatocyte cells to normal hepatocyte cells with respect to space and time. Figure 12A shows a spatial difference graph for calcium concentration variation due to obese and normal hepatocyte cells. The graph shows that the difference in calcium concentration from an obese to a normal hepatocyte cell is largest close to the source and gradually reduces as one moves away from the source and becomes zero as calcium concentration attains an equilibrium state in both obese and normal hepatocyte cells. Figure 12B shows a temporal difference graph for calcium concentration variation. The Fig. 12B shows that the behaviour of the fluctuation in calcium concentration is similar to Fig. 1B. Initially, difference in calcium increases upto 400 ms then attains steady state at 400 ms.

Fig. 12

Difference of calcium concentration due to obese and normal hepatocyte

Figure 13 shows a difference of DAG net growth rate variation due to obese and normal hepatocyte cells with respect to space and time. Figure 13A shows a spatial difference graph for DAG net growth rate variation. The graph illustrates that the initial difference in calcium concentration near the source increases and reaches its peak at approximately 5 $\mu$ m then starts decreasing due to obese and normal hepatocyte cells and becomes zero. Figure 13B shows a temporal difference graph for DAG net growth rate variation. It is noticed from the figure that the behaviour of the DAG net growth rate variation is similar to Fig. 10B. It is seen from the curves that the difference in net growth rate increases more gradually and smoothly compared to the temporal calcium profile in Fig. 1B

Fig. 13

Difference of DAG net growth rate due to obese and normal hepatocyte

Figure 14 displays calcium concentration distribution in normal and obese hepatocyte cells. Figure 14A shows calcium concentration variation with respect to space for normal and obese cells. The Fig. 14A demonstrates that the concentration of calcium increases in obese cells as ER becomes leaky in obesity. Figure 14B shows calcium concentration variation with respect to time for normal and obese cells. The behaviour of the curves is similar to that in the Fig. 1B.

Fig. 14

Calcium concentration variation in normal and obese hepatocyte

Figure 15 shows DAG net growth rate variation in normal and obese hepatocytes. Figure 15A shows DAG net growth rate variation with respect to space for normal and obese cells. It is observed from the figure that the DAG net growth rate is high in the case of obese cells. DAG net growth rate is highest at the source. When going away from the source DAG net growth rate decreases and attains a fixed value that is $\approx$ 0.6 $\mu$ M sec^-1. Figure 15B shows DAG net growth rate variation along time. It is observed that initially difference in DAG net growth rate in the obese and normal cells was not much but as time increases difference increases. It is noticed that in obese hepatocyte cells, DAG net growth rate increases in comparison to normal hepatocyte cells.

Fig. 15

DAG net growth rate variation in normal and obese hepatocyte

Figure 16 shows a 3-d plot among calcium concentration, buffer concentration and time at $x$ = 0, 0.1875, 0.9375 and 1.6875 m$\mu$. The figure illustrates that the concentration of calcium is a maximum $\approx$ 0.5 $\mu M$ and the buffer value is smallest around 0 $\mu M$ at time t = 0 ms. With the increase in time, calcium concentration reaches its equilibrium value i.e. 0.1 $\mu M$ and buffer value increase with the increase in time. An inverse relationship is observed between calcium and buffer. As a high quantity of calcium is toxic to the cell, buffers bind with calcium and form a calcium-bound buffer. Therefore, when calcium concentration is high, the free buffer value will be low and when the buffer value is high, calcium concentration will attain a small value (Tables 1, 2, and 3).

Fig. 16

Graph among calcium and buffer concentrations and time at different spatial positions

Table 1 Physiological parameters for calcium and buffer variation (Jagtap and Adlakha 2019; Smith et al. 1996)

Table 2 Physiological parameters for the comparative study of normal and obese hepatocyte cells (Han and Periwal 2019)

Table 3 Error analysis for calcium profile with 80 elements and 90 elements

Figure 17 shows a 3-d plot of calcium concentration, buffer concentration and time at $x$=0 m$\mu$ for the source influx’s different values. It is analyzed from figure that at $t$=0 ms the concentration of calcium is highest $\approx$ 0.5 $\mu M$ and the buffer value is smallest around 0 $\mu M$. With the increase in time, calcium concentration reaches its equilibrium value i.e. 0.1 $\mu M$ and buffer value increases with the increase in time. With the increase in the value of source influx, a gradual and smooth increase in the concentration of buffer is observed with respect to time. The concentration of calcium increases with an increase in source influx, hence buffers take more time to form a calcium-bound buffer. An inverse relationship is observed between calcium and buffer. As a high quantity of calcium is toxic to the cell, buffers bind with calcium and form a calcium-bound buffer. Therefore, when calcium concentration is high, the free buffer value will be low and when the buffer value is high, calcium concentration will attain a small value.

Fig. 17

Graph among calcium and buffer concentrations and time at x = 0

Error and stability analysis

Error analysis is done for $t$= 0.1, 0.2, 0.3, 0.4 and t = 0.5 s at $x$=0. The finite element method is found effective in this problem as accuracy with 80 linear elements for calcium profile is found as 99.96% and for buffer profile accuracy is 99.47% as displayed in Table 4. The spectral radius for the finite element method is 0.9959 which is less than one therefore, the method is stable.

Table 4 Error analysis for buffer concentration profile with 80 elements and 90 elements

Validation

The concentration profiles of $[C{a}^{2+}]$ obtained for the parameter values taken by Smith et al. (Smith et al. 1996) at x = 0, 0.5, 1, 2 and 15 m$\mu$, are compared to earlier research by Smith et al. (Smith et al. 1996) at time t = 50 s and findings are in good accord, as demonstrated in Table 5.

Table 5 Validation of calcium dynamics with Smith et al. at t = 50 s (Smith et al. 1996)

Conclusion

The existing model (Smith et al. 1996; Lopez-Caamal et al. 2014) is modified by incorporating IP3R, SERCA pump, RyR and calcium buffering fluxes and reaction term to propose a new system dynamics model for numerical simulation of calcium, buffer and DAG dynamics due to obese and normal hepatocyte cells. The outcomes were discovered to be consistent with cellular biological phenomena (Naraghi and Neher 1997; Neher and Augustine 1992; Smith et al. 1996). The results lead to the following basic conclusions:

• (i) As source inflow increases, it also raises the concentration of free calcium.

• (ii) With an increase in free buffer concentration, free calcium concentration falls.

• (iii) With an increase in calcium’s diffusion coefficient, free calcium concentration drops.

• (iv) (iv)The concentration of free calcium decreases as the buffer’s diffusion coefficient rises.

• (v) Near the source, the concentration of the calcium is largest and calcium diffuses towards other end of the cell ($x$= 15 $\mu m$) and reaches an equilibrium state, whereas free buffer concentration diffuses towards calcium source.

• (vi) Free calcium and buffer reach at steady state at the same time period with a slight change in temporal behaviour.

The analysis of numerical results leads to the following novel conclusions:

• (i) The spatial locations where calcium concentration is high, there consequently the free buffer concentration is low because free buffer concentration decreases due to high buffering activity to lower the free calcium concentration at those locations.

• (ii) The spatial locations where the rise in calcium concentration is high, there consequently rise in free buffer concentration is slower because most of the free buffer binds with free calcium. Similarly, wherever buffer concentration is rising rapidly consequently calcium concentration rises slowly.

• (iii) Free calcium and free buffer are interdependent depending on their domination at various locations.

• (iv) Free calcium and free buffer fluctuate dynamically concerning one another based on the rate of a gradual rise in buffer activity. The difference in calcium profile and DAG net growth rate due to realistic dynamic buffering process and idealistic constant buffering process is quite significant. Thus, it implies that the proposed model provides more realistic simulation results as compared to the existing models.

• (v) Due to an increase in calcium-elevating mechanisms brought on by obesity, the amount of free calcium concentration is higher in the obese cell than it is in the normal hepatocyte cell.

• (vi) DAG growth rate is higher in obese cells as compared to normal hepatocyte cells due to increase in calcium concentration causing an increase in DAG net growth rate in obese cells.

• (vii) The effect of changes in parameters like source, total buffer concentration, SERCA pump etc. on calcium profiles is transferred in a synergistic manner to the net growth rate of DAG. Thus changes in these parameters cause significant changes in the net growth rate of DAG leading to various disorders of the liver like obesity, diabetes etc.

• (viii) Obese mice’s liver cells had an ER content that was 50% lower. The obesity-related aberrant increase in MAM (mitochondria associated membrane) production induces increased Ca²⁺ flow from the ER to the mitochondria (Arruda et al. 2014). As a result, only a 10% increase in the calcium content of a hepatocyte cell’s cytoplasm was anticipated, the same is evident in Fig. 14.

Thus proposed model is quite effective in estimating the levels of concentration of calcium in obesity and normal conditions of the cell. The numerical approach consisting of finite element and Crank- Nicolson method is competent enough to solve the proposed model for generating useful results. The ensuing model excels among others as it is able to incorporate the effect of dynamic variations in free buffer concentration on free calcium concentration and vice versa in normal and obese hepatocyte cells and provide the more realistic dynamics of calcium and buffers in these cells. Similar models can be developed further for other liver disorders like diabetes etc. to generate crucial information for therapeutic applications.