An emerging view of the mathematics that teachers use in their work acknowledges its special character (Ball & Cohen, 1999; Lampert, 2001; Ma, 1999). Consistent with the argument made by Ball and Bass (2003) that “mathematical knowledge for teaching has features that are rooted in the mathematical demands of teaching itself” (p. 4), new approaches to structuring teachers’ learning opportunities, often referred to as practice-based professional development, engage teachers in activities that replicate or resemble components of their daily work (Smith, 2001). Advocates for this approach argue that learning experiences that are highly connected to and contextualized in professional practice can better enable mathematics teachers to make the kinds of complex, nuanced judgments required in teaching (Ball & Bass, 2003; Little, 1993).

Using the work of teaching as a central resource, practice-based approaches attempt to coordinate and link different facets of teacher knowledge to each other and to the settings in which the knowledge is used. In traditional approaches to teacher education in North America, for example, the knowledge domains of mathematics content, mathematics pedagogy, and student thinking tend to be treated separately. In particular, teachers take some specific courses to learn mathematics, different ones to learn pedagogy, and others to gain information about how students learn. Moreover, the content of the mathematics courses is usually provided apart from any deep consideration of its use in the work of teaching. One consequence of such a treatment of knowledge is that the learner is burdened with the responsibility for making the needed connections across domains and recognizing the settings in which the knowledge could be appropriately used. In contrast, in practice-based approaches the knowledge domains are treated as intertwined, and they are tied to settings in which they appear in the work of teaching. Although the separation of knowledge domains in teacher preparation is an especially acute problem in the U.S.Footnote 1, there is worldwide interest in teacher learning in, from, and for professional practice. For example, the theme of “professional learning in and for practice” was one of the major organizational strands in the International Commission on Mathematics Instruction (ICMI) Study 15 on mathematics teacher education (ICMI, 2004), which drew nearly 150 researchers from more than 30 countries.

A key element in practice-based professional development is a well-designed, well-facilitated professional learning task (PLT) (Ball & Cohen, 1999). PLTs are organized around artifacts of practice such as curriculum materials, video or narrative records of classroom teaching episodes, and samples of student work. They make the work of teaching (e.g., designing, preparing to teach, or enacting classroom lessons or larger units of instruction; analyzing evidence of student thinking from verbal statements or written products) available for investigation and inquiry (Smith, 2001). PLTs are complex tasks that create opportunities for teachers to ponder pedagogical problems and their potential solutions through processes of reflection, knowledge sharing, and knowledge building.

Although advocates for practice-based approaches have made a strong case for its adoption, a number of fundamental issues remain largely unexplored. For example, given the centrality of teachers’ knowledge in the work of mathematics teaching, it is critical to examine the ways in which teachers’ engagement in professional learning tasks affords them opportunities to enhance their mathematical knowledge. In this paper, we examine data from a practice-based professional development initiative to illuminate how the PLTs used therein made available opportunities for teachers to work on and learn about mathematical ideas.

Context: The BIFOCAL Project

BIFOCAL (Beyond Implementation: Focusing on Challenge and Learning) was a multi-year practice-based professional development initiative intended to support teachers of mathematics in the middle grades (grades 6–8). In this paper, we focus on the first year of the project (May 2003 to May 2004). In that year we worked with 12 teachers from 5 middle schools that had been using Connected Mathematics (Lappan, Fey, Fitzgerald, Friel, & Phillips, 1996) for at least three years. This mathematics curriculum features many complex, contextualized problems and mathematical investigations. Participants met about once per month in a series of day-long sessions, during which they typically engaged in two main sets of activities designed to assist them to improve their teaching practice: (1) case analysis and discussion and (2) modified lesson study.Footnote 2

BIFOCAL was built on a foundation of prior work in the Quantitative Understanding: Amplifying Student Achievement and Reasoning (QUASAR) and Cases Of Mathematics Instruction to Enhance Teaching (COMET) projects, particularly regarding the effective classroom use of cognitively demanding tasks (e.g., Silver & Stein, 1996; Stein, Grover & Henningsen, 1996; Stein, Smith, Henningsen, & Silver, 2000). A basic premise of BIFOCAL was that teachers would benefit from opportunities to consider the challenges and opportunities associated with teaching mathematics using cognitively challenging tasks. Because they were using curriculum materials that provided a rich supply of such tasks, an initial focus of our work was the ways in which teachers’ use of such tasks could enhance or constrain students’ opportunities to learn mathematics.

Professional Learning Tasks Incorporating Narrative Cases: Opportunities to Learn Mathematics

We frequently used narrative cases as anchors for PLTs in the BIFOCAL project (Silver et al., 2006).Footnote 3 In general, narrative cases offer a means of drawing teachers’ attention to key aspects of mathematics teaching and learning. The cases we used were developed in the QUASAR and COMET projects to illustrate core issues and persistent challenges embedded in the use of cognitively demanding tasks in the mathematics classroom. These narrative cases describe instructional episodes depicting a teacher facilitating student engagement with a mathematical task or problem. Additionally, they portray the interactions among the teacher, the students, and a mathematical task.

Although our focus in BIFOCAL was primarily on the effective use of cognitively demanding tasks in the classroom – essentially a pedagogical issue with mathematical entailments – the PLT cycle used in the project did provide opportunities for participants to learn mathematics. With respect to the PLTs anchored by narrative cases, for example, teachers encountered mathematical ideas through the mathematical tasks and through the teachers’ and students’ work embedded in the cases.

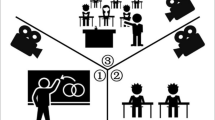
We identify four distinct, though highly interrelated, opportunities for BIFOCAL participants to learn mathematics within the project’s PLT cycle when anchored by a narrative case. These opportunities are illustrated in Figure 1 as four embedded activity segments. The first activity segment (triangle 1 in Figure 1) is the Opening Activity (OA), during which teachers are asked to solve a nontrivial mathematics problem. The OA offers an opportunity for teachers to engage directly in mathematical problem solving, which has the potential to provoke deep thinking on their part regarding at least one mathematical idea. Initially, teachers solve the problem individually, and then discuss with others their solution methods. In this respect, teachers have the opportunity to tease out the mathematical ideas embedded in the problem and consider them directly without necessarily considering pedagogical entailments. Furthermore, by serving as a preview of the mathematical task in the case, the OA prepares teachers for the next activity—reading and analyzing the case.

Fig. 1
figure 1

Opportunities to learn mathematics in a case-anchored BIFOCAL PLT cycle

Full size image

The second activity segment (triangle 2 in Figure 1) is individual reading and analysis of the narrative case. Each case describes a classroom instructional episode in which students and a teacher enact a cognitively demanding mathematics problem, similar to the one given in the OA. The depiction of teaching, including dilemmas and challenges, as well as the portraits of student thinking and learning during enactment of the problem, allow readers to encounter the mathematical ideas associated with the problem in an instructional context. To guide the reading and analysis of the case, we provide the teachers with focus questions to draw their attention to key facets within the case. As they read, teachers consider the mathematical ideas at play in the lesson, and as depicted in the case, in relation to the mathematical ideas that emerged in the OA. Usually, the teachers start by individually reading the case and then discuss it with other project participants.

The third activity segment (triangle 3 in Figure 1) is whole-group case discussion. The whole-group discussion provides an occasion for further relating OA experiences to the lesson depicted in the case, clarifying concepts, introducing additional ideas, or problematizing issues related to mathematics content, pedagogy, or student learning. When teachers comment on issues arising in the case in a manner that ties to their own teaching, they anticipate the next activity.

The fourth activity segment (triangle 4 in Figure 1) consists of a structured opportunity for participants to consider the case in relation to their own instructional practice. During this activity segment, teachers engage in a collaborative lesson planning and debriefing cycle consisting of selecting a target lesson, planning the lesson collaboratively, teaching the target lesson in their classrooms (between BIFOCAL sessions), reflecting on their instructional moves in relation to evidence of students’ thinking and understanding, and analyzing their lessons in discussions with colleagues. During collaborative lesson planning and debriefing, teachers often propose and explore ideas related to instruction that arose from the case discussion and then analyze and test the applicability of these ideas in their lesson planning. In a subsequent BIFOCAL session, teachers analyze the efficacy of the ideas as they were represented in the lessons they taught and revisit the ideas in ensuing cases, thereby refining and extending their understanding of the ideas. We employed lesson planning tools, such as the Thinking through a Lesson Protocol (Smith & Bill, 2004), to focus and support teachers as they engage in lesson planning, reflection, and analysis.

Throughout all four PLT activity segments, teachers often draw on their practice to enrich the discussions that transpire. It is common for teachers to consider how students in their classrooms might solve the problem in the OA or how pedagogical practices they have utilized with similar mathematics content influence student learning. As they move back and forth between PLTs offered in BIFOCAL sessions and their classroom teaching, teachers have further opportunities to grapple with a host of mathematical ideas and potentially expand and deepen their mathematical knowledge for teaching.

Theoretical Perspectives on Teachers’ Opportunities to Learn Mathematics

In the space available we can only summarize briefly the theoretical perspectives on human learning that inform practice–based approaches to teacher education. Sociocultural theories, emerging largely from the work of Vygotsky (1934/1962, 1978), underscore the situated nature of teacher knowledge and the culturally embedded processes by which one comes to participate fully in a community. In addition, cognitive theories, with origins in the work of Piaget (1950, 1952), underscore the key role that individual reflection and cognitive conflict can play in stimulating conceptual development and change. Though scholarly debates have erupted regarding the apparent conflict between these two theoretical stances, we agree with Sfard (1998) that the acquisition (cognitive) and participation (sociocultural) perspectives on learning can be productively viewed as complementary rather than contradictory. In fact, we see practice-based approaches to teacher professional development as a strong example of how the two different theoretical perspectives can co-exist in the service of learning goals.

These perspectives illuminate why it might be possible for teachers to have opportunities to learn mathematics in practice-based professional development. From a cognitive perspective, a critical aspect of PLTs is their potential to provide opportunities for teachers to treat a particular situation as problematic - as something they need to think deeply about and carefully consider rather than something that calls for a scripted solution. Commentators on human learning, stretching back at least to Plato, have long noted that disequilibrium can be an impetus for accommodation, and contemporary research on conceptual change has confirmed that learning often occurs when individuals sense a difficulty or impasse that they need to resolve (e.g., Vosniadou & Verschaffel, 2004). In the BIFOCAL PLT cycle that we describe above, participants have opportunities to treat classroom instructional situations as problematic and consequently to experience dissonance, which cognitive learning theorists view as a pathway to conceptual growth and change. The dissonance may arise in the OA as teachers try to solve a challenging mathematics problem. Or the dissonance might occur later in the PLT activity cycle, arising as one compares one’s own practice to the practice of the teacher depicted in the case, or from questions or observations offered by other participants. Opportunities for this dissonance may also arise in the final stage of the cycle in one’s attempt to experiment with new ideas in one’s own practice.

Complementary to this cognitive depiction of learning opportunities is a consideration of the critical role that conversation with and mediation by others can play in supporting conceptual change. Sociocultural accounts of learning draw attention to the role that discussion, debate, and negotiation can play in interactions between learners and their peers, especially those deemed to be more capable (Tharp & Gallimore, 1989). Thus, we would expect that peer interaction and skilful facilitation would both be important factors in fostering opportunities to learn in practice-based professional learning environments.

With regard to teachers’ opportunities to learn mathematics, much of the presumed power of PLTs of the form described above resides in their allowing teachers to examine specific mathematics ideas from several different perspectives: as a doer of mathematics, as an observer of mathematics teaching and learning, and as a teacher whose work entails assisting students to learn mathematics. Moreover, as we noted at the outset, practice-based professional development integrates and interweaves several domains of knowledge germane to teaching: mathematics, pedagogy, and student thinking. These two features of PLTs – multiple perspectives and interwoven knowledge strands – can be seen as related to the enhanced knowledge that one intends to result from professional development; namely, knowledge that is well-organized and connected to settings of use.

The organization and connectedness of knowledge is critical to its usability. One of the key findings of several decades of research on complex human performance is that expert competence rests on a knowledge base that is distinctive in its organization and connectedness: “Experts know the conditions of applicability of their knowledge, and they are able to access the relevant knowledge with considerable ease” (Bransford, Brown, & Cocking, 2000, p. 237). In contrast, non-experts may know as much as experts, but they are often unable to use their knowledge: “Learners do not always relate the knowledge they possess to new tasks, despite its possible relevance. This ‘disconnect’ has important implications for understanding differences between usable knowledge (which is the kind of knowledge that experts have developed) and less-organized knowledge, which tends to remain ‘inert’” (Bransford et al., 2000, p. 237).

This characterization suggests a useful perspective from which to view teacher learning in and through practice-based approaches; namely, the connection of knowledge to settings of usability. Thus, in considering how such practice-based approaches might afford opportunities for teachers to learn mathematics, we need to examine how these opportunities promote the connection of mathematical ideas to each other and the connection of mathematical ideas to settings in which these ideas are used in the work of teaching, which also involve issues of pedagogy and student thinking.

Data Sources and Analysis Method

To probe the nature of project participants’ opportunities to learn mathematics, several different kinds of data were examined. The corpus of data used in this study consisted of:

  • Video and textual records: Each professional development session was videotaped and transcribed. The video camera focused on large-group interactions, supplemented by field notes that detailed small-group interactions.

  • Post-session reflections: Written reflections were solicited and collected at the end of each session. Participants were usually asked to comment on each day’s activity in relation to their instructional practice, their students’ mathematical learning, or other pertinent themes.

  • Interviews: Semi-structured interviews were conducted individually with participants in May 2004. The interviews were audiotaped and transcribed. An interviewer probed participants’ perceptions of the nature and impact of project experiences across the year. Memory prompts included a chart summarizing major project activities over the year (e.g., the specific problems, cases, and lessons considered) to which teachers referred as they were asked to identify and comment on activities that they judged to have contributed to their learning.

In our examination of how opportunities to learn mathematics were made available in BIFOCAL, we focus on the PLTs and associated activities in two consecutive sessions (February and March 2004). We selected these sessions for two reasons. First, these sessions were among those most often identified as influential in participant interviews at the end of the first year. Second, the sessions encompass the activity segments of the BIFOCAL PLT cycle shown in Figure 1: initial problem solving; case analysis and discussion; and collaborative lesson planning and debriefing. In addition, both sessions addressed in some way the same mathematical topic, proportionality, and considered the entailments of the pedagogical practice of having students share multiple solution methods. Transcriptions of the videotaped sessions and associated field notes were the primary data sources for this analysis.

To sharpen our presentation of findings regarding learning opportunities and to reduce the density of the data to be analyzed, we highlight one teacher, Natalie. We use her interactions with the PLTs, her colleagues, and the facilitators to illustrate the nature of opportunities to learn mathematics in the various activity segments. Natalie was an active participant in both sessions, thereby ensuring a data stream suitable for analysis.

Findings and Discussion

In this section we use data from the February and March 2004 sessions to illuminate opportunities to learn mathematics within three directly observable activity segments in the BIFOCAL PLT cycle: initial problem solving, case analysis and discussion, and lesson planning and debriefing. Each activity segment is discussed in turn.

Initial Problem Solving (February 2004)

The opening activity for the February 2004 session was the Candy Jar Problem (Figure 2). The problem consists of three questions that can be correctly answered in several different ways using ratios, fractions, decimals, and percentages.

Fig. 2
figure 2

The Candy Jar Problem

Full size image

Participants solved the problem in several different ways. Figure 3 displays three of their methods to answer questions 1 and 2. After participants solved the problem, the facilitator asked several participants to display and explain their solution methods. Helen went first and explained that she added 5 Jolly Ranchers (JR) and 13 Jawbreakers (JB) to each previous combination of JR and JB to obtain the next. This was characterized as an additive approach. Next, Natalie shared her solution. Initially, she stated that she had followed “the same approach” as Helen’s, with the only difference being the arrangement of the numbers in the table. However, in further explaining her approach, she pointed out that she had actually multiplied the initial number of JB and JR by different factors each time, until she found some useful shortcuts (i.e., she multiplied the 25 JR and the 65 JR by a factor of 4 or the 20JR and the 72 JR by a factor of 10). Following this, Kendra presented a solution that also involved multiplication. She indicated that the factor of 20 was needed to transform 5 JR into 100 JR, and then multiplied the original number of JB by this same factor to determine the number of JB. She used a parallel process to answer the second question. Other participants also presented a few solutions to the Candy Jar problem.

Fig. 3
figure 3

Three Solutions Produced by Participants

Full size image

Following the solution presentations, the facilitators orchestrated a discussion of the various methods. Several points about the relationships among the solutions were noted. For example, participants commented on the difference between the additive and the multiplicative approaches pursued by Helen and Natalie. Recall that Natalie did not accentuate this difference when presenting her solution; instead she said that hers and Helen’s solutions were essentially the same. However, a short time later, after Kendra presented her solution, Natalie remarked that she and Kendra both “followed a scale-factor approach.”

In order to probe and challenge participants’ solution methods one of the facilitators noted that many of the solution methods involved what he called a jump. In Natalie’s approach, for instance, there is a “jump” from 25 JR to 100 JR. To provoke participants to articulate the mathematical idea that underlies such “jumps,” the facilitator shifted attention to students and how this idea might be explained to them:

  • Facilitator: There is something about that move that depends on understanding, something pretty fundamental about ratios. Everybody agrees that it’s okay. But why is it okay? … There is something at the heart of all of them [these solutions] that it’s really fundamental to this. Is this something that 6th graders just have no trouble with? I mean, they might accept it, but do they get it?

The facilitator’s comment sought to sharpen their examination of the various solution methods and help them consider two different types of connections. First, it suggested that, in addition to the connections outlined before, participants should also delve deeper into the mathematics of each approach teasing out the core mathematical ideas underpinning these approaches. In so doing, the facilitator was, in essence, urging these teachers to build more underlying, fundamental, connections within the domain of mathematics. And second, by asking if students understand this fundamental idea, he deliberately brought into play issues of student thinking and pedagogy. In this way, his comment opened an opportunity for participants to build connections between student thinking and the mathematics at stake in the discussion.

In responding to the facilitator’s comment, participants drew on their experience in teaching these ideas. At one point Natalie claimed that it was not until seventh grade that students are able to gain a conceptual understanding of these ideas. The facilitator asked her to explain how she fostered the development of conceptual understanding in her students, and she replied that she often relied on drawings and diagrams, but she did not provide a clear explanation of how she could use diagrams or drawings to illustrate the core mathematical idea that legitimates the “jump.” In fact, none of the participants articulated the mathematical idea lurking at the root of this step, nor did they clarify how this mathematical idea might be explained to students.

To advance the conversation beyond this impasse, the facilitator commented that it was critical to remember that the problem involved more than numbers – the numbers are attached to quantities, and the problem is about the multiplicative relationships between and among the quantities. Saying that two ratios are equivalent is saying that the relationship between quantities expressed by each ratio is identical in the two ratios. That is, the absolute size of the quantities may vary between the ratios, but the relative relationship between corresponding quantities is preserved.

There were no immediate comments from participants about what the facilitator said, so the facilitator resumed the conversation about comparing different solution methods. After several minutes of this renewed discussion, Natalie interjected a comment:

  • Natalie: Can I say something about the scale factor? This just popped to the front of my brain. Conceptually … the reason we can multiply by 20 in the numerator and 20 in the denominator is because you are really multiplying by 1. And we are not changing the size of the fraction … we are changing the size of the pieces. … So, the whole is the same but the parts are smaller.

In this comment one can see how Natalie interpreted the facilitator’s statement regarding the constant relationship between quantities in two equivalent ratios, connecting it to other elements of her prior knowledge about fractions (which were never mentioned by the facilitator), or some combination of both. It appears that Natalie was trying to assimilate the facilitator’s comment into her existing knowledge of pertinent mathematical ideas, especially fractions.

Natalie’s introduction of the word “fraction” into the conversation was consequential for the group’s opportunity to learn mathematics. The facilitator cautioned that the relationship between ratios and fractions was subtle and prone to misunderstanding. He noted that Natalie’s explanation would be accurate in describing fractional equivalences – multiplying a denominator by a whole number can be thought of as subdividing the size of the parts in a fraction – but the quantities in the Candy Jar Problem do not conform to this depiction. In that problem, the candies are not being subdivided. Instead, multiplying one term of a ratio by a whole number increases the number of candies. The facilitator noted that if you think about quantities, and not only numbers, you see an important difference between ratios and fractions in how you interpret the meaning of the “scale factor” jump encountered in solutions of the Candy Jar Problem.

Natalie pursued this idea further by noting that fractions and ratios often seem to be used interchangeably in mathematics books, and she had not thought much about this distinction in her teaching. She elaborated, “We often write ratios as fractions, when we say part to whole, it feels like a fraction.” Several other participants also commented, suggesting that they also used these concepts interchangeably. This exchange between Natalie and the facilitator appears to mark a clear moment of cognitive dissonance for her and at least some of the other participants. The facilitator responded by suggesting that at times the distinction between ratios and fractions is largely invisible, such as when working with equivalence. The distinction however becomes critically important when trying to interpret the meaning of the numbers in relation to the quantities they represent and when engaging in operations on and with the quantities these numbers represent. To illustrate, he contrasted the addition of fractions (where adding numerators and denominators leads to error) with the combination of ratios (in which one can, under certain conditions, add corresponding quantities to produce a correct result). He elaborated this distinction by using examples from real life where combining two ratios makes sense and others where adding fractions would be more reasonable.

In this brief account of the opening activity segment of the February 2004 session, it is clear that a number of mathematical ideas – including ratio, proportion, multiplicative relationship, scale factor, and fraction – were under consideration by the participants. Also, participants considered and compared several different solution strategies for a few mathematics problems, and they reflected on the complexity of each approach both from their perspective as doers of mathematics and from the perspective of teachers whose work entails assisting students to learn mathematics. In addition, their attention was drawn to the important relationship between the numbers and the quantities they represent in ratio, proportion, and fraction problems. We also saw in this episode evidence of Natalie attempting to reconcile new and old ideas to make sense of the mathematics at stake in the session and to resolve the emergent cognitive dissonance. At several points during this activity segment, participants were offered opportunities to connect the mathematics at stake in the discussion to their pedagogical practices and their understanding of their students’ thinking.

The opportunities for teachers to work on the mathematics in this activity segment were supported by the social mediation that characterized their interactions. In one respect, the whole group discussion mediated teachers’ access to practices and ideas as they were negotiated between the group members. In another respect, facilitation of the PLT played another mediating role in the way the facilitators challenged teachers’ solutions and prompted them to consider them in relation to student learning. The facilitators pressed the teachers to consider not only the methods of solving specific problems, but also why these methods make sense and what pedagogical entailments they may have for supporting student thinking.

Narrative Case Analysis and Discussion (February 2004)

In the next activity segments participants read and discussed a case (triangles 2 and 3 in Figure 1). Introducing Ratios and Proportions: The Case of Marie Hanson (Smith et al., 2005b, pp. 26–43) depicts a sixth-grade teacher using a mathematics task that introduces her students to ideas of ratio and proportionality in the context of a complex problem, Candy Jar Problem (Figure 2). The case portrays Marie’s students using a variety of problem-solving strategies and representations – verbal descriptions, tables and diagrams. Yet some of their approaches are incorrectly based on an additive rather than a multiplicative rationale. Marie is thus confronted with several instructional challenges: Which solutions should she ask students to share? How should she orchestrate the sharing of these solutions? Should she ask students to present incorrect approaches? How could she help the students who solved the problem using an additive approach develop understanding and, at the same time, ensure that the rest of the class will not get confused or bored?

This case was selected for use in the February session for two reasons. First, it provided an opportunity for participants to continue working in the domain of proportionality, which had also been the focus of the previous session in January 2004. Second, the case provided an opportunity to deal explicitly with the pedagogical practice of having students share several solutions to a problem. This pedagogical issue surfaced in the first project session in May 2003, and resurfaced in January 2004, so it appeared to be ripe for further work.

After reading the case, the teachers were invited to comment on aspects of the case that they found interesting or important. Some participants commented on Marie’s encouragement of students to use different representations; others attended more to her questioning strategies and her skillful highlighting of connections among students’ solutions. Natalie noted Marie’s decision making regarding the order in which solutions would be presented:

  • Natalie : One thing that I noticed, and that I don’t know if I pay enough attention to, is that she [Marie] mentioned she wanted to expose her students to multiple strategies. [Natalie reads from the case]: “As the time to share solution strategies approached, I struggled with the decision as to which solution strategies to get out publicly and in what order.” I guess I saw that as a choice – Do I or do I not pay attention as to what order I share solutions? And does it make a big difference or not in the students’ thinking? If I do it, should I start with the most simplistic way and move up the ladder, or is a random presentation just as good? I guess in my classroom I don’t consider that so much, but maybe I should.

Noting that she did not think much about this issue in her own teaching, Natalie wondered whether the deliberate ordering of solution methods might make a difference, and if so, whether there is an optimal way to order students’ solutions.

The facilitator redirected the question to the other participants, prompting them to consider Marie’s rationale for the order in which her students’ solutions were presented. Several participants suggested reasons having to do with the complexity of different solution methods and the ease of grasping the underlying mathematical rationale. In this way, the participants were tying mathematical ideas to issues of pedagogy and student thinking that were evident in the case.

Natalie commented that she thought that Marie’s decision to have an erroneous method presented first reflected her desire to allow students to address a fundamental misconception. That is, Marie capitalized on one student’s error to allow all students to address this misconception. Appropriating language introduced by the facilitator during the opening activity that morning, she referred to Marie’s intention to expose students to both additive and multiplicative approaches. This comment prompted a vigorous discussion among participants about Marie’s decision to expose the student error and common misconception first. Some participants worried that exposing the error early might accentuate some students’ confusion:

  • Nina: I agree that she [Marie] needed to get the addition fallacy out of the way, or whatever, but I don’t know that I would have started with that. Because if people are on the verge of seeing it but a little bit confused and they see that I am afraid that is just going to completely confuse them.

Other participants wondered whether it would have been better to avoid exposure of the misconception to the class.

The facilitator decided to probe this issue a bit further by asking whether exposing students to incorrect approaches could help solidify their understanding of correct approaches. Noting that the concern about student confusion might be reasonable, he asked if there weren’t also some costs or risks associated with leaving the error invisible to the class:

  • Facilitator: [If the erroneous solution is not shared] the work of figuring out why that solution is wrong [is left] as a private matter for those kids that made that error … How can the rest of the class … benefit from the contrast of additive vs. multiplicative thinking if they don’t have access to it? They don’t know what the problem is that these other guys over here are working on because it isn’t out in a public space where it can be worked on as a group.

In this brief account of these activity segments, we can see that reading and discussing the case not only provided participants with opportunities to encounter once again the mathematical ideas met in the opening activity but also to connect these ideas to a range of pedagogical and student-related issues. The PLT anchored in the narrative case allowed participants to consider mathematical ideas in light of the thinking of students and the decision making of the teacher as the case unfolds.

The case discussion and analysis afforded the participants a space in which they could also make connections to their own practice. Embedded in this aspect of the activity were further opportunities to consider mathematics. Consider, for instance, Natalie’s comments on the ordering of students’ solutions. Natalie’s public comments appear to focus on pedagogy and they reflect a degree of dissonance. She expresses interest in taking up different practices in her classroom, particularly increased attentiveness to and use of students’ solutions, and she suggests the need to develop more sensitive filters that allow her to sequence student solutions in instructionally effective ways. Yet it is also important to note the critical mathematical entailments of her remarks, though the mathematical considerations are subtler than in her OA comments in which she attempted to make sense of specific mathematical concepts. If she is to take up these new practices, she must more deeply consider what it means for a solution to be “simplistic” versus other solutions that are further “up the ladder” – judgments that are essentially mathematical.

In these segments of the BIFOCAL PLT activity cycle, the facilitators appeared to play a critical role in assisting participants to overcome impasses and in challenging them to make connections within and across knowledge domains relevant to their practice. In this episode we noted that the facilitators pressed teachers to consider actions like addressing students’ erroneous solutions in light of not only pedagogical considerations (e.g., other students might get confused), but also mathematical ones. The mediation of the facilitator in teachers’ opportunities to learn mathematics was evident in the way the facilitators directed participants’ attention to critical mathematics-related aspects of the case (e.g., mathematics-based decisions regarding how to sequence students’ solutions).

In sum, the discussion of the case made clear that pedagogical decisions could and should be informed by the mathematical ideas and concepts at stake in a lesson. We speculate that this phase of the PLT helped participants organize their (individual and collective) knowledge of the ideas of proportionality and connect that knowledge to settings of use in teaching, by interweaving mathematical considerations, pedagogical concerns, and issues of student thinking. If so, then we would expect that their knowledge could become more usable for the purposes of their practice.

Debriefing Lesson Enactment (March 2004)

The final activity segment in the BIFOCAL PLT cycle (triangle 4 in Figure 1) was intended to promote the application of learning derived from other activity segments. During this segment, participants collaboratively planned lessons, decided how to evaluate the effectiveness of the lesson, and shared information with each other about the enactment of these lessons. In March 2004 participants discussed the enactment of lessons that had been planned at the February session.

Natalie’s lesson involved the problem shown in Figure 4. Natalie explained how the lesson unfolded and displayed posters created by her seventh-grade students to illustrate and explain their solution methods. As her students worked on the problem, she walked around the room and noted the different solution approaches that students were using.

Fig. 4
figure 4

The problem Natalie assigned to her seventh-grade students

Full size image

Natalie “ranked” students’ solution approaches according to her judgment of their sophistication:

  • Natalie : I have them do a poster. And as I was doing it, I was consciously walking around putting numbers on their posters. Because what we talked about the last time, I was trying to set up the presentations in a specific order from the simple to the advanced. So, for example, this group here [pointing to a poster of student work] got a 1 because you see they kind of struggled a little bit.

  • Facilitator: The question was “The spread of the largest white oak is greater than that of the largest Coast Redwood by a ratio of about 3 to 2.”

  • Natalie: So they knew that the numbers that it showed in the problem had to 3 to 2 had also to be 120 to 80. And they rounded it.

  • Teachers:They also rounded right here, this was 119.

  • Natalie:Yeah, they took 119 and made it 120. So this was the simplest understanding the ratio 3 to 2. Three dots, two dots, and they continued all the way until they got … 120 and 80 [dots]. So I thought this was the simplest way, yet correct and a very good way of solving it. Then, there were some number 2’s where …[students] found out that if we multiply by forty which means there are forty sets of 3 and forty sets of 2, we are going to get to a similar ratio. … And then there were some 3’s that showed and I had never showed them this before. So they took both parts and divided them and came out with 1.5 both times. So they said therefore they are the same ratio.

  • Teachers: How do you think they came to that?

  • Natalie: Well, I asked them that and what they said was if you kind of think of it as a fraction – and a fraction is a division problem – so if I did two division problems you get the same answer and they have to be the same ratio.

For solution methods she deemed the simplest, Natalie placed a “1” on the student paper; she designated as “2” those methods that were more complex, and she used “3” for the even more complex solution methods. Using this scheme, she asked several students to display their solutions to the entire class, beginning with those labeled “1” and moving “up the ladder” to those with higher numbers denoting more complexity. After clustering students’ solutions according to their level of complexity, she orchestrated a whole class discussion and comparison of solution methods.

Natalie’s lesson debriefing showcases how certain ideas discussed in the February session appear to have been influential and useful in her teaching of this lesson. Although we did not directly assess Natalie’s knowledge of the core mathematical ideas related to proportional reasoning (e.g., fractions, ratios, scale-factor, unit-rate, etc), one can see in Natalie’s report that many of the mathematical ideas discussed in February were embedded in her students’ solutions, and she seemed to handle these ideas well in her teaching. For example, the consistent relationship between two quantities that is preserved in a proportion was a common mathematical idea that she threaded through the three student solutions that she shared. In the first solution, this relationship is evident in the repeating pattern of “two dots to three dots.” In the second solution, the constant relationship is conveyed by the constant factor by which students multiplied the two components of the ratio 3:2. And in the third solution, her students considered each ratio as a quotient and compared the two quotients (i.e., 3/2 compared to 119/80) to realize that these were approximately the same.

There are many difficulties inherent in the practice of having students share several solutions to a problem, and this practice is difficult to achieve (Silver, Ghousseini, Gosen, Charalambous, & Strawhun, 2005). Given that Natalie noted in February that she had not previously intended to decide the sequence in which students would share solutions, Natalie’s lesson suggests considerable growth on her part. She exhibited both mathematical knowledge and pedagogical proficiency in her lesson.

Natalie’s rationale for ordering students’ solutions was largely mathematical though her decisions and actions were quintessentially pedagogical, and both were connected to her students’ ideas and solution methods. Natalie analyzed the solutions generated by her students to identify the mathematical ideas and representations underpinning each, and then rank-ordered the solutions accordingly from simplest to most complex. We infer that Natalie’s interactions with the PLTs, the facilitators and the other participants at the February session helped her to clarify, solidify or perhaps establish connections among ideas in the domain of proportionality, and also to consider the instructional implications of these connections.

Two types of connections – within the mathematics, and between the mathematics and matters of pedagogy and student thinking – appear to have played a role in rendering her knowledge to serve as a usable resource. This assertion was supported by a statement made by Natalie during her end-of-year interview.

  • Natalie : We were working on the mathematics because we were getting a deeper understanding of the algorithm. We were getting a deeper understanding of the math behind it and the different representations of whatever kind of math we were working on. But at the same time that is also pedagogy.

  • Interviewer: How is it at the same time pedagogy?

  • Natalie: Because if I want a deeper understanding of a math topic, you need to know how to get that from kids. So we were not only working on, for example, the [problem from an early BIFOCAL session] with ratios, that was not just about 3 cups of concentrate and 2 cups of water, it was about how we represented that, all the different ways, all the different strategies. So I learned all that – how it looked as a percent, as a fraction and all that. But to pull that out, you had to learn how to question kids and had to learn how to present all of the student work. Then we pulled out what order you present the student work. So that is the pedagogy part, to get to the mathematics part. So it was both. It was both.

In her comment, Natalie underscores the nature of the opportunities she had to learn mathematics. She described those opportunities as ones where she (and her colleagues) considered the mathematics in connection to student thinking and pedagogy. In some sense, Natalie broke down the way she came to encounter these ideas in two phases. First, she came to know the relationship between the mathematical ideas – their different representations and approaches (i.e. knowing them from the perspective of a doer of mathematics). Second, she needed to consider how to teach these mathematical ideas to students (i.e. considering them from the perspective of a teacher whose work entails assisting students to learn mathematics). Hence, she learned about making pedagogical decisions on the basis of these mathematical ideas: what questions to use and how to order student work.

Conclusion

The analysis presented here illustrates some ways in which teachers can learn mathematics as participants in practice-based professional development. We have shown that teachers can consider mathematical ideas in relation to the ways in which students think about these ideas, the pedagogical entailments of these ideas, and the consequences of teachers’ decisions based on these ideas. Our trace of Natalie’s experiences in the BIFOCAL project serve as empirical support of the hypothesis that the mathematics used in teaching can be found in the “unique understanding that intertwines aspects of teaching and learning with content” (Ball & Bass, 2003, p. 4).

Teachers had significant opportunities to learn mathematics – to build or strengthen connections among related mathematical ideas and to consider these ideas in relation to how students think about the ideas and to a range of pedagogical actions and decisions that affect students’ opportunities to learn. Our examination of the design and enactment of PLTs in BIFOCAL has illustrated some of the opportunities that participants had to connect mathematical ideas to each other and to settings in which these ideas are used in the work of teaching. In this way, participants not only considered and organized a complex, nuanced constellation of mathematical ideas related to ratio and proportion, but they also connected these ideas to the work of classroom teaching.

From our work alone, we cannot disentangle a number of factors that may have influenced the outcomes. Several factors were evident and appeared to be important in our analysis of BIFOCAL project sessions – the consistent, long-term use of PLTs that made mathematics salient; the coordination of all aspects of the professional development sessions around a core set of foundational ideas and frameworks; the roles of the facilitators in keeping a focus on mathematical ideas and on the mathematical basis for pedagogical decisions; the high levels of participant engagement and interaction; and the willingness of participants to work and reflect on their mathematical knowledge and instructional practice in a public setting. We suspect that many, perhaps all, of these are critical factors, but only further research, and a more complex research design, would allow us to analyze and understand the contribution of each factor.

We have seen that professional learning tasks of the sort used in BIFOCAL can provide opportunities for teachers to rethink and reorganize the mathematics that they encounter in their practice, thereby allowing them to render their mathematical knowledge more useful and usable. Through successive opportunities to consider mathematical ideas in relation to the activities of classroom practice, our participants came to see their pedagogical work as permeated by mathematical considerations. Another important question for future research is if and how teachers who have such professional development experiences can continue to learn in and through their own classroom teaching practice. If teachers become more adept at learning mathematics in this way, they can improve their practice continuously over time. Given that teachers spend far more time in their classrooms than in carefully developed and orchestrated professional development settings, it is critical to understand how they can access and benefit from opportunities to learn mathematics in their daily practice.