Point Cloud Registration Using Virtual Interest Points from Macaulay’s Resultant of Quadric Surfaces

Abstract

A novel formulation called Virtual Interest Point is presented and used to register point clouds. An implicit quadric surface representation is first used to model the point cloud segments. Macaulay’s resultant then provides the intersection of three such quadrics, which forms a virtual interest point (VIP). A unique feature descriptor for each VIP is computed, and correspondences in descriptor space are established to compute the rigid transformation to register two point clouds. Each step in the process is designed to consider robustness to noise and data density variations, as well as computational efficiency. Experiments were performed on 12 data sets, collected with a variety of range sensors, to characterize robustness to noise, data density variation, and computational efficiency. The data sets were extracted from both natural scenes, including plants and rocks, and indoor architectural scenes, such as cluttered offices and laboratories. Similarly, several 3D models were tested for registration to demonstrate the generality of the technique. The proposed method significantly outperformed a variety of alternative state-of-the-art approaches, such as 2.5D SIFT-based RANSAC method, Super 4-Point Congruent Sets and Super Generalized 4PCS, and the Go-ICP method in registering overlapping point clouds with both a higher success rate and reduced computational cost.

1 Introduction

Registration is the process of rigidly transforming the coordinate reference frames of two or more partially overlapping 3D point clouds, such that their intersecting regions overlap correctly. Once registered, the point clouds can be merged into a single convenient frame and can be used for further processing for many applications, such as object reconstruction, segmentation, SLAM, and recognition [1, 2]. To do so, detection of the area of overlap between two point clouds plays an important role. This is done by finding corresponding points between the two-point clouds, using one of two approaches. The first approach assumes that the point clouds are initially approximately aligned and applies the nearest neighbor search to establish point correspondences based on their proximity in 3D space. The registration process is completed when a convergence criterion is satisfied, such as a minimal threshold of the average separation between correspondences, or a maximum threshold on the number of iterations. Such techniques can be termed non-feature-based registration. Iterative closest point (ICP) method and its many variations are based on this approach [3, 4].

The second approach is feature based registration, in which the data sets are processed to extract interest points and feature descriptors. In this approach, there is no requirement for an initial approximate alignment of the data sets, and the correspondences are established by determining matches in descriptor space [5, 6]. A relatively small number of repeatable representative points in the point cloud are first detected, called interest points¹. For each interest point, a feature descriptor is computed that contains the salient and distinct properties based on the neighborhood of that point. Feature descriptors between the two point clouds are then matched to determine correspondences. A transformation is calculated using the correspondences. Typically, this process is wrapped in a robust framework such as RANSAC, to accommodate any false correspondences (i.e., outliers) that result from occasional and inevitable mismatches in descriptor space.

The existence of noise in point cloud data is one source of outliers and presents challenges in determining correspondences for both feature-based and non-feature-based registration. Noise is present in the data for several reasons, such as the fundamental physics and measurement technique upon which the sensor is based, which is referred to collectively as sensor-specific noise [7]. Sensor-specific noise includes pixel position error, axial noise, and quantization error. Alternately, scene-specific noise is a result of the sensor’s limitation to correctly observe certain areas in the scene such as corners, edges, and reflective objects [8]. Feature-based registration techniques generally identify interest points in regions with large shape variations. Unfortunately, these regions of large variation are among those which are the most highly affected by scene-specific noise, thereby increasing the chances of feature mismatches and registration inaccuracies and failures.

Data density variation significantly affects the registration process. Data density also varies from sensor to sensor, as each sensor has a predefined resolution and offset between points. Furthermore, data density is also scene-dependent, as it relies on the distance to the sensors. The higher the density and the resolution of the sensor, the higher the details around each data point. The descriptor is computed normally based on the neighborhood of an interest point. If data is dense, the neighborhood contains a notable description. On the other hand, coarse data makes the descriptor less descriptive. Thus, density highly affects the descriptor which is used to compute correspondences. Feature-based registration techniques are highly affected when data, collected using different sensors, is registered.

In this paper, a novel method is proposed for registering two noisy point clouds. The main idea is to observe the underlying structure of the scene, extract implicit surfaces, identify the intersection of multiple implicit surfaces as virtual interest points, and then use these virtual interest points to register the original point clouds. Implicit surfaces such as planar surfaces are the most stable areas in the scene because they contain minimal shape variation and are therefore less susceptible to both sensor-specific and scene-specific noise [7]. Large shape variation areas are filtered from the cloud so that implicit surfaces are computed only for the most stable areas in the scene. Furthermore, implicit surfaces do not depend on the data density variation. The stability of the underlying implicit surfaces can result in stable and repeatable virtual interest points, which leads to accurate registration results. In addition, only one correct correspondence of virtual interest points is sufficient to register two point clouds, which significantly improves the computational efficiency.

2 Related Work

The most widely used approach for non-feature-based registration of two point clouds is the ICP algorithm [3], and many variants of ICP have been developed that use different error functions and point selection strategies. The three most commonly used distance functions are point-to-point, point-to-plane and plane-to-plane [3, 9, 10]. The transformation is iteratively refined by applying the computed transformation and recalculating the correspondences. For large initial offsets between two noisy point clouds, however, ICP-based approaches will fail to converge [10].

For feature-based registration, there exist a number of different 3D interest point operators that are based on different properties of the data, and yet extracting interest points repeatably among multiple point clouds is a challenge. The local surface patch (LSP) approach [1] searches for areas with large shape variations as measured by shape indices, which are calculated through principal curvature. Intrinsic shape signatures (ISS) [11] addresses the detection of view-invariant interest points. 2.5D SIFT [12] detects interest points using an enhanced version of the Lowe’s scale-invariant feature transform (SIFT) algorithm [13]. A discrete scale-space representation by using Gaussian smoothing and difference of Gaussian (DOG) pyramid techniques is first created, and maxima are detected within the DOG scale-space. The interest points are finally validated and located by comparing the ratio of the principal curvatures with a predefined threshold.

Once extracted, the support region for each interest point is used to compute a unique feature descriptor. Again there are a number of methods for feature descriptor computation. Signature based methods describe the local neighborhood of an interest point by encoding one or more geometric measures computed individually at each point of a subset of the neighborhood [14]. Histogram based methods describe the local neighborhood of an interest point by accumulating geometric or topological measurements into histograms [15]. A comprehensive overview of a number of interest point and feature descriptor techniques is given in [16]. Given two sets of feature descriptors from two acquired scans, correspondences are computed to find overlapping parts in the data. For matching in feature descriptor space, brute force matching and k-d tree nearest-neighbor search (e.g., FLANN) have been applied [17]. Since incorrect correspondences can negatively affect the estimation of the final transformation, some outlier rejection method such as RANSAC is required. The last step is to compute the transformation based on the best correspondences, typically minimizing some least square measure of error.

The proposed method falls under the category of feature-based registration. Virtual interest points (VIPs) are identified by observing the underlying structure of the scene. The use of the term virtual highlights that these points do not exist in the original point cloud data; rather, they are 3D points that are injected at distinct locations based on a computation. The VIPs between two point clouds are further annotated, based on the properties of their supporting implicit surfaces, and are matched in feature descriptor space. A rigid transformation to register two point clouds can be computed from a single true VIP correspondence. As discussed in Sect. 5, experimentation has shown improvements in both registration success and computational efficiency over ICP [3], GICP [9], and conventional feature-based registration techniques [12].

The remainder of this paper is organized as follows: In Sect. 3, the mathematical foundation of quadric surface representation and intersection is described. In Sect. 4, the methodology of the novel interest point operator is explained, as is the criteria to compute VIPs, and the steps of registration using VIPs. In Sect. 5, experimental evidence demonstrates that the method registers noisy point clouds accurately and efficiently compared to other well-known techniques. Finally, Sect. 7 concludes the paper with a summary and discussion of future work.

3 Quadric Surface Intersection

Quadric surface intersection is a well-known technique and has been used in a number of computer vision applications such as absolute pose estimation of a calibrated camera, multi-camera pose estimation and generalized structure from motion [18]. In our case, we are considering the intersections to form virtual interest points, which we are using to compute the registration of two noisy point clouds, which is a different application of quadric surface intersection than has previously been considered. The mathematical formulation to calculate quadric surface intersections and that allows their use as virtual interest points is detailed in the following sections.

3.1 Quadric Surface Representation

A bivariate quadric surface is represented by a quadratic equation of three variables, two of which are of degree two with the remaining variable of degree one. In contrast to general quadrics (three variables each of degree two) which represent volumes, bivariate quadrics represent surfaces, and are therefore used here to naturally model 2.5D point clouds.

A bivariate quadric is represented implicitly as:

$$\begin{aligned} p^TQp \left\{ \begin{array}{lll} < 0 &{} \iff &{} p \ \text{ lies } \text{ below } \text{ the } \text{ surface } \\ = 0 &{} \iff &{} p \ \text{ lies } \text{ on } \text{ the } \text{ surface } \\ > 0 &{} \iff &{} p \ \text{ lies } \text{ above } \text{ the } \text{ surface } \end{array} \right. \end{aligned}$$

(1)

where Q is a $4\times 4$ matrix called the discriminant of the quadric surface. Q is symmetric and for any real nonzero scalar $\beta$, the quantity $\beta Q$ is equivalent to Q, since they describe the same surface. Satisfaction of Eq. (1) implicitly determines membership of point p on the quadric surface defined by Q. Expanding the elements of Eq. (1) gives:

$$\begin{aligned} \begin{bmatrix} x&y&z&1 \end{bmatrix} \begin{bmatrix} a &{} b &{} c &{} d \\ b &{} e &{} f &{} g\\ c &{} f &{} h &{} k \\ d &{} g &{} k &{} j \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = 0 . \end{aligned}$$

(2)

The upper-left $3 \times 3$ principal submatrix of Q, called the subdiscriminant $Q_u$, contains all of the second-order terms:

$$\begin{aligned} Q_u = \begin{bmatrix} a &{} b &{} c \\ b &{} e &{} f \\ c &{} f &{} h \end{bmatrix} \end{aligned}$$

(3)

The ranks of Q and $Q_u$, along with the sign of the determinant of the discriminant $\det (Q)$, are helpful in classifying the quadric surface. There are 17 standard types as listed in Table 1, with the planar, elliptic paraboloid and hyperbolic paraboloid types being well-suited to the 2.5D point cloud representation.

Table 1 Quadric surfaces type with their canonical equation is given for rank of discriminant $\Delta =\mathrm{{rank}}(Q)$ and subdiscriminant $\Delta _u =\mathrm{{rank}}(Q_u)$, and sign of the determinant of discriminant $\rho = \mathrm{{sgn}}(\det (Q))$

For a point set $P\!=\!\{p_i\}_1^n$ drawn from a quadric surface, Eq. (2) can be expanded into the form $A C\!=\!0$, where A is the $n\times \!10$ matrix comprising the point components, and C is a column vector representing the unknown discriminant coefficients:

$$\begin{aligned} \begin{bmatrix} x_1^2 &{} x_1y_1 &{} x_1z_1 &{} x_1 &{} y_1^2 &{} y_1z_1 &{} y_1 &{} z_1^2 &{} z_1 &{} 1 \\ x_2^2 &{} x_2y_2 &{} x_2z_2 &{} x_2 &{} y_2^2 &{} y_2z_2 &{} y_2 &{} z_2^2 &{} z_2 &{} 1 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ x_n^2 &{} x_ny_n &{} x_nz_n &{} x_n &{} y_n^2 &{} y_nz_n &{} y_n &{} z_n^2 &{} z_n &{} 1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e\\ f\\ g\\ h\\ k \\ j \end{bmatrix} = 0 \end{aligned}$$

(4)

For $n \ge 9$, the elements of C can be estimated using numerical methods, such as by applying Singular Value Decomposition (SVD) on matrix A.

3.2 Intersection of Three Quadric Surfaces

When three quadric surfaces intersect, calculating the set of intersection points can be more or less involved, depending on the types of the three surfaces involved, revealed by the ranks of their respective Q and $Q_u$ matrices and the signs of their determinants $\det (Q)$, as listed in Table 1. In the following two subsections, the calculation will be described first for the simplest case of three intersecting planes, and then for the most general case of three intersecting non-planar quadrics.

3.2.1 Planar Intersections

When considering three planes $\Pi _i = \begin{bmatrix}a_i&b_i&c_i&d_i\end{bmatrix}, i\!=\!1\ldots 3$, the existence of a common point of intersection can be determined by examining the coefficient matrix $M_c$ and the augmented matrix $M_a$:

$$\begin{aligned} M_c= & {} \left[ \begin{array}{ccc} a_1 &{} b_1 &{} c_1 \\ a_2 &{} b_2 &{} c_2 \\ a_3 &{} b_3 &{} c_3 \end{array} \right] \end{aligned}$$

(5)

$$\begin{aligned} M_a= & {} \left[ \begin{array}{ccc} a_1 &{} b_1 &{} d_1 \\ a_2 &{} b_2 &{} d_2 \\ a_3 &{} b_3 &{} d_3 \end{array} \right] \end{aligned}$$

(6)

The three $\Pi _i$ can only intersect at a point if both $M_c$ and $M_a$ are of full rank. Further, $M_c$ contains the row unit normals for each plane, and so the closer $\det (M_c)$ is to one, the closer are the three planes to being mutually perpendicular.

If a common point of intersection is determined to exist, then its value can be recovered as:

$$\begin{aligned} \left[ \begin{array}{c} x\\ y\\ z \end{array} \right] = M_c^{-1} \left[ \begin{array}{c} -d_1 \\ -d_2 \\ -d_3 \end{array} \right] \end{aligned}$$

(7)

3.2.2 Non-planar Quadric Intersections

When all three surfaces are non-planar, as revealed by an examination of the ranks of their discriminants and subdiscriminants, then a more involved method is required to compute their intersections. By Bezout’s Theorem, three quadric surfaces intersect at either at most eight, or infinitely many points [19]. There are three known approaches to calculate these points, the first of which is to calculate the intersection of two of the three surfaces, which results in a curve known as a Quadric Surfaces Intersection Curve (QSIC). This QSIC is substituted into the expression for the third surface, yielding a polynomial of maximum degree four which is then solved to yield the points of common intersection [20].

In the second approach, three QSICs are calculated from the set of possible intersections of all pairs of the three surfaces. The curve–curve intersections of pairs of QSICs are then calculated and compared, and those points common to all three pairs of curve–curve intersections are the common points of intersections of all three surfaces.

The third approach is to apply elimination methods to arrange the three quadric surface equations into a linear system, which can then be solved directly. A particular case of Macauley’s resultant, which is one of the main tools of effective elimination theory, is applied to concisely solve the intersections of three implicit quadric surfaces by simultaneously computing the intersection of three polynomials of degree two in three variables [21]. For convenience, we will reorder the variables and relabel the coefficients to express an $i^{th}$ implicit quadric surface as:

$$\begin{aligned}&c_{i,1}x^2+c_{i,2}y^2+c_{i,3}z^2+c_{i,4}xy+c_{i,5}xz\nonumber \\&\quad +c_{i,6}yz+c_{i,7}x+c_{i,8}y+c_{i,9}z+c_{i,10}=0 \end{aligned}$$

(8)

where the $c_{i,j}$ coefficients above correspond to the (reordered) elements of vector C in Eq. (4). The intersections of three such surfaces can be expressed as the solution to the system of equations:

$$\begin{aligned} \begin{bmatrix} c_{1,1} &{} c_{1,2} &{} \ldots &{} c_{1,10} \\ c_{2,1} &{} c_{2,2} &{} \ldots &{} c_{2,10} \\ c_{3,1} &{} c_{3,2} &{} \ldots &{} c_{3,10} \\ \end{bmatrix} \begin{bmatrix} x^2 \\ y^2 \\ z^2 \\ xy \\ xz \\ yz \\ x \\ y \\ z \\ 1 \end{bmatrix} = 0 . \end{aligned}$$

(9)

Equation (8) can be rearranged so as to isolate the variable x, known as freezing x as an indeterminate constant coefficient:

$$\begin{aligned}&c_{i,2}y^2+c_{i,3}z^2+c_{i,6}yz+\left( c_{i,4}x+c_{i,8}\right) y\nonumber \\&\quad + \left( c_{i,5}x+c_{i,9}\right) z+\left( c_{i,1}x^2+c_{i,7}x+c_{i,10}\right) =0. \end{aligned}$$

(10)

The system of Eq. (9) can be similarly arranged as:

$$\begin{aligned}&\begin{bmatrix} -c_{1,2} &{} -c_{1,3} &{} -c_{1,6} \\ -c_{2,2}\ &{} -c_{2,3} &{} -c_{2,6} \\ -c_{3,2} &{} -c_{3,3} &{} -c_{3,6} \end{bmatrix} \begin{bmatrix} y^2 \\ z^2 \\ yz \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} c_{1,4}x+c_{1,8} &{} c_{1,5}x+c_{1,9} &{} c_{1,1}x^2+c_{1,7}x+c_{1,10} \\ c_{2,4}x+c_{2,8} &{} c_{2,5}x+c_{2,9} &{} c_{2,1}x^2+c_{2,7}x+c_{2,10} \\ c_{3,4}x+c_{3,8} &{} c_{3,5}x+c_{3,9} &{} c_{3,1}x^2+c_{3,7}x+c_{3,10} \end{bmatrix} \begin{bmatrix} y \\ z \\ 1 \end{bmatrix}\nonumber \\ \end{aligned}$$

(11)

or more succinctly as:

$$\begin{aligned} A\left[ \begin{array}{c} y^2 \\ z^2 \\ yz \end{array} \right] =P(x)\left[ \begin{array}{c} y \\ z \\ 1 \end{array} \right] . \end{aligned}$$

(12)

Assuming A to be of full rank and therefore invertible, Eq. (12) can be manipulated further into the form:

$$\begin{aligned} \left( B\left( x\right) A^{-1}P\left( x\right) -C\left( x\right) \right) \begin{bmatrix} y \\ z \\ 1 \end{bmatrix} = 0 \end{aligned}$$

(13)

where the terms of B(x) and C(x) comprise first- and second-order polynomials of the terms of $A^{-1}P\left( x\right)$. This leads to the definition of Macauley’s resultant M(x) as:

$$\begin{aligned} M\left( x\right) =B\left( x\right) A^{-1}P\left( x\right) -C\left( x\right) . \end{aligned}$$

(14)

The above formulation of Macauley’s resultant elegantly addresses the intersection of three quadric surfaces through the solution of the roots of the single univariate polynomial:

$$\begin{aligned} \det (M\left( x\right) )=0 \end{aligned}$$

(15)

where $\det (M(x))$ is a polynomial of degree eight. Up to eight-ordered nonlinear equations can be computed as the eigenvalues of its companion matrix, or using Sturm sequences in some feasible interval. This gives a set of x values, which can then be substituted into M(x) thereby allowing for the solution of the linear system for both y and z.

Since the existence of a solution requires polynomials with necessary vanishing conditions, each root x of the resultant corresponds to a solution of indeterminate variable, for $x\ne 0$. Thus, the intersection problem reduces to solving for the root of a single univariate polynomial, provided that resultant is a non-zero non-constant polynomial. Similarly, x can be replaced with y or z as an indeterminate constant. The resultant, a polynomial in x, may have infinitely many roots, called the identically zero resultant.

The intersection of three quadric surfaces has at most eight intersection points [22], all eight of which become virtual interest points. Within a given point cloud, there will be several VIPs depending upon the number of intersections of sets of three quadric surfaces. Out of at most eight VIPs from an intersection of three quadric surfaces, only one VIP is used to register the point cloud, as described in Sect. 4.3. Any of these intersection points, once matched to the target intersection points, are potential candidates for computing the registration matrix of two point clouds. We select the best pair that minimizes the reprojection error between the two point clouds in a RANSAC fashion.

4 Global Registration with VIPs

Equipped with a method to calculate the points of intersection of three quadric surfaces, this section now describes a process to use these intersection points for the efficient and robust global registration of two point clouds. These points of intersection are called Virtual Interest Points (VIPs), as they do not exist in the original point cloud data.

The proposed method limits the search space when detecting interest points by avoiding noisy areas in the point clouds. A significant amount of noise exists in areas with large shape variations, which occur in regions normally composed of corners, edges, and extremas, and so such regions are not targeted here to find interest points. Conversely, smooth regions with small surface variation contain relatively less noise. Such regions are less affected by sensor-specific and scene-specific noise and are thus considered as the most stable regions to support a search for repeatable interest points [23]. It is these less noisy regions that are modeled into quadric surface representations. Only a few points from these regions are required to support a quadric surface model, and so the quadric representation does not require any specific or significant data density. Similarly, the quadric surface fitting absorbs the effects of noise. Once the surface representation has been extracted, the remainder of the algorithm then only depends on the estimated parameters of the extracted quadrics.

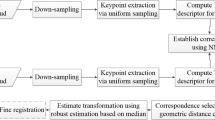
The two point clouds are first segmented into a set of implicit quadric surfaces, with each segment represented by a quadratic equation. Within each point cloud, two pairs of quadric surfaces are also compared together to avoid spurious calculations. A refined set of quadratic equation parameters is then added to a segment database, one for each point cloud, based on a qualification criterion such that the represented segments will likely intersect at real isolated points. Once the two segment databases are populated with quadric surface equations, intersections of combinations of three such surfaces within each segment database are processed using Macaulay’s resultant to extract VIPs. A descriptor for each VIP is also computed, and the VIPs along with their descriptors are then added to a distinct VIP database for each point cloud. The two VIP databases are next passed to a VIP matching process, in which a k-d tree is used to establish VIP correspondences in descriptor space. The correspondences are further refined using a geometric consistency clustering technique. The group of consistent VIP correspondences is then processed using a RANSAC framework to determine the rigid transformation matrix that minimizes the global registration error between the two point clouds.

The main steps of this global registration process are described in greater detail in the following subsections.

4.1 Segmentation

The segmentation of 2.5D surfaces is a well-explored problem, and a number of effective solution methods exist. In the surface splatting approach [24], the input points are grown to construct a continuous surface. Each of these grown points, now consisting of a volume and a normal, is called a surface splat. The most intuitive and simple technique is to let the points grow as spheres until there are no more holes in the surface. The drawback of this technique is that it does not generate a hole-free approximation.

As an alternative, the moving least squares technique builds a local fit for every point on the surface using higher-order polynomials [25, 26]. To reconstruct a smooth surface from the input set of points, the geometric error of the approximation is minimized. This makes it computationally fast and the locality of the neighborhood is responsible for the reconstruction properties. The continuity of the surface can be adjusted based on the kernel function, such that if sharp edges need to be reconstructed, the method becomes computationally expensive.

The approach taken here uses region growing segmentation based on characterizing the surface curvature of points in a region. The three eigenvalues of the covariance matrix in the neighborhood of a point p are computed, and the surface curvature $\gamma = curvature(p)$ is calculated as the ratio of the smallest to the sum of all eigenvalues. The segmentation process alternates between specifying a seed point, and then identifying all points in the neighborhood of that seed that satisfy a smoothness criterion. Initially, all points and their associated $\gamma$ values are added to a list, which is sorted by increasing $\gamma$. The point of minimum curvature which therefore lies in the flattest region is identified as the initial seed point and is extracted from the point list. This initial seed point is used to segment each region as shown in Algorithm 1.

In line 4 of Algorithm 1, we have used a value of $k=50$. The condition in line 6 prevents corners and edges from being added to the region whereas the condition in line 9 helps to grow the region beyond the current neighborhood of the seed point. The region returned by Algorithm 1 is added to the set of regions. The algorithm is repeated by extracting the next point with minimum surface curvature $\gamma$ value from the point list as the initial seed point for the next region. The process continues until the point list is empty.

In order to find an optimal number of regions, we use a scale-space approach inspired by Lowe [13]. For the first iteration, a small neighborhood is selected for curvature estimation so that abrupt changes in curvature are identified resulting in only very smooth regions being segmented. The neighborhood size is increased gradually in subsequent iterations so that a large number of valid regions can be identified, which are not detectable with a small neighborhood radius for the curvature estimate. The output of the algorithm is a set of regions, as illustrated in Fig. 1.

Fig. 1

Region Growing Segmentation. a A frontal view of the Watermelon Kid model. b Regions extracted for surface representation and depicted in color-codes as segmentation

4.1.1 Segment Pair Qualification

Once the quadric surface coefficients have been computed for each segment using the method described in Sect. 3.1, the surface database is then populated. Each surface in the database has to pass a qualification criterion, before being considered further to compute intersections.

For all pairs of quadric surfaces in the database, the criterion checks the potential for intersection of the surfaces based on the directions of their normals, which is calculated as the eigenvector associated with the smallest eigenvalue of the covariance matrix of those points comprising the quadric surface. If the magnitude of the solid angle between the normals of the two surfaces is less than a certain threshold, then they are either parallel (in the case of planar surfaces) or their intersection is far away, and the surface pair is considered disqualified.

Those surface pairs that do not pass the above two criteria are grouped together and considered as a single surface for subsequent computations, so that their intersection calculations can be avoided. For each point cloud, a surface database is then populated with the following information:

• Group indexParallel (non-intersecting) surfaces are grouped together so that spurious calculations can be avoided;

• Surface coefficientsCoefficients of the quadratic equations, that are used to compute the VIPs;

• Number of points $N_s$A trust measure, such that a greater value of $N_s$, indicates a more stable surface.

4.2 VIP Descriptor

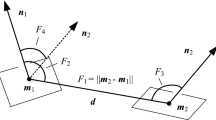
Once calculated from the intersection of three intersecting quadric surfaces $S_1$, $S_2$, and $S_3$, each VIP is added to a VIP database along with its associated feature descriptor, which is composed of the following three properties:

• Angles $\theta$, $\phi$, and $\rho$ between the normals of $S_1$, $S_2$, and $S_3$;

• Degree of Orthogonality of the three surfaces, measured as $\text {det}(M_c)$, where matrix $M_c$ stacks the first three parameters of the normals $(a_i,b_i,c_i)$ of each corresponding intersecting surface $S_i$:

  $$\begin{aligned} M_c = \left[ \begin{array}{ccc} a_1 &{} b_1 &{} c_1 \\ a_2 &{} b_2 &{} c_2 \\ a_3 &{} b_3 &{} c_3 \end{array} \right] \end{aligned}$$

  (16)

• Trust Factor $t_f$, calculated as

  $$\begin{aligned} t_f = \frac{|S_1|+|S_2|+|S_3|}{|P|} \end{aligned}$$

  (17)

  where $|S_i|$ is the cardinality (number of points) of surface $S_i$, and |P| is the cardinality of the complete point cloud. The higher the value of $t_f$, the more reliable the VIP is considered to be.

Surfaces composed of fewer points can contain higher amounts of noise compared to those with more points. The trust factor quantifies the importance of certain VIPs over others.

4.3 VIP Correspondences

A nearest-neighbor search mechanism is employed to match the VIPs across two point clouds. A k-d tree is populated where each property of the feature descriptor serves as a dimension, and source image VIPs are matched with the nearest target image VIPs in descriptor space. Only one correct correspondence is required to recover the registration transformation, and an obvious selection of the best correspondence is that with the minimum distance in feature space. It is possible, however, that correspondence selection based on only minimum descriptor space distance might return an outlier, and so a RANSAC framework is employed to increase robustness.

The correspondences are first grouped using a geometric consistency checking algorithm that enforces simple geometric constraints between pairs of correspondences [1]. Candidate corresponding pairs are filtered based on the geometric constraint:

$$\begin{aligned} \mid \parallel {s_1-s_2}\parallel - \parallel {t_1-t_2}\parallel \mid < \epsilon , \end{aligned}$$

(18)

where $s_1$ and $s_2$ are two VIPs from the source point cloud, $t_1$ and $t_2$ are their two corresponding VIPs from the target point cloud. $\parallel {s_1-s_2} \parallel$ and $\parallel {t_1-t_2} \parallel$ are the Euclidean distances between the two VIPs and $\epsilon = 5.0$ cm is a threshold for allowable difference between the two distances. This consistency check guarantees that the distances $\parallel {s_1-s_2} \parallel$ and $\parallel {t_1-t_2} \parallel$ are similar within each point cloud, and therefore the correspondence across the point clouds is not inconsistent. Potential corresponding pairs are grouped together, and the larger the group is, the more likely it will be to contain a number of true correspondences.

As only one true VIP pair correspondence is required to register two point clouds, a rigid transformation is computed for a randomly selected correspondence from this largest group. The transformation involves a three-step registration process, with one translation and two rotations. The translation is calculated trivially as the difference between the two VIPs, i.e., $T = v_{1_{xyz}} - v_{2_{xyz}}$. To calculate the two rotations, first it is recognized that query and matching VIPs have three quadric surfaces in common, so that three angles between the normals of the matched quadric surfaces are computed as

$$\begin{aligned} \alpha _i = \cos ^{-1}{\left( \frac{(n_{1_i} \cdot n_{2_i})}{\sqrt{(n_{1_i} \cdot n_{1_i})*(n_{2_i} \cdot n_{2_i})}}\right) } \end{aligned}$$

(19)

where $\alpha _i$ is the angle between the $i \in \{1,2,3\}$ normals $n_{1_i}$ and $n_{2_i}$ of the two matched VIPs. We used RANSAC mechanism to choose the order for normal angles, i.e., orders were randomly selected and tested, and that transformation on the VIPs was selected that minimize the projection error.

Next, we select the two largest angles and calculate the rotation matrix R using Rodrigues’ rotation formula, in which rotation in one axis is given by:

$$\begin{aligned} R = I + \sin \alpha _1 [k]_\times + (1 - \cos \alpha ) (k k^\mathsf {T}-I) \end{aligned}$$

(20)

where $k = (n_1 \times n_2)$ is the cross-product of two normals and $[k]_\times$ is a cross-product matrix of k:

$$\begin{aligned} {[}k]_{\times }={\begin{bmatrix}\,\,0&{}\!-k_{z}&{}\,\,\,k_{y}\\ k_{z}&{}0&{}\!-k_{x}\\ \!-k_{y}&{}\,\,k_{x}&{}\,\,0\end{bmatrix}}. \end{aligned}$$

(21)

Two point clouds are registered together by using the translation matrix T and the rotation matrix R. Only one true correspondence is therefore required to register two-point clouds which significantly reduces the computational cost of the registration process.

The residual error is minimized by applying a number of iterations of ICP to all points in the neighborhood, and this process is repeated for a number of randomly selected correspondences from this group. That correspondence which leads to the minimum ICP residual error is considered to return the best transformation.

Table 2 Seven data sets were used to test the proposed method

5 Experimental Results

The proposed VIP method was tested under different challenging conditions for robustness to noise and data density variation, as well as computational efficiency. A total of twelve (12) data sets were collected from both natural and architectural scenes, as well as models from different sensors for registration with known ground truth. The VIP technique was compared with state-of-the-art feature-based registration and non-feature-based registration techniques. Furthermore, registration was performed by using VIPs for noisy pairs of point clouds as well as those with different data density variations.

The algorithms’ running times and performance were recorded for the different data sets. The proposed method was implemented using C++ and compared with efficient, optimized C++ implementations of other techniques provided by the authors. A Quad Intel Corei5-3330 CPU with a speed of 3.00 GHz and 8 gigabytes of RAM was used to run the experiments.

All experiments were verified by using ground truth registration, generated using manual alignment. Four-point correspondences were precisely selected manually in two frames and using correspondences the point clouds are aligned. The transformation computed using four point correspondences are considered as ground truth transformation. As described by Mohamad et al. [27], automatic registration was considered a success if the rotation and translation errors were less than 5 degrees and 5 cm, respectively. We define the convergence rate of a given experiment as the percentage of trials that successfully satisfy this criterion.

Seven data sets were used to test the proposed method in architectural and natural environments along with 3D models, as shown in Table 2. Two data sets, Object and Plant, were collected using a Microsoft Kinect version 2. The Object data set consists of 8 pairs of point clouds of a small area of a graduate student laboratory where various objects with different shapes such as spheres, cylinders, boxes, and planes are captured. A natural scene with mostly non-planer surfaces is captured by the Plant data set which has 8 pairs of point clouds of an indoor plant. A data set using the (noisier) Microsoft Kinect version 1 of the cubical in a laboratory, called Lab, was tested. This data set has a total of 9 pairs of point clouds. Four data sets of 3D models, Goose, Elmo, Rabbit, and Sailor of abstract shapes were captured using a NextEngine 3D sensor with 4, 8, 8, and 4 pairs of point clouds, respectively. Some registration results from these tests are shown in Fig. 2.

Fig. 2

Successful registration of various data set using VIP technique. The row in the blue presents one view of the objects, while the second row in orange color represents another view which is captured from a slightly different angle, and the third row represents the registration of the above two views into a registered point cloud. The quality of the registration is highlighted by showing two clouds in two different colors

5.1 Comparison to Feature-Based Registration Techniques

VIP technique was compared for registration with state-of-the-art interest point operators and feature descriptors for two RGB-D data sets, Office and Storage, captured using a Kinect version 1. We also tested two standard Stanford registration data sets, Stanford-office and Stanford-stage. The interest point operators Harris 3D [28], Harris 6D, intrinsic shape signature (ISS) [11], and SIFT 2.5D [12] were used in combination with feature descriptors FPFH [15], SHOT [14], and SpinImages [29] to register pairs of point clouds. Combinations of interest points (IPs) and feature descriptors (FDs) were applied to register 9 and 7 pairs of point clouds of Office and Storage data sets, respectively. The results were compared with the VIP technique for convergence and performances, as shown in Table 3. All techniques were successfully able to register all pairs of Office data set, although the computational efficiency of most of the techniques is significantly lower than that of VIPs. Only Harris 3D with SpinImages had slightly better computational efficiency than VIPs in some tests, albeit this efficiency improvement always accompanied a reduced convergence rate. For the Storage data set, VIPs outperformed all the other techniques for computational efficiency and convergence. Several combinations of interest points and feature descriptors failed to achieve 100% convergence. Most techniques failed to converge on the Stanford data sets because the overlapping region between the two clouds was significantly small. It can be noticed that the convergence for Stanford-stage is slightly higher than Stanford-office for all the techniques. The reason is that Stanford-stage has higher inter-frame overlap and is captured in an indoor environment without any presence of sunlight. On the other hand, Stanford-office has a smaller inter-frame overlap and direct sunlight is present in the room that downgrades IR-based sensors, such as the Kinect . In both data sets, VIP-based registration failed only for one pair of point cloud each. VIP-based registration requires at least three identical surfaces in two point clouds in order to perform correct registration. We manually inspected the failure cases and identified that failures occurred due to a smaller overlap and a lack of similar surfaces. The VIP convergence rate was still considerably better than that of all other techniques. The performance of the VIP-based technique was also more efficient than other techniques except for the Harris3D with SpinImages combination, which was 3.91 s. However, this combination of Harris3D with SpinImages was only able to converge on 1 pair of point clouds and was therefore not very effective.

Table 3 Two data sets were used to compare the proposed method with a number of feature-based registration techniques for computational efficiency (average time in s) and convergence rate

Table 4 Running time in seconds achieved by SUPER 4PCS (S4PCS), SUPER G4PCS (SG4PCS), Go-ICP, and VIP for different data sets. (Speedup of VIP in brackets.)

In our previous work [30], planar-VIP method does not apply to non-planar data sets mostly used in these experiments. However, we compared registration on the Office data set, which is composed of mostly planar regions, with planar-VIP. The planar-VIP was faster (2.6 s) than proposed VIP (5.8 s). The reason for the higher computational expense of proposed more general VIP over the planar VIP was because it did not reject any surfaces. In this work, which is inspired by our recent work [31], we fit quadrics to all clusters, subsequently, these quadrics are grouped together to find the intersections. The discriminant and sub-discriminant are used to find the type of the quadric. The intersection of planar is computed using the methods explained in Sect. 3.2.1 and for non-planar quadrics, the intersection is computed using Macaulay’s resultant as explained in Sect. 3.2.2. The proposed VIP was slightly slower but it considered all possible surfaces to find interest points, and thus overcame the limitation of planar VIP by registering pairs of point clouds that are composed of non-planar surfaces.

5.2 Comparison to Non-feature Based Registration Techniques

Three data sets of the models were used to compare the proposed technique with non-feature-based techniques such as Super 4PCS, Super Generalized 4PCS [27] and Go-ICP [32]. The data sets Elmo, Rabbit, and Sailor of abstract shapes were captured using a NextEngine 3D sensor with 8, 8, and 4 pairs of point clouds, respectively.

In order to fairly compare the algorithms, the parameters for S4PCS and SG4PCS were optimized, respectively, for each algorithm, so that the comparison was of the most efficient version and tuning of each algorithm. Several trials were executed for each algorithm, and a trial was considered successful if the error in the resulting transformation was within the rotation and the translation threshold of the ground truth transformation.

In Table 4, a comparison of running time (in s) for S4PCS, SG4PCS, Go-ICP, and VIP is given when the registration rate of the algorithms was 100%. The ratio of each method’s running time over that of the VIP running time for that data set is shown in brackets. The first two columns indicate the number of points in the two frames being registered. VIP was more efficient than S4PCS, and significantly more efficient than Go-ICP for all data sets. It was also more efficient than SG4PCS for the Rabbit and Elmo data sets, although it was slightly slower than SG4PCS for the Sailor data set. The rotation and translation error for all three data sets were less than 1 degree and 3 cm, respectively. The initial pose estimated by VIP was further refined by using ICP with only five iterations. Some results of the registration using VIP are illustrated in Fig. 2. In this figure, each object is shown in three views, with the top two rows representing two views of the same objects captured from different view points, such that there is sufficient overlap where repeatable virtual interest points can be extracted. The bottom view is generated using matched VIPs from both top views, which are registered together into a single frame. The distinct color of above two views is maintained in the third view to highlight their overlapping merged regions, as well as to illustrate the non overlapping regions.

To further explore the relative performance of SG4PCS and the proposed VIP method, the WaterMelonKid data set shown in Fig. 3a–c was captured using Microsoft Kinect v2. and tested. A total of 14 pairs were registered using both techniques. The convergence rates of VIP and SG4PCS were 100% and 84%, respectively. The VIP approach executed in 2.8 s, whereas SG4PCS executed in 8.67 s, for a 3 times speedup of VIP over SG4PCS. VIP therefore outperformed SG4PCS with respect to both accuracy and efficiency on this data set.

Fig. 3

Registration using Implicit Quadric Surfaces. In a and b two point clouds of the WaterMellonKid data set with implicit quadric surfaces are shown where different colors highlights surfaces. Whereas in c registration result of the two point cloud are shown

5.3 Robustness to Noise

Another experiment was performed to test convergence in the presence of noise. Gaussian white noise with zero mean and standard deviation $\sigma$ ranging from 0.0001 m to 0.07 m was added to the two point clouds of Lab data sets. The proposed technique is compared to eight feature-based registration techniques for robustness to noise, with the results plotted in Fig. 4. The two plots show the rotation error and translation error with the increase in the noise in the data. The registration using VIP was successful for up to $\sigma =0.01$ m as shown in Fig. 5. However, other techniques failed to converge to a global minimum as the $\sigma$ is increased. The reason for the convergence for VIP was that the saliency measure of extracting implicit surfaces was less affected by noise (Fig. 6).

Fig. 4

Robustness to noise is shown by plotting a rotation error in degrees and b translation error in meters for Noise standard deviations $\sigma$ from 0.0001 to 0.07 m

Fig. 5

Robustness to noise. Noise standard deviations $\sigma = 0.0001~\text {m}, 0.001~\text {m}, \text { and } 0.01~\text {m}$ are added to two point clouds of the Lab data set and registered using VIP

Fig. 6

Robustness to data density variation is shown by plotting a rotation error in degrees and b translation error in meters for downsampled percentage

Fig. 7

Robustness to data density variation. a Original size, b 46% of original size of the second point cloud of the pair and c registration using VIP, converged to a global minimum

Table 5 Computational complexity of various modules of the technique

5.3.1 Robustness to Data Density Variation

The approach was further tested by downsampling one of the point clouds in the pair to reduce the data density. The results for the Sailor data set are illustrated in Fig. 7. In Fig. 7b, the point cloud was downsampled to 46% of the original size. The pair of point clouds converged to a global minimum with translation and rotation errors of 0.24 degrees and 0.003 cm. This experiment was performed on two data sets, Lab and Sailor, for different downsampling percentages, and rotation error and translation error are plotted in Fig. 6. It can be seen that the error was within the acceptance threshold for up to 35% of downsampled point clouds for the Sailor data set. However, when the point cloud was further downsampled, the error increased significantly. The rotation error and translation error were very low even when downsampled to 10% of the original point cloud size. It is worth mentioning here that feature-based techniques were also tested for robustness to data density variation but none of the feature-based technique converged to a global minimum because feature matching failed in descriptor space.

5.4 Computational Complexity

VIP technique has shown significant improvements in terms of computational cost over the state-of-the-art techniques, as shown in Tables 2, 3 and 4. The average iterations and running time of all the modules are given in Table 5.

The first module of the proposed technique is surface extraction using region growing segmentation algorithm. The number of iterations and computational cost for this module is proportional to the surfaces found in the point cloud. If the point cloud is of an architectural structure, which is composed of a few surfaces, the algorithm will require fewer iterations to compute the surfaces. On the contrary, if the point cloud is composed of a natural structure, which has a significant number of surfaces, the algorithm will require more iterations and higher computational cost. Another important factor in the computational complexity is point density of a point cloud. A dense point cloud will require more computation as compared to a coarse point cloud. This is depicted in Table 2 where Goose data set is composed of 8152 points per view on the average and thus computation time for registration is less than a second. On the other hand, Lab and Object data sets are composed of average sizes of 307,200 and 214,877 points per view, respectively, so each has a computation time of more than 5 s. It can be noticed that Lab data set with more points has lower computation time because it is composed of an architectural structure while the Object data set is composed of objects with varying geometry such as spheres, cylinders, etc. so, it requires more computation time.

The next module is quadratic surface parameter extraction. It is not an iterative process; however, it depends on the number of surfaces to be processed within a point cloud. Once the surface parameters are extracted, the rest of the technique only works with parameters. This significantly improves the computational cost as compared to the state-of-the-art techniques.

The next module is VIP computation which requires surface filtering. The filtering process filters quadric surfaces that result in spurious virtual interest points. Surfaces that are not potentially useful for VIP computation are parallel surfaces or surfaces with similar curvature. Therefore, three quadric surfaces with a very high degree of orthogonality are only considered for VIP computation module. As a result, only a few quadric surfaces qualify for computing the repeatable and distinct virtual interest points. This module also includes descriptor computation for each VIP extracted.

The next module is VIP matching module which is an iterative process that depends on minimizing the reprojection error in a RANSAC fashion. The complexity depends on the number of VIPs extracted in the previous module as well as the accuracy of matches. The last module is a refinement module which is based on five iterations of ICP.

6 Discussion

VIP outperforms all other tested techniques in terms of computational efficiency for most of the data sets. In the noisy data sets where measurement noise and quantization error was very high, VIP is converged to a global minimum. Implicit surfaces absorb the effect of noise. Furthermore, VIPs are not based on a single implicit surface but a group of three, which is the reason for the good repeatability of VIPs even in the presence of a significant amount of noise. Similarly, the surface fitting does not rely on the density of the surface unless the curvature is maintained. This makes the technique robust to data density variations.

The limitation of VIP is that it requires at least three non-parallel implicit surfaces in the point cloud to compute a single VIP. In the presence of only parallel surfaces, it normally fails which is an issue to be addressed in future work. Nevertheless, point clouds normally acquired from natural and artificial environments are rich in areas that exhibit non-parallel surfaces. Using ICP as a post-processing step for further refinement improves the quality of registration and may also register only parallel surfaces, but decreases the running time of the algorithm. Parallel surface cases may be solved by adopting the planes correspondences determination technique [33].

7 Conclusion

A novel robust feature-based registration method is presented. The method is robust to noise because avoiding noisy areas is one of the key aspect considered in design criteria. The VIPs are computed by observing the most stable regions in the scene, and therefore the performance of the algorithm degrades gracefully in the presence of noise and reduced resolution. Furthermore, the feature descriptors are computed in such a way that only one true correspondence is required for registration of noisy point clouds. As a result, compared to other commonly used registration methods, the proposed method is both stable and computationally efficient. The method was experimentally evaluated and shown to outperform the PCL versions of ICP, GICP, and 2.5D SIFT, with respect to both convergence behavior and efficiency.

In future work, this method will be expanded to solve the aforementioned cases by including other types of parametric surfaces, such as lines, spheres, and conics. The technique will also be tested against other natural scenes, and generalized for object recognition purposes.