Tomographic Image Reconstruction with a Spatially Varying Gamma Mixture Prior

Abstract

A spatially varying Gamma mixture model prior is employed for tomographic image reconstruction, ensuring effective noise elimination and the preservation of region boundaries. We define a line process, modeling edges between image segments, through appropriate Markov random field smoothness terms which are based on the Student’s t-distribution. The proposed algorithm consists of two alternating steps. In the first step, the mixture model parameters are automatically estimated from the image. In the second step, the reconstructed image is estimated by optimizing the maximum-a-posteriori criterion using the one-step-late expectation–maximization and preconditioned conjugate gradient algorithms. Numerical experiments on various photon-limited image scenarios show that the proposed model outperforms the compared state-of-the-art reconstruction models.

1 Introduction

Emission tomography (ET) and tomographic reconstruction have gained tremendous attention in the last decades. This is due to the crucial role that medical imaging has come to play in the diagnosis of human disease, as well as in monitoring the progress of therapeutic methods. From a computational-model point of view, tomographic reconstruction is a typical inverse problem. After noisy emission data are collected, the goal is to reconstruct the original object, thereby inverting in this sense the image generation process [10, 16, 19].

Several approaches have been proposed for tomographic reconstruction, a considerable part of which focuses on methods based on iterative image reconstruction. This family of methods involves an iterative procedure of repeated projections and backprojections that progressively refines the image estimate [2, 38]. Iterative tomographic reconstruction techniques are separated into two basic categories: algebraic and statistical [1, 40], with the latter having proved to be the most popular. Shepp and Vardi have defined the problem in terms of maximization of a likelihood function [35], proposing the widely used maximum likelihood expectation–maximization (MLEM) algorithm. In EM and its variants, a probabilistic model is solved with an iterative scheme of alternating steps: the expectation (E-step) and the maximization step (M-step). In the E-step, moments of latent model variables are computed with respect to the current non-latent parameter estimate. In the M-step, non-latent parameters are optimized, with respect to current latent variable moments. The two interrelated steps are iterated until convergence. In practice, slight variants of the basic EM algorithm are used, such as MAP-EM, where part of the model random variables can be treated as parameters to be optimized, and their prior plays the standard role of a penalty term.

The ordered subsets EM (OSEM) algorithm has been proposed [14, 17] as an efficient variation of the MLEM algorithm, reducing the reconstruction time and the computational cost, as well as facilitating clinical use. The kernel-based EM algorithm that has been presented in [37] for PET image reconstruction is also of note. The row action maximum likelihood algorithm (RAMLA) [5] has been proposed as another MLEM variation, further speeding up convergence rate. Furthermore, with respect to speeding up reconstruction, also notable is the parallel tomographic reconstruction technique that has recently been proposed in [26], suitable for use with GPU-ready machines.

Bayesian maximum a posteriori methods, tantamount to penalized maximum likelihood [4], have been employed for tomographic reconstruction. Methods of this family impose a prior probability density function (pdf) on the reconstruction, encouraging image smoothness or other desirable traits (e.g., sharp edges). When the reconstruction problem is posed as an inverse problem, prior pdfs are in fact not only useful but necessary as well, as reconstruction from projections is in general an ill-posed problem. As such, in order to proceed a form of regularization is required [8,9,10]. In this sense of posing tomographic reconstruction as an inverse problem, a prior pdf acts as an objective function regularizer. With respect to traits that are deemed desirable for the reconstruction, image smoothness is perhaps one of the most usual constraints. The image smoothness constraint is based on the preassumption that high-frequency components in the reconstruction are more likely to be present due to noise. A common smoothness prior is the Markov random field (MRF) prior, formulated as a Gibbs distribution. Numerous Gibbs/MRF-based methods have been proposed, using various potential functions [12, 13, 21]. Under Gibbs/MRF priors, local differences between neighboring pixels are penalized in order to encourage small values, hence enforcing output image smoothness.

Another popular prior is the total variation (TV) prior [6, 11, 25, 28, 36, 39], with application to many imaging tasks, including tomographic reconstruction. The motivation behind using TV priors is that they provide a principled, coherent way to favor a smooth solution with sharper edges, in the premise that such solutions should have lower total intensity variation [6]. The penalty associated with total variation is in practice typically formulated as the discrete sum of gradient norms over the reconstructed image. In tomographic reconstruction with TV priors, the objective function is the weighted sum of the TV prior term and a data term. The data term is formulated as the distance between the reconstructed object and the original projections [11, 36]. Prior models and associated algorithms that can’t readily be categorized as Gibbs/MRF or TV priors have otherwise been proposed [7, 15]. A notable example is the clustered intensity histogram algorithm [15], where Gamma-distributed priors are used to enforce emission positivity constraints.

More complex prior models are in general possible, formulated as hierarchical probabilistic models [3]. In hierarchical probabilistic models, multiple stochastic and deterministic parameters may interact to model the reconstruction as a data generation process. The expectation–maximization (EM) algorithm is typically used to solve hierarchical probabilistic models [30], provided the model is suitably constructed (for example, pdf conjugacy requirements need to be met [3]). The tomographic reconstruction model and algorithm proposed in the current work is a hierarchical probabilistic model, solved with a MAP-EM algorithm. We propose a spatially varying mixture model [22, 23, 27, 32, 33] based on a Gamma mixture prior. In order to account for the modeling of edges between image segments, appropriate MRF smoothness priors on pixel label mixing proportions are defined. These priors model edges as random, latent variables, an assumption known in the literature as a ${ line \; process}$ model. The proposed model is based on a MAP tomographic reconstruction formula that uses a Gamma mixture prior and encourages edge preservation by modeling edge presence as a Student’s t-distribution on the pixel contextual mixing proportions.

In the proposed model, parameters are automatically estimated from the observed data. In effect, this yields location-dependent smoothing which cannot be modeled by the standard Gibbs distribution. The image reconstruction process integrates this prior in a standard MAP-EM iterative algorithm, where the proposed spatially varying Gamma mixture model (SVGammaMM) parameters and the unknown image are estimated in an alternating scheme. Numerical experiments using photon-limited images validate the method’s usefulness with respect to results using common state-of-the-art MRF-based priors.

The remainder of this paper is organized as follows. The image formation model and proposed reconstruction method is presented in Sect. 2. We present numerical results in Sect. 3, testing our model and comparing it against other well-known reconstruction models. In Sect. 4, we discuss our conclusions and perspectives for future work.

2 Image Formation Model and Image Reconstruction

Let $\mathbf{f}$ be the vectorized form of the image to be reconstructed. Let also $\mathbf{g}$ be the observed projections (sinogram), also in vectorized form, and let $\mathbf{H}$ represent the projection matrix. Penalized likelihood models rely on a stochastic interpretation of reconstruction regularization by introducing an appropriate prior $p(\mathbf{f})$ for the image $\mathbf{f}$. The likelihood function $p(\mathbf{g}|\mathbf{f})$ is related to the posterior probability $p(\mathbf{f}|\mathbf{g})$ by the Bayes rule, $p(\mathbf{f}|\mathbf{g})\propto p(\mathbf{g}|\mathbf{f})p(\mathbf{f})$.

In emission tomography, the likelihood $p(\mathbf{g}|\mathbf{f})$ is a Poisson distribution if the detector counts are mutually independent and not corrupted by additional data errors. Formally, we can write:

$$\begin{aligned} p(\mathbf{g}|\mathbf{f})= \prod _{m=1}^{M} \left( [\mathbf{Hf}]_{m}\right) ^{g_{m}} \frac{\exp (-[\mathbf{Hf}]_{m})}{g_{m}!}, \end{aligned}$$

(1)

with respect to $\mathbf{f}$, where M is the number of projection measurements, $g_{m}$ is the $m^{\text {th}}$ component of $\mathbf{g}$ and $[\mathbf{Hf}]_{m}$ is the $m^{\text {th}}$ component of the vector $\mathbf{Hf}$. MAP estimates for the image $\mathbf{f}$ may be obtained by maximizing the log-posterior:

$$\begin{aligned} \log p(\mathbf{f}|\mathbf{g})=\log p(\mathbf{g}|\mathbf{f})+\log p(\mathbf{f}) + const. \end{aligned}$$

(2)

We assume that the N intensity values $\{ { f}_n \}_{n=1}^N$ of the reconstructed image $\mathbf{f}$ are independent and identically distributed. These can be assumed to be generated by a finite mixture model [20]:

$$\begin{aligned} p({{ f}_n})= \sum _{j=1}^{J} \pi _j{\phi {({ f}_n;\theta _j)}} \end{aligned}$$

(3)

where $\pi =\lbrace \pi _{\mathbf{j}} \rbrace _{\mathbf{j}=1}^{\mathbf{J}}$ is the prior probability vector of a pixel membership on class j. The $\lbrace \theta _j \rbrace _{j=1}^J$ parameters control the shape of the kernel functions $\phi$. Thus, there is a natural correspondence between pixel class-membership and kernels, and we can classify the pixels according to posterior class memberships [32]. A standard and well-known choice of a kernel function are the Gaussian distribution [32] or the Gamma distribution [3]. The Gamma distribution is nonzero valued on positive real numbers only, the positivity constraint of the reconstruction problem is inherently satisfied. The general form of a mixture-of-Gammas prior pdf is:

$$\begin{aligned} p(\mathbf{f}| \theta ) = \prod _{n=1}^{N} \sum _{j=1}^{J}\pi _j \mathscr {G}({ f}_n| q_{j}, r_{j}). \end{aligned}$$

(4)

In Eq. (4), the set of parameters $\theta$ involves the vector q, with elements $\{ q_j \}_{j=1, \ldots , J}$ and the vector r, $\{ r_j \}_{j=1, \ldots , J}$, which parameterize the gamma density. The gamma density is defined only for $\mathbf{f}>0$. Furthermore, $r_j>0$ is the mean and $r_j^2/q_j$ the variance of the j-th component. Like other positivity preserving priors, it motivates a slight bias due to the difference between mean and mode. The mixing proportions (weights) $\pi _j$ are positive and satisfy the constraint:

$$\begin{aligned} \sum _{j=1}^{J}\pi _j = 1. \end{aligned}$$

(5)

In this paper, we extend the above assumptions (Eqs. 3, 4, 5) which assumes global mixing weights $\pi _j$ and assume that mixing proportions vary pixel-wise. Formally, we assume that the conditional distribution of $\mathbf f$ given a latent variable $\mathbf{z}$ is:

$$\begin{aligned} p({\mathbf{f}|\mathbf{z}})= \prod _{j=1}^{J}\prod _{n=1}^{N} {\phi {({ f}_n;\theta _j)}^{{z}_j^n}} \end{aligned}$$

(6)

where the prior distribution for the latent variable $\mathbf{z}$ is multinomial [32]:

$$\begin{aligned} p({\mathbf{z}|\pi })= \prod _{j=1}^{J}\prod _{n=1}^{N} {({\pi _j^n})^{{z}_j^n}} \end{aligned}$$

(7)

where ${z}^n$ is a binary vector $[{z}^n_1 {z}^n_2 \ldots {z}^n_J]^T$ with a single component equal to 1, ${z}^n_j=1$ and all others equal to 0, i.e., a “one-hot” vector representation. Pixel n is estimated to be part of segment j if and only if ${z}^n_j=1$. Note that, while the vector ${z}^n$ is binary and one-hot, the corresponding ${\pi }^n$ vector $[{\pi }^n_1 {\pi }^n_2 \ldots {\pi }^n_J]^T$ is a probability vector with $\pi ^n_j \in [0,1] \forall j \in [1,J]$ and $\sum _{j=1}^J \pi ^n_j = 1$. Also, as a direct consequence of Eq. (7), the two vectors are related by $<z^n_j> = \pi ^n_j$, where $<\cdot>$ denotes random variable expectation.

Our model differs from the standard Gamma mixture model in the definition of the mixing proportions. More precisely, each pixel $f_n$, $n=1,\ldots ,N$ has a distinct vector of mixing proportions denoted by $\pi _{j}^{n}$, $j=1,\ldots ,J$, with J being the number of Gamma kernels. We call these parameters contextual mixing proportions to distinguish them from the mixing proportions of a standard Gamma mixture model.

Apart from inherently assuming an image segmentation by means of the Gamma mixture prior, the edges in the image are preserved because the local differences of the contextual mixing proportions are considered to follow a univariate Student’s t-distribution (or referred to as simply t-distribution for brevity). Following the definition of the Student’s t-distribution [18], we can write the Student’s t as a two-step generative process:

$$\begin{aligned}&\pi _{j}^n - \pi _{j}^k \sim \mathscr {N}(0, \beta _{jd}^2/u_j^{nk}), \nonumber \\&u_j^{nk} \sim \mathscr {G}(\nu _{jd}/2,\nu _{jd}/2),\;\; \forall n,j,d,\; k\in \gamma _d(n), \end{aligned}$$

(8)

where $\gamma _d(n)$ is the set of neighbors of the pixel indexed by n, with respect to the $d{\mathrm{th}}$ adjacency type. This model first draws $u_j^{nk}$ from a Gamma distribution parameterized by $\nu _{jd}$ and then considers that the local differences of the mixing proportions follow a Gaussian distribution with zero mean and standard deviation $\beta _{jd}^2/u_j^{nk}$. We consider D different adjacency types (e.g., horizontal, vertical, diagonal). For example, if d=“horizontal adjacency” and n is a non-border pixel, we have $|\gamma _d(n)|=2$ as pixel n has one horizontal neighbor to its left pixel and one horizontal neighbor to its right. The total number of neighbors for all adjacency types $d \in [1,D]$ is considered equal to $\varGamma$.

Note that Eq. (8) effectively defines a Gibbs distribution on the contextual mixing proportions $\pi$. The Gibbs distribution has the general form $e^{-\int \beta V(f(x,y), \gamma (x,y))dxdy}$ where $\beta$ and $V(\cdot )$ are Gibbs parameters and clique potentials, respectively. In the current model, these are defined by a zero-centered normal distribution on neighbor differences (8), parametrized by $\beta _{jd}$ and line process $\mathbf{u}$. Note that this use is quite different from the typical use of the Gibbs distribution, which is defined directly over pixel value estimates.

Formally, the Student’s t-distribution is defined as

$$\begin{aligned} p(u; \mu , \sigma ^2, \nu ) = \frac{ \varGamma (\frac{\nu }{2} + \frac{1}{2})}{|\sigma |(\frac{\varGamma }{2})^\frac{1}{2} [1 + \frac{(u-\mu )^2}{\nu \sigma ^2}] } \end{aligned}$$

(9)

The t-distribution is heavy-tailed, which means that it is more likely to generate values that fall far from its mean. As the number of degrees of freedom $\nu$ increases, the t-distribution approaches the normal distribution [3]. On the contrary, the closer $\nu$ is to zero, the more heavy-tailed the distribution is.

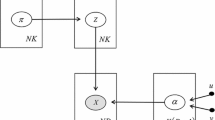
The proposed generative model can be examined in Fig. 1. The model imposes edge preservation through the Student’s t-distribution on the difference of the mixing proportions. The variables $u_j^{nk}$, effectively modeling a continuous line process, provide a detailed description of the boundary structure of the image.

Fig. 1

Graphical model for the continuous line process edge preserving model (SVGammaMM). $f_n$ are the N reconstructed object pixel intensities, assumed to be Gamma distributed an parametrized by $q_j, r_j$. Each of the N pixels of the reconstruction belongs to one of J image segments. This relationship is encoded as the multinomially distributed $z^n_j$ values, parametrized by the Gibbs-distributed $\pi ^n_j$. Parameters $\pi ^n_j$ depend on Gibbs parameters $\beta ^2_{jd}$ and on line process $u^{nk}_j$, over D pixel adjacency types and $\varGamma$ neighbors per pixel. The line process intensity is locally controlled by the “degrees of freedom” parameters $\nu _{jd}$. The reconstruction and all parameters are automatically estimated with the proposed MAP EM-based algorithm. See text for more details

Estimation of model parameters is obtained through a standard MAP-EM approach, consisting of a two-step alternating optimization scheme. In the first step, the parameters of the SVGammaMM model are estimated using the EM algorithm [32] given a fixed image estimate $\mathbf {f}$. In the second step, the image estimate $\mathbf {f}$ is updated while the model parameters are kept fixed.

The EM algorithm consists of performing alternating E-steps and M-steps until model likelihood convergence. In the E-step, moments of the hidden variables $\mathbf{z}$ and $\mathbf{u}$ are computed:

$$\begin{aligned} {\langle z_j^n \rangle }^{(t)}= & {} \frac{{\pi _j^{n{(t)}}}\mathscr {G}({ f}_n;q_j^{(t)},r_j^{(t)})}{\sum _{l=1}^{J}{\pi _l^{n{(t)}}}\mathscr {G}({ f}_n;q_l^{(t)},r_l^{(t)})}, \end{aligned}$$

(10)

$$\begin{aligned} {\langle u_j^{nk} \rangle }^{(t)}= & {} {\zeta ^{nk(t)}_j}/{\eta ^{nk(t)}_j}, \end{aligned}$$

(11)

$$\begin{aligned} {\langle \ln u_j^{nk} \rangle }^{(t)}= & {} {\psi }({\zeta ^{nk(t)}_j})-\ln {\eta ^{nk(t)}_j}, \end{aligned}$$

(12)

where t denotes iteration index. $\psi (\cdot )$ denotes the digamma function, while z, $\eta$ are determined by:

$$\begin{aligned} {\zeta ^{nk(t)}_j}= & {} \frac{1}{2}{(\nu _{jd}^{(t)}+1)}, \phantom {kk} \forall k \in \gamma _d(n), \end{aligned}$$

(13)

$$\begin{aligned} {\eta ^{nk(t)}_j}= & {} {2}{\left( \nu _{jd}^{(t)}+\frac{{(\pi _j^{n(t)}-\pi _j^{k(t)})^2}}{\beta _{jd}^{2(t)}}\right) }, \phantom {kk} \forall k \in \gamma _d(n). \end{aligned}$$

(14)

In the M-step, the non-stochastic parameters r, q, $\beta$ are updated with:

$$\begin{aligned} r_j^{(t)}= & {} \frac{\sum _{n=1}^N{\langle z_j^n \rangle ^{(t)}}{ f}_n}{{\langle z_j^n \rangle }^{(t)}}, \end{aligned}$$

(15)

$$\begin{aligned} q_j^{(t)}= & {} \sum _{n=1}^{N}\log {{ f}_n}{\langle z_j^n \rangle ^{(t)}}- {\langle z_j^n \rangle ^{(t)}}\log r_j^{(t)} \nonumber \\&- {\langle z_j^n \rangle ^{(t)}}\psi {(q_j^{(t)})}, \end{aligned}$$

(16)

$$\begin{aligned} {\beta _{jd}^{2(t+1)}}= & {} \frac{\sum _{n=1}^{N}\sum _{k\in \gamma _d(n)}{{{\langle u_j^{nk} \rangle }^{(t)}}{(\pi _j^{n(t)}-\pi _j^{k(t)})^2}}}{\sum _{n=1}^{N}{\left| \gamma _d(n) \right| }}. \end{aligned}$$

(17)

In addition, the degrees of freedom parameter $\nu _{jd}^{(t+1)}$ are estimated as the solution of the below equation:

$$\begin{aligned}&\ln {(\nu _{jd}^{(t+1)}/2)} - \psi {(\nu _{jd}^{(t+1)}/2)}+\nonumber \\&\quad \frac{\sum _{n=1}^{N}\sum _{k\in \gamma _d(n)}{({{\langle \ln u_j^{nk} \rangle }^{(t)}-{\langle u_j^{nk} \rangle }^{(t)})}}}{\sum _{n=1}^{N}{\left| \gamma _d(n) \right| }} + 1 = 0 \end{aligned}$$

(18)

Thereafter, the MAP estimate for the random process $\pi$ is computed. The elements of $\pi$ are updated by solving the following quadratic equation:

$$\begin{aligned} a_j^n{(\pi _j^{n(t+1)})^2} + b_j^n{(\pi _j^{n(t+1)})} + c_j^n = 0 \end{aligned}$$

(19)

with coefficients:

$$\begin{aligned} a_j^n= & {} - \sum _{d=1}^{D}{\left\{ (\beta _{jd}^{(t)})^{-2} \sum _{k\in \gamma _d(n)}{\langle u_j^{nk} \rangle }^{(t)}\right\} }, \end{aligned}$$

(20)

$$\begin{aligned} b_j^n= & {} \sum _{d=1}^{D}{\left\{ (\beta _{jd}^{(t)})^{-2} \sum _{k\in \gamma _d(n)}{\langle u_j^{nk} \rangle }^{(t)}\pi _j^{k(t)}\right\} }, \end{aligned}$$

(21)

$$\begin{aligned} c_j^n= & {} \frac{1}{2}{\langle z_j^n \rangle }^{(t)}. \end{aligned}$$

(22)

While the vector elements of $\pi$ are probability distributions, the real nonnegative solutions will not, in general, satisfy the sum-to-unity constraint. In order to get proper mixing weight vectors, we perform a projection step onto the constraints subspace using the quadratic programming algorithm described in [32].

After having updated the SVGammaMM parameters with the updates presented above, the next step consists in estimating the reconstruction $\mathbf {f}$ given these parameters. An update for $\mathbf {f}$ should maximize Eq. 2. The intensity of the $n^{\text {th}}$ pixel of the unknown image can therefore be updated as follows:

$$\begin{aligned} \hat{{ f}}_n^{(t+1)} = \frac{\hat{{ f}}_n^{(t)}}{\sum _{i'}{ H}_{i'n} + \left. \frac{\partial \log p}{\partial f_n}\right| _{f_{n}=\hat{f}_{n}^{(t)}}}\sum _i{{ H}_{in}\frac{{ g}_i}{\sum _k{{ H}_{ik}}\hat{{ f}}_k^{(t)}}}. \end{aligned}$$

(23)

This “one-step-late” (OSL) update [12, 38] uses the previous image estimate to evaluate the derivative term in Eq. (23).

Algorithm 1 summarizes the steps of the proposed tomographic reconstruction algorithm. The algorithm stops when the estimated image does not change significantly or when a predefined number of iterations is reached.

3 Numerical Results

Fig. 2

a Shepp–Logan phantom. b Elliptical phantom

The performance of the proposed spatially varying mixture models for the tomographic reconstruction problem was evaluated using the well-known Shepp-Logan phantom and a phantom consisting of three regions of relative intensities, represented by a hot disk, a cold disk and a background ellipse (Fig. 2). We call this phantom Elliptical phantom. The resolution of the reconstructed objects $\mathbf{f}$, for both cases is $256 \times 256$ pixels. Projections are observed for tilt angles {$0^\circ$, $1^\circ$, $2^\circ$, $\ldots$, $179^\circ$}. The observed sinograms $\mathbf{g}$ are of size $367 \times 180$, for both cases again. We have set $J = 3$ and $J = 5$ clusters for the mixture models taking into account the segments of the two phantoms. The algorithm stopped when $\epsilon =10^{-3}$ or when 60 iterations were reached. The presented algorithm, namely the spatially varying Gamma mixture model (SVGammaMM), was evaluated with respect to the standard MLEM [35], the established MAP-EM algorithm with a Gibbs [12] and a TV prior [25]. The MLEM method solves the problem by performing a maximum likelihood fit over the Poisson-distributed emissions. The Gibbs and TV prior models penalize the solution according to a prior distribution model. The Gibbs prior term is defined as a MRF over the reconstruction itself [12], contrary to the proposed hierarchical model, as:

$$\begin{aligned} p_{Gibbs}(f) = e^{-\int \beta V(f(x,y), \gamma (x,y))dxdy} \end{aligned}$$

(24)

where $\beta$ is a parameter controlling prior weight with respect to the data term. $V(\cdot )$ is a clique potential function, penalizing reconstruction pixel values that are different from their neighbors, denoted here as $\gamma (x,y)$. The TV prior term takes the form [6, 25]:

$$\begin{aligned} p_{TV}(f) = e^{-\int \beta |\nabla f(x,y)| dx dy} \end{aligned}$$

(25)

Furthermore, we have compared our algorithm to a spatially varying Gaussian mixture model (SVGMM) [24], a standard Gaussian mixture model (GMM) and a standard Gamma mixture model (GammaMM). The latter two models define likelihood according to Eq. 3, with different choices for the kernel function $\phi$.

For the image estimation step (see algorithm 1) we have tried employing two alternatives. We ran tests either using an OSL update (Eq. 23) or preconditioned conjugate gradients (PCG) to compute the image estimate. Concerning parameters of the competing algorithms (e.g., the weight parameter between data term and total variation term in the TV prior method), tests were run over different parameter values, and the optimal ones, result-wise, were chosen to be presented for comparison.

A number of performance indices were used. To this end, degraded images were generated from the initial images by modifying the total photon counts. More specifically, images having 75, 55, 35 and 15 photons/pixel on average were generated to degrade the signal quality, and for the Elliptical phantom, 80, 56, 36 and 24 photons/pixel were simulated. Since the various performance indices are so similar for the whole set of photon counts, only comparative statistics for one rate of photons per pixel is illustrated (75 photons/pixel for the Shepp–Logan phantom and 80 photons/pixel for the Elliptical phantom).

Furthermore, we have artificially degraded the original phantoms by smoothing with a Gaussian blur filter. We have used two different levels of smoothing, $\sigma =2$ and $\sigma =4$. We have run tests corresponding to the original, non-smoothed phantoms as well as the smoothed phantoms, in order to test for our algorithm’s robustness also to this type of degradation.

Fig. 3

Comparative statistics for various performance indices for the Shepp–Logan phantom for 75 photons per pixel. a ISNR (mean values of the 40 experiments), b bias, c variance

Fig. 4

Comparative statistics for various performance indices for the Elliptical phantom for 80 photons per pixel. a ISNR (mean values of the 40 experiments), b bias, c variance

Fig. 5

Comparative statistics for various performance indices for the Shepp–Logan phantom for 75 photons per pixel, smoothed with a Gaussian filter ($\sigma =2$). a ISNR (mean values of the 40 experiments), b bias, c variance

Fig. 6

Comparative statistics for various performance indices for the Shepp–Logan phantom for 75 photons per pixel, smoothed with a Gaussian filter ($\sigma =4$). a ISNR (mean values of the 40 experiments), b bias, c variance

At first, the algorithms were put in test in terms of the improvement in signal to noise ratio (ISNR) with respect to a reconstruction obtained by a simple filtered backprojection using the Ram–Lak filter:

$$\begin{aligned} \text {ISNR}=10\log _{10}\frac{||\mathbf{f}-\mathbf{f}_{FBP}||^{2}}{||\mathbf{f}-\hat{\mathbf{f}}||^{2}}, \end{aligned}$$

(26)

where $\mathbf{f}$ is the ground truth image, $\mathbf{f}_{FBP}$ is the reconstructed image by filtered backprojection and $\hat{\mathbf{f}}$ is the reconstructed image using the proposed image model. Practically, ISNR measures the improvement (or deterioration) in the quality of the reconstruction of the proposed method with respect to the reconstruction obtained by filtered backprojection.

Moreover, the consistency of the method was measured by the bias (BIAS) and the variance (VAR) of the reconstructed images:

$$\begin{aligned} \text {BIAS}= & {} ||\mathbf{f}-\bar{\mathbf{f}}||,\,\,\, \end{aligned}$$

(27)

$$\begin{aligned} \text {VAR}= & {} \sum _{k=1}^{K}||\bar{\mathbf{f}}-\hat{\mathbf{f}}^{k}||^{2}, \end{aligned}$$

(28)

with

$$\begin{aligned} \bar{\mathbf{f}}=\frac{1}{K}\sum _{k=1}^{K}\hat{\mathbf{f}}^{k}, \end{aligned}$$

(29)

where ${\mathbf{f}}$ is the ground truth image and $\hat{\mathbf{f}}^{k}$, for $k=1,\ldots ,K$, is the $k^{\text {th}}$ reconstructed image, obtained from $K=40$ different realizations for each noise level. Finally, we also considered for the evaluation the structural similarity index (SSIM) [34], which represents the visual distortion between the reconstructed image and the ground truth. It is computed to be close to 1 for all the resulted images except from MLEM and MAP-EM with Gibbs prior, hence it is not included in the illustrated comparative results.

The statistical comparisons for the aforementioned algorithms are shown in Fig. 3 for the Shepp–Logan phantom. For all the quantities, their mean values over the $K=40$ experiments are shown. All of the obtained ISNR values are very close to the mean values as their standard deviations over the whole set of experiments are very small. The ISNR, bias and variance for the Shepp–Logan phantom, for 75 photons per pixel on average, are shown. The statistical comparisons for the Elliptical phantom for 80 photons per pixel are illustrated in Fig. 4. It may be observed from all these indices for both phantoms that the proposed spatially varying mixture model performs better with respect to the other priors. Specifically, for the Shepp–Logan phantom with 75 photons per pixel and for the Elliptical phantom with 80 photons, ISNR reaches its peak for the spatially varying Gamma mixture model, carried out by a preconditioned conjugate gradient optimizer (SVGammaMM (PCG)), as shown in Figs. 3a and 4a. The spatially varying Gamma mixture methods have similar ISNR values but always larger than the other algorithms. The proposed methods similarly outperform the competition for the case where we perform reconstructions over the blur-degraded versions of the phantoms, for either blur intensity (Figs. 5, 6, 7, 8).

The same stands for the bias which yields its minimum through the SVGammaMM (PCG) for both phantoms as it can be observed in Figs. 3c and 4c. Furthermore, the variance of the estimates is relatively consistent for the spatially varying mixture model for both phantoms. This is due to the mixture nature of the priors. The results confirm the effectiveness of the proposed model.

Fig. 7

Comparative statistics for various performance indices for the elliptical phantom for 80 photons per pixel, smoothed with a Gaussian filter ($\sigma =2$) a ISNR (mean values of the 40 experiments), b bias, c variance

Fig. 8

Comparative statistics for various performance indices for the Elliptical phantom for 80 photons per pixel, smoothed with a Gaussian filter ($\sigma =4$) a ISNR (mean values of the 40 experiments), b bias, c variance

Fig. 9

The reconstructed images for the Shepp–Logan phantom (degraded with Gaussian smoothing, $\sigma =2$) with 75 photons per pixel

Fig. 10

The reconstructed images for the Elliptical phantom (degraded with Gaussian smoothing, $\sigma =2$) with 80 photons per pixel

Fig. 11

Comparison of horizontal profiles between the original Shepp–Logan phantom and the reconstructed images provided by the proposed SVGammaMM and the Gibbs prior for 75 counts per pixel

In general, the images provided by the proposed spatially varying mixture model are visually sharper. Estimated images obtained using this model (SVGammaMM, PCG) are illustrated in Figs. 9 and 10, where we show reconstructions on input data degraded with Gaussian blur ($\sigma =2$). For comparison, estimates obtained using MLEM, MAP-EM with a Gibbs prior and a TV prior and a filtered backprojections (FBP) estimate are shown in the same Figures. Note that the performance of SVGammaMM (OSL) is always very close to SVGammaMM (PCG), with only small differences, and with at times slightly better performance.

Fig. 12

Comparison of horizontal profiles between the original Elliptical phantom and the reconstructed images provided by the proposed SVGammaMM and the Gibbs prior for 75 counts per pixel

In addition, to highlight the accuracy of the proposed model, the estimated image intensities along a scan line for both phantoms are shown in Figs. 11 and 12. Results using the SVGammaMM (PCG) model and a MAP-EM with a Gibbs prior are compared. It can be observed that the spatially varying Gamma mixture model provides values which are closer to the ground truth.

Finally, the required execution time of the proposed models on a standard PC using MATLAB without any optimization is on average 4 minutes, which is explained by the number of required computations for the EM or PCG for the reconstruction and the EM for the estimation of the model parameters.

4 Conclusion and Future Work

The main goal of this work was to explore the possibility of the development of a robust model for tomographic image reconstruction purposes. We have proposed an alternative hierarchical and spatially constrained mixture model in order to enforce them to preserve image edges. We have presented a spatially varying Gamma mixture model with a Student’s t MRF-based prior governing the contextual mixing proportions. Spatially varying mixture models are characterized by the dependence of their mixing proportions on location (contextual mixing proportions) and they have been previously successfully used in image segmentation.

The main contribution of this work is the effectiveness of the adaptive MRF priors which may capture spatial coherence and preserve image boundaries, retaining them unsmoothed. The proposed Gamma mixture component of the model assumes a multiple-mode histogram in the object, and enforces positivity naturally. Furthemore, an important property of the proposed model is the automatic estimation of model parameters from the data which is crucial, as many state-of-the-art reconstruction algorithms rely on empirical parameter selection. Numerical experiments on various photon-limited image scenarios showed that the proposed models are more accurate than the corresponding results of the compared methods.

With regard to directions for future improvements, an important perspective of this study would be to explore how to automatically estimate the number of components of the mixture model assumed in the image reconstruction framework. This remains an important open problem in the mixture modeling literature [3, 29].

Furthermore, the space complexity of the proposed algorithm could perhaps be improved upon. Taking into account that for each iteration we require space for the Markov random field values $\pi$ and the line process $\mathbf {u}$, we can easily see that our space complexity is $O(NJ\varGamma )$. For values $J=5$ and a standard $8-$ neighborhood, this may mean a requirement of up to $\sim 50$ times the space of the reconstruction. Perhaps a grid-update strategy [31] could be envisaged and improved upon to save on required space.