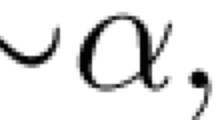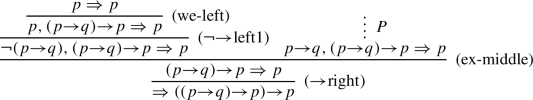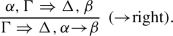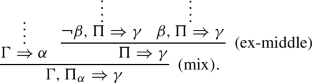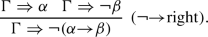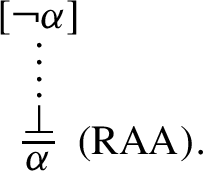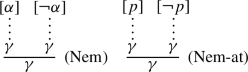Abstract
A unified and modular falsification-aware single-succedent Gentzen-style framework is introduced for classical, paradefinite, paraconsistent, and paracomplete logics. This framework is composed of two special inference rules, referred to as the rules of explosion and excluded middle, which correspond to the principle of explosion and the law of excluded middle, respectively. Similar to the cut rule in Gentzen’s LK for classical logic, these rules are admissible in cut-free LK. A falsification-aware single-succedent Gentzen-style sequent calculus fsCL for classical logic is formalized based on the proposed framework. The calculus fsCL is obtained from the existing falsification-aware single-succedent Gentzen-style sequent calculus GN4 for Nelson’s paradefinite (or paraconsistent) four-valued logic N4 by adding the rules of explosion and excluded middle. A falsification-aware single-succedent Gentzen-style sequent calculus GN3 for Nelson’s paracomplete three-valued logic N3 is also obtained from GN4 by adding the rule of explosion. The cut-elimination theorems for fsCL, GN3, and some of their neighbors as well as the Glivenko theorem for fsCL are proved.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rules of Explosion and Excluded Middle: In this study, we introduce a unified and modular falsification-aware single-succedent Gentzen-style framework for classical, paradefinite, paraconsistent, and paracomplete logics. This framework is composed of the following two special inference rules, which are referred to as the rules of explosion and excluded middle, respectively.

The rules (explosion) and (ex-middle) correspond to the principle of explosion \((\lnot \alpha {\wedge }\alpha ) {\rightarrow } \beta \) and the law of excluded middle \(\lnot \alpha {\vee }\alpha \), respectively. The rule (explosion) is introduced in this study as the dual counterpart of (ex-middle). The rule (ex-middle) was originally introduced by von Plato (1999); Negri and von Plato (2001) in constructing some single-succedent Gentzen-style sequent calculi for classical logic.Footnote 1
Significance of the Rules of Explosion and Excluded Middle: Similar to the cut rule in Gentzen’s sequent calculus LK (Gentzen, 1969) for classical logic, the rules (explosion) and (ex-middle) are admissible in cut-free LK. This means that these rules are regarded as critical, natural, and plausible components of Gentzen-style sequent calculi. These rules are similar to the following cut rule in Gentzen’s sequent calculus LJ (Gentzen, 1969) for intuitionistic logic.

The rules (cut), (explosion), and (ex-middle) are, in a sense, regarded as (or intended to becoming) structural rulesFootnote 2 and are primarily concerned with critical notions of consistency, paraconsistency, and paracompleness, respectively. Thus, using the rules (explosion) and (ex-middle), we can clarify and compare the essential differences and similarities of classical, paradefinite, paraconsistent, and paracomplete logics.
Results of this Study: In this study, we introduce a falsification-aware single-succedent Gentzen-style sequent calculus fsCL for classical logic. The proposed calculus fsCL is obtained from the existing falsification-aware single-succedent Gentzen-style sequent calculus GN4 for Nelson’s paradefinite (or paraconsistent) four-valued logic N4 (Almukdad & Nelson, 1984; Nelson, 1949) by adding (explosion), (ex-middle), and the standard right-weakening rule (we-right). In addition, we introduce two falsification-aware single-succedent Gentzen-style sequent calculi GN3 and GLP for Nelson’s paracomplete three-valued logic N3 (Almukdad & Nelson, 1984; Nelson, 1949) and an extension of the logic of paradox LP (Asenjo, 1966; Priest, 1979), respectively. The proposed calculus GN3 is obtained from GN4 by adding (explosion) and (we-right). The proposed calculus GLP is obtained from GN3 by replacing (explosion) with (ex-middle). We then prove the cut-elimination theorems for fsCL, GN3, and GLP as well as the Glivenko theorem for fsCL. We also observe that some falsification-aware single-succedent Gentzen-style sequent calculi for Belnap–Dunn logic BD (Belnap and Dunn’s four-valued logic, first-degree entailment logic, or Dunn–Belnap logic) (Belnap, 1977a, b; Dunn, 1976, 2019), Kleene’s strong three-valued logic K\(_3\) (Kleene, 2009), and the logic of paradox LP (Asenjo, 1966; Priest, 1979) can be obtained as subsystems of the \({\rightarrow }\)-less fragment of fsCL by deleting (explosion), (ex-middle), and/or (we-right).
Nelson’s Paradefinite Four-Valued Logic N4: The logic N4, which is regarded as an extension of BD by adding \({\rightarrow }\), is obtained from the positive fragment of intuitionistic logic by adding the following axiom schemesautoedited,:Footnote 3\(\lnot \lnot \alpha \leftrightarrow \alpha \), \(\lnot (\alpha {\wedge } \beta ) \leftrightarrow \lnot \alpha {\vee }\lnot \beta \), \(\lnot (\alpha {\vee } \beta ) \leftrightarrow \lnot \alpha {\wedge }\lnot \beta \), and \(\lnot (\alpha {\rightarrow } \beta ) \leftrightarrow \alpha {\wedge }\lnot \beta \). Some Gentzen-style sequent calculi for N4 are naturally constructed from the positive fragment of LJ by adding negated logical inference rules that correspond to the axiom schemes previously mentioned. These calculi for N4 are formalized based on the single-succedent (or intuitionistic) sequents of the form \( \Gamma \Rightarrow \gamma \), where \( \Gamma \) is a sequence of formulas and \( \gamma \) is a formula or the empty sequence. These calculi are regarded as single-succedent Gentzen-style sequent calculi similar to LJ. For more information on Gentzen-style sequent calculi for N4, see (Kamide & Wansing, 2012, 2015).
Paradefinite, Paraconsistent, and Paracomplete Logics: The logic N4 is known as a paradefinite logic, which is a specific type of paraconsistent logic (Priest, 2002). Paradefinite logics incorporate the properties of both paraconsistency, which rejects the principle of explosion, and paracompleteness, which rejects the law of excluded middle. Because of these properties, paradefinite logics are useful for handling indefinite information (Arieli & Avron, 2016; Avron et al., 2018). They are also known to have multiple names: referred to as paradefinite logics by Arieli and Avron (2016, 2017), paranormal logics by Béziau (2009), and non-alethic logics by da Costa. In this study, based on traditional naming, we refer to paraconsistent logics and paracomplete logics as logics that reject the principle of explosion and the law of excluded middle, respectively. For example, the logic N3, which is regarded as an extension of K\(_3\) by adding \({\rightarrow }\), is regarded as a paracomplete logic because N3 is obtained from N4 by adding the principle of explosion as an axiom scheme (i.e., N3 has no law of excluded middle).Footnote 4 In addition, the logic LP, which is considered an extension of BD by adding the law of excluded middle, is regarded as a paraconsistent logic because it has no principle of explosion.
Falsification-Awareness of Logics: Some of the previously proposed Gentzen-style sequent calculi for N4 and the proposed calculus fsCL are regarded as falsification-aware. Thus, the notion “falsification-awareness” should be explained. The notion of falsification and an adequate representation of falsification-aware reasoning are critical in the field of philosophy (Wansing, 2010; Horn & Wansing, 2017; Kapsner, 2014; Łukowski, 2002; Shramko, 2005). Thus, falsification-aware proof systems and semantics are required to analyze these philosophical issues. Based on some traditional studies, Kamide Kamide (2022) has suggested that proof systems and/or semantics are falsification-aware if they are capable of providing or representing direct or explicit falsifications or refutations of given negated formulas (excluding the negated atomic formula).
Falsification-Aware Gentzen-Style Sequent Calculi: The following logics are traditionally known to have falsification-aware Gentzen-style sequent calculi and (Kripke-style) semantics, which provide a clear understanding of falsification-aware reasoning within the underlying logic: Nelson’s N4 and N3 (Almukdad & Nelson, 1984; Nelson, 1949; Wansing, 1993; Kamide, 2005b; Kamide & Wansing, 2012, 2015), Belnap–Dunn logic BD (Belnap, 1977a, b; Dunn, 1976, 2019), bi-intuitionistic logics (Rauszer, 1974, 1977, 1980; Łukowski, 2002; Wansing, 2010, 2016), and dual-intuitionistic logics (or falsification logics) (Czermak, 1977; Goodman, 1981; Urbas, 1996; Shramko, 2005, 2016). In addition, Kamide (2022) introduced two types of falsification-aware multiple-succedent Gentzen-style sequent calculi for classical logic. However, a falsification-aware single-succedent Gentzen-style sequent calculus for classical logic has yet to be proposed. For more information on falsification-aware Gentzen-style sequent calculi for BD and its extensions and neighbors, see (Kamide, 2018, 2023a, b).
Single-Succedent Gentzen-Style Sequent Calculi for Classical Logic: On the one hand, Gentzen’s LK for classical logic was formalized based on the standard multiple-succedent (or classical) sequents of the form \( \Gamma \Rightarrow \Delta \), where \( \Gamma \) and \( \Delta \) are sequences of formulas. On the other hand, some non-falsification-aware single-succedent Gentzen-style sequent calculi for classical logic, which are constructed based on Gentzen’s LJ, were traditionally proposed and studied by Curry (1963); Felscher (1975); Gordeev (1987); Africk (1992); Negri and von Plato (2001), and Kamide (2005a). These single-succedent calculi for classical logic are useful when the focus is on the essential differences between classical and intuitionistic logics. For a comprehensive survey of single-succedent Gentzen-style sequent calculi for classical and intermediate logics, see Sect. 4.
Paper Structure: The remainder of this paper is organized as follows. In Sect. 2, we introduce fsCL, compare fsCL and GN4, and present some basic properties of (explosion) and (ex-middle). In addition, we introduce three alternative falsification-aware single-succedent Gentzen-style sequent calculi fsCL\(^e\), fsCL\(^s\), and fsCL\(_s\) for classical logic, two falsification-aware single-succedent Gentzen-style sequent calculi GN3 and GN3\(^s\) for N3, and a falsification-aware single-succedent Gentzen-style sequent calculus GLP for an extension of LP with the sddition of \({\rightarrow }\). We also observe that falsification-aware single-succedent Gentzen-style sequent calculi for BD, K\(_3\), and LP can be obtained as subsystems of fsCL. In Sect. 3, we present our main theorems. First, we prove the explosion- and excluded-middle-elimination theorems for LK, which are theorems for eliminating (explosion) and (ex-middle) in cut-free LK (i.e., these rules are admissible in cut-free LK). Next, we prove the equivalence between fsCL and classical logic using the explosion- and excluded-middle-elimination theorems for LK. We then prove the cut-elimination theorem for fsCL using Africk’s proof method (Africk, 1992), which is a simple embedding-based method. In addition, we prove the cut-elimination theorems for fsCL\(^e\), fsCL\(_s\), GN3, and GLP. We next prove the Glivenko theorem for fsCL, which is a theorem for embedding fsCL into LJ. In Sect. 4, we present a comprehensive survey of the traditionally proposed non-falsification-aware single-succedent Gentzen-style sequent calculi for classical and intermediate logics. In Sect. 5, we conclude the study and address related works on Łukasiewicz-style refutation systems, which are regarded as alternative falsification-aware proof systems.
2 Gentzen-Style Sequent Calculi
2.1 Falsification-Aware Single-Succedent Gentzen-Style Sequent Calculus for Classical Logic
Formulas of the logics discussed in this study are constructed from countably many propositional variables by the logical connectives \({\wedge }\) (conjunction), \({\vee }\) (disjunction), \({\rightarrow }\) (implication), and \(\lnot \) (negation). Small letters p, q, ... are used to denote propositional variables, Greek small letters \(\alpha , \beta ,...\) are used to denote formulas, and Greek capital letters \( \Gamma , \Delta ,...\) are used to represent finite (possibly empty) multisets of formulas. An expression \(\lnot \Gamma \) is used to denote the multiset \(\{ \lnot \gamma ~\mid ~ \gamma \in \Gamma \}\). The symbol \(\equiv \) is used to denote the equality of symbols.
A single-succedent (or intuitionistic) sequent (simply called sequent) is an expression of the form \( \Gamma \Rightarrow \gamma \) where \( \gamma \) is a formula or the empty multiset. An expression \(L \vdash S\) is used to represent that a sequent S is provable in a Gentzen-style sequent calculus L. In this expression, L will occasionally be omitted. An expression \(\alpha \Leftrightarrow \beta \) is used to represent the abbreviation of the sequents \( \alpha \Rightarrow \beta \) and \( \beta \Rightarrow \alpha \).
Two Gentzen-style sequent calculi \(L_1\) and \(L_2\) are said to be theorem-equivalent if \(\{S~\mid ~L_1\vdash S\}\) = \(\{S~\mid ~L_2\vdash S\}\). A rule R of inference is said to be admissible in a Gentzen-style sequent calculus L if the following condition is satisfied: For any instance

of R, if \(L \vdash S_i\) for all i, then \(L \vdash S\). Furthermore, R is said to be derivable in L if there is a derivation from \(S_1, \ldots , S_n\) to S in L. In this study, a Gentzen-style sequent calculus is occasionally identified with the logic determined by it.
We introduce a falsification-aware single-succedent Gentzen-style sequent calculus fsCL for classical logic.
Definition 1
(fsCL) In this definition, we use the symbol \( \gamma \) to represent an arbitrary formula or the empty multiset, and the symbol p to represent an arbitrary propositional variable.
The initial sequents of fsCL are of the form:
The explosion and excluded middle inference rules of fsCL are of the form:

The structural inference rules of fsCL are of the form:

The non-negated logical inference rules of fsCL are of the form:

The negated logical inference rules of fsCL are of the form:

We have the following important observation.
Observation 1
(Relationship between classical logic and N4) A Gentzen-style sequent calculus GN4 for Nelson’s paradefinite (paraconsistent) four-valued logic N4 can be obtained from fsCL by deleting (explosion), (ex-middle), and (we-right).
Remark 1
We make the following remarks.
-
1.
The system fsCL is indeed a system for classical logic. This fact will be shown in Theorem 15.
-
2.
The system fsCL has no standard negation inference rules (\(\lnot \)left) and (\(\lnot \)right) used in Gentzen’s LJ for intuitionistic logic. But, we will show in Proposition 12 that (\(\lnot \)left) and (\(\lnot \)right) are derivable in fsCL.
-
3.
The following is an example proof in fsCL for \( \Rightarrow ((p{\rightarrow }q){\rightarrow }p){\rightarrow }p \) where p and q are distinct propositional variables.
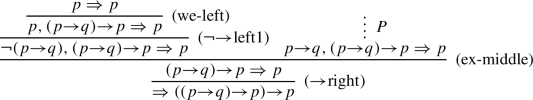
where P is:

-
4.
Note that the sequent \( \Rightarrow ((p{\rightarrow }q){\rightarrow }p){\rightarrow }p \) is also provable in a sequent calculus GLP \(=\) fsCL − (explosion), where GLP is a sequent calculus for an extension of the logic LP (Asenjo, 1966; Priest, 1979). GLP and the corresponding logic of it will be discussed.
-
5.
The following basic properties hold for GN4.
-
(a)
For any formula \(\alpha \), GN4 − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
-
(b)
The rule (cut) is admissible in cut-free GN4.
For more detailed information on the latter property (i.e., the cut-elimination theorem for GN4), see e.g., Kamide and Wansing (2012, 2015).
-
(a)
Next, we show some basic propositions for fsCL.
Proposition 1
For any formula \(\alpha \), fsCL − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
Proof
We show this by induction on \(\alpha \). We have to consider the cases for \(\alpha \equiv p\), \(\alpha \equiv \beta _1{\wedge } \beta _2\), \(\alpha \equiv \beta _1{\vee } \beta _2\), \(\alpha \equiv \beta _1{\rightarrow } \beta _2\), and \(\alpha \equiv \lnot \beta \). Since the cases for \(\alpha \equiv p\), \(\alpha \equiv \beta _1{\wedge } \beta _2\), \(\alpha \equiv \beta _1{\vee } \beta _2\), and \(\alpha \equiv \beta _1{\rightarrow } \beta _2\) are obvious, we show only the case for \(\alpha \equiv \lnot \beta \). To show this, we have to consider the subcases for \( \beta \equiv p\), \( \beta \equiv \gamma _1{\wedge } \gamma _2\), \( \beta \equiv \gamma _1{\vee } \gamma _2\), \( \beta \equiv \gamma _1{\rightarrow } \gamma _2\), and \( \beta \equiv \lnot \gamma \). The subcase for \( \beta \equiv p\) is obvious, because \( \lnot p \Rightarrow \lnot p \) is an initial sequent. In what follows, we show only the subcases for \( \beta \equiv \lnot \gamma \) and \( \beta \equiv \gamma _1{\rightarrow } \gamma _2\), because the other cases can be treated similarly.
-
1.
Subcase \( \beta \equiv \lnot \gamma \):

-
2.
Subcase \( \beta \equiv \gamma _1{\rightarrow } \gamma _2\):

\(\square \)
Proposition 2
For any formulas \(\alpha \) and \( \beta \),
-
1.
fsCL − (cut) \(\vdash \) \( \Rightarrow (\lnot \alpha {\wedge }\alpha ) {\rightarrow } \beta \),
-
2.
fsCL − (cut) \(\vdash \) \( \Rightarrow \lnot \alpha {\vee }\alpha \).
Proof
-
1.
Case \( \Rightarrow (\lnot \alpha {\wedge }\alpha ){\rightarrow } \beta \):

-
2.
Case \( \Rightarrow \lnot \alpha {\vee }\alpha \):

\(\square \)
Proposition 3
-
1.
The rule (explosion) is derivable in explosion-free fsCL using the sequents of the form \( \lnot \alpha {\wedge }\alpha \Rightarrow \gamma \) where \(\alpha \) is an arbitrary formula and \( \gamma \) is an arbitrary formula or the empty multiset.
-
2.
The rule (ex-middle) is derivable in ex-middle-free fsCL using the sequents of the form \( \Rightarrow \lnot \alpha {\vee }\alpha \) where \(\alpha \) is an arbitrary formula.
Proof
-
1.
Case (explosion):

-
2.
Case (ex-middle):

\(\square \)
2.2 Alternative Falsification-Aware Single-Succedent Gentzen-Style Sequent Calculi for Classical and Other Logics
First, we introduce two alternative falsification-aware single-succedent Gentzen-style sequent calculi fsCL\(^e\) and fsCL\(^s\) for classical logic.
Definition 2
(fsCL\(^e\) and fsCL\(^s\)) A falsification-aware single-succedent Gentzen-style sequent calculus fsCL\(^e\) or fsCL\(^s\) for classical logic is obtained from fsCL by replacing (explosion) with the following rule, referred to as the empty explosion rule or the single-formula explosion rule, respectively.

where \( \beta \) is a formula.
Proposition 4
Let L be fsCL\(^e\) or fsCL\(^s\). For any formula \(\alpha \), L − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
Proof
Similar to the proof of Proposition 1. \(\square \)
We obtain the following theorem for fsCL\(^e\).
Theorem 5
(Cut-free equivalence between fsCL\(^e\) and fsCL) For any sequent \( \Gamma \Rightarrow \gamma \), fsCL\(^e\) − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \) iff fsCL − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \).
Proof
This theorem is obtained from the facts that (1) (e-explosion) is an instance of (explosion) and (2) (explosion) is derivable in cut-free fsCL\(^e\) by using (e-explosion) and (we-right). \(\square \)
Remark 2
The same theorem as Theorem 5 does not hold for fsCL\(^s\). A counterexample is \( \lnot p, p \Rightarrow \) where p is a propositional variable. Actually, this sequent is provable in cut-free fsCL\(^e\), but not provable in cut-free fsCL\(^s\). It is unknown whether \( \lnot p, p \Rightarrow \) is provable in fsCL\(^s\) or not, because it is unknown the “full” cut-elimination theorem for fsCL\(^s\) holds or not. See Remark 10.
We obtain the following theorem for fsCL\(^s\), which represents the formula-based weak form of equivalence between fsCL\(^s\) and fsCL.
Theorem 6
(Weak cut-free equivalence between fsCL\(^s\) and fsCL) For any formula \(\alpha \), fsCL\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \) iff fsCL − (cut) \(\vdash \) \( \Rightarrow \alpha \).
Proof
To prove this theorem, it is sufficient to prove the following statements.
-
1.
For any sequent \( \Gamma \Rightarrow \gamma \), if fsCL\(^s\) − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \), then fsCL − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \).
-
2.
For any formula \(\alpha \), if fsCL − (cut) \(\vdash \) \( \Rightarrow \alpha \), then fsCL\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \).
The statement (1) is obvious because fsCL\(^s\) − (cut) is a subsystem of fsCL − (cut). Thus, we prove (2) by induction on the proofs P of \( \Rightarrow \alpha \) in cut-free fsCL. We distinguish the cases according to the last inferences of P. Then, it is sufficient to consider the case (explosion), especially the case (e-explosion). But, we do not have to consider this case, because (e-explosion) cannot apply to the sequent \( \Rightarrow \alpha \). Therefore, we obtain the required fact. \(\square \)
Next, we introduce two falsification-aware single-succedent Gentzen-style sequent calculi GN3 and GN3\(^s\) for Nelson’s paracomplete three-valued logic N3 (Almukdad & Nelson, 1984; Nelson, 1949).
Definition 3
(GN3 and GN3\(^s\)) Falsification-aware Gentzen-style sequent calculi GN3 and GN3\(^s\) for Nelson’s paracomplete three-valued logic N3 are defined as follows.
-
1.
GN3 is obtained from fsCL by deleting (ex-middle).
-
2.
GN3\(^s\) is obtained from fsCL\(^s\) by deleting (ex-middle) and (we-right).
Remark 3
We can obtain the following alternative definitions of GN3 and GN3\(^s\) using GN4.
-
1.
GN3 is obtained from GN4 by adding (explosion) and (we-right).
-
2.
GN3\(^s\) is obtained from GN4 by adding (s-explosion).
Proposition 7
Let L be GN3 and GN3\(^s\). For any formula \(\alpha \), L − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
Proof
Similar to the proof of Proposition 1. \(\square \)
Remark 4
The logic N3 is obtained from N4 by adding the principle of explosion as an axiom scheme. Thus, the system GN3\(^s\) is indeed a Gentzen-style sequent calculus for N3 because (1) \( \Rightarrow (\lnot \alpha {\wedge }\alpha ){\rightarrow } \beta \) is provable in GN3\(^s\) as presented in the proof of Proposition 2 and (2) (s-explosion) is derivable from the sequents of the form \( \lnot \alpha {\wedge }\alpha \Rightarrow \beta \) as presented in the proof of Proposition 3.
We obtain the following theorem, which represents the formula-based weak form of equivalence between GN3 and GN3\(^s\).
Theorem 8
(Weak cut-free equivalence between GN3 and GN3\(^s\)) For any formula \(\alpha \), GN3\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \) iff GN3 − (cut) \(\vdash \) \( \Rightarrow \alpha \).
Proof
We can prove this theorem in a similar way as for the proof of Theorem 6. Thus, we consider only the following statement.
For any formula \(\alpha \), if NG3 − (cut) \(\vdash \) \( \Rightarrow \alpha \), then GN3\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \).
We prove this statement by induction on the proofs P of \( \Rightarrow \alpha \) in cut-free GN3. We distinguish the cases according to the last inferences of P. Then, it is sufficient to consider the case (we-right) because the case (explosion) is the same as the proof of Theorem 6. But, we do not have to consider this case because (we-right) cannot apply to the sequent \( \Rightarrow \alpha \). Namely, the upper sequent \( \Rightarrow \) of \( \Rightarrow \alpha \) in (we-right) is not provable in cut-free GN3. Therefore, we obtain the required fact. \(\square \)
Remark 5
We make the following remarks.
-
1.
The same statement as that of Theorem 6 cannot be shown for GN3\(^s\) because, as shown in the proof of Theorem 8, we need the fact that the upper sequent \( \Rightarrow \) of \( \Rightarrow \alpha \) in (we-right) is not provable in cut-free GN3.
-
2.
We can also consider the following “intermediate” alternative falsification-aware Gentzen-style sequent calculi for N3: GN4 \(+\) (s-explosion) \(+\) (we-right) and GN4 \(+\) (explosion). But, we do not discuss them.
Next, we introduce another falsification-aware single-succedent Gentzen-style sequent calculus fsCL\(_s\) for classical logic.
Definition 4
(fsCL\(_s\)) A falsification-aware single-succedent Gentzen-style sequent calculus fsCL\(_s\) for classical logic is obtained from fsCL by replacing (ex-middle) with the following rule, referred to as the the single-formula excluded-middle rule.

where \( \beta \) is a formula.
Proposition 9
For any formula \(\alpha \), fsCL\(_s\) − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
Proof
Similar to the proof of Proposition 1. \(\square \)
Remark 6
We make the following remarks.
-
1.
The system fsCL\(_s\) is indeed a falsification-aware single-succedent Gentzen-style sequent calculus for classical logic. This fact will be shown in Theorem 16.
-
2.
We can also consider the falsification-aware single-succedent Gentzen-style sequent calculus fsCL\(_e\) that is obtained from fsCL by replacing (ex-middle) with the following rule, refereed to as the the empty excluded-middle rule.

However, fsCL\(_e\) is not a system for classical logic because the sequents of the form \( \Rightarrow \lnot p{\vee }p \) are not provable in cut-free fsCL\(_e\).
Next, we introduce a falsification-aware single-succedent Gentzen-style sequent calculus GLP for an extension ELP of the logic of paradox LP (Asenjo, 1966; Priest, 1979), where ELP is obtained from LP by adding \({\rightarrow }\).
Definition 5
(GLP) A falsification-aware single-succedent Gentzen-style sequent calculus GLP for an extension ELP of the logic of paradox LP is obtained from fsCL by deleting (explosion).
Proposition 10
For any formula \(\alpha \), GLP − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
Proof
Similar to the proof of Proposition 1. \(\square \)
Remark 7
We make the following remarks.
-
1.
We can obtain the following alternative definitions of GLP using GN4 and GN3.
-
(a)
GLP is obtained from GN4 by adding (ex-middle) and (we-right).
-
(b)
GLP is obtained from GN3 by replacing (explosion) with (ex-middle).
-
(a)
-
2.
The \({\rightarrow }\)-less fragment of GLP is regarded as a falsification-aware single-succedent Gentzen-style sequent calculus for LP. We can also consider similar systems such as the system that is obtained from GLP by replacing (ex-middle) with (s-ex-middle).
-
3.
The logic ELP, the sequent calculus of which is GLP, is not a new logic. It was referred to as PI\(^s\) by Batens (1980), RM\(^{\supset }_3\) and Pac by Avron (1986, 1991),Footnote 5 and PCont by Rozonoer (1989). It was also studied by D’Ottaviano and da Costa (1970), by da Costa (1974), and by Asenjo and Tamburino (1975). PCont was also studied by Bolotov and Shangin (2012) and by Kürbis and Petrukhin (2021).
-
4.
Following (Avron, 1991), we now consider a Hilbert-style axiomatic system for ELP (i.e., PI\(^s\), RM\(^{\supset }_3\), Pac, or PCont). Such a Hilbert-style axiomatic system (for Pac) is obtained from a Hilbert-style axiomatic system HBe introduced by Avron (1991) by adding the axiom scheme \(\lnot \alpha {\vee }\alpha \) or \((\alpha {\rightarrow } \beta ){\rightarrow }((\lnot \alpha {\rightarrow } \beta ){\rightarrow } \beta )\). HBe is defined in Avron (1991) by the following axiom schemes and inference rule:
-
(a)
\(\alpha {\rightarrow }( \beta {\rightarrow }\alpha )\),
-
(b)
\((\alpha {\rightarrow }( \beta {\rightarrow } \gamma )){\rightarrow }((\alpha {\rightarrow } \beta ){\rightarrow }(\alpha {\rightarrow } \gamma ))\),
-
(c)
\(((\alpha {\rightarrow } \beta ){\rightarrow }\alpha ){\rightarrow }\alpha \),
-
(d)
\((\alpha {\wedge } \beta ){\rightarrow }\alpha \),
-
(e)
\((\alpha {\wedge } \beta ){\rightarrow } \beta \),
-
(f)
\(\alpha {\rightarrow }( \beta {\rightarrow }(\alpha {\wedge } \beta ))\),
-
(g)
\(\alpha {\rightarrow }(\alpha {\vee } \beta )\),
-
(h)
\( \beta {\rightarrow }(\alpha {\vee } \beta )\),
-
(i)
\((\alpha {\rightarrow } \gamma ){\rightarrow }(( \beta {\rightarrow } \gamma ){\rightarrow }((\alpha {\vee } \beta ){\rightarrow } \gamma )\),
-
(j)
\(\lnot (\alpha {\vee } \beta ) \leftrightarrow (\lnot \alpha {\wedge }\lnot \beta )\),
-
(k)
\(\lnot (\alpha {\wedge } \beta ) \leftrightarrow (\lnot \alpha {\vee }\lnot \beta )\),
-
(l)
\(\lnot \lnot \alpha \leftrightarrow \alpha \),
-
(m)
\(\lnot (\alpha {\rightarrow } \beta ) \leftrightarrow (\alpha {\wedge }\lnot \beta )\),
-
(n)

where \(\alpha \leftrightarrow \beta \) stands for \((\alpha {\rightarrow } \beta ){\wedge }( \beta {\rightarrow }\alpha )\). Note that all the sequents that correspond to these axiom schemes for Pac are provable in GLP.
-
(a)
-
5.
A multiple-succedent Gentzen-style sequent calculus for ELP (i.e., PI\(^s\), RM\(^{\supset }_3\), Pac, or PCont) was originally introduced by Avron (2003) as the I-less part of GM\(_3^{t, I}\) where I is a certain constant. This sequent calculus by Avron is defined based on the sequents of the form \( \Gamma \Rightarrow \Delta \) where \( \Gamma \) and \( \Delta \) represent sets of formulas. This sequent calculus is defined by the standard structural rules of cut and weakening and the initial sequents and logical inference rules of the form:

The rules of GLP are either instances of the rules of this calculus or can be easily shown to be derivable or admissible in this calculus. For example, (ex-middle) is derivable using \( \Rightarrow \lnot \alpha , \alpha \) by:

-
6.
By both the just mentioned fact (i.e., GLP is a subsystem of the above system) and the above-mentioned fact (i.e., all the sequents that correspond to the axiom schemes of Pac are provable in GLP), we obtain that ELP is logically-equivalent to Pac, RM\(^{\supset }_3\), PI\(^s\), and PCont.
-
7.
Avron considered an infinitely-valued logic RM\(^{\supset }\), the three-valued version of which is RM\(^{\supset }_3\). It can be obtained from the above-mentioned Hilbert-style axiomatic system for ELP by replacing \(((\alpha {\rightarrow } \beta ){\rightarrow }\alpha ){\rightarrow }\alpha \) and \(\lnot (\alpha {\rightarrow } \beta ) \leftrightarrow (\alpha {\wedge }\lnot \beta )\) with the axiom schemes of the form: \((\alpha {\wedge }\lnot \beta ) {\rightarrow }\lnot (\alpha {\rightarrow } \beta )\), \(\lnot (\alpha {\rightarrow } \beta ){\rightarrow }\lnot \beta \), and \(\lnot (\alpha {\rightarrow } \beta ){\rightarrow }((\alpha {\rightarrow } \beta ){\rightarrow }\alpha )\). As shown in Avron (1986), RM\(^{\supset }_3\) can be obtained from RM\(^{\supset }\) either by replacing \(\lnot (\alpha {\rightarrow } \beta ){\rightarrow }((\alpha {\rightarrow } \beta ){\rightarrow }\alpha )\) with \(\lnot (\alpha {\rightarrow } \beta ) {\rightarrow }\alpha \) or by adding \(((\alpha {\rightarrow } \beta ){\rightarrow }\alpha ){\rightarrow }\alpha \). Thus, \(((\alpha {\rightarrow } \beta ){\rightarrow }\alpha ){\rightarrow }\alpha \) is a dependent axiom scheme in the Hilbert-style axiomatic system for RM\(^{\supset }_3\).
2.3 Standard Gentzen-Style Sequent Calculi for Classical and Intuitionistic Logics
In the following, we introduce the standard Gentzen-style sequent calculi LK and LJ for classical and intuitionistic logics, respectively. These calculi will be used to show the equivalence between fsCL and classical logic. The systems LJ and LK, which will be defined in Definitions 6 and 7, are non-essential modifications of Gentzen’s original LJ and LK (Gentzen, 1969), respectively. We use the same names LJ and LK for these modified systems as the original ones.
First, we introduce LJ.
Definition 6
(LJ) A Gentzen-style sequent calculus LJ for intuitionistic logic is obtained from fsCL by replacing (ex-middle), (explosion), the negated logical inference rules (\(\lnot \lnot \)left), (\(\lnot \lnot \)right), (\(\lnot {\wedge }\)left), (\(\lnot {\wedge }\)right1), (\(\lnot {\wedge }\)right2), (\(\lnot {\vee }\)left1), (\(\lnot {\vee }\)left2), (\(\lnot {\vee }\)right), (\(\lnot {\rightarrow }\)left1), (\(\lnot {\rightarrow }\)left2), (\(\lnot {\rightarrow }\)right), and the initial sequent \( \lnot p \Rightarrow \lnot p \) with the following logical inference rules:

Next, we introduce LK. Prior to introducing LK, we have to modify the notion of sequent as follows. A multiple-succedent (classical) sequent (simply called sequent) is an expression of the form \( \Gamma \Rightarrow \Delta \). We use the same names for the structural and logical inference rules for LK as those for fsCL and LJ, although the forms of these rules are different.
Definition 7
(LK) In this definition, we use the symbol p to represent an arbitrary propositional variable.
The initial sequents of LK are of the form:
The structural inference rules of LK are of the form:

The logical inference rules of LK are of the form:

Remark 8
The main differences between Gentzen’s LK and our LK are as follows. In Gentzen’s LK, (1) the sequent \( \Gamma \Rightarrow \Delta \) is defined using sequences \( \Gamma \) and \( \Delta \) of formulas (instead of multisets of formulas), (2) the formula-based initial sequents of the form \( \alpha \Rightarrow \alpha \) for any formula \(\alpha \) (instead of the propositional variable-based initial sequents) are used, (3) the left and right exchange rules are used, (4) the multiplicative version of (cut) is used, and (5) the multiplicative version of (\({\rightarrow }\)left) is used. These differences do not change the provability of sequents (i.e., Gentzen’s LK and our LK are logically-equivalent) and the admissiblity of the cut rule (i.e., the cut-elimination theorem for Gentzen’s LK implies that of our LK). Similar situations and facts hold for Gentzen’s LJ and our LJ.
Proposition 11
Let L be LJ or LK.
-
1.
For any formula \(\alpha \), L − (cut) \(\vdash \) \( \alpha \Rightarrow \alpha \).
-
2.
The rule (cut) is admissible in cut-free L.
Proof
(1) can be proved by induction on \(\alpha \). (2) is obtained from Gentzen’s original results (Gentzen, 1969) and the cut-free equivalence between the original systems and our systems LJ and LK. \(\square \)
3 Main Theorems
3.1 Equivalence Theorems
Prior to proving a theorem for equivalence between fsCL and classical logic, we have to show a proposition for fsCL and two theorems for LK.
First, we show the following proposition for fsCL.
Proposition 12
The following rules (\(\lnot \)left) and (\(\lnot \)right) are derivable in cut-free fsCL:

Proof
-
1.
Case (\(\lnot \)left):

-
2.
Case (\(\lnot \)right):

\(\square \)
We then show the following explosion-elimination theorem for LK.
Theorem 13
(Explosion-elimination theorem for cut-free LK) The rule (explosion) is admissible in cut-free LK.
Proof
Suppose LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \lnot \alpha \) and LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \alpha \). Then, we obtain LK \(\vdash \) \( \Gamma \Rightarrow \gamma \) using (cut) by:

Thus, by the cut-elimination theorem for LK, we obtain the required fact LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \). \(\square \)
Next, we show the following excluded-middle-elimination theorem for LK.
Theorem 14
(Excluded-middle-elimination theorem for cut-free LK) The rule (ex-middle) is admissible in cut-free LK.
Proof
Suppose LK − (cut) \(\vdash \) \( \lnot \alpha , \Gamma \Rightarrow \gamma \) and LK − (cut) \(\vdash \) \( \alpha , \Gamma \Rightarrow \gamma \). Then, LK \(\vdash \) \( \Gamma \Rightarrow \gamma \) using (cut) by:

where the fact that LK − (cut) \(\vdash \) \( \Rightarrow \lnot \alpha {\vee }\alpha \) is obvious and well-known. Thus, by the cut-elimination theorem for LK, we obtain the required fact LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \). \(\square \)
Remark 9
Theorems 13 and 14 can also be obtained using the proofs of Proposition 3 because the proofs of Theorems 13 and 14 also derive LK-proofs with the addition of the proofs of \( \Rightarrow \lnot \alpha {\vee }\alpha \) and \( \lnot \alpha {\wedge }\alpha \Rightarrow \gamma \). The same theorem as Theorem 13 holds for LJ. But, the same theorem as Theorem 14 does not hold for LJ.
We then obtain the following equivalence theorem.
Theorem 15
(Equivalence between fsCL and classical logic) The system fsCL is indeed a Gentzen-style sequent calculus for classical logic.
Proof
It is sufficient to show the following two items.
-
1.
First, we show that LK (i.e., classical logic) is stronger than or equals to fsCL (i.e., fsCL is a Gentzen-style sequent calculus for a logic weaker than or equals to classical logic). The rule (explosion) of fsCL is admissible in cut-free LK by Theorem 13 (also derivable in LK by Proposition 3 (2)). The rule (ex-middle) of fsCL is admissible in cut-free LK by Theorem 14 (also derivable in LK by Proposition 3 (1)). The negated logical inference rules of fsCL are derivable in LK. The initial sequents of the form \( \lnot p \Rightarrow \lnot p \) are provable in LK. Thus, LK is stronger than or equals to fsCL.
-
2.
Next, we show that fsCL is stronger than or equals to LK (i.e., fsCL is a Gentzen-style sequent calculus for a logic stronger than or equals to classical logic). By Proposition 12, it is obvious that fsCL is stronger than LJ (i.e., intuitionistic logic). Thus, it is sufficient to show that fsCL \(\vdash \) \( \Rightarrow \lnot \alpha {\vee }\alpha \), because it is well-known that classical logic can be obtained from intuitionistic logic by adding the law of excluded middle \(\lnot \alpha {\vee }\alpha \). This is obtained by Proposition 2 (1). Thus, fsCL is stronger than or equals to LK.
\(\square \)
Theorem 16
(Equivalence between fsCL\(_s\) and classical logic)
The system fsCL\(_s\) is indeed a Gentzen-style sequent calculus for classical logic.
Proof
Similar to the proof of Theorem 15. \(\square \)
Theorem 17
(Equivalence among fsCL\(^e\), fsCL\(^s\) and classical logic) The systems fsCL\(^e\) and fsCL\(^s\) are indeed Gentzen-style sequent calculi for classical logic.
Proof
By Theorems 15, 5, and 6. \(\square \)
3.2 Cut-Elimination Theorems
Next, we prove the cut-elimination theorem for fsCL using Africk’s method (1992). Prior to proving this theorem, we have to prove the following lemma.
Lemma 18
For any sequent \( \Gamma \Rightarrow \Delta \), if LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \Delta \), then fsCL − (cut) \(\vdash \) \( \lnot \Delta , \Gamma \Rightarrow \) .
Proof
We prove this lemma by induction on the proofs P of \( \Gamma \Rightarrow \Delta \) in cut-free LK. We show some cases.
-
1.
Case (co-right): The last inference of P is of the form:

By induction hypothesis, we have fsCL − (cut) \(\vdash \) \( \lnot \alpha , \lnot \alpha , \lnot \Delta , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
2.
Case (\({\wedge }\)right): The last inference of P is of the form:

By induction hypotheses, we have fsCL − (cut) \(\vdash \) \( \lnot \alpha , \lnot \Delta , \Gamma \Rightarrow \) and fsCL − (cut) \(\vdash \) \( \lnot \beta , \lnot \Delta , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
3.
Case (\({\vee }\)right): The last inference of P is of the form:

By induction hypothesis, we have fsCL − (cut) \(\vdash \) \( \lnot \alpha , \lnot \beta , \lnot \Delta , \Gamma \Rightarrow \) Then we obtain the required fact by:

-
4.
Case (\({\rightarrow }\)left): The last inference of P is of the form:

By induction hypotheses, we have fsCL − (cut) \(\vdash \) \( \lnot \alpha , \lnot \Delta , \Gamma \Rightarrow \) and fsCL − (cut) \(\vdash \) \( \beta , \lnot \Delta , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
5.
Case (\({\rightarrow }\)right): The last inference of P is of the form:
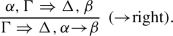
By induction hypothesis, we have fsCL − (cut) \(\vdash \) \( \alpha , \lnot \beta , \lnot \Delta , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
6.
Case (\(\lnot \)left): The last inference of P is of the form:

By induction hypothesis, we obtain the required fact: fsCL − (cut) \(\vdash \) \( \lnot \alpha , \lnot \Delta , \Gamma \Rightarrow \).
-
7.
Case (\(\lnot \)right): The last inference of P is of the form:

By induction hypothesis, we have fsCL − (cut) \(\vdash \) \( \alpha , \lnot \Delta , \Gamma \Rightarrow \). Then we obtain the required fact by:

\(\square \)
Theorem 19
(Cut-elimination theorem for fsCL) The rule (cut) is admissible in cut-free fsCL.
Proof
Suppose fsCL \(\vdash \) \( \Gamma \Rightarrow \gamma \) for any sequent \( \Gamma \Rightarrow \gamma \). Then, we have LK \(\vdash \) \( \Gamma \Rightarrow \gamma \) by Theorem 15. We obtain LK − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \) by the cut-elimination theorem for LK. We thus obtain fsCL − (cut) \(\vdash \) \( \lnot \gamma , \Gamma \Rightarrow \) by Lemma 18. Then, we obtain the required fact fsCL − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \) as follows. Since the case when \( \gamma \) is the empty multiset is obvious, we show only the case when \( \gamma \) is a formula.

\(\square \)
We can also obtain the following cut-elimination theorem for fsCL\(_s\).
Theorem 20
(Cut-elimination theorem for fsCL\(_s\)) The rule (cut) is admissible in cut-free fsCL\(_s\).
Proof
Similar to the proof of Theorem 19. \(\square \)
We also obtain the following cut-elimination theorem for fsCL\(^e\).
Theorem 21
(Cut-elimination theorem for fsCL\(^e\)) The rule (cut) is admissible in cut-free fsCL\(^e\).
Proof
Suppose fsCL\(^e\) \(\vdash \) \( \Gamma \Rightarrow \gamma \). Then, we have fsCL \(\vdash \) \( \Gamma \Rightarrow \gamma \) because fsCL\(^e\) is a subsystem of fsCL. By Theorem 19, we obtain fsCL − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \). Thus, we obtain the required fact fsCL\(^e\) − (cut) \(\vdash \) \( \Gamma \Rightarrow \gamma \) by Theorem 5. \(\square \)
Remark 10
We can also obtain the following formula-based weak cut-elimination theorem for fsCL\(^s\).
For any formula \(\alpha \), if fsCL\(^s\) \(\vdash \) \( \Rightarrow \alpha \), then fsCL\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \).
This theorem can be proved as follows. Suppose fsCL\(^s\) \(\vdash \) \( \Rightarrow \alpha \). Then, we have fsCL \(\vdash \) \( \Rightarrow \alpha \) because fsCL\(^s\) is a subsystem of fsCL. By Theorem 19, we obtain fsCL − (cut) \(\vdash \) \( \Rightarrow \alpha \). Thus, we obtain the required fact fsCL\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \) by Theorem 6.
We also obtain the following cut-elimination theorem for GN3.
Theorem 22
(Cut-elimination theorem for GN3) The rule (cut) is admissible in cut-free GN3.
Proof
(Sketch). We can prove this theorem by using a similar method as introduced by Gentzen (1969) for LJ. We now present a rough sketch of the proof. Let GN3\(^{\sharp }\) be a sequent calculus similar to Gentzen’s LJ. Namely, GN3\(^{\sharp }\) is based on the formula-sequence-based sequent, the formula-based initial sequent, the multiplicative implication left rule, the multiplicative cut rule of the form:

and the left exchange rule of the form:

Then, GN3\(^{\sharp }\) is logically-equivalent to GN3 and, since (m-cut) and (cut) are deductively equivalent, the cut-elimination for GN3\(^{\sharp }\) implies that for GN3 (i.e., to show the cut-elimination for GN3, it is sufficient to show that for GN3\(^{\sharp }\)). Next, we introduce a sequent calculus GN3\(^{\sharp \sharp }\) that is obtained from GN3\(^{\sharp }\) by replacing the multiplicative cut rule with the following mix rule:

where \( \Pi \) has at least one occurrence of \(\alpha \), and \( \Pi _{\alpha }\) is a sequence of formulas obtained from \( \Pi \) by deleting all occurrences of \(\alpha \). Then, GN3\(^{\sharp \sharp }\) is logically-equivalent to GN3\(^{\sharp }\) and GN3, and the mix-elimination for GN3\(^{\sharp \sharp }\) implies the cut-elimination for GN3\(^{\sharp }\) and GN3 (i.e., to show the cut-elimination for GN3, it is sufficient to show the mix-elimination for GN3\(^{\sharp }\)). Thus, we show the admissiblity of (mix) in GN3\(^{\sharp \sharp }\) below. The standard notions of rank and grade are assumed in the following discussion. We now consider the proof P of the form:

where \(P_1\) and \(P_2\) have no occurrence of (mix). Then, it is sufficient to show that (mix) can be eliminated by proof transformation. We prove this by double induction on the rank and grade. We show some cases below.Footnote 6
-
1.
The last inference of the left upper sequent of (mix) is (explosion):

This proof can be transformed into the following mix-free proof:

-
2.
The last inference of the right upper sequent of (mix) is (explosion):

This proof can be transformed into the following proof:

Then, (mix) in this proof can be eliminated because the rank concerning this mix is less than that of the proof presented above.
\(\square \)
Remark 11
We can also obtain the following formula-based weak cut-elimination theorem for GN3\(^s\).
For any formula \(\alpha \), if GN3\(^s\) \(\vdash \) \( \Rightarrow \alpha \), then GN3\(^s\) − (cut) \(\vdash \) \( \Rightarrow \alpha \).
This theorem can be proved in a similar way as the proof as presented in Remark 10. We use Theorems 22 and 8.
We also obtain the following cut-elimination theorem for GLP.
Theorem 23
(Cut-elimination theorem for GLP) The rule (cut) is admissible in cut-free GLP.
Proof
(Sketch). Similar to the proof of Theorem 22. We assume the same setting as that for GN3. Namely, we introduce the systems GLP\(^{\sharp }\) and GLP\(^{\sharp \sharp }\) that are logically-equivalent to GLP. We show the mix-elimination for GLP\(^{\sharp \sharp }\) by double induction on the grade and rank. We show some cases below.
-
1.
The last inference of the left upper sequent of (mix) is (ex-middle):

This proof can be transformed into the following proof:

Then, (mix) in this proof can be eliminated because the rank concerning this mix is less than that of the proof presented above.
-
2.
The last inference of the right upper sequent of (mix) is (ex-middle):
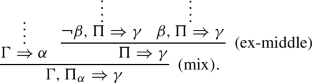
-
(a)
Case \(\alpha \not \equiv \beta \) and \(\alpha \not \equiv \lnot \beta \): This proof can be transformed into the following proof:

Then, (mix) in this proof can be eliminated because the rank concerning this mix is less than that of the proof presented above
-
(b)
Case \(\alpha \equiv \lnot \beta \): This proof can be transformed into the following proof:

Then, (mix) in this proof can be eliminated because the rank concerning this mix is less than that of the proof presented above
-
(c)
Case \(\alpha \equiv \beta \): This proof can be transformed into the following proof:

Then, (mix) in this proof can be eliminated because the rank concerning this mix is less than that of the proof presented above.
-
(a)
\(\square \)
Remark 12
Let GBD, GK\(_3\), and GP be the \({\rightarrow }\)-less parts of GN4, GN3, and GLP, respectively. Then, GBD, GK\(_3\), and GP are falsification-aware single-succedent Gentzen-style sequent calculi for the logics BD, K\(_3\), and LP, respectively. By the cut-elimination theorems for GN4, GN3, and GLP, we can obtain the fact that GN4, GN3, and GLP are conservative extensions of GBD, GK\(_3\), and GP, respectively. Then, we can also obtain the cut-elimination theorems for GBD, GK\(_3\), and GP.
3.3 Glivenko Theorem
Next, we prove the Glivenko theorem for fsCL. Prior to proving this theorem, we have to prove the following lemma.
Lemma 24
For any sequent \( \Gamma \Rightarrow \gamma \), if fsCL \(\vdash \) \( \Gamma \Rightarrow \gamma \), then LJ \(\vdash \) \( \lnot \gamma , \Gamma \Rightarrow \).
Proof
We prove this lemma by induction on the proofs P of \( \Gamma \Rightarrow \gamma \) in fsCL. We show some cases.
-
1.
Case (ex-middle): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \lnot \alpha , \lnot \gamma , \Gamma \Rightarrow \) and LJ \(\vdash \) \( \alpha , \lnot \gamma , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
2.
Case (explosion): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \lnot \lnot \alpha , \Gamma \Rightarrow \) and LJ \(\vdash \) \( \lnot \alpha , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
3.
Case (\(\lnot \lnot \)left): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \alpha , \lnot \gamma , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
4.
Case (\(\lnot \lnot \)right): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \lnot \alpha , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
5.
Case (\(\lnot {\wedge }\)left): The last inference of P is of the form:

By induction hypotheses, we have LJ \(\vdash \) \( \lnot \alpha , \lnot \gamma , \Gamma \Rightarrow \) and LJ \(\vdash \) \( \lnot \beta , \lnot \gamma , \Gamma \Rightarrow \). Then we obtain the required fact by:

where R is:

and S can be straightforwardly obtained (i.e., \( \lnot (\alpha {\wedge } \beta ), \lnot \lnot \alpha {\wedge }\lnot \lnot \beta \Rightarrow \) is provable in LJ).
-
6.
Case (\(\lnot {\wedge }\)right1): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \lnot \lnot \alpha , \Gamma \Rightarrow \). Then we obtain the required fact by:

where Q is:

-
7.
Case (\(\lnot {\rightarrow }\)left1): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \alpha , \lnot \gamma , \Gamma \Rightarrow \). Then we obtain the required fact by:

-
8.
Case (\(\lnot {\rightarrow }\)left2): The last inference of P is of the form:

By induction hypothesis, we have LJ \(\vdash \) \( \lnot \beta , \lnot \gamma , \Gamma \Rightarrow \). Then we obtain the required fact by:

where Q is:

-
9.
Case (\(\lnot {\rightarrow }\)right): The last inference of P is of the form:
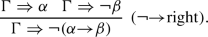
By induction hypotheses, we have LJ \(\vdash \) \( \lnot \alpha , \Gamma \Rightarrow \) and LJ \(\vdash \) \( \lnot \lnot \beta , \Gamma \Rightarrow \). Then we obtain the required fact by:

where Q is:

\(\square \)
Theorem 25
(Glivenko theorem for fsCL) For any formula \(\alpha \), fsCL \(\vdash \) \( \Rightarrow \alpha \) if and only if LJ \(\vdash \) \( \Rightarrow \lnot \lnot \alpha \).
Proof
-
1.
(\(\Longrightarrow \)): Suppose fsCL \(\vdash \) \( \Rightarrow \alpha \). Then, we have that LJ \(\vdash \) \( \lnot \alpha \Rightarrow \) by Lemma 24. Thus, we obtain the required fact LJ \(\vdash \) \( \Rightarrow \lnot \lnot \alpha \) by applying (\(\lnot \)right).
-
2.
(\(\Longleftarrow \)): Suppose LJ \(\vdash \) \( \Rightarrow \lnot \lnot \alpha \). Then, we have fsCL \(\vdash \) \( \Rightarrow \lnot \lnot \alpha \), because LJ (intuitionistic logic) is regarded as a subsystem of fsCL (classical logic). Thus, we obtain the required fact fsCL \(\vdash \) \( \Rightarrow \alpha \) by:

\(\square \)
4 Related Works
Some single-succedent Gentzen-style sequent calculi for classical logic can be obtained from Gentzen’s LJ for intuitionistic logic by adding one of the following inference rules.Footnote 7

The rule (Peirce), which corresponds to the Peirce formula \(((\alpha {\rightarrow } \beta ){\rightarrow }\alpha ){\rightarrow }\alpha \), was introduced and studied by Curry (1963); Felscher (1975); Gordeev (1987); Africk (1992). The cut-elimination theorem for LJ + (Peirce) was proved and investigated by them. The subformula property for a version of LJ + (Peirce) without the falsity constant \(\bot \) was shown by Gordeev. Specifically, Gordeev (1987) showed that \( \beta \) in (Peirce) can be restricted to a subformula of formulas in (\( \Gamma , \alpha \)).
The rule (r-Peirce) was introduced by Curry (1963) and further studied by Gordeev (1987) and Africk (1992). They then proved the cut-elimination theorem for LJ + (r-Peirce). Through the cut-elimination theorem, a weak subformula property allowing negation formulas can be obtained for LJ + (r-Peirce). A simple embedding-based proof of the cut-elimination theorems for LJ + (Peirce) and LJ + (r-Peirce) was proposed by Africk (1992). This method is used in the present study to prove the cut-elimination theorem for fsCL.
The rule (r-Peirce) is regarded as an instance of (ex-middle) because it is derivable in cut-free fsCL by:

Similar to (ex-middle), the rule (r-Peirce) is admissible in cut-free LK. This can be shown in a similar manner as that for (ex-middle) because (r-Peirce) can be derived using (cut) and (\(\lnot \)right) in LK.
The rule (Raa) was studied by Negri and von Plato (2001). As mentioned in Negri and von Plato (2001), obtaining a direct proof of cut-elimination theorems for some Gentzen-style sequent calculi with (Raa) is difficult. They showed that the structural rules, including the cut rule, are admissible in a Gentzen-style sequent calculus G3ip (for intuitionistic logic) with an inference rule of the form:

where p is a propositional variable. They also showed that G3ip + (Raa-at) is not a system of classical logic but rather a system of intermediate logic referred to as stable logic.
Some single-succedent Gentzen-style sequent calculi for classical logic can also be obtained from LJ by adding one of the following inference rules.

where \( \gamma \) is a formula or the empty multiset and p is a propositional variable.
The rules (ex-middle) and (ex-middle-at) were introduced by von Plato (1999); Negri and von Plato (2001), and (ex-middle) is re-investigated in the present study. In von Plato (1999); Negri and von Plato (2001), he showed that a cut rule and (ex-middle) are admissible in some versions of cut-free LJ with (ex-middle-at). Through these results, he proved that a weak subformula property allowing propositional variables and negations of propositional variables holds for these versions.Footnote 8
Some single-succedent Gentzen-style sequent calculi for classical logic can also be obtained from LJ by adding one of the following inference rules, which are slightly modified versions of the previous rules.

where \( \gamma \) is a formula or the empty multiset.
The rules (g-Dmt) and (g-Peirce), which Kamide (2005a) referred to as the generalized Dummett rule and generalized Peirce rule, respectively, are generalized versions of (ex-middle). The rule (s-Peirce), which in Kamide (2005a) was referred to as the specialized Peirce rule, is a specialized version of (r-Peirce) and (Raa). The rule (s-Peirce) was originally studied by Gordeev (1987) based on a different cut-free formulation of LJ with a specialized negation-cut rule. The rule (s-Peirce) of Gordeev is not very different from (Raa) of Negri and von Plato, but (s-Peirce) has the advantage of being able to derive a weak subformula property without \(\bot \). The cut-elimination theorems for LJ + (g-Dmt), LJ + (g-Peirce), and LJ + (s-Peirce) were proved by Kamide (2005a) using Africk’s proof method (1992). He also showed that LJ + (s-Peirce) has a weak subformula and Craig interpolation properties. Note that \( \beta \) in (g-Dmt) and (g-Peirce) can be restricted to \(\bot \) and that \( \delta \) in (g-Dmt) can be restricted to \(\top \) (i.e. the provability is not changed by these restrictions). The cut-elimination theorem holds for LJ with one of these restricted rules. Similar to (ex-middle), the rule (s-Peirce) is admissible in cut-free LK. This can be shown in a similar manner as for (ex-middle) because (s-Peirce) can be derived using (cut) and (\(\lnot \)right) in LK.
A single-succedent Gentzen-style sequent calculus for Dummett’s LC can be obtained from LJ by adding the following inference rule, which is regarded as an instance of (g-Dmt).

where \( \gamma \) is a formula or the empty multiset. The rule (Dmt) corresponds to the law of linearity \((\alpha {\rightarrow } \beta ) \vee ( \beta {\rightarrow }\alpha )\). The rule (Dmt) and a multiple-succedent Gentzen-style sequent calculus, G3ipm with (Dmt), for Dummett’s LC were discussed in Negri and von Plato (2001).
We can consider the following rules, which are restricted and specialized versions of (Dmt).

However, we have yet to obtain the cut-elimination theorems for LJ + (r-Dmt) and LJ + (s-Dmt), as they remain open problems.
A single-succedent Gentzen-style sequent calculus for the logic of weak excluded middle can be obtained from LJ by adding the following inference rule, which is regarded as an instance of (ex-middle).

where \( \gamma \) is a formula or the empty multiset. The rule (we-ex-middle) corresponds to the law of weak excluded middle \(\lnot \lnot \alpha {\vee }\lnot \alpha \). The cut-elimination theorem for LJ + (we-ex-middle) was shown by Negri and von Plato (2001).
We can consider the following rules, which are restricted and specialized versions of (we-ex-middle).

However, we have yet to obtain the cut-elimination theorems for LJ + (w-r-Peirce) and LJ + (w-s-Peirce), as they remain open problems.
5 Concluding Remarks
In this study, we introduced the falsification-aware single-succedent Gentzen-style sequent calculus fsCL for classical logic. The proposed calculus fsCL was obtained in a simple manner from the existing falsification-aware single-succedent Gentzen-style sequent calculus GN4 for Nelson’s paradefinite (or paraconsistent) four-valued logic N4 (Almukdad & Nelson, 1984; Nelson, 1949) by adding the rules (explosion), (ex-middle), and (we-right). The rules (explosion) and (ex-middle), which are referred to as the rules of explosion and excluded middle, correspond to the principle of explosion and the law of excluded middle, respectively. Similar to the cut rule in Gentzen’s LK for classical logic, we addressed the explosion- and excluded-middle-elimination theorems for LK. These theorems state that the rules (explosion) and (ex-middle) are admissible in cut-free LK. We then proved the cut-elimination and Glivenko theorems for fsCL.
We also introduced the falsification-aware single-succedent Gentzen-style sequent calculi GN3 and GLP for Nelson’s paracomplete three-valued logic N3 (Almukdad & Nelson, 1984; Nelson, 1949) and an extension ELP (i.e., PI\(^s\) (Batens, 1980), RM\(^{\supset }_3\) (Avron, 1986), Pac (Avron, 1991), or PCont (Rozonoer, 1989)) of the logic of paradox LP (Asenjo, 1966; Priest, 1979), respectively. The proposed calculus GN3 was obtained from GN4 by adding (explosion) and (we-right), and the proposed calculus GLP was obtained from GN3 by replacing (explosion) with (ex-middle). We then proved the cut-elimination theorems for GN3 and GLP.
We also observed that some falsification-aware single-succedent Gentzen-style sequent calculi for Belnap–Dunn logic BD (Belnap, 1977a, b; Dunn, 1976, 2019), Kleene’s strong three-valued logic K\(_3\) (Kleene, 2009), and the logic of paradox LP (Priest, 1979) can be obtained as subsystems of the \({\rightarrow }\)-less fragment of fsCL by deleting (explosion), (ex-middle), and/or (we-right). Thus, we showed that the proposed falsification-aware single-succedent Gentzen-style framework, which is constructed based on (explosion) and (ex-middle), is regarded as a unified and modular framework for formalizing and handling classical, paradefinite, paraconsistent, and paracomplete logics.
Figure 1 shows the relationship among the logics discussed in this study. CL and CL\(^-\) in Fig. 1 denote classical logic and the \({\rightarrow }\)-less fragment of classical logic, respectively. In addition, exp and ex-m in Fig. 1 denote the principle of explosion and the law of excluded middle, respectively. The arrow denoted as \(L_1 \longrightarrow L_2\) in Fig. 1 indicates that \(L_2\) is an extension of \(L_1\) (i.e., \(L_1 \subseteq L_2\)). For example, K\(_3\) and LP are obtained from BD by adding the principle of explosion and the law of excluded middle, respectively, and BD, K\(_{3}\), and LP are regarded as the \({\rightarrow }\)-less fragment of N4, the \({\rightarrow }\)-less fragment of N3, and the \({\rightarrow }\)-less fragment of ELP, respectively.
In the following, we illustrate another approach to falsification-aware formal systems. Some falsification-aware systems based on Łukasiewicz-style refutation systems have been proposed (Łukasiewicz, 1987; Goranko, 1994; Skura, 1995, 2002, 2011, 2017; Goranko, 2019; Goranko et al., 2020; Moore, 2021). Compared with the proposed falsification-aware single-succedent Gentzen-style sequent calculi, Łukasiewicz-style refutation systems have the following inference rules, referred to as reverse substitution and reverse modus ponense, respectively.

where \(\dashv \) and \(\vdash \) represent refutation and verification, respectively, and \(e(\alpha )\) represents a substitution instance of \(\alpha \). The rule of reverse modus ponense intuitively means that if a conditional is provable and its consequent is refutable, then its antecedent is refutable.
For example, some Łukasiewicz-style refutation systems (Łukasiewicz, 1987) for modal logics including S4 were introduced in Goranko (1994); Skura (1995, 2002). A Łukasiewicz-style refutation system for Wansing’s nonmonotonic modal logic W (Wansing, 1995) was introduced by Skura (2017), wherein the decidability and finite model property were proved for W using the refutation system. The logic W is regarded as an extension of Nelson’s N4. A basic theory (and a meta proof theory) for hybrid deductive-refutation systems was proposed by Goranko (2019), wherein the concept of a hybrid derivation system of natural deduction for classical logic was illustrated. Hybrid deductive-refutation systems for FDE-based logics (i.e., logics based on first-degree entailment logic or Belnap–Dunn logic) were introduced and investigated by Moore (2021), wherein a unified framework for formalizing and handling classical, paradefinite, paraconsistent, and paracomplete FDE-based logics was obtained. The present study was inspired by this idea of a unified framework. For a comprehensive survey of Łukasiewicz-style refutation systems, see (Goranko et al., 2020).
Finally, we address certain problems that have yet to be solved. The first problem is to construct a cut-free falsification-aware single-succedent Gentzen-style sequent calculus for intuitionistic logic. This type of calculus cannot be obtained based on GN4 because Gentzen’s LJ is not an extension of GN4. The second problem is to construct cut-free falsification-aware single-succedent Gentzen-style sequent calculi for some intermediate logics including Dummett’s LC and the logic of weak excluded middle. The final problem is to construct modal extensions of fsCL, GN4, and GN3.
Notes
(cut) is well-known to be a structural rule. However, the proposal for saying that (explosion) and (ex-middle) are structural rules has an issue. These two rules involve the negation and the validity of the rules depends on the definition of the negation. Thus, in this aspect, they seem to rather logical inference rules. Besides, the corresponding properties of paraconsistency and paracompleteness are the properties that deal not only with consequence relation, but also with the negation. Thus, the issue with classification of these rules is not clear or simple.
The logic N4 was originally introduced as a first-order predicate logic refereed to as N\(^-\) (Almukdad & Nelson, 1984; Nelson, 1949) which has the following axiom schemes: \(\lnot \forall x \alpha (x) \leftrightarrow \exists x \lnot \alpha (x)\) and \(\lnot \exists x \alpha (x) \leftrightarrow \forall x \lnot \alpha (x)\).
Avron also used the name Pac for the implication-less fragment of this logic.
Since the cut-elimination theorem for GN4 holds, it is sufficient to check the additional cases for (we-right) and (explosion) in GN3.
(Peirce), (r-Peirce), (Raa), as well as (ex-middle) can be seen as the sequent calculus rule versions of the corresponding natural deduction rules. For example, (Raa) is the sequent calculus rule version of the well-known natural deduction rule of the form:
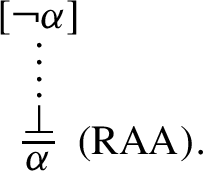
In von Plato (1999); Negri and von Plato (2001), he also introduced the following natural deduction rules (Nem) and (Nem-at) that correspond to (ex-middle) and (ex-middle-at), respectively.
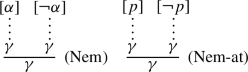
where p is a propositional variable. He construct natural deduction systems (for classical logic) with these rules and proved a normalization theorem for the natural deduction system with (Nem-at).
References
Africk, H. (1992). Classical logic, intuitionistic logic, and the Peirce rule. Notre Dame Journal of Formal Logic, 33(2), 229–235.
Almukdad, A., & Nelson, D. (1984). Constructible falsity and inexact predicates. Journal of Symbolic Logic, 49(1), 231–233.
Arieli, O., & Avron, A. (2016) Minimal paradefinite logics for reasoning with incompleteness and inconsistency. In Proceedings of the 1st international conference on formal structures for computation and deduction (FSCD), Leibniz International Proceedings in Informatics (LIPIcs) 52, pp. 7:1-7:15.
Arieli, O., & Avron, A. (2017). Four-valued paradefinite logics. Studia Logica, 105(6), 1087–1122.
Asenjo, F. G. (1966). A calculus of antinomies. Notre Dame Journal of Formal Logic, 7, 103–106.
Asenjo, F. G., & Tamburino, J. (1975). Logic of antinomies. Notre Dame Journal of Formal Logic, 16(1), 17–44.
Avron, A. (1986). On an implicational connective of RM. Notre Dame Journal of Formal Logic, 27(2), 201–209.
Avron, A. (1991). Natural 3-valued logics: Characterization and proof theory. Journal of Symbolic Logic, 61(1), 276–294.
Avron, A. (2003) Classical Gentzen-type methods in propositional many-valued logics. Studies in Fuzziness and Soft Computing, pp. 117–155
Avron, A., Arieli, O., & Zamansky, A. (2018). Theory of effective propositional paraconsistent logics. Studies in Logic - Mathematical Logic and Foundations, Volume 75, 550 pages, College Publications.
Batens, D. (1980). Paraconsistent extensional propositional logics. Logique et Anal., 23(90–91), 195–234.
Belnap, N. D. (1977). A useful four-valued logic, In Modern uses of multiple-valued logic, G. Epstein and J. M. Dunn (eds.), Dordrecht: Reidel, pp. 5–37.
Belnap, N. D. (1977). How a computer should think. In G. Ryle (ed.) Contemporary aspects of philosophy, Oriel Press, Stocksfield, pp. 30–56
Béziau, J.-Y. (2009) Bivalent semantics for De Morgan logic (The uselessness of four-valuedness), In W.A. Carnieli, M.E. Coniglio and I.M. D’Ottaviano (Eds.), The many sides of logic, pp. 391–402, College Publications.
Bolotov, A., & Shangin, V. (2012). Natural deduction system in paraconsistent setting: Proof search for PCont. Journal of Intelligent Systems, 21(1), 1–24.
Czermak, J. (1977). A remark on Gentzen’s calculus of sequents. Notre Dame Journal of Formal Logic, 18, 471–474.
Curry, H. B. (1963). Foundations of mathematical logic. McGraw-Hill.
da Costa, N. C. A. (1974). On the theory of inconsistent formal systems. Notre Dame Journal of Formal Logic, 15(4), 497–510.
D’Ottaviano, I. M. L., & da Costa, N. C. A. (1970). Sur un probléme de Jaśkowski. Comptes Rendus Acad. Sci. Paris., 270A, 1349–1353.
Dunn, J. M. (1976). Intuitive semantics for first-degree entailment and ‘coupled trees’. Philosophical Studies, 29(3), 149–168.
Dunn, T. J. M. (2019) The Algebra of intensional logics, a republication of a Ph.D. thesis, which was originally defended at the University of Pittsburgh in 1966, College Publications, London, UK.
Felscher, W. (1975). Kombinatorische Konstruktionen mit beweisen und schnittelimination. Lecture Notes in Mathematics, 500, 119–151.
Gentzen, G. (1969) Collected papers of Gerhard Gentzen. In M. E. Szabo (Ed.), Studies in logic and the foundations of mathematics, North-Holland (English translation).
Goodman, N. D. (1981). The logic of contradiction. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 27, 119–126.
Goranko, V. (1994). Refutation systems in modal logic. Studia Logica, 53, 299–324.
Goranko, V. (2019). Hybrid deduction-refutation systems. Axioms, 8(4) 118–119.
Goranko, V., Pulcini, G., Skura, T. (2020) Refutation systems: An overview and some applications to philosophical logics, In Knowledge, proof and dynamics, pp. 173–197.
Gordeev, L. (1987). On cut elimination in the presence of Peirce rule. Archiv für Mathematische Logik und Grundlagenforsch, 26, 147–164.
Horn, L. R., Wansing, H. (2017). Negation, The Stanford Encyclopedia of Philosophy (Spring 2017 Edition), Edward N. Zalta (editor), Last modified on January, https://plato.stanford.edu/archives/spr2017/entries/negation/.
Kamide, N. (2005). Cut-free single-succedent systems revisited. Bulletin of the Section of Logic, 34(3), 165–175.
Kamide, N. (2005). Natural deduction systems for Nelson’s paraconsistent logic and its neighbors. Journal of Applied Non-Classical Logics, 15(4), 405–435.
Kamide, N. (2018). Proof theory of paraconsistent quantum logic. Journal of Philosophical Logic, 47(2), 301–324.
Kamide, N. (2022). Falsification-aware semantics and sequent calculi for classical logic. Journal of Philosophical Logic, 51(1), 99–126.
Kamide, N. (2023). Falsification-aware calculi and semantics for normal modal logics including S4 and S5. Journal of Logic, Language and Information, 32(3), 395–440.
Kamide, N. (2023). Refutation-aware Gentzen-style calculi for propositional until-free linear-time temporal logic. Studia Logica, 111(6), 979–1014.
Kamide, N., & Wansing, H. (2012). Proof theory of Nelson’s paraconsistent logic: A uniform perspective. Theoretical Computer Science, 415, 1–38.
Kamide, N., Wansing, H. (2015). Proof theory of N4-related paraconsistent logics. Studies in Logic, 54, College Publications, pp. 1–401.
Kapsner, A. (2014). Logics and falsifications: A new perspective on constructivist semantics. Trends in Logic Book 40, Springer.
Kürbis, N., & Petrukhin, Y. (2021). Normalisation for some quite interesting many-valued logics. Logic and Logical Philosophy, 30(3), 493–534.
Kleene, S. C. (2009). Introduction to Metamathematics (with a new foreworded by M. Beeson). ISHI Press International.
Łukasiewicz, J. (1987). Aristotle’s syllogistic from the standpoint of modern formal logic, Oxford, 1951 (Aristotle’s syllogistic from the standpoint of modern formal logic - Greek & Roman philosophy, Taylor & Francis).
Łukowski, P. (2002). A deductive-reductive form of logic: General theory and intuitionistic case. Logic and Logical Philosophy, 10, 59–78.
Moore, E. (2021). Hybrid deduction-refutation systems for FDE-based logics. The Australasian Journal of Logic, 18(6), 597–615.
Negri, S., & von Plato, J. (2001). Structural proof theory. Cambridge University Press.
Nelson, D. (1949). Constructible falsity. Journal of Symbolic Logic, 14, 16–26.
Odintsov, S. P. (2002). On the embedding of Nelson’s logics. Bulletin of the Section of Logic, 31(4), 241–248.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8(1), 219–241.
Priest, G. (2002) Paraconsistent logic. In D. Gabbay and F. Guenthner (Eds.) Handbook of Philosophical Logic (Second Edition), vol. 6, Kluwer, Dordrecht, pp. 287–393.
Rauszer, C. (1974). A formalization of the propositional calculus of H-B logic. Studia Logica, 33, 23–34.
Rauszer, C. (1977). Applications of Kripke models to Heyting–Brouwer logic. Studia Logica, 36, 61–71.
Rauszer, C. (1980). An algebraic and Kripke-style approach to a certain extension of intuitionistic logic. Dissertations Mathematicae, Polish Scientific Publishers, pp. 1–67.
Rozonoer, L. I. (1989). On interpretation of inconsistent theories. Information Sciences, 47(3), 243–266.
Shramko, Y. (2005). Dual intuitionistic logic and a variety of negations: The logic of scientific research. Studia Logica, 80(2–3), 347–367.
Shramko, Y. (2016). A modal translation for dual-intuitionistic logic. Review of Symbolic Logic, 9(2), 251–265.
Skura, T. F. (1995). A Łukasiewicz-style refutation system for the modal logic S4. Journal of Philosophical Logic, 24, 573–582.
Skura, T. F. (2002). Refutations, proofs, and models in the modal logic K4. Studia Logica, 70(2), 193–204.
Skura, T. F. (2011). Refutation systems in propositional logic. Handbook of Philosophical Logic, 16, 115–157.
Skura, T. F. (2017). Refutations in Wansing’s logic. Reports on Mathematical Logic, 52, 83–99.
Urbas, I. (1996). Dual-intuitionistic logic. Notre Dame Journal of Formal Logic, 37(3), 440–451.
von Plato, J. (1999). Proof theory of full classical propositional logic. Manuscript, 16 pages.
Wansing, H. (1993). The logic of information structures. Lecture Notes in Artificial Intelligence 681, 163 pages.
Wansing, H. (1995). Semantics-based nonmonotonic inference. Notre Dame Journal of Formal Logic, 36, 44–54.
Wansing, H. (2010). Proofs, disproofs, and their duals. Advances in Modal Logic, 8, 483–505.
Wansing, H. (2016). Falsification, natural deduction and bi-intuitionistic logic. Journal of Logic and Computation, 26(1), 425–450.
Acknowledgements
We would like to thank the anonymous referees for their valuable comments. Specifically, the relationship among ELP, PI\(^s\), RM\(^{\supset }_3\), Pac, and PCont was pointed out by a referee. This research was supported by JSPS KAKENHI Grant Number 23K10990.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kamide, N. Rules of Explosion and Excluded Middle: Constructing a Unified Single-Succedent Gentzen-Style Framework for Classical, Paradefinite, Paraconsistent, and Paracomplete Logics. J of Log Lang and Inf 33, 143–178 (2024). https://doi.org/10.1007/s10849-024-09416-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-024-09416-6