A joint particle filter and expectation maximization approach to machine condition prognosis

Abstract

This paper presents a probabilistic model based approach for machinery condition prognosis based on particle filter by integrating physical knowledge with in-process measurements into a state space framework to account for uncertainty and nonlinearity in machinery degradation process. One limitation of conventional particle filter is that condition prognosis is performed based on the model with predetermined parameters obtained from simulation studies or lab-controlled tests. Due to the stochastic nature of machinery defect propagation under varying operating conditions, model parameters may vary in practice which causes prediction errors. To address it, an integrated state prediction and parameter estimation framework based on particle filter and expectation-maximization algorithm is formulated and investigated. The model parameters are adaptively estimated based on expectation-maximization algorithm utilizing hidden degradation state and available in-process measurements. Particle filter is then performed on the identified model with estimated parameters following Bayesian inference scheme to improve the robustness and accuracy of machinery condition prognosis. The effectiveness of the developed method is demonstrated through a simulation study and an experimental run-to-failure bearing test in a wind turbine.

Introduction

Machinery condition prognosis refers to the estimation of time to failure of the machine, as well as the risk associated with existing or future failure modes (Heng et al. 2009). It is critical to establishing optimized maintenance plans to enhance production, minimize costly downtime, and avoid catastrophic damage. Different sensing techniques have been integrated into the manufacturing system for timely acquisition of its working status to improve the system reliability. According to the sensing parameters, these sensing techniques can be categorized into direct sensing approach and indirect sensing approach (Teti et al. 2010). In the direct sensing approach, the actual quantities, such as crack length, tool wear width, etc. are measured. Such direct sensing approach could directly indicate the machinery condition, however, it is usually performed offline, and usually interrupts the normal operation of the machine. On the contrary, the auxiliary in-process quantities such as force, vibration, acoustic emission, and motor current, are measured in the indirect sensing approach. The indirect sensing approach can online monitor the machinery, thus it is more suitable for practical applications. Since the indirect sensing parameters are the indirect indicators of machinery condition, the machinery condition is then deduced using different data processing techniques.

Fig. 1

Comparison of different approaches for machinery condition prognosis

Numerous efforts have been made to develop a variety of methods for machinery condition prognosis. In Jurkovie et al. (2016), the performance of three different machine learning methods including support vector regression, polynomial regression and artificial neural network have been investigated for the prediction of independent output cutting parameters in a high speed turning process. In Vogl et al. (2016), it reviews the challenges, needs, methods and best practice for PHM within manufacturing systems highlighted by diagnostics, prognostics, dependability analysis, data management, and business. An integrative method of logical analysis and non-parametric cumulative incidence functions is presented to address the multiple failure modes issue in prognosis and the results shows the competitive performance of presented method over neural network and support vector machine (Ragab et al. 2016). The prognostics-based decision support methods are summarized for condition based maintenance and a decision tree learning method is provided to guide the model selection (Bousdekis et al. 2016).

According to the utilization of sensing information, these prognosis techniques can be categorized into physics based approach, data driven approach, and model based approach (also known as physics-data integrative approach) Peng et al. (2010) as illustrated in Fig. 1. Physics based approach typically uses empirical models to describe system physics and these empirical models are usually expressed by a series of ordinary or partial differential equations (Peng et al. 2010). For instance, the bearing degradation could be described by Paris’ formula (Paris et al. 1961) or empirical equation L10 to model the crack growth or predict spalling initiation during the bearing life test. Data driven approach derives model from online and offline historical measurements based on artificial intelligence techniques without physical knowledge needed (Heng et al. 2009; Lever et al. 1997). Different artificial intelligence techniques have been investigated for machinery condition prognosis, including artificial neural network (Zhang et al. 2013), support vector regression (Benkedjouh et al. 2015), ARMA/GARCH model (Pham and Yang 2010), hidden Markov model (Peng and Dong 2011), Naïve Bayes (Mehta et al. 2015), fuzzy logic (Gokulachandran and Mohandas 2015), and adaptive neuro-fuzzy inference system (Sarkeyli et al. 2015), etc.

As shown in Fig. 1, physics based approach usually utilizes curve fitting to identify parameters in an empirical equation using offline sensing measurements through extensive experiments. The machinery condition prognosis is then estimated based on deterministic model with determined parameters. In practice, physics based approach may not be the most practical solution since the parameters in the model are validated by large sets of data (Peng et al. 2010). However, it is usually difficult or impossible to obtain sufficient offline measurement data in real application. Compared with physics based approach, data driven approach may be more available in some practical cases in which it is relatively easier to gather data than to build accurate physics models (Heng et al. 2009). However, there are still some limitations. (1) A large amount of historical data (more than physics based techniques needed) is required to train the model in data driven approach and the performance of prediction highly relies on the quality of training data. But it is usually a costly and time consuming process to obtain the required run-to-failure experimental data. (2) The model is derived in a deterministic fashion and only applicable under specific operating conditions. On the other hand, physics based approach and data driven approach do not consider the uncertainty due to component variation and varying operating conditions in the model construction, and are usually difficult to quantify the uncertainty in the mechanical degradation process.

In comparison, model based approach takes advantage of the merits in physics based approach and data driven approach, and addresses their limitations. Given that the physical knowledge governing defect propagation has been established in physics based approach, model based approach integrates physical knowledge and in-process measurements into a state space model. Since the machinery defect status is usually not directly accessible using in-process measurements, defect status needs to be estimated or predicted from in-process measurements, to which Bayesian inference provides a rigorous mathematic solution. Based on Bayesian inference, the present defect status is estimated based on previous defect status in one-step-ahead prediction. The estimated defect status is then updated using in-process measurements based on Bayes rule. For multi-step-ahead prediction, recursive process is applied to predict the defect propagation in the desired prediction horizon. Depending on the system type and noise assumption, different methods including Kalman filter (for linear system and Gaussian noise) (Kalman 1960), extended Kalman filter (for weak nonlinear system and Gaussian noise) (Julier and Uhlmann 1997), and particle filter (for nonlinear system and non-Gaussian noise) (Gordon et al. 1993) have been investigated to implement model based prognosis. Different from the above-mentioned two methods, model based approach doesn’t require too much data, and the uncertainty could be well quantified by way of probability distribution.

Particle filter (PF) is a numerical approximation method based on Bayesian inference using point mass (or ‘particle’) representation of probability densities to tackle the nonlinearity and non-Gaussianity in modeling system dynamics (Gordon et al. 1993). It has been investigated for condition prognosis and remaining useful life prediction in different applications. In Orchard and Vachtsevanos (2009), a particle filter framework is investigated to analyse the axial crack growth in a planetary carrier plate. A regularized auxiliary particle filter is presented for battery remaining life prediction in Liu et al. (2011). In the previous work, model parameters are usually pre-determined from lab controlled test or FEA simulation analysis. However, model parameters may vary in practice due to various factors, including different material properties, component-to-component variations, or different operating conditions in the machinery degradation process.

To accommodate parameter variations and improve tracking performance, the level of noise associated with the system state and measurement models for degradation modeling can be increased. The drawback of such an approach, however, is that it also decreases the prediction accuracy and precision. Joint state and parameter estimation techniques have been investigated to address the aforementioned issue, and these methods can be categorized into Bayesian estimation and maximum likelihood estimation. In the Bayesian estimation approach, an auxiliary particle filtering using shrinkage modification of kernel smoothing technique is firstly presented in Liu and West (2001) for sequential Bayesian learning about time-varying state vectors and fixed model parameters simultaneously. Particle filter is then investigated in Storvik (2002) for dynamic state space model by marginalizing the unknown static parameter as part of the state vector. Following the similar idea, a Matlab-based tutorial for model-based prognostic is presented in An et al. (2013) by combining a physical model with observed data to identify model parameter using Bayesian estimation in particle filter. A mean-square filter is investigated in Basin et al. (2013) for joint state and parameter estimation in uncertain stochastic nonlinear polynomial system by incorporating the unknown parameters into extended polynomial state vector. Parameter estimation is investigated for batch processes in Zhao et al. (2013) through the maximum likelihood method which is accomplished by Expectation-Maximization algorithm. Prior efforts on joint state and parameter estimation mainly focus on filtering and control applications.

In line with the above efforts, this study investigates a joint state prediction and parameter estimation framework based on particle filter and expectation-maximization (EM) algorithm for machinery condition prognosis. To account for the stochastic property of machinery degradation process, the system is firstly modelled with unknown parameters. Model parameters are then estimated based on the degradation status (hidden information) and available in-process measurements using expectation-maximization algorithm. Machinery degradation status is then predicted by recursively updating the identified model with in-process measurements, following Bayesian inference scheme in particle filter. A simulation study and an experimental bearing run-to-failure test in a wind turbine gearbox are used to demonstrate the effectiveness of the developed method.

The merits of this study rest on the following. (1) A stochastic state space model is constructed for machinery defect prognosis comparing with predetermined models in prior studies. (2) To the best knowledge, it is the first study of integrative particle filter and EM algorithm investigated for machinery condition prognosis. (3) Performance comparison between Bayesian estimation and presented integrative PF and EM method is discussed. The rest of the paper is constructed as follows. After introducing the theoretical background of particle filter and expectation-maximization algorithm in Sect. 2, the details of the proposed mathematical framework for joint state prediction and parameter estimation is discussed in Sect. 3. Additionally, the construction of state space model based on physical knowledge and in-process data analysis is also discussed respectively. The effectiveness of the developed method is experimentally demonstrated based on bearing run-to-failure data acquired in a wind turbine gearbox in Sect. 4. To further demonstrate the performance of the presented method, performance comparison with conventional approach is discussed, and their Pros and Cons are summarized in Sect. 5. Finally, conclusions are drawn in Sect. 6.

Theoretical framework

In machinery condition prognosis, defect status is usually impossible to be directly observed unless it is measured offline by costly equipment (e.g., microscope, surface profiler). On the other hand, online sensing techniques, such as vibration, acoustic emission, dynamic force, temperature and wear debris, are readily measured in-process. However, online measurements are usually the indirect indicators of machinery status. Such scenario can be well described using state space model in a Bayesian framework (Arulampalam et al. 2002) as follows.

• a) A state equation describing the underlying machinery degradation process with time:

  $$\begin{aligned} x_t =f(x_{t-1},u_{t-1} ) \end{aligned}$$

  (1)

where t is time index, and $x_{t}$ is the defect status at time step t. $f(\bullet )$ describes the state transition function from state $x_{t-1}$ to $x_{t}$ considering order-one Markov process. $u_{t-1 }$ is the process noise representing uncertainty in degradation process. The state transition probability $p(x_{t}{\vert }x_{t-1})$ is the intrinsic property of machinery degradation, and can be derived from Eq. (1). The state equation is usually constructed based on physical knowledge of the degradation process (e.g., Paris’ formula).

• b) A measurement equation linking online measurement to unobservable defect status:

  $$\begin{aligned} z_t =h(x_t,v_t ) \end{aligned}$$

  (2)

where $\hbox {z}_{\mathrm{t}}$ denotes the online measurement at time step t. $h(\bullet )$ is a measurement function representing the relationship between online measurements $z_{t}$ and unobservable defect status $x_{t}$. ${\nu }_{t}$ is the sequence of measurement noise. The measurement $z_{t}$ is considered to be conditionally independent given the degradation state $x_{t}$ which is described as measurement probability $p(z_{t}{\vert }x_{t})$.

• c) A set of available online measurements acquired in the experiments:

  $$\begin{aligned} {{\varvec{Z}}}=\left\{ {z_1,z_2,\ldots ,z_N} \right\} \end{aligned}$$

  (3)

Equations (1–2) describe the system equation and measurement equation with known model parameters. In case of unknown parameters, the general state space models can be described as follows.

$$\begin{aligned} x_t= & {} f(x_{t-1},\theta ,u_{t-1} ) \end{aligned}$$

(4)

$$\begin{aligned} z_t= & {} h(x_t,\theta ,v_t ) \end{aligned}$$

(5)

where $\theta$ represents the unknown parameters need to be estimated. $z_{t}$ is the available in-process measurement at time step t. $x_{t}$ denotes the hidden defect status. The state transition probability is denoted as $p_{\theta }(x_{t}{\vert }x_{t-1})$ while the measurement probability is described as $p_{\theta }(z_{t}{\vert }x_{t})$.

Particle filter

In machinery defect prognosis, the idea is to find the posterior probability distribution $p(x_{t+l}{\vert }z_{t})$ of future defect status given the present measurements in the state space model with known parameters. The posterior probability distribution is recursively computed in two stages: prediction and update. Given the posterior probability distribution $p(x_{t}{\vert }z_{t})$ at time t, the prediction stage is to estimate the probability distribution $p(x_{t+1}{\vert }z_{t})$ via the Chapman–Kolmogorov equation (Arulampalam et al. 2002) as:

$$\begin{aligned} p(x_{t+1} |z_t )=\int {p(x_{t+1} |x_t )p(x_t |z_t )dx_t } \end{aligned}$$

(6)

Upon the new measurement $z_{t+1}$ is available, the posterior probability distribution $p(x_{t+1}{\vert }z_{t})$ of defect state $x_{t+1}$ is updated via Bayes rule (Arulampalam et al. 2002).

$$\begin{aligned} p(x_{t+1} |z_{t+1} )=\frac{p(x_{t+1} |z_t )p(z_{t+1} |x_{t+1} )}{p(z_{t+1} |z_t )} \end{aligned}$$

(7)

where $p(z_{t+1}{\vert }z_{t})$ is the normalizing factor which can be calculated as:

$$\begin{aligned} p(z_{t+1} |z_t )=\int {p(x_{t+1} |z_t )p(z_{t+1} |x_{t+1} )dx_{t+1}} \end{aligned}$$

(8)

As discussed above, Eqs. (6–8) give the exact analytic Bayesian solution for linear system with Gaussian noise. However, for nonlinear system, the integral operation in Eq. (6) is usually intractable due to high dimensional computation. Particle filter is developed using sequential Monte Carlo sampling method based on random samples (particle) representation of probability densities for nonlinear or non-Gaussian system. It has been widely studied in different applications such as mobile robot localization (Kwok et al. 2003), and object tracking (Hue et al. 2002), which involve nonlinear system and/or non-Gaussianity noise. Based on Monte Carlo approximation, the integral operation in Eq. (6) is transformed into the summarization to address complex high-dimensional computation in nonlinear system. In particle filter, the posterior probability distribution $p(x_{t}{\vert }z_{t})$ at time t is represented by a set of random samples or particles $x_t^i$, $i=1,2,\ldots ,M$, with the corresponding weight $w_t^i$. Then, Eq. (6) can be reformulated as Arulampalam et al. (2002):

$$\begin{aligned} p(x_{t+1} |z_t )= & {} \int {p\left( x_{t+1} |x_t\right) p\left( x_t |z_t\right) dx_t}\nonumber \\\approx & {} {\mathop {\sum }\limits _{i=1}^{M}} w_t^i \delta \left( x_t -x_t^i\right) p\left( x_{t+1} |x_t\right) \nonumber \\= & {} {\mathop {\sum }\limits _{i=1}^{M}} w_t^i p\left( x_{t+1} |x_t^i\right) \end{aligned}$$

(9)

where i is the index of particle, and M is the total number of particles which affects the accuracy of represented probability distribution function and the efficiency of computation. $\delta (\bullet )$ is the delta function. In the update step, the weight of each particle is then updated based on the likelihood of the observation $z_{t+1}$ at time step $t+1$ as:

$$\begin{aligned} w_{t+1}^i \propto w_t^i p\left( z_{t+1} |x_{t+1}^{i}\right) \end{aligned}$$

(10)

In implementation, resampling is applied in every step to obtain equally weighted samples so as to avoid particle degeneracy issue of particle filter (Arulampalam et al. 2002). The particles are resampled from importance distribution with associated importance weights. Those particles with very small weights are eliminated, while those particles with high weights are duplicated. Therefore, particle filter is a recursive numerical method based on the Bayesian inference to estimate posterior probability density function of a state which is represented by a set of random samples (named particles) with associated weights (Wang and Gao 2013). Particle filter gives the complete solution of state estimation in the state space model with known model parameters.

Table 1 Illustration of EM algorithm

Expectation-maximization algorithm

Because of the stochastic property of machinery degradation process, the parameters of state space model are unknown. To solve this issues, the maximum likelihood estimation (MLE) could be used to deduce the most likely parameters which satisfy the distribution of in-process measurements. However, in practice, the measurements are usually incomplete data which will seriously affect the accuracy of estimation. On the other hand, the likelihood function is sometimes too complicated to solve the MLE of corresponding parameters. Expectation-maximization (EM) algorithm (Dempster et al. 1977; Moon 1996), an iterative algorithm, is developed for obtaining the MLE of parameters using incomplete data. Using this method, the complex problem of maximizing likelihood function is translated into the optimization of a series of simple functions. The essence of EM algorithm is the postulation of hidden defect state X and in-process measurements Z to form a complete data set $\{{{\varvec{ X}}}, {{\varvec{ Z}}}\}$, then the log-likelihood function is expressed through marginalizing the joint distribution $p_{\theta }({{\varvec{ X}}}, {{\varvec{ Z}}})$.

$$\begin{aligned} L_\theta (X,Z)=\log p_\theta (X,Z) \end{aligned}$$

(11)

where X is denoted as the N-dimensional hidden degradation state vector $\{x_{1},x_{2},{\ldots },x_{N}\}$ while Z represents the in-process measurement vector $\{z_{1},z_{2},{\ldots },z_{N}\}$. To estimate the parameters, EM algorithm maximizes the cost function ${Q(\theta , \theta }_{k})$ which is formulated as the conditional mean of the log-likelihood function $L_{\uptheta }({{\varvec{ X}}}, \mathbf{Z})$ (Schon et al. 2011).

$$\begin{aligned} Q(\theta ,\theta _k )= & {} \int {L_\theta (X,Z)} p_{\theta _k } (X|Z)dX \nonumber \\= & {} \int {\log p_\theta (X,Z)} p_{\theta _k } (X|Z)dX \end{aligned}$$

(12)

where $\uptheta _{k}$ is the sequence of estimated parameters. There are mainly two major steps in parameter estimation. In the first step, also known as E-step, cost function ${Q(\theta , \theta }_{k})$ is computed as shown in Eq. (12) by estimating the joint probability density of state and in-process measurements based on initial estimated parameters. Then, in the following M-step, the cost function ${Q(\theta , \theta }_{k})$ is maximized using a gradient ascent algorithm to obtain the new estimated parameters $\theta _{k+1} =\arg \max Q(\theta ,\theta _k )$. These two steps are iterated until the parameters converge which means the changes of parameters after each iteration remain within a specified tolerance level.

One challenge in EM algorithm is to calculate the cost function $Q(\theta , \theta _{k})$. Based on Bayes’ rule and Markov property, the joint distribution $p_{\theta }({{\varvec{X}}}, {{\varvec{ Z}}})$ is derived as:

$$\begin{aligned} p_\theta ({{\varvec{X}}},{{\varvec{Z}}})=p_\theta ({{\varvec{X}}})p_\theta ({{\varvec{Z}}}|{{\varvec{X}}}) \end{aligned}$$

(13)

where

$$\begin{aligned} p_\theta ({{\varvec{X}}})= & {} p_\theta (x_1 )\prod _{t=\hbox {1}}^{N\hbox {-1}} {p_\theta (x_{t\hbox {+1}} |x_t )} \end{aligned}$$

(14)

$$\begin{aligned} p_\theta ({{\varvec{Z}}}|{{\varvec{X}}})= & {} p_\theta (z_1 |x_1 )\prod _{t=\hbox {2}}^N {p_\theta (z_t |x_t )} \end{aligned}$$

(15)

Similarly, the log-likelihood function can be computed as:

$$\begin{aligned} L_\theta ({{\varvec{X}}},{{\varvec{Z}}})= & {} \log p_\theta ({{\varvec{X,Z}}})=\log p_\theta ({{\varvec{Z}}}|{{\varvec{X}}})+\log p_\theta (X) \nonumber \\= & {} \log p_\theta (x_1 )+\sum _{t=1}^{N-1} {\log p_\theta (x_{t+1}|x_t )} \nonumber \\&+\sum _{t=1}^N {\log p_\theta (z_t |x_t )} \end{aligned}$$

(16)

According to Eqs. (12) and (16), the cost function ${Q(\theta , \theta }_{k})$ is then transformed as Schon et al. (2011):

$$\begin{aligned} Q(\theta ,\theta _k )=I_1 +I_2 +I_3 \end{aligned}$$

(17)

where

$$\begin{aligned} I_1= & {} \int {\log p{ }_\theta (x_1 )p} _{\theta _k } (x_1 |{{\varvec{Z}}})dx_1 \end{aligned}$$

(18)

$$\begin{aligned} I_2= & {} \sum _{t=1}^{N-1} {\int {\int {\log p{ }_\theta (x_{t+1} |x_t )p} _{\theta _k } (x_{t+1},x_t |{{\varvec{Z}}})dx_t dx_{t+1} } }\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} I_3= & {} \sum _{t=1}^N {\int {\log p_\theta (z_t |x_t )p_{\theta _k } (x_t |{{\varvec{Z}}})dx_t } } \end{aligned}$$

(20)

For linear system with Gaussian noise, the cost function ${Q(\theta ,\theta }_{k})$ can be calculated analytically, and the explicit equations for parameter estimation in EM algorithm can be developed. However, for nonlinear state space model in machinery defect prognosis, the integral operation in Eqs. (18–20) is intractable to get a complete solution which poses challenge in EM algorithm. In such case, particle filter plays an import role in computation of the cost function, which will be discussed in the next section of the integrated framework of particle filter and expectation-maximization algorithm for machinery defect prognosis. The details of EM algorithm are given in Table 1.

Formulation of prognosis model

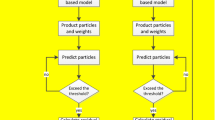
In order to accommodate model dynamics (parameter variations) and reduce prognosis uncertainty, this paper presents a computational framework of joint state prediction and parameter estimation for machinery condition prognosis based on particle filter and EM algorithm as shown in Fig. 2.

Fig. 2

Computational framework for joint state prediction and parameter estimation in machinery condition prognosis

According to the inherent physical knowledge of different applications, a state space model consisting of system equation and measurement equation is constructed firstly. With the available in-process measurements, system identification is performed to identify the model parameters using expectation-maximization algorithm in the learning stage. After the model parameters are identified, the system state is then predicted based on particle filter in the desired prediction horizon. The details of the joint state prediction and parameter estimation framework are discussed below.

Construction of state space model

As discussed in Sect. 2, system equation and measurement equation are essential to construct the state space model which describes the machinery degradation process.

System equation

System equation describes machinery defect state evolving behavior which is usually impossible to be measured directly through online measurements. Take defect prognosis of rolling element bearing as an example, spalling area is a direct indicator of bearing defect severity. Since the bearing defect grows slowly and the physics governing its behavior is known, a physics-based model governing fatigue crack propagation based on Paris’ formula is given by Li et al. (1999):

$$\begin{aligned} \frac{dx}{dt}=\alpha (\Delta k)^{m} \end{aligned}$$

(21)

where t is the number of cycles related to bearing running time, and dx / dt is the defect growth rate. The parameters $\alpha$ and m are related to material properties, and $\Delta k$ is the amplitude of the stress intensity factor. In the case of bearing defect propagation, it is difficult to estimate the stress intensity factor. To circumvent it, an empirical model is developed as Li et al. (1999):

$$\begin{aligned} \frac{dx}{dt}=cx^{m} \end{aligned}$$

(22)

where x represents the spalling area. The defect growth rate is an exponential function of the existing spalling area. The model parameters c and m are initialized as unknown variables. Take integration operation on both sides after separating variables, Eq. 22 can be rewritten in a state transition form as:

$$\begin{aligned} x_t =\left[ {x_{t-1}^{(1-m)} +c(1-m)} \right] ^{1/{(1-m)}}+u_{t-1} \end{aligned}$$

(23)

where t is the time index, and $u_{t-1}$ represents the noise in the state evolving process.

Measurement equation

During machinery degradation process, in-process measurements carrying defect signatures have been widely employed. However, due to the complexity and the low signal to noise ratio (SNR) of raw measurements, it is difficult to model the relationship between the measurements and machinery defect status. To tackle this problem, effective data processing and feature representation techniques are performed to reduce data dimensionality without losing the information of defect signature. The relationship between extracted feature and defect state is expected to be modelled using a simple function.

Different features from time domain, frequency domain, and time-frequency domain have been investigated for bearing defect diagnosis and prognosis. Time domain methods involve statistical features such as root mean square (RMS), Kurtosis, skewness, crest factor, peak–peak value, and entropy. The frequency domain methods take advantage of spectrum/time-frequency analysis and extract the energies at bearing defect characteristic frequencies (e.g. the ball-pass frequency of outer ring $f_{BPFO}$, ball-pass frequency of inner ring $f_{BPFI}$, and ball-spin frequency $f_{BSF})$ as features. A number of features are extracted from the measurements to represent the bearing defect. However, these features may contain redundant information. For improved computational efficiency in machinery condition prediction, a proper feature selection/fusion strategy is needed to lower the dimension of feature space. Different feature selection techniques have been investigated in the literature, including genetic algorithm (Liao 2014), principle component analysis (PCA) (Malhi et al. 2011), and health index (Bechhoefer and Bernhard 2007), etc. Generally, it is difficult to determine which feature is more sensitive to bearing defect propagation. A good feature should present a consistent trend with defect propagation, and is expected to describe the measurement equation using a simple function. The assumption on linear relationship between bearing defect status and selected feature, which is often used in the literature (Pedregal and Carnero 2006), is also adopted in this study.

$$\begin{aligned} z_t =x_t +v_t \end{aligned}$$

(24)

where $z_{t}$ denotes the selected feature from in-process measurements, and $\nu _{t}$ represents the measurement noise.

Fig. 3

The simulated data and defect state

Formulation of joint parameter estimation and state prediction

The state space model with unknown parameters has been constructed. To predict the machinery condition based on available observation, a mathematic framework based on particle filter and expectation-maximization algorithm for joint state prediction and parameter estimation is investigated in this study. To estimate the parameters in the nonlinear state space model, the cost function $Q(\theta , \theta _{k})$ described in Eqs. (17–20) is computed based on the sequential importance resampling method in particle filter. From Eqs. (17–20), it is seen that the computation of quantities $I_{1}$, $I_{2}$, and $I_{3}$ depends primarily on the smoothed density function $p_{\theta k}(x_{t}{\vert }{{\varvec{ Z}}}{} \mathbf{)}$. To estimate the density function $p_{\theta }(x_{t}{\vert }{{\varvec{ Z}}})$, a forward–backward smoother algorithm is investigated and proofed in Schon et al. (2011).

$$\begin{aligned} p_\theta (x_t |{{\varvec{Z}}})= & {} \int {p_\theta (x_{t} |x_{t+1},{z_{{1}:_t}} )p_\theta (x_{t+1} |{{\varvec{Z}}})dx_{t+1} }\nonumber \\= & {} \int {\frac{p_\theta (x_{t+1} |x_t )p_\theta (x_t |z_{{1:}t} )}{p_\theta (x_{t+1} |z_{1:t} )}p_\theta (x_{t+1} |{{\varvec{Z}}})dx_{t+1} } \nonumber \\= & {} p_\theta (x_t |z_{1:t} )\int {\frac{p_\theta (x_{t+1} |x_t )p_\theta (x_{t+1} |{{\varvec{Z}}})}{p_\theta (x_{t+1} |z_{1:t} )}dx_{t+1} }\nonumber \\ \end{aligned}$$

(25)

Hence, the smoothed density function can be obtained as the function of filtered state density $\hbox {p}_{\uptheta }(\hbox {x}_{\mathrm{t}}{\vert }\hbox {z}_{1:\mathrm{t}})$ at time t, smoothed density $\hbox {p}_{\uptheta }(\hbox {x}_{\mathrm{t}+1}{\vert }{} \mathbf{Z})$ at time t+1, and state prediction density $\hbox {p}_{\theta }(\hbox {x}_{\mathrm{t}+1}{\vert }\hbox {x}_{\mathrm{t}})$. Based on particle approximation in particle filter, the smoothed density function $p_{\theta }(x_{t}{\vert }Z)$ can be obtained following the recursive approximated density function $p_{\theta }(x_{t+1}{\vert }{{\varvec{ Z}}})$ as:

$$\begin{aligned} p_\theta (x_t |{{\varvec{Z}}})\approx \sum _{i=1}^M {\omega _{t|N}^i \delta \left( x_t -x_t^i\right) } \end{aligned}$$

(26)

where

$$\begin{aligned} \omega _{t|N}^i =\omega _t^i \sum _{k=1}^M {\omega _{t+1|N}^k \frac{p_\theta \left( x_{t+1}^k |x_t^i\right) }{\sum _{i=1}^M {\omega _t^i p_\theta \left( x_{t+1}^k |x_t^i \right) } }} \end{aligned}$$

(27)

Similarly, the quantities $I_{1}$, $I_{2}$ and $I_{3}$ which constitute the cost function $Q(\theta , \theta _{k})$ can be obtained accordingly as Schon et al. (2011):

$$\begin{aligned} Q(\theta ,\theta _k )=I_1 +I_2 +I_3 \end{aligned}$$

(28)

where

$$\begin{aligned} I_1= & {} \sum _{i=1}^M {\omega _{1|N}^i \log p_\theta \left( x_1^i\right) } \end{aligned}$$

(29)

$$\begin{aligned} I_2= & {} \sum _{t=1}^{N-1} {\sum _{i=1}^M {\sum _{j=1}^M {\frac{\omega _t^i \omega _{t+1|N}^j p_{\theta _k } \left( x_{t+1}^j |x_t^i\right) }{\sum _{l=1}^M {\omega _t^l p_{\theta _k } \left( x_{t+1}^j |x_t^l \right) } }\log p_\theta \left( x_{t+1}^j |x_t^i\right) } } } \nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} I_3= & {} \sum _{t=1}^N {\sum _{i=1}^M {\omega _{t|N}^i \log p_\theta \left( z_t |x_t^i\right) } } \end{aligned}$$

(31)

By recursively maximizing the cost function $Q(\theta ,\theta _{k})$ using optimization algorithm, such as gradient descent algorithm (Qian 1999), the parameter vector $\theta$ can be determined when it converges.

$$\begin{aligned} \theta _{k+1} =\theta _k -\gamma \cdot \nabla Q(\theta ,\theta _k ) \end{aligned}$$

(32)

where $\gamma$ is the step size, $\nabla (\cdot )$is the gradient function. In machinery condition prognosis, we are interested in degradation state prediction with the identified model parameter vector $\theta$. For l-step ahead prediction, the posterior probability distribution $p_{\uptheta }(x_{t+l}{{\vert }z}_{t})$ can be obtained according to Eqs. (4–6) as Zio and Peloni (2011):

$$\begin{aligned} p_\theta (x_{t+l} |z_t )=\int \cdots \int {\prod _{t=N}^{N+l} {p_\theta (x_{t+1} |x_t )p_\theta (x_t |z_t )} \prod _{t=N}^{N+l} {dx_t } } \end{aligned}$$

(33)

To eliminate the computation of integral operation in nonlinear system, particle filter is used to calculate the posterior probability distribution $p_{\uptheta }(x_{t+l}{{\vert }z}_{t})$ as:

$$\begin{aligned} p_\theta (x_{t+l} |z_t )\approx \sum _{i=1}^M {w_{t+l-1}^i p_\theta \left( x_{t+l} |x_{t+l-1}^i\right) } \end{aligned}$$

(34)

Simulation study

To evaluate the performance of the developed joint state prediction and parameter estimation algorithm, the state space model described in Eqs. (23–24) is used as an example.

$$\begin{aligned}&\underset{z_t =x_t +v_t }{x_{t+1} =\left[ {x_t^{(1-m)} +c(1-m)} \right] ^{1/{(1-m)}}} +u_t \left[ {{\begin{array}{l} {u_t } \\ {v_t } \\ \end{array} }} \right] \nonumber \\&\quad \sim \mathrm{N}\left( {\left[ {{\begin{array}{l} 0 \\ 0 \\ \end{array} }} \right] ,\left[ {{\begin{array}{cc} q&{}0 \\ 0&{}r \\ \end{array} }} \right] } \right) \end{aligned}$$

(35)

here, the parameters q and r are the variances of noises in system equation and measurement equation, respectively. The simulated data is firstly generated by the above model with preset parameters in order to be similar with the experimental data in Sect. 4. The parameters are preset as:

$$\begin{aligned} \theta ^{*}=[m^{*},c^{*},q^{*}, r^{*}]=[0.9305,0.0053,0.0015,0.252] \end{aligned}$$

(36)

By setting the initial state $x_{1}$ as 0.27, the simulated data z and defect state x can be generated as shown in Fig. 3.

The developed algorithm is investigated to determine the parameters and to predict the future state x on the basis of available observation $\hbox {z}_{1:200}$. Using EM algorithm, it is straightforward to estimate the parameters as described in Table 2. It is seen that the estimated parameters match well with the preset values. It is noted that the estimated variance q of the state vector is less than the preset value with an error of 13.3 % which means the estimated state is smoother than the simulated state.

Table 2 The preset and estimated parameters used in the simulation study

Next, particle filter is used to estimate the future state based on available observation and estimated parameters. Figure 4 shows the quantified uncertainty of predicted state on the basis of available observation $z_{\textit{1:250}}$ under 50 steps ahead prediction. Since the estimated states follow probability distributions, the probability distributions of the estimated states ${\times }150$, ${\times }250$ and ${\times }300$ are illustrated in the zoomed regions.

Fig. 4

Uncertainty quantification of predicted state in simulation study

To quantify the prediction accuracy, root mean square error (RMSE) is defined as the square root of the average of the square of all difference between predicted state $\hat{{x}}$ and simulated state x.

$$\begin{aligned} {\textit{RMSE}}=\sqrt{\frac{1}{N}{\mathop {\sum }\nolimits _{j=1}^{N}} {(\hat{{x}}_j -x_j )^{2}} } \end{aligned}$$

(37)

Figure 5 shows the root mean square error of the predicted state under different-steps-ahead prediction (e.g., 10, 20, 50, 100, and 150 steps) using the developed algorithm. It is found that the prediction error in short term prediction (e.g., around 0.05 % in 10, 20, and 50 steps ahead) is less than that of long term prediction (e.g., around 0.2 % in 100 and 150 steps ahead). The prediction error is relative small in all cases which demonstrates the effectiveness of the developed algorithm in parameter estimation and state prediction.

Fig. 5

Prediction error of the developed algorithm under different-step-ahead prediction

Experimental evaluation

To experimentally evaluate the joint state prediction and parameter estimation method based on particle filter and expectation-maximization algorithm, a set of vibration signals measured on a wind turbine gearbox in a run-to-failure test is analyzed, and the analysis results are discussed as below.

Experimental setup

Experimental data measured on a wind turbine gearbox was made available in a field test. The tested turbine is a stall-controlled, three-bladed, upwind machine with 2 MW rated power. The wind turbine gearbox is composed of one low speed planetary stage and two parallel stages, and its detailed configuration is described in Fig. 6. The defect was initiated from a rolling element bearing A in the high speed shaft as shown in Fig. 6b. The tested bearing run continuously for about 107 million revolutions in the field to the end of service life.

Fig. 6

Illustration of the tested wind turbine gearbox, a 3D gearbox structure, b internal configuration

Data preprocessing

With the growth of bearing defect, the energies at bearing defect characteristic frequencies are increased, and thus they can be extracted as the representative features of bearing status. Due to the varying speed operating conditions of the wind turbine, an integrated approach of complex wavelet transform and computed order tracking can be used to extract the energies at the bearing defect characteristic frequencies as representative features (Wang et al. 2014). Figure 7 shows the extracted energies at bearing defect characteristic frequencies as the indicators of bearing status in the run-to-failure test. It is found that the energies at the frequency $\hbox {f}_{\mathrm{BPFI}}$ show a clearly increasing trend which means bearing experienced a defect on the inner raceway. The defect may propagate into the cage and the outer raceway since the energies at the frequencies $f_{{\textit{FTF}}}$ and $f_{{\textit{BPFO}}}$ also show an increasing trend.

Fig. 7

The extracted energies at bearing defect characteristic frequencies

The extracted energies at defect characteristic frequencies are denoted as condition indicators (CI) which mean these features indicate the bearing conditions. However, each CI only contains partial information of bearing status or it is sensitive to only one failure mode of bearing. To comprehensively describe the degradation process, the health index (HI) algorithm illustrated in Bechhoefer and Bernhard (2007) is used to fuse all these CIs:

$$\begin{aligned} {\textit{HI}}=\sqrt{{\textit{CI}}^{T}\Sigma ^{-1}{\textit{CI}}}\times 0.7/v \end{aligned}$$

(38)

where vector CI represents the energies at bearing defect characteristic frequencies $f_{{\textit{FTF}}}$, $f_{{\textit{BSF}}}$, $f_{{\textit{BPFI}}}$ and $f_{{\textit{BPFO}}}$, and $\Sigma$ is the sample covariance from a set of nominal bearings. The term v is a normalized factor (Bechhoefer and Bernhard 2007). The obtained fused feature describes a clearly trend representing bearing defect growth as shown in Fig. 8.

Fig. 8

The fused feature obtained in health index algorithm

Fig. 9

Uncertainty quantification of predicted state using integrative PF and EM method

Based on statistical information (e.g., probability distribution of feature), the fused feature is scaled to represent the defect severity. Based on the rule which has been successfully implemented in aerospace condition monitoring (Beckhoefer et al. 2011), the amplitude in the range of [0 0.5] is set as normal or healthy condition, while the range of [0.5 0.75] is set as mild defective condition, and the amplitude above 0.75 is considered as severely defective condition. The value greater than 1 indicates that the continuous operations may result in collateral damage to other components in the gearbox. Therefore, the threshold is set as 1 to determine the component remaining useful time. It is seen that the fused feature presents dominant noise which causes computational difficulties of the remaining useful life (RUL). However, due to the dominant noise in fused feature, it is difficult to determine the remaining useful life from the fused feature. The developed joint state prediction and parameter estimation algorithm can quantify the uncertainty of defect growth and reduce the noise variance in fused feature, and thus reduce the false alarm rate in threshold setting as discussed below.

Fig. 10

The probability distribution of bearing remaining useful life

Fig. 11

Predicted bearing defect growth using the ARMA model

Fig. 12

Distribution of model parameters ${\bar{m}}$ and ${\bar{c}}$ using conventional PF approach

Analysis results

The fused features from time steps [300 500] are chosen as the available observation to predict the bearing defective status in future. The bearing defect growth process is modeled by the system equation and measurement equation in the state space model as described in Eq. 35. According to available observation, the parameters in the state space model are firstly estimated using EM algorithm as:

$$\begin{aligned} {\hat{\theta }}=[\hat{{m}},\hat{{c}},\hat{{q}},\hat{{r}}] =[0.9322,0.0052,0.021,0.2512] \end{aligned}$$

(39)

Thus, the state space model can be identified as:

$$\begin{aligned}&\underset{z_t =x_t +v_t }{x_{t+1} =\left[ {x_t^{{0.0678}} +{0.0052*0.0678}} \right] ^{1/{{0.0678}}}}\nonumber \\&\quad +\,u_t\left[ {{\begin{array}{l} {u_t } \\ {v_t } \\ \end{array} }} \right] \sim \mathrm{N}\left( {\left[ {{\begin{array}{l} 0 \\ 0 \\ \end{array} }} \right] ,\left[ {{\begin{array}{cc} 0.021&{} 0 \\ 0&{}0.2512 \\ \end{array}}}\right] } \right) \end{aligned}$$

(40)

Next, particle filter is used to predict the future bearing defective state based on available observation and identified state space model. The predicted bearing defect status with quantified uncertainty in next 100 steps is shown in Fig. 9, and the probability distributions of estimated bearing states are illustrated in zoomed regions. It is found that the predicted bearing defect state using integrative PF and EM method closely follows the trend of observation with highly reduced variance in uncertainty. Because of the defect accumulating effect in the system equation, the predicted bearing defect status grows monotonically since mechanical defect could not heal itself. It can facilitate the remaining useful life (RUL) calculation of the bearing. Bearing RUL is defined as the service time until the defect state reaches the threshold as illustrated in Fig. 9.

$$\begin{aligned} {\textit{RUL}}(t)=t_{r }-t_{s} \end{aligned}$$

(41)

where $t_{s}$ is the present time and $t_{r}$ is the time when the bearing defect state reaches the threshold. By setting the threshold as 1, the probability distribution of the bearing remaining useful life can be computed as shown in Fig. 10. It is seen that the remaining useful life of bearing is around 33 time steps (e.g., about 180,000 REV.) by selecting the highest probability distribution.

A data driven approach is also investigated for the machinery condition prediction using the same experimental data for performance comparison. Given the limited number of experimental data set, an autoregressive moving average (ARMA) model is used to predict the bearing defect growth, and the results are shown in Fig. 11. It is found that the prediction results of the ARMA model follow the trend closely; however, it could not quantify prediction uncertainty. The up and down trend also causes the difficulty to determine the remaining useful life of bearing.

From the above analysis, the integrated PF and EM algorithm can incorporate the estimation of model parameters and prediction of hidden defect state in one framework. By taking advantage of physical knowledge, the hidden defect state of bearing can be inferred from noisy measurement based on Bayesian inference. The estimated defect state with threshold setting can be used to determine the remaining useful life of bearing. The uncertainty of remaining useful life is also quantified in a probabilistic manner. Therefore, the developed method can facilitate the threshold setting with estimated defect state (reduced variance) instead of noisy measurement to reduce false alarm rate and improve the maintenance strategy in practice.

Discussions

To compare the performance of developed method, the conventional PF approach, which takes the unknown parameters as the part of state vector based on Bayesian estimation, is investigated here. The conventional method still uses the state space model denoted by Eq. 35 as its system equation and measurement equation. The same fused features are chosen as training data of the conventional particle filter to predict the RUL of bearing. In the conventional method, the initial parameters of model are set as probability distributions. If no prior information is available, uniform distribution is usually chosen and the probability parameters of lower and upper bounds are empirically selected. With the prior knowledge about parameter estimated using EM algorithm, the uniform distributions of parameters are determined as:

$$\begin{aligned} {\bar{\theta }}=[{\bar{m}}\sim (0.7,1),{\bar{c}}\sim (0.003,0.005)] \end{aligned}$$

(42)

Fig. 13

Uncertainty quantification of predicted state using conventional PF approach

Table 3 The comparison between the conventional approach and presented method

Here, the terms ${\bar{m}}$ and ${\bar{c}}$ represent the parameters in system equation. The process noise u and the measurement noise v are ignored since they can be handled through the uncertainty in model parameters. With the available measurement information, model parameters could be updated based on Bayesian estimation and the results are shown in Fig. 12. It is found that the probability distribution of model parameters ${\bar{m}}$ and ${\bar{c}}$ fluctuate continuously during the learning stage, but they remain constant during the prediction stage because no measurement is available to update the model parameters. Thus, in the prediction stage, the state space model is determined and particle filter is used for bearing defect prognosis. Figure 13 shows the long-term bearing defect prediction results using the conventional PF approach. It is found that the median of the predicted bearing defect state closely follows the trend of observation, and the uncertainty of prediction result is well demonstrated through the 90 % confidence interval.

Comparing the integrated PF and EM algorithm with the conventional particle filter, it is found that both methods could follow the bearing defect propagation trend closely and quantify the uncertainty of prediction process in the form of confidence intervals. However, the distribution interval of predicted RUL using the integrated PF and EM algorithm is much smaller than that using the conventional particle filter. On the other hand, the prediction accuracy of conventional particle filter approach highly relies on the initial selection of model parameters since the estimation error of model parameters could be propagated in the sequential Bayesian estimation process. In essence, the conventional algorithm and the presented algorithm are based on Bayesian estimation and maximum likelihood estimation, respectively. Bayesian estimation could adapt to the local variation (e.g., the variation of measurement) and update the relevant parameters. Therefore, there are fluctuations during the learning stage as shown in Figs. 12 and 13. On the contrary, maximum likelihood estimation calculate model parameters as deterministic value. Once parameters are determined, they will not change during the prediction process. Because of the comprehensive consideration of all available measurements in parameters determination, maximum likelihood estimation has the global property in parameter estimation. The parameters with the maximum likelihood probability are determined during the learning stage, thus the estimation error is not propagated. The Pros and Cons of these two approaches are summarized in Table 3.

Conclusions

Data analytic methods have been extensively investigated to complement sensing techniques for improved systems diagnosis, prognosis, and reliability. This paper presents a joint state prediction and parameter estimation method to address nonlinearity and stochastic properties that are typically associated with machine degradation processes, based on integrated particle filtering (PF) and expectation maximization (EM). From the results obtained, following conclusion can be drawn:

• 1. The presented method makes use of prior physical knowledge about the system being estimated as well as new measurement data, and presents solution in a Bayesian framework. Uncertainty associated with the degradation state prediction can be quantified in terms of probability distribution functions.

• 2. The integration of EM with PF improves the accuracy of system parameter estimation based on measurements. As a result, the presented method can be applied to degradation prediction of systems with limited known model parameters.

• 3. The presented method can minimize the effect of variance in prediction, caused by measurement noise, thus improving the overall robustness in sensing data thresholding for alarm triggering and maintenance scheduling.

The performance of the presented method has been verified using both simulation and a run-to-failure experimental test on a bearing for wind turbines. Several limitations remain to be further investigated. For example, the computational efficiency of the presented method is low, due to the low convergence rate of the EM algorithm. It was also noted that initial selection of parameters during the model parameters estimation process can significantly affect the computational efficiency. Future research will be directed towards improving the computational efficiency by e.g., replacing the EM algorithm with methods of higher convergence rate, such as Expectation Conditional Maximization (ECM) or Expectation/Conditional Maximization Either (ECME) (Mkhadri 1998). Further systematic experiments will be performed to investigate the robustness of the developed method.