Introduction

The globalization of market, information technologies, advertisements etc. directly or indirectly influence the price of commodities; stimulate rivalry among manufacturers, vendors and retailers; and stimulate humor of customers, also. As a result, the parameters of inventory system rapidly (randomly or imprecisely or both) change over time. Whereas changing scenarios elongate complexity of inventory modeling problem. On the other side, it emboldens to use more appropriate mathematical methods and adequate tools. Consideration of either randomness or fuzziness in the involved key parameters is not a more pertinent tool to deal with the real life situations at all. In 1978, Kwakernaak introduced the notion of fuzzy random variable (FRV) that underlines randomness as well as fuzziness in the perception of an event. The notion of FRV is further enhanced, extended and explained with more unambiguity by Gil et al. (2006), Yoshida et al. (2006) and Shapiro (2009). FRV is a hybrid type uncertainty, in which statistical uncertainty as well as linguistic impreciseness both appear simultaneously. According to Shapiro (2009), randomness models the stochastic variability of all possible outcomes of a situation and describes the inherent variation associated with the environment under consideration. On the other hand, fuzziness relates to the unsharp boundaries of the parameters of the model. In brief, we can realize that FRV as an ideal instrument for dealing with the real life business transactions.

A SC (supply chain) is concerned with a network of facilities or key business activities that sequentially performs the functions of procurement of raw materials, conversion of raw materials into intermediate and finished product, and finally distribution of finished products to the customers. These ventures of SC are accomplished at different stages by several individuals (called entities of SC) such as supplier, manufacturer, distributor, merchandiser etc. As per requirement, different kind of items are stored at various places. Accordingly, decisions concerning to shipment time, shipment size etc. are taken by the administration. The decision making process is characterized as either centralized or decentralized. The centralized decision making process assumes a unique decision-maker managing the whole SC with the objective to minimize (maximize) the total SC cost (profit), whereas in the decentralized decision making process, there are multiple decision- makers whose objectives are conflicting (Mishra and Raghunathan 2004). In the centralized decision making process, the cooperation among the entities is indispensable in order to optimize the total cost of whole SC. Numerous of results have been published on the coordination and cooperation between the manufacturer and the buyer suggesting the joint channel-optimal ordering, shipment and lot sizing policies in the deterministic environment. Goyal (1977) established a joint economic lot-size (JELS) formula to minimize the integrated relevant costs for both the vendor and the buyer. Banerjee (1986) determined the JELS for the single-vendor and the single-buyer integrated system, wherein the vendor produces to order for the buyer on a “lot-for-lot” basis. Goyal (1988) enhanced Banerjee (1986) JELS policy by relaxing the assumption “lot-for-lot”. The above discussed three models lay down the foundation of integrated SC, and are the most cited articles. However, we are intended to develop a two-echelon integrated procurement production (IPP) that deals with stochastic and then fuzzy stochastic demand rate. So, keeping it in mind, in Sect. 2, we provide the detailed literature review toward the our research objective. Remainder of paper arranged as follows: Sect. 3 provides the basics about FRV and evaluation of its expectation incorporating the possibilistic mean and probabilistic expectation. We also establish a result in this section that will be used in cost function determination in later section. Section 4 provides the notations and assumptions that are used throughout the article. Then, next two sections are devoted to the mathematical formulation of model for random demand and its extension in fuzzy random environment, respectively. In Sect. 7, solution procedure is discussed and an algorithm is proposed to find the optimal solution. The next section illustrates the solution procedure with numerical example. Finally, Sect. 9 makes concluding remarks and suggest future scope of this study.

Literature review

A production–inventory system that incorporates the procurement of raw material, in the literature, it is termed as IPP. An adequate number of articles addressed IPP covering variant circumstances in deterministic framework. Lee (2005) developed an IPP for the single-manufacturer and the single-buyer by considering conversion factor of raw material to finished product. In literature, conversion factor is defined as fraction of raw material that is converted to as finished product. Hajji et al. (2009) studied the perturbation in supplier and the transformation stage which occur due to internal difficulties or market constraints, and established the replenishment policies for the manufacturer and downstream stage. Ben-Daya and Al-Nassar (2008) studied a three-stage IPP in the context of each stage having more than one firm, and the number of shipment in each stage is integer multiple of adjacent downstream stage. A single shipment of raw material in a scheduling period increases the carrying charge of raw material. In order to reduces this charge, Ben-Daya et al. (2013) amended the model of Ben-Daya and Al-Nassar (2008) by considering raw material shipment times as a decision variable. Recently, Yu et al. (2012) developed an vendor managed inventory (VMI) IPP in which vendor’s inventory of raw materials continuously decreases due to the deterioration and its conversion into the finished products. Above discussion indicates that there is an ample scope to deal with IPP by considering demand factor as stochastic, fuzzy or fuzzy stochastic. However, we now need a brief review of literature concentrating to fuzzy and fuzzy stochastic framework.

Consideration of deterministic constant demand is not very appreciable in the realistic volatile market scenarios, on the other hand, usage of probability theory needs a great deal with past data records. But, it may happen that the historical data record is not available at all (specially newly start business), and if it is available, then the exact estimation of forthcoming demand can not be taken as granted. Fuzzy set theory that relaxes the essentiality of complete information (but it is essential for use of probability theory) as well as provides a flexibility (in the parameters), is a panacea to tackle the real life situations. It also provides a framework to deal with dynamical systems wherein impreciseness or ill-known data such as demand is about \(d\) units per unit time, holding cost is about Rs. \(h\) and so on. In recent years, the implementation of fuzzy sets theory and techniques in supply chain inventory management (SCIM) lodge a great interest among the practitioners. Mahata et al. (2005) extended Banerjee (1986) JELS policy in fuzzy environment by incorporating the buyer’s order quantity as a fuzzy variable. Mahata and Goswami (2007) addressed a trade credit financing for the retailer and customers, wherein annual demand and cost parameters were considered as fuzzy numbers. Pan and Yang (2008) extended Yang and Pan (2004) integrated model for the single-vendor and the single buyer by assuming fuzzy production rate and fuzzy expected annual demand. Supplier selection in a supply chain is crucial because supplier play a key role in regard of competitive advantage (Kubat and Yuce 2012). Kubat and Yuce (2012), Pang and Bai (2013) design supply chains in which fuzziness is inherent in supplier selection that are examined by fuzzy analytic hierarchy or fuzzy performance evaluation. Yang and Liu (2013) address a supply chain network design (SCND) for fuzzy demand and transportation cost, and accordingly construct a fuzzy mathematical programming to demonstrate the situation. Bandyopadhyay and Bhattacharya (2013) developed a bi-objective supply chain, first objective is to minimize the total cost and second objective is to minimize the bullwhip effect, whereas order quantity is taken as fuzzy number. Ayag et al. (2013) determined the supply chain management strategies for dairy industry, wherein fuzzy quality function deployment (QFD) is used to maximize the customer satisfaction. Arikan (2013) studied a multiple sourcing supplier selection problem, wherein the retailer faced fuzzy demand rate.

In the real life situations, key parameters of a business activities are not linguistically imprecise, only, but it may have a random fluctuation, also. As we discussed at the beginning of the article, FRV is a hybrid type uncertainty that comprises fuzziness as well as randomness in itself, is used as a pioneer tool in recent trend of inventory modeling problem. Chang et al. (2006) and Dutta et al. (2007) extended the continuous review inventory system in fuzzy random environment. Chang et al. (2006) enhanced the normally distributed lead time demand as a FRV and annual expected demand as a fuzzy number, while Dutta et al. (2007) considered lead time demand as a fuzzy variable and annual demand as a discrete FRV. Lin (2008) and Dey and Chakraborty (2009) extended the periodic review inventory system in fuzzy random framework. Dey and Chakraborty (2011) further extended the continuous review inventory system by considering demand rate as a continuous FRV. Wang (2011) discussed a continuous review inventory system for imperfect quality items in fuzzy random environment, and used the concept of fuzzy random renewal process in determination of desired cost function. Recently, Kumar and Goswami (2013) developed a production–inventory model by considering machine shifting hazard in fuzzy random environment, in which shifting time is considered as a FRV. While an adequate number of research papers have incorporated hybrid uncertainty in inventory modeling problem, but unfortunately this advantage is not carrying out in SC modeling. However, authors such as Xu et al. (2008), Gumus and Guneri (2009) and Xu et al. (2011) developed some SC models in mixed environment of randomness and fuzziness. Xu et al. (2008) considered normally distributed demand rate with fuzzy parameter and shipping cost between the entities of network as FRVs. Gumus and Guneri (2009) considered demand, lead time and expediting cost as FRVs, and in this context artificial neural networks and neuro-fuzzy integration have been explained. Xu et al. (2011) considered demand and cost parameters as FRVs and the model is interpreted with genetic algorithm. Hu et al. (2010) established the vendor-buyer coordination for single-period in the centralized decision making process by incorporating the buyer fulfills fuzzy random demand of customers. Recently, Nagar et al. (2014) addressed an integrated SC in multi-objective framework by considering demand rate as scenario dependent FRV.

This paper models an IPP for the single-manufacturer and the single-buyer integrated inventory system in fuzzy random framework. The entire schema of supply chain is delineated in Fig. 1. The manufacturer purchases raw material from outside supplier. Through the production processes raw material is converted into finished product, and then finally delivers to the buyer who fulfills customers demand. As an evidence of literature review and the best of our knowledge, no SCIM model have been developed in fuzzy random environment under these circumstances. According to Lee (2005), the proportion of raw material and finished product is defined as conversion factor. In many enterprise such as steel industries, food processing and packaging etc., the conversion factor is always less than one. As an instance, we consider a manufacturer purchases paddy (raw material) from outside supplier (or local farmers), and through the production process converts its into rice (finished product). As we know a fraction of material called scrap is obtained during the process. Due to space constraint (limited space), scraps are instantly withdrawn from the warehouse. The “lot-for-lot” policy would not optimize the SCIM problem, especially when manufacturer’s setup cost is significantly higher than the buyer’s ordering cost (Banerjee 1986). In this context, the model determines the raw material lot size in such of a way that the finished product is an integer multiple of buyer’s order quantity. The centralized integrated-inventory management resulted lower mean total cost than that of planning separately for both integrating manufacturer’s production and buyer’s ordering, and integrating manufacturer’s raw material procurement and its production (Lee 2005, and referances therein). Thus, we assume that the model works under the centralized decision making process to determine the optimal policy. The objective of this IPP is to minimize the joint expected total costs of setup (including ordering costs of raw material), carrying of raw and finished items, buyer’s ordering, holding and backordering costs. We first discuss the model in random framework, then further extend it in fuzzy random environment.

Fig. 1
figure 1

Graphical representation of manufacturer–buyer coordination

Full size image

Preliminaries

Triangular fuzzy number

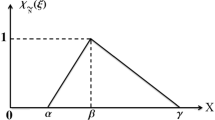
A triangular fuzzy number \(\tilde{a}=(a_1,a_2,a_3)\) where \(a_1\leqslant a_2\leqslant a_3\), is identified as a fuzzy subset on real line \(\mathbb {R}\), whose membership function \(\mu _{\tilde{a}}\) satisfies the following properties (Kaufmann and Gupta 1991):

  1. 1.

    \(\tilde{a}\) is normal, i.e., there exist \(x\in \mathbb {R}\) such that \(\mu _{\tilde{a}}(x)=1\).

  2. 2.

    \(\mu _{\tilde{a}}\) is a continuous mapping from \(\mathbb {R}\) to \([0, 1]\) which is defined as

    $$\begin{aligned} \mu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} L(x)=\frac{x-a_1}{a_2-a_1}, &{} a_1 \leqslant x \leqslant a_2; \\ R(x)=\frac{a_3-x}{a_3-a_2}, &{} a_2 \leqslant x \leqslant a_3; \\ 0, &{} \hbox {otherwise,} \end{array} \right. \end{aligned}$$
    (3.1)

    where \(L(x)\) is strictly increasing on \([a_1, a_2]\) called left spread function of \(\tilde{a}\), and \(R(x)\) is strictly decreasing on \([a_2, a_3]\) called right spread function.

  3. 3.

    \(\tilde{a}\) is a convex fuzzy subset on \(\mathbb {R}\).

  4. 4.

    Support of \(\tilde{a}\), \(supp\tilde{a}=cl\{x\in \mathbb {R}:\mu _{\tilde{a}}(x)>0\}\) where \(cl\) represents the closure of the set, is compact.

The \(\alpha \)-cut of \(\tilde{a}\), \(a_\alpha =[a_{\alpha }^-,a_{\alpha }^+]=[a_1+(a_2-a_1)\alpha , a_3-(a_3-a_2)\alpha ]\) where \(\alpha \in [0, 1]\), is a closed interval on \(\mathbb {R}\), \(a_{\alpha }^-\) is left and \(a_{\alpha }^+\) is right end points of \(a_{\alpha }\). Without loss of generality, we consider all imprecise key parameters as a triangular fuzzy number throughout this article.

Possibilistic mean value of a fuzzy number

Yoshida et al. (2006) enhanced Carlsson and Fuller’s (2001) interval-valued possibilistic mean value of a fuzzy number in the fuzzy measure framework. The fuzzy measure evaluates a confidence degree that the fuzzy number takes in an interval. Let \(\tilde{a}\) be a fuzzy number with compact support and the closed interval \(a_{\alpha }=[a_{\alpha }^-, a_{\alpha }^+]\) is its \(\alpha \)-cut, then possibility evaluation measure induced from the fuzzy number \(\tilde{a}\) is defined as

$$\begin{aligned} M_{\tilde{a}}^{P}(a_{\alpha })=\sup _{x\in a_{\alpha }} \mu _{\tilde{a}}(x). \end{aligned}$$
(3.2)

The mean value of a fuzzy number \(\tilde{a}\) with respect to possibility evaluation measure \(M_{\tilde{a}}^{P}\) is defined (Yoshida et al. 2006) as

$$\begin{aligned} M(\tilde{a}) = \frac{\int _0^1 M_{\tilde{a}}^P(\lambda a_{\alpha }^- + (1-\lambda )a_{\alpha }^+)d\alpha }{\int _0^1 M_{\tilde{a}}^Pd\alpha }, \end{aligned}$$
(3.3)

where \(\lambda a_{\alpha }^- + (1-\lambda )a_{\alpha }^+\) is called \(\lambda \)-weighting function. If \(\lambda =1/2\), then Eq. (3.3) becomes Carlsson and Fullér (2001) possibilistic mean value. We now propose a proposition that stated as below.

Proposition 3.1

If \(\tilde{a}\) is a triangular fuzzy number with compact support, and \(k\in \mathbb {R}\), then

$$\begin{aligned} M(k\tilde{a})&= k M(\tilde{a})\end{aligned}$$
(3.4)
$$\begin{aligned} \mathrm{and}\quad M(k+\tilde{a})&= k+M(\tilde{a}). \end{aligned}$$
(3.5)

Proof

Let us denote \(\tilde{b}=k\tilde{a}\). The \(\alpha \)-cut of \(\tilde{a}\) is \(a_{\alpha }=[a_{\alpha }^-, a_{\alpha }^+]\), this implies \(b_{\alpha }=[ka_{\alpha }^-, ka_{\alpha }^+]\). By using the extension principle, Kaufmann and Gupta (1991) have proved

$$\begin{aligned} \mu _{\tilde{b}}(x) = \mu _{\tilde{a}}(x/k). \end{aligned}$$
(3.6)

According to possibility evaluation measure (Yoshida et al. 2006), we have,

$$\begin{aligned}&M_{\tilde{b}}^P(b_{\alpha })\!=\!\sup _{x\in b_{\alpha }}\mu _{\tilde{b}} (x)=\sup _{x \in b_{\alpha }}\mu _{\tilde{a}}(x/k)\nonumber \\&\quad =\sup _{t \in a_{\alpha }}\mu _{\tilde{a}}(t)\!=\! M_{\tilde{a}}^P(a_{\alpha }). \end{aligned}$$
(3.7)

Hence,

$$\begin{aligned} M(\tilde{b})&= \frac{\int _0^1 M_{\tilde{b}}^P(b_{\alpha })[\lambda b_{\alpha }^{-}+ (1-\lambda )b_{\alpha }^+]d\alpha }{\int _0^1 M_{\tilde{b}}^P (b_{\alpha })d\alpha }\\&= \frac{k \int _0^1 M_{\tilde{a}}^P(a_{\alpha })[\lambda a_{\alpha }^- + (1-\lambda )a_{\alpha }^+]d\alpha }{\int _0^1 M_{\tilde{a}}^P (a_{\alpha })d\alpha } = k M(\tilde{a}). \end{aligned}$$

Now, let us denote \(\tilde{c}=\tilde{a} + k\). The \(\alpha \)-cut of \(\tilde{c}\) is \(c_{\alpha }=[c_{\alpha }^-, c_{\alpha }^+] =[a_{\alpha }^- + k, a_{\alpha }^+ + k]\) and \(\mu _{\tilde{c}}(x)=\mu _{\tilde{a}}(x-k)\). Hence,

$$\begin{aligned}&M_{\tilde{c}}^P(c_{\alpha }) = \sup _{x \in c_{\alpha }} \mu _{\tilde{c}}(x)\nonumber \\&\quad = \sup _{x \in c_{\alpha }}\mu _{\tilde{a}}(x-k) = \sup _{t \in a_{\alpha }}\mu _{\tilde{a}}(t) = M_{\tilde{a}}^P (a_{\alpha }). \end{aligned}$$
(3.8)

Now,

$$\begin{aligned} M(\tilde{c})&= \frac{\int _0^1 M_{\tilde{c}}^P(c_{\alpha })[\lambda c_{\alpha }^- + (1-\lambda )c_{\alpha }^+]d\alpha }{\int _0^1 M_{\tilde{c}}^P (c_{\alpha })d\alpha }\\&= \frac{ \int _0^1 M_{\tilde{a}}^P(a_{\alpha })[\lambda (a_{\alpha }^- + k) + (1-\lambda )(a_{\alpha }^++k)]d\alpha }{\int _0^1 M_{\tilde{a}}^P (a_{\alpha })d\alpha }\\&= M(\tilde{a}) + k. \end{aligned}$$

Hence, the proof is complete. \(\square \)

Fuzzy random variable

Kwakernaak (1978) introduced the notations of FRV. Later, various authors such as Gil et al. (2006), Yoshida et al. (2006) and Shapiro (2009) enhanced Kwakernaak (1978) and explained with more intelligibly. Roughly one can say, a FRV is an imprecise perception on the outcomes in the real-valued random variable. However, the mathematical (axiomatic) definition which is presented in simplest way by Gil et al. (2006) and is based on Kwakernaak (1978) view is discussed here.

Let \(\mathcal {K}(\mathbb {R}^n)\) denotes the class of non-empty compact subsets of \(n\)-dimensional Euclidean space \(\mathbb {R}^n\), and let \(\mathcal {K}_c(\mathbb {R}^n)\) be subclass of convex set in \(\mathcal {K}(\mathbb {R}^n)\). Further, let \(\mathcal {F}(\mathbb {R}^n)\) is the class of fuzzy values whose membership function is upper semi-continuous functions in \([0, 1]^{\mathbb {R}^n}\), i.e.,

$$\begin{aligned} \mathcal {F}(\mathbb {R}^n)\!=\!\Big \{\tilde{a}: \mu _{\tilde{a}}:\mathbb {R}^n \rightarrow [0, 1], a_{\alpha } \in \mathcal {K}(\mathbb {R}^n), \forall \alpha \in [0, 1] \Big \}. \end{aligned}$$
(3.9)

Now consider a case for one-dimension, \(\mathcal {F}_c(\mathbb {R})=\big \{\tilde{a}: \mu _{\tilde{a}}:\mathbb {R}\rightarrow [0, 1], a_{\alpha }\in \mathcal {K}_c(\mathbb {R}), \forall \alpha \in [0, 1]\big \}\). i.e., \(\mathcal {F}_c(\mathbb {R})\) is the class of upper semi-continuous convex function in \([0, 1]\) with compact \(supp~\tilde{a}\). Further, let us assume that \((\Omega , \mathcal {B}, P)\) be a probability space, where \(\mathcal {B}\) is the \(\sigma \)-algebra of the subsets of sample space \(\Omega \) and \(P\) is the probability measure. A mapping \(\tilde{X}:\Omega \rightarrow \mathcal {F}_c(\mathbb {R})\), is called a FRV if for all \(\alpha \in [0, 1]\), the two real-valued mappings \(X_{\alpha }^-:\Omega \rightarrow \mathbb {R}\) and \(X_{\alpha }^+:\Omega \rightarrow \mathbb {R}\) are real-valued random variables (Gil et al. 2006). For every \(\omega \in \Omega \), \(\tilde{X}_{\alpha }(\omega )=(\tilde{X}(\omega ))_{\alpha }\), and \(X_{\alpha }^-(\omega )=\inf (\tilde{X}(\omega ))_{\alpha }\), \(X_{\alpha }^+(\omega )=\sup (\tilde{X}(\omega ))_{\alpha }\). The expectation \(\widetilde{EX}\) of a FRV \(\tilde{X}\) is a unique fuzzy number that can be represented (see decomposition principle, Kaufmann and Gupta 1991), as \(\widetilde{EX}=\bigcup _{\alpha \in [0, 1]}\big [EX_{\alpha }^-, EX_{\alpha }^+\big ]=\bigcup _{\alpha \in [0, 1]}\big [E[X_{\alpha }^-], E[X_{\alpha }^+]\big ]\).

A FRV is a bearer of two types of uncertainties, one is randomness which can be interpreted through probability distribution function and other one is fuzziness that can be described through membership function (or possibility distribution function). In order to use FRV in decision making problem, its scalarization must be required. Yoshida et al. (2006) proposed an evaluation method where randomness is estimated by probabilistic expectation and fuzziness is estimated by possibilistic mean value. If \(\tilde{X}\) is a FRV, then the mean value of \(\tilde{X}\) is

$$\begin{aligned} E[M(\tilde{X})]=E\left[ \frac{\int _0^1 M_{\tilde{X}}^P (X_{\alpha }^- + X_{\alpha }^+)d\alpha }{2\int _0^1 M_{\tilde{X}}^P d\alpha } \right] . \end{aligned}$$
(3.10)

Notations and assumptions

Notations

\(D\) :

expected demand per unit time for the buyer

\(\beta \) :

conversion factor of raw material to finished product, \(0 < \beta < 1\)

\(P\) :

production rate per unit time of the manufacturer

\(A_v\) :

ordering cost of raw material per order

\(S_v\) :

the manufacturer’s set-up cost per set-up

\(h_f\) :

holding cost per unit per unit time of finished item for the manufacturer

\(h_r\) :

holding cost per unit per unit time of raw material for the manufacturer \((h_r < h_f)\)

\(A\) :

the buyer’s ordering cost per order

\(h_b\) :

holding cost per unit per unit time for the buyer

\(c_b\) :

unit shortage cost for the buyer

\(Q\) :

the buyer’s order quantity (decision variable)

\(Q_v\) :

the manufacturer’s order quantity of raw material (decision variable)

\(r\) :

reorder level in the buyer’s inventory system (decision variable)

\(\tau \) :

production run time

\(T\) :

cycle length of one production period

\(L\) :

constant lead time

\(m\) :

number of shipments in which the finished product is dispatched to the buyer in one production cycle (discrete decision variable)

\(X\) :

lead time demand which has normal distribution function with mean \(D_L=DL\) and standard deviation \(\sigma _L=\sigma \sqrt{L}\)

\(S=A_v + S_v\). \(\tilde{X}(\omega )=\big (X(\omega )-\Delta _1, X(\omega ), X(\omega )+\Delta _2\big )\), where \(X \sim N(D_L, \sigma _L^2)\) (normally distributed with mean \(D_L\) and variance \(\sigma _L^2\)), fuzzy random demand during lead time. \(\tilde{D}=(D-\Delta _3, D, D+\Delta _4)\), fuzzy expected demand per unit time. \(x^+=\max \{ x,0\}\).

Assumptions

  1. 1.

    There are the single-manufacturer and the single-buyer who deals with a single product.

  2. 2.

    The buyer orders a lot of size \(mQ\), and the manufacturer produces this quantity in one set-up and replenished to the buyer in \(m\) shipment each of size \(Q\). That is, in one production cycle \(T\), the manufacturer incurs one set-up (including raw material ordering) cost \(S\), while the buyer have to pay \(m\) times ordering cost.

  3. 3.

    The manufacturer receives a lot of raw material of size \(Q_v\), and through the production process converts its into finished product. The consumption rate of raw material is \(P\). The conversion factor \(\beta \), of raw material to finished product is less than one. Hence, production rate \(\beta P\) is less than consumption rate of raw material \(P\).

  4. 4.

    Machine produces finished product with the rate \(\beta P\) up to time \(\tau \). A fraction \((1-\beta )\) of \(P\), called scraps are obtained and thrown out instantly from the stocks.

  5. 5.

    To avoid the shortages during the production up time, a restriction is employed as \(\beta P > D +\Delta _4\).

  6. 6.

    The buyer’s inventory level is continuously reviewed, and an order is placed when it reaches to a certain level \(r\), called reorder level.

  7. 7.

    Shortages are allowed in the buyer’s inventory system and it is completely backlogged.

  8. 8.

    Demand rate per unit time follows normal distribution with mean \(D\) and variance \(\sigma ^2\). Lead time demand is convolution of \(L\) and demand rate. Thus, lead time demand, \(X\) is normally distributed with mean \(D_L=DL\) and variance \(\sigma _L^2=\sigma ^2 L\).

  9. 9.

    The time horizon is infinite.

  10. 10.

    Transportation cost from the vendor to the buyer is constant over time. Hence, transportation cost per unit time is ignored.

Model formulation

An IPP for the single-manufacturer single-buyer integrated system is mathematically derived here in random framework. The objective of this SC is to determine the optimal order quantity for both parties, reorder level for the buyer’s inventory system and number of shipments to the buyer in order to keep the JTRC as low as possible. The manufacturer’s inventory levels of both raw and finished items, delivery schemes to the both parties, and the buyer’s inventory level and reordering strategy are delineated in Fig. 2. The upper portion of Fig. 2 shows the manufacturer’s inventory levels of both type items with respect to time, whereas the lower portion shows the buyer’s inventory level and reordering strategies. In each cycle \(T\), the manufacturer procures once a lot of raw material of size \(Q_v\), and instantly starts the production process that is continued up to production up time \(\tau \). During this \(\tau \), inventory of raw material is continuously depleted with the consumption rate \(P\), and is reached at zero level at the end of the period. But, a fraction \(1-\beta ,~(0<\beta <1)\) called scrap fraction is obtained during production process. Hence, inventory of finished item is raised with the rate \(\beta P\). The production and demand satisfaction are synchronized. Whenever buyer’s inventory level reaches at reorder level \(r\), he/she places an order to the manufacturer, which is arrived after lead time \(L\). Thus, the manufacturer ships a batch of finished product of size \(Q\) to the buyer at every expected time interval \(Q/D\). In one production cycle, the manufacturer produces \(mQ\) quantity that delivers to the buyer in \(m\) shipment. During the production downtime, the manufacturer’s finished product inventory is flat if there is no replenishment, and is depleted by a quantity \(Q\) if a replenishment occurs. At the end of cycle \(T\), the manufacturer’s inventory reaches at zero level. After that the cycle repeats itself continuously.

Fig. 2
figure 2

The manufacturer’s and the buyer’s inventory position

Full size image

The manufacturer’s expected total cost

As we discussed above, the manufacturer’s produced quantity \(\beta Q_v\) is replenished to the buyer in \(m\) shipments each of size \(Q\). Hence, \(\beta Q_v=mQ\), this implies

$$\begin{aligned} Q_v=\frac{mQ}{\beta }. \end{aligned}$$
(5.1)

The inventory of raw material \(Q_v\) is consumed with the rate \(P\). Thus, the consumption time of \(Q_v\) or equivalently, the production runtime is

$$\begin{aligned} \tau =\frac{Q_v}{P}. \end{aligned}$$
(5.2)

Keeping consistency in production process as well as to heighten the customers service level, the manufacturer is carrying the inventory of raw material as well as finished product. The behavior of inventory level of both types of good opposes each other as shown in Fig. 2. Inventory of raw material continuously decreases whereas finished product’s is raw-tooth pattern. Thus, the holding cost of raw material and finished product (see Ouyang et al. 2004, 2007) is

$$\begin{aligned} H_v&= h_r\frac{1}{2}Q_v\tau + \frac{h_f mQ^2}{2D}\Big [m\Big (1-\frac{D}{\beta P}\Big )-1+\frac{2D}{\beta P}\Big ]\nonumber \\&= h_r\frac{m^2Q^2}{2P\beta ^2}\!+\!\frac{h_f mQ^2}{2D}\Big [m\Big (1\!-\!\frac{D}{\beta P}\Big )\!-\!1\!+\!\frac{2D}{\beta P}\Big ].\quad \end{aligned}$$
(5.3)

The manufacturer’s expected cycle length is \(mQ/D\). The expected total cost comprises with the sum of set-up cost, holding cost of raw material and finished product. So, the expected total cost per unit time is

$$\begin{aligned}&ETC_v(Q, m)\nonumber \\&\quad =\frac{D}{mQ}\Big [S + \frac{h_rm^2Q^2}{2P\beta ^2}+\frac{h_f mQ^2}{2D}\Big [m\Big (1-\frac{D}{\beta P}\Big )-1+\frac{2D}{\beta P}\Big ]\Big ]\nonumber \\&\quad =\frac{SD}{mQ} + \frac{h_rmQD}{2P\beta ^2}+\frac{h_fQ}{2} \Big [m\Big (1-\frac{D}{\beta P}\Big )-1+\frac{2D}{\beta P}\Big ]. \end{aligned}$$
(5.4)

The expected total cost for the buyer

As described in Fig. 2, the buyer orders a quantity \(Q\) whenever inventory reaches to a critical level \(r\), called reorder level. But, due to the order preparation, order transit, transportation etc., he/ she receives this quantity after elapsed time \(L\). The buyer’s expected cycle length is \(\frac{Q}{D}\). The expected ordering cost per unit time is \(\frac{AQ}{D}\). The expected net-inventory just before and after the arrival of order are \(r-D_L\) and \(Q+r-D_L\), respectively. Hence, the buyer’s expected net-inventory over the cycle is \(\frac{Q}{2}+r-D_L\). Shortages will occur when lead time demand, \(x>r\). The expected shortages in the buyer’s cycle is \(E(X-r)^+=\int _r^{\infty }(x-r)f(x)dx\). Thus the expected shortages per unit time is \(\frac{Q}{D}E(X-r)^+\). The expected total cost per unit time for the buyer comprises with ordering cost, holding cost and backordering cost as

$$\begin{aligned} ETC_b(Q,r)\!=\!\frac{AD}{Q}\!+\!h_b\Big (\frac{Q}{2}\!+\!r\!-\!D_L\Big )\!+\!\frac{c_bD}{Q}E(X\!-\!r)^+.\nonumber \\ \end{aligned}$$
(5.5)

Joint total relevant cost

The centralized decision making process demands coordination and cooperation between the parties. Coordination and cooperation amplify effectiveness and efficacious of SC which is desirable to tackle the difficulties such as short product life cycle, intense competition and heightened attention to customers. On the other side, it confers more financial benefits to the entire SC. Thus, we consider the situation in which both the manufacturer and the buyer belong to the single decision-maker system in which central planner make all decisions to minimize the total expected cost. In this policy the joint expected total cost per unit time for the manufacturer and the buyer is

$$\begin{aligned} JTRC(Q, r, m)&= ETC_b(Q, r) \!+\! ETC_v(Q, m)\nonumber \\&= \frac{AD}{Q}\!+\!h_b\Big (\frac{Q}{2}\!+\!r-D_L\Big )\nonumber \\&\quad +\,\frac{c_bD}{Q}E(X-r)^+ \!+\! \frac{SD}{mQ} \!+\! \frac{h_rmQD}{2P\beta ^2}\nonumber \\&\quad +\,\frac{h_fQ}{2}\Big [m\Big (1\!-\!\frac{D}{\beta P}\Big )-1\!+\!\frac{2D}{\beta P}\Big ].\qquad \end{aligned}$$
(5.6)

Model in mixed environment of fuzziness and randomness

There are mainly two sources of uncertainty that perturb the inventory control system and influence decision making process of SC, one is randomness (that taken as account in the previous section) and another one is fuzziness. This twofold uncertainty is often intrinsic in key parameters of business activities. To capture this feature, we now incorporate fuzziness in the model discussed in the previous section. Demand is the vitality of inventory management and SC, because of this, inventory is kept and inventory control problem exists. Demand may be internal or extraneous as the manufacturer faces in this model. Thus, a veritable realization of demand is desirable (especially when we talk about long-term strategic businesses) to maximize the profit. In real-life business transaction, it is very difficult for decision makers to find out the exact value of the demand (or expected demand). Usually, decision makers collect demand information from the experts’ opinion or previous data records. Experts’ experiences may conclude some imprecise information like ‘the demand is about \(D\)’, and this imprecise realization may vary randomly (by expert to expert or experience to experience). However, the description of demand rate as a FRV is more reliable compared to either random or fuzzy (see Chang et al. 2006). In this section, we first incorporate fuzziness in random lead time demand, and then discuss fuzzy expected demand rate. Let us denote that lead time demand as, \(\tilde{X}(\omega )=(X(\omega )-\Delta _1, X(\omega ), X(\omega )+\Delta _2)\), where \(X \sim N(D_L, \sigma ^2)\), and \(0 \leqslant \Delta _1, \Delta _2 \leqslant D_L\). The fuzzy random lead time demand steers JTRC as a FRV. As discussed in preliminaries section, we use possibilistic mean to estimate the fuzziness and probabilistic expectation to estimate the randomness of fuzzy random JTRC. If \(E[M(\tilde{X})]\) denotes the fuzzy expected value of \(\tilde{X}\) and \(\widetilde{JTRC}_L(Q, r, m)\) denotes the joint fuzzy expected total cost per unit time, then from Eq. (5.6), we have,

$$\begin{aligned} \widetilde{JTRC}_L(Q, r, m)&= \frac{A D}{Q}+h_b\Big (\frac{Q}{2}+r-E[M(\tilde{X})] \Big )\nonumber \\&\quad +\,\frac{c_bD}{Q}E[M((\tilde{X}-r)^+)] + \frac{SD}{mQ}+\frac{h_rmQD}{2P\beta ^2}\nonumber \\&\quad +\,\frac{h_fQ}{2}\Big [m\Big (1-\frac{D}{\beta P}\Big )-1+\frac{2D}{\beta P}\Big ]. \end{aligned}$$
(6.1)

For each \(\omega \in \Omega \), the \(\alpha \)-cut of \(\tilde{X}(\omega )=(x-\Delta _1, x, x+\Delta _2)\) is \(X_\alpha =[x-\Delta _1+\Delta _1\alpha , x+\Delta _2-\Delta _2\alpha ]\). The membership function \(\mu _{\tilde{X}}\) of \(\tilde{X}\) is

$$\begin{aligned} \mu _{\tilde{X}}(t)=\left\{ \begin{array}{ll} \frac{t-x+\Delta _1}{\Delta _1}, &{} x-\Delta _1 \leqslant t \leqslant x; \\ \frac{x+\Delta _2-t}{\Delta _2}, &{} x \leqslant t \leqslant x+\Delta _2; \\ 0,&{}\hbox {otherwise.} \end{array} \right. \end{aligned}$$
(6.2)

Since, \(M_{\tilde{X}}^P(X_\alpha )=\sup _{t\in X_\alpha }\mu _{\tilde{X}}(t)=1\). Hence,

$$\begin{aligned} M(\tilde{X})&= \frac{\displaystyle \int _0^1 M_{\tilde{X}}^P(X_\alpha )\Big (\frac{X_{\alpha }^-+X_{\alpha }^+}{2}\Big )d\alpha }{\displaystyle \int _0^1 M_{\tilde{X}}^P(X_\alpha )d\alpha }\nonumber \\&= x+\frac{\Delta _2-\Delta _1}{4}.\end{aligned}$$
(6.3)
$$\begin{aligned} \therefore ~ E[M(\tilde{X})]&\!=\!&E\left[ x\!+\!\frac{\Delta _2\!-\!\Delta _1}{4}\right] \!=\!D_L\!+\!\frac{\Delta _2\!-\!\Delta _1}{4}.\quad \end{aligned}$$
(6.4)

Evaluation of \(\varvec{E[M((\tilde{X}-r)^+)]}\)

Due to fuzzy random demand rate, shortage occurrence in the buyer’s inventory system during lead time is a random phenomenon which inherits fuzziness also, and it will happen when \(\tilde{X} > r\). If shortage occurs, then shortage quantity \((\tilde{X}-r)^+\) is a FRV. Let us denote \(\tilde{Y}=(\tilde{X}-r)^+\), where \(\tilde{X}-r=(x-\Delta _1-r, x-r, x+\Delta _2-r)\). Since, \(x\) is a variable, so, for fixed \(r,~\Delta _1\) and \(\Delta _2\), there are four possible cases (i) \(x \in [r+\Delta _1,\infty )\), (ii) \(x \in [r, r+\Delta _1]\), (iii) \(x \in [r-\Delta _2,r]\) and (iv) \(x \in (-\infty , r-\Delta _2]\) as delineated in Fig. 3.

Fig. 3
figure 3

Fuzzy shortage quantity: a when \(x\in [r+\Delta _1,\infty )\), b when \(x\in [r,r+\Delta _1]\), c when \(x\in [r-\Delta _2,r]\) and d when \(x\in (-\infty ,r-\Delta _2]\)

Full size image

Case i. When \(x \in [r+\Delta _1 , \infty )\), then the membership function \(\mu _{\tilde{Y}}\) of \(\tilde{Y}\) is shown in Fig. 3a, and is defined as

$$\begin{aligned} \mu _{\tilde{Y}}(y)=\left\{ \begin{array}{ll} \frac{y-(x-\Delta _1-r)}{\Delta _1}, &{} x-\Delta _1-r \leqslant y \leqslant x-r ; \\ \frac{(x+ \Delta _2-r) -y}{\Delta _2}, &{} x-r \leqslant y \leqslant x+\Delta _2-r; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$
(6.5)

The \(\alpha \)-cut of \(\tilde{Y}\) for this case is \(Y_{\alpha }=[Y_\alpha ^-, Y_\alpha ^+]=[x-\Delta _1-r+\Delta _1 \alpha , x+\Delta _2-r-\Delta _2\alpha ], ~0 \leqslant \alpha \leqslant 1\). Hence, \(M_{\tilde{Y}}^P(Y_\alpha )=\sup _{y\in Y_\alpha }\mu _{\tilde{Y}}(y)=1\), and

$$\begin{aligned} M(\tilde{Y})&= \frac{\displaystyle \int _0^1 \Big (\frac{Y_\alpha ^- + Y_{\alpha }^+}{2}\Big )M_{\tilde{Y}}^P(Y_\alpha )d\alpha }{\int _0^1M_{\tilde{Y}}^P(Y_\alpha )d\alpha }\nonumber \\&= \frac{1}{2}\int \limits _0^1(x\!-\!\Delta _1\!-\!r\!+\!\Delta _1\alpha \!+\! x\!+\!\Delta _2\!-\!r\!-\!\Delta _2\alpha )d\alpha \nonumber \\&= x-r+\frac{\Delta _2-\Delta _1}{4}. \end{aligned}$$
(6.6)

Case ii. When \(x \in [r, r+\Delta _1 ]\), then Fig. 3b shows the membership function \(\mu _{\tilde{Y}}\) of \(\tilde{Y}\) by smooth line of triangle, and is obtained as

$$\begin{aligned} \mu _{\tilde{Y}}(y)=\left\{ \begin{array}{ll} \frac{y-(x-\Delta _1-r)}{\Delta _1},&{}0 \leqslant y \leqslant x-r ; \\ \frac{(x+ \Delta _2-r) -y}{\Delta _2}, &{} x-r \leqslant y \leqslant x+\Delta _2-r; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$
(6.7)

The \(\alpha \)-cut of \(\tilde{Y}\) for this case is

$$\begin{aligned} Y_{\alpha }\!=\!\left\{ \begin{array}{ll} \left[ 0, x\!+\!\Delta _2-r-\Delta _2 \alpha \right] , &{} 0 \leqslant \alpha \leqslant \frac{r\!+\!\Delta _1\!-\!x}{\Delta _1}\leqslant 1; \\ \left[ x\!-\!\Delta _1\!-\!r\!+\!\Delta _1 \alpha , x\!+\!\Delta _2-r-\Delta _2 \alpha \right] , &{} 0 \leqslant \frac{r+\Delta _1-x}{\Delta _1} \leqslant \alpha \leqslant 1. \end{array} \right. \nonumber \\ \end{aligned}$$
(6.8)

So, \(M_{\tilde{Y}}^P(Y_\alpha )=\sup _{y\in Y_\alpha }\mu _{\tilde{Y}}(y)=1\). Hence,

$$\begin{aligned} M(\tilde{Y})&\!=\!&\frac{1}{2}\displaystyle \int \limits _0^{\frac{r+\Delta _1-x}{\Delta _1}}(x+\Delta _2-r-\Delta _2 \alpha )d\alpha \nonumber \\&\quad +\frac{1}{2}\displaystyle \int \limits _{\frac{r+\Delta _1-x}{\Delta _1}}^1[x-\Delta _1-r+\Delta _1 \alpha + x+\Delta _2-r-\Delta _2 \alpha ]d\alpha \nonumber \\&= \frac{1}{2}\Big (x+\frac{\Delta _2}{2}-r\Big )-\frac{(x-\Delta _1-r)^2}{4\Delta _1}. \end{aligned}$$
(6.9)

Case iii. When \(x \in [r-\Delta _2, r ]\), then the membership function \(\mu _{\tilde{Y}}\) of \(\tilde{Y}\) is shown by the smooth line of triangle in Fig. 3c, and is defined as

$$\begin{aligned} \mu _{\tilde{Y}}(y)=\left\{ \begin{array}{ll} \frac{x+\Delta _2-r-y}{\Delta _2}, &{} 0 \leqslant y \leqslant x+\Delta _2-r ; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$
(6.10)

The \(\alpha \)-cut of \(\tilde{Y}\) for this case is

$$\begin{aligned} Y_\alpha =\left\{ \begin{array}{ll} [0, 0], &{} 0 \leqslant \frac{x-r+\Delta _2}{\Delta _2} \leqslant \alpha \leqslant 1; \\ \left[ 0, x+\Delta _2-r-\Delta _2\alpha \right] , &{} 0 \leqslant \alpha \leqslant \frac{x-r+\Delta _2}{\Delta _2} \leqslant 1. \end{array} \right. \end{aligned}$$
(6.11)

\(M_{\tilde{Y}}^P(Y_\alpha )=\sup _{y\in Y_\alpha }\mu _{\tilde{Y}}(y)=\frac{x-r+\Delta _2}{\Delta _2}\). Hence,

$$\begin{aligned} M(\tilde{Y})&= \frac{\displaystyle \int _0^1\Big (\frac{Y_\alpha ^-+Y_\alpha ^+}{2}\Big )M_{\tilde{Y}}^P(Y_\alpha )d\alpha }{\displaystyle \int _0^1M_{\tilde{Y}}^P(Y_\alpha )d\alpha }\nonumber \\&= \frac{\displaystyle \int _0^{\frac{x-r+\Delta _2}{\Delta _2}}\Big (\frac{0\!+\!x\!+\!\Delta _2 -r-\Delta _2\alpha }{2}\Big )\frac{x-r\!+\!\Delta _2}{\Delta _2}d\alpha }{\displaystyle \int _0^{\frac{x-r\!+\!\Delta _2}{\Delta _2}}\frac{x-r\!+\!\Delta _2}{\Delta _2}d\alpha }\nonumber \\&= \frac{x-r+\Delta _2}{4}. \end{aligned}$$
(6.12)

Case iv. When \(x\in (-\infty , r-\Delta _2]\), then as shown in Fig. 3d, membership value \(\mu _{\tilde{Y}}\) of \(\tilde{Y}\) is equal to zero. So, for this case \(M(\tilde{Y})=0\).

In the above discussed four cases, for \(\omega \in \Omega \), we have found possibilistic mean value of \(\tilde{Y}(\omega )\) according to location of \(r\). We now combine all cases to find the expected value of possibilistic mean \(M(\tilde{Y})\). We have from the Eqs. (6.6), (6.9) and (6.12),

$$\begin{aligned}&E[M((\tilde{X}-r)^+)]= \int \limits _{r+\Delta _1}^{\infty }\Big (x-r+\frac{\Delta _2-\Delta _1}{4} \Big )f(x)dx\nonumber \\&\quad +\int \limits _r^{r+\Delta _1}\Big [\frac{1}{2}\Big (x+\frac{\Delta _2}{2}-r\Big ) -\frac{(x-\Delta _1-r)^2}{4\Delta _1}\Big ]f(x)dx\nonumber \\&\quad +\int \limits _{r-\Delta _2}^r \frac{x-r+\Delta _2}{4}f(x)dx\nonumber \\&\quad = \int \limits _{r}^{\infty }\Big (x-r+\frac{\Delta _2-\Delta _1}{4} \Big )f(x)dx\nonumber \\&\qquad -\frac{1}{4\Delta _1}\int \limits _r^{r+\Delta _1}(x-r)^2f(x)dx\nonumber \\&\qquad +\frac{1}{4}\int \limits _{r-\Delta _2}^r (x-r+\Delta _2)f(x)dx \end{aligned}$$
(6.13)
$$\begin{aligned}&=-\left( r-D_L-\frac{\Delta _2-\Delta _1}{4}\right) \nonumber \\&\quad +\frac{(r-D_L+\Delta _1)^2 +\sigma _L^2+\Delta _1(r-D_L)}{4\Delta _1}\Phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad -\,\frac{1}{4\Delta _1}[(r-D_L)^2+\sigma _L^2]\Phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big )\nonumber \\&\quad +\,\left( \frac{r-D_L-\Delta _2}{4}\right) \Phi \Big (\frac{r-D_L-\Delta _2}{\sigma _L}\Big )\nonumber \\&\quad +\,\sigma _L\left( \frac{r-D_L+3\Delta _1}{4\Delta _1}\right) \phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad -\,\sigma _L\left( \frac{r-D_L-\Delta _1}{4\Delta _1}\right) \phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big )\nonumber \\&\quad +\,\frac{\sigma _L}{4}\phi \Big (\frac{r-D_L-\Delta _2}{\sigma _L}\Big ) = G(r)~\mathrm{(say)}, \end{aligned}$$
(6.14)

where \(\phi (z)=\frac{1}{\sqrt{2\pi }}e^{-\frac{1}{2}z^2}\) and \(\Phi (z)=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^{z}e^{-\frac{1}{2}t^2}dt\) are standard normal distribution and cumulative normal distribution functions, respectively. Equation (6.14) is a function of the decision variable \(r\), for simplicity, we denote this quantity by \(G(r)\). Hence, the defuzzified value of Eq. (6.1) can be rewritten as

$$\begin{aligned}&JTRC_L(Q,r,m)=\left[ \frac{1}{Q}\left( A+c_b G(r) +\frac{S}{m} \right) \right. \nonumber \\&\quad \left. +\,\frac{h_r m Q}{2\beta ^2 P} \!-\!\frac{h_f Q(m\!-\!2)}{2\beta P}\right] D\nonumber \\&\quad +\,h_b\left( \frac{Q}{2} \!+\!r \!-\!D_L \!-\! \frac{\Delta _2\!-\!\Delta _1}{4}\right) \!+\!\frac{h_f Q(m\!-\!1)}{2}. \end{aligned}$$
(6.15)

Fuzzy expected demand rate

In the earlier discussed contiguity, instead a precise average demand per unit time, we consider here this is a triangular fuzzy number as \(\tilde{D}=(D-\Delta _3,D,D+\Delta _4)\), where \(\Delta _3\) and \(\Delta _4\) are decided by decision makers, but it must be restricted as \(0\leqslant \Delta _3 \leqslant D\) and \(\Delta _4 \geqslant 0\). From Eq. (6.15), the fuzzy JTRC can be written as

$$\begin{aligned}&\widetilde{JTRC}(Q, r, m)\nonumber \\&\quad \!=\!\left[ \frac{1}{Q}\left( A\!+\!c_b G(r) \!+\!\frac{S}{m} \right) \!+\!\frac{h_r m Q}{2\beta ^2 P} \!-\!\frac{h_f Q(m\!-\!2)}{2\beta P} \right] \tilde{D}\nonumber \\&\quad \!+\,h_b\left( \frac{Q}{2} \!+\!r \!-\!D_L \!-\! \frac{\Delta _2\!-\!\Delta _1}{4}\right) \!+\!\frac{h_f Q(m\!-\!1)}{2}. \end{aligned}$$
(6.16)

Now, we use the Proposition 3.1 to find the possibilistic mean of above fuzzy cost function. Let us denote this as \(JRTC(Q, r, m)\), then

$$\begin{aligned}&JTRC(Q, r, m)\nonumber \\&\quad =\Big [\frac{1}{Q}\left( A+c_b G(r) +\frac{S}{m} \right) +\frac{h_r m Q}{2\beta ^2 P} -\frac{h_f Q(m-2)}{2\beta P}\Big ]M(\tilde{D})\nonumber \\&\quad +\,h_b\left( \frac{Q}{2} +r -D_L - \frac{\Delta _2-\Delta _1}{4}\right) +\frac{h_f Q(m-1)}{2}. \end{aligned}$$
(6.17)

\(\tilde{D}\) is a normal fuzzy number with compact support and \(\alpha \)-cut of \(\tilde{D}\) is \(D_{\alpha }=[D_{\alpha }^-, D_{\alpha }^+]=[D-\Delta _3 + \Delta _3 \alpha , D+\Delta _4 - \Delta _4 \alpha ]\), so, it must be \(M_{\tilde{D}}^P(D_{\alpha })=1\). Hence, \(M(\tilde{D})=\int _0^1\frac{1}{2}(D_{\alpha }^- + D_{\alpha }^+)d\alpha \) \(=D + \frac{\Delta _4 - \Delta _3}{4}\). For sake of simpler notation, Eq. (6.17) can be rewritten as

$$\begin{aligned} JTRC(Q, r, m)= \frac{H(m)Q}{2} + h_b(r-\gamma ) + \frac{1}{Q}\Big (A + c_b G(r) + \frac{S}{m}\Big )\Gamma \end{aligned}$$
(6.18)

where

$$\begin{aligned} \Gamma&= D + \frac{\Delta _4- \Delta _3}{4},~~ \gamma = D_L + \frac{\Delta _2 - \Delta _1}{4}\nonumber \\ \mathrm{and ~~}H(m)&= h_b + h_f (m-1) + \Big (\frac{h_r m}{\beta ^2 P} - \frac{h_f (m-2)}{\beta P} \Big )\Gamma . \end{aligned}$$
(6.19)

Solution procedure

Proposition 7.1

For fixed values of \(r\) and \(m\), \(JTRC(Q,r,m)\) is convex over \(Q\), and

$$\begin{aligned} Q(r, m)=\sqrt{2\Big (A + c_b G(r) + \frac{S}{m}\Big )\Gamma /H(m)}. \end{aligned}$$
(7.1)

Proof

It can be easily proved. \(\square \)

Now, we substitute the value of \(Q(r, m)\) in Eq. (6.18), this gives

$$\begin{aligned} JTRC(r, m)=\sqrt{2\Big (A + c_b G(r) + \frac{S}{m}\Big )\Gamma H(m)} + h_b(r-\gamma ). \end{aligned}$$
(7.2)

\(JTRC(r, m)\) is a function of a continuous variable \(r\) and a discrete variable \(m\). An elaborative method in order to determination of \(r\) for a fixed \(m\) is discussed now. For this, we first find the derivatives of \(JTRC(r, m)\) with respect to \(r\).

$$\begin{aligned} \frac{dJTRC(r, m)}{dr}=\frac{c_b G^{'}(r)\sqrt{\Gamma H(m)}}{\sqrt{2\Big (A+c_bG(r)+\frac{S}{m}}\Big )}+h_b \end{aligned}$$
(7.3)

and

$$\begin{aligned} \frac{d^2JTRC(r, m)}{dr^2}&= \frac{c_b G^{''}(r)\sqrt{\Gamma H(m)}}{\sqrt{2\Big (A+c_bG(r)+\frac{S}{m}}\Big )}\nonumber \\&\quad - \frac{c_b \sqrt{\Gamma H(m)}G^{'^2}(r)}{\Big [2\Big (A + c_bG(r) + \frac{S}{m}\Big )\Big ]^{3/2}} \end{aligned}$$
(7.4)

where

$$\begin{aligned} G^{'}&= \frac{dG(r)}{dr}=-1+\frac{2(r-D_L)+3\Delta _1}{4\Delta _1}\Phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad -\,\frac{r-D_L}{2\Delta _1}\Phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big )\nonumber \\&\quad +\,\frac{1}{4}\Phi \Big (\frac{r-D_L-\Delta _2}{\sigma _L}\Big )\nonumber \\&\quad +\,\frac{\Delta _1^2+2\sigma _L^2}{4\Delta _1\sigma _L}\phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad -\,\frac{\Delta _1^2+2\sigma _L^2}{4\Delta _1\sigma _L}\phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big ) \end{aligned}$$
(7.5)

and

$$\begin{aligned} G^{''}&= \frac{d^2G(r)}{dr^2}=\frac{1}{2\Delta _1}\Phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad -\frac{1}{2\Delta _1}\Phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big )\nonumber \\&\quad +\frac{3\sigma _L^2-\Delta _1(r-D_L)}{4\sigma _L^3}\phi \Big (\frac{r-D_L}{\sigma _L}\Big )\nonumber \\&\quad +\frac{\Delta _1(r-D_L)+2\sigma _L^2+\Delta _1^2}{4\sigma _L^3}\phi \Big (\frac{r-D_L+\Delta _1}{\sigma _L}\Big )\nonumber \\&\quad +\frac{1}{4\sigma _L}\phi \Big (\frac{r-D_L-\Delta _2}{\sigma _L}\Big ). \end{aligned}$$
(7.6)

The necessary condition, to obtain the value of \(r\) is \(\frac{d JTRC}{dr} = 0\). This implies \(G^{'} = - \frac{h_b \sqrt{2\big (A + c_b G(r) + S/m\big )}}{ c_b \sqrt{\Gamma H(m)}}\). Moreover, the sufficient condition for optimality of \(r\) from Eq. (7.4) becomes as

$$\begin{aligned} \frac{d^2JTRC(r, m)}{dr^2}=\frac{\Gamma H(m)c_b G^{''}(r) - h_b^2}{\sqrt{2 \Gamma H(m)} \sqrt{A + c_b G(r) + S/m}} > 0. \end{aligned}$$
(7.7)

\(\Gamma \) is the possibilistic mean value of fuzzy expected demand, so, it must be \(\Gamma >0\). \(H(m)\) can be written as \(h_b + h_f(m-1)\big (1- \Gamma /\beta P \big ) + \big (h_r m /\beta ^2 P + h_f/\beta P\big )\Gamma \). Now, \(\Gamma = D + (\Delta _4 - \Delta _3)/4 = D + \Delta _4 -(3 \Delta _4 + \Delta _3)/4\) \( < D +\Delta _4 < \beta P\) (due to assumption 5). This implies \(\Gamma / \beta P < 1\). Hence, \(H(m) > 0\). Also, \(G(r) = E[M((\tilde{X}-r)^+)] > 0\). Thus the denominator of Eq. (7.7) is positive. Therefore, \(d^2JTRC / dr^2 > 0\) if and only if \(\Gamma H(m)c_b G^{''}(r) > h_b^2\).

Furthermore, since \(m\) is a decision variable which must be a positive integer. Hence for a given \(r\), optimum \(m\) that minimizes JTRC must satisfy the following conditions.

$$\begin{aligned}&JTRC(r,m) \leqslant JTRC(r, m -1)~\mathrm{and~}JTRC(r, m)\nonumber \\&\quad \leqslant JTRC(r, m +1).\nonumber \\ \end{aligned}$$
(7.8)

\(JTRC(r, m) \leqslant JTRC(r, m -1)\) implies

$$\begin{aligned} m(m-1)\leqslant \frac{S\Big [h_b-h_f+\frac{2h_f\Gamma }{\beta P} \Big ]}{[A+c_bG(r)] \Big [h_f+\Big (\frac{h_r}{\beta ^2P}-\frac{h_f}{\beta P}\Big )\Gamma \Big ]} \end{aligned}$$
(7.9)

and \(JTRC(r, m) \leqslant JTRC(r, m +1)\) implies

$$\begin{aligned} \frac{S\Big [h_b-h_f+\frac{2h_f\Gamma }{\beta P} \Big ]}{[A+c_bG(r)] \Big [h_f+\Big (\frac{h_r}{\beta ^2P}-\frac{h_f}{\beta P}\Big )\Gamma \Big ]}\leqslant m(m+1). \end{aligned}$$
(7.10)

Combining the relations (7.9) and (7.10), the optimality condition for \(m\) becomes as

$$\begin{aligned} m(m\!-\!1)\leqslant \frac{S\Big [h_b-h_f\!+\!\frac{2h_f\Gamma }{\beta P} \Big ]}{[A\!+\!c_bG(r)] \Big [h_f\!+\!\Big (\frac{h_r}{\beta ^2P}\!-\!\frac{h_f}{\beta P}\Big )\Gamma \Big ]}\leqslant m(m\!+\!1). \end{aligned}$$
(7.11)

Let us denote

$$\begin{aligned} F(r) = \frac{S\Big [h_b-h_f+\frac{2h_f\Gamma }{\beta P} \Big ]}{[A+c_bG(r)] \Big [h_f+\Big (\frac{h_r}{\beta ^2P}-\frac{h_f}{\beta P}\Big )\Gamma \Big ]}. \end{aligned}$$
(7.12)

It is now necessary to summarize the above discussion systematically in order to access the global optimal policy, for this purpose we develop an algorithm. In general, the decision maker would not wish a negative safety stock. So, one can start with \(r_1=D_L + (\Delta _2 - \Delta _1)/4\), accordingly to find \(m_1\) such that the relation (7.11) holds, and can access the optimal solution in the following way.

Algorithm

Step 1. :

Set \(i=1\), \(r_1=D_L+(\Delta _2-\Delta _1)/4\) and corresponding \(m_1\). Then correspondingly find \(Q_1(r_1, m_1)\) and \(JTRC(Q_1, r_1, m_1)\).

Step 2. :

Set \(i=i+1\), and find \(r_i\) from the equation \(c_b G^{'}(r)\sqrt{\Gamma H(m_{i-1})}/\sqrt{2\big (A+c_bG(r)+S/m_{i-1}}\big )+\!h_b = 0\) by using Mathematica software. Check whether \(r_i > D_L + (\Delta _2-\Delta _1)/4\), if yes, go to step 3, otherwise go to step 6.

Step 3. :

Evaluate \(m_i\) in such a way that the relation \(m_i(m_i-1) \leqslant F(r_i) \leqslant m_i(m_i+1)\) must be satisfied, and then evaluate the correspondingly \(Q_{i}(r_i, m_i)\).

Step 4. :

If \(\Gamma H(m_{i}) c_b G^{''}(r_{i}) \leqslant h_b^2\), then go to step 6. Otherwise compute \(JTRC(Q_{i}, r_{i}, m_{i})\).

Step 5. :

If \(JTRC(Q_{i}, r_{i}, m_{i})\approx JTRC(Q_{i-1}, r_{i-1}, m_{i-1})\), then \(Q^{*}=Q_{i},~r^{*}=r_{i},\) \(m^{*}=m_{i}\) and \(JTRC^{*}=JTRC(Q_i, r_i, m_i)\). Otherwise goto step 2.

Step 6. :

\(r^* = r_{i-1}\), \(m^*=m_{i-1}\), \(Q^*=Q(r_{i-1}, m_{i-1})\) and \(JTRC^{*}=JTRC(Q_{i-1}, r_{i-1}, m_{i-1})\), where superscript \(^*\) denotes optimal solution.

Remark 7.1

If we consider no fuzziness in the random demand, i.e., \(\Delta _3=\Delta _4=0\), \(\Delta _1=\Delta _2=\Delta \rightarrow 0\), no carrying charge for raw material, i.e., \(h_r=0\) and conversion factor \(\beta =1\), then Eq. (6.19) reduce as: \(\Gamma =D,~\gamma =D_L\), \(H(m)=h_b+h_f\Big (m(1-D/P)-1+2 D/P\Big )\) and \(G(r)=\int _r^{\infty }(x-r)f(x)dx\). The order quantity (7.1) becomes \(\sqrt{2\big [A + c_b G(r)+S/m\big ]D/H(m)}\). This is Ouyang et al. (2004) order quantity. Thus, our model is a generalization of earlier models.

Illustrative example

This study aims to consider a situation where farmers are bringing items say paddy to near by a rice mill where its are converted into rice. 20 % husk is obtained during conversion process. The manufacturer who accomplishes conversion process keeps stocks of paddy as well as rice. Such a situation has been taken into account and accordingly following essential parameters are given: \(D=1,000\) bags/year, \(P=3,200\) bags/year, \(\sigma =7\) bags/week, where each bag contains 100 Kg. All cost parameters are taken in INR. \(A=25\) per order, \(A_v=400\) per order, \(h_b=5\)/bag/unit time, \(h_f=4\)/bag/unit time, \(h_r=2\)/bag/unit time, \(c_b=7\)/bag, \(S_v=100\) per setup, \(L=4\) week, \(\Delta _3=300,~\Delta _4=300\). Thus, \(S = 500\), the expected demand during lead time, \(D_L=\frac{DL}{50}=80\) and standard deviation of lead time demand, \(\sigma _L=\sigma \sqrt{L}=14\), \(\Delta _1 = \frac{\Delta _3 L}{50}=24,~\Delta _2 = \frac{\Delta _4 L}{50}=24\). Since 20 % husk is obtained during conversion process, this implies conversion factor is \(\beta =0.8\). As discussed in Algorithm, we start with \(r_1=80\Rightarrow m_1=3\), the output of each iteration is shown in Table 1. The optimal policy is: \(m^{*}=4,~r^{*}=106.96,~Q^{*}=132.86\) and the joint total expected cost is \(2497.17\). The manufacturer order quantity of raw material is, \(Q_v^{*}=\frac{m^{*}Q^{*}}{\beta }=664\).

Table 1 Iterative procedure
Full size table

Sensitivity of raw material procurement and holding costs: When \(h_r=0=S_v\), i.e., no procurement and holding charges for raw material are included (such as Lee 2005) in SC, then Table 2 yields \(r^{*}=108.90,~m^{*}=5\), \(Q^{*}=116.51\), \(JTRC^{*}=2045.10\) and \(Q_v^{*}=728\). A little difference in our optimal policy and Lee (2005) optimal policy is noticed. It is because of we have considered fuzzy random demand rate wherein shortage is not prohibited, whereas Lee (2005) has taken deterministic and constant demand wherein shortage is prohibited. When procurement cost increases from 100 to 1,500, then \(r^{*}=108.74,~Q^{*}=117.83\), \(m^*=9,~JTRC^*=4,250.16\) and \(Q_v^{*}=1,325\). Increment in procurement cost increases procurement quantity and number of shipment to the buyer, consequently, \(JTRC^*\) also increases. Finally, when holding cost increases from 2 to 3, then \(r^{*}=107.75,~m^{*}=4\), \(Q^{*}=125.9\), \(JTRC^{*}=2623.43\) and \(Q_v^{*}=630\). Thus, the manufacturer’s procurement and carrying costs highly influences the entire SC, and the buyer’s ordering as well as reordering policy also has significant impact.

Table 2 Sensitivity of ordering and holding costs
Full size table

Sensitivity of spreads of fuzzy demand: How the spreads \(\Delta _1,\Delta _2, \Delta _3\) and \(\Delta _4\) of fuzzy demand influence the optimal policy is tested here. When \(\Delta _1\), \(\Delta _3\) are fixed and \(\Delta _2\), \(\Delta _4\) increase, then buyer’s reorder level significantly increases, buyer’s order quantity and JTRC increase also, whereas shipment times to the buyer’s remains constant as shown in Table 3. When \(\Delta _2,~\Delta _4\) are fixed and \(\Delta _1,~\Delta _3\) increase, then \(r^{*}\) and \(JTRC^{*}\) decrease, shipment times to the buyer changes, also. Demand uncertainty highly influences reorder level, it varies from 94.19 to 124.58 as Table 3 delineates. Moreover, we can say that left spread of demand in more sensitive compare to right spread. Hence, fuzzy random demand mark a significant efficacy in the optimal policy.

Table 3 Sensitivity of spreads of fuzzy random demand
Full size table

Conclusion

This article addressed a two-echelon IPP for the manufacturer–buyer integrated inventory system, who work under the centralized decision making process. This study adorn with advantage to integrate the concepts of raw material procurement, its maintenance and stochastic customers’ demand, together, wherein shortage is not prohibited. Furthermore, this two-echelon SC extends customers’ demand as a fuzzy random variable. Contextually, fuzzy expectation based on probabilistic expectation and possibility evaluation measure coalesce to mathematically interpret the proposed model. A new methodology have been proposed to evaluate the fuzzy expected shortage quantity during stock out period. We have established a multi-ordering policy for the buyer in the manufacturer’s one production cycle in such a way that JTRC for both parties is minimum. An efficient and effective solution procedure is discussed to derive the order quantity, reorder level, number of shipment to the buyer and order quantity of raw material which minimizes the JTRC. The proposed model and algorithm are illustrated with numerical example. The sensitivity for changing parameters are carried out and discussed, also. A significant changes in the optimal policy for changing parameters are pointed out. This model is distinct from the existing models, one can easily notice this through the numerical analysis as discussed in Sect. 8. In many manufacturing systems such as chemical industries, steel industries, food processing and packaging etc., the conversion factor of raw material to finished item is plausible. Thus the proposed SCIM model can be applied in such type of enterprises.

JIT (Just-in-time) delivery system focuses immediate consumption of required item, and it is widely accepted by Japanese Companies. JIT require to reduce the lead-time yield to immediate use of item. In this account, this model can be further extended in the direction of lead-time reduction. One more possible extension of this SC, to incorporate lead time as a FRV.