1 Introduction

Electric circuit design is greatly supported by circuit simulators. One of the widely established codes is SPICE [1], and it is based on the elementary nodal relations between electronic devices. Every component is dealt as a black box having an input and output. The response of every single component is known. Parallel or in series, connections of different components create an integrated circuit design and the elementary rules in electric engineering establish an overall system response computed by, for example, SPICE algorithm. The general idea is based on Kirchhoff’s law, which states that the total electric current entering a node and the total electric current leaving that node are equal. This balance is fundamental, and for every single node, this basic law generates one equation to fulfill. In a circuit with hundreds of components, we have a system of only hundreds of equations solved in less than a minute with a regular laptop. Hence, such a circuit simulator is a powerful support in engineering design. It is simple, fast, and reliable for non-dissipative systems. Before the production stage, one can test and develop the suggested design at (nearly) no cost.

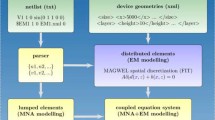
A circuit simulator reduces the complexity of a system by means of four assumptions. First of all, the components are analyzed as being isolated, i.e., the components have no interactions with each other. Second, the components are simplified and their geometric shape is completely ignored in a circuit simulator. Third, all components are modeled as rigid bodies. Fourth, connections (solders, pads, traces, and vias) are perfect conductors such that no dissipation is modeled. These assumptions are shown in Fig. 1; we want to discuss their effects to the accuracy.

Fig. 1
figure 1

Diagram of assumptions necessary for the circuit simulator SPICE

Full size image

It is important to remark that in the industry, these simplifications are seen critical and different strategies are used to overcome the inaccuracy determined with the aid of experiments. Especially in nanometer length scale, the deficiencies are well known, and in field effect transistors like CMOS, MOSFET, FinFET, the reduced size introduces many challenges in predicting the system response accurately. Many amendments to the usual SPICE model needs to be made, for example, see [2,3,4,5]. The justification of the model is established by using numerical simulations of more sophisticated models. We want to start a discussion in the micrometer length scale, where quantum mechanical effects can be neglected and continuum mechanics approach holds. Especially in designs of an IC, the thermal management is of paramount importance. In this work, we want to test the aforementioned assumptions and their effects on heat production. Therefore, we will use the dissipation computed by SPICE and compare it to a numerical solution of the detailed model based on finite element method (FEM).

The first assumption, isolated components, results in a system response in any length scale. Considering high-frequency applications, we know that an induced magnetic field affects the distribution of electric charges in wires. Instead of a bundle, litz wires are used to minimize this effect. In low-frequency applications, induced magnetic effects are small such that they are negligible even in short distances. As a natural consequence of miniaturization, the components are built denser and interaction between components might be necessary even in the case of low-frequency applications. We will investigate this condition by varying the frequency and observe that the total amount of the dissipated heat remains equal although the charge distribution alters. The second assumption eliminates any deformation. We will model the complex geometry with all connections as a deformable continuum body and determine that no significant changes occur owing to the small displacements in a realistic design. The third assumption reduces the system to a nodal analysis by neglecting the geometric shape. We will model a resistor widely used with all its connections and soldering as well as board and traces. Additionally, the fourth assumption ignores all different connections, and by modeling all connections of the resistor with their material properties (electric and thermal conductivity) as rigid bodies, we will find out that the second and fourth assumptions are responsible for inaccuracies in the heat generation.

Since a circuit simulator computes a simplified system, it is fast with respect to the FEM computation. Therefore, it is of interest to pair SPICE and FEM. Especially, the assumption of no dissipation is overcome by first obtaining the Joule’s loss (power, heat) from SPICE and then running FEM analysis to compute the temperature distribution in the system, see [6, 7]. In a rigid and isothermal system, the dissipation consists of Joule’s loss, and for many applications, the results are appropriate, see [8]. Generally speaking, dissipation consists terms due to the heat conduction as well as due to the irreversible deformation. In order to solve SPICE and FEM separately, we have to accept that the system is decoupled, see [9, Sect. 2.4]. In order to involve the deformation, again after assuming that mechanics and electromagnetism can be decoupled, in a similar fashion one needs to introduce SPICE-like models based on several FEM calculations, see [10]. In this setting, mechanics and electromagnetism are treated separately with a weak coupling. If the application deserves a more accurate coupling, an iterative scheme is used, for example, see [11]. It is challenging to justify the decoupling as we will see the dissipation results in an inherent coupling of mechanics, thermodynamics, and electromagnetism.

For most of the applications, aforementioned assumptions are adequate and the suggested designs work. From smartphones to controllers in a spaceship, various technological devices are constructed by using several assumptions. Increasing complexity of ICs introduces yet to be solved problems, see [12]. For example in printed circuit boards (PCBs) used in high frequency, so-called S-parameters are introduced to match the inaccuracy of response function to the experimental values. We aim at comprehending the taken assumptions such that we can judge their feasibility and even ignite newer modeling methods without introducing correction parameters. Consider a transformer embedded in an epoxy. We can simulate the system response under the assumption of a rigid system. The design would work as expected, with an unexpected consequence of an audible noise, see [13]. Electromagneto-restriction is a shape change of the electronic components, and this deformation creates a noise. In a laptop, a sophisticated motherboard design consists of hundreds of components creating a specific noise by operating, commonly called “coil whine.” Not only unpleasant, this effect is a security problem, see [14].

A transient, nonlinear, and coupled system of deformable bodies subject to electromagnetic fields is modeled in [15, Chap. 3]. In this work, we exploit the strategy and apply for micrometer length-scale systems in order to test the usual assumptions and simplifications done in SPICE models.

2 Governing equations

For a solid continuum body, we aim at computing electric potential \(\phi \) in V(olt), magnetic potential \(\varvec{A}\) in T(esla) m(eter), displacement \(\varvec{u}\) in m, and temperature T in K(elvin). We simply list the necessary equations and refer to [15, Chap. 3] for their elaborate derivation. All quantities are expressed in a Cartesian coordinate system, and we use the standard tensor notation with the summation convention. The electromagnetic potentials are used to obtain electric field \(E_i\) and magnetic flux (area density) \(B_i\) as follows:

$$\begin{aligned} E_i = -\frac{\partial \phi }{\partial X_i} - \frac{\partial A_i}{\partial t},\quad B_i = \epsilon _{ijk} \frac{\partial A_k}{\partial X_j}, \end{aligned}$$
(1)

where \(X_i\) indicates the reference position of particles. The current position is denoted by \(x_i\) such that the displacement reads \(u_i=x_i-X_i\). We will have small displacements with respect to the geometric dimensions in the applications such that we neglect any geometric nonlinearities. Hence, a derivative in \(X_i\) and \(x_i\) is identical. From the electric field and magnetic flux, we acquire charge potential \(D_i\) and current potential \(H_i\) by means of Maxwell–Lorentz aether relations:

$$\begin{aligned} D_i = \varepsilon _0 E_i,\quad H_i = \frac{1}{\mu _0} B_i. \end{aligned}$$
(2)

The specific electric charge, z, in C(oulomb)/k(ilo)g(ram) is separated into free and bound charges. In the same fashion, we can propose to separate the charge and current potentials,

$$\begin{aligned} D_i = \mathfrak {D}_i - P_i ,\quad \ H_i = \mathfrak {H}_i + \mathcal {M}_i, \end{aligned}$$
(3)

into potentials caused by the free charges, \(\mathfrak {D}_i\), \(\mathfrak {H}_i\), and potentials effected by the bound charges, \(P_i\), \(\mathcal {M}_i\). Since we have the aforementioned Maxwell–Lorentz aether relations, we need constitutive equations either for \(\mathfrak {D}_i\), \(\mathfrak {H}_i\) or for \(P_i\), \(\mathcal {M}_i\). For computing the electric potential, we use the balance of electric charge and one Maxwell equation

$$\begin{aligned} \frac{\partial \rho z}{\partial t} + \frac{\partial J_i}{\partial X_i} = 0 ,\quad \rho z = \frac{\partial D_i}{\partial X_i}. \end{aligned}$$
(4)

For the total electric current in the laboratory frame, we use

$$\begin{aligned} J_i= & {} J_i^{\tiny \text {fr.}}+ \frac{\partial P_i}{\partial t} + \epsilon _{ijk}\frac{\partial \mathcal {M}_k}{\partial X_j},\nonumber \\ J_i^{\tiny \text {fr.}}= & {} \mathcal {J}_i^{\,{\tiny \text {fr.}}} + \rho z^{\tiny \text {fr.}}v_i = \mathcal {J}_i^{\,{\tiny \text {fr.}}} + \frac{\partial \mathfrak {D}_j}{\partial X_j} v_i, \end{aligned}$$
(5)

where we need a constitutive equation for the electric current of free charges in the material frame, \(\mathcal {J}_i^{\,{\tiny \text {fr.}}}\). For computing the magnetic potential, we use another Maxwell equation:

$$\begin{aligned} -\frac{\partial D_i}{\partial t} + \epsilon _{ijk} \frac{\partial H_k}{\partial X_j} = J_i. \end{aligned}$$
(6)

After inserting Maxwell–Lorentz aether relations and Lorenz’s gauge:

$$\begin{aligned} \varepsilon _0 \frac{\partial \phi }{\partial t} + \frac{1}{\mu _0} \frac{\partial A_i}{\partial X_i} = 0, \end{aligned}$$
(7)

we obtain

$$\begin{aligned} \varepsilon _0 \frac{\partial ^2 A_i}{\partial t^2} - \frac{1}{\mu _0} \frac{\partial ^2 A_i}{\partial X_j\partial X_j} = J_i, \end{aligned}$$
(8)

as the governing equation for the magnetic potential \(A_i\). For computing the displacement, we use the balance of linear momentum:

$$\begin{aligned} \rho \frac{\partial ^2 u_i}{\partial t^2} + \frac{\partial (\varvec{\mathfrak {D}}\times \varvec{B})_i}{\partial t} - \frac{\partial (\sigma _{ji}+m_{ji})}{\partial X_j} - \rho f_i = 0, \end{aligned}$$
(9)

where we have introduced the electromagnetic momentum density (per volume), \((\varvec{\mathfrak {D}}\times \varvec{B})_i\), and Maxwell stress:

$$\begin{aligned} m_{ji} = -\frac{1}{2} \delta _{ji} (H_k B_k + D_k E_k) + H_i B_j + D_j E_i. \end{aligned}$$
(10)

For the Cauchy stress, \(\sigma _{ji}\), we need a constitutive equation. The specific body force, \(f_i\), is due to gravitation, and its value is known. For computing the temperature, we are going to use the balance of entropy:

$$\begin{aligned} \rho \frac{\partial \eta }{\partial t} + \frac{\partial \Phi _i}{\partial X_i} - \rho \frac{r}{T} = \Sigma , \end{aligned}$$
(11)

where the entropy flux is given by \(\Phi _i = q_i/T\) with the heat flux \(q_i\). For the specific entropy, \(\eta \), as well as for the heat flux, \(q_i\), we need constitutive equations. The entropy production:

$$\begin{aligned} \Sigma= & {} -\frac{q_i}{T^2} \frac{\partial T}{\partial X_i} + \frac{1}{T} \left( \,^{\tiny \text {d}}\!\sigma _{ji} - P_j E_i + \mathcal {M}_i B_j\right) \frac{\partial v_i}{\partial X_j} \nonumber \\&+ \frac{1}{T} \mathcal {E}_i \mathcal {J}_i^{\,{\tiny \text {fr.}}} , \end{aligned}$$
(12)

will be determined after defining constitutive equations for the heat flux, \(q_i\), for the dissipative stress, \(\,^{\tiny \text {d}}\!\sigma _{ji}\), for the electric polarization, \(P_i\), for the magnetic polarization, \(\mathcal {M}_i\), and for the free electric current in the material frame, \(\mathcal {J}_i^{\,{\tiny \text {fr.}}}\). The electric field in the material frame is given by,

$$\begin{aligned} \mathcal {E}_i = E_i + \epsilon _{ijk} v_j B_k. \end{aligned}$$
(13)

After a thermodynamical investigation as in [15, Sect. 3.5], for an elastic material, we acquire the following linear constitutive equations:

$$\begin{aligned} q_i= & {} -\, \kappa \frac{\partial T}{\partial X_i} + \varsigma \pi T , \ \mathcal {J}_i^{\,{\tiny \text {fr.}}} = \varsigma \pi \frac{\partial T}{\partial X_i}+\varsigma \mathcal {E}_i,\nonumber \\ \,^{\tiny \text {d}}\!\sigma _{ji}= & {} P_j E_i - \mathcal {M}_i B_j, \nonumber \\ \sigma _{ji}= & {} P_j E_i-\mathcal {M}_i B_j - C_{jikl} \alpha _{kl} (T-T_\text {ref.}) + C_{jikl} \varepsilon _{kl}\nonumber \\&-\,\tilde{T}_{kji} E_k - \tilde{S}_{kji} B_k, \nonumber \\ \eta= & {} c\ln \left( \frac{T}{T_\text {ref.}}\right) +\frac{1}{\rho }C_{ijkl} \alpha _{kl} \epsilon _{ij} - \frac{1}{\rho }\tilde{T}_{ijk} \alpha _{jk} E_i \nonumber \\&-\,\frac{1}{\rho }\tilde{S}_{ijk} \alpha _{jk} B_i, \nonumber \\ P_i= & {} -\,\tilde{T}_{ijk}\alpha _{jk}(T-T_\text {ref.}) + \tilde{T}_{ijk} \varepsilon _{jk} +\varepsilon _0 \chi ^{\tiny \text {el.}}_{ij} E_j \nonumber \\&+ \,\tilde{R}_{ji} B_j, \nonumber \\ \mathcal {M}_i= & {} -\,\tilde{S}_{ijk} \alpha _{jk} (T-T_\text {ref.}) + \tilde{S}_{ijk} \varepsilon _{jk}\nonumber \\&+\,\tilde{R}_{ij} E_j + \left( \varvec{\mu }^{-1}_{\tiny \text {mag.}}\right) _{ik} \chi ^{\tiny \text {el.}}_{kj} B_j, \end{aligned}$$
(14)

under the assumption that polarization is reversible, in other words, we neglect electromagnetic hysteresis. Material parameters, namely thermal conductivity \(\kappa \), electrical conductivity \(\varsigma \), Peltier or thermoelectric parameter \(\pi \), stiffness tensor \(C_{ijkl}\), coefficients of thermal expansion \(\alpha _{ij}\), piezoelectric tensor \(\tilde{T}_{ijk}\), piezomagnetic tensor \(\tilde{S}_{ijk}\), specific heat capacity c, electric susceptibility \(\chi ^{\tiny \text {el.}}_{ij}\), magnetoelectric coupling \(\tilde{R}_{ij}\), magnetic susceptibility \(\chi ^{\tiny \text {mag.}}_{ij}\), magnetic permeability \(\mu ^{\tiny \text {mag.}}_{ij}\), need to be determined by experiments. For a homogeneous material, the parameters are constant in space.

3 Numerical method of solution

The governing equations augmented by the constitutive equations form a set of differential equations called the field equations. We obtain them from Eqs. (4), (8), (9), (11) as follows:

$$\begin{aligned}&\frac{\partial \mathfrak {D}_{i,i}}{\partial t} + \Big ( \mathcal {J}_i^{\,{\tiny \text {fr.}}} + v_i \mathfrak {D}_{j,j} + \epsilon _{ijk} \mathcal {M}_{k,j} \Big )_{,i} =0,\nonumber \\&\varepsilon _0 \frac{\partial ^2 A_i}{\partial t^2}- \frac{1}{\mu _0} A_{i,jj} = \mathcal {J}_i^{\,{\tiny \text {fr.}}} + v_i \mathfrak {D}_{j,j} + \frac{\partial P_i}{\partial t} + \epsilon _{ijk} \mathcal {M}_{k,j},\nonumber \\&\rho _0 \frac{\partial ^2 u_i}{\partial t^2} + \epsilon _{ijk} \frac{\partial \mathfrak {D}_j B_k}{\partial t} - (\sigma _{ji} + m_{ji})_{,j} - \rho _0 f_i = 0,\nonumber \\&\rho _0 \frac{\partial \eta }{\partial t}+ \Phi _{j,j} - \rho _0 \frac{r}{T} = \Sigma , \end{aligned}$$
(15)

where we have introduced the notation “i,” indicating a partial differentiation with respect to \(X_i\). These field equations for the primitive variables, \(\{\phi , A_i, u_i, T\}\), are coupled and nonlinear partial differential equations in space and time. We will solve them by using finite difference method in time and finite element method in space. We refer to [16] for an elaborate derivation of the integral forms presented in the following.

For the time discretization, we use the so-called backward Euler scheme, which is stable for real-valued problems. For the space discretization, we multiply each field equation with a test function, \(\{\updelta \phi , \updelta A_i, \updelta u_i, \updelta T\}\), and use an integration by parts in order to reduce the differentiability condition of the terms. In other words, we weaken the formulation. We obtain the weak form for \(\phi \),

$$\begin{aligned} F_\phi= & {} \int _\Omega \bigg ( -\left( \mathfrak {D}_i-\mathfrak {D}_i^0\right) \updelta \phi _{,i} - \Delta t \mathcal {J}^{\,{\tiny \text {fr.}}}_i \updelta \phi _{,i}\nonumber \\&-\, \left( u_i-u_i^0\right) \mathfrak {D}_{j,j} \updelta \phi _{,i} - \Delta t \epsilon _{ijk} \mathcal {M}_{k,j} \updelta \phi _{,i} \bigg ) \, \mathrm {d}V \nonumber \\&+ \int _{\partial \Omega ^I} N_i \Delta t \epsilon _{ijk} \llbracket \mathcal {M}_{k,j} \rrbracket \updelta \phi \, \mathrm {d}A, \end{aligned}$$
(16)

and for \(A_i\),

$$\begin{aligned} F_{\varvec{A}}= & {} \int _\Omega \bigg ( \varepsilon _0 \frac{A_i - 2 A_i^0 + A_i^{00}}{\Delta t \Delta t} \updelta A_i + \frac{1}{\mu _0} A_{i,j} \updelta A_{i,j} \nonumber \\&-\, \mathcal {J}_i^{\,{\tiny \text {fr.}}} \updelta A_i - \frac{u_i-u_i^0}{\Delta t} \mathfrak {D}_{j,j} \updelta A_i - \frac{P_i-P_i^0}{\Delta t} \updelta A_i \nonumber \\&+\, \epsilon _{ijk} \mathcal {M}_k \updelta A_{i,j} \bigg ) \, \mathrm {d}V, \end{aligned}$$
(17)
Fig. 2
figure 2

Diagram of different types of FEM analysis leading to more sophisticated models

Full size image

where jump conditions are applied over the interface \(\Omega ^I\) between two different materials and \(\llbracket \dots \rrbracket \) indicates the difference of the value between two adjacent materials. Models will be embedded in air, so the computational domain’s boundary is far away from the object under investigation. On boundary of the computational domain, \(\phi \) and \(A_i\) are set to zero since we expect electromagnetic potentials to diminish far away from the continuum body. With the analogous approach, we obtain the weak form for \(u_i\),

$$\begin{aligned} F_{\varvec{u}}= & {} \int _\Omega \bigg ( \rho _0 \frac{u_i - 2 u_i^0 + u_i^{00} }{\Delta t \Delta t} \updelta u_i -\bar{\sigma }_{ji,j} \updelta u_i + \tau _{ji} \updelta u_{i,j}\nonumber \\&-\,\rho _0 f_i \updelta u_i \bigg ) \, \mathrm {d}V + \int _{\partial \Omega ^I} N_j \llbracket \bar{\sigma }_{ji} \rrbracket \updelta u_i \, \mathrm {d}A. \end{aligned}$$
(18)

where the total stress \(\sigma ^{\tiny \text {tot.}}_{ji}=\sigma _{ji}+m_{ji}\) is decomposed into terms consisting of derivatives of the primitive variables, \(\tau _{ji}\), and consisting only the primitive variables but no derivatives, \(\bar{\sigma }_{ji}\), as follows:

$$\begin{aligned} \tau _{ji}= & {} -\frac{1}{2} \delta _{ji} (H_k B_k + D_k E_k) + \mathfrak {H}_i B_j + \mathfrak {D}_j E_i\nonumber \\&+\, C_{jikl} \varepsilon _{kl} - \tilde{T}_{kji} E_k - \tilde{S}_{kji} B_k, \nonumber \\ \bar{\sigma }_{ji}= & {} - \,C_{jikl} \alpha _{kl} (T-T_\text {ref.}). \end{aligned}$$
(19)

This approach is of importance in order to apply the integration by parts only to the terms where it is needed. On the boundary \(\Omega \), we assume that the deformation of the air is given; concretely, we set it zero. Although we compute the displacement of the embedding air by using a fictitious modulus, its value is not accurate and will not be presented as a result. In the same fashion, we acquire a weak form for T after implementing the condition that the heat flux toward surface normal is continuous

$$\begin{aligned} F_T= & {} \int _\Omega \bigg ( \rho _0 \left( \eta - \eta ^0\right) \updelta T - \Delta t \Phi _i \updelta T_{,i} - \Delta t \rho _0 \frac{r}{T} \updelta T\nonumber \\&-\, \Delta t \Sigma \updelta T \bigg ) \, \mathrm {d}V, \end{aligned}$$
(20)

and assume that on the boundary of the embedding air, the temperature is given by \(T_\text {ref.}=300\) K. A simulation starts with the given initial conditions, namely \(\phi =0\), \(A_i=0\), \(u_i=0\), and \(T=T_\text {ref.}\), within the whole computational domain. The primitive variables are computed over time such that the weak forms are fulfilled.

Now we have the possibility to solve different problems in various settings. For example, a rigid and isothermal body can be solved by using

$$\begin{aligned} \text {Form} = F_\phi + F_{\varvec{A}}. \end{aligned}$$
(21)

If the temperature distribution is necessary, we can model the body as rigid and solve

$$\begin{aligned} \text {Form} = F_\phi + F_{\varvec{A}} + F_T. \end{aligned}$$
(22)

The most general solution is of course

$$\begin{aligned} \text {Form} = F_\phi + F_{\varvec{A}} + F_{\varvec{u}} + F_T. \end{aligned}$$
(23)

We have compiled these different types of FEM solutions in Fig. 2, which will be used in the next section for testing the SPICE models for resistor. As expected, more complexity increases the computation time as well as the accuracy of the model problem. By setting one or more material parameters in the constitutive equations, we can test the importance of assumptions about the system response.

4 Applications

In this section, we will examine some common design simplifications in the electric circuit design. We mainly compare results from a one-dimensional SPICE simulation to the three-dimensional transient FEM computation. We focus on the dissipation in a circuit design, since the thermal management is a critical issue in electronic design. In the most general case, the dissipated power, \(T\Sigma \), alters the temperature. As aforementioned, for an elastic material, we obtain

$$\begin{aligned} T\Sigma = -\frac{1}{T} q_i T_{,i} + \mathcal {E}_i \mathcal {J}_i^{\,{\tiny \text {fr.}}}. \end{aligned}$$
(24)

In a conductor, we expect that the production by the electric current is homogeneous. Based on this, we may approximate the temperature distribution in a conductor as constant leading to suppression of the first term in the production, \(T\Sigma \). Then, the production or generated power is given by the so-called Joule’s heat (loss), \(\mathcal {E}_i \mathcal {J}_i^{\,{\tiny \text {fr.}}}\). Since \(\mathcal {E}_i\) is in V/m and \(\mathcal {J}_i^{\,{\tiny \text {fr.}}}\) is in A(mpere)/m\(^2\), the contraction \(\mathcal {E}_i\mathcal {J}_i^{\,{\tiny \text {fr.}}}\) results in a power density (per volume). In FEM computation, we will integrate over the continuum body and calculate the dissipated power in W(att). By using a circuit simulator, we can calculate the electric field and current giving us Joule’s loss in W at a node for a comparison with the FEM computation.

We use PySPICE with NG-SPICE coded in Python for all SPICE calculations, [17]. For FEM, we use FEniCS in Python and visualize in ParaView 5.3, [18,19,20]. Geometries are constructed in Salome 7.5. All codes and geometries used in this section are publicly available in [21] licensed under [22] in order to encourage scientific exchange.

4.1 Skin and proximity effects

Consider a surface mount technology (SMT) resistor, like a metal electrode leadless face (MELF), of type 103, i.e., 10 k\(\Omega \) resistor on a circuit. We simulate resistor as a rigid and isothermal body, i.e., only electromagnetic potentials \(\phi \) and \(A_i\) are computed within the computational domain. Two cylindrical resistors are embedded in air as seen in Fig 3. The resistors and air are modeled as rigid, isothermal bodies, leading to

$$\begin{aligned}&c=0 ,\quad \kappa = 0 ,\quad C_{ijkl}=0,\quad \tilde{T}_{kji}= 0 ,\quad \tilde{S}_{kji}=0, \end{aligned}$$
(25)

for air as well as resistors. Moreover, we choose

$$\begin{aligned} \varsigma = 3\times 10^{-15}\,\text {mS/mm} ,\quad \chi ^{\tiny \text {el.}}= 0 ,\quad \chi ^{\tiny \text {mag.}}= 0, \end{aligned}$$
(26)

for air and

$$\begin{aligned} \varsigma= & {} \frac{\ell }{R\, a} ,\quad a = \uppi r^2 ,\quad r=0.01\,\text {mm} \nonumber \\\Rightarrow & {} R=10\,\text {k}\Omega \,{\hat{=}}\,10\,\text {mS}^{-1}, \nonumber \\ \chi ^{\tiny \text {el.}}= & {} 0 ,\quad \chi ^{\tiny \text {mag.}}= 1\times 10^{-5}, \end{aligned}$$
(27)

for the resistors based on the values of copper with the length of the resistor \(\ell \), and radius r. The inertial term in the balance of charge, namely the time rate of divergence of free charge potential, becomes dominating if the electromagnetic fields vary quickly in time. For higher frequencies, the divergence term results in concentration of free charge on the surface of the resistors with round cross-sectional profiles. This phenomenon is called skin effect. Alternate current (AC) generates electromagnetic fields varying in time. This implies a magnetic field, which alters the charge distribution in the environment. Therefore, both resistors affect each other, which is known as proximity effect. Skin and proximity effects are addressed in a transient three-dimensional solution as shown in Fig 3. In SPICE, such effects are ignored under the assumption that these effects are negligible. If the tests show a significance, it is possible to determine S-parameters for future designs such that the skin and proximity effects are involved for the electromagnetic response function. For a thermal management, i.e., for computing the dissipation, there are no such parameters known to the best knowledge of authors. Herein, we want to examine the inaccuracy introduced to the dissipation by neglecting skin and proximity effects.

Fig. 3
figure 3

Left: geometry of two rigid and isothermal resistors connected in parallel, modeled in mm. Right: distribution of electric current due to the skin and proximity effects

Full size image

We model the resistors as connected in parallel by excluding the connecting vias from the FEM simulation. We simply generate a potential difference by setting the electric potential on one end of each resistors,

$$\begin{aligned} \phi = A \sin (2\uppi \nu t) ,\quad A=12\,\text {V}, \end{aligned}$$
(28)

and by grounding the other end, i.e., setting as 0 V. In a low-frequency excitation, the distribution of the electric current is homogeneous; however, in a high-frequency application, it concentrates to the surface far from the neighboring conductor, as presented in Fig 3 for \(\nu =500\) MHz at the end of one period, \(t=2\times 10^{-9}\) s. Although the distribution changes, the total amount of the electric current remains the same, so the overall dissipation is not affected from the skin and proximity effects. We run several simulations in different frequencies and compare them with their SPICE calculations as seen in Fig 4. No significant difference can be seen between SPICE and FEM, for 500 Hz and 500 MHz AC excitations.

Fig. 4
figure 4

Frequency variations and comparing SPICE to FEM in order to test the skin and proximity effects

Full size image

4.2 Size effects

We have used a relatively simple geometry, a cylinder as the MELF resistor. Circuit simulator determines the current and potential, such that the dissipation is computed by means of them. For the 2 cylinders as MELFs, we simply have

$$\begin{aligned} 2 I U = \frac{2 U^2}{R}, \end{aligned}$$
(29)

where I is the total amount of electric current flowing through the cross-sectional area of one resistor and R is the resistance of this resistor. In each resistor \(U=12\) V varying harmonically and \(R=10\) k\(\Omega \) as set by the type of the MELF. We have calculated the electrical conductivity

$$\begin{aligned} \varsigma = \frac{\ell }{R\, a} ,\quad a = \uppi r^2, \end{aligned}$$
(30)

by using the length of resistor \(\ell \), as well as cross-sectional area a. Therefore, the dissipation may depend on the geometric length scale. We simulate different length scales, namely length is 0.1 and radius is 0.01 in m, and in mm. The results of these two simulations in different length scales can be seen in Fig. 5. No significant difference is observed such that the miniaturization seems to be adequate for SPICE models, as long as the quantum mechanical effects can be neglected.

Fig. 5
figure 5

Size scale variations and comparing SPICE to FEM in order to examine the effect of geometrical length scale

Full size image

4.3 Geometrical simplification

As is usually the case, we have ignored the real geometry and modeled the MELF resistor as a cylinder. This assumption is justified as a consequence of having negligible resistance in the conductor with respect to the resistor. In order to make the ideas more concrete, in reality, MELF is a ceramic cylinder placed on top of an epoxy-based composite board as soldered to the copper traces. Copper traces carry the electric signals, and this transmission is assumed to be perfect for small distances as in an IC. Since MELF is ceramic (insulator), the electrical contact is established through metallic caps at the both ends of the cylinder. Inside the ceramic cylinder, a thin sheet (usually copper) is laser-cut in the middle such that the effectively conducting area is precisely constructed, leading to an accurate resistivity. We skip a modeling of the inner of the cylinder and apply the electrical conductivity of the MELF to the ceramic cylinder as a whole. A realistic micro-MELF resistor of type MMU 0102 is seenFootnote 1 in Fig. 6. Since the conductivities of the traces, pads, solders, and caps are much higher than the cylinder, their CAD accuracies are not important. The objective is to determine the geometric effect of the cylinder with caps having an electric contact only on a fraction of the faces.

Fig. 6
figure 6

Geometry of micro-MELF soldered on a piece of epoxy board and all geometry is embedded in air (transparent gray). Colors: board is green, traces and solder pads are yellow, solder is white, ceramic MELF is light blue, and metallic caps on the MELF are orange (Color figure online)

Full size image
Table 1 Material parameters for the rigid and isothermal simulation
Full size table
Table 2 Additional material parameters for the non-isothermal case
Full size table
Table 3 Additional material parameters for the deformable structure
Full size table

SPICE implementation is identical to the previous case; only for a single resistor, we obtain the half of the power dissipation. In FEM, we conduct three different simulations. First, we model a rigid and isothermal body of the presented geometry in mm for a half period. Air embeds the polyimide board with Al\(_2\)O\(_3\) ceramic MELF and its nickel-steel caps, which is soldered by SnAg35 lead-free solder to the copper pad and traces. MELF is a cylinder of radius 0.55 mm with the cross-sectional area a. For the rigid and isothermal simulation, material parameters are compiled in Table 1. In order to cause significant temperature rise, we use \(R=100\) \(\Omega \) as the resistance of the resistor. In each time step, Joule’s loss is computed within the whole ceramic cylinder. In order to ensure the reliability of the FEM implementation, we perform several test simulations. First, we validate the solution in the case of different materials by using a simple geometry after a comparison of the numerical solution to the analytic solution. Second, we generate meshes with different space discretization by increasing the degrees of freedom and test the convergence. Both tests perform well and are discussed further in Appendix.

The second FEM computation addresses the thermodynamics and illustrates that the temperature deviates from the reference value. In addition to the already mentioned parameters, we use the material parameters in Table 2. In this simulation, we neglect the thermoelectric coupling \(\pi =0\) V/K for every material. Only conductors have a thermoelectric coupling in reality.

The third FEM computation involves the elastic deformation. We avoid to implement piezomagnetic, piezoelectric, and magnetoelectric effects, i.e., \(\tilde{T}_{kij}=0\), \(\tilde{S}_{kij}=0\), and \(\tilde{R}_{ij}=0\), respectively. We model all materials as isotropic,

$$\begin{aligned} \alpha _{ij}= & {} \alpha \delta _{ij} ,\quad C_{ijkl}= \lambda \delta _{ij}\delta _{kl} + \mu \delta _{ik}\delta _{jl} + \mu \delta _{il}\delta _{jk}, \nonumber \\ \mu= & {} G=\frac{E}{2(1+\nu )}, \nonumber \\ \lambda= & {} \frac{2\mu \nu }{1-2\nu } = \frac{(E-2G)G}{3G-E} = \frac{E\nu }{(1+\nu )(1-2\nu )}, \end{aligned}$$
(31)

with only two of \(E, G, \nu \), see Table 3 for the implemented material parameters. For air, we simply set the realistic parameter \(\alpha =3.2\times 10^{-3}\) K\(^{-1}\) and the artificial values \(\lambda =\mu =0.1\) MPa, which are very small with respect to the moduli of other materials. Therefore, embedding air fails to restrict motion of other components. Although we calculate a fictitious displacement in the embedding air, we never evaluate this.

We observe significant differences between SPICE and FEM approaches, see results in Fig. 7. Obviously, the underlying geometry alters the dissipated power greatly. The main reason behind lies in the assumption that the electric current be homogeneous within the resistor. Although we have modeled the cylinder as a homogeneous material of 100 \(\Omega \) resistance and the potential difference is implemented nearly homogeneous by means of nickel-steel caps of nearly zero resistance, the distribution of the electric current is heterogeneous as seen in Fig. 8 at the quarter period, when maximum electric potential difference occurs. The geometry of the metallic caps and their contact surfaces affects the distribution of the electric current within MELF. Moreover, Joule’s loss is concentrated in the core of MELF between caps. Therefore, in reality, the dissipated power is greater than determined in a circuit simulator. By involving temperature distribution and displacement, the dissipation within MELF fails to change significantly. This fact is due to the small displacements, see Fig. 9, as well as due to almost homogeneous temperature distribution in the core, see Fig. 10. Although displacements are small, coefficients of thermal expansion are different between the adjacent components leading to thermal stresses. By computing the displacements, inspection of thermal stresses is possible. If the sole purpose is to determine the produced power, then a rigid and isothermal computation on three-dimensional geometry is sufficient.

Fig. 7
figure 7

MELF modeled with SPICE versus FEM as a rigid, isotherm; rigid, thermal; elastic, thermal system

Full size image
Fig. 8
figure 8

Electric current distribution as colors and denoted by the scaled arrows on a cut of the ceramic MELF, electric potential’s distribution as colors on a cut on the circuit board, at the quarter period (Color figure online)

Full size image
Fig. 9
figure 9

Displacement at the half of the period in the micro-MELF, scaled 3000 times for the sake of visualization

Full size image
Fig. 10
figure 10

Temperature distribution on a cut in the middle of the MELF, at the half of the period

Full size image

Generally, in a circuit simulator, the resistor is modeled as a one-dimensional component such that the cylinder is a line segment with beginning and ending nodes. The difference in electric potentials at these boundary nodes implies an electric field with generated heat. If we want to mimic this behavior in 3-D, we use a cylinder with boundary conditions applied on the entire beginning and ending faces. In reality, only the contact area between solder and caps is supplying the electric current. This difference is the root cause of the inaccuracy, and we wish to explain it by considering a simplified model. For this purpose, the micro-MELF is modeled as a ceramic cylinder and we simply suppress board, solder, pads, and caps. On this geometry, two simulations with different boundary conditions are performed: One uses only the contact area between MELF and solder, we call it type A; another uses the whole front and back faces for boundary conditions, we name it type B. For the sake of clarity, we mark these different selection of surfaces in Fig. 11. MELF is modeled as a rigid and isothermal material embedded in air; we perform simulations, where \(\phi \) is set on both sides. On one side, it is the same harmonic function, and on the other, it is grounded. As seen in Fig. 12, the significant difference is due to the model reduction to one-dimensional continuum. We have selected one single component, namely MELF, out of various devices used on a circuit board. The simplification to one-dimensional components in circuit simulators relies on the fact that the whole cross section is used in MELF. In reality, within MELF, only a thin sheet conducts current. For a better comparison, we modeled MELF as a ceramic material with a given resistance such that the whole cross section conducts. However, the implementation of boundary conditions affects the heat generation greatly. We have observed that only boundary conditions are relevant for a mismatch between SPICE and FEM. Otherwise, SPICE is doing an invaluable job for determining the overall system response of an IC. In thermal analysis, we recall that there are stark differences between SPICE and FEM. This fact is due to Joule’s loss being quadratic in the electric field. Therefore, for an accurate thermal analysis, production of heat should be computed by using a transient electromagnetism code such as ours. In order to encourage more research, we make our codes available in [21] licensed under [22].

Fig. 11
figure 11

Boundary conditions of type A (left) and type B (right) for the simplified MELF model

Full size image
Fig. 12
figure 12

Comparison of FEM results with type A and type B boundary conditions to SPICE results

Full size image

5 Conclusion

A circuit simulator such as SPICE performs a fast and reliable computation of a complex system response under several assumptions, namely isolated components, simplified geometry, rigid bodies, and neglecting dissipation. Especially on an IC, thermal management is of great importance and we have investigated the possible inaccuracies introduced by these assumptions. For a micro-MELF, we have presented a realistic, three-dimensional, coupled, and nonlinear solution based on the finite element method (FEM) for electromagneto-thermomechanical fields, viz., electric potential \(\phi \), magnetic potential \(A_i\), displacement \(u_i\), and temperature T. The same system is simplified by assuming a rigid body, \(u_i=0\), and rigid as well as isothermal system, \(u_i=0\) and \(T=T_\text {ref.}\). After a comparison of the dissipation in these three-dimensional simulations to Joule’s loss obtained from a one-dimensional computation on a circuit simulator, we have found out that cutting down on the detailed geometry leads to inaccurate results. For different electronic components, we expect analogous results.

We want to emphasize, according to the presented observation, the strategy of a thermal analysis with the obtained power from a circuit simulator is prone to inaccuracies. The main reason for this phenomenon is the simplification of the geometry leading to different boundary conditions than in reality. We have modeled MELF as a ceramic cylinder with homogeneous electric conductance. Actually, even this model is an assumption since only a thin metallic sheet inside the ceramic cylinder is conducting electric current. We want to start a discussion and increase the awareness that the geometry simplification can be held responsible for the inaccuracies in thermal management of ICs. Assumption of rigid bodies as well as isolated components is appropriate for the micrometer length scale. Due to the nature of the used materials, we have neglected piezoelectric, piezomagnetic, magnetoelectric, and thermoelectric couplings in the simulations. We encourage further studies to determine limits of the very powerful circuit simulators in order to let designers know, how far and whether to use or avoid them in certain analyses.