1 Introduction

Due to some defects and scaling limitation of current CMOS technology, wide- range researches are going on making nanoscale devices using techniques such as quantum dot cellular automata (QCA), tunneling phase logic (TPL), single electron tunneling (SET) and carbon nanotube (CNT). Among them, QCA would be more interesting because of its attractive features of high speed operation, low power consumption and small dimension. In 1993, Lent et al. proposed a physical implementation of an automaton using quantum-dot cells. The automaton quickly gained popularity among researchers worldwide and it was first fabricated in 1997 [1].

1.1 QCA building blocks

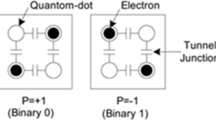
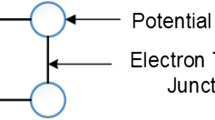
A basic QCA cell is shown in Fig. 1. As shown into the figure, QCA cell consists of four quantum dots which are arranged in square pattern. The cell has two extra electrons inside it by tunneling them which resides diagonally to each other due to their mutual electrostatic repulsive force between them. These two electrons tend to keep the furthest distance with each other in the square pattern grid and produce two different logical states (logic 0 and logic 1). We can get a proper logical expression by arranging these electrons properly. Information is passed in QCA cells by propagation of polarized charge instead of flow of current, so they require lower energy and higher processing speed.

QCA wire needed to transmit a signal consists of chain of cells which are coupled to each other is shown in Fig. 2. Information is passed from cell to cell due to the coulomb interactions through the wire.

For designing any QCA circuit, we require two primary QCA gates: (a) QCA Inverter (b) QCA majority gate.

(a) QCA Inverter

A QCA inverter is combination of cells which inverters the topology of an input from one logic to another. Generally, two types of inverter are used [2, 3], which has been utilized for implementation of many structures as a basic cell [4–11]:

Fig. 1
figure 1

QCA cell a empty, b logic ‘0’, c logic ‘1’

Full size image
Fig. 2
figure 2

QCA binary wire

Full size image
Fig. 3
figure 3

a Simple inverter, b robust inverter

Full size image
Fig. 4
figure 4

QCA majority gate

Full size image

Figure 3a shows the simple structure of inverter but there is a probability for each QCA to get fail, so a more robust double path inverter has been designed in Fig. 3b.

(b) QCA Majority gate:

Another primary gate in QCA is QCA majority gate. Two types of majority gates are there in general (Fig. 4 ).

QCA majority gate is made of five QCA cells with a cross shape structure. Polarity of the central cell, as known as device cell is enforced, via the coulomb repulsion to be equal to the output cell. Table 1 shows the input and output cells combinations. ‘0’ means logic ‘0’ and ‘1’ indicates logic ‘1’ in the table. Therefore, a combination of QCA majority gate and an inverter is sufficient to make a complete logic set for designing any circuit.

The rest of this presentation is organized as follows: Sect. 2 briefly gives physical proofs of some basic QCA designs with the introduction of proposed novel 5-input majority gate. Section 3 provides details about previously available full adder (FA) designs and proposes a new FA based on the proposed 5-input majority gate. Results based on QCADesigner tool are given in Sect. 4 followed by conclusion in Sect. 5. At last Acknowledgment of the work is given.

Fig. 5
figure 5

QCA cells connected in series as a binary wire for a logic ‘1’ and b logic ‘0’ value in cell-2

Full size image
Table 1 Input and output cells combinations in 3-input majority gate
Full size table

2 General proofs

2.1 Proof 1

According to Fig. 5, if we assume that logic ‘1’ is provided at the input side to cell-1, so cell-2 will follow the same logic as input because it is connected in series with cell-1. Physical proof has been provided as below for this.

For physical proofs, assume that all the cells are similar and length of each one is a (a = 18nm) and there is a space of x (x = 2nm) between each two neighbour cells. In all the figures, rectangles show the QCA cell and the circles inside shows the position of electrons inside that particular cell. In order to achieve more stability, electrons of QCA cell are arranged in such a manner that their potential energy should be at minimum level.

The potential energy between two electron charges is calculated using relation (1a). In this equation, U is the potential energy, k is fixed colon, q1 and q2 are electric charges and r is the distance between two electric charges. By putting the values of k and q, we obtain Eq. (1b). \(\hbox {U}_{\mathrm{T}}\) is the summation of potential energies that is calculated from Eq. (2) [12–14].

$$\begin{aligned}&U=\frac{kq_1 q_2 }{r} \end{aligned}$$
(1a)
$$\begin{aligned}&kq_1 q_2 =9\times 10^{9}\times \left( {1.6} \right) ^{2}\times 10^{-38}\nonumber \\&\quad \quad \quad \quad =23.04\times 10^{-29}=A=cte \end{aligned}$$
(1b)
$$\begin{aligned} U_T =\sum \nolimits _{i=1}^n U_i \end{aligned}$$
(2)

Assumption 1: If cell-2 is logic ‘1’ as in Fig. 5a.

Figure 5a (electron x)

Figure 5a (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{38.05\times 10^{-9}}=0.60\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{18.11\times 10^{-9}}=0.60\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_{T11} =\sum \limits _{i=1}^2 U_i =1.41\times 10^{-20}J\)

\(U_{T12} =\sum \limits _{i=1}^2 U_i =1.41\times 10^{-20}J\)

\(U_{T1} =\sum \limits _{i=1}^2 U_i =2.82\times 10^{-20}J\)

Assumption 2: If cell-2 is logic ‘0’ as in Fig. 5b.

Figure 5b (electron x)

Figure 5b (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_{T21} =\sum \limits _{i=1}^2 U_i =2.292\times 10^{-20}J\)

\(U_{T22} =\sum \limits _{i=1}^2 U_i =1.07\times 10^{-20}J\)

\(U_{T2} =\sum \limits _{i=1}^2 U_i =3.364\times 10^{-20}J\)

With comparison to the above result, we can conclude that the potential energy of cell-2 in Fig. 1a is lower. So, cell-2 will be logic ‘1’. Same as if cell-1 is logic ‘0’, so we can take cell-2 as logic ‘0’ if they are connected in series with each other.

2.2 Proof 2

According to Fig. 6a, if we assume that logic ‘1’ is provided at the input side to cell-1 (Proof 1), so if the cell-2 will follow the same logic as input because it is connected cross to cell-1. Physical proof is provided below:

Fig. 6
figure 6

Simple QCA inverter for a logic ‘1’ and b logic ‘0’ value in cell-2

Full size image

Assumption 1: If cell-2 is logic ‘1’ as in Fig. 6a.

Figure 6a (electron x)

Figure 6a (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_{T11} =\sum \limits _{i=1}^2 U_i =1.682\times 10^{-20}J\)

\(U_{T12} =\sum \limits _{i=1}^2 U_i =1.682\times 10^{-20}J\)

\(U_{T1} =\sum \limits _{i=1}^2 U_i =3.364\times 10^{-20}J\)

Assumption 2: If cell-2 is logic ‘0’ as in Fig. 6b.

Figure 6b (electron x)

Figure 6b (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{53.74\times 10^{-9}}=0.42\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{2.82\times 10^{-9}}=8.14\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_{T21} =\sum \limits _{i=1}^2 U_i =8.95\times 10^{-20}J\)

\(U_{T22} =\sum \limits _{i=1}^2 U_i =1.23\times 10^{-20}J\)

\(U_{T2} =\sum \limits _{i=1}^2 U_i =10.18\times 10^{-20}J\)

2.3 Proof 3

If two cells are connected as crossing to a single cell as shown in Fig. 3. So what will the value of cell-3 if values of other two cells crossing to it are different from each other? We have taken cell-1 as logic ‘1’ and cell-2 as logic ‘0’. We will find out the value of cell-3 if it is logic ‘0’ or logic ‘1’.

Assumption 1: If cell-3 is logic ‘1’ (Fig. 7a).

By taking into consideration, the mathematical terms for physical proof provided same as in Proof 1 above, we can give physical proof here as below:

Figure 7a (electron x)

Figure 7a (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{38.05\times 10^{-9}}=0.6\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{38.05\times 10^{-9}}=0.6\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_3 =\frac{A}{r_3 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_3 =\frac{A}{r_3 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_4 =\frac{A}{r_4 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_4 =\frac{A}{r_4 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_{T11} =\sum \limits _{i=1}^4 U_i =3.702\times 10^{-20}J\)

\(U_{T12} =\sum \limits _{i=1}^4 U_i =2.482\times 10^{-20}J\)

\(U_{T1} =\sum \limits _{i=1}^2 U_i =6.184\times 10^{-20}J\)

Fig. 7
figure 7

Two cells connected as crossing to a single cell cell-3 taken as a logic ‘1’ b logic ‘0’

Full size image

Assumption 2: If cell-3 is logic ‘0’ (Fig. 7b).

Figure 7b (electron x)

Figure 7b (electron y)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_1 =\frac{A}{r_1 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{20.09\times 10^{-9}}=1.146\times 10^{-20}J\)

\(U_2 =\frac{A}{r_2 }=\frac{23.04\times 10^{-29}}{42.94\times 10^{-9}}=0.536\times 10^{-20}J\)

\(U_3 =\frac{A}{r_3 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_3 =\frac{A}{r_3 }=\frac{23.04\times 10^{-29}}{38.05\times 10^{-9}}=0.6\times 10^{-20}J\)

\(U_4 =\frac{A}{r_4 }=\frac{23.04\times 10^{-29}}{38.05\times 10^{-9}}=0.6\times 10^{-20}J\)

\(U_4 =\frac{A}{r_4 }=\frac{23.04\times 10^{-29}}{28.28\times 10^{-9}}=0.81\times 10^{-20}J\)

\(U_{T21} =\sum \limits _{i=1}^4 U_i =3.702\times 10^{-20}J\)

\(U_{T22} =\sum \limits _{i=1}^4 U_i =2.482\times 10^{-20}J\)

\(U_{T2} =\sum \limits _{i=1}^2 U_i =6.184\times 10^{-20}J\)

From above analysis, we can observe that, the potential energy is same in both the cases, So cell-3 value can be assumed either as a logic ‘0’ or as a logic ‘1’ according to our convenience. Same as above, we can give physical proof for the different values of cell-3 when cell-1 and cell-2 has different values as given in Table 2.

2.4 Proposed 5 input majority gate

Majority gate depends on the choice of number of inputs given, which are major as a logic ‘0’ or logic ‘1’. In this scheme, we have taken five inputs labelled as A, B, C, D and E and the output is labelled as Y (Output). Seven middle cells are also provided and number is given to them according to their polarization changing priority based on inputs given. Polarization of all the input cells is fixed according to the given input from user but middle cells are free to change polarization.

Fig. 8
figure 8

a Proposed 5-input majority gate and b schematic symbol for the majority gate

Full size image

In this design the middle cells has effect of other input cells as given in following Table 3.

Table 2 Values of cell-3, based on values of cell-1 and cell-2
Full size table
Table 3 Effect of other cells on the given cell
Full size table

The majority voting function can be shown in terms of fundamental Boolean logic operator as below

$$\begin{aligned} M\left( {A,B,C,D,E} \right)= & {} \textit{ABC}+\textit{ABD}+\textit{ABE}+\textit{ACD}+\textit{ACE}\nonumber \\&+\,\textit{ADE}+\textit{BCD}+\textit{BCE}+\textit{BDE}+\textit{CDE}\nonumber \\ \end{aligned}$$
(3)

A schematic symbol of a five-input majority gate is given in Fig. 8b. We can implement three input AND gate and three input OR gate using this majority gate which are as follows as shown in Fig. 9a, b accordingly:

$$\begin{aligned}&M\left( {A,B,C,1,1} \right) =A+B+C\\&M\left( {A,B,C,0,0} \right) \hbox { }=\hbox { }ABC \end{aligned}$$

Simulation results for the output for OR and AND gate is given in Fig. 10 a,b.

Fig. 9
figure 9

Three input a OR gate and b AND gate

Full size image
Fig. 10
figure 10figure 10

Simulation results for the 5-input majority gate a OR gate b AND gate

Full size image

2.5 Physical proof for 5-input majority gate

As a 5-input Majority gate has 32 different input states, we should check all the states to verify the correctness of the proposed gate for physical proof. Here, we have checked only one state for inputs (A=1, B=0, C=1, D=1, E=1) and the other states can also be proved as same.

Based on Proof nos. 1, 2 and 3, we can predict values of different middle cell no. 1, 2, 3, 4, 5, 6, 7 as shown in Fig. 11.

Physical proofs of the proposed gate can also be given and the conditions and parameters value of cell size and distance between two cells is same as taken in above Proofs 1 and 2.

We have taken here values of cell no. 1 and 2 as logic ‘0’ as per our convenience from Proof 3. So from it, we can judge that output will come here as logic ‘1’ as cell no. 7 is logic ‘0’ and so that according to Proof 2, Output will be gain opposite value to cell no .7. We can predict the output value same as above for all the input values provided at input cells (A, B, C, D, E).

3 One bit QCA full adder

We have implemented full adder using our proposed design of five-input majority gate. First of all other FAs are presented and then our design is compared with them. A one bit FA can be defined as:

Input: Operand bit (A, B) and carry bit is shown as C.

Output: Sum and Carryout (Cout).

3.1 A QCA FA with seven gates

In a classical design of [4], author has implemented one bit FA as shown in Fig. 12a using five, three input majority gates and three inverters. It has been simplified and implemented in [6] using four, three input majority gates and three inverters in a more simple and robust manner as in Fig. 12b.

Fig. 11
figure 11

Value of different middle cells

Full size image

In the above design, the FA has been implemented using only inverters and majority gates. Using only AND/OR gates can increase the total number of QCA cells.

3.2 A QCA FA with five gates

In [6], author has used a method to decrease the numbe of gates for implementing FA and proposed a FA design using three, 3-input majority gates and two inverters as in Fig. 13. layout of this figure has 4 clocking phases.

Fig. 12
figure 12

a One bit QCA FA with eight gates b modified one bit QCA FA with seven gates

Full size image

3.3 A QCA FA with three gates

In [15], a novel design of one bit FA using only three gates has been implemented using one inverter, one 3-input majority gate and one 5-input majority gate as in Fig. 14. Author has tried to implement a novel 5-input majority gate besides the conventional gates.

Fig. 13
figure 13

One bit QCA FA with five gates

Full size image
Fig. 14
figure 14

One bit QCA FA with three gates

Full size image
Fig. 15
figure 15

a 1 bit QCA FA cell layout, b 3D schematic

Full size image

3.4 A QCA FA with one gate

In one of the latest design [16], author has implemented one bit FA using three layers in its layout and taking only one 5-input majority gate in first layer, connection from layer 1 to layer 3 in layer 2 and proposed a mechanism for getting \(\hbox {C}_{\mathrm{out}}\) in layer 3 as shown in Fig. 15a, b. Author has proposed a new methodology for implementing FA here. The number of total cells are only 24 here having area of \(0.04\,\upmu \hbox {m}^{2}\) only. Drawback of this design is that it is sometime hard to implement a design with 3 layers in its layout.

Fig. 16
figure 16

Proposed one bit QCA FA schematic design

Full size image
Fig. 17
figure 17

Proposed one bit QCA FA

Full size image

3.5 Proposed QCA FA

Table 4 Comparison of various QCA FA design
Full size table
Fig. 18
figure 18

Simulation result for proposed 5-input majority gate

Full size image
Fig. 19
figure 19

Simulation result for FA based on proposed 5-input majority gate

Full size image

A novel 5-input Majority gate has been proposed here (Fig. 9). By means for checking this 5-input Majority gate, a new and efficient FA is designed. Schematic design of the proposed FA is presented in Figs. 16 and 17 illustrates the layout of the proposed FA. The proposed FA is best in terms of total number of cell count it uses for its design (48) taking into consideration that it uses only three clock phases for its implementation. Proposed FA layout can be implemented on a single layer only which is other advantage compared to some other latest techniques available. Comparison of proposed FA with that of other FA is given in Table 4.

4 Simulation results

A simulation tool for QCA circuits, QCADesigner version 2.0.3 [17], is used here for the proposed circuit layout and functionality checking of FA. The following parameters are used for bistable approximation: no. of samples: 12,800, convergence tolerance: 0.001000, radius of effect: 65.00 nm, relative permittivity: 12.90, clock high: \(9.8\times 10^{-22}\), clock low: \(3.8\times 10^{-23}\), clock shift: 0.00 + 00, clock amplitude factor: 2.0, layer separation: 11.50, Max. iterations per sample: 100. Most of the default parameters are given as a default values in QCADesigner tool.

Figures 18 and 19, shows simulation results of proposed 5-input majority gate and 1-bit FA constructed using the proposed gate accordingly.

5 Conclusion

A novel design for 5-input majority gate has been proposed here and tried to give its physical proof from Proofs 1, 2 and 3. We can design more sophisticated QCA circuits by utilizing this 5-input majority gate. To illustrate the usefulness of the proposed gate, a new FA has been implemented which is robust in nature and uses 48 cells and a single layer with utilizing only 3 clock phases in its structure. Area and complexity of proposed FA is also small compared to most of the previous approaches available and thus the proposed FA has some superiority over the previous designs and shows consideration improvements.