1 Introduction

Designing and fabricating complementary metal oxide semiconductor (CMOS)-based logic devices at nanoscale (Lent and Tougaw 1997) has issues like oxide thickness, thermal reliability and power dissipation (Joachim et al. 2000). Hence, the industries are in search of new techniques which could aid the scaling of CMOS. Researchers are well-aware that the CMOS technology could be continued only for a decade. Some of the alternate technologies like QCA, single-electron tunneling (SET) and carbon nanotubes (CNT) came into existence. QCA is one of the competitive alternate technologies (Bourianoff 2003) that has none of the above-said problems. The benefit of QCA devices over regular CMOS circuits is the absence of electron flow for charge transfer and absence of metallic interconnects which are the main sources of IR losses with low power consumption (Huang et al. 2007). Hence, QCA (Walus et al. 2004) is more prudent than CMOS technology.

Many QCA logic designs have been implemented during recent years. Various five-input majority gates in (Navi et al. 2010a, b; Akeela and Wagh 2011; Roohi et al. 2014; Angizi et al. 2015; Hashemi and Navi 2015; Sen et al. 2013; Hashemi et al. 2012; Sheikhfaal et al. 2015; Bahar and Waheed 2016), one-bit full-adder designs in (Hennessy and Lent 2001; Navi et al. 2010a, b; Akeela and Wagh 2011; Angizi et al. 2015; Sen et al. 2013; Sheikhfaal et al. 2015; Vetteth 2002; Azghadi et al. 2012; Farazkish and Navi 2012; Zhang et al. 2004; Cho and Swartzlander 2007; Mohammadyan et al. 2015; Timler and Lent 2002; Farazkish 2014; Zhang 2005; Wang et al. 2003; Hänninen and Takala 2010; Sayedsalehi et al. 2015; Abdullah-Al-Shafi and Bahar 2016), multiplier designs (Cho and Swartzlander 2009; Cho 2006; Abdullah-Al-Shafi et al. 2017a, c), RAM cell structures in (Shamsabadi et al. 2009; Vankamamidi et al. 2008), flip flops (Vetteth et al. 2003; Yang et al. 2010; Hashemi and Navi 2012; Abdullah-Al-Shafi and Bahar 2017) and logic circuits in (Abdullah-Al-Shafi et al. 2017b; Bahar et al. 2017) are presented. In the above work, most of the circuits were not potent, and hence susceptible to various defects at fabrication level because of the wire-crossing structures of QCA cells. Here, an effective use of cross-overs can reduce the number of QCA cells, complexity and total cost. Multiple cross-over wire designs result in various fabrication defects (Dysart and Kogge 2007) and area overhead. One can replace these multilayer structures with 45° rotated cells which result in coplanar cross-over designs. Such coplanar cross-over designs are utilizing two types of QCA cells which result in a problem of increased fabrication cost and reduced robustness (Crocker et al. 2008). Hence, there is a need to design robust single-layer QCA structures which uses only single-type QCA cells (that is 90° cells). The basic idea is to propose a design of a robust and energy efficient five-input majority gate and investigate the energy dissipation of the existing majority gate with PMG. The PMG proposed in this paper is utilizing lesser area with reduced power dissipation as compared to the best designs reported in the literature. The correctness of PMG is validated by designing a one-bit full adder based on proposed gate.

In this work, a coplanar five-input novel and efficient majority gate is proposed. To measure its effectiveness, one-bit novel full-adder structure is designed using PMG. The remaining paper is arranged as follows: Section 2 shows the basic concept of QCA structure and the clocking concepts. Section 3 describes the existing QCA-based five-input majority gates. Section 4 describes a proposed five-input novel majority gate design, simulation results, its physical proof and energy dissipation analysis. The energy dissipation analysis is carried out using QCAPro tool. Section 5 represents a new robust full-adder circuit design using the PMG, its simulation, energy dissipation analysis and comparison of proposed robust full-adder circuit with the existing designs in terms of area and delay. Section 6 compares the result of PMG with the existing designs in terms of occupational area and interference. The conclusion is given in Sect. 7.

2 Review of a QCA Cell

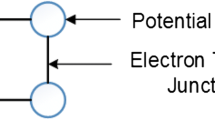
QCA cell is the fundamental nanostructure which can construct all elements of a circuit (wiring and computing). A basic QCA cell is having four quantum dots placed at the extreme edges of a quantum cell. Out of which, two quantum dots contain free electrons in a diagonal direction. These two electrons can exchange their positions by lowering the barrier potential between them to achieve P = + 1 (logic 0) or P = − 1 (logic 1) polarization state (Hennessy and Lent 2001) as shown in Fig. 1. These two free electrons confines with in a QCA cell and can never tunnel between the adjacent QCA cells. Hence, when array of QCA cells placed adjacent to one another to form a wire, only a polarization state (columbic charge) will travel along the wire. Such an array of QCA cells can be used to construct wire or any logic structure. Hence, there is less power dissipation because of the change in the polarization and propagation of columbic charge (absence of flow of electrons). Therefore, a QCA technology can be an alternative to that of a CMOS technology. The digital structure in QCA is designed by joining these cells in cascade.

Fig. 1
figure 1

QCA cells with two polarization states (Huang et al. 2007)

Full size image

2.1 Basic Structures

By connecting basic QCA cells in cascade, a wire is formed as shown in Fig. 2a. Other QCA structures like inverter and majority gate of three inputs can also be constructed using these quantum cells. An inverter circuit shown in Fig. 2b inverts its state because the output cell is in the diagonal orientation (interaction) with respect to the adjacent QCA cell. A majority gate works on the principle that the value of the output cell is true if majority of the input QCA cells are true. The QCA structure of a three-input majority gate is shown in Fig. 2c. This gate can be further configured to form AND and OR gate structures. The function of three-input majority gate is exhibited by the following equation:

$$M(A,B,C) = AB + BC + AC$$
(1)
Fig. 2
figure 2

a QCA wire, b inverter gate, c three-input majority gate and d five-input majority gate (Huang et al. 2007)

Full size image

The majority gate with five-input-based designs are much faster and are having less area as compared to the same designs made using the majority gate with three inputs. Figure 2d represents a basic structure of five-input majority gate. Its Boolean function is given in Eq. (2)

$$MG\left( {A,B,C,D,E} \right) = ABC + ABD + ABE + ACD + ACE + ADE + BCD + BCE + BDE + CDE$$
(2)

2.2 Clocking

In switch phase, the barrier potential of a QCA cell starts increasing, hence moving from unpolarized state to polarized state. In this state, the polarization state of the QCA cell will depend upon its neighboring cells. In hold phase, the barrier potential will remain constant and the QCA cell is completely polarized. Now, it becomes independent of its neighboring cells. In release phase, the barrier potential of QCA cell starts reducing, hence moving from polarized state to unpolarized state. In relax phase, the barrier potential of the QCA cell becomes zero, and hence the cell will be unpolarized as shown in Fig. 3.

Fig. 3
figure 3

QCA clocking with four phases (Hennessy and Lent 2001)

Full size image

3 Existing Five-Input Majority Gates Based on QCA

In addition to three-input majority gate design, many researchers tried to implement the digital circuits using five-input majority gate. The purpose of designing digital circuits using five-input majority gate is reduced area, latency and faster speed of operation than the traditional designs. Various five-input majority gates existing in the literature are described in this section. Many digital circuits implementing five-input majority gate using Eq. (2) are designed in Navi et al. (2010a, b), Farazkish and Navi (2012), Mohammadyan et al. (2015) and Farazkish (2014).

The design (Navi et al. 2010a) shown in Fig. 4a is utilizing only ten QCA cells with an area of 0.01 µm2. This five-input majority gate is having a drawback that its output QCA cell is trapped by the input QCA cells, hence limiting the access of output cell in a single layer only. The majority gate design (Navi et al. 2010b) shown in Fig. 4b also utilizes ten QCA cells with an area of 0.01 µm2 but it causes an interference between the input QCA cells as they are too close to each other. However, the design presented in Mohammadyan et al. (2015) shown in Fig. 4c tries to overcome the previous disadvantages but at the cost of increased area from 0.01 to 0.02 µm2. The designs in Farazkish and Navi (2012) and Farazkish (2014) shown in Fig. 4d, e also show the improvement in terms of no interference and accessibility to single-layer as well as multilayer designs. These designs are not so encouraging because of their increase up to 0.03 µm2. The design in Farazkish and Navi (2012) is utilizing 42 QCA cells, whereas the design in Farazkish (2014) is using 51 QCA cells.

Fig. 4
figure 4

Various five-input majority gates a design (Navi et al. 2010a), b design (Navi et al. 2010b), c design (Mohammadyan et al. 2015), d design (Farazkish and Navi 2012) and e design (Farazkish 2014)

Full size image

4 Proposed Five-Input Majority Gate (PMG)

4.1 Structural Analysis

The five-input novel majority gate proposed in this paper is utilizing 17 QCA cells having an area of 0.01 µm2 as shown in Fig. 5a. It has no interference between the input cells and can be used for both single-layer as well as multilayer designs. Figure 5b shows the simulation waveform for the PMG. From the simulation results, it is clear that when a majority number of inputs are at high logic, the output is also at logic high.

Fig. 5
figure 5

Proposed five-input majority gate a structure and b simulation results

Full size image

4.2 Physical Proof

The proposed five-input coplanar majority gate (PMG) has 25 = 32 input combinations. Accuracy of these 32 input combinations needs to be verified but due to insufficient space, only one state is proven for consideration. Rest of the other states can be similarly verified.

All the QCA cells of PMG are of equal size (18 nm × 18 nm) and are separated from each other by 2 nm space. The electrons in each cell are positioned in a manner that they must acquire minimum potential energy to become stable. The lesser the potential energy of a QCA cell, the more stable it is. The potential energy between two electron charges in a QCA cell is calculated as:

$$U = \frac{{kq_{1} q_{2} }}{r} = \frac{A}{r}$$
(3)
$${\text{where}}\;A = kq_{1} q_{2} = 9 \times 10^{9} \times \left( {1.6} \right)^{2} \times 10^{ - 38} = 23.04 \times 10^{ - 29}$$
(4)

where U = potential energy, K = Coulomb’s law constant, r = distance between two electrons and q1 and q2 are charges of electrons.

$$U_{T} = \mathop \sum \limits_{i = 1}^{n} U_{i}$$
(5)

where UT = summation of potential energies from Eq. (3) (Srivastava et al. 2009; Shamsabadi et al. 2009).

In this section, the stability analysis of proposed PMG is done on one state that is A = B = C = E = 1 and D = 0, by finding the potential energy between input cells (i.e., A, B, C, D and E) and their corresponding middle cells (i.e., cell nos. 1, 2, 3, 9 and 11). Figure 6a, b shows Cell 1 with electrons x and y in two different states. Next step is to find which state is more stable by calculating their potential energies separately.

Fig. 6
figure 6

Two states of Cell 1 a Cell 1 = Logic “1” and b Cell 1 = Logic “0”

Full size image

Firstly, the potential energy of Cell 1 (highlighted with yellow color) in Fig. 6a will be calculated, when the value of Cell 1 is logic “1.” The polarization of Cell 1 is affected by input cell A only because it is the only adjacent input cell for Cell 1. The potential energy of electron x (Ux) is calculated with reference to electron e1 and e2 called as Ux1 and Ux2. In the similar way, potential energy of electron y (Uy) is calculated with reference to electron e1 and e2 called as Uy1 and Uy2. The calculation of potential energies Ux1, Ux2, Uy1 and Uy2 is given below:

$$\begin{aligned} U_{x1} & = \frac{A}{r1} = \frac{{23.04 \times 10^{ - 29} }}{20} \approx 1.152 \times 10^{ - 20} \left( J \right) \\ U_{x2} & = \frac{A}{r1} = \frac{{23.04 \times 10^{ - 29} }}{18.11} \approx 0.07024 \times 10^{ - 20} \left( J \right) \\ U_{x} & = \mathop \sum \limits_{i = 1}^{2} U_{xi} = 1.222 \times 10^{ - 20} \left( J \right) \\ U_{y1} & = \frac{A}{r1} = \frac{{23.04 \times 10^{ - 29} }}{42.04} \approx 0.5479 \times 10^{ - 20} \left( J \right) \\ Uy_{2} & = \frac{A}{r1} = \frac{{23.04 \times 10^{ - 29} }}{20} \approx 1.152 \times 10^{ - 20} \left( J \right) \\ U_{y} & = \mathop \sum \limits_{i = 1}^{2} U_{yi} = 1.6999 \times 10^{ - 20} \left( J \right) \\ U_{T11} & = U_{x} + U_{y} = 2.92219 \times 10^{ - 20} \left( J \right) \\ \end{aligned}$$

where UT11 is the total potential energy of Cell 1 when it is at the “1” state.

Similarly, the results of Ux1, Ux2, Uy1 and Uy2 are calculated when the value of Cell 1 is at logic “0” as shown in Fig. 6b.

$$\begin{aligned} U_{x} & = \mathop \sum \limits_{i = 1}^{2} U_{i} = 12.376 \times 10^{ - 20} \left( J \right) \\ U_{y} & = \mathop \sum \limits_{i = 1}^{2} U_{i} = 1.46258 \times 10^{ - 20} \left( J \right) \\ U_{T10} & = U_{x} + U_{y} = \mathop \sum \limits_{i = 1}^{2} U_{1i} = 13.8388 \times 10^{ - 20} \left( J \right) \\ \end{aligned}$$

where UT10 is the total potential energy of Cell 1 when it is at the “0” state. The results show that the potential energy of UT11 is lower than the UT10. So the Cell 1 will acquire the polarization state of “1” because it achieves lower potential energy with more stability.

In the same way, the potential energies of other middle cells which are adjacent to input cells will be calculated by assuming them to be at the state “1” and “0,” respectively. The final results of potential energies for adjacent middle cells (2, 3, 9, and 11) are given below.

Cell 2::

At Logic “1” \(U_{T21} = 4.1239 \times 10^{ - 20} \left( j \right)\)

At Logic “0” \(U_{T20} = 13.8387 \times 10^{ - 20} \left( j \right)\)

Cell 3::

At Logic “1” \(U_{T31} = 4.1241 \times 10^{ - 20} \left( j \right)\)

At Logic “0” \(U_{T30} = 13.8387 \times 10^{ - 20} \left( j \right)\)

Cell 9::

At Logic “1” \(U_{T91} = 13.8387 \times 10^{ - 20} \left( j \right)\)

At Logic “0” \(U_{T90} = 4.1240 \times 10^{ - 20} \left( j \right)\)

Cell 11::

At Logic “1” \(U_{T111} = 4.1241 \times 10^{ - 20} \left( j \right)\)

At Logic “0” \(U_{T110} = 13.8387 \times 10^{ - 20} \left( j \right)\)

From the above results, it is clear that when the inputs are A = B = C = E = 1 and D = 0, Cell 2, Cell 3 and Cell 11 will remain at the logic 1 because potential energies UT21, UT31 and UT111 are less than UT20, UT30 and UT110, respectively, whereas Cell 9 will be at the logic 0 because UT90 is lesser than UT91. This is practically true also because its adjacent input Cell D is at logic 0. By considering the achieved results, the proposed QCA structure for implementing five-input novel majority gate is fully correct and results in a precise output.

4.3 Energy Dissipation Analysis

Low power dissipation, even below traditional KT, is one of the main features of QCA nanotechnology. QCAPro is one of the accurate power estimation tools which uses non-adiabatic power dissipation model (Srivastava et al. 2009) to estimate the switching power loss in QCA. The basics of this model were taken from quasi-adiabatic model in Timler and Lent (2002). According to this model, the expectation energy value of cell for every clock cycle is described as:

$$E = \frac{\hbar }{2} \cdot \vec{\varGamma } \cdot \vec{\lambda }$$
(6)

where \(\vec{\lambda } = {\text{coherence}}\;{\text{vector}}\), \(\vec{\varGamma } = 3{\text{D}}\;{\text{energy}}\;{\text{vector}}\).

Now, the total power of single QCA cell at any instant is:

$$P_{\text{total}} = \frac{{{\text{d}}E}}{{{\text{d}}t}} = \frac{\text{d}}{{{\text{d}}t}}\left[ {\frac{\hbar }{2}. \vec{\varGamma } \cdot \vec{\lambda }} \right] = \frac{\hbar }{2}\left[ {\frac{{{\text{d}}\vec{\varGamma }}}{{{\text{d}}t}} \cdot \vec{\lambda }} \right] + \frac{\hbar }{2}\left[ {\vec{\varGamma } \cdot \frac{{{\text{d}}\vec{\lambda }}}{{{\text{d}}t}}} \right] = P_{1} + P_{2}$$
(7)

The first term, i.e., \(P_{1} = \frac{\hbar }{2}\left[ {\frac{{{\text{d}}\vec{\varGamma }}}{{{\text{d}}t}} \cdot \vec{\lambda }} \right]\) indicates two components; first is transfer of power from clock signal to the QCA cell and the second is power gain due to the difference in input and output signal power.

The second term \(P_{2} = \frac{\hbar }{2}\left[ {\vec{\varGamma } \cdot \frac{{{\text{d}}\vec{\lambda }}}{{{\text{d}}t}}} \right]\) indicates instantaneous power dissipation. In one clock cycle, the energy dissipation in a QCA cell is calculated by integrating P2 over time. Therefore,

$$E_{\text{diss}} = \int_{ - T}^{T} {P_{2} {\text{d}}t} = \frac{\hbar }{2}\int_{ - T}^{T} {\vec{\varGamma } \cdot \frac{{{\text{d}}\vec{\lambda }}}{{{\text{d}}t}} {\text{d}}t}$$
(8)
$$E_{\text{diss}} = \frac{\hbar }{2}\left( {\left[ {\vec{\varGamma } \cdot \vec{\lambda }} \right]_{ - T}^{T} - \int_{ - T}^{T} {\vec{\lambda } \cdot \frac{{{\text{d}}\vec{\varGamma }}}{{{\text{d}}t}} {\text{d}}t} } \right)$$
(9)

The value of energy dissipation is maximum for maximum changing rate of \(\vec{\varGamma }\). So the upper bound power dissipation is given by:

$$P_{\text{diss}} = \frac{{E_{\text{diss}} }}{{T_{\text{cc}} }}\left\langle\frac{\hbar }{{2T_{\text{cc}} }}\vec{\varGamma }_{ + } \times \left[ { - \frac{{\vec{\varGamma }_{ + } }}{{\left| {\vec{\varGamma }_{ + } } \right|}}\tanh \left( {\frac{{\hbar \left| {\vec{\varGamma }_{ + } } \right|}}{{k_{\text{B}} T}}} \right) + \frac{{\vec{\varGamma }_{ - } }}{{\left| {\vec{\varGamma }_{ - } } \right|}}\tanh \left( {\frac{{\hbar \left| {\vec{\varGamma }_{ - } } \right|}}{{k_{\text{B}} T}}} \right)} \right] \right\rangle$$
(10)

where \(k_{\text{B}}\) represents Boltzmann Constant, and T represents temperature. Srivastava (2011) presented a power dissipation model in which total power is classified as leakage power and switching power. Here, leakage power is a power loss at clock transitions at leading edge or trailing edge of the pulse, and switching power loss is due to the switching state of the cell. Based on this, a tool called QCAPro is developed which estimates average power dissipation of the circuit.

In this paper, the energy dissipation of proposed five-input coplanar majority gate is analyzed. For this switching energy, leakage energy and total energy dissipation are calculated for three different tunneling energies (shown in Table 1) at temperature T = 2 K. Also the results of proposed five-input coplanar majority gate are compared with the existing structures proposed in Navi et al. (2010a, b), Farazkish and Navi (2012), Mohammadyan et al. (2015) and Farazkish (2014). Table 1 presents energy dissipation analysis of PMG and the previous existing designs. The comparative results of leakage, switching and total energy dissipation are also shown in Fig. 7a, b, c respectively. The results calculated in Table 1 conclude that the proposed five-input coplanar majority gate design has 20.1% less switching energy, 10.5% less leakage energy and 21.1% less total energy dissipation than the best conferred design in Zhang (2005) for single-layer as well as multilayer designs at 1.0Ek tunneling energy level. The existing designs in Navi et al. (2010a, b) cannot be used for single-layer design. So in the graph (Fig. 7), our results are compared only with the designs that can be used for single-layer as well as multilayer structures.

Table 1 Energy dissipation analysis of proposed five-input coplanar majority gate (PMG) and previous designs at temperature, T = 2 K
Full size table
Fig. 7
figure 7

a Leakage energy dissipation, b switching energy dissipation and c total energy dissipation of the PMG at three different tunneling energies (at T = 2.0 K)

Full size image

Figure 8 shows the thermal layout of proposed five-input majority gate at temperature 2.0 k with tunneling energy of 0.5Ek. In this, the darker QCA cells indicate more average energy dissipation, whereas white cells represents the inputs.

Fig. 8
figure 8

Thermal layout of PMG at temperature 2 K (tunneling energy = 0.5Ek)

Full size image

5 Single-Bit QCA Full Adder

5.1 Proposed One-Bit Full Adder

The correctness of proposed coplanar majority gate (PMG) is validated by designing a full-adder structure using the proposed gate. The structure of proposed full adder (PFA) using PMG is shown in Fig. 9a. Its QCA equivalent and simulations are given in Fig. 9b, c. The PFA circuit adds the two input bits A and B and carry C. The output is taken from SUM and CARRY bits. The PFA structure outperforms the previous designs with 58 QCA cells, occupational area of 0.05 µm2, gate count of 4 and input-to-output delay of 1 clock cycle. Its energy dissipation analysis is also done using QCAPro tool, and its results are shown in Table 2. The PFA dissipates 129.97 meV energy at 0.5Ek tunneling energy, 154.73 meV energy at 1.0Ek tunneling energy and 186.61 meV energy at 1.5Ek tunneling energy at the temperature of 2 K.

Fig. 9
figure 9

Proposed full adder a circuit diagram, b QCA implementation and c simulation results of proposed one-bit full adder

Full size image
Table 2 Energy dissipation analysis of PFA design for tunneling energies 0.5Ek, 1.0Ek and 1.5*Ek at T = 2 K
Full size table

Here, the existing QCA-based full-adder designs are compared with a new full-adder design based on PMG. The proposed full-adder design (PFA) outperforms the existing presented designs in terms of latency and occupational area. The comparison of PFA with the existing designs is shown in Table 3. The PFA design shows 16.6% enhancement in occupational area and 33.3% enhancement in latency in comparison with the best design conferred in Hashemi and Navi (2015) for single-layer as well as multilayer designs.

Table 3 Comparison of proposed full adder with the existing layout
Full size table

6 Comparison of PMG with Existing Designs

The proposed five-input coplanar majority gate is verified by a QCADesigner tool. The simulation is done for bistable and coherence vector simulation engine setup for which the total number of samples taken is 32,000 with temperature of 2 K. The simulations of PMG are done at the default value of relative permittivity of 12.9 for GaAs and AlGaAs heterostructure implementation. Table 4 depicts the comparison of PMG with the existing designs. It is illustrated that the PMG design occupies an area of 0.01 (µm2) which is 50% less as compared to the best design presented in Mohammadyan et al. (2015) for single-layer as well as multilayer designs.

Table 4 Comparison of PMG with the existing layouts
Full size table

7 Conclusion

In this paper, a novel five-input coplanar majority gate design with its physical proof is presented. The detailed analysis and energy dissipation of proposed gate were performed. To authenticate the correctness of the proposed gate, a full-adder circuit is designed, and their power analysis is also carried out. The results proved that the proposed designs have outgrown all previously mentioned structures and show remarkable improvement in terms of latency, occupational area, complexity and average energy dissipation. The designs have been verified at three different tunneling energies, that is, 0.5Ek, 1.0Ek and 1.5Ek at the temperature of 2 K. The total energy dissipation of the circuit is computed as the sum of average leakage energy and switching energy dissipation. The PMG design has 21.1% less total energy dissipation than the best reported circuits in Mohammadyan et al. (2015) at a tunneling energy level of 1.0Ek.