1 Introduction

Single-electron circuits are an important topic in electronics and physics research due to their small size and ultra-low power consumption. The field of solid state single-electronics began in 1985 when Averin and Likharev applied the orthodox theory [1] on the transfer of discrete charge through energy barriers along metallic conductors separated by \(\sim \)1 nm of insulating material, which is known as a “tunnel junction” [2]. They also predicted the “single-electron tunneling (SET) oscillations” phenomenon [3]. In 1987, their theoretical work was supported by Fulton and Dolan experiments [4] when the first single-electron transistor was implemented.

To simplify the equations of single-electron circuits without limiting the description, the orthodox theory neglects the cotunneling (simultaneous quantum tunneling events), the electron energy quantization inside the conductor, and the time of electron tunneling through the barrier [5].

For many experiments, quantum mechanics only predicts the probability of any outcome; therefore, the Monte Carlo (MC) method, which is a stochastic technique, is a more suitable method to simulate quantum systems. It is based on random inputs which may obey any type of distribution according to the nature of the investigated problem. Repeating this “mathematical experiment” many times and using good random numbers generator enhance the results.

The main disadvantage of MC algorithms is the long simulation time. Thus the point here is how the simulation time can be shortened. In this paper two strategies are considered. As for the first, the rare events are neglected so MC is not needed. This method is sufficient for small circuits with few islands; but for large circuits we are forced to use MC because rare events cannot be neglected. This leads to the second strategy where the simulation time can be shortened by using the results of the average values for small number of tunnelling events instead of considering large number of events. These strategies are applied on single-electron circuits which are divided into three types. The first is the single-electron circuits with single output and few islands (up to five islands) as for example NAND and NOR circuits. The second type is a single output but it has more than five islands as is the case with the majority logic gate (MLG) circuits. The multi output circuits such as decimal to binary coded decimal (BCD) encoders represent the third type of circuits.

All the results are obtained by our simulator MUSES which was presented earlier in [6] and compared with the widely accepted MC simulator for single-electronics SIMON [7, 8].

2 Simulation process

The current in the single-electron circuits depends only on quantum tunneling phenomena, and the occurrence probability of a certain tunnel event is a function of Helmholtz free energy before and after the tunnel event \(\Delta {F}\).

$$\begin{aligned} \Delta F=\Delta E-W \end{aligned}$$
(1)

where \(W\) is the work done by the power sources and \(\Delta E\) is the change of the total energy stored in the circuit and can be approximated to equal the change of the electrostatic energy of the circuit (if the change in the Fermi energy in the charging nodes and the effect of quantum confinement energies are neglected).

The electrons tunneling rate \(\varGamma \) through a single-electron device depends on the change of Helmholtz free energy \(\varGamma =f(\Delta F)\). Based on the Fermi golden role and orthodox theory, the tunneling rate through the \(i\)th tunnel junction is derived as [9].

$$\begin{aligned} \varGamma _i =\frac{\Delta F}{e^{2}R_T \left( {1-exp\left( {\frac{-\Delta F}{kT}} \right) } \right) } \end{aligned}$$
(2)

where \(R_{T}\) is the tunnel resistance.

The interval between two successive tunnel events “silence time” or the duration to the next tunnel event when rare events are considered is expressed as:

$$\begin{aligned} t=-\frac{\ln r}{\varGamma } \end{aligned}$$
(3)

where \(r\) is a random number with uniform distribution and \(\varGamma \) is the tunnel rate [10].

If rare events are neglected (MC not considered), the silence time is expressed as:

$$\begin{aligned} t=\frac{1}{\varGamma } \end{aligned}$$
(4)

The simulation process can be summarized in few steps. First, the capacitance matrix of the circuit is extracted and all possible tunneling events are determined. Then, the initial condition of the charging nodes is used to calculate the system electrostatic energy. In the third step, the time to the next tunnel event for each possible event is computed and the tunnel event with shortest silence time is the happened tunnel event. The nodes charges are updated according to the happened tunnel event. The last two steps should be repeated until the computations are done for all the required voltages [6].

3 Results

To simplify the analysis, the investigated circuits are divided into three types. The first is the single-electron circuits with single output and few islands. The second circuit type is a single output with more islands than the first circuit type. The third type is the multi output circuits. The last subsection is concerned with enhancing the results of the third type.

3.1 First type (small single output circuits)

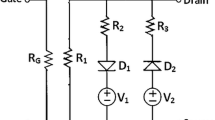
Single-electron circuits with single output and few islands like NAND and NOR can be simulated without using MC algorithms as in Eq. 4. Figure 1 shows a diagram for NAND and NOR single-electron circuits. The circuit represents a NOR gate when \(\hbox {V}_{\mathrm{control}}\) equals \(\hbox {V}_{\mathrm{bias}}\) (0.5 V) but if \(\hbox {V}_{\mathrm{control}}\) is grounded, the circuit behaves as NAND gate [11]. The MUSES results for NAND and NOR gates are shown in Fig. 2 and they are comparable to the SIMON results [12] as shown in Fig. 3.

Fig. 1
figure 1

Single-electron circuit works as a NAND \((\hbox {V}_{\mathrm{control}}=0)\) and NOR \((\hbox {V}_{\mathrm{control}}=\hbox {V}_{\mathrm{bias}})\) with parameter: \(\hbox {C}_{\mathrm{in}}=2\) aF, \(\hbox {C}_{\mathrm{bias}}=\hbox {C}_{\mathrm{in}}\), \(\hbox {C}_{\mathrm{out}}=0.3\) aF, \(\hbox {C}_{\mathrm{g}}=0.15\) aF, TJ \((\hbox {R}_{\mathrm{TJ}}=10^{5} \quad \Omega \), \(\hbox {C}_{\mathrm{TJ}}=0.01\) aF), \(\hbox {V}_{\mathrm{bias}}\)=0.5 V, \(\hbox {V}_{1}\) and \(\hbox {V}_{2}\) are digital inputs with maximum values = \(\hbox {V}_{\mathrm{bias}}\)

Full size image
Fig. 2
figure 2

MUSES results for NAND and NOR gates

Full size image
Fig. 3
figure 3

SIMON results for NAND and NOR gates

Full size image

3.2 Second type (large single output circuits)

In this type, the number of islands is more than the first type as the example of the MLG-n (7 islands) [13] shown in Fig.  4. This Artificial Neural Network ANN circuit has \(\hbox {C}_{\mathrm{x}1}\) and \(\hbox {C}_{\mathrm{x}2}\) for hidden neuron and output neuron respectively. Figures 5 and 6 illustrate the results of MUSES and SIMON for MLG3 and MLG7. The results of MUSES are done at working temperature \(300^\circ \hbox {K}\) without using MC (Eq. 4 are considered) and the value of \(\hbox {C}_{\mathrm{FB}}\) is taken 1.5 aF for MLG3 and 2.5 aF for MLG7 and the working temperature is \(300\,^\circ \hbox {K}\). The changes of \(\hbox {C}_{\mathrm{FB}}\) in MUSES may derive from the non-mentioned parameter [13] (for example: the working temperature).

Fig. 4
figure 4

The schematic diagram of the n-input SE ANN majority logic gate (MLGn) with parameter: \(\hbox {C}_{\mathrm{g}}(\hbox {MLG}3)=0.5\) aF, \(\hbox {C}_{\mathrm{g}}(\hbox {MLG}7)=0.2\) aF, \(\hbox {C}_{\mathrm{int}}=10\) aF, \(\hbox {C}_{\mathrm{b}}=4.25\) aF, \(\hbox {C}_{\mathrm{out}}=9\) aF, \(\hbox {C}_{\mathrm{FB}}=0.5\) aF, \(\hbox {TJ}_{1}(\hbox {R}_{\mathrm{TJ}}=10^{5} \quad \Omega \), \(\hbox {C}_{\mathrm{TJ}}=0.1\) aF), \(\hbox {TJ}_{2}(\hbox {R}_{\mathrm{TJ}}=10^{5} \quad \Omega \), \(\hbox {C}_{\mathrm{TJ}}=0.5\) aF), \(\hbox {V}_{\mathrm{bias}}=16\) mV, and \(\hbox {V}_{1}\), \(\hbox {V}_{2}, {\ldots }., \hbox {V}_{\mathrm{N}}\) are digital inputs with maximum values = \(\hbox {V}_{\mathrm{bias}}\)

Full size image
Fig. 5
figure 5

MUSES results for MLG3 and MLG7. a MLG3, b MLG7

Full size image
Fig. 6
figure 6

SIMON results for MLG3 and MLG7 [13]. a MLG3, b MLG7

Full size image

3.3 Third type (the multi output circuits)

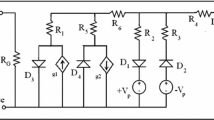
Figure 7 shows logic diagram of the single-electron SE decimal-to-BCD encoder using NOR gates. This multi output circuit has 4 outputs and 16 islands. The SIMON results [12] are shown in Fig. 8. Figure 9 shows the MUSES results without MC method. The error in the results without using randomness can not be accepted so we are forced to use the MC method. Figure 10 illustrates the MUSES results with considering MC method (Eq. 3) and 20,000 tunnel event per each computation of voltage. The simulation time is 36 min using computer HP Compaq Elite 8300 SFF with Intel(R) Core(TM) i7-3770 CPU @ 3.4 GHz, 4 GB of RAM.

Fig. 7
figure 7

Logic diagram of the decimal-to-BCD encoder using NOR gates

Full size image
Fig. 8
figure 8

The SIMON results for the SE decimal-to-BCD encoder using NOR gates

Full size image
Fig. 9
figure 9

MUSES results without using Monte Carlo for the SE decimal-to-BCD encoder using NOR gates

Full size image
Fig. 10
figure 10

MUSES results using Monte Carlo for the SE decimal-to-BCD encoder using NOR gates (with 20,000 tunnel event per each computation of voltage and the simulation time is 36 min using computer HP Compaq Elite 8300 SFF with Intel(R) Core(TM) i7-3770 CPU @ 3.4 GHz, 4 GB of RAM)

Full size image

3.4 Enhancing the results of the third type

Enhancing the results can be accomplished with a small price of the accuracy where the simulation time can be shortened by computing the upper and lower values for the digital outputs. This can be done by using the average values for small number of tunnelling events instead of considering large number of events. Figure 11 represents MUSES results using MC for the SE decimal-to-BCD encoder using NOR gates where the number of tunnel events per each computation of circuit voltages is 270 events per each computation of the voltage and the simulation time is 23 s. Figure 12 compares the results of 20,000 events per each computation and 270 events results after optimizing the results of Fig. 11.

Fig. 11
figure 11

MUSES results using Monte Carlo for the SE decimal-to-BCD encoder using NOR gates (with 270 tunnel event per each computation of voltage and the simulation time is 23 s using a computer HP Compaq Elite 8300 SFF with Intel(R) Core(TM) i7-3770 CPU @ 3.4 GHz, 4 GB of RAM)

Full size image
Fig. 12
figure 12

Comparison between the MUSES results using Monte Carlo for the SE decimal-to-BCD encoder using NOR gates with 20,000 tunnel events per each computation (dots) and 270 events after optimizing the results by computing the upper and lower average values of the outputs (solid)

Full size image

4 Discussion

The simulation results for single output circuits with few islands are accepted even if the rare events are completely neglected. But for multi output circuits, rare events must be considered.

The non-random technique is valid for single output circuits but for multi output circuits the situation is different. As tunnel rates are high in some parts of the circuit and low in other parts the non-random method means that only events with the highest tunnel rates will occur. This neglects the rare events completely and takes the simulation in the highest tunnel rates route so only single output is correct and the rest are not as shown in Fig. 9. So there is no choice, considering rare events and using MC method in multi output and large circuits are a must.

The long simulation time can be minimized by using the results of the average values for a small number of tunnelling events instead of considering large number of events. This technique is a success when using optimized results for 270 events instead of using 20,000 events as shown in Fig. 12. The optimized method takes less than 1.1 % of the time of the method with a large number of events.

Fast simulation methods such as eliminating all randomness method for small circuits and optimized MC method for large circuits are attractive techniques by taking the advantage of short simulation time and less complication analysis. On the other hand, this may run the risk that certain complex interactions are being missed particularly if the operation of the circuit is not well known. So it was advised to use classical MC method for exploratory simulations of new circuits and applications of SET devices and fast simulation methods to tweak and optimize parameters of well understood circuits.

5 Conclusion

Simulation of single-electron circuits can be made more effective by speeding up the calculation. For single-electron circuits with single output, the simulation can be done without using the Monte Carlo method. The simulation time is short with very good approximate results.

In the simulation of multi output circuits, the rare events cannot be neglected and MC must be used. Also the simulation time can be shortened by using average values of a small number of tunnelling events instead of using a large number. This technique saves more than 98.9 % of the simulation time with a little loss on the simulation accuracy.