Optimal income taxation and migration

Abstract

We tackle the issue of optimal dynamic taxation of capital income in an economy with disconnection as in Weil (J Public Econ 38:183–198, 1989), generated by migration and intra-family altruism. We show that, when the government aims at correcting such a disconnection using time-varying weights in the social welfare function, then there is room for nonzero capital income taxation, both in the short and in the long run.

1 Introduction

Starting from the seminal works by Judd (1985) and Chamley (1986), the issue of dynamic optimal capital income taxation has been analysed by a number of researchers. In particular, Judd (1999) has shown that the zero-tax rate result stems from the fact that a tax on capital income is equivalent to a tax on future consumption: thus, capital income should not be taxed if the (general equilibrium) elasticity of consumption is constant over time. In infinitely lived representative agent (ILRA) models,¹ along the transition path, this condition holds only if the utility function is assumed (weakly) separable in consumption and leisure and homothetic in consumption. It is, instead, necessarily satisfied in the long run, thus leading to the well-known result of optimal zero capital income taxes.

The result appears at odds with reality, since the existence of positive capital income taxes is often observed. Several theoretical models have tried to find a rationale for capital income taxation.

One avenue has been allowing the government’s discount rate to differ from the households’ one. De Bonis and Spataro (2005) find that the zero capital tax result does not generally hold when the government discount rate differs from the individual one, due to “Pigouvian” arguments²: along the transition path, even with separable and homothetic utility functions, capital income is taxed (subsidized) when the government is less (more) impatient than individuals are. Instead, they obtain an asymmetry as for the steady state, since in the long run only the case for subsidizing capital is confirmed. This is because, when the government discounts the future more heavily than private agents do, the explosive distortionary effect of taxation impedes to hit capital income.³ Reis (2012) finds that capital income taxes are positive even in the long run if one introduces lack of commitment for the government alongside the difference in the discount rates: if the government is more impatient than households are, it will increase debt, but the lack of commitment will force it to save to make future policies credible. This will prevent the government from becoming too indebted, which would force it to resort only to the more efficient labour taxes.⁴

Another avenue to obtain the result of the violation of the zero tax rule also in the long run is abandoning the standard ILRA framework in favour of overlapping generations models with life cycle (OLG-LC).⁵ This outcome can be understood by reckoning that in such a set-up optimal consumption and labour, or, more precisely, the (general equilibrium) elasticity of consumption, are generally not constant over life and even at the steady state, due to life-cycle behaviour.

Both ILRA and OLG-LC models are characterized by very simple population dynamics. In this work, we extend the previous analysis on optimal taxation to a model with a “disconnected”⁶ economy, generated by migration and limited altruism. More precisely, we consider a model with individuals who are altruistic only towards their own descendants and disregard the well-being of immigrants.⁷ Hence, the entrance of new dynasties in each period prevents the economy from behaving as a single representative individual one and creates an “overlapping dynasties” mechanism.

The literature has widely analysed the interconnections between migration and fiscal policies, in particular those stemming from differences between natives and immigrants.⁸ In this paper, however, we only consider the different time of entry into the economy as a heterogeneity dimension. This is because the paper aims at analysing the effects of the disconnectedness caused by migration on capital income taxation once the policymaker, differently from residents, aims at correcting it by taking the utility of new entrants properly into account in the social welfare function. The issue of the weight to be assigned to future generations has long been debated and addressed in recent works.⁹ However, so far the literature has assumed a constant social discount rate (see, for instance, Erosa and Gervais 2002). We depart from the traditional approach by assuming that the social discount rate is time-varying and, precisely, inversely correlated with the age of the dynasty.¹⁰ In particular, we consider the case in which such weights coincide with the actual demographic weights of dynasties, which, due to immigration flows, are declining through time.¹¹ In fact, such an assumption, which seems reasonable and consistent with a Benthamite approach, turns out to be equivalent to assuming a constant intergenerational discount rate and a social intertemporal discount rate that differs from the individual one.

In this scenario, the main result we find is that the capital income tax can be nonzero, even in the absence of life-cycle behaviour. The result directly stems from Pigouvian arguments: declining dynasty’s weights lead the government to correct private accumulation of capital. More precisely, since the government cares less about the future well-being of the dynasty than the dynasty does, it wishes to tax future consumption more than present one, which implies a positive capital income tax.

Even if the rationale is the same as in the ILRA framework in De Bonis and Spataro (2005), disconnection in the economy generates positive capital income taxes also in the long run. Differently from the result obtained in Reis (2012), lack of commitment is not necessary to obtain the outcome.

The work proceeds as follows: in the section that follows, we present the model and derive the equilibrium conditions for the decentralized economy. Next, we characterize the Ramsey problem by adopting the primal approach. Finally, we present the results by focusing on the new ones. Concluding remarks and a technical Appendix will end the work.

2 The model

We consider a neoclassical production-closed economy in which there is a large number of agents and firms. Private agents, who are identical in their preferences and have infinite lives, differ as for their date of entry into the economy, s; natives are supposed to have entered the economy at time $s = -1$, while migrants start entering at time 0 at a given rate $\alpha$; both types of individuals have a constant rate of growth n: as a consequence, the population growth rate is equal to $\gamma \equiv (1 + \alpha ) (1 + n) - 1$; the whole population at time t has cardinality:

$$\begin{aligned} N_{t} = (1 + \gamma )^{t+1}, \end{aligned}$$

with the size of population at time − 1 normalized to 1; the size of each dynasty (started by the entry of the founder) is¹²:

$$\begin{aligned} P_{s,t} = \alpha ^{d} ({1+\alpha })^{d\cdot s}\cdot ({1+n})^{t+1};t\ge 0,-1\le s\le t \end{aligned}$$

with $d = 0$ if $s =-\,1$, 1 otherwise. Moreover, all individuals offer labour and capital services to firms by taking the net-of-tax factor prices, $\tilde{w}_{s,t}$ and $\tilde{r}_{s,i}$ as given. Firms, which are identical to each other, own a constant return to scale technology F satisfying the Inada conditions and which transforms factors into production–consumption units. Finally, the government can finance an exogenous stream of public expenditure $G_{t}$ by issuing internal debt $B_{t}$ and by raising proportional taxes both on interests and wages, referred to as $\tau _{s,t}^k$ and $\tau _{s,t}^l$, respectively. Notice that taxes can be conditioned on the date of birth of dynasties.

2.1 Private agents

Agents’ preferences can be represented by the following instantaneous utility function:

$$\begin{aligned} U \, (c_{s,t}, \, l_{s,t}), \end{aligned}$$

where $c_{s,t}$ and $l_{s,t}$ are instantaneous consumption and labour supply, respectively, of the dynasty founded in period s, as of instant t. Such a utility function is strictly increasing in consumption and decreasing in labour, strictly concave, and satisfies the standard Inada conditions. Since we assume that individuals care about the well-being of their children, agents maximize the following utility function:

$$\begin{aligned} \max \limits _{\{{c_{s,t} ,l_{s,t}}\}_s^\infty } \sum _{t=s}^\infty \left( {\frac{1+n}{1+\beta }} \right) ^{t-s} \, U(c_{s,t} ,l_{s,t}) \end{aligned}$$

(1)

sub:

$$\begin{aligned}&a_{s,t} =\frac{({1+\tilde{r}_{s,t}})}{({1+n})}a_{s,t-1} +\tilde{w}_{s,t} l_{s,t} -c_{s,t}, \nonumber \\&\lim \limits _{t\rightarrow \infty } a_{s,t} \frac{(1+n)^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} =0, \quad a_{s,s-1} =0, \quad a_{0,-1} ={\bar{k}}_{-1}, \end{aligned}$$

(2)

where $\beta$ is the intertemporal discount rate, with $1> \beta> n > 0$, a is the agent’s wealth, while $\tilde{w}_{s,t} =w_{t} (1- \tau _{s,t}^l)$ and $\tilde{r}_{s,i} = r_{t} (1 - \tau _{s,t}^k)$ are the net-of-tax factor prices.

The FOCs of this problem imply:

$$\begin{aligned} \left( {\frac{1+n}{1+\beta }}\right) ^{t-s}U_{c_{s,t}}= & {} p_{s,t} \end{aligned}$$

(3)

$$\begin{aligned} \left( {\frac{1+n}{1+\beta }}\right) ^{t-s}U_{l_{s,t}}= & {} -p_{s,t} \tilde{w}_{s,t} \end{aligned}$$

(4)

$$\begin{aligned} \frac{({1+\tilde{r}_{s,t+1}})}{({1+n})}p_{s,t+1}= & {} p_{s,t}, \end{aligned}$$

(5)

where the expression $U_{i_t}$ is the partial derivative of the utility function with respect to argument $i=c, l$ at time t and $p_{s,t}$ is the shadow price of wealth. These conditions yield:

$$\begin{aligned} \frac{U_{c_{s,t}}}{U_{c_{s,t+1}}}= & {} \frac{({1+\tilde{r}_{s,t+1}})}{1+\beta } \end{aligned}$$

(6)

$$\begin{aligned} \frac{U_{l_{s,t}}}{U_{c_{s,1}}}= & {} -\tilde{w}_{s,t}. \end{aligned}$$

(7)

which provide the usual relations between individual’s marginal rate of substitution and prices along an optimal trajectory.

2.2 Firms

We assume that firms are identical and operate in a competitive environment; they hire capital and labour services according to their market prices (gross of taxes). This means that, for each firm i, profit maximization yields:

$$\begin{aligned} \frac{\mathrm{d}F(K_{t-1}^i ,L_t^i )}{\mathrm{d}K_{t-1}^i}= & {} r_t \end{aligned}$$

(8)

$$\begin{aligned} \frac{\mathrm{d}F(K_{t-1}^i ,L_t^i )}{\mathrm{d}L_t^i}= & {} w_t. \end{aligned}$$

(9)

Note that capital is assumed to enter the production process with a one period lag. Assuming a CRS technology, such conditions can also be expressed for the economy as a whole, in per capita terms:

where $l_t \equiv \frac{L_t}{N_t} = \sum \limits _{s=0}^t {\nu _{s,t} l_{s,t}}$ and $k_t \equiv \frac{K_t}{N_t} =\sum \limits _{s=0}^t {\nu _{s,t} k_{s,t}}$, with $\nu _{s,t} \equiv \frac{P_{s,t}}{N_t} =\frac{\alpha ^{d}}{(1+\alpha )^{t+1-d\cdot s}}$ and $d=0$ if $s =-1$, 1 otherwise, the weight of dynasty s in the economy population at period t.

2.3 The government and market clearing conditions

The government is assumed to finance an amount of exogenous public expenditure by levying taxes on capital and labour income and by issuing debt in the absence of lump sum taxation. In order to rule out the problem of time inconsistency, we suppose that the government has access to a commitment technology that ties it to the announced path of distortionary tax rates whenever the possibility of lump sum taxation arises. The only constraints on the possibility of debt issuing are the usual no-Ponzi game condition and the initial condition $B_0 = {\bar{B}}$. Thus, one obtains the usual equation for the dynamics of aggregate debt:

$$\begin{aligned} B_{t} = (1 + r_{t}) B_{t-1} + G_{t}-T_{t}, \end{aligned}$$

(10)

where $T_t =\sum \limits _{s=0}^t {P_{s,t}} [{\tau _{s,t}^l w_t l_{s,t} +\frac{\tau _{s,t}^k r_t a_{s,t-1}}{(1+n)}}]$, Eq. (10) can also be written, in per capita terms:

$$\begin{aligned} b_t = \left( {\frac{1+r_t}{1+\gamma }}\right) b_{t-1} +g_t -\tau _t. \end{aligned}$$

(11)

Finally, the market clearing condition implies that, at each date, the sum of capital and debt equals aggregate private wealth, that is:

$$\begin{aligned} A_{t}=K_{t-1}+B_{t}. \end{aligned}$$

(12)

3 The Ramsey problem

Since we adopt the primal approach to the Ramsey (1927) problem,¹³ a key point is restricting the set of allocations among which the benevolent government can choose to those that can be decentralized as a competitive equilibrium.¹⁴ Thus, in this paragraph we define a competitive equilibrium and the constraints that must be imposed on the policymaker problem in order to achieve such a competitive outcome.

The first constraint is the implementability constraint, i.e. the dynasty budget constraint with prices substituted for by exploiting the individual FOCs (for the derivation see Appendix):

$$\begin{aligned} \sum _{t=s}^\infty {\left( {\frac{1+n}{1+\beta }} \right) }^{t-s} ({U_{c_{s,t}} c_{s,t} +U_{l_{s,t}} l_{s,t}})=0,\forall s \end{aligned}$$

(13)

which is referred to as the “implementability constraint”.¹⁵

As for the second constraint, summing Eq. (2) over population to get aggregate wealth, subtracting Eq. (10) and exploiting the market clearing condition, we get:

$$\begin{aligned} y_t \ge c_t +k_t -\frac{k_{t-1}}{1+\gamma } +g_t, \end{aligned}$$

(14)

where y is output in per worker terms. Such an expression is usually referred to as the “feasibility constraint” (see Appendix for a formal derivation).

We can now give the following definition, supposing that the policy is introduced in period 0:

Definition 1

A competitive equilibrium is: a) an infinite sequence of policies $\pi = \{{\tau _{s,t}^k ,\tau _{s,t}^l ,b_t}\}_{t=0}^\infty$, b) allocations $\{{c_{s,t} ,l_{s,t}, k_t}\}_{t=0}^\infty$ and c) prices $\{{w_t ,r_t}\}_{t=0}^\infty$ such that, at each instant t: b) satisfies Eq. (1) subject to (2), given a) and c); c) satisfies Eq. (8’) and (9’); Eqs. (14) and (11) are satisfied.

In the light of the definition given above, the following proposition holds:

Proposition 1

An allocation is a competitive equilibrium if and only if it satisfies implementability and feasibility.

Proof

The first part of the proposition is true by construction. The proof of the reverse (any allocation satisfying implementability and feasibility is a competitive equilibrium) is provided in Appendix. $\square$

3.1 Solution

We now assume that the policymaker maximizes a utilitarian social welfare function, which is a weighted sum of the dynasties’ utilities, subject to the constraints presented above.¹⁶ By defining the auxiliary function:

$$\begin{aligned} W_s =\sum _{t=s}^\infty {\left( {\frac{1+n}{1+\beta }} \right) ^{t-s} [{\mu _{s,t} U(c_{s,t} ,l_{s,t} )+\lambda _s (U_{c_{s,t}} c_{s,t} +U_{l_{s,t}} l_{s,t} )}]}, \end{aligned}$$

the policymaker’s problem is the following:

$$\begin{aligned} \max \limits _{\{{c_{s,t} ,l_{s,t} ,k_t}\}_0^\infty } \sum _{s=0}^\infty {W_s} \end{aligned}$$

sub:

$$\begin{aligned}&y_t =c_t +k_t -\frac{k_{t-1}}{1+\gamma } +g_t , \quad \forall t \\&\lim \limits _{t\rightarrow \infty } \frac{k_t}{\prod \limits _{i=1}^t {({1+f_{k_i}})}} =0, \quad k_{-1} ={\bar{k}}. \end{aligned}$$

where $\mu _{s,t}$ is the weight that the government attaches to dynasty s.¹⁷ Note that, differently from previous works, $\mu _{s,t}$ is allowed to vary with time.

The FOCs of the problem with respect to consumption and capital are, respectively:

$$\begin{aligned} \frac{\partial W_t}{\partial c_{s,t}}= & {} 0\Rightarrow \left( {\frac{1+n}{1+\beta }} \right) ^{t-s}U_{c_{s,t}} [{\mu _{s,t} +\lambda _s ({1+H_{c_{s,t}}})}] = \phi _t \nu _{s,t} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial W_t}{\partial k_t}= & {} 0\Rightarrow \phi _t = \left( {\frac{1}{1+\gamma } +f_{k_t}} \right) \phi _{t+1} \end{aligned}$$

(16)

where $\lambda _{s}$ is the multiplier associated with the implementability constraint, $H_{c_{s,t}} =\frac{U_{cc_{s,t}} c_{s,t} +U_{lc_{s,t}} l_{s,t}}{U_{c_{s,t}}}$, which is usually referred to as the “general equilibrium elasticity of consumption,” and $\phi _{t}$ is the multiplier associated with the feasibility constraint.

By taking the first order condition relative to consumption as for period $t+1$ and dividing Eq. (15) by it, we get¹⁸:

$$\begin{aligned} \frac{\left( {\frac{1+n}{1+\beta }} \right) ^{t-s}U_c [{\mu +\lambda ({1+H_c})}]}{\left( {\frac{1+n}{1+\beta }} \right) ^{t+1-s}U_c^{+1} \left[ {\mu ^{+1} +\lambda \left( {1+H_c^{+1}}\right) }\right] } = \frac{\phi _t \nu }{\phi _{t+1} \nu ^{+1}} \end{aligned}$$

(17)

and, by exploiting Eqs. (6), (8’) and (16) and by reckoning that $\frac{\nu }{\nu ^{+1}}= ({1+\alpha })$, we get:

$$\begin{aligned} \frac{1+\tilde{r}^{+1}}{1+r^{+1}}=\frac{\mu ^{+1} +\lambda \left( {1+H_c^{+1}}\right) }{\mu +\lambda ({1+H_c})} \end{aligned}$$

(18)

which provides the implicit expression for the optimal capital income tax.

4 Discussion of the results

We now discuss the results concerning capital income taxation at the steady state.

By inspection of the tax equation, it emerges that there are two independent forces determining the level of $\tau ^{k}$: (1) the dynamics of $H_{c}$ and (2) the dynamics of the social intergenerational weight, which is new.

We can now state the following proposition:

Proposition 2

If the economy converges to a steady state, along the transition path, for $t > t_{0}$, and at the steady state the tax on capital income is different from zero unless $\frac{\mu ^{+1} +\lambda ({1+H_c^{+1}})}{\mu +\lambda ({1+H_c})}=1$.

Proof

The proof is straightforward by inspection of Eq. (18). $\square$

Factor 1) has been widely discussed in the literature: $H_c= H_c^{+1}$ obtains, for example, by assuming homotheticity in consumption and (weak) separability in consumption and leisure in the utility function. Otherwise, future consumption is taxed/subsidized if consumption demand is getting more/less inelastic. Moreover, as recalled above, this factor marks the difference between the ILRA and the OLG-LC models as for the steady-state result: in fact, in OLG models $H_{c}$ can vary with age even at the steady state. However, as shown in Eq. (18), even in the absence of a life cycle, in the present model the nonzero tax rule can still apply.

The role of factor 2) can be isolated by supposing $H_c =H_c^{+1}$.¹⁹ Then, $\frac{1+\tilde{r}^{+1}}{1+r^{+1}}=\frac{\mu ^{+1} +\lambda ({1+H_c})}{\mu +\lambda ({1+H_c})}$. As for the choice of the social weight, we consider two exemplifying cases, chosen to allow the government to distinguish either on the basis of the dynasty only (only the index s of the weight $\mu$ varies), or of both the dynasty and its age (both s and t vary).

• (a) $\mu _{s,t} = \mu$. The weight assigned to each dynasty by the government is constant through time. Then, $\frac{1+\tilde{r}^{+1}}{1+r^{+1}}=$ 1, which implies the absence of capital income taxation. The assumption of a constant $\mu$ is made in the existing OLG-LC models (see, in particular, Erosa and Gervais 2002 and Garriga 2003).²⁰

• (b) $\mu _{s,t} \ne \mu _{s,t+1}$. The weight assigned to the dynasty varies through time, that is, through the age of the dynasty. In this case, the capital income tax is different from zero. Let us consider the Benthamite case in which the social weight of each dynasty is equal to its actual demographic weight within the population, i.e. $\mu _{s,t} = \nu _{s,t}$. Given our assumption of a constant rate of migration arrivals $\alpha$, the relative size of each dynasty is decreasing through time, so that $\mu ^{+1}/\mu = 1/(1 + \alpha )$ for each dynasty. Hence, the tax rate is, in general, positive. This result stems from the fact that the government cares less about the future utilities of the dynasty than the dynasty does and therefore discriminates future consumption in favour of the present one. Given that the dynasty’s weight decreases with time, also the tax on each dynasty’s capital income will decrease with age and will tend to zero for ${t-s} \rightarrow \infty$, that is, for the oldest dynasties (since their social weight tends to zero).

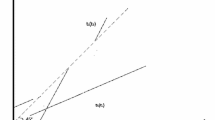
For illustrative purposes, in Fig. 1 we report the dynamics of the capital income tax for a generic dynasty born in year s, endowed with a CES utility function with separable consumption and leisure. According to this example, in which the government uses demographic weights as social weights, the capital income tax would halve in fifty years and halve again in the next fifty years, then tending asymptotically to zero. Notice that the same figure can be interpreted as the steady-state tax structure as a function of the age (i.e. size) of each dynasty. We again notice that the capital income tax will be nonzero and tending asymptotically towards zero as age increases.

Fig. 1

Dynamics of the capital income tax for a generic dynasty. Parameters specification: ${s}=1$, $\sigma =2$, $\lambda =0.05$, $\alpha =2\%$, $r = 5\%$

Another way to grasp the forces delivering this result is to note that the presence of a social weight declining over time corresponds to a government time discounting that differs from the private one. This can be seen by rewriting the problem of the policymaker as follows:

$$\begin{aligned} \max \limits _{\{{c_{s,t}, l_{s,t}, k_t}\}_0^\infty } \sum _{s=0}^\infty {\hat{{\mu }} _s \hat{{W}}_s} \end{aligned}$$

where $\hat{{\mu }}_s = \alpha ^{d} ({1+\alpha })^{s}$ and

$$\begin{aligned} \hat{{W}}_s =\sum _{t=s}^\infty {\left( {\frac{1+n}{1+\beta }} \right) ^{t-s} \left[ {({1+\alpha })^{-t}U_{s,t} +\frac{({1+\alpha })}{\alpha ^{d}}^{-s}\lambda _s \left( {U_{c_{s,t}} c_{s,t} +U_{l_{s,t}} l_{s,t}}\right) }\right] }. \end{aligned}$$

Hence, our result can be interpreted in terms of Pigouvian correction: since the government is less patient than individuals are, it is optimal to hit capital income in order to slow down the accumulation of private capital and, thus, increase present consumption. Finally, note that our result would still apply if lump sum taxes were available. In fact, the result would hold even if the implementability constraint did not bind, i.e. for the case of $\lambda = 0$, i.e. if lump sum taxes were available.

Thus, the case of constant dynasty weights corresponds to a social discount rate that is equal to the private one; consequently, if the elasticity of consumption is constant, there is no reason for correcting individual choices.

In the case of time-varying dynasty weights, instead, if these are chosen based on the dynasty relative size, the social intertemporal discount rate is smaller than the private one. Therefore, the government discriminates against future consumption.

Finally, we can provide the shape of the labour income tax under sufficiently general assumptions on the utility function (that is, weak complementarity between consumption and leisure):

Proposition 3

Suppose that the utility function is such that $U_{c,l} \le 0$; if the economy converges to a steady state, then the optimal labour tax is positive.

Proof

Taking the first derivative with respect to labour supply yields:

$$\begin{aligned} \frac{\partial W_t}{\partial l_{s,t}} =0\Rightarrow \left( {\frac{1+n}{1+\beta }} \right) ^{t-s}U_{l_{s,t}} [{\mu _{s,t} +\lambda _s ({1+H_{l_{s,t}}})}] = -\phi _t \nu _{s,t} f_{l_t} \end{aligned}$$

(19)

where $H_{l_{s,t}} = \frac{U_{ll_{s,t}} l_{s,t} +U_{lc_{s,t}} c_{s,t}}{U_{l_{s,t}}}$ is “general equilibrium elasticity of labour.” Combining (19) with (15), exploiting (7) and (9’) and collecting terms it descends that:

$$\begin{aligned} \tau _{s,t}^l =\lambda _s \frac{H_{l_{s,t}} -H_{c_{s,t}}}{\mu _{s,t} +\lambda _s ({1+H_c})} \end{aligned}$$

(20)

By (19), the denominator of (20) is positive and so is $\lambda _s$. Exploiting the definitions of $H_l$ and $H_c$, it can be seen that a sufficient condition for the numerator of (20) to be positive is $U_{c,l} \le 0$. $\square$

5 Conclusions

We reconsider the issue of optimal capital income taxation in an OLG economy with dynastic altruism and migration applying the primal approach to the Ramsey problem.

The thrust of the paper is that the Chamley–Judd zero tax rule comes out not to apply if the policymaker wishes to correct the disconnection of the economy by attaching to each dynasty a social weight that varies with time. Moreover, if the latter corresponds to each dynasty’s actual share within the population the optimal rule prescribes positive taxation of capital income, even in the absence of life-cycle behaviour, and positive taxation of labour income as well.

Taking into account the dynamics of population in the social welfare function, while being absent in both “representative agent” and traditional OLG models, besides being interesting per se, seems appropriate for models in which population “matters” and can represent a useful criterion for normative prescriptions concerning the real world, in which the dynamics of the population are typically very complicated. In particular, our model might be extended by connecting the date of entry into the economy to some population characteristics that are relevant to taxation policy (heterogeneity in tastes, skills, income and wealth levels).

Appendix

1.1 Derivation of the implementability constraint

In order to obtain the implementability constraint, write Eq. (2) in its intertemporal form:

$$\begin{aligned} \sum _{t=s}^\infty {\frac{({c_{s,t} -\tilde{w}_{s,t} l_{s,t}})}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} =0}. \end{aligned}$$

(21)

Since:

$$\begin{aligned} \frac{U_{c_{s,t}}}{U_{c_{s,t+1}}} \frac{({1+\beta })}{({1+n})} = \frac{p_{s,t}}{p_{s,t+1}} =\frac{({1+\tilde{r}_{t+1}})}{({1+n})}, \end{aligned}$$

we have

$$\begin{aligned} \frac{1}{({1+n})^{t-s}}\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})} =\frac{p_{s,s}}{p_{s,s+1}} \frac{p_{s,s+1}}{p_{s,s+2}} ...\frac{p_{s,t-1}}{p_{s,t}}. \end{aligned}$$

By substituting into Eq. (21), we obtain

$$\begin{aligned} \sum _{t=s}^\infty {\frac{({c_{s,t} -\tilde{w}_{s,t} l_{s,t}}) p_{s,t}}{p_{s,s}} =0} \end{aligned}$$

and exploiting the FOCs from the individual maximization problem, we get

$$\begin{aligned} \sum _{t=s}^\infty {\left( {\frac{1+n}{1+\beta }} \right) ^{t-s} ({U_{c_{s,t}} c_{s,t} +U_{l_{s,t}} l_{s,t}})=0}. \end{aligned}$$

which is Eq. (13) in the text.

1.2 Derivation of the feasibility constraint

To derive the feasibility constraint, first aggregate Eq. (2) over population at time t (notice that $a_{s,s-1} = 0$):

$$\begin{aligned} \sum _{s=0}^t {P_{s,t} a_{s,t} =\sum _{s=0}^t {P_{s,t} \left[ {\frac{({1+r_t})}{({1+n})}a_{s,t-1} +w_t l_{s,t} -c_{s,t} -\frac{\tau _{s,t}^k r_t a_{s,t-1}}{1+n}-\tau _{s,t}^l w_t l_{s,t}} \right] }}. \end{aligned}$$

(22)

and by recalling that $A_t \equiv \sum \limits _{s=0}^t {P_{s,t} a_{s,t}}$, $P_{s,t} =P_{s,t-1} ({1+n})$ and $P_{t,t-1} =0$, so that $\sum \limits _{s=0}^t {P_{s,t-1} a_{s,t-1}} =A_{t-1}$ we can rewrite Eq. (22) as follows

$$\begin{aligned} A_t = ({1+r_t})A_{t-1} +w_t L_t -C_t -T_t \end{aligned}$$

where $C_{t}$ is aggregate consumption. Finally, by subtracting Eq. (10) and exploiting the market clearing condition we obtain

$$\begin{aligned} K_t = ({1+r_t})K_{t-1} +w_t L_t -C_t -G_t \end{aligned}$$

which, in per capita terms, becomes

$$\begin{aligned} k_t =\frac{({1+r_t})}{({1+\gamma })}k_{t-1} +w_t l_t -c_t -g_t \end{aligned}$$

where $\frac{r_t k_{t-1}}{({1+\gamma })} +w_t l_t \equiv y_t$ due to CRS.

1.3 Proof of Proposition 1

Proof

Since a competitive equilibrium (or implementable allocation) satisfies both the feasibility and the implementability constraints by construction, in this “Appendix” we demonstrate the reverse of Proposition 1: any feasible allocation satisfying implementability is a competitive equilibrium.

Suppose that an allocation satisfies the implementability and the feasibility constraints. Then, define a sequence of after tax prices as follows: $\tilde{w}_{s,t} =-\frac{U_{l_{s,t}}}{U_{c_{s,t}}}$, $\tilde{r}_{s,t} =\frac{p_{s,t}}{p_{s,t+1}} ({1+n})-1$, with $p_{s,t} =U_{c_{s,t}} ({\frac{1+n}{1+\beta }})^{t-s}$, $\forall s$ and $\forall t$, and a sequence of before tax prices: $f_{k_{t-1}} =\frac{r_t}{1+\gamma }$, $f_{l_t} =w_t$. Therefore, by construction such allocation satisfies both the consumers’ and firms’ optimality conditions.

The second step is to show that the allocation satisfies the consumer budget constraint. Take the implementability constraint and substitute $U_{c_{s,t}}$ and $U_{l_{s,t}}$ by using the expressions above:

$$\begin{aligned} \sum _{t=s}^\infty {({p_{s,t} c_{s,t} -\tilde{w}_{s,t} p_{s,t} l_{s,t}})=0} \quad \forall s. \end{aligned}$$

Then, by recursively using the expression $p_{s,t} =\frac{p_{s,s} ({1+n})^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}}$ we get

$$\begin{aligned} \sum _{t=s}^\infty {\frac{({1+n})^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} p_{s,s} ({c_{s,t} - \tilde{w}_{s,t} l_{s,t}})=0}. \end{aligned}$$

Finally, by eliminating $p_{s,s}$ and defining $c_{s,t} -\tilde{w}_{s,t} l_{s,t} = -\,({1+n}) q_{s,t} + ({1+\tilde{r}_{s,t}}) q_{s,t-1}$, we get

$$\begin{aligned} \sum _{t=s}^\infty {\frac{({1+n})^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} [{- ({1+n})q_{s,t} + ({1+\tilde{r}_{s,t}}) q_{s,t-1}}]=0} \end{aligned}$$

that turns out to be:

$$\begin{aligned} -\lim \frac{({1+n})^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} q_{s,t} +q_{s,s} =0 \end{aligned}$$

which holds if $q_{s,t} = a_{s,t}$ and $\lim \frac{({1+n})^{t-s}}{\prod \limits _{i=s+1}^t {({1+\tilde{r}_{s,i}})}} a_{s,t} =0$.

As for the public sector budget constraint, by aggregating the individuals’ budget constraints over population at time t and expressing them in per capita terms, we get

$$\begin{aligned} a_t =\frac{({1+r_t})}{({1+\gamma })}a_{t-1} +w_t l_t -c_t -\tau _t. \end{aligned}$$

(23)

Finally, by subtracting the feasibility constraint

$$\begin{aligned} k_t =\frac{({1+r_t})}{({1+\gamma })}k_{t-1} +w_t l_t -c_t -g_t \end{aligned}$$

and defining $b_t =-\,k_{t-1} +a_t$, we obtain

$$\begin{aligned} b_t =\frac{({1+r_t})}{({1+\gamma })}b_{t-1} +g_t -\tau _t \end{aligned}$$

which is Eq. (11) in the text. $\square$