1 Introduction

One of the major challenges in conventional non-reversible circuits is the issue of internal energy dissipation, which becomes more evident with increasing the number of transistors per area unit. Landauer showed that in irreversible circuits, the loss of every bit of information would generate at least KTLn2 Jules of heat energy in which K = 1.3806505 × 10−23 (Joules/Kelvin) is Boltzmann constant and T is absolute temperature [1]. Afterwards, Bennett proved that the design of the circuits should be reversible to avoid energy dissipation, since the energy loss in the reversible circuits is zero. The reversible logic is considered as a new way to reduce the amount of physical entropy [2]. Hence, reversible logic is used in many areas such as low-power CMOS circuits, optical information processing, quantum processing, etc. [3, 4].

A circuit is reversible if any input is mapped to a unique output. In the reversible circuits, the number of inputs and outputs are equal. The design of reversible circuits is more complicated than irreversible ones because fan-out and feed back is not permitted in these circuits. In order to properly synthesize the reversible circuits, it is necessary to minimize the criteria such as the number of gate count (GC), number of constant inputs (CI), number of garbage outputs (GO) and hardware complexity (HC). One of the most important issues in the reversible circuits is the error-detection capability. Parity preserving is recognized as one of the low-cost approaches for creating error-detection potential in reversible circuits. A gate or block is called parity preserving gate (or block), if Ex-or of inputs equals to Ex-or of outputs.

So far, several reversible computing circuits have been presented, such as adders, multipliers, dividers, ALUs. Meanwhile, the multiplier circuit is considered as one of the most important computational units that comprises many calculations. In the following, some of the most important reversible multipliers will be reviewed.

In 2005, Thapliyal and Srinivas proposed a 4-bit Vedic multiplier using the FRG, NG and TG gates [5]. Also, in 2006, they introduced another design of 4-bit multiplier in which the partial product network consists of the FRG gates as well as TSG blocks is used as FA in the summation network [6].

In 2008, Shams et al. suggested a 4-bit multiplier in which PG gate is used for generating partial products and MKG block is utilized as FA in the summation network [7].

A 4-bit signed multiplier proposed by Pourali-akbar et al. in 2011 based on Wallace’s technique. In its partial product network, the PG and TG gates are used, and in its summation network, the HNG block is used as FA [8].

In 2012, Babazadeh and Haghparast proposed a 4-bit parity preserving multiplier, which the FRG gate has been used in its partial product network and MIG gate in its summation network as FA [9].

A 5-bit parity preserving multiplier presented by Qi et al. based on Wallace’s technique in 2012, which its partial product consists of the FRG, MNFT and F2G gates, as well as the MIG and F2PG blocks as FAs in the summation network [10].

In 2013, Saligram and Rakshith proposed a 4-bit parity preserving multiplier based on Vedic technique, which its multiplication partial network consisted of the FG, PG, BVPPG, and NFT gates, and in its summation network, the PG and HNG blocks have been used as FA [11].

In 2013, Haghparast and Shams proposed a 4-bit parity preserving reversible Vedic multiplier in which the FG, NFG and IG gates are used for designing 2-bit parity preserving Vedic multiplier and the IG gate is used as FA in the summation network [12].

In 2014, Panchal and Nayak provided a 4-bit parallel multiplier without parity preserving potential based on Wallace’s technique, which the PG and TG gates have been used in its partial product network and the DPG and PG gates have been used in its summation network [13].

Parallel parity preserving multiplier provided in 2014 by Srikanth and Kumar based on the Vedic technique that the PG and FG gates have been used in its partial product network and the FRG gate has been used as FA in its summation network [14].

In 2014, Bhardwaj and Singh provided a parallel parity preserving multiplier based on Wallace’s technique, that the FRG gate has been used in its partial product network and the IG and PG gates have been used as HA and FA in its summation network [15].

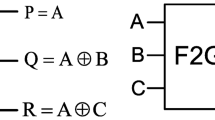
A 4-bit parity preserving multiplier presented by A. Sahu and A.K. Sahu in 2014 based on Vedic technique, that the NFT, DFG and IG gates have been used in its partial product network and the NFT and F2G gates have been used in its summation network [16]. In addition, 8-bit, 16-bit, 32-bit and 64-bit multipliers have been realized by them in 2015 [17].

Valinataj proposed a parity preserving multiplier based on array technique in 2017, that the FRG, F2G and LMH gates have been used in its partial product network and the ZCG, F2G and ZPLG blocks have been used in its summation network [18].

In 2017, Babu and Surendra provided a multiplier without parity preserving potential based on Vedic technique that the TG and PG gates have been used in its partial product network and the HNG block has been used in its summation network [19].

In this paper, two effective 4-bit reversible multipliers are presented based on the Vedic technique so that the first proposed design lacks error-detection capability, while the second proposed design has error-detection capability using the parity preserving technique. A 4-bit Vedic multiplier consists of four 2-bit Vedic multipliers and three 4-bitRCAs. In the first multiplier, we have utilized the TG, PG and FG gates for designing an effective 2-bit reversible Vedic multiplier as well as the PG gate and HNG block as HA and FA in the 4-bit RCAs. Also, in the second design, 2-bit parity preserving reversible Vedic multipliers have been designed using the FRG, DFG, ZCG and PPTG gates as well as ZCG and ZPLG blocks have been utilized as HA and FA in the4-bit RCAs. Moreover, in the proposed designs, the FG and DFG gates have been used as copy gates in the proposed multipliers.

This paper contains the following sections: in Section 2, primary definitions of the reversible logic as well as the basis of Vedic multipliers are presented. The proposed Vedic multipliers are presented in Section 3. In Section 4, the effectiveness of the proposed multipliers is compared with the existing ones. Finally, the paper ends with the conclusion section.

2 Preliminaries

2.1 An Introduction to Reversible Logic

A circuit is reversible if the number of inputs and outputs is equal and there is a one-to-one correspondence between inputs and outputs [20]. Not only can outputs be obtained in a unique way from inputs, but inputs can be obtained from the recovery of outputs. Reversible circuits are evaluated based on various criteria such as gate counts, number of constant inputs, number of garbage outputs, quantum cost, latency, and hardware complexity.

The total number of reversible gates required to analyze a reversible circuit is the number of gates. The constant inputs are equal to the input lines, which are represented as 0 or 1 at the input side of the circuit. Outputs that are not considered for further calculations are called garbage outputs. The linear quantum cost of a quantum circuit is defined as the sum of the initial quantum gates required for the analysis of a reversible circuit. The quantum cost of a 2 × 2 basic gate such as CNOT, Controlled-V, and Controlled-V + is all equal to one. In addition, V × V=V+ × V+ = NOT and V × V+ = V+ × V=I, where I is a unitary matrix. The NOT gate is a basic 1 × 1 quantum gate and its quantum cost is equal to one. Latency or delay is considered as the maximum number of gates in the critical path from the input to the output.

The total number of logic operators in a reversible circuit is defined as the hardware complexity. In the hardware complexity, the parameters are as follows [21]:

α:

A 2-input XOR gate calculation

β:

A 2-input AND gate calculation

δ:

A NOT gate calculation

Therefore, computational complexity is introduced as follows:

$$ \mathrm{Hardware}\ \mathrm{Complexity}=\mathrm{N}\left(\upalpha \right)\upalpha +\mathrm{N}\left(\upbeta \right)\upbeta +\mathrm{N}\left(\updelta \right)\updelta $$
(1)

in which N (.) is equal to the number of operators in the reversible circuit.

So far, several reversible gates and blocks have been introduced that can be used to design reversible circuits. In the following, some of the most important of these gates and blocks will be investigated.

FG Gate

The FG gate is a 2 × 2 reversible gate with Iv input and Ov output as follows:

Iv:

(A, B)

Ov:

(P = A, Q = A⊕B)

The quantum realization and the circuit representation of the FG gate are shown in Fig. 1.

Fig. 1
figure 1

FG gate (a) circuit display and b quantum realization

Full size image

It should be noted, when the B input of FG gate is considered to be ‘0’, it is used as copy gate (fan-out).

The quantum cost of the reversible FG gate is 1. Its hardware complexity is also as follows:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{FG}}=1\upalpha $$
(2)

TG Gate

The TG gate, also known as the CNOT gate, is a 3 × 3 reversible gate with Iv input and Ov output as follows [22]:

Iv:

(A, B, C)

Ov:

(P = A, Q = B, R = AB⊕C)

The quantum realization and the circuit representation of the TG gate are shown in Fig. 2.

Fig. 2
figure 2

TG gate (a) circuit display and b quantum realization

Full size image

As can be seen in Fig. 3, when the C input of TG gate is considered to be ‘0’, the reversible AND gate is obtained.

Fig. 3
figure 3

The generation of a reversible AND gate by TG gate

Full size image

The quantum cost of the reversible TG gate is five. Its hardware complexity is also as follows:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{TG}}=1\upalpha +1\upbeta $$
(3)

PG Gate

The PG gate, also known as the new Toffoli gate (NTG), is a 3 × 3 reversible gate with Iv input and Ov output as follows [23]:

Iv:

(A, B, C)

Ov:

(P = A, Q = A⊕B, R = AB⊕C)

The circuit representation and quantum realization of the PG gate are shown in Fig. 4.

Fig. 4
figure 4

PG gate (a) circuit display and b quantum realization

Full size image

As shown in Fig. 5, the reversible PG gate can be used as a half-adder (HA) and AND gate in reversible circuits, when its input C is set to ‘0’.

Fig. 5
figure 5

Generate a reversible half-adder by the PG gate

Full size image

The quantum cost of a reversible PG gate is four. Also, its hardware complexity is expressed as:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{PG}}=2\upalpha +1\upbeta $$
(4)

HNG Block

The HNG block is a 4 × 4 reversible block with the input of the Iv and Ov output as follows [24]:

Iv:

(A, B, C, D)

Ov:

(P = A, Q = B, R = A ⊕ B ⊕ C, S = (A ⊕ B)C ⊕ AB⊕D)

The quantum realization and the circuit representation of the HNG gate are shown in Fig. 6.

Fig. 6
figure 6

HNG block (a) circuit display and b quantum realization

Full size image

The quantum cost of this block is six. The hardware complexity of this block is calculated from Eq. (4):

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{HNG}}=5\upalpha +2\upbeta $$
(5)

If the input D of the HNG block is set as ‘0’, the HNG block will be used as a reversible full-adder (FA) (Fig. 7).

Fig. 7
figure 7

HNG block as a reversible full-adder

Full size image

DFG Gate

The DFG gate is a 3 × 3 parity preserving reversible gate with Iv input and Ov output as follows:

Iv:

(A, B, C)

Ov:

(P = A, Q = A⊕B, R = A⊕C)

The quantum realization and the circuit representation of the DFG gate are shown in Fig. 8.

Fig. 8
figure 8

DFG gate (a) circuit display and b quantum realization

Full size image

It should be noted, when the B or C inputs of DFG gate is considered to be ‘0’, it is used as copy gate (fan-out).

The quantum cost of the parity preserving reversible DFG gate is 2. Its hardware complexity is also as follows:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{DFG}}=2\upalpha $$
(6)

FRG Gate

The FRG gate is a 3 × 3 parity preserving reversible gate with the input of the Iv and Ov output as follows [25]:

Iv:

(A, B, C)

Ov:

(P = A, Q = AB⊕AC, R = AC ⊕ AB)

The quantum realization and the circuit representation of the FRG gate are shown in Fig. 9. The quantum cost of this gate is five and its hardware complexity is calculated from the following equation:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{FRG}}=2\upalpha +4\upbeta +2\upgamma $$
(7)
Fig. 9
figure 9

FRG gate (a) circuit display and b quantum realization

Full size image

As can be seen in Fig. 10, if the A input of FRG gate is considered to be ‘0’, this gate can act as a buffer.

Fig. 10
figure 10

FRG gate as a buffer

Full size image

ZCG Gate

The ZCG block is a 4 × 4 parity preserving reversible circuit with Iv input and Ov output as follows [26]:

Iv:

(A, B, C, D)

Ov:

(P = AB’ ⊕ C, Q = A ⊕ B, R = AB⊕C, S = A ⊕ C ⊕ D)

The quantum realization and the circuit representation of the ZCG block are shown in Fig. 11.

Fig. 11
figure 11

ZCG block (a) circuit representation and b quantum realization

Full size image

The quantum cost of this gate is six and its hardware complexity is calculated from the following equation:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{ZCG}}=5\upalpha +2\upbeta +1\upgamma $$
(8)

As can be seen in Fig. 12, by setting the C and D inputs as ‘0’, it can be used to implement parity preserving reversible half-adder.

Fig. 12
figure 12

Parity preserving reversible half-adder by the ZCG block

Full size image

ZPLG Block

The ZPLG block is a 5 × 5 parity preserving reversible gate with Iv input and Ov output as follows [26]:

Iv:

(A, B, C, D, E)

Ov:

(P = A ⊕ D, Q = A ⊕ B ⊕ D, R = A ⊕ B ⊕ C ⊕ D, S = (A ⊕ D)(B ⊕ C) ⊕ BC ⊕ D, T = (A ⊕ D)(B ⊕ C) ⊕ BC’ ⊕ D ⊕ E)

The quantum realization and circuit representation of the ZPLG block is shown in Fig. 13.

Fig. 13
figure 13

ZPLG block (a) circuit representation and b quantum realization

Full size image

The quantum cost of this gate is equal to eight, and its hardware complexity is calculated from the following equation:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{ZPLG}}=9\upalpha +3\upbeta +1\upgamma $$
(9)

As shown in Fig. 14, by setting the D and E inputs as zero, it can be converted to a parity preserving reversible full-adder:

Fig. 14
figure 14

parity preserving reversible full-adder by ZPLG block

Full size image

PPTG Gate

The PPTG block is a 4 × 4 parity preserving reversible gate with Iv input and Ov output as follows [27]:

Iv:

(A, B, C, D)

Ov:

(P = A, Q = B, R = AB⊕C, S = AB⊕D)

The quantum realization and the circuit representation of the PPTG block are shown in Fig. 15.

Fig. 15
figure 15

PPTG block (a) circuit display and b quantum realization

Full size image

The quantum cost of this gate is equal to seven, and its hardware complexity is calculated from the following equation:

$$ {\mathrm{Hardware}\ \mathrm{Complexity}}_{\mathrm{PPTG}}=2\upalpha +1\upbeta $$
(10)

2.2 Vedic Multiplier

The Urdhva Tiryakbhayam (UM) algorithm is a method of multiplying numbers based on the old Vedic mathematics, which is suitable for multiplying the hexadecimal, decimal, and binary numbers [28]. The Sanskrit words of Urdhva and Tiryakbhayam are termed as “vertical” and “crossed” respectively. This algorithm is used to multiply two “vertical” and “crossed” operations. This method is based on the concept in which the production of partial product and summations is performed simultaneously, which increases the speed of the multiplication. This feature of UT algorithm is compatible with digital systems. The UT algorithm based multipliers are also called Vedic multipliers.

Consider two n-bit numbers of A = (an-1, …. a1, a0) and B = (bn-1, …, b1, b0). The multiplication result of these two binary numbers can be expressed by the binary sequence of P = (p2n-1,…,p1,p0) so that we have:

$$ {p}_j=\Big\{{\displaystyle \begin{array}{ll}{\sum}_{i=0}^j{a}_i{b}_{j-1}& if\;j=0,1\\ {}{C}_{j-1}+{\sum}_{i=0}^j{a}_i{b}_{j-i}& if\;j=2.\cdots \cdot \cdot .n-1\\ {}{C}_{j-1}+{\sum}_{i=0}^{2n-j-2}{a}_{i+j-n+1}{b}_{n-1-i}& if\;j=2.\cdots \cdot \cdot .2n-2\\ {}{C}_{j-1}& if\;j=2n-1\end{array}} $$
(11)

That Cj represents the carry of the j-th step.

According to the presented relations in Eq. (11), the operation of a 2-bit Vedic multiplier with A = (a1,a0) and B = (b1,b0) is as follows:

$$ {\displaystyle \begin{array}{c}{p}_0={a}_0{b}_0\\ {}{p}_1={a}_0{b}_1\oplus {a}_1{b}_0\\ {}{p}_2={C}_1\oplus {a}_1{b}_1={a}_0{b}_1{a}_1{b}_0\oplus {a}_1{b}_1\\ {}{p}_3={C}_2={a}_0{b}_1{a}_1{b}_0\end{array}} $$
(12)

Hardware implementation of 2-bit Vedic multiplier requires two half-adder (HA) and four AND gate, as shown in Fig. 16.

Fig. 16
figure 16

The structure of 2-bit Vedic multiplier

Full size image

Moreover, block diagram of a 4-bit Vedic multiplier is shown in Fig. 17 [29].

Fig. 17
figure 17

Architecture of a 4-bit Vedic multiplier [29]

Full size image

3 Proposed Reversible Vedic Multipliers

As shown in Fig. 17, a modular design of a 4-bit Vedic multiplier is made up of three levels, in which four 2-bit Vedic multipliers have been used in the first level, two 4-bit RCAs in the second level, and one 4-bit RCA in the third level. In the following, two proposed 4-bit reversible Vedic multipliers are described.

3.1 Proposed 4-Bit Reversible Vedic Multiplier

In order to implement the reversible Vedic multiplier provided in Fig. 17, it is necessary to implement all the used modules in it with reversible circuits. The implementation of proposed reversible for the 2-bit Vedic multiplier module is shown in Fig. 18.

Fig. 18
figure 18

The proposed reversible circuit for implementing 2-bit Vedic multiplier

Full size image

As can be seen, the proposed circuit is composed of a reversible TG gate and five reversible PG gates. The number of its constant input and its garbage outputs is equal to 5. In addition, its quantum cost is 22.

Also, implementation of a reversible 4-bit RCA using the HNG block and PG gate is shown in Fig. 19.

Fig. 19
figure 19

Implementation of 4-bit reversible RCA using the HNG block and PG gate

Full size image

Therefore, the 4-bit reversible RCA has constant input number equal to 4, the garbage output of 7 and the quantum cost of 22.

Block diagram of the proposed 4-bit reversible Vedic multiplier is shown in Fig. 20.

Fig. 20
figure 20

Architecture of the proposed 4-bit reversible Vedic multiplier

Full size image

Therefore, the quantum cost of the proposed reversible Vedic multiplier is calculated as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{QC}\left(\mathrm{proposed}\ 4-\mathrm{bit}\ \mathrm{reversible}\ \mathrm{Vedic}\ \mathrm{multiplier}\right)\\ {}=8\mathrm{QC}\left(\mathrm{FG}\right)+4\mathrm{QC}\left(\mathrm{proposed}\ 2-\mathrm{bit}\ \mathrm{reversible}\ \mathrm{Vedic}\ \mathrm{multiplier}\right)\\ {}\kern6em +3\mathrm{QC}\left(4-\mathrm{bit}\ \mathrm{reversible}\ \mathrm{RCA}\right)=\\ {}=8(1)+4(22)+3(22)=162\end{array}} $$

3.2 Proposed Parity Preserving Reversible 4-Bit Vedic Multiplier

The proposed circuit is shown in Fig. 21 for implementing reversible 2-bit Vedic multiplier module with the parity preserving ability.

Fig. 21
figure 21

The proposed reversible circuit to implement 2-bit parity preserving reversible Vedic multiplier

Full size image

The proposed circuit consists of a PPTG block, three FRG gates and two ZCG blocks, all of which are capable of parity preserving. The number of constant inputs as well as garbage outputs is equal to 8. In addition, the quantum cost is 30.

Also, the reversible implementation of a 4-bit RCA using ZCG and ZPLG blocks is shown in Fig. 22.

Fig. 22
figure 22

The reversible implementation of a 4-bit parity preserving reversible RCA with ZCG and ZPLG blocks

Full size image

As can be inferred from Fig. 22, the number of constant inputs and garbage outputs of the 4-bit parity preserving reversible RCA are equal to 8 and 11, respectively. Moreover, its quantum cost is [(3 × 8) + 6] =30.

Block diagram of the proposed 4-bit parity preserving reversible Vedic multiplier is shown in Fig. 23.

Fig. 23
figure 23

Architecture of the proposed 4-bit parity preserving reversible Vedic multiplier

Full size image

Therefore, the quantum cost of the proposed 4-bit parity preserving reversible Vedic multiplier is calculated as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{QC}\left(\mathrm{proposed}\ 4-\mathrm{bit}\ \mathrm{parity}\ \mathrm{preserving}\ \mathrm{reversible}\ \mathrm{Vedic}\ \mathrm{multiplier}\right)\\ {}=8\mathrm{QC}\left(\mathrm{DFG}\right)+4\mathrm{QC}\left(\mathrm{proposed}\ 2-\mathrm{bit}\ \mathrm{Vedic}\right)\\ {}\kern6em +3\mathrm{QC}\left(4-\mathrm{bit}\ \mathrm{parity}\ \mathrm{preserving}\ \mathrm{reversible}\ \mathrm{RCA}\right)=\\ {}=8(2)+4(30)+3(30)=226\end{array}} $$

4 Evaluation and Comparison Results

In this section, the proposed 4-bit reversible Vedic multipliers are compared with previous works in terms of gate counts, number of constant inputs, number of garbage outputs, quantum cost and hardware complexity.

The evaluation results of the proposed 4-bit reversible multiplier in comparison with previous designs are provided in Table 1. It should be noted that in the most of the previous designs, the issue of copying of the inputs (fan out) is not met. Therefore, in order to make a fair comparison, the designs which this issue has not been seen in them, have been modified using the FG gate and, accordingly, the results of the evaluations, have been reported which in some cases, the results are different from the presented values in their papers.

Table 1 The comparison results of the 4-bit reversible multipliers
Full size table

As shown in Table 1, the proposed reversible Vedic multiplier is superior to the other available designs in terms of the number of gates, number of constant inputs, the number of garbage outputs and quantum cost. In addition, the improvement percentage of proposed reversible Vedic multiplier is shown in Fig. 24.

Fig. 24
figure 24

Improvement of the proposed reversible Vedic multiplier compared to other designs

Full size image

Moreover, the evaluation results of the proposed 4-bit parity preserving reversible multiplier in comparison with the existing designs are shown in Table 2.

Table 2 Comparison results of 4-bit parity preserving reversible multipliers
Full size table

As can be seen in Table 2, although the proposed parity preserving reversible multiplier is close to the proposed designs in [9, 12] in terms of number of constant inputs and garbage output, however, is superior to all designs in terms of the gate counts and quantum cost (Fig. 25).

Fig. 25
figure 25

Improvement of the 4-bit proposed parity preserving reversible Vedic multiplier in comparison with existing design

Full size image

5 Conclusion

In this paper, two efficient 4-bit reversible Vedic multipliers were presented. The first multiplier was a reversible multiplier without parity preserving capability in which the FG, TG and PG gates were used to design 2-bit reversible Vedic multiplier as well as the PG gate and HNG block were used as HA and FA in the summation network. The second design was a 4-bit parity preserving reversible Vedic multiplier, in which the DFG, FRG and PPTG gates were utilized to design 2-bit parity preserving reversible Vedic multiplier and the ZCG and ZPLG blocks were used as HA and FA in the summation network. The comparison results show that the proposed reversible multipliers are superior in term of criteria such as gate count, number of constant inputs, number of garbage output and quantum cost compared to other existing designs. In the future, we plan to develop efficient designs of signed reversible multipliers and then apply them in the more complex reversible circuits such as adaptive digital filter and ALU.