Entanglement Dynamics of Two Spins in Initially Correlated Wheel-Shaped Spin Baths

Abstract

We study the effects of the initial correlations in environment on the entanglement dynamics of spin system. The correlated environment is novelly simulated by two correlated wheel-shaped spin baths, each consisting of an intermediate spin interacting with a spin-ring. The correlations in environment are achieved by the entanglement between two intermediate spins. The spin system includes two system-spins, and the interaction between the spin system and the environment is implemented by the coupling between the system-spin and the intermediate spin. Firstly, we analyze the influences of the initial entanglement between the two intermediate spins, the coupling parameters and the temperature of the baths on the entanglement dynamics of the two system-spins in equivalent subsystems. It is demonstrated that the initial entanglement between the baths can act as a resource for the generation and the revivals of the entanglement of the system-spins. Moreover, the amount of the generation and the revivals of the entanglement of the system-spins can be enhanced by regulating the coupling constants and the temperature of the baths. In addition, we also investigate the influences of different coupling ratios in non-equivalent subsystems, it is found that changing the coupling ratios of two subsystems has a significant effect on the generation and revivals of entanglement of system-spins.

1 Introduction

Due to long decoherence time and scalability, spin systems have been widely applied in various fields of quantum computation and quantum information processing [1–3]. As other quantum systems, realistic spin systems are not isolated and they are inevitably influenced by their surrounding environments [4–6], especially the spin environments [7–12]. As a result, their entanglement and coherence will be irretrievably lost, even vanished [9–11]. Recently, it has been observed that two spin qubits initially in the maximal entangled states will completely disentangle in a finite time [13–15]. This phenomenon is called the entanglement sudden death (ESD). As entanglement is the most important resource for quantum computation and quantum communication, the appearance of ESD puts a limitation to the time when entanglement could be usefully exploited.

Extensive works have been put forward to protect entanglement or coherence in spin systems [16–23]. And it has been found that strong system-environment couplings [17], low temperatures [18] and initial system-environment correlations [20] play an important role in the dynamics of spin systems. In addition, some meaningful proposals show that the dynamics of entanglement can be frozen and inhibit their relaxation into the environment by tuning the interaction parameters and the detuning [22, 23].

However, most previous literatures assumed that each spin locally couples to its own environment and the environments for different spins are initially uncorrelated. The assumption of independent environments may be much restrictive in realistic experiments. The initial correlations between environments have been studied in the electromagnetic field [24–26]. Interestingly, it has been shown that initial environmental correlations can be used as a new resource for bringing memory effects in the dynamics of open quantum systems [24] and can induce correlations between the initially uncorrelated atoms [25]. Moreover, it has been verified experimentally that the information initially held in the environment can induce nonlocal memory effects in a photonic open system [26]. So we are very interested in what effects will be performed on the entanglement dynamics of the spin systems if there are initial environmental correlations.

In this work, we consider a novel model, as shown in Fig. 1, two system-spins interact respectively with their own environments. The environments are described with wheel-shaped spin-baths and there are initial correlations between them. This model can be reduced from realistic quantum system, e.g., coupled electron spins, with one of them coupled to a bath of N nuclear spins in a quantum dot or nuclear magnetic resonance(NMR) system [20]. In this paper, we study the effects of the initial correlations of spin-baths on the entanglement dynamics of the two system-spins. The paper is organized as follows. In Section 2, we describe our model in detail and present the Hamiltonian. In Section 3, we derive the time-dependent expression of the reduced density matrix of the two system-spins. In Section 4, we discuss the effects of various factors on the entanglement dynamics of the two system-spins. Conclusions are given in Section 5.

Fig. 1

(Color online) Sketch of the model. The system-spin (A or B) interacts with an intermediate spin (a or b), and the intermediate spin also interacts with the spin-ring ( R ₁ or R ₂). The wavy line between a and b indicates that there are initial correlations between them

2 The Model and Hamiltonian

The model we consider is shown in Fig. 1. The system consists of two subsystems (1 and 2). In each subsystem, a system-spin (A or B) interacts with an intermediate spin (a or b), and the intermediate spin locates in the center of a spin-ring ( R ₁ or R ₂) and interacts with the spin-ring. The intermediate spin and the spin-ring form a wheel-shaped spin-bath for the system-spin. We assume that the separation between the two subsystems is large enough so that there is no direct interaction between them. However, there are initial correlations between the two baths. The Hamiltonian for the whole system can be written as

$$ {H}= {H_{1}} + {H_{2}} , $$

(1)

where H ₁ and H ₂ are the subsystem Hamiltonians, they can be written as

$$ {H_{l}}= {H_{S}} + {H_{I}} + {H_{SI}} + {H_{IR}} + {H_{R}}, $$

(2)

here, l=1,2 denotes the subsystems 1 and 2. H _S (S=A,B), H _I (I=a,b) and H _R (R=R ₁,R ₂) are the Hamiltonians for the system-spin, the intermediate spin and the spin-ring, respectively. H _{S I} describes the interaction between the system-spin and the intermediate spin, H _{I R} denotes the interaction between the intermediate spin and the spin-ring. They have following forms

$$ {H_{S}} = {\mu_{0}}{S_{0}^{z}}, $$

(3)

$$ {H_{I}} = {\mu_{I}}{S_{I}^{z}}, $$

(4)

$$ {H_{SI}} = {\alpha_{l}} (S_{0}^{+}S_{I}^{-}+ S_{0}^{-}S_{I}^{+}), $$

(5)

$$ {H_{IR}} = \frac{{\beta_{l}} }{{\sqrt{N}}}(S_{I}^{+}{J_{-}} + S_{I}^{-}{J_{+}}), $$

(6)

$$ {H_{R}} = \frac{{\gamma }}{N}({J_{+}}{J_{-}} + {J_{-}}{J_{+}}), $$

(7)

where μ _0, μ _I are proportional to the external magnetic field applied on the system-spin and the intermediate spin along the z direction, respectively. For simplicity, we take μ ₀=μ _I =μ. α _l is the coupling constant between the system-spin and the intermediate spin. β _l stands for the interaction strength between the intermediate spin and the spin-ring , and γ is the coupling constant between the bath spins. ${S_{0}^{z}}$, $S_{0}^{+}$ and $S_{0}^{-}$ are the operators of the system-spin, ${S_{I}^{z}}$, $S_{I}^{+}$ and $S_{I}^{-}$ are the operators of the intermediate spin. ${J_ \pm } = \sum \nolimits _{i = 1}^{N} {S_{i}^{\pm }}$ are the collective angular momentum operators of the spin-ring, in which $S_{i}^{\pm }$ are the corresponding operators of the ith spin in the ring, N is the number of the spins in the ring. In our model, we assume that all the spins have the value 1/2, and all the spins in the ring have the same coupling to the intermediate spin, and all the couplings among the spins in the ring are the same, as considered in Refs [9, 22]. By using the Holstein-Primakoff transformation ${J_{+}} = {b^{\dag } }\sqrt {N - {b^{\dag } }b}$, ${J_{-}} = (\sqrt {N - {b^{\dag } }b}) b,$ with [b,b ^‡]=1, and in the limit $N \to \infty$, the bath can be described by a single-mode boson field, then we have

$$ {H_{IR}} = \beta_{l}(S_{I}^{+}b + S_{I}^{-}{b^{+}}), $$

(8)

$$ {H_{R}} = 2\gamma {b^{\dag} }b. $$

(9)

In this work, we only consider the on-resonant case μ=2γ, which is much easier to study in the interaction picture. The interaction Hamiltonian for the subsystem can be written as

$$ {H_{l}^{\prime}} = \alpha_{l} (S_{0}^{+}S_{I}^{-}+ S_{0}^{-}S_{I}^{+})+ \beta_{l} (S_{I}^{+}b +S_{I}^{-}{b^{+}}). $$

(10)

The transformed Hamiltonian describes two coupled spins, with one of them interacting with a single-mode boson field.

3 Analysis on the State Evolution

Under the assumption of non-interacting subsystems, the time evolution operator for the whole system $1\cup 2$ can be expressed as U _{t o t} (t)=U ₁(t)⊗U ₂(t) with U ₁(t) and U ₂(t) having the same form $exp( - iH_{l}^{\prime }t)$. Further, we assume initial state of the total system as

$$ {\kern 15pt} {\rho_{tot}}(0) = {\rho_{AB}}(0) \otimes {\rho_{ab}}(0) \otimes {\rho_{R_{1}}} \otimes {\rho_{R_{2}}}, $$

(11)

where ${\rho _{AB}}(0) =\left | {{{\Psi }_{AB}}(0)} \right \rangle \left \langle {{{\Psi }_{AB}}(0)} \right |$ and ${\rho _{ab}}(0) =\left | {{{\Phi }_{ab}}(0)} \right \rangle \left \langle {{{\Phi }_{ab}}(0)} \right |$ are the initial density matrix of the system-spins and the intermediate spins with

$$ {\kern 10pt} \left| {{{\Psi}_{AB}}(0)} \right\rangle = {c_{1}}\left| {00} \right\rangle + {c_{2}}\left| {11} \right\rangle, {\kern 11pt}\left| {{{\Phi}_{ab}}(0)} \right\rangle = {d_{1}}\left| {01} \right\rangle + {d_{2}}\left| {10} \right\rangle, $$

(12)

here $\phantom {\dot {i}\!}{|c_{1}|^{2}} + {|{c_{2}}|^{2}} = 1$ and $\phantom {\dot {i}\!}{|d_{1}|^{2}} + {|d_{2}|^{2}} = 1$. $\phantom {\dot {i}\!}{\rho _{{R_{1}}}}$ ($\phantom {\dot {i}\!}{\rho _{{R_{2}}}}$) is the density matrix of the spin-ring $\phantom {\dot {i}\!}{R_{1}}({R_{2}})$ satisfying the Boltzmann distribution, $\phantom {\dot {i}\!}{\rho _{{R_{1}}}} = {\rho _{{R_{2}}}} = {e^{- {H_{R}}/T}}/Z$ where $\phantom {\dot {i}\!}Z = Tr({e^{- {H_{R}}/T}})$ is the partition function and the Boltzmann constant has been set to 1.

Although the absence of direct interaction, subsystems 1 and 2 still display dynamical correlations when the system-spins A and B (the intermediate spins a and b) are initially prepared in entangled states. The entanglement revivals of the system-spins may come from two sources, one is the initial entanglement of the system-spins itself, the other comes from the transfer of the entanglement that initially stored in the intermediate spins. The different forms of the entangled states |Ψ _{A B} (0)〉 and |Φ _{a b} (0)〉 will help us to distinguish the origin of the contributions to the entanglement revivals of the two system-spins.

The time evolution of the density matrix for the whole system is given by

$$ {\rho_{tot}}(t) = {{\mathrm{U}}_{tot}}(t){\rho_{tot}}(0){\mathrm{U}}_{tot}^{\dag} (t), $$

(13)

where the exact expression of evolution operator U _{t o t} (t) of the whole system is obtained by using the method proposed in reference [20] and the details are provided in the Appendix. The reduced density matrix of the two system-spins is calculated by tracing over the environments consisting of a,b,R₁,R₂, namely

$$ {\rho_{AB}}(t) = t{r_{ab{R_{1}}{R_{2}}}}{{{\mathrm{U}}_{tot}}(t){\rho_{tot}}(0){\mathrm{U}}_{tot}^{\dag} (t)}\\ = \left( {\begin{array}{*{20}{c}} {{\rho_{11}}(t)}&0&0&{{\rho_{14}}(t)}\\ 0&{{\rho_{22}}(t)}&{{\rho_{23}}(t)}&0\\ 0&{\rho_{23}^ *(t)}&{{\rho_{33}}(t)}&0\\ {\rho_{14}^ * (t)}&0&0&{{\rho_{44}}(t)} \end{array}} \right), $$

(14)

The explicit expressions of the matrix elements are collected in the Appendix and they are related to the initial state of the whole system, the coupling parameters and the temperature of the baths. When the reduced density matrix is determined, the physical quantity of the system-spins can be readily found out. In Section 4, we discuss the entanglement dynamics of the system-spins with different initial conditions.

4 Numerical Analysis on the Entanglement Dynamics

In order to analyse the entanglement dynamics of the system-spins, we use the concurrence [27] to measure the entanglement. The initial density matrix of the system-spins have the special X-structure, which is maintained during the evolution [22]. By virtue of the symmetries of such density matrix, the concurrence of the two system-spins can be simplified as C _{A B} (t)=C _Ψ(t)+C _Φ(t) [25], where

$$ {C_{\Psi} }(t) = 2\max \{ 0,[\left| {{\rho_{14}}(t)} \right| - \sqrt{{\rho_{22}}(t){\rho_{33}}(t)} ]\}, $$

(15)

$$ {C_{\Phi} }(t) = 2\max \{ 0,[\left| {{\rho_{23}}(t)} \right| - \sqrt{{\rho_{11}}(t){\rho_{44}}(t)} ]\}, $$

(16)

here, C _Ψ(t) represents the concurrence preserved in the system-spins during evolution, while C _Φ(t) denotes the concurrence transferred from the initial entangled intermediate spins. It is found that C _Ψ(t) and C _Φ(t) cannot be positive simultaneously, so that we can distinguish them easily. In this paper, we mainly concern the influence of initial concurrence between the intermediate spins on the entanglement of the system-spins.

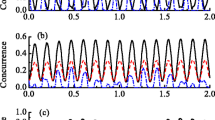
We first consider the case in which the system-spins are initially prepared in a product state i.e., c ₁=1, c ₂=0, and the two subsystems are completely identical. Figure 2a shows the influence of the different initial degree of entanglement of the intermediate spins on the entanglement dynamics of the system-spins. Due to there is no initial entanglement and coupling between the two system-spins, the only origin of the concurrence of the system-spins is the transfer of the entanglement that initially stored in the intermediate spins. It can be observed that the entanglement of the system-spins emerges and oscillates with the scaled time β t, and can be enhanced by increasing the degree of entanglement of the intermediate spins. Meanwhile, we plot the concurrence of the intermediate spins with the scaled time β t in Fig. 2b. By comparing Fig. 2a and b, one can explicitly find that a part of the entanglement in the intermediate spins is transferred to the system spins through the system-intermediate coupling.

Fig. 2

(Color online) a Time evolution of concurrence C _{A B} (t) for two system spins initially in $\left | {{{\Psi }_{AB}}(0)} \right \rangle = \left | {00} \right \rangle$ with different initial correlation between intermediate spins (1) ${d_{1}} = \frac {1}{{\sqrt {2}}},{d_{2}} = \frac {1}{{\sqrt {2}}}$ (dot curve), (2) ${d_{1}} = \sqrt {\frac {1}{5}}, {d_{2}} = \sqrt {\frac {4}{5}}$ (dashed curve), (3) ${d_{1}} = \sqrt {\frac {1}{{10}}}, {d_{2}} = \sqrt {\frac {9}{{10}}}$ (solid curve). b The corresponding time evolution of concurrence C _{a b} (t) for two intermediate spins initially in different states. Other parameters: μ=2γ, α ₁=α ₂=α, β ₁=β ₂=β, α/β=1 , T=1γ

Figure 3 illustrates the change of the concurrence of the system-spins as a function of both scaled time β t and the ratio α/β with different temperatures. With increasing the value of α/β, the generation of the entanglement in the system-spins is more rapid and the concurrence is larger. A comparison among Fig. 3a-c shows that higher temperature will suppress the generation and the revivals of the entanglement in the system-spins.

Fig. 3

(Color online) Concurrence C _{A B} (t) as a function of scaled time β t and the coupling ratio α/β with different temperatures a T=0.1γ, b T=1γ, c T=10γ. Other parameters: μ=2γ, c ₁=1,c ₂=0, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$, α ₁=α ₂=α, β ₁=β ₂=β

Then we study the entanglement dynamics of the system-spins in non-equivalent subsystems. For non-equivalent subsystems, we consider two cases (1) α ₁≠α ₂,β ₁=β ₂ and (2) β ₁≠β ₂, α ₁=α ₂. In Fig. 4 we plot the concurrence C _{A B} (t) as a function of scaled time β ₁ t with fixed coupling ratio α ₁/β ₁ and different coupling ratios α ₂/β ₂. In the first case, Fig. 4a shows that the magnitude and generated time of entanglement of the system-spins with α ₁=α ₂ are better than other non-equivalent coupling ratios. For the second case, Fig. 4b shows that decreasing the value of β ₂ is benefit for the entanglement generation of the system-spins.

Fig. 4

(Color online) Concurrence C _{A B} (t) as a function of scaled time β ₁ t with the coupling ratio α ₁/β ₁=2 and the different coupling ratios α ₂/β ₂ a β ₂=β ₁, α ₂/β ₂=1.5,2 and 2.5 (dot, solid and dashed curve); b α ₂=α ₁, α ₂/β ₂=1.5,2 and 2.5 (dot, solid and dashed curve). Other parameters: μ=2γ, T=1γ, c ₁=1,c ₂=0, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$

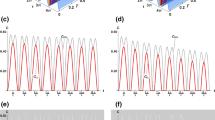
Now we consider the situation in which the system-spins are initially prepared in a maximal entangled state, namely ${c_{1}} = {c_{2}} = {1/{\sqrt {2}}}$ . Firstly, we also analyze how the initial entanglement in the intermediate spins make effects on the entanglement dynamics of the system-spins in equivalent subsystems. Figure 5a shows the concurrence of the system-spins as a function of scaled time β t with different initial entangled states of the intermediate spins and the concurrence of the system-spins strongly depends on the initial correlations between the intermediate spins. For greater initial correlation of the intermediate spins, the revived entanglement of the system-spins reaches a higher maximum and the revived time lasts longer, but the decay of the concurrence of the system-spins gets quicker. These results suggest that the initial correlations in environment can act as a resource for promoting the revivals of entanglement in the system-spins. On the other hand, the initial entanglement of system-spins also transfer to the intermediate spins. In Fig. 5b, we plot the entanglement evolution of the intermediate spins for observing the entanglement flow between the system-spins and intermediate spins. By comparing Fig. 5a and b, it can be found that both of the concurrence of system-spins and the intermediate spins consist of two part. One is the concurrence of the entanglement preserved in themselves during evolution, and the other as the bold lines in Fig. 5a and b denote the transferred from each other.

Fig. 5

(Color online)a Time evolution of the concurrence C _{A B} (t) of the two system-spins initially in $\left | {{{\Psi }_{AB}}(0)} \right \rangle = \frac {1}{{\sqrt {2}}}(\left | {00} \right \rangle + \left | {11} \right \rangle )$ with intermediate spins in different states ${d_{1}}= 1/{\sqrt {2}}, {d_{2}}= 1/{\sqrt {2}}$ (dashed curve); ${d_{1}} = \sqrt {1 / 10}, {d_{2}} = \sqrt {9 / 10}$ (dot-dashed curve); d ₁=1,d ₂=0 (solid curve). The Bold lines denote the concurrence transferred from the initial entangled intermediate spins. b The corresponding time evolution of concurrence C _{a b} (t) for two intermediate spins initially in different states. The Bold lines denote the concurrence transferred from the initial entangled system-spins. Other parameters: μ=2γ,T=1γ, α ₁=α ₂=α, β ₁=β ₂=β, α/β=2.5

Then we discuss how the entanglement dynamics of the system-spins are influenced by the ratio α/β of the coupling parameters. Here the intermediate spins are initially prepared in the Bell state with ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$. In the α/β≤1 regime, the concurrence of the system-spins is plotted as a function of scaled time β t and the ratio α/β in Fig. 6a. It is shown that, the smaller the value of the ratio α/β is, the better the entanglement is preserved. In order to figure out the origin of the entanglement C _{A B} (t) of the system-spins, we plot the time evolution of C _Ψ(t) and C _Φ(t) in Fig. 6b and c. One can see clearly that the initial entanglement in the system-spins contributes to the most of C _{A B} (t) while the initial entangled intermediate spins contribute little. The reason is that when α≪β, the entanglement of the intermediate spins loses quickly to the ring.

Fig. 6

(Color online) In the α/β≤1 regime, a Concurrence C _{A B} (t) as a function of β t and the coupling ratio α/β; b Concurrence C _Ψ(t) as a function of β t and the coupling ratio α/β; c Concurrence C _Φ(t) as a function of β t and the coupling ratio α/β. Other parameters: μ=2γ, T=1γ, ${c_{1}} = {c_{2}} = \frac {1}{{\sqrt {2}}}$, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$, α ₁=α ₂=α, β ₁=β ₂=β

In the α/β≥1 regime, the decay rate of the concurrence of the system-spins increases and the revivals of the entanglement of the system-spins become much stronger when the value of the ratio α/β is larger, as shown in Fig. 7. From Fig. 7b and c, we can see that both C _Ψ(t) and C _Φ(t) contribute to the entanglement revivals, and the time period of their contribution to the entanglement revivals is complementary because that C _Ψ(t) and C _Φ(t) cannot be positive simultaneously. The difference between Figs. 6c and 7c shows that the strong coupling between the system-spin and the intermediate spin make the entanglement of the intermediate spins transfer to the system-spins. The effect of the temperature on the entanglement dynamics of the system-spins is shown in Fig. 8, it demonstrates that high temperatures depress the revivals of the entanglement.

Fig. 7

(Color online) In the α/β≥1 regime, a Concurrence C _{A B} (t) as a function of β t and the coupling ratio α/β; b Concurrence C _Ψ(t) as a function of β t and the coupling ratio α/β; c Concurrence C _Φ(t) as a function of β t and the coupling ratio α/β. Other parameters: μ=2γ, T=1γ, ${c_{1}} = {c_{2}} = \frac {1}{{\sqrt {2}}}$, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$, α ₁=α ₂=α, β ₁=β ₂=β

Fig. 8

(Color online) Concurrence C _{A B} (t) as a function of scaled time β t and the coupling ratio α/β with different temperature a T=0.1γ, b T=1γ, c T=10γ. Other parameters: μ=2γ, ${c_{1}} = {c_{2}} = \frac {1}{{\sqrt {2}}}$, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$, α ₁=α ₂=α, β ₁=β ₂=β

Finally, we also discuss the effect of non-equivalent subsystems with coupling ratio α ₁/β ₁≠α ₂/β ₂ on entanglement dynamics of the system-spins. Like as the situation of system-spins prepared in product state, Fig. 9a and b demonstrate that keeping α ₁=α ₂ and decreasing the value of β ₂ are effectively promoted to the revivals of entanglement of the system-spins.

Fig. 9

(Color online) Concurrence C _{A B} (t) as a function of scaled time β ₁ t with the coupling ratio α ₁/β ₁=3 and the different coupling ratio α ₂/β ₂ a β ₂=β ₁, α ₂/β ₂=2,3 and 4 (dot, solid and dashed curve); b α ₂=α ₁, α ₂/β ₂=2,3 and 4 (dot, solid and dashed curve). Other parameters: μ=2γ, T=1γ, ${c_{1}} = {c_{2}} = \frac {1}{{\sqrt {2}}}$, ${d_{1}} = {d_{2}} = \frac {1}{{\sqrt {2}}}$

5 Conclusions

In summary, we have studied the effects of initial environmental correlations on the entanglement dynamics of the system-spins. The entangled environment is constructed by two entangled intermediate spins, each embedded in the center of a wheel-shaped bath. The interaction between the system-spin and the environment is simulated by the coupling between the system-spin and the intermediate spin.

In this work, we firstly analysed numerically the time evolution of concurrence of the system-spins influenced by the initial correlations in environment, the coupling ratio α/β, and the temperature of the baths in equivalent subsystems. It is shown that when we increase the initial degree of entanglement in environment, the amount of generation and revivals of the entanglement of the system-spins become stronger and the revived time lasts longer, but the decay rate of the concurrence gets quicker. Moreover, with increasing the value of the coupling ratio α/β which regulates the degree of non-Markovian characteristics of the system, the entanglement of the intermediate spins transferring to the system-spins can be evidently enhanced. While the high temperature of the bath always suppresses the transfer of the concurrence from the initial entangled intermediate spins. These results suggest that the initial correlations in environment can act as a resource for generating entanglement and promoting the revivals of entanglement in the system-spins, and we can enhance the non-Markovian effects of the spin system by increasing the coupling ratio α/β or decreasing the temperature of the baths. In addition, we investigated the effects of different coupling ratios for non-equivalent subsystems on the entanglement dynamics of system-spins. It is found that keeping coupling constant α ₁=α ₂ and decreasing the value of β ₂ are benefit for the generation and revivals of entanglement of the system-spins.

Appendix

In the Appendix we provide the method to obtain the exact time evolution operator and the reduced density matrix of the system-spins. Note that the environment is constituted by the intermediate spins and the spin-rings, it is difficult to trace over them together directly. Here, we adopt a skillful method to handle this problem. Firstly, we take the two system-spins and the two intermediate spins as a whole, and their reduced density matrix can be written as

$$ {\rho_{AaBb}}(t) = t{r_{{R_{1}}{R_{2}}}}[{U_{1}}(t) \otimes {U_{2}}(t){\rho_{AB}}(0)\otimes {\rho_{ab}}(0){\otimes\rho_{{R_{1}}}} \otimes {\rho_{{R_{2}}}}U_{1}^{\dag} (t) \otimes U_{2}^{\dag} (t)]. $$

(17)

Since there is no interaction between the subsystems 1 and 2 , we first concentrate on the time evolution operator of a single subsystem only. We use U _{i j} to denote the components of the single time evolution operator U _l acting on the basis $\{ \left | {00} \right \rangle$, $\left | {01} \right \rangle$, $\left | {10} \right \rangle$, $\left | {11} \right \rangle \}$, here |m n〉 corresponds to the states of the system-spin and the intermediate spin [20]. From the Schrodinger equation we obtain

$$\begin{array}{@{}rcl@{}} \frac{d}{{dt}}{U_{1j}} &=& - i{\kern 1pt} {\kern 1pt} \beta_{l} {b^ + }{U_{2j}}, \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} \frac{d}{{dt}}{U_{2j}} &=& - i{\kern 1pt} {\kern 1pt} [ - \beta_{l} b{U_{1j}} + \alpha_{l} {U_{3j}}], \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} \frac{d}{{dt}}{U_{3j}} &=& - i{\kern 1pt} {\kern 1pt} [\alpha_{l} {U_{2j}} + \beta_{l} {b^ + }{U_{4j}}], \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} \frac{d}{{dt}}{U_{4j}} &=& - i{\kern 1pt} {\kern 1pt} \beta_{l} b{U_{3j}} . \end{array} $$

(21)

Here, j=1,2,3,4 is the number of the column of the evolution operator U _l in the chosen basis. Differentiating the equations (19) and (20), we obtain

$$\begin{array}{@{}rcl@{}} \frac{d}{{d{t^{2}}}}{U_{2j}} &=& - i{{\beta_{l}^{2}}}(1 + \hat n){U_{2j}} - i\alpha_{l} \frac{d}{{dt}}{U_{3j}} \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} \frac{d}{{d{t^{2}}}}{U_{3j}} &=& - i{{\beta_{l}^{2}}}\hat n{U_{3j}} - i\alpha_{l} \frac{d}{{dt}}{U_{2j}} \end{array} $$

(23)

where $\hat n=b^ + b$. By combining with the equations (18) and (21), we can get the explicit expressions of the evolution operator

$$\begin{array}{@{}rcl@{}} {U_{11}}\! &=&\! \frac{{({A_{1}} + {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1}}_ + t}}{{\sqrt{2}}})+({A_{1}} - {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}})}}{{2{A_{1}}}}, \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} {U_{21}}\! &=&\! \frac{{ - ib\beta_{l} [({A_{1}} + {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}}){B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) + ({A_{1}} - {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}}){B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{\sqrt{2}{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} {U_{31}}\! &=&\! \frac{{\alpha_{l} \beta_{l} b [\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - \cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}}}, \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} {U_{41}}\! &=&\! \frac{{ - i\sqrt{2}\alpha_{l} {{\beta_{l}^{2}}}bb[{B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - {B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} {U_{12}} \!&=&\!\! \frac{{ - i\beta_{l}{b^ + }[({A_{1}}\! +\! {{\alpha_{l}^{2}}}\! +\! {{\beta_{l}^{2}}}){B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}})\! +\! ({A_{1}} - {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}}){B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{\sqrt{2}{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} {U_{22}}\! &=&\! \frac{{({A_{1}} + {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) + ({A_{1}} - {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})}}{{2{A_{1}}}}, \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} {U_{32}}\! &=&\! {U_{23}} = \frac{{i\alpha_{l} [{B_{1 - }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - {B_{1 + }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{\sqrt{2}{A_{1}}}}, \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} {U_{42}} &=& \frac{{\alpha_{l} \beta_{l} b [\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - \cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}}}, \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} {U_{13}}\! &=&\! \frac{{\alpha_{l} \beta_{l} {b^ + } [\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - \cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}}}, \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} {U_{33}}\! &=&\! \frac{{ ({A_{1}} + {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) + ({A_{1}} - {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})}}{{2{A_{1}}}}, \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} {U_{43}}\! &=&\! \frac{{ - i\beta_{l} b [({A_{1}} + {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}}){B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) + ({A_{1}} - {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}}){B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{\sqrt{2}{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(34)

$$\begin{array}{@{}rcl@{}} {U_{14}}\! &=&\! \frac{{ - i\sqrt{2}\alpha_{l} {{\beta_{l}^{2}}}{b^ + }{b^ + }[{B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - {B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} {U_{24}}\! &=&\! \frac{{\alpha_{l} \beta_{l} {b^ + }[\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) - \cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{{A_{1}}}}, \end{array} $$

(36)

$$\begin{array}{@{}rcl@{}} {U_{34}}\! &=&\! \frac{{ - i\beta_{l} {b^ + } [({A_{1}} + {{\alpha_{l}^{2}}}\! -\! {{\beta_{l}^{2}}}){B_{1 + }}\sinh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}})\! +\! ({A_{1}}\! -\! {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}}){B_{1 - }}\sinh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})]}}{{\sqrt{2}{A_{1}}{B_{1 - }}{B_{1 + }}}}, \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}} {U_{44}}\! &=&\! \frac{{({A_{1}} - {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 - }}t}}{{\sqrt{2}}}) + ({A_{1}} + {{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}})\cosh (\frac{{{B_{1 + }}t}}{{\sqrt{2}}})}}{{2{A_{1}}}}. \end{array} $$

(38)

In the above equations we have used the notation

$${A_{1}} = \sqrt{{{({{\alpha_{l}^{2}}} + {{\beta_{l}^{2}}})}^{2}} + 4{{\alpha_{l}^{2}}}{{\beta_{l}^{2}}}\hat n},{\kern 10pt}{B_{1, \pm }} = \sqrt{ - {{\alpha_{l}^{2}}} - {{\beta_{l}^{2}}}(1 + 2\hat n) \pm {A_{1}}} $$

Having determined the exact analytical form of the evolution coefficients U _{i j} of the single subsystem, we could get the total components of the time evolution operator U _{t o t} (t). And after the trace over the intermediate spins, we can find the explicit reduced density matrix of the two system-spins as

$$\begin{array}{l} {\rho_{AB}}(t) = \left( {\begin{array}{*{20}{c}} {{\rho_{11}}(t)}&0&0&{{\rho_{14}}(t)}\\ 0&{{\rho_{22}}(t)}&{{\rho_{23}}(t)}&0\\ 0&{\rho_{23}^ *(t)}&{{\rho_{33}}(t)}&0\\ {\rho_{14}^ * (t)}&0&0&{{\rho_{44}}(t)} \end{array}} \right) \end{array}$$

where

$$\begin{array}{l} {\rho_{11}}(t) = {|{c_{1}}|^{2}}{f_{1}}(t) {f_{2}}(t) + {|{c_{2}}|^{2}}{f_{3}}(t) {f_{4}}(t), \end{array}$$

$$\begin{array}{l} {\rho_{44}}(t) = {|{c_{1}}|^{2}}{g_{1}}(t) {g_{2}}(t) + {|{c_{2}}|^{2}}{g_{3}}(t) {g_{4}}(t), \end{array}$$

$$\begin{array}{l} {\rho_{22}}(t) = {|{c_{1}}{d_{1}}|^{2}}{f_{1}}(t) {g_{2}}(t) + {|{c_{1}}{d_{2}}|^{2}}{f_{2}}(t) {g_{1}}(t)\\ {\kern 20pt}+{|{c_{2}}{d_{1}}|^{2}}{f_{3}}(t) {g_{4}}(t) + {|{c_{2}}{d_{2}}|^{2}}{f_{4}}(t) {g_{3}}(t), \end{array}$$

$$\begin{array}{l} {\rho_{33}}(t) = {| {{c_{1}}{d_{2}}} |^{2}}{f_{1}}(t) {g_{2}}(t) + {| {{c_{1}}{d_{1}}}|^{2}}{f_{2}}(t) {g_{1}}(t) \\ {\kern 20pt}+{|{c_{2}}{d_{2}}|^{2}}{f_{3}}(t) {g_{4}}(t) + {|{c_{2}}{d_{1}}|^{2}}{f_{4}}(t) {g_{3}}(t), \end{array}$$

$$\begin{array}{l} {\rho_{23}}(t) = {|{c_{1}}|^{2}}{d_{1}}d_{2}^ * {h_{3}^{2}}(t) + {|{c_{2}}|^{2}}{d_{1}}d_{2}^ * {h_{4}^{2}}(t), \end{array}$$

$$\begin{array}{l} {\rho_{14}}(t) = \rho_{41}^ * (t) = {c_{1}}c_{2}^ * {h_{1}}(t){h_{2}}(t), \end{array}$$

and

$$\begin{array}{l} {f_{1}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{11}}} U_{11}^{\dag} {e^{- 2\gamma n/T}} +\sum\limits_{n = 1}^{\infty} {{U_{21}}} U_{21}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {f_{2}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{12}}} U_{12}^{\dag} {e^{- 2\gamma n/T}}+ \sum\limits_{n = 0}^{\infty} {{U_{22}}} U_{22}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {f_{3}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{13}}} U_{13}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 0}^{\infty} {{U_{23}}} U_{23}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {f_{4}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{14}}} U_{14}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 0}^{\infty} {{U_{24}}} U_{24}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {g_{1}}(t) = \frac{1}{Z}(\sum\limits_{n = 1}^{\infty} {{U_{31}}} U_{31}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 2}^{\infty} {{U_{41}}} U_{41}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {g_{2}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{32}}} U_{32}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 1}^{\infty} {{U_{42}}} U_{42}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {g_{3}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{33}}} U_{33}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 1}^{\infty} {{U_{43}}} U_{43}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {g_{4}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{34}}} U_{34}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 0}^{\infty} {{U_{44}}} U_{44}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {h_{1}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{11}}} U_{33}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 1}^{\infty} {{U_{21}}} U_{43}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$${h_{2}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{12}}} U_{34}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 0}^{\infty} {{U_{22}}} U_{44}^{\dag} {e^{- 2\gamma n/T}}), $$

$$\begin{array}{l} {h_{3}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{11}}} U_{32}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 1}^{\infty} {{U_{21}}} U_{42}^{\dag} {e^{- 2\gamma n/T}}), \end{array}$$

$$\begin{array}{l} {h_{4}}(t) = \frac{1}{Z}(\sum\limits_{n = 0}^{\infty} {{U_{13}}} U_{34}^{\dag} {e^{- 2\gamma n/T}} + \sum\limits_{n = 0}^{\infty} {{U_{23}}} U_{44}^{\dag} {e^{- 2\gamma n/T}}). \end{array}$$

In the above expressions, $Z = \frac {1}{{1 - {e^{- 2\gamma /T}}}}$.