An efficient wavelet-based adaptive filtering algorithm for automatic blind speech enhancement

Abstract

In this paper, we address the problem of speech enhancement by adaptive filtering algorithms. A particular attention has been paid to the backward blind source separation (BBSS) algorithm and its use in crosstalk resistant speech enhancement applications. In this paper, we propose to implement the BBSS algorithm in the wavelet-domain. The proposed backward wavelet BBSS (WBBSS) algorithm is then used in speech enhancement application when important crosstalk interferences are presents. The new WBBSS algorithm shows better performances in terms of convergence speed and steady state in comparison with the classical BBSS one. The performances properties of the proposed algorithm are evaluated in term of segmental SNR (SegSNR), segmental mean square error (SegMSE), and cepstral distance (CD) criteria. The obtained results have confirmed the best performance of the proposed WBBSS algorithm in a lot of situations when blind noisy observations are available.

1 Introduction

Various speech enhancement and acoustic noise reduction techniques have been developed in the previous years as speech enhancement is a core target in many challenging areas such as telecommunications, speech and speaker recognitions, teleconferencing and hand-free telephony (Loizou 2007). In such applications, we aim to recover a speech signal from observations corrupted by different noises components. The unusual noise components can be of various classes that are often present in the environment (Djendi et al. 2013).

Numerous algorithms and techniques were proposed to resolve the problem of corrupted speech signals (Dixit et al. 2014; Bactor and Garg 2012; Scalart and Filho 1996). Moreover, techniques of single or multi-microphones are proposed to improve the behavior of the speech enhancement algorithms and also to reduce the acoustic noise components even in very noisy conditions. The most popular single channel techniques that are widely known in speech enhancement application is the spectrum subtraction (SS) that needs only one channel signal (Boll 1979). It has been embedded in some high-quality mobile phones for the same application. However, the SS technique is only suitable for stationary noise environments. Moreover, it certainly introduces music noise problem. In fact, the higher the noise is reduced, the greater the distortion is brought to the speech signal and accordingly the poorer the intelligibility of the enhanced speech is obtained (Zhang and Zhao 2012; Cappé 1994). As a result, ideal enhancement can hardly be achieved when the signal-to-noise-ratio (SNR) of the noisy speech is relatively low; below 5 dB. In contrast, it has quite good result when the noisy speech SNR is relatively high; above 15 dB.

The SS and others speech enhancement techniques that are based on SS principal have improved the decision directed (DD) techniques in reducing the musical noise components (Ephraim and Malah 1984, 1985; Ephraim et al. 2014; Selva Nidhyananthan et al. 2014). Several and recent algorithms that improve the DD techniques are proposed in (Wolfe and Godsill 2003). In Dong et al. (2009), a speech enhancement algorithm based on high-order cumulant parameter estimation is proposed. In (Davila 1984; Doclo and Moonen 2002), a subspace method, which is based on well-known singular value decomposition (SVD) techniques is proposed; the signal is enhanced when the noise subspace is removed, and accordingly, the clean speech signal is estimated from the noisy speech subspace.

Another approach that has been largely studied in speech enhancement application is the adaptive noise cancellation (ANC) approach that was firstly proposed in (Widrow and Goodlin 1975; Widrow 1985). Furthermore, most important speech enhancement techniques and algorithm use adaptive approaches to get the tracking ability of non-stationary noise properties (Lee and Gan 2004; Weinstein et al. 1993). Several adaptive algorithms have been proposed for speech enhancement application, we can find time domain algorithm (21), frequency domain adaptive algorithms (Plapous et al. 2004; Al-Kindi and Dunlop 1989; Plapous et al. 2005; Djendi et al. 2015, 2016) or adaptive spatial filtering techniques (Tong et al.2015; Goldsworthy 2014) that often use adaptive SVD techniques to separates the speech signal space from the noisy one.

Another direction of research combines the blind source separation techniques with adaptive filtering algorithms to enhance the speech signal and to cancel efficiently the acoustic echo components (Van Gerven and Compernolle 1992; Djendi et al. 2006; Zoulikha and Djendi 2016; Jin et al. 2014). This approach uses at least two microphones configuration to update the adaptive filtering algorithms. Also, a multi-microphone speech enhancement approach has been proposed for the same purpose and have improves the existing one-channel and two-channel speech enhancement and noise reduction adaptive algorithms (Benesty and Cohen 2017; Lee and Dae Na 2016). We can also find several papers that highlighted the problem of speech enhancement on a simple problem of mixing and unmixing signals with convolutive and instantaneous noisy observations (Jutten and Herrault 1991; Nguyen Thi and Jutten 1995; Mansour et al. 1996).

In last ten years, a new direction of research have proven the efficiency of the wavelet domain as a new efficient mean that can improves the techniques of speech enhancement, and several techniques and algorithms have been proposed for the same purpose (Bouzid and Ellouze 2016; Ghribi et al. 2016). In this paper, we propose a new implementation of the backward blind source separation (BBSS) algorithm in the wavelet domain.

The presentation of this paper is given as follows: after the introduction, we present, in Sect. 2, the noisy observations generation process that we use in this paper. Section 3 is reserved to describe the classical and original backward blind source separation (BBSS) algorithm. Section 4 presents the proposed wavelet transform domain of the BBSS (WBBSS) algorithm that works in the wavelet domain and its mathematical formulation and derivation. In Sect.  5 , the obtained results of the proposed WBBSS algorithm are presented, and finally we conclude our work in Sect. 6.

2 Noisy observations

In this work, we consider two noisy observations m₁(n) and m₂(n) available at the output of two sources and two sensors configuration mixing model. The mixing model uses two uncorrelated sources s(n) and b(n) that are the speech signal and the noise respectively. These two signals are considered real and statistically independent, i.e. $E\left[ {s\left( n \right)\,b\left( {n - m} \right)} \right]=0$. The two mixing signals ${m_1}\left( {\text{n}} \right)$ and ${m_2}\left( n \right)$ at the sensor outputs of this model are given as follows (Djendi et al. 2013):

$${m_1}\left( {\text{n}} \right)={\text{s}}\left( {\text{n}} \right)+{\mathbf{h}}_{{21}}^{T}\left( n \right){\text{ }}{\mathbf{b}}\,\left( n \right)$$

(1)

$${m_2}\left( n \right)=b\left( n \right)+{\mathbf{h}}_{{12}}^{T}\left( n \right){\text{ }}{\mathbf{s}}\,\left( n \right)$$

(2)

where ‘*’ is the convolution operator. ${\mathbf{h}}_{{12}}^{{}}\left( n \right)={\left[ {h_{{12}}^{{[1]}}\left( n \right){\text{ }}...{\text{ }}h_{{12}}^{{[L]}}\left( n \right)} \right]^T}$ and ${\mathbf{h}}_{{21}}^{{}}\left( n \right)={\left[ {h_{{21}}^{{[1]}}\left( n \right){\text{ }}...{\text{ }}h_{{21}}^{{[L]}}\left( n \right)} \right]^T}$ represent the cross-coupling effects between the channels, and L is their length. The vectors ${\mathbf{b}}\left( n \right)={\left[ {b\left( n \right)...b\left( {n - L+1} \right)} \right]^T}$ and ${\mathbf{s}}\left( n \right)={\left[ {s\left( n \right){\text{ }}...{\text{ }}s\left( {n - L+1} \right)} \right]^T}$ are the punctual noise and the speech source signals. This mixing model allows to say the the first microphone is close to the speech signal, and the punctual noise is close to the second microphone. This configuration is very realistic as in a car or in an office (Djendi et al. 2013).

3 Description of the BBSS algorithm

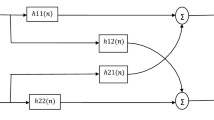
The general block diagram configuration of the multi-inputs multi-outputs (MIMO) and simplified two-inputs two-outputs (TITO) backward blind source separation (BBSS) algorithm is given in Fig. 1. The aim of this approach is to recover the original sources estimates by using only noisy observations.

Fig. 1

Block diagram of the BBSS algorithm in the case of MIMO configuration

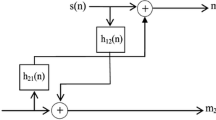
In this paper, we study a particular two-inputs two-outputs (TITO or 2 × 2) BBSS algorithm that aims to separate the original sources estimates of one source signal s(n) and one punctual noise $b\left( n \right)$ by using only two available noisy observed signals m₁(n) and m₂(n) at the input as given by Fig. 2.

Fig. 2

Block diagram of the BBSS algorithm in the case of TITO configuration

The TITO BBSS algorithm is mainly based on the assumptions that the source signals, $s\left( n \right)$ and $b\left( n \right)$, are statistically independents, and the mixing and unmixing models H and W respectively, are linear systems (Plapous et al. 2004). In a previous work, we have published a work on the implementation of the forward blind source separation (FBSS) algorithm in the wavelet-domain (Djendi et al. 2006; Mansour et al. 1996). However, in this paper, we will focus our interest on the BBSS algorithm of Fig. 3 and its implementation in the wavelet-domain.

Fig. 3

Backward blind source separation (BBSS) algorithm. Two inputs and two output (TITO) configuration

In the blind source separation model of Fig. 2, the output signals ${v_1}(n)$ and ${v_2}(n)$ of the BBSS algorithm are given by the following relations (Djendi et al. 2006; Zoulikha et al. 2014):

$${v_1}\left( {\text{n}} \right)={m_1}\left( n \right) - {\mathbf{w}}_{{21}}^{T}\left( n \right){\text{ }}{\mathbf{v}}_{2}^{{}}\left( {n - 1} \right)$$

(3)

$${v_2}\left( {\text{n}} \right)={m_2}\left( n \right) - {\mathbf{w}}_{{12}}^{T}\left( n \right){\text{ }}{\mathbf{v}}_{1}^{{}}\left( {n - 1} \right)$$

(4)

where ${\mathbf{v}}_{1}^{{}}\left( n \right)={\left[ {v_{1}^{{}}\left( n \right)...v_{1}^{{}}\left( {n - L+1} \right)} \right]^T}$ and ${\mathbf{v}}_{2}^{{}}\left( n \right)={\left[ {v_{2}^{{}}\left( n \right)...v_{2}^{{}}\left( {n - L+1} \right)} \right]^T}$ are the two outputs vectors of the BBSS algorithm. The vectors ${\mathbf{w}}_{{12}}^{{}}\left( n \right)={\left[ {w_{{12}}^{{[1]}}\left( n \right){\text{ }}...{\text{ }}w_{{12}}^{{[L]}}\left( n \right)} \right]^T}$ and ${\mathbf{w}}_{{21}}^{{}}\left( n \right)={\left[ {w_{{21}}^{{[1]}}\left( n \right){\text{ }}...{\text{ }}w_{{21}}^{{[L]}}\left( n \right)} \right]^T}$ are the adaptive cross-filters of the BBSS algorithm. The output signals v₁(n) and ${v_2}\left( n \right)$ of Fig. 2 are obtained by inserting relations (1) and (2) into (3) and (4), respectively. In order to get the original speech signal $s\left( n \right)$ at the output ${v_1}\left( n \right)$ and the noise component $b\left( n \right)$ at the output v₂(n) without distortions, we have to use a voice activity detector (VAD) that updates alternatively the cross-filters ${w_{21}}\left( n \right)$ and ${w_{12}}\left( n \right)$. We recall here that the optimal solutions of the adaptive filters are obtained when ${w_{12}}\left( n \right)={h_{12}}\left( n \right)$ and ${w_{21}}\left( n \right)={h_{21}}\left( n \right)$ and we get:

$${v_1}\left( n \right)=s\left( n \right)$$

(5)

$${v_2}\left( n \right)=b\left( n \right)$$

(6)

According to Fig. 2, and by using a vector notation, the BBSS algorithm updates the cross-filters ${w_{21}}\left( n \right)$ and ${w_{12}}\left( n \right)$ by the following relations:

$${{\mathbf{w}}_{12}}\left( {n+1} \right)={{\mathbf{w}}_{12}}\left( n \right)+2{\theta _1}\frac{{{v_2}\left( n \right)\;{{\mathbf{v}}_1}\left( n \right)}}{{{\mathbf{v}}_{1}^{T}\left( n \right)\;{{\mathbf{v}}_1}\left( n \right)+{\varsigma _1}}}$$

(7)

$${{\mathbf{w}}_{21}}\left( {n+1} \right)={{\mathbf{w}}_{21}}\left( n \right)+2{\theta _2}\frac{{{v_1}\left( n \right)\;{{\mathbf{v}}_2}\left( n \right)}}{{{\mathbf{v}}_{2}^{T}\left( n \right)\;{{\mathbf{v}}_2}\left( n \right)+{\varsigma _2}}}$$

(8)

where the scalar ${\theta _1}$ and ${\theta _2}$ are the step sizes of the BBSS algorithm and selected as follows: $0{\text{<}}{\theta _1}{\text{<}}1$, $0{\text{<}}{\theta _2}{\text{<}}1$. The scalar ${\varsigma _1}$ and ${\varsigma _2}$ are small constants used to avoid division by zeros. In this paper, we propose to use automatic VAD technique that is inspired from (Zoulikha and Djendi 2016). We recall here that we can alternate the obtained original source signals by inverting the control of the adaptive filters. In Table 1, we summarize the BBSS algorithm.

Table 1 The BBSS algorithm (Djendi et al. 2006)

4 Proposed WBBSS algorithm

The proposed Wavelet-domain implementation of the BBSS (WBBSS) algorithm is given in Fig. 4. We use the discrete wavelet transform (DWT) to convert the mixing signals m₁(n) and m₂(n) into wavelet domain with several number of scales then we apply the BBSS structure. The proposed WBBSS algorithm uses approximations and details that are generated by DWT of m₁(n) and m₂(n) to update two cross-adaptive filters, w₁₂(n) and w₂₁(n). The two cross-filters are therefore used to enhances the speech signal at the output v₁(n). To reconstruct the temporal version of the enhanced speech signal, we apply the inverse DWT at the output. We recall here that we propose to use a new voice activity detector (VAD) system to control the adaptive filter w₂₁(n) to get the speech signal at the output v₁(n) because we focus only on the speech enhancement signal recovered at the first output v₁(n).

Fig. 4

Bloc diagram of the proposed WBBSS algorithm. DWT discrete wavelet transform, IDWT the inverse of DWT, VAD a voice activity detector

4.1 Derivation of the proposed WBBSS algorithm

A detailed scheme of the proposed WBBSS algorithm is given in Fig. 5. The formulation of the proposed WBBSS algorithm is done in several steps.

Fig. 5

Proposed WBBSS algorithm. DWT discrete wavelet transform, IDWT the inverse of DWT, VAD a voice activity detector

In the first, we apply discrete wavelet transform (DWT) of scale N to the two mixing signal vectors m₁(n) and m₂(n). If the scale DWT number is denoted N, we can write for$\left\{ {{\text{J, K}}} \right\}={\text{0, 1, 2, 3, }}...{\text{, N-1}}{\text{.}}$:

$$M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)=\sum\limits_{{{\text{J, k}}}} {{m_{\text{1}}}\left( {\text{n}} \right)\upphi _{{{\text{J,K}}}}^{\Theta }\left( {\text{n}} \right)} ,$$

(9)

$$M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)=\sum\limits_{{{\text{J, k }}}} {{m_{\text{2}}}\left( {\text{n}} \right){\text{ }}\upphi _{{{\text{J,K}}}}^{\Theta }\left( {\text{n}} \right)} ,$$

(10)

where $\upphi _{{{\text{J,}}\,{\text{k}}}}^{{}}\left( {\text{n}} \right)={{\text{2}}^{{{ - {\text{J}}} \mathord{\left/ {\vphantom {{ - {\text{J}}} {\text{2}}}} \right. \kern-0pt} {\text{2}}}}}\upphi \,\left( {{2^{ - {\text{J}}}}{\text{n-k}}} \right)$ is the wavelet basis function, and ‘$\Theta$’ symbolizes complex conjugate. J and k indicate scale and translation respectively of the mother wavelet function $\upphi$. The two mixing signals m₁(n) and m₂(n) of length L are given by ${{\text{m}}_1}\left( {\text{n}} \right)={\left[ {{{\text{m}}_1}\left( {\text{n}} \right),{{\text{m}}_1}\left( {{\text{n}}-1} \right), \ldots {{\text{m}}_1}\left( {{\text{n}}-{\text{L}}+1} \right)} \right]^{\text{T}}}$, and ${{\text{m}}_2}\left( {\text{n}} \right)={\left[ {{{\text{m}}_2}\left( {\text{n}} \right),{{\text{m}}_2}\left( {{\text{n}}-1} \right), \ldots {{\text{m}}_2}\left( {{\text{n}}-{\text{L}}+1} \right)} \right]^{\text{T}}}$. The two (N x L) DWT matrices (where L is the length of the DWT vector for J scales) $M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)$ and $M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)$of the mixing signals m₁(n) and m₂(n), respectively, are defined as follows: $M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right){\text{=}}{\left[ {m_{{{\text{0, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right){\text{,}}\,m_{{{\text{1, K}}}}^{{\left( {\text{1}} \right)}}\left( {{\text{n}}-{\text{1}}} \right){\text{,}} \ldots m_{{{\text{N-1, K}}}}^{{\left( {\text{1}} \right)}}\left( {{\text{n}}-{\text{L}}+{\text{1}}} \right)} \right]^T}$ and $M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right){\text{=}}{\left[ {m_{{{\text{0, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right){\text{,}}\,m_{{{\text{1, K}}}}^{{\left( {\text{2}} \right)}}\left( {{\text{n}}-{\text{1}}} \right){\text{,}} \ldots m_{{{\text{N-1, K}}}}^{{\left( {\text{2}} \right)}}\left( {{\text{n}}-{\text{L}}+{\text{1}}} \right)} \right]^T}$, where N is the DWT number scale, i.e., $\left\{ {{\text{J, K}}} \right\}={\text{0, 1, 2, 3, }}...{\text{, }}N{\text{-1}}{\text{. }}$

In the second step we apply the FBSS structure to the two converted DWT mixing signals $M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)$ and $M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)$.This procedure generates the approximations and the detail parts of the two mixing DWT observations, $M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)$ and $M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)$, then we use them to estimate, at each iteration, the filtering errors vectors which are given as follows:

$${{\mathbf{v}}_1}{\text{ }}\left( {\text{n}} \right){\text{=}}{{\mathbf{m}}_{\text{1}}}\left( {\text{n}} \right) - \sum\limits_{{\text{J}}} {{\mathbf{w}}_{{21,{\text{ J}}}}^{{}}\left( {\text{n}} \right){\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)}$$

(11)

$${{\mathbf{v}}_2}{\text{ }}\left( {\text{n}} \right){\text{\,=\,}}{{\mathbf{m}}_{\text{2}}}{\text{(n) }} - \sum\limits_{{\text{J}}} {{\mathbf{w}}_{{12,{\text{ J}}}}^{{}}\left( {\text{n}} \right){\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)}$$

(12)

After the filtering errors vector computation, then we apply the BBSS algorithm to the two wavelets-domain mixing signals ${\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)$ and ${\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)$. We use approximations and details information of noisy observations, ${\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)$ and ${\mathbf{M}}_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)$, to update the cross-adaptive filters ${{\mathbf{w}}_{{\text{12,J}}}}\left( {\text{n}} \right)$, and ${{\mathbf{w}}_{{\text{21,J}}}}\left( {\text{n}} \right)$ at each sub-scale J:

$${\mathbf{w}_{{\text{12,J}}}}\left( {{\text{n}}+{\text{1}}} \right)={\mathbf{w}_{{\text{12,J}}}}\left( {\text{n}} \right)+2\,{\mu _{12}}{\mathbf{v}_2}\left( {\text{n}} \right)\frac{{M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)}}{{{\xi _1}+M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)M_{{{\text{J, K}}}}^{{{\text{T}}\left( {\text{1}} \right)}}\left( {\text{n}} \right)}}$$

(13)

$${\mathbf{w}_{{\text{21,J}}}}\left( {{\text{n}}+{\text{1}}} \right)={\mathbf{w}_{{\text{21,J}}}}\left( {\text{n}} \right)+2\,{\mu _{21}}{\mathbf{v}_1}\left( {\text{n}} \right)\frac{{M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)}}{{{\xi _2}+M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)M_{{{\text{J, K}}}}^{{{\text{T}}\left( {\text{2}} \right)}}\left( {\text{n}} \right)}}$$

(14)

The step-sizes ${\mu _{12}}$ and ${\mu _{21}}$ are used to control the adaptation process of the convergence of the cross adaptive filters${\mathbf{w}_{{\text{12,J}}}}\left( {\text{n}} \right)$, and ${\mathbf{w}_{{\text{21,J}}}}\left( {\text{n}} \right)$ in each DWT scale, respectively. The two-step-sizes ${\mu _{12}}$ and ${\mu _{21}}$ must verify the following relations: $0<{\text{ }}{\mu _{12}}<1$ and $0<{\text{ }}{\mu _{21}}<1$. The parameter $\xi$ is a small scalar used to avoid division by zero. In last step, and in order to extract the speech signal at the output v₁(n) and the noise component at the output v₂(n), we propose to do a modification in relations (13) and (14) by applying an automatic VAD system that is proposed recently in (Jin et al. 2014). We normalized each relations (13) and (14) of the cross adaptive filters ${\mathbf{w}_{{\text{12,J}}}}\left( {\text{n}} \right)$, and ${\mathbf{w}_{{\text{21,J}}}}\left( {\text{n}} \right)$ by the norm of the corresponding error vectors ${\mathbf{v}_2}\left( {\text{n}} \right)$ and ${\mathbf{v}_1}\left( {\text{n}} \right)$, respectively. The new update formulas of the cross adaptive filter ${\mathbf{w}_{{\text{12,J}}}}\left( {\text{n}} \right)$ and ${\mathbf{w}_{{\text{21,J}}}}\left( {\text{n}} \right)$ at each wavelet scale are given as follows:

$${\mathbf{w}_{{\text{12,J}}}}\left( {{\text{n}}+{\text{1}}} \right)={\mathbf{w}_{{\text{12,J}}}}\left( {\text{n}} \right)+2\,{\mu _{12}}{\mathbf{v}_2}\left( {\text{n}} \right){{\mathbf{D}}_{12}}\left( {\text{n}} \right)$$

(15)

$${\mathbf{w}_{{\text{21,J}}}}\left( {{\text{n}}+{\text{1}}} \right)={\mathbf{w}_{{\text{21,J}}}}\left( {\text{n}} \right)+2\,{\mu _{21}}{\mathbf{v}_1}\left( {\text{n}} \right){{\mathbf{D}}_{21}}\left( {\text{n}} \right)$$

(16)

where the ${{\mathbf{D}}_{12}}\left( {\text{n}} \right)$ and ${{\mathbf{D}}_{21}}\left( {\text{n}} \right)$ are given by the following relations:

$${{\mathbf{D}}_{12}}\left( {\text{n}} \right)\frac{{M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)}}{{{\xi _1}+\left\| {{{\varvec{v}}_2}\left( {\text{n}} \right)} \right\|_{2}^{2}+M_{{{\text{J, K}}}}^{{\left( {\text{1}} \right)}}\left( {\text{n}} \right)M_{{{\text{J, K}}}}^{{{\text{T}}\left( {\text{1}} \right)}}\left( {\text{n}} \right)}}$$

(17)

$${{\mathbf{D}}_{21}}\left( {\text{n}} \right)\frac{{M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)}}{{{\xi _2}+\left\| {{{\varvec{v}}_1}\left( {\text{n}} \right)} \right\|_{2}^{2}+M_{{{\text{J, K}}}}^{{\left( {\text{2}} \right)}}\left( {\text{n}} \right)M_{{{\text{J, K}}}}^{{{\text{T}}\left( {\text{2}} \right)}}\left( {\text{n}} \right)}}$$

(18)

where $\left\| . \right\|_{2}^{2}$ is the mathematical squared norm operator. ${\mathbf{v}}_{j}^{{}}\left( n \right)={\left[ {v_{j}^{{}}\left( n \right){\text{ }}... v_{j}^{{}}\left( {n - L+1} \right)} \right]^T}$ with $j=\left\{ {1{\text{, 2}}} \right\}$ are the output BBSS signal vectors. The scalar ${\xi _1}$ and ${\xi _2}$ are small constants used to avoid division by zeros. In Table 2, we summarize the proposed WBBSS algorithm.

Table 2 The proposed WBBSS algorithm [In this paper]

5 Analysis of simulation results

We have done intensive experiments on the proposed WBBSS algorithm in comparison with the original version [i.e. BBSS (Djendi et al. 2006)], and the two-step noise reduction (that is called TSNR) algorithm (Plapous et al. 2004) that use only one microphone to enhance the corrupted speech signal, also this TSNR algorithm is mainly based on the use of the Wiener function gain to estimate in two times the correcting gain of the corrupted speech signal, this algorithm I well explained in (Plapous et al. 2004). The comparison of the proposed algorithm with BBSS (Djendi et al. 2006) and TSNR (Weinstein et al. 1993) is based on the evaluation of the convergence speed performance and the segmental mean square error of the output speech signals of each algorithm. The comparison is based on the following criteria: (i) the segmental mean square error (SegMSE), (ii) the segmental signal-to-noise-ratio (SegSNR), and (iii) the cepstral distance (CD) (Hu and Loizou 2007, 2008). All of the simulations are used the same parameters as given in Table 3 for the algorithms, i.e. the TSNR, the BBSS and the proposed WBBSS.

Table 3 Simulation parameters of BBSS (Djendi et al. 2006), TSNR (Plapous et al. 2004), and proposed WBBSS algorithms

5.1 Description of the signals used in simulation

In Fig. 6 we show the original speech signal and the USASI (United State of America Standard Institute, now ISI) noise signals that are used in simulation. On Fig. 7, we show an example of real impulse responses that we used in our experiments. These source signals are sampled at 16 kHz and coded on 16 bit. The speech signals are taken from the AURORA database. These signals are measured in real situations and often used in the domain of adaptive filtering and speech enhancement to test the performance of algorithms. We recall here that the used voice activity detector in the BBSS algorithm is manual.

Fig. 6

Simulated impulse responses in the spaced microphones case; [Left]: ${{\text{h}}_{{\text{12}}}}\left( {\text{n}} \right)$, [Right]: ${{\text{h}}_{{\text{21}}}}\left( {\text{n}} \right)$. The real filters length is L = 128. ${\text{fs}}={\text{8 kHz}}$

Fig. 7

Original speech signal taken from Aurora data-base [In left], and the USASI (United State of America Standard Institute now ANSI) noise [In right]

In order to show the performance of the proposed WBBSS algorithm in comparison with the classical BBSS (Djendi et al. 2006), and the TSNR (Plapous et al. 2004), we have reported on Figs. 8 and 9 the output speech signal ${v_1}\left( \text{n} \right)$ obtained by the two algorithms (i.e. the classical BBSS, TSNR, and the proposed WBBSS). In the proposed WBBSS algorithm, the DWT scale is N = 2 (the results are shown on Fig. 8) and N = 4 (the results are shown on Fig. 9). The simulation parameters for each algorithm are given in Table 3.

Fig. 8

Outputs of BBSS [in black], TSNR [in blue] and proposed WBBSS [in green] for N = 2. (Color figure online)

Fig. 9

Outputs of BBSS [in black], TSNR [in blue] and proposed WBBSS [in green] for N = 4. (Color figure online)

According to Figs. 8 and 9, we can well see that the estimated speech signal ${v_1}\left( \text{n} \right)$ is quickly denoised by the proposed WBBSS algorithm in comparison with TSNR and BBSS algorithms that take more times to converge especially in the case of N = 4. This experiment leads to say that the three algorithms (BBSS, TSNR, and proposed WBBSS) are good enough, to reduce acoustic noise components at the output. To give insight of the proposed WBBSS algorithm, we present in the next sections intensive simulations that are carried out with other objective criteria.

5.2 Segmental MSE (SegMSE) evaluation

In order to quantify the convergence speed performance of the adaptive filters of the proposed algorithm and its original version, i.e. the BBSS (Djendi et al. 2006), we have used the SegMSE criterion. As the output speech signal v₁(n) is controlled by the adaptive filters w₂₁(n), we concentrate on the evaluation of the SegMSE criterion calculated on the output of this filter, i.e. w₂₁(n). This SegMSE criterion is evaluated by the following relation (Hu and Loizou 2007, 2008):

$${\text{SegMS}}{{\text{E}}_{{\text{dB}}}}=\frac{{10}}{{\text{M}}}\mathop \sum \limits_{{{\text{m}}=0}}^{{{\text{M}} - 1}} {\text{lo}}{{\text{g}}_{10}}\left( {\frac{1}{{\text{Z}}}\mathop \sum \limits_{{{\text{n}}={\text{Zm}}}}^{{{\text{Zm}}+{\text{Z}} - 1}} {{\left| {{{\text{v}}_1}\left( {\text{n}} \right)} \right|}^2}} \right)$$

(19)

where ‘Z’ is the time averaging frame length of the output v₁(n) or the segment length, and ‘M’ is the number of segments when speech signal is absent. We note that the SegMSE criterion is estimated in noise-only presence periods. This good property is achieved thanks to the speech signal intermittence property. All the simulation parameters of both algorithms are summarized in Table 3. The used noise types are White, Babble, USASI (United Sate of America Signal Institute now ANSI), and street. All the noises that we use in all the simulation of this paper are real and sampled at 8 kHz.

The obtained results of the SegMSE for four noises types are reported on Fig. 8. According to this experiment of Fig. 10, we can say that the proposed WBBSS algorithm behaves more efficiently than the BBSS, especially when the DWT scale is selected high (N = 4). This is true for all of the other DWT scales and for all noise types.

Fig. 10

SegMSE of BBSS (Djendi et al. 2006) and proposed WBBSS algorithms for DWT scales N = 2 and 4. [Top left]: white; [Top right]: USASI; [Bottom left]: Babble; [Bottom right]: Street

5.3 SegSNR evaluation

We have evaluated the performance of the two-step noise reduction (TSNR) algorithm (Plapous et al. 2004), BBSS (Djendi et al. 2006) and the proposed WBBSS algorithm in terms of output segmental signal-to-noise ratio (SegSNR) criterion. The SegSNR allows quantifying the acoustic noise reduction amounts at the output. As we are interested on speech enhancement signal, we focus only on the SegSNR output of the output v₁(n). The SegSNR criterion is evaluated according to the following relation (Hu and Loizou 2007, 2008):

$${\text{SegSN}}{{\text{R}}_{{\text{dB}}}}=\frac{{10}}{{\text{M}}}\mathop \sum \limits_{{{\text{m}}=0}}^{{{\text{M}} - 1}} {\text{lo}}{{\text{g}}_{10}}\left( {\frac{{\mathop \sum \nolimits_{{{\text{n}}={\text{Zm}}}}^{{{\text{Zm}}+{\text{Z}} - 1}} {{\left| {{\text{s}}\left( {\text{n}} \right)} \right|}^2}}}{{\mathop \sum \nolimits_{{{\text{n}}={\text{Zm}}}}^{{{\text{Zm}}+{\text{Z}} - 1}} {{\left| {{\text{s}}({\text{n}}) - {{\text{v}}_1}\left( {\text{n}} \right)} \right|}^2}}}} \right)$$

(20)

where ${\text{s}}({\text{n}})$ and ${{\text{v}}_1}\left( {\text{n}} \right)$ are the original and the enhanced speech signals, respectively. The parameters ‘M’ and ‘Z’ are the number of segments and the segment length, respectively. We note that at the output, we get ‘M’ values of the SegSNR criterion, each one is mean averaged on ‘N’ samples. The symbol $\left| {\,.\,} \right|$ represents the magnitude operator. We recall here that all the ‘M’ segments correspond to only speech signal presence periods. The log10 symbol is the base 10 logarithm of a given number. The same parameters of each algorithm that are summarized in Table 3 are used in the simulation. The obtained results of the SegSNR are given in Fig. 11 for three input SNR values, i.e. -6 dB, 0 dB, and 6 dB.

Fig. 11

SegSNR evaluation of the BBSS (Djendi et al. 2006), TSNR (Plapous et al. 2004), and the proposed WBBSS algorithms for WDT scale N = 2 and 4. [Top left]: white; [Top right]: USASI; [Bottom left]: Babble; [Bottom right]: Street

According to Fig. 11, we note the best performances of the proposed WBBSS algorithm when the DWT scale is selected equal to N = 2. However, the SegSNR values decrease when the DWT scale increases. We have also noted that in low and high DWT scales, the general order values of the output SegSNR are superior to 40 dB, which means that the proposed algorithms (with different DWT scales) and both of TSNR (Plapous et al. 2004) and BBSS (Djendi et al. 2006) algorithms lead to a good reduction of the acoustic noise components. The important advantage of the proposed WBBSS algorithm is the speech convergence property that was highlighted in the SegSNR and well shown in the SegMSE criterion of Sect. 5.2 for each input SNR.

5.4 CD evaluation

In order to quantify the distortion amount introduced in the output speech signal by the proposed WBBSS algorithm in comparison with the BBSS (Djendi et al. 2006) and the TSNR (Plapous et al. 2004) ones, we have evaluated the cepstral distance criterion. The CD criterion is computed by the log-spectrum distance between the original speech signal ${\text{s(n)}}$and the output of the proposed WBBSS and BBSS algorithms, i.e. ${\text{v}_{\text{1}}}{\text{(n)}}$. The CD criterion is evaluated by the following relation (Hu and Loizou 2007, 2008):

$${\text{CD}}_{{{\text{dB}}}} = \frac{{10}}{{\text{M}}}\sum\limits_{{{\text{m}} = 0}}^{{{\text{M}} - 1}} {{\text{log}}} 10\sum\limits_{{{\text{n}} = {\text{Zm}}}}^{{{\text{Zm}} + {\text{Z}} - 1}} {\left( {{\text{c}}_{{\text{s}}} ({\text{n)}} - \left( {{\text{c}}_{{{\text{v}}1}} ({\text{n)}}} \right)^{2} } \right)}$$

(21)

where ${{\text{c}}_{\text{s}}}({\text{n}})=\frac{1}{{2\pi }}\mathop \smallint \limits_{{ - \pi }}^{\pi } \log \left| {{\text{S}}\left( \omega \right)} \right|{{\text{e}}^{{\text{j}}\omega {\text{n}}}}{\text{d}}\omega$ and ${{\text{c}}_{{\text{v}}1}}({\text{n}})=\frac{1}{{2\pi }}\mathop \smallint \limits_{{ - \pi }}^{\pi } {\text{log}}\left| {{{\text{V}}_1}\left( \omega \right)} \right|{{\text{e}}^{{\text{j}}\omega {\text{n}}}}{\text{d}}\omega$ are the nth real cepstral coefficients of the signals s(n) and v₁(n), respectively. We recall here that ${\text{S}}(\omega )$ and ${{\text{V}}_1}(\omega )$ present the short Fourier transform of the original speech signal ${\text{s}}({\text{n}})$ and the enhanced one${\text{~}}{{\text{v}}_1}({\text{n}})$, respectively. The parameter ‘Z’ is the mean averaging value of the CD criterion and ‘M’ represents the number of segment where only speech is present. The simulations parameters of this experiment are the same as given in Table 3. In order to well see the output speech signal distortion evolution of the proposed WBBSS algorithm, we have selected the DWT scale to be equal to N = 2 and then to N = 4. The simulation results of this experiment for three input SNR values, i.e. − 6, 0, and 6 dB are shown on Fig. 12.

Fig. 12

CD evaluation of the BBSS (Djendi et al. 2006), the TSNR (Plapous et al. 2004), and the proposed WBBSS algorithms. [Top left]: white; [Top right]: USASI; [Bottom left]: Babble; [Bottom right]: Street

From this experiment and according to Fig. 12, we conclude that the proposed WBBSS algorithm has almost the lower CD values for different scale of the DWT, with a slight superiority in the case when the DWT scale is selected N = 2. These results show that the proposed WBBSS algorithm outperforms the conventional BBSS (Djendi et al. 2006) and TSNR (Plapous et al. 2004) for each DWT scale. However, we observe a decrease of the CD values when the number of DWT scale is chosen low, i.e. N = 2. We have also noted that for high input SNR situations, the CD values are low thus signifying a superior intelligibility performance of the output speech signal of the proposed WBBSS algorithm. We have also observed that the enhanced speech signals of the proposed WBBSS algorithm sound much clearer with much less speech distortion than the BBSS (Djendi et al. 2006) and TSNR (Plapous et al. 2004) algorithms.

6 Conclusion

In this paper, we have proposed a new wavelet based BSS (WBBSS) algorithm that is based on a wavelet implementation of the backward blind source separation (BBSS) algorithm. The theoretical derivation and intensive experimental validation of the proposed WBBSS algorithm have been presented along this paper. The proposed WBBSS algorithm has shown best performances in terms of segmental signal-to-noise ratio, segmental mean square error and cepstral distance criteria. We have also shown the best convergence speed performance property of the WBBSS algorithm through the evaluation of the system mismatch criterion. This new work allows improving the convergence speed of the WBBSS algorithm even when very noisy observations are available. The drawback of the proposed WBBSS algorithm is a degradation of the criterion CD, SegMSE, SegSNR when the discrete wavelet transform (DWT) scale is selected high. Also, we have noted that the proposed WBBSS outperforms the BBSS and the TSNR algorithms with low DWT scales, and comparable performances when high DWT scales are selected. We have also noted that both of BBSS and TSNR algorithms use a manual VAD to give such performances, however, the proposed WBBSS algorithm detect activity and silence periods of the speech signal automatically thanks to the modifications that we have reported on the update relation of the cross-filters (See relations 15, 16). This means that the new WBBSS algorithm can be used directly in practice as its work automatically without need of any VAD systems. In order to improve the behavior of the proposed WBBSS algorithm when the DWT scales are selected high, we can envisage using a variable step-size to correct this problem in our future works.