1 Introduction

The highly parallel compute throughput and memory bandwidth of GPUs make them a desirable platform to accelerate data-parallel, compute-intensive applications. For the past few years, general-purpose computing on GPUs (GPGPU) has shown successes in various application domains, including image and video processing, data mining, bioinformatics, numerical simulations and so on. Most of these applications map well to GPUs’ SIMD architectures and programming models and achieve performance speedups on GPUs compared to CPUs. Recent research efforts have advanced GPU computing into the areas of SIMD-unfriendly workloads [1, 2]. Graph applications are an emerging set of such irregular workloads. They are used in social network analysis, knowledge discovery, business analytics, infrastructure planning and engineering simulation. Many big-data applications involve graph processing on large datasets. In contrast to regular applications, programming and optimizing these graph applications tend to be a challenge. In addition, understanding how efficiently these applications can leverage GPUs is essential to improve hardware and software for irregular workloads.

In parallel computing, designers increasingly face the challenge of balancing performance and programming efforts. Highly tuned applications for a particular platform achieve high performance but require significant engineering. Possible side effects include complex code and poor performance portability. High-level languages and APIs make programming easier, but may cause additional overhead due to extra layers of abstraction. For graph applications, most prior GPGPU research took problem-specific approaches for parallelization and optimizations of individual problems. These advanced techniques usually are not intuitive for regular programmers because significant effort is needed to restructure SIMD computation and memory accesses. Ideally, programmers need an easy way to program graph applications while in the meantime achieve high-performance and portability.

This paper resolves these issues by developing and fine-tuning a set of linear-algebra building blocks shared by many important graph algorithms. Our goal is to provide a framework which allows programmers to achieve good programmability, performance and portability for GPGPU graph processing. Inspired by the prior work [3–5], we adopt the concept and development of graph algorithm research in the linear-algebra language. Though there could be alternative abstractions for solving graph problems [6], primitives designed in linear algebra are promising to map relatively well to SIMD architectures with optimizations. We develop the BelRed library, encapsulating common programming primitives into reusable functions. We demonstrate the usage of these functions to program a set of representative graph algorithms for GPUs. BelRed enables programmers to focus on high-level algorithms rather than device-specific mapping and optimization. Improving performance of individual API functions (e.g. by software vendors) leads to better overall performance, while preserving modularity. The library can also be easily extended to support multiple machine nodes. This paper makes several contributions:

  • We present the BelRed library framework and describe a set of important routines (e.g., diverse sparse-matrix and vector operations) for graph processing. We present their GPU parallelization and optimization techniques.

  • We present several representative graph applications and their GPU implementations. We use several case studies on how to build them with the BelRed API.

  • We show application performance on an AMD discrete GPU with comparisons to the Pannotia [2] library. We discuss performance implications of device-specific optimizations, data layouts and access patterns. We show that the diverse data structures provided by BelRed offer the capabilities to process different graphs efficiently.

2 Background

In this section, we describe the GPU architecture with an AMD GPU as an example and OpenCL. We also present some common features shared by many graph applications.

2.1 AMD GPUs and OpenCL

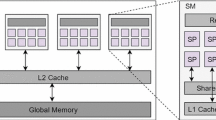
AMD Radeon™ HD 7000 series and later GPUs use the AMD Graphics Core Next (GCN) architecture [7], which is a radically new design compared to prior AMD designs based on very long instruction word (VLIW) architectures. The AMD GPU includes multiple SIMD compute units (CUs). Each CU contains one scalar unit and four vector units [8]. Each vector unit contains an array of 16 processing elements (PEs). Each PE consists of one ALU. The four vector units use SIMD execution of a scalar instruction. Each CU contains a single instruction cache, a data cache for the scalar unit, a L1 data cache and a local data share (LDS) (i.e., software-managed scratchpad). All CUs share a single unified L2 cache. The GPU supports multiple DRAM channels.

OpenCL is a programming model to develop applications for GPUs and other accelerators [9]. In OpenCL, a host program launches a kernel with work-items over an index space (NDRange). Work-items are grouped into work-groups. OpenCL supports multiple memory spaces (e.g., the global memory space shared by all work-groups, the per-work-group local memory space, the per-work-item private memory space, etc.). In addition, there are constant and texture memory spaces for read-only data structures. The original OpenCL uses two types of barrier synchronizations in different scopes: local barriers for all the threads (i.e., work-items) within a work-group and global barriers for all the threads launched in a kernel. The new OpenCL 2.0 defines an enhanced execution model and a subset of the C/C++11 memory modes. It supports work-item atomics and synchronizations visible to other work-items in a work-group, across work-groups executing on a device, or for sharing data between the OpenCL device and host [9].

2.2 Graph Applications

Graph applications are an emerging application domain, thanks to recent developments generally referred to as “big data”. Graphs with millions of vertices and edges are common. Graph algorithms are applied to solve a variety of problems, including intelligence (e.g., data analytic, security, and knowledge discovery), social network, life science and healthcare (e.g., bioinformatics), infrastructure (e.g., road network and energy supply) and scientific and engineering simulations in high-performance computing. These graph applications, which process a large amount of data in parallel, require massive computation power and memory. Recent studies [1, 2, 10–13] show that GPUs can be powerful to compute structured, regular data-parallel applications and also promising to accelerate irregular applications such as graph processing.

Graph applications present certain characteristics not in other regular GPU workloads. For example, they present low arithmetic intensity, that is, relatively less arithmetic compared to memory operations. This imposes much pressure on off-chip memory bandwidth. Certain applications present poor data reuse. Access patterns are hard to predict. This makes it difficult to exploit on-chip data locality. In addition, SIMD underutilization is a common issue in many graph workloads. The reasons can be due to branch divergence which occurs when threads in the same wavefront take different execution paths, or due to different amounts of work assigned to different threads. In these cases, some GPU threads must be masked off, leading to a subset of active SIMD lanes [8]. Another issue is memory divergence due to undesirable memory coalescing. Uncoalesced memory accesses require multiple memory transactions to supply data with poor cache-line utilization. Efficient coupling between data layouts and access patterns is needed.

However, the above inefficiencies are difficult to remove entirely for SIMD execution. Our primitives based on sparse-matrix and vector operations are relatively friendly to SIMD architectures. Furthermore, we provide several solutions to optimize data layouts and access patterns and perform GPU-specific optimizations.

3 BelRed

BelRed is a library of sparse-matrix and vector operations, consisting of diverse and optimized functions necessary for graph applications on GPUs. The goal is to allow GPU programmers to leverage these functions to construct their applications. The actual implementation is transparent to programmers. In addition, another contribution is that we provide a set of representative graph applications implemented using BelRed. BelRed uses graph algorithms in linear algebra [4], and supports diverse graph formats and data layouts. The current API is implemented on top of OpenCL, but can be extended to any programming model (e.g., C++, CUDA, Python, or Matlab). It is not restricted to GPU uses and thus implementations can target any computer architecture or dedicated hardware. BelRed has multiple advantages:

Programmability The BelRed library provides a high-level abstraction and programming primitives for GPGPU graph processing. Programmers can construct GPU graph applications with the BelRed API easily with minimum programming efforts.

Performance The BelRed implementation applies various optimizations to achieve high performance for each individual library function.

Portability Applications which use BelRed are portable across different GPUs and accelerator devices. Performance portability can be achieved by offering library implementations optimized for different devices (e.g., by library vendors).

Our library does not target algorithm-level functions (e.g. single-source shortest path, breadth first search, etc.). It is focused on low-level primitives useful for these graph algorithms. In addition, they can be useful for other sparse-matrix problems.

3.1 Formal Definitions

BelRed represents graphs using matrices. Graphs can be stored in sparse matrices. We first define operations mathematically for easy notation and explanation. We use a similar form by Kepner and Gilbert [4] and Matlab. We use U, \(\mathbf {u}\) and u to denote a 2-D matrix, a vector, and scalar element, respectively. For example, given a \({m \times n}\) matrix M and a vector \(\mathbf {w}\) with dimension n, the product \({M\mathbf {w}}\) (i.e., \({M +.*\mathbf {w}}\) ) is a vector of dimension m (see Sect. 4.1). Besides multiplication, other operations are also supported. For example, \({M min.+\mathbf {w}}\) is a m-wide vector whose ith element is \({min(M(i, j)+\mathbf {w}(j): 1 \le j \le N)}\) (see Sect. 4.2). For vector \({\mathbf {v}}\) with dimension m and vector \({\mathbf {w}}\) with dimension n, the outer product of \({\mathbf {v}}\) and \({\mathbf {w}}\) is described as \({\mathbf {v} \circ \mathbf {w}}\), which is a \(m \times n\) matrix whose (i, j) element is the result of \({\mathbf {v}(i) * \mathbf {w}(j)}\). In this paper, we show outer sum, in which the multiplication operation is substituted by addition (see Sect. 4.5). If A and B are matrices of the same size, the element-wise product \(A .\times B\) is the matrix C with \(C(i, j) = A(i, j) * B(i, j)\) where \(1 \le i \le m\) and \(1 \le j \le n\). Similar notation applies to other element-wise binary operators (e.g., \(C = A .min B\)). There are similar element-wise operations for vectors, for instance, the AND and OR of two vectors v and w can be denoted as \( \mathbf {v} \& \mathbf {w}\) and \(\mathbf {v} | \mathbf {w}\) respectively (see Sect. 4.3). For vector-wise operations, they generate a value with all the elements in a vector, for instance, \({max(\mathbf {w}(i): 1 \le i \le N)}\) (i.e., the max for a vector).

Table 1 Sample BelRed API functions and descriptions
Full size table
Table 2 Operations and current data structure support
Full size table

3.2 BelRed Functions

This section summarizes the BelRed functions. Table 1 shows a subset of library functions and their descriptions (see Fig. 2 for a graphical representation). Programmers can call these functions on the host. This is by no means a complete list for graph processing; BelRed is extensible to support other operations, and each function may be extended to different variants (e.g., semirings [4] ) with replacement of other operators (e.g., \({\times , +, min}\)). For example, OuterSum may have a variant of OuterProduct. Similarly, \(min.+\) may have a variant of \(max.+\). It may also be useful to provide user-defined functions for matrices or vectors. Software vendors can provide highly optimized implementations for individual functions which target specific devices. In addition, with BelRed, application behavior and performance become relatively easy to predict with a breakdown into individual functions. In Sects. 4 and  5, we show how we implement and optimize these functions and how to use them to build a variety of graph algorithms.

3.3 Data Structure Layout

The BelRed framework currently supports a few data structures internally to store graphs. We found that different algorithms and traversal patterns may prefer different memory layouts. These include the compressed sparse row (CSR), coordinates list (COO) and ELLPACK (ELL) formats to store sparse graph structures (e.g., in Bellman–Ford, Maximal Independent Set, Coloring and PageRank). BelRed is extensible to other data layouts. In Sect. 7.2, we discuss the reasons why we choose these data layouts and their pros and cons. Figure 1 shows a graphical representation of these data layouts. Other operations support regular 2-D adjacency list and 1-D vector. Table 2 lists the BelRed functions and the associated data structures they currently support. Future BelRed development will extend the framework to other data structures (e.g. diagonal and hybrid formats).

3.4 Graph Inputs

BelRed includes support for widely used graph formats: DIMACS Challenge [14, 15], METIS [16] and Matrix Market [17] formats. The library contains utility routines to parse graph inputs in these formats. BelRed uses many real-world graphs for different problems (e.g, co-author and citation graphs, road networks, numerical simulation meshes, clustering instances, web, etc.). We include sample graphs from the DIMACS Implementation Challenges [14, 15] for shortest-path, graph partitioning, and clustering problems. Some graphs are obtained from the University of Florida Sparse Matrix Collection [18]. GTGraph [19] is used to generate random graphs.

Fig. 1
figure 1

Different data structures supported by BelRed (e.g., 2-D adjacency matrix, compressed-sparse row, coordinate and ELLPACK). Some format such as ELL requires padding and storage in the column-major format

Full size image
Fig. 2
figure 2

Sample BelRed operations: a matrix-vector multiply, b \(min.+\), c segmented min reduction, d vector-vector AND, and e outer sum. For b and c, the blank regions represent big numbers (i.e., \(\infty \)) while for (a), (d) and (e), the blank regions represent zeroes. The 2-D matrices can be stored in a sparse format.

Full size image

4 Graph Building Blocks

In this section, we present some key operations and functions in the BelRed API. Each function is implemented and optimized for the GPU and can be called in a GPU program. Figure 2 shows the graphical representation of sample operations. 2-D matrices in the figure can be represented in compact sparse formats.

Fig. 3
figure 3

Pseudocode examples of min.+ (b \(=\) data \(min.+\) a) in CSR (top) and ELL (bottom)

Full size image

4.1 SpMV

Sparse matrix-vector product (SpMV) is a computational kernel that is critical to many scientific and engineering applications. Figure 2a is a graphical view of SpMV. SpMV-type operation is a natural fit for graph applications in which vertices have data exchanges with their neighbors. For example, SpMV can be used to expand the neighbor list (e.g., in breadth-first search [4]). Also, SpMV can be modified with other operators to meet different purposes. For instance SpTouch can be defined by substituting \(\times \) and \(+\) in the inner loop with |. There can be multiple GPU implementations for SpMV. The outer loop of SpMV can be unfolded such that each GPU thread is responsible for processing one row. An alternative is that each wavefront is responsible for one row. In this case, intra-wavefront parallel reduction is needed to calculate the sum. Prior studies [20–22] demonstrate approaches to optimize SpMV on GPUs. It is one of the useful building blocks for graph processing. The implementation of SpMV in this paper is currently for dense vector V. Recent work by Yang et al. [23] studies an approach to improve sparse-matrix and sparse-vector multiplication (SpMSpV); we leave the evaluation of SpMSpV for future work.

4.2 min.+

As discussed in Sect. 3.1, the \(min.+\) operation is another important programming primitive for graph processing [4]. Vertex-value comparison is a common operation in shortest-path and graph-partitioning algorithms. For each row in the adjacency matrix and a dense vector, \(min.+\) sums each pair of two elements in the row and vector, and then performs a reduction with a min operation across all pairs. Two pseudocode examples for \(min.+\) are shown in Fig. 3. The first example uses CSR to store the matrix, and each thread is responsible for processing one row. The second example uses ELL, and each thread is responsible for one row as well. The ELL matrix is stored in a column-major order with additional padding. This helps improve memory coalescing when multiple threads in a wavefront access data elements in the cache simultaneously. Also, there is no divergent branch but with additional redundant computation.

Figure 2b is a graphical representation of the \(min.+\) operation. We use \(min.+\) to implement the Bellman–Ford algorithm, which solves the single-source shortest path (SSSP) problem. We also use it as an example to show performance impacts of using different graph data structures in Sect. 7.2.

4.3 Element-Wise Operations

Element-Wise matrix-matrix operations take two matrices and generate a result matrix with an operator (e.g., \(\times , +, min\)) applied on each pair of elements from two matrices. To implement element-wise GPU operations, each thread is assigned to compute each result element in parallel. Element-wise vector–vector operations are also very common in many graph algorithms. For instance, an algorithm may decide which vertices are active or inactive. Figure 2d is graphical view of an AND operation. GPU implementations of these operations seem to be straightforward with threads processing different regions of an array or vector. But the performance will be suboptimal if inappropriate parameters are chosen, such as OpenCL workgroup size and the amount of work (data chunk in bytes) assigned for each workitem. BelRed relieves programmers from dealing with device-specific tunings.

4.4 Segmented Reduction

Segmented reduction calculates a vector with each its element calculated by reducing the elements in a segment of the vector (e.g., each segment can be a row in a sparse matrix). One useful operation in many graph partitioning problems is to compare the values of all the vertices in a row and calculate the maximum or minimum. For example, given a 2-D adjacency matrix, \(SegReduc\_Min\) produces a vector with each element being the minimum of the elements in each row (see Fig. 2c).

4.5 Outer Sum

The outer sum operation calculates an \(m \times n\) matrix using two 1-D vectors as inputs, with a size of m and n respectively. It is useful for calculating all-to-all relationship. Figure 2e shows the outer-sum operation in which for a 2-D matrix M and two vectors \(\mathbf {v}\) and \(\mathbf {w}\), the element M(i, j) is the sum of \(\mathbf {v}(i)\) and \(\mathbf {w}(j)\) where \(i \in [1, m]\) and \(j \in [1, n]\). For a GPU implementation, an \(m \times n\) 2-D ND-Range is configured to launch an OpenCL kernel. All the points in the computation domain are mapped to 2-D indices and processed concurrently. The Floyd–Warshall algorithm, which computes the all-pairs shortest-path (APSP) problen can use the outer sum operation.

4.6 Other Building Blocks

Prior studies investigated other basic building blocks for irregular applications. Our work is complementary to theirs. For instance, one famous example is a set of scan primitives developed by Sengupta [24]. They implemented the classic scan and segmented-scan operations for GPUs. Merrill et al. [12] developed a highly optimized Breadth-First algorithm with prefix-sum. Bolt C++ [25] and Thrust [26] implemented a GPU API similar to the C++ standard template library (STL). Our library is designed particularly for graph processing.

5 Graph Algorithms with BelRed

In this section, we present several case studies which use BelRed to program graph applications.

5.1 PageRank

PageRank (PRK) is an algorithm to calculate probability distributions representing the likelihood that a person randomly clicking on links arrives at any particular page. In a typical implementation, the value of each vertex first is initialized to \(\frac{1}{num\_vertices}\). In each step of the main computation loop, each vertex assigned to a GPU thread sends along its outgoing edges the current PageRank value divided by the number of its outgoing edges [27]. Each thread then sums the values arriving at each vertex, and calculates a new PageRank value. The algorithm terminates when convergence is determined by an aggregator or after running a user-specified number of iterations. Each GPU thread can traverse the neighbor list of a vertex and atomically adds the associated PageRank amount \(\frac{PgRankVal}{num\_outgoing\_edges}\) to each neighbor in the neighbor list [2]. With BelRed, this step can be substituted with a SpMV operation on the GPU. A preprocessing step is conducted first to compute a matrix which stores the percentage of PageRank a vertex transfers to each of its neighbors. A transpose is performed first so that the ith row of the new matrix represents the information for all the vertices which have an outgoing edge to the ith vertex. Then the algorithm goes into the main loop, launching SpMV followed by an update kernel to calculate PageRanks. The update kernel is written by the user and finalizes the PageRank value for each vertex at the end of an iteration. This uses the equation \(PageRank[tid] = (1-d)/num\_vertices + d * PageRank\prime [tid] \), where d is a damping factor (0.85 in our study) and tid is the GPU thread id.

5.2 Bellman–Ford

The SSSP algorithm is a common subroutine in various graph applications. Given a user-specified source vertex, the algorithm searches the shortest path between the source vertex and all the other vertices in the graph. SSSP keeps track of a distance array, saving the shortest distances while the program proceeds. In a typical SSSP implementation [2], each vertex in the graph is assigned to a GPU thread. Starting at the source vertex, GPU threads gradually explore frontiers while a vector keeps track of the active vertices. Each thread processes an active vertex, traverses the neighbor list and performs edge relaxation. If the shortest distance of the active vertex to the source plus the edge weight to a particular neighbor is less than the recorded distance, a new shortest distance is updated atomically by a GPU thread.

In this study, we use the Bellman–Ford algorithm [1, 28] to solve the single-source shortest path problem. Figure 4 is an example showing four iterations of Bellman–Ford on a sample graph with six vertices and eleven edges. The core of the algorithm is performing the \(min.+ \) operation on a matrix M and a vector \(\mathbf {w}\) on the GPU. The vector \(\mathbf {w}\) stores the shortest distances of all the vertices to the source. The source vertex i in \(\mathbf {w}\) is initialize to 0 (i.e., zero distance to itself), while all the other vertices are initialized to a \(\infty \) value (i.e., a big integer). \(\mathbf {w}^{\prime } = M min.+ \mathbf {w}\) produces the shortest distances for all the vertices directly connected to the source at the end of the first iteration. Similarly, \(\mathbf {w}'' = M min .+ \mathbf {w}^{\prime }\) produces the shortest distances after traversing two layers of vertices from the source. The same process repeats until convergence. A check_convergence GPU kernel following min.+ in the main loop is used to determine program termination. The \(min.+\) operation is a basic primitive useful for solving a variety of problems; Bellman–Ford is used as case to show its usage. Recent work shows a new GPU technique to solve SSSP [29] which is of better computational complexity than Bellman–Ford. On the other hand, it is interesting to compare their execution times and memory requirements when computing concurrent SSSPs ( given multiple sources), which may be efficient and easy to do using \(min.+ \) with multiple vectors. We leave this comparison for future work.

Fig. 4
figure 4

Conduct \(min.+\) repeatedly to implement the single-source shortest path (SSSP) algorithm. We use a square adjacency matrix for demonstration. The actual storage can be in a sparse-matrix format. For an element (j, i) with value w, it means vertex i connects to vertex j with an edge weight of w. All the elements along the diagonal are initialized to zeroes with the rest initialized to a big number. The source vertex in this example is vertex 3

Full size image

5.3 Coloring

Graph coloring (CLR) partitions the vertices of a graph such that no two adjacent vertices share the same color. We use an algorithm similar to that used in prior work [30]. In the initialization step, each vertex is labelled with a random integer. The algorithm takes multiple iterations to solve the problem, with each iteration labelling vertices with one color. For each vertex, a GPU thread compares its vertex value with that of its neighbors. If the value of a given vertex happens to be the largest (or smallest) among its neighbors, it labels itself with the color of the current iteration. The algorithm converges when all vertices are colored.

In fact, the step of determining whether a vertex is a local maximum or minimum can leverage a BelRed library function. To achieve this, given a matrix M, the \(SegReduc\_Min\) operation spanned across multiple rows calculates a temporary vector \(\mathbf {u}\). Each element i in \(\mathbf {u}\) is max/min for the elements in each individual row of M (i.e., the neighbor list for each vertex). Each GPU thread (or wavefront) can be responsible for a row. The algorithm then compares the temporary vector with the vector that stores the current vertex values, and decides if a vertex is local maximum or minimum in order to label a color. In this problem, we use a specific version of GPU vector-wise max/min. We maintain a mask vector recording the activeness of each vertex. The max/min operation is applied only to those vertices active in a given iteration.

5.4 Maximal Independent Set

An independent set are vertices in a graph in which none are adjacent. In Maximal Independent Set (MIS), it is not possible to add another vertex to the set without violating that property. This algorithm is commonly used to solve problems in graph partitioning and task scheduling. A typical MIS implementation uses Luby’s algorithm [31]. Each vertex is labelled with a random integer and each GPU thread compares the value of a vertex to its neighbors and determines whether it should be added to the set (based on the local maximum/minimum). For each vertex added to the set, each thread visits its neighbor list and marks all the neighbors inactive, which will not be evaluated in the next iteration.

With BelRed, Maximal Independent Set can be implemented using the same building block as Coloring to calculate local max/min. However, in this study, we use another algorithm described by Shah et al. [32, 33]. In our implementation, the program first selects a subset of vertices, select, randomly as an initial set. It conducts SpTouch with a graph M and the vector select as inputs. Remember that SpTouch is used to expand the neighbor list of the selected vertices. The algorithm marks the touched neighbors as “visited” vertices, and subsequently determines whether the expanded neighbors and selected vertices overlap. This can be achieved through an AND operation (i.e., \( select \& SpTouch(M, select)\)). For the result, we evaluate the overlapped vertices and keep only those with higher degrees, \(final\_select\), which is implemented with a specific kernel. Then we add them to the set mis. This step is achieved through an OR operation (i.e., \(mis | final\_select\)). All neighbors of \(final\_select\) are discarded; the following iterations process the remaining vertices, until all the vertices are evaluated.

5.5 Floyd–Warshall

Floyd–Warshall (FW) solves the all-pairs shortest paths (APSP) problem. This problem can be solved in a manner of dynamic programming in 2-D matrix operations [11]. For instance, given a graph G(V, E), a function shortestPath(i, j, k) returns the shortest possible path from i to j using vertices from the set 1, 2 , ..., k as intermediate vertices. Each step is to find the shortest path from each i to each j using vertices 1 to \(k + 1\) with increasing k. The shortest path for \(k + 1\) is either a path that uses vertices in the set 1, 2,..., k or a path that goes from i to \(k + 1\) and then from \(k + 1\) to j [2]. This operation is summarized as:

figure a

In our implementation, a 2-D distance array is used to keep track of the shortest distances from all possible sources to all possible destinations. Floyd–Warshall uses two major BelRed operations. The first is an outer sum on the GPU calculating an \(n \times n\) matrix with two n-wide vectors as inputs. The second is a parallel element-wise min operation on the GPU applied on each pair of elements from two 2-D matrices M1 and M2. Each element in the result matrix is calculated with min(M1(i, j), M2(i, j)), (\(i, j \in [1, n]\)). We use FloydWarshal as an example to show the overhead of launching GPU kernels. We also implemented APSP using the R-Kleen algorithm [34] which uses the \(min.+ \) semiring, but we found that it is slower than the version using outer sum.

6 Experimental Setup

In this paper, the experimental results are measured on real hardware using an AMD Radeon HD 7950 discrete GPU. The AMD Radeon HD 7950 features 28 GCN CUs with 1792 processing elements running at 800 MHz with 3 GB of device memory. We compare the results to those obtained from four CPU cores on an AMD A8-5500 with a 3.2-GHz clock rate and 2 MB L2 cache. We use AMD APP SDK 2.8 with OpenCL 2.1 support. AMD APP Profiler v2.5 is used to collect profiling results. In addition, this study is restricted to cases when the working sets of applications do not exceed the capacity of the GPU device memory. We leave graph partitioning for multi-node processing for future work.

7 Results

In this section, we discuss performance benefits of using BelRed. We also discuss issues related to the choice of data layouts, kernel launch overhead and impacts of device-specific parameters.

7.1 Performance Improvement

Performance is evaluated on five graph algorithms constructed with BelRed (see Sect. 5). We calculate performance speedups by running applications on a AMD Radeon HD 7950 discrete GPU, and comparing them to running applications on four CPU cores of an AMD A8-5500. We focus on the main computation part, and exclude file I/Os and graph parsing. For the AMD Radeon HD 7950, we include the PCI-E data-transfer overhead when calculating speedups. We choose the inputs used in Che et al. [2] for comparison. Figure 5 shows the performance speedups for all the applications and inputs. The arithmetic mean of speedups for all program-input pairs is approximately 4\(\times \). Application performance is also input-dependent (i.e., graph structures). For example, for Bellman–Ford, road-NW achieves a 6\(\times \) speedup, while road-CAL achieves a 10\(\times \) speedup. This is similar to Coloring with shell (8\(\times \)) and ecology (4.5\(\times \)). Maximal Independent Set achieves only 10 % performance improvement due to in-loop CPU computation and kernel-call overhead. Figure 6 shows the execution-time breakdown due to CPU computation, GPU computation and PCI-E transfer for the main computation part across different applications. The portion of GPU computation is up to 99 %. For Coloring and Floyd–Warshall, a small portion of execution time is spent on the initial setup and data preprocessing. Maximal Independent Set has some opportunity for additional GPU offloads, which we leave for future work.

We also compare performance between BelRed and Pannotia [2]. BelRed shows a comparable performance to Pannotia (see Table 3) which provides algorithm-specific implementations. For fair comparison, we use the same data structure when comparing the same algorithm; however, BelRed supports more diverse data structures, which may yield better performance for certain inputs (see Sect. 7.2). Specifically, Bellman–Ford with BelRed is on average 30 % faster than Pannotia. For PageRank, the performance is similar. For instance, for the coAuthor data set, the BelRed version is 12 % slower than Pannotia, while for the 2k dataset, BelRed is 22 % faster than Pannotia. Similar behaviors are present in Graph Coloring as well. The Pannotia version is 2\(\times \) faster than BelRed for Floyd–Warshall, due to that BelRed breaks the problem into smaller kernels. We did not compare Maximal Independent Set, because they use two different algorithms, which is not a fare comparison ( though each will generate a different, though valid result for Maximal Independent Set. For a graph, there can be multiple “maximal” independent sets). In general, applications programmed with BelRed achieve competitive performance and show good programmability.

Fig. 5
figure 5

Performance speedups of running graph applications on the GPU compared to the CPU

Full size image
Fig. 6
figure 6

Application execution time breakdown in CPU execution, GPU kernel execution, and PCI-E transfer

Full size image
Table 3 BelRed versus Pannotia runtime comparison (ms)
Full size table

7.1.1 Kernel Launching

Terminating a kernel call is essentially forcing all the threads to synchronize. An efficient implementation of an application uses a small number of kernel calls. Our BelRed API encapsulates common functionally into well-defined functions for reuse, productivity and maintainability. However, the cost of maintaining modularity is the possibly resultant overhead of GPU kernel call invocation and extra device-memory accesses. Therefore, an application using BelRed may launch more kernels than a version otherwise implemented with cross-function optimizations and fewer kernels. For Floyd–Warshall, calculation of each individual element is independent of others. Therefore the two BelRed kernels actually can be merged into a big kernel if not using the BelRed API. This leads to about 2\(\times \) slowdown for the BelRed version. Thus, GPU vendors may focus on reducing the cost associated with kernel launching. Recently AMD proposes Heterogeneous System Architecture (HSA) [35], supporting low-overhead user-space queuing on the GPU side; HSA may help address this concern benefiting library designers. In addition, because of dividing kernels, extra global memory writes and reads may be needed between kernels to pass the intermediate results from one kernel to another.

7.2 Data Layouts and Accesses

Efficient memory accesses are important for GPUs to achieve high performance. This study examines the performance impact of using different data structures. We consider three popular data layouts for sparse graphs—COO, CSR, and ELL. Each structure has their unique advantage when solving different problems. COO and CSR are more general and flexible formats than ELL. Compared to ELL, they also require less memory capacity to store graphs and sparse matrices. On the other hand, for GPU processing, the ELL format (similar to the diagonal format) generally is more efficient, especially for structured or semi-structured graphs. For unstructured graphs, sometimes COO or CSR is preferable given the limited GPU memory capacity. Discussions of different data structures and their implications to GPU performance can be found in prior research [20, 22]. Figure 7 shows degree distributions of two sample graphs for G3-Circuit and coAuthor; they represent typical characteristics of structured and unstructured graphs respectively. For G3-Circuit, most non-zero points are distributed along the diagonal of the 2-D adjacency matrix. The degree of vertices ranges from two to five. On the other hand, for coAuthor, a majority of vertices have small degrees, while there is a long tail with small number of vertices of large degrees. Many real-world graphs (e.g., power-law graphs) present similar characteristics.

Fig. 7
figure 7

Degree distribution of two graph inputs G3-Circuit and coAuthor. The y-axis shows vertex counts while the x-axis shows degrees. The ranges of y axes are [0, \(1.2\times 10^{6}\)] and [0, \(6\times 10^{4}\)] for the left and right figures, respectively. The long tail of the coAuthor dataset is only shown up to 50 for demonstration purpose. The largest degree is 240

Full size image

We develop multiple versions of GPU kernels for SpMV, \(min.+\) and other operations to process graphs that are stored in different data structures. For example, we apply some techniques from prior work [20, 22] to improve performance of sparse-matrix operations. Also, for \(min.+\) and row reduction, we optimize them to take advantage of the per-SIMD scratchpad memory (local data share in AMD GPUs) to perform parallel addition and min operations. We also organize ELL in a column-major layout with padding to remove memory divergence. This organization allows better memory coalescing without load imbalance but at the cost of redundant computation.

We use \(min.+\) as an example for result demonstration. Figure 8 reports execution times of \(min.+\) in CSR, COO, and ELL over a variety of graph inputs. As shown in the figure, performance depends on different layout-input pairs. In general, the ELL format is more SIMD-friendly than CSR and COO for GPU computation, especially for many structured graphs (e.g., fem-3D-thermal and denaunay). For unstructured graphs (e.g., email-eron and wiki-vote), the COO or CSR format achieves the best performance. For coAuthor and Wikipedia, the points for the ELL format are missing; the available OpenCL buffer is not big enough to hold the working sets for these two problems, because ELL requires much padding capacity for unstructured graphs. This can be shown in Fig. 9 that unstructured graphs with ELL are not very efficient, showing more DRAM reads and writes. The results are measured with the AMD APP Profiler using hardware counters. For many problems, program execution time is directly related to the amount of off-chip memory traffic (the applications are memory-bound).

Fig. 8
figure 8

Performance of the \(min.+\) operation over different inputs and graph formats

Full size image
Fig. 9
figure 9

The total kilobytes read from and written to the GPU device memory for the \(min.+\) operation

Full size image

We also measure SIMD utilization (i.e., the percentage of active threads in a wavefront) for all the layout-input combinations (see Fig. 10). In general, the ELL format achieves 100 % utilization for all the cases. All the SIMD lanes are active with certain redundant computation for the padding data. The average utilization for COO is approximately 60 %. This is due to underutilized SIMD lanes when doing parallel reductions in the GPU local data share. The CSR format achieves an average of 43 % of SIMD utilization. The data presents large variance depending on irregularity of graphs, ranging from 7 % for Wiki-Vote to 90 % for fem-3D-thermal.

Fig. 10
figure 10

SIMD utilization of different inputs and graph formats

Full size image

In another experiment, we measure the L2 cache behavior and the three data formats also show different characteristics. The average L2 cache hit rates are 36, 40 and 53 % for CSR, COO and ELL, respectively. For the CSR format, since threads in a wavefront may touch different lines depending on the sizes (i.e., number of nonzeros) of matrix rows and a line may be partially used in the cache, this format tends to require more cache misses than other formats. ELL achieves better average hit rates because it presents better data locality for threads in a wavefront.

7.3 Impact of GPU Parameters

Though support for some primitives (e.g., vector operations) seems to be straightforward for the GPU, the performance would be suboptimal without careful implementation and performance tuning. In this study, we evaluate typical vector operations, + and&. The workgroup size is varied from 64 (the wavefront size for the AMD GPU) to 256 and the amount of work done per thread is varied by performing vector operations on different data types (int, int2, int4 and int8). The total amount of work (a 256 k matrix) is fixed for different experiments. We found that the differences between the best and worst performance points can be quite significant, with 25 % for + and 20 % for&, respectively. For example, the best-performing configurations for these two operations are (workgroup_size, data_type) = (256, int2) and (64, int4) on an AMD Radeon 7950. The best choice of combination is highly-architecture dependent; therefore, functions have to be tuned for a specific GPU device [36]. However, this is a one-time cost for library designers per implementation and per GPU. This is a benefit of BelRed’s high-level abstraction, which relieves programmers from dealing with hand-optimized codes.

7.4 Convergence

A typical pattern in many graph algorithms is that it takes multiple iterations to solve a problem. The program needs to determine when to converge using the loop condition. For instance, Coloring and Maximal Independent Set finish processing when all the vertices are evaluated. This is achieved by updating a global variable shared by multiple GPU threads. This variable is also shared by both the CPU and the GPU and used to determine loop termination at the end of each iteration. For Bellman–Ford, a convergence kernel is added after the \(min.+\) kernel to determine if there are newer shortest paths updated. Algorithmically, Bellman–Ford requires N (i.e. \(N = no. vertices\)) iterations to converge. However, many real-world graphs do not require N iterations.

8 Related Work

Combinatorial BLAS [3] is graph library offering a powerful set of linear algebra primitives for graph analytics. Graph BLAS [5] is a recent effort of defining standard linear-algebra building blocks for graph processing. The area of research on graph algorithms in linear algebra is documented in the work by Kepner and Gilbert [4]. Our work is unique in that we target a practical implementation for the GPU and also include several workloads as case studies.

Prior benchmarking efforts (e.g. the Rodinia [37], Parboil [38], and SHOC [39] frameworks) included and evaluated only a few graph or tree-based algorithms. Burtscher et al. [1] performed a quantitative study of irregular programs on GPUs. Pannotia [2] is a recent work on developing and characterizing graph algorithms on the GPU. Other works studied how to accelerate graph algorithms efficiently on GPUs. Harish et al. [11] parallelized several graph algorithms on the GPU. Merrill et al. [12] proposed an optimized breadth-first search implementation with scan on both single and multiple GPU nodes. Burtscher et al. [10] presented an efficient CUDA implementation of a tree-based Barnes-Hut n-body algorithm. Other works studied GPU acceleration for connected component labelling [40], minimum-spanning tree [13], B+tree searches [41] and so on. All these works are problem-specific solutions. In contrast, we propose an API and library for GPGPU graph processing.

Several researchers built libraries of parallel graph algorithms for CPUs. These include the Parallel Boost Graph Library [42], the SNAP library [43], and the Multi-threaded Graph Library [44]. Other works studied graph algorithms on big machine clusters. For instance, Pregel [27] is a system to process large graphs. GraphLab [6] uses a gather-apply-scatter model and scale graph problems to multiple nodes. GraphChi [45] is a disk-based system for processing large graphs by breaking graphs into small chunks and using a parallel-sliding window method. In contrast, our work targets sparse-matrix building blocks for SIMD architectures.

9 Conclusion and Future Work

Graph applications are a set of emerging workloads in data processing. It is important to understand and improve their performance on GPUs and other manycore architectures. Programming irregular graph algorithms tends to be a challenge for GPU programmers. This paper presents a library, BelRed which includes GPU implementation of common software building blocks useful for programming graph applications. We show that diverse graph algorithms can be constructed with these modularized functions and achieve performance speedups on a GPU. We also discuss approaches to optimize these building blocks and study performance issues and impacts related to uses of different data structures and device-specific parameters. In addition, applications that use BelRed present good code portability across platforms. Programmers are relieved from writing error-prone, device-specific GPU kernels. Instead, programmers can focus on high-level algorithm design and describe the problem with BelRed functions.

BelRed can be integrated into existing GPU sparse-matrix libraries to enhance their support for graph processing. It can also be treated as an intermediate interface, translated from higher level languages and APIs. Besides taking ad-hoc approaches to solve individual problems, research and efforts are needed for a common programming abstraction and interface for GPU graph processing. One thing to note is that linear algebra is a useful framework for expressing some graph algorithms, but not all. For example, a heavy-weight maximal matching is simple to compute in parallel using greedy methods but resists expression through sparse-matrix products. Users may need to choose the best solution appropriate for their problems.

General sparse matrix-sparse matrix multiplication SpGEMM [46] is another important building block we plan to include. To make sparse-matrix and sparse-matrix multiplication perform well on the GPU requires significant effort of optimizations and is a hot topic of research. This routine is useful for building various graph applications such as triangle counting and enumeration [47], K-Truss, and Jaccard coefficient [48] which can be used for social-network analysis. In the meantime, these applications can take advantage of the existing routines (e.g., element-wise and vector operations) we developed.

Future directions include adding support for more functions (e.g., sub-matrix extraction and assignment), evaluating them using more graph applications (e.g., social network), supporting more graph formats and data structures, optimizing BelRed for different platforms (e.g., APUs, GPUs and other types of architectures) and studying its extension to multiple machine nodes.