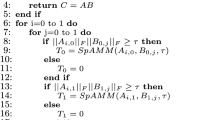1 Introduction

Modern Graphics Processing Units (GPUs) use multiple streaming multiprocessors (SMs) with potentially hundreds of cores. The key features are the fast context switching and the high memory bandwidth, which are used to hide long latency operations by switching to other threads [15]. Hiding the latency of main memory is based on an efficient zero-overhead switching mechanism, which uses a context register window. GPUs are primarily designed to run numerical computations having abundant data parallelism, i.e. having no recurrences or only marginal data dependencies. The hybrid CPU-GPU execution model allows data dependent computations to run on a host CPU, while the massive data parallel parts are efficiently run on the GPU. The Compute Unified Device Architecture (CUDA) framework supports this hybrid CPU-GPU approach of model execution. A Cooperative Heterogeneous Computing (CHC) framework [18] has also been proposed for explicitly processing CUDA applications in parallel on sets of heterogeneous processors including \(\times 86\) based general-purpose multi-core processors and GPUs.

During the past few years the many-core accelerators like the GPU (Nvidia) and Xeon Phi (Intel) [12, 13] proved to be efficient in running parallel numerical applications. Orders of magnitude acceleration have been reported compared to traditional multi-core computers. Many numerical algorithms have been designed for simulating a wide range of application domains such as fluid dynamics, reservoir simulation, as well as many problems that are solved using Cellular Automata (CA) algorithms [8].

A large class of numerical techniques boil down to repeatedly solving a large system of linear equations with billions of unknowns. This very demanding computational task involves dense and sparse linear algebra solvers (LAS). Modern parallel computing is concerned with the analysis and development of efficient implementations of state-of-the-art numerical simulations on massively parallel computers (MPC). The efficient implementation of LAS on MPCs is obviously a challenging task which promises a significant performance gain in many-core accelerators as compared to classical shared-memory multiprocessors (SMP) and distributed-memory systems [11, 13]. The iterative solvers have abundant matrix and vector operations which are known to be communication bound. Minimizing communication overhead and storage require new storage schemes for efficient implementation of large sparse matrix-vector (SpMV) operations. A communication reduction approach proved to be very useful on computing clusters with accelerators [6].

Matrix-Matrix multiplication (MM) is one fundamental component for linear algebra solvers, combinatorial optimizations, and graph algorithms. MM is the basic kernel that has \(O(N^3)\) operations as per the standard MM algorithm for \(N \times N\) arrays. Significant efforts have been made to obtain efficient MM implementations such as the Hybrid MM (HMM) algorithms. HMM generally consists of a 2-level approach: (1) a recursive algorithm which reduces the number of multiplications at the cost of some increase in the number of additions, and (2) a high-performance MM such as CuBLAS, MKL, and GotoBLAS.

In 1969, Strassen proposed an \(O(N^{log_27})\) algorithm for MM [27] that reduces the matrix multiplications but with some extra matrix additions. Several improvements have also been proposed on the original Strassen MM algorithm [31] and further developed newly optimized algorithms [24]. At present, the best upper bound kernel is \(O(N^{2.376})\) [7]. A general methodology for analyzing Coppersmith-Winograd-type algorithms has been developed [30] that improves the matrix-multiplication time to \(O(N^{2.373})\) steps. However, the practical benefit of these methods lies in their applicability to some very large matrices. Hence, the Strassens algorithm can be considered as one of the most practical approaches for fast matrix multiplication. It is believed that an MM optimal algorithm will run in essentially \(O(N^2)\) time [26].

Due to the additional matrix additions the original Strassen algorithm and its Winograd variant have relatively weaker numerical properties in comparison to the standard \(O(N^3)\) algorithm [19]. HMM algorithms are known to be less accurate than the canonical MM algorithm. Tiling MM is widely used due to small cache memory. However, adding tiles strongly impacts the forward error bound. Improving the accuracy of HMM is challenging because of the difficulties of adapting the algorithm without increasing the execution time and storage requirements. For this, a pairwise tile summation (PTS) that shortens the path from the summand to the total is proposed [2]. PTS is adapted in a top-down implementation, called recursive matrix multiplication, which allows dropping the error bound to \(O(log_2(N))\) as compared to \(O(\sqrt{N})\) for the GotoBLAS. Evaluation shows that performance improves if the leaf size at which recursion breaks is fixed as opposed to an implementation controlled using a fixed number of recursions. Overall, performance improves by 10 % with increased accuracy compared to the fastest high-performance MM.

Dumitrescu et. al [10] have implemented fast MM based on Strassen [27] and Winograd [31] algorithms using the ring and torus topologies on MIMD distributed-memory multi-computers with the generalization of Hyper-Torus. The results show a good asymptotic behavior in terms of complexity and efficiency. The parallel implementations achieved speedup of 75x over the canonical MM algorithm and 30x over an improved canonical implementation. These results are consistent with those reported by Bailey [3] for the same matrix dimension on a Cray-2 supercomputer. Unlike the standard algorithm that is easily customizable, these parallel implementations are applicable only on a fixed number of processors. The design of fast matrix multiplication (FMM) algorithms is emphasized while recognizing the difficulties of the implementation on MIMD computers. Achieving scalable performance is challenging due to the difficulty in FMM implementation on MIMD distributed-memory systems.

Communication cost of the Strassen algorithm has been estimated [5] using graph expansion analysis, and a lower bound on their communication costs was obtained. The calculated lower bounds show that not only does the Strassen algorithm reduce computation, but also creates an opportunity for reducing communication. In addition, the lower bound becomes tighter as the amount of available memory grows, suggesting that using extra memory may also allow for faster algorithms. Using the above analysis, a new algorithm (CAPS) [4] based on Strassen fast MM has been proposed. CAPS minimizes communication and attains theoretical lower bounds as identified in [5]. CAPS traverses the recursion tree of Strassen sequential algorithm in two ways that are the Breadth-First-Step (BFS) and the Depth-First-Step (DFS). BFS step requires more memory but reduces communication costs while a DFS step requires little extra memory but is less communication-efficient. The implementation of the above algorithm on Cray XT4 enhanced the execution time by 24–184 % for a fixed matrix dimension of size 94080. Lipshitz et. al [21] also evaluated the Strassen MM algorithm on Hopper (Cray XE6), Intrepid (IBM BG/P), and Franklin (Cray XT4) machines. A few other approaches for optimizing MM on MIC have been reported. Manually optimized library of operators [12] has been implemented on MIC, which allowed achieving approximately similar performance to MKL.

Matrix multiplication kernels have been investigated extensively on GPUs and several optimizations have been proposed [9, 16, 20, 22, 32] including GEMM implementation in MAGMA and CUBLAS libraries. Out of these implementations, CUDA BLAS (CUBLAS) library includes a highly optimized matrix multiplication kernel [23] based on the Volkov Demmel’s algorithm [28] on Tesla architecture. Panel Factorization (PF) has been efficiently implemented using BLAS1 and BLAS2. These are bandwidth bound on GPU, i.e. performance strongly depends on the flop:word ratio. Due to complexity of optimizations on GPUs, micro-benchmarking is used to reveal the memory latency and bandwidth, pipeline latency, and synchronization overheads. The above parameters allowed optimizing PF by adapting a blocked MM to match with the best block size, using memory alignment with short vectors, and loading blocks of data into the register file instead of the shared memory. Overall, Volkov Demmel’s kernel is implemented on a hybrid CPU-GPU model with efficient use of tiling due to the small cache memory on GPU. Volkov’s hybrid implementation of Cholesky factorization has been further enhanced [29] on the Fermi architecture using newer improvement strategies. A speedup of 3.85x is reported on Cholesky factorization of a square matrix of dimension \(10^4\).

Li et. al [19] presented both Strassen algorithm and its Winograd variant on NVIDIA C1060 GPU for integer and single-precision floating point data arrays. Strassen implementation achieved a speedup of 32–35 % while Winograd variant achieved a speedup of 33–36 % over CUBLAS 3.0 SGEMM implementations. The maximum numerical error was about twice that achieved by SGEMM for single-precision and zero for integer matrix multiplication. A GPU implementation of Strassen MM was first optimized by using multi-kernel streaming at the lowest level of recursion to exploit thread block parallelism [17]. Kernel synchronization was used to preserve dependencies. A cutoff prediction allowed finding the point at which the recursion breaks and the high-performance MM is activated. Basically, Strassens algorithm applies to power-of-2 sized matrices. In the above work, arbitrarily sized matrices were handled by using dynamic peeling. Evaluation shows a 1.27\(\times \) speedup for SPFP and 1.42\(\times \) speedup for DPFP over the CUBLAS-5.0 on a Tesla K10 GPU.

In this paper we propose a method for optimizing the performance of basic Strassen MM algorithm. The DFS approach is used due to the limited global memory space on the GPU and MIC. The proposed implementation is based on three optimization steps. First, the function invocation overhead is reduced by using a small set of basic functions (matrix multiplication, matrix addition, and matrix aggregation). Second, one of the most optimized libraries (CUBLAS 5.5) is invoked and embedded into the code using static device functions. This reduces the overhead of dynamic linking at runtime. Third, parametric kernels are generated and parameter-tuning techniques are applied to find the most profitable resource parameters that improves resource utilization. In the evaluation we show that 1-level of Strassen MM (S-MM) and other variants with CUBLAS as the basic library outperforms the native CUBLAS for two dimensional arrays. Similar results have been achieved when running the proposed approach on MIC and invoking the MKL library. This suggests that the proposed approach can be used as an optimization technique to further enhance the performance of CUBLAS and MKL libraries for basic algebra operations.

The rest of the paper is organized as follows: Sect. 2 describes the Strassen matrix multiplication method and its derivations. Section 3 presents the proposed Strassen implementations. Section 4 presents GPU and MIC architecture and programming models and optimizations. Section 5 presents the performance evaluation and discusses the obtained results. In Sect. 6, we conclude our work.

2 Strassen Matrix Multiplication Method

In 1969, Volker Strassen developed a recursive matrix multiplication algorithm (S-MM) [27] based on a divide and conquer strategy.

The objective is the computation of the resultant product matrix C as follows:

$$\begin{aligned} C = A B \quad A,B,C \quad \epsilon \quad R^{2^n \times 2^n} \end{aligned}$$
(1)

where A and B are square matrices over a ring R with \(N=2^n\).

All three matrices will be sub-divided into equally sized blocks of matrices in such a way that

$$\begin{aligned} \tiny A = \left( \begin{array}{cc} A_{1,1} &{} A_{1,2} \\ A_{2,1} &{} A_{2,2} \\ \end{array} \right) ,\quad B = \left( \begin{array}{cc} B_{1,1} &{} B_{1,2} \\ B_{2,1} &{} B_{2,2} \\ \end{array} \right) ,\quad C = \left( \begin{array}{cc} C_{1,1} &{} C_{1,2} \\ C_{2,1} &{} C_{2,2} \\ \end{array} \right) \end{aligned}$$
(2)

with

$$\begin{aligned} A_{i,j}, \quad B_{i,j}, \quad C_{i,j} \qquad \epsilon \quad R^{2^{n-1} \times 2^{n-1}} \end{aligned}$$
(3)

then

$$\begin{aligned} C_{1,1}= & {} A_{1,1} B_{1,1} + A_{1,2} B_{2,1} \nonumber \\ C_{1,2}= & {} A_{1,1} B_{1,2} + A_{1,2} B_{2,2} \nonumber \\ C_{2,1}= & {} A_{2,1} B_{1,1} + A_{2,2} B_{2,1} \nonumber \\ C_{2,2}= & {} A_{2,1} B_{1,2} + A_{2,2} B_{2,2} \end{aligned}$$
(4)

In the above construction eight multiplications are needed to calculate \(C_{i,j}\) matrices. In order to reduce the number of multiplications, the following new matrices have to be defined.

$$\begin{aligned} M_1= & {} (A_{1,1} + A_{2,2})(B_{1,1} + B_{2,2}) \nonumber \\ M_2= & {} (A_{2,1} + A_{2,2}) B_{1,1} \nonumber \\ M_3= & {} A_{1,1}(B_{1,2} - B_{2,2}) \nonumber \\ M_4= & {} A_{2,2}(B_{2,1} - B_{1,1}) \nonumber \\ M_5= & {} (A_{1,1} + A_{1,2})B_{2,2} \nonumber \\ M_6= & {} (A_{2,1} - A_{1,1})(B_{1,1} + B_{1,2}) \nonumber \\ M_7= & {} (A_{1,2} - A_{2,2})(B_{2,1} + B_{2,2}) \end{aligned}$$
(5)

Now, using only the above 7 multiplications, \(C_{i,j}\) can be expressed in terms \(M_k\) as follows:

$$\begin{aligned} C_{1,1}= & {} M_1 + M_4 - M_5 + M_7 \nonumber \\ C_{1,2}= & {} M_3 + M_5 \nonumber \\ C_{2,1}= & {} M_2 + M_4 \nonumber \\ C_{2,2}= & {} M_1 - M_2 + M_3 + M_6 \end{aligned}$$
(6)

The sub-division process can be done recursively until the sub-matrices degenerate into numbers. The complexity of the S-MM algorithm in terms of addition and multiplication operations can be calculated as follows:

$$\begin{aligned} f(n) = 7 f(n-1) + l 4^n \end{aligned}$$
(7)

where f(n) denotes the number of additions performed at each level l of the algorithm.

$$\begin{aligned} g(n) = (7 + O(1))^n \end{aligned}$$
(8)

where g(n)denotes the number of multiplications performed at each level.

Thus, the asymptotic complexity for multiplying matrices with \(N=2^n\) is \(O([7 + O(1)]^n) = O(N^{log_27 + O(1)}) \approx O(N^{2.8074})\). However, this reduction in multiplications has been achieved with some reduction in the numerical stability of the algorithm and an increased need for additional memory in comparison to the canonical MM algorithm of \(O(N^3)\). The arithmetic complexity of the algorithm per iteration is:

$$\begin{aligned} t_m(n) = n^{log_27} \qquad t_a(n) = 6n^{log_27} - 6n^2 \end{aligned}$$
(9)

where \(t_m(n)\) and \(t_a(n)\) respectively denote the number of matrix multiplications and the number of matrix additions.

Winograd [31] proposed an alternative approach to S-MM, which is denoted as W-MM, that reduces the number of matrix additions to 15 which has been proved to be the minimum for any of the rank 7 algorithms. Table 1 shows the comparison of operations in both Strassen and Winograd approaches in each recursion. The following equations describe the ordered steps of the W-MM algorithm:

$$\begin{aligned} \begin{aligned} S_1&= A_{2,1}+A_{2,2} \\ S_2&= S_1-A_{1,1} \\ S_3&= A_{1,1}-A_{2,1} \\ S_4&= A_{1,2}-S_2 \\ S_5&= B_{1,2}-B_{1,1} \\ S_6&= B_{2,2}-S_5 \\ S_7&= B_{2,2}-B_{1,2} \\ S_8&= S_6-B_{2,1} \end{aligned}\qquad \begin{aligned} M_1&= S_2 \times S_6 \\ M_2&= A_{1,1} \times B_{1,1} \\ M_3&= A_{1,2} \times B_{2,1} \\ M_4&= S_3 \times S_7 \\ M_5&= S_1 \times S_5 \\ M_6&= S_4 \times B_{2,2} \\ M_7&= A_{2,2} \times S_8 \\ \end{aligned}\quad \begin{aligned} V_1&= M_1+M_2 \\ V_2&= V_1+M_4 \\ C_{1,1}&= M_2+M_3 \\ C_{1,2}&= V_1+M_5+M_6 \\ C_{2,1}&= V_2-M_7 \\ C_{2,2}&= V_2+M_5 \\ \end{aligned} \end{aligned}$$
(10)

The complexity of W-MM algorithm is as follows:

$$\begin{aligned} t_m(n) = n^{log_27} \qquad t_a(n) = 5 n^{log_27} - 5 n^2 \end{aligned}$$
(11)
Table 1 Number of Multiplications and additions/subtractions of each approach
Full size table

We are interested in a few iterations of S-MM implementation for which odd-sized matrices pose a problem. In this case, dynamic peeling [17] seems to provide an acceptable solution. At each level of recursion, dynamic peeling strips off the extra row and/or column from the input matrices to make them evenly sized. Hence S-MM is applied to even-sized matrices, which represent the majority of the computation, while the vector and scalars are separately computed and patched back into the resulting matrix.

3 Strassen Matrix Multiplication Optimization Method

A previous implementation of S-MM and W-MM algorithms (referred to as H-S-MM) on GPUs [19] uses 10 different user-defined matrix algebra kernels. These kernels are manually optimized for the basic matrix multiplication and matrix addition. H-S-MM has been implemented using some reordering of the matrix operations of the original Strassen to reduce memory allocation. H-S-MM kernels implement the following operations:

$$\begin{aligned} Z= & {} X + Y \nonumber \\ Z= & {} X - Y \nonumber \\ Z= & {} X \times Y \nonumber \\ (Y+, Z+)= & {} W \times X \nonumber \\ (Y+, Z-)= & {} W \times X \nonumber \\ (Y, Z-)= & {} W \times X \nonumber \\ (Y, Z+)= & {} W \times X \nonumber \\ Z= & {} W \times X + Y \nonumber \\ W= & {} U \times V; Y += W; Z += Y; Y += X \nonumber \\ Y= & {} X - V \times W; Z += X \end{aligned}$$
(12)

These implementations were run on NVIDIA C1060 GPU and the performance of H-S-MM was compared with CUBLAS 3.0 SGEMM kernel.

To further enhance the S-MM performance we propose the following optimization steps:

  1. 1.

    A small set of basic algebra operators. A set of three basic functions is used to provide the needed functionality as the basic matrix algebra kernels. These kernels are the matrix multiplication (MM), matrix addition (Madd/sub), and matrix aggregation (Magg). The objective is to reduce the overhead associated with the library invocation. We also define two special matrix algebra kernels for matrix add composition (Maddcomp) and matrix composite addition (Mcompadd) to combine the repetitive addition of different matrices into the same matrix and to reduce overhead of kernel termination and invocation.

  2. 2.

    Embedding of optimized library. Earlier approaches used manually optimized kernels for matrix multiplication and matrix addition. In our approach we use some of the most optimized libraries to date, i.e. the CUBLAS 5.5 which is optimized at the level of the CUDA assembly language. This library is invoked for each MM operation in the S-MM and W-MM algorithms. We used the available static device functions of CUBLAS instead of the external library to reduce the overhead of dynamic linking of library at runtime.

  3. 3.

    Optimizing GPU occupancy. Kernel optimization is based on (1) the design of a thread grip organization that match the structure of the data results, (2) partitioning the grid into thread blocks to provide parallelism, and (3) setting up the thread block size to improve resource utilization. For the above the performance of CUDA programs strongly depends on grid organization, number of blocks, and thread block size. To provide a systematic approach for optimizing the above resource parameters, we developed a matrix-aggregation (Magg) operator as a parametric kernel, and use parameter-tuning technique (Sect. 3.2) to find the best possible number of blocks and number of threads in each block that maximize GPU resource occupancy [1]. This approach allows us to find an optimal tile size for Magg kernel to guarantee the best GPU resource utilization.

3.1 Basic GPU Kernels

In the following we present the details of each algebra operator.

  • Madd/sub: This kernel performs the single-precision matrix-matrix addition/subtraction to compute the intermediate sub matrices for each of the multiplications proposed in Strassen and Winograd algorithms. To achieve the best possible performance, we used cublasSgeam function of CUBLAS 5.5. The function can be used to perform one of the following operations:

    $$\begin{aligned} \begin{aligned} C&= \alpha A + \beta B \qquad&or \\&= \alpha A^T + \beta B \qquad&or \\&= \alpha A + \beta B^T \qquad&or \\&= \alpha A^T + \beta B^T \end{aligned} \end{aligned}$$
    (13)

    where \(\alpha \) and \(\beta \) are scalars, and A, B, and C are matrices stored in column major format with dimensions \(m \times n\). In our implementation, we have used this function for addition or subtraction of submatrices (Z = X + Y or Z = X\(-\)Y) by setting \(\alpha =\beta =1\) or \(\alpha =1, \beta =-1\) and also for copying the submatrices as required for the multiplications mentioned in Sect. 2 by setting \(\alpha =1, \beta =0\).

  • MM: This kernel performs the single precision MM using the cublasSgemm function of CUBLAS 5.5. The function can be used to perform one of the following operations:

    $$\begin{aligned} \begin{aligned} C&= \alpha AB + \beta C \qquad&or \\&= \alpha A^TB + \beta C \qquad&or \\&= \alpha AB^T + \beta C \qquad&or \\&= \alpha A^TB^T + \beta C \end{aligned} \end{aligned}$$
    (14)

    where \(\alpha \) and \(\beta \) are scalars, and A, B, and C are matrices stored in column major format with dimensions A \(m \times k\), B \(k \times n\) and C \(m \times n\). In our implementation, we have used this function with only non-transpose case for seven multiplications \((M_1 - M_7)\) mentioned in Sect. 2 by setting \(\alpha =1, \beta =0\).

  • Magg: This is a set of four similar kernels to perform the final four operations (C11, C12, C21, C22) at the recursion termination mentioned in Sect. 2. All of these kernels load each operand from the global memory to the shared memory and then to the register file by applying the related operation (addition or subtraction). Then the result will be stored back to the global memory. These kernels take two parameters that define the width (TILE_X) and height (TILE_Y) of the tile to be loaded into shared memory. Code Listings 1–4 show the kernel functions for these operations. Based on the restructuring algorithm [1], we have used TILE_X = 32 and TILE_Y = 16 that give the best performance of these kernels using optimal resource utilization. The kernels are invoked with block dimension (TILE_X x TILE_Y) and grid dimension (N/TILE_X x N/TILE_Y) where N is the dimension of submatrices.

    figure a
    figure b
    figure c
    figure d

  • Maddcomp: this kernel is defined to perform the operation \((\alpha X+, \beta Y+) = Z\) that adds matrix Z in one or both X and Y based on the values of \(\alpha \) and \(\beta \). Code Listing 5 shows the kernel function for this operation.

    figure e

  • Mcompadd: this kernel is defined to perform the operation \(Z = (\alpha X+, \beta Y+)\) that adds one or both matrices X and Y in matrix Z based on the values of \(\alpha \) and \(\beta \). Code Listing 6 shows the kernel function for this operation.

    figure f

3.2 Parameters Tuning Algorithm

figure g

Algorithm 1 determines the optimal parameters (TILE_X and TILE_Y) for the generated parametric CUDA kernel. The kernel will be executed with TILE_X x TILE_Y block dimension and N/TILE_X x N/TILE_Y grid dimension.

The algorithm evaluates the generated parametric kernel with various possible combinations of TILE_X and TILE_Y. The pruning of the list of possible parameters is used at three levels to reduce the repeated compilation and execution of the kernel. The three levels of pruning are as follows:

  1. 1.

    Array Block Level: This skips those values of TILE_X and TILE_Y which do not equally distribute the number of resultant elements among all threads (see step 3 and 7).

  2. 2.

    Kernel Block Level: This skips those values of TILE_X and TILE_Y which do not distributed the number of resultant elements among all kernel blocks (see step 11).

  3. 3.

    Active Block Level: This skips those combinations of parameters which require more than the available resources such as number of registers, shared memory and number of threads per SM (see step 32).

The algorithm takes kernel source file, resultant matrix dimension (N) and GPU Compute Capability (CC) for the target GPU device. It first loads the parameters (see Algorithm 1) for the given compute capability such as Register Allocation Unit Size, Threads Per Warp, Warps Per SM, Maximum Shared Memory Per Block, Register File Size, etc. It then loops over all possible combinations of TILE_X and TILE_Y limiting to the range given by the user with appropriate pruning (Array Block Level and Kernel Block Level) of the parameters as explained above. For each combination, it compiles the kernel with ptx information to determine the required number of Registers Per Thread (RPT) and Shared Memory (ShM) per block (see step 14). Then, it calculates and stores the restricted number of Active Blocks by Warp (ABW), Active Blocks by Shared Memory (ABShM), and Active Blocks by Registers (ABR) into a structured list (CompleteParamsList) (see steps 15–20). Then, it performs parameters pruning at Active Block Level and generates a list of possible optimal parameters (CandidateParamsList) (see steps 23–27). Finally, it executes the kernel for each combination of parameters in CandidateParamsList and determines the final optimal parameters (OptimalParams) that give the minimum execution time (see steps 29–36).

3.3 Algorithm Implementations

3.3.1 Strassen Adaptation (S-MM)

Algorithm 2 shows the pseudo code of S-MM implementation. Following the Strassen block partitioning, the function starts by calculating the dimension of current matrix blocks that is dividing each dimension by 2 (step 1). The current implementation works only for square matrices. Then, in step 2, it performs global memory allocations to store the intermediate results of seven multiplications (m1–m7) and also for their operands that result from some addition or copy operations on matrix blocks (m1a, m1b, m2a, m2b, m3a, m3b, m4a, m4b, m5a, m5b, m6a, m6b, m7a, m7b). Each of these sub-matrices are of the dimension subWidth x subWidth. These operands will be calculated in step 3 and 4. In Step 5–7, the threshold of current matrix dimension (BLOCK_THRESHOLD) is checked to decide whether to continue with recursion or terminate. After recursion termination, synchronization among all threads is required to avoid data hazards (step 16) as it may be possible that elements of matrices \(m_1\) to \(m_7\) be read by some threads which may be calculated by some other threads in different thread blocks. In step 17, the resultant matrix C is computed and the global memory resources is de-allocated in step 18.

figure h

3.3.2 Strassen with Reordering Steps (R-S-MM)

The original implementation of Strassen suffers from memory usage, and it is not practical due to the size of memory it needs for large matrices. We implemented a reordering Strassen algorithm that reduces the memory allocations at each level of recursion [19]. In each level of recursion only two matrices (T1,T2) of size (N/2L) are needed as intermediate sub-matrices, where L is the level of recursion and N is dimension of the matrix. Algorithm 3 shows the pseudo code of R-S-MM.

figure i

3.3.3 Winograd Adaptation (W-MM)

Algorithm 4 shows the pseudo code of W-MM. The implementation of W-MM is similar to that described for S-MM with the following exceptions:

  • In step 2, it allocates only 15 submatrices (\(m_1\) to \(m_7\) and \(S_1\) to \(S_8\)) instead of 21 submatrices.

  • In step 3, it performs only 8 addition/subtraction operations instead of 14 addition/subtraction/copying operations.

figure j

3.4 Tradeoffs Between Time-Bound and Storage-Bound Implementations

The proposed S-MM algorithm consists of traversing the recursion tree sequentially using the depth-first scheme DFS and executing each step using all available memory and processing cores. S-MM computes a linear combination of pairwise MM and combines intermediate matrices as a linear combination to produce the final sub-matrices. S-MM is based on a traversal of the recursion tree where all the cores work in parallel on assembling each of the seven sub-matrices, which are computed in sequence. S-MM repeatedly applies the DFS steps, which reduces the required storage of intermediate results by assembling one single matrix at a time. DFS requires allocation of only one sub-matrix because each of the intermediate results is computed in sequence. Thus there is no redistribution of work and all cores participate in computing each resulting matrix. Each core computes the local additions and subtractions associated with the intermediate sub-matrices. In contrast, in the BFS the cores work on different subsets of matrices in parallel, which requires extra memory but with reduced data motion among the cores, while DFS leads to large data motion among the cores to gather the resulting sub-matrices [4, 21].

A time-bound (TB) implementation aims at minimizing execution time by reducing the recursive function calls at base level (1-Level) of the algorithm. In addition it avoids any unnecessary stack operations that might increase the execution time and the required storage. TB assumes boundless storage. Thus TB can be used for S-MM and W-MM to highlight the implementation that produces the least execution time. Examples of TB implementations are S-MM and W-MM which are evaluated in the next section.

The storage-bound (SB) implementation aims at minimizing the used storage by reordering the original steps and using some of the resultant matrices to accumulate the intermediate results of multiplication operations and the final aggregation operations. However, this approach requires additional overhead of recursive function calls among other execution steps such as additions and subtractions. This option is useful if one may tolerate an increase in execution time provided that the minimum storage is being used which allows an implementation to use a larger problem size. Example of SB implementation is the R-S-MM.

At each computation level, S-MM (W-MM) repeatedly performs all the 18 (15) matrix additions before carrying out one in-depth recursion until reaching the deepest recursion level which is defined by a threshold on the smallest operable matrix size. When recursion pops up, S-MM (W-MM) performs one MM. Recursion pops up until reaching the original matrix, where it proceeds on another depth-first path. The process is repeated until assembling the resulting matrix. In contrast, R-S-MM repeatedly performs partial matrix additions in preparation of the single MM before carrying out one in-depth recursion. This process of partial computing and recursion repeats until reaching the deepest recursion level. When recursion pops up, R-S-MM completes partial work for the matrix multiplication as well as all needed matrix additions. The pop up process continues until returning to the original matrix at the top level. The process is re-iterated from the top level in a similar manner to S-MM.

The performance of each of the implementations depends on the number of additions/subtractions, multiplications and function recursive calls. Table 2 shows the number of additions/subtractions, multiplications, function recursive calls and additional memory allocations of each of the implementations based on the matrix dimension (N) and the level of recursion (k).

W-MM requires less number of arithmetic operations and recursive calls than S-MM and hence it has better performance. S-MM and R-S-MM have an equal number of arithmetic operations. R-S-MM has additional overheads of stack operations due to the additional recursive calls compared the S-MM.

Table 2 Algorithm complexity analysis
Full size table

4 An Overview of GPU and MIC

4.1 GPU and CUDA

GPU is organized into an array of highly threaded Streaming Multiprocessors (SMs). Each SM has a number of Streaming Processors (SPs) that share control logic and instruction cache. Each GPU currently comes with up to 4.8 GB of graphics double data rate (GDDR) DRAM referred to as global memory (GM) that is visible to all threads in all blocks. Each SM has a read/write shared memory (ShM) which is visible to all threads running within SM. ShM is much faster than GM but smaller in size.

A CUDA program is a unified source code encompassing both the host and the device code. The device code is written using ANSI C extended with keywords for labeling data-parallel functions, called kernels, and their associated data structures [15]. Each kernel initiates a set of blocks defined by the programmer as grid dimension. Another parameter is the number of threads to be executed within each block while invoking the device kernel function. The block scheduler dynamically schedules each thread block to one SM based on the availability of resources. Each block is broken down into subsets of 32 thread forming warps. Warps execute in SIMD mode. The warp is the unit of thread scheduling in SMs. Each warp consists of 32 threads of consecutive thread ids. An SM can handle at most 16 blocks at a time. Also, the possible number of concurrent blocks per SM depends on the number of warps per block, number of registers per block, and the shared memory usage per block.

Each SM schedules one warp at a time with zero overhead warp scheduling. In the case of higher dimensional kernels, warps are retrieved from blocks according to the row major numbering. As warps execute in SIMD fashion, if there is a high latency exception such as loading or storing data with GM then the warp is suspended and its context preserved. A DMA operation is initiated by the SM whenever it finds one or more threads within a running warp that are subject to long latency memory transfer. In this case, SM schedules another ready warp with zero-overhead context switching [15].

4.2 Xeon Phi and Programming Model

Intel Many Integrated Core (MIC) Architecture is based on a 64-core cache-coherent SMP, where each core features hybrid 4-way hyperthreading with wide 512-bit vectorization unit (VPU) to exploit data parallelism [12, 13, 25]. All coherence notifications, control, address, and data are transferred on a set of 10 fast ring networks. Each core has an in-order dual-issue unit with two level L1 and L2 caches. Each core can access all other L2 caches via the ring network which makes a collective L2 cache size with up to 32MB. VPU has 32 512-bit SIMD registers. VPU supports Fused Multiply-Add (FMA) operations. The sustainable peak performance using Stream Triad benchmark2 is about 20 GFLOPS. Eight memory controllers support up to 16 GDDR5, which deliver up to 5.5 GT/s.

A host CPU interfaced to a MIC operates in three modes: (1) the offload mode in which the host transfers part of its computing code to MIC, (2) the symmetric mode uses MPI to communicate with other MICs, and (3) the native mode in which the application is locally run on MIC. There are three ways for thread assignments. First, scattering consists of evenly distributing the threads across all cores. Second, in compact mode consecutive threads are distributed over a minimal number of cores with four treads per core. Third, in balanced mode threads are scattered across all cores such that successive threads are assigned to the same core. In our work we used OpenMp programming paradigm which uses a fork-join execution model.

Because MIC has 5.6 GB of memory, the largest matrix that can be handled by S-MM is 3072. The R-S-MM is based on re-using some storages that saves the memory allocation and allows the use of larger matrices with up to 10240. In this work we focus on using R-S-MM for the above reasons. The R-S-MM algorithm for MIC is denoted as Str_mkl with the invocation of the MKL function CBLAS_DGEMM for single precision.

The number of recursion levels L depends on the threshold value of the smallest matrix size the algorithm can handle. For each recursion level, the new matrix size and the scope of sub matrices are passed as illustrated on Table 3.

Table 3 Submatrix indices
Full size table

5 Performance Evaluation

In this section we evaluate the performance of proposed algorithm implementations S-MM, R-S-MM, and W-MM on an NVIDIA GPU and an Intel Xeon Phi. The GPU used is a Kepler K20c with 4.8 GB of GM, 48 KB of ShM, and 13 SM. The Xeon Phi accelerator is 7110 with 60 cores and 5.6 GB of main memory. Each core is running at 1.3 GHz with 32KB L1 cache and 512KB L2 cache. In the following sub-sections we present the performance evaluation of proposed approaches.

5.1 Evaluation on GPU

Proposed algorithms S-MM, R-S-MM, and W-MM were implemented using the optimized libraries CUBLAS SGEMM (version 5.5) and NVIDIA SDK MM (version 5.5). Ideally, the above algorithms are run with different BLOCK_ THRESHOLD (BT) at which the recursions break and the high-performance MM (CUBLAS or MKL) is applied. However, to ease the interpretation of the results we refer to the recursion level for each run.

Fig. 1
figure 1

Speedup of our implementations with 1-Level Recursion over CUBLAS Sgemm

Full size image

Figure 1 shows the speedup achieved by S-MM, R-S-MM, and W-MM over native CUBLAS SGEMM versus the matrix size using one recursion level. Figure 2 presents a comparison of the execution times of S-MM, R-S-MM, W-MM, and CUBLAS SGEMM. Note that W-MM has the shortest execution time for the studied range of matrix size. CUBLAS is faster than S-MM only for matrices where \(N \le 3072\) (for S-MM) and \(N \le 2048\) (for W-MM). For matrices with \(N > 2048\), W-MM becomes up to twice as fast as CUBLAS. S-MM becomes also faster (speedup of 1 to 1.9) than CUBLAS for \(N > 3072\). On the other hand, R-S-MM only outperforms CUBLAS when \(N > 6144\) due to reordering which incurs some overhead in copying data. For \(N \ge 2048\), the three implementations satisfy the following condition \(T_{W-MM} \le T_{S-MM} \le T_{R-S-MM}\), where \(T_{X}\) is the execution time of implementation X. The proposed algorithms scale well with increase in the problem size of up to the largest size that the above GPU can handle. R-S-MM was ranked last because of it’s SB implementation, which is due to additional overhead of recursive function calls, as compared to S-MM and W-MM which are based on TB implementation (see Sect. 3.4).

Fig. 2
figure 2

Comparison of our implementations with 1-Level Recursion and CUBLAS

Full size image
Fig. 3
figure 3

Performance FLOPs for our implementations with 1-Level Recursion and CUBLAS

Full size image

Figure 3 shows the performance in FLOPS of proposed Strassen/Winograd implementations with CuBLAS versus the matrix size. Sorting the above implementations in descending order of best achieved performance gives W-MM, S-MM, R-S-MM, and CuBLAS with best score 2.35 TFLOPS, 1.95 TFLOPS, 1.45 TFLOPS, and 1.35 TFLOPS, respectively. The above performance scores represent 67, 55, 41, and 38 % of peak performance for Kepler K20c GPU (3.52 TFLOPS). These results confirm the effectiveness of proposed kernel optimizations because significant fraction of peak GPU performance is achieved.

Figure 4 shows the speedup achieved by S-MM, R-S-MM, W-MM, and CUBLAS SGEMM over the NVIDIA SDK library. Notice that S-MM, W-MM, CUBLAS, and R-S-MM are 80\(\times \), 60\(\times \), 41\(\times \), and 38\(\times \) faster than the NVIDIA SDK library when \(N \ge 4096\), respectively. Additionally, by inspecting Figs. 1 and 4 we note that the performance of our proposed implementations scales much better than CUBLAS versus an increase in array size.

Fig. 4
figure 4

Comparing speedup over NVIDIA SDK by CUBLAS and our implementations with 1-Level Recursion

Full size image

However, as we increase the level of recursion the execution time is also increased due to the overhead of additional operations in both Strassen and Winograd implementations. The reason is that the reduction in one matrix multiplication using Strassen and Winograd is not large enough to offset the overhead of the matrix additions and the stack overhead due to recursive invocations when two recursion levels or more are executed. Also note that the high-performance MM CUBLAS_Sgemm is highly optimized at a very low level of programming.

Figure 5 shows the percentage increase of the execution time when two recursion levels are used over one recursion level implementations. The results show that our implementations are more profitable and scalable with additional levels of recursion when there is an increase in matrix size. Also, W-MM shows a zero balance between matrix addition overhead and the saving in the one matrix multiplication. Unfortunately we are bound by N = 10240 due to limitations of device memory on the Kepler K20c GPU.

Fig. 5
figure 5

Percentage increase in execution time with 2nd level of recursion

Full size image

5.2 Evaluation on Xeon Phi

In this section we compare the performance of proposed Strassen MM algorithm to that of MKL on MIC for 2D arrays. As stated before, the reordering algorithm Str_mkl (R-S-MM) has been implemented using C++ with OpenMp on MIC. Recall that Str_mkl is similar to R-S-MM with the difference that it invokes the MKL high-performance matrix multiplication function CBLAS_DGEMM. On MIC, the memory allocation (malloc) for two dimensional array does not allocate contiguous memory when 2D indexing is used. This causes some performance degradation due to address translation overhead for large array sizes. For this, we used explicit 1D array indexing instead of the standard 2D array indexing to reduce the above mentioned overheads. All the experiments were run by disabling the factorization unit and using the O2 level of compiler optimization. Also, the thread affinity was set to “compact” to enhance the data locality among the threads. In the case of compact affinity, a minimum number of cores is used for assigning four consecutive threads to each core. In all the experiments, each core is running 4 OpenMp threads which bind to the hardware threads depending on the OS scheduling criteria. Finally, it is noticed that OpenMp incurs a relatively small overhead for scheduling, managing, and synchronizing threads under Linux.

To assess the Str_mkl, we ran the experiments with different matrix sizes and different numbers of threads or cores. We experience the Str_mkl algorithm with the first five level of recursions and compare execution time to that achieved by directly invoking MKL for standard MM. Figures 6, 7, 8, 9 show the execution time of Str_mkl, for 1–5 recursion levels, and MKL for 8, 16, 32, and 60 MIC cores, respectively. In these Figures, the execution time of Str-mkl is shown with different recursion levels versus MKL CBLAS_DGEMM execution time.

For one recursion level, Str_mkl is faster than MKL by a smaller factor which is between 4 and 8 % for all the experimented number of cores. The reason is that the MIC memory is not fully utilized to take advantage of using deeper recursion levels with Str_mkl. For two recursion levels, Str_mkl is faster than MKL by 14–26 % when the array size \(N \ge 1024\) for all the experimented number of cores. In this case, there is a matching between the MIC available memory and the storage of intermediate arrays required by the Str_mkl depth-first recursive kernels. Vtune run-time profiler was used to validate the efficient use of the memory in the case of one or two recursion levels. The number of L1 and L2 misses is dramatically lower than that noticed in the case of deeper recursion levels. For three recursion levels, Str_mkl achieves shorter execution times only for matrix sizes satisfying N\(>=\)16000 and for all number of cores. Specifically, Str_mkl is 6–12 % faster than MKL. For four or more recursion levels the overhead of matrix additions seem to offset the benefit of saving on matrix multiplication, where MKL times are shorter than those of proposed Str_mkl for all problem sizes and all the experimented number of cores.

Fig. 6
figure 6

Execution time of Strassen with MKL using 8 cores

Full size image
Fig. 7
figure 7

Execution time of Strassen with MKL using 16 cores

Full size image
Fig. 8
figure 8

Execution time of Strassen with MKL using 32 cores

Full size image
Fig. 9
figure 9

Execution time of Strassen with MKL using 60 cores

Full size image
Fig. 10
figure 10

Execution time of cublas_dgemm MKL library function

Full size image

Proposed algorithm Str-mkl is based on a traversal of the recursion tree where all the MIC cores work in parallel on computing each of the sub-matrices, which are processed one after the other in sequence. DFS reduces the required storage of intermediate results by assembling one sub-matrix at a time because it allocates storage for each of the resulting four sub-matrices. Thus, DFS leads to aggregate data motion among all the cores to gather the resulting matrix. In MIC the inter-core communication is carried out implicitly by the coherence protocol, which is supported by eight fast ring networks. The above mechanism seems to be efficiently aggregating the core sub-matrices. With four threads assigned to each core, a thread which is exposed to a high latency exception (like a remote data fetching) is temporarily suspended and another thread is started using a fast context switching. For the first two recursion of Str-mkl, it is clear that the above MIC latency hiding technique seems to be profitable in trading one matrix multiplication at the cost of 18 extra matrix additions. However, with three or more recursion levels str-mkl is no longer profitable as compared to MKL due to the following reasons:

  1. 1.

    The reduction in one matrix multiplication seems not sufficient to offset the overhead of additional smaller matrix additions,

  2. 2.

    The transfer of large data (coherence protocol) involved when aggregating the intermediate arrays and assembling the current working matrix.

  3. 3.

    The increase in time of the CBLAS_DGEMM library when the size of the matrix is smaller than 2048 especially when using a large number of cores. Figure 10 shows how the CBLAS_DGEMM library performs with matrices smaller than 2048 when run on larger number of threads.

  4. 4.

    The increase in time due to the stack operation overhead that is caused by the recursive Strassen invocations and the less efficient cache utilization when DFS works with small arrays.

We have also run the same experiments on Intel Xeon E5 CPU with 16 cores and found similar trends of execution time with respect to the level of recursion in the Strassen kernel execution. Figure 11 shows the execution time of Strassen implementation and MKL CBLAS_DGEMM kernel library. Like Xeon Phi results, Strassen implementation with up to 2 levels of recursion outperforms MKL CBLAS_DGEMM kernel.

Fig. 11
figure 11

Execution time of Strassen with MKL using 16 cores on Xeon E5 CPU

Full size image

Figure 12 shows the performance in FLOPS of proposed Str-mkl and MKL implementations for fixed matrix size of N= 16384 versus the number of MIC cores. Sorting the above implementations in descending order of best achieved performance gives MKL, str-MM(N/4), str-MM(N/2), str-mkl(N/8), str-mkl(N/16) with best FLOPS score of 0.5, 0.45, 0.42, 0.35, and 0.2 TFLOPS respectively. The above performance scores represent 21, 19, 17.5, 15, and 8.5 % of peak performance for Xeon Phi 7110 (2.4 TFLOPS). Here also, these results confirm the effectiveness of proposed code optimization because significant fraction of peak MIC performance is achieved.

Fig. 12
figure 12

Flops comparison of Strassen with MKL under different cores

Full size image

5.3 Accuracy of Strassen Implementation

It is well known that the hybrid MM algorithms like Strassen algorithm have weak numerical properties compared to the canonical algorithm or the high-performance MM like MKL. We assessed the numerical accuracy of three MM implementations: str-mkl with the first four recursion levels, MKL and the canonical algorithm.

We used the single precision test matrix defined in [14]. The test consists of initializing two operand matrices of arbitrary size to some predefined values so that their product is the identity matrix. Table 4 shows the maximum absolute differences between the elements of the product matrix as computed by each of the above implementations and the exact product. For each of the above implementations, the test was run using 60 cores with 240 threads.

MKL and the canonical algorithm have comparable accuracy to the advantage of MKL. The str-mkl errors are substantially larger than that produced by MKL. Specifically, MKL is at least one order of magnitude more accurate than str-mkl. Referring to str-mkl, the errors increase up to one order of magnitude when recursion are increased from one to four levels. In other word, the errors are about three times for each additional recursion level. Also the errors increase with the array size. Although, str-mkl with two recursions achieves between 14 and 25% speedup over MKL, but the errors are 7 to 27 times compared to those achieved by MKL for the studied range of matrix sizes.

Table 4 Maximum absolute errors of MM implementations
Full size table

6 Conclusion

Hybrid matrix multiplication using Strassen MM algorithm has \(O(N^{2.807})\) time complexity instead of \(O(N^3)\) for the canonical approach. The depth first traversal is used for the hybrid MM method using Strassen and Winograd algorithms. In this case, all cores work in parallel on computing each of the \(N \times N\) sub-matrices, which are computed in sequence. Although this approach reduces the needed storage, it requires substantial data motion to gather and aggregate the results. The proposed Strassen and Winograd implementations are based on three optimizations: (1) using a small set of basic algebra functions to reduce overhead, (2) invoking efficient library (CUBLAS 5.5) for basic functions, and (3) using parameter-tuning of parametric kernel to improve GPU resource occupancy. Evaluation of S-MM and W-MM is carried out on GPU and MIC. For GPUs, W-MM and S-MM with one recursion level are up to twice as fast as CUBLAS 5.5 Library for arrays satisfying \(N > 2048\) and \(N > 3072\), respectively. Similar trends are observed for S-MM with reordering, which is used to save storage. Compared to NVIDIA SDK library, S-MM and W-MM achieved a speedup between 20\(\times \) and 80\(\times \) for the above array sizes. For MIC, two-recursion S-MM with reordering outperforms MKL library by 14–26 % for \(N >= 1024\). Similar encouraging results are obtained for 16-core Xeon-E5 server with enhanced computation scalability. The best achieved performance FLOPS are 2.35 TFLOPS for W-MM (67 % of peak) and 1.95 TFLOPS (55 % of peak) for S-MM on GPU and 0.5 TFLOPS on MIC (21 % of peak). This shows the profitability of proposed S-MM implementation with limited recursion levels as a hybrid MM algorithm. We conclude that proposed S-MM and W-MM implementations with a few recursion levels can be used to further optimize the performance of basic algebra libraries. The number of recursion levels can be increased for very large matrices.