1 Introduction

After a period of time, if a solid material is placed in a controlled relative humidity environment, such material will achieve the equilibrium condition with the environment. The equilibrium relationship between the moisture content of the solid material (MD) and the relative humidity (RH) at the equilibrium state is known as sorption isotherm.

Sorption isotherms are important for manufactures of foodstuffs, pharmaceutical, building, agriculture products, among others, because they are useful for their handling, storage, preservation, processing and transportation.

In the field of foodstuffs, the definition of water activity is preferred because it allows their classification according to the water content available to determine its microbiology stability. In this paper we will use the term equilibrium relative humidity instead of water activity, because it is considered a more suitable concept for a wider range of materials.

The sorption process includes absorption, adsorption and desorption. In the absorption the water molecules are incorporated to the material matrix, while in adsorption water molecules are deposited only on the material’s surface; desorption is related to the evaporation or releasing of water from the material. In the interaction between water vapor and the solid material, the vapor is added to the matrix of the solid material by electrostatic forces mainly by absorption, giving rise to the formation of a composite by a chemical reaction.

Given the complexity of the sorption process and the lack of a general theory that properly describes this process for all materials, a possible option is to find the corresponding sorption isotherm for each set of materials. In fact, many of sorption isotherms are found by empirical realizations [1,2,3].

To obtain the mathematical models for the sorption isotherms, some factors are involved, such as the chemical composition, the physical–chemical state, the physical structure, temperature effects, pressure effects [1]. For such reason the sorption models can be complex and the uncertainty estimation under the framework of the Guide to the Expression of Uncertainty in Measurement (GUM) [4] is not a proper method for most of the developed models (theoretical-, semi-theoretical- and empirical-based) which are nonlinear [1,2,3].

Although there exist a vast number of papers related to the sorption isotherms, most of them only deal with the fitting parameters and do not give information to estimate the uncertainty of MD when the RH is known, and vice versa, that is very important for the conditioning of samples used in the calibration of moisture meters and for the preparation of reference materials with known moisture content. In addition, given the nonlinearity of sorption models, it is necessary to use a suitable method to carry out the uncertainty estimation properly.

For the correct application of the GUM, one of the main requirements is that the measurand’s model is linear, but most of the sorption models are not.

The framework of the GUM can be applied to nonlinear models; however, in many cases the uncertainty estimation is complex due to the calculation of derivatives involved. Thus, it is recommended to use another method that can be applied to nonlinear models and whose sensitivity coefficients (derivatives of the model) are less complicated; such option is the Monte Carlo method (MC).

In this paper, the moisture content uncertainty estimation of a solid material exposed at known relative humidity of three sorption isotherm models is analyzed. The uncertainty analysis is performed under the GUM framework and also with the MC method.

The statistical shape and sensitivity coefficients, as a measure of nonlinear models, are discussed as well.

2 Sorption Isotherms

The Henderson (Eq. 1), Chung-Pfost (Eq. 2) and Oswin (Eq. 3) models are widely used in the foods field [5]; in particular, they are important during handling, storage and processing of cereal grains. In this paper is carried out the moisture content (MD) uncertainty estimation of the above-mentioned models applied to wheat samples placed at a known RH atmosphere.

2.1 Modified Henderson’s Model

It is a semi-theoretical model developed in 1952 for biological materials, taking the adsorption theory of Gibbs [6] as a basis. In Eq. 1 the modified Henderson’s model is given, which allows to calculate the RH at equilibrium, as a function of the dry basis moisture content (MD) and the sample’s temperature (t).

$$ RH = 1 - \exp \left[ { - A(t + C) \cdot (M_{D} )^{B} } \right] $$
(1)

For wheat, the uncertainty of fitting using this model is uRH = 3.8 % of RH [7].

2.2 Modified Chung-Pfost’s Model

It is a theoretical model developed in 1967 which relates the surface free energy changes to the moisture content [6]. The modified Chung-Pfost’s model is given in Eq. 2.

$$ RH = \exp \left[ { - \frac{A}{t + C}\exp ( - B \cdot M_{D} )} \right] $$
(2)

For wheat, the uncertainty of fitting using this model is uRH = 0.93 % of RH [7].

2.3 Modified Oswin’s Model

It is an empirical model developed in 1946. At the beginning this model included two constants, but later it was modified to correct temperature effects as given in Eq. 3 [2, 6].

$$ RH = \left[ {\left( {\frac{A + B \cdot t}{{M_{D} }}} \right)^{c} + 1} \right]^{ - 1} $$
(3)

For wheat, the uncertainty of fitting using this model is uRH = 0.83 % of RH [7].

In Eqs. 1, 2 and 3, A, B and C are the calibration constants that depend on the type of grain (see Table 1) [7].

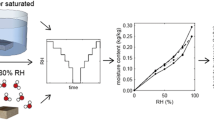
Table 1 Calibration constants of sorption isotherm models for samples of hard red wheat [6]
Full size table

Figure 1 shows the sorption isotherms described by Eqs. 1, 2 and 3 for samples of hard red wheat at a temperature of 20 °C.

Fig. 1
figure 1

Sorption isotherm for hard red wheat

Full size image

As shown in Fig. 1, the three models are approximately linear over the range from 10 % to 80 % RH; however, at higher values of RH the isotherms deviate from the linearity, with the Oswin’s model showing the largest deviations. The lack of linearity at high relative humidity could be due to the elevated pressure of water vapor in that range.

2.4 Uncertainty Estimation

Some methods used for the uncertainty estimation of a measurement are as follows: the method of the Taylor’s series expansion described in the GUM [4], the MC simulation method (non-deterministic analysis), the Bayesian inference method and the interval analysis method [8]. The choice depends on the available information about the influence quantities and the mathematical model of the measurand.

Most used methods are the GUM, the Bayesian inference and the MC. The GUM method is used for linear models and allows the Taylor’s series expansion in terms of higher order when the model deviates from linearity. In addition, the GUM method requires that the uncertainty values of the influence quantities must be of the same order of magnitude. In particular, those having a probability distribution different from a Gaussian or t-Student must be smaller than the others and in this way, the central limit theorem applies that generates a normal distribution.

The Bayesian inference is a method of statistical analysis that allows to derive the probability density function of the measurand, taking into account the level of unknowledge of the input quantities, under the assumption that they are random variables; this method is applicable to linear and nonlinear models and does not have limitations with the uncertainty values, neither with the probability density functions of them.

The MC is a numerical method, which can also be applied to linear and nonlinear models if the uncertainty of influence quantities and the probability density function are known; in this method, the probability distribution of the measurement depends on the available information on input quantities. The application of Monte Carlo method is described in the framework of GUM Supplement 1 [9]. This method can be straightforwardly implemented in commercial datasheets (e.g., Excel). It also has the advantage of not requiring the calculation of sensitivity coefficients, although if needed, it is possible to calculate them.

In this paper, the GUM framework and Monte Carlo method were used for the uncertainty estimation of moisture content (MD) given the RH of three sorption isotherms.

2.5 GUM Framework

The law of propagation of uncertainty for the moisture content (dry basis), given a known relative humidity and the temperature, is given by Eq. 4.

$$\begin{aligned} uM_{D} = \sqrt {\left( {\frac{{\partial M_{D} }}{\partial RH}} \right)^{2} u^{2} RH + \left( {\frac{{\partial M_{D} }}{\partial t}} \right)^{2} u^{2} t + u_{{{\text{fit}}(M_{D} )}}^{2} + 2\left( {\frac{{\partial M_{D} }}{\partial RH}} \right)\left( {\frac{{\partial M_{D} }}{\partial t}} \right) \cdot r(RH,t)u(RH)u(t)}\\ \end{aligned}$$
(4)

where u(RH) is the uncertainty of the relative humidity measurement, u(t) is the uncertainty of the temperature measurement, ufit(MD) is the uncertainty of the fitting of model, r(RH, t) is the correlation coefficient between the relative humidity and the temperature, and ∂MD/∂RH, ∂MD/∂t are the sensitivity coefficients with respect to the temperature and the relative humidity, respectively.

Equation 4 includes the uncertainty of equation fitting, which takes into account the uncertainty of the parameters A, B and C involved in Eqs. 1–3.

The sensitivity coefficients of the Henderson’s modified model (Eq. 1) are given by

$$ \frac{{\partial M_{D} }}{\partial RH} = \frac{1}{AB(t + C)(1 - RH)}\left( { - \frac{{{\text{In}}(1 - RH)}}{A(t + C)}} \right)^{{\frac{1 - B}{B}}} $$
(5)
$$ \frac{{\partial M_{D} }}{\partial t} = \frac{{{\text{In}}(1 - RH)}}{AB(t + C)}\left( { - \frac{{{\text{In}}(1 - RH)}}{A(t + C)}} \right)^{{\frac{1 - B}{B}}} $$
(6)

The sensitivity coefficients for the Chung-Pfost’s modified model (Eq. 2) are given by

$$ \frac{{\partial M_{D} }}{\partial RH} = \frac{1}{{B(RH) \cdot {\text{In}}\;RH}} $$
(7)
$$ \frac{{\partial M_{D} }}{\partial t} = \frac{1}{B(t + C)} $$
(8)

The sensitivity coefficients for the Oswin’s modified model (Eq. 3) are given by

$$ \frac{{\partial M_{D} }}{\partial RH} = \frac{A + Bt}{C} \cdot \left( { - \frac{RH}{1 - RH}} \right)^{{\frac{1 - C}{C}}} $$
(9)
$$ \frac{{\partial M_{D} }}{\partial t} = B \cdot \left( {\frac{RH}{1 - RH}} \right)^{1/C} $$
(10)

In Figs. 2 and 3 are shown the sensitivity coefficients of ∂MD/∂RH and ∂MD/∂t for the analyzed models.

Fig. 2
figure 2

Sensitivity coefficients ∂MD/∂RH of sorption models

Full size image
Fig. 3
figure 3

Sensitivity coefficients ∂MD/∂RH of sorption models

Full size image

In Fig. 2 is observed clearly that the sorption isotherms described above are not linear at relative humidity of 80 % RH. In Fig. 3, the sensitivity coefficients (∂MD/∂t) are approximately linear.

2.6 Monte Carlo Method

For this analysis it is assumed that the input quantities have normal probability distributions. With this assumption, the input quantities (ξ) in the sorption model are described by

$$ \zeta_{i} = x_{j} + u_{j} z_{i} $$

where uj is input quantity uncertainty, xj, and zi the ith are pseudo random numbers. The pseudo random numbers set shall satisfy the condition N(0, 1); i.e., they must follow a normal probability distribution with zero mean and variance equal to one.

Although the pseudo random numbers can be generated with several algorithms [10, 11], in this paper these numbers were generated with a commercial software (MATLAB) and the uncertainty estimation calculations were performed with commercial data spreadsheets (Excel). The application of Excel for the MC method can be found in [11] with satisfactory results.

3 Results

Tables 2, 3 and 4 show the results for the uncertainty estimation with both methods (GUM and MC) and the skewness and kurtosis coefficients as well.

Table 2 Uncertainty estimation for the modified model of Henderson
Full size table
Table 3 Uncertainty estimation of the modified model of Chung-Pfost
Full size table
Table 4 Uncertainty estimation of the modified model of Oswin
Full size table

According to Tables 2, 3 and 4, the results of the GUM framework and MC method are in good agreement in a wide range of relative humidity. However, some differences are observed at 95 % RH. In particular, the Oswin’s model shows significant differences, due to the nonlinearity of this model.

To verify such statement and considering that it is possible to relate the skewness and kurtosis coefficients to the lack of linearity [12], the corresponding coefficients were estimated, and their results are given in the same tables.

The obtained results show that the lack of linearity in the isotherm models has an influence on the uncertainty. Therefore, it is more reliable to use the MC method in those models that deviate from linearity. This statement was confirmed with the calculation of the statistical shape coefficients (kurtosis and skewness). Figure 4 shows a frequency histogram where a non-symmetric distribution is observed, with a high skewness, which is representative of a nonlinear measurand.

Fig. 4
figure 4

Frequency histogram for a nonlinear model of measurand

Full size image

4 Discussion

4.1 Evaluation of Sensitivity Coefficients

Under the GUM framework, the sensitivity coefficients of a given measurement model are very important to estimate the uncertainty, because they allow to convert the units of the input quantities into units of the measurand. In addition, these give information about the rate of change of measurand with respect to the input quantities.

With the traditional GUM method, the evaluation of sensitivity coefficients can be challenging when the model is complex, but simple with the MC method because the sensitivity coefficients are obtained by making changes in the quantity of interest and keeping constant the other [10]. The quotient between the standard deviations of the measurand and the quantity of interest allows the calculation of the sensitivity coefficient.

Then, the sensitivity coefficients are calculated by using Eq. 11 with the results given in Table 5.

$$ \frac{dM}{d\xi } \approx \frac{{\sigma_{Mx} (\xi )}}{{\sigma (\xi_{x} )}} $$
(11)

where M(ξ1, ξ2,…, ξx,…,ξn) is the function which relates the measurand to the input quantities, σM(ξx) is the standard deviation of M, keeping constant all input quantities except one (ξx), and σ(ξx) is the standard deviation of ξx

Table 5 Sensitivity coefficients of Eqs. 1, 2 and 3
Full size table

As shown in Table 5, the sensitivity coefficients have similar values in almost all cases; however, it can be found some differences over the range of high relative humidity (RH > 80 %), i.e., in the range where the models are not linear.

5 Conclusions

The uncertainty estimation of three sorption models was performed, evaluated for hard red wheat under the GUM framework and the MC method.

Both methods give good agreement over the range where the mathematical model is linear (RH≤ 80 %), while there exist significant differences at higher values of relative humidity, in particular for the Oswin’s model where differences of about 0.2 % of moisture content were found.

In order to verify that the differences are due to the model’s nonlinearity, the skewness and kurtosis coefficients were estimated, finding that these coefficients have high values in the high nonlinearity range. The statement was confirmed with a frequency histogram.

The sensitivity coefficients were also estimated by analytical and numerical methods. In most of the cases, the results were similar but showing again some differences at high relative humidity values, due to the model’s nonlinearity.