Second Law Analysis in Mixed Convection Through an Inclined Porous Channel

Abstract

The paper provides a numerical investigation of the entropy generation analysis due to mixed convection with viscous dissipation effect of a laminar viscous and incompressible fluid, flowing in an inclined channel filled with a saturated porous medium. The Darcy–Brinkman model is employed. The Navier–Stokes and energy equations are solved by classic Boussinesq incompressible approximation. A special attention is given to the study of the influence of the channel inclination angle on the transient and the steady-state entropy generation. The fluctuations of the transient total entropy generation are investigated when the inclination angle is varied from $0^{\circ }$ to $180^{\circ }$. Moreover, the entropy generation and the Bejan number were studied as a function of the inclination angle of the channel, in the steady state of mixed convection. It was found that the total entropy generation is maximum at inclination angle close to $70^{\circ }$ and minimum at $0^{\circ }$ and $180^{\circ }$.

1 Introduction

Entropy generation is closely associated with the thermodynamic irreversibility because it encountered in all heat transfer processes. The different sources responsible for the entropy generation are heat transfer and viscous effect. References (Nield and Bejan [1], Bejan and Kraus [2] and Ingham et al. [3]) excellently described the extent of the research information in this area. The viscous dissipation effects are important in geophysical flows and also in certain industrial operations. In the literature, extensive research works are available to examine the effect of mixed convection on flow in porous channel with viscous dissipation effect. Ingham et al. [4] studied mixed convection in a vertical porous channel in the presence of viscous dissipation effects. He used the Darcy flow model and determined the basic flow and temperature fields. Al-Hadhrami et al. [5] investigated the mixed convection of a fully developed Newtonian fluid in a vertical porous channel with viscous dissipation and Darcy effects taken into consideration. He combined the Brinkman equation and the energy equation in the porous medium to form a fourth-order non-linear Ordinary Differential Equation. Based on the Brinkman model a new form of the viscous dissipation term was given so that it possesses the correct asymptotic behaviors for the clear fluid region $({\mu } \rightarrow \infty )$ and for the Darcy limit $({\mu }\rightarrow 0)$. Nield et al. [6] studied the effect of the viscous dissipation term to the thermal energy equation for the problem of forced convection in a parallel-plate channel, with the temperature held constant at the walls that is in the absence of viscous dissipation. He shows that the variation of Nusselt number is small with the Darcy number but it is increasing as Peclet number decreases. He concluded that the effect of viscous dissipation has a significant effect on the developing Nusselt number. Okedayo et al. [7] studied the viscous dissipation effect on flow through a horizontal porous channel with constant wall temperature and a periodic pressure gradient. Effects of various parameters such as the Darcy, Reynolds, Prandtl, and Eckert numbers were also studied. Elbashbeshy [8] has investigated the mixed convection along a vertical plate embedded in non-Darcian porous medium with suction and injection. Makinde and Osalusi [9] analyzed the entropy generation in a liquid film falling along an inclined porous heated plate and concluded that the entropy generation is enhanced by viscous dissipation and generally reduced by increasing wall suction. However, mixed convection and entropy generation in the Poiseuille–Benard channel in different angles are studied numerically by Nourollahi et al. [10]. They studied the variations of entropy generation and the Bejan number as a function of inclination angle. Moreover, they discussed the positive and negative effects of buoyancy force on flow field, Nusselt number, and entropy generation. It shows that the entropy generation due to heat transfer is localized at the areas where heat exchanged between the walls and the flow is maximum, while the entropy generation due to fluid friction is maximum at areas where the velocity gradients are maximum such as vortex centers. A numerical investigation of double-diffusive convection through an inclined porous cavity was carried out by Mchirgui et al. [11]. They found that the entropy generation exhibits an oscillatory behavior for lower $({Da}=10^{-4})$ and higher $({Da}=10^{-2})$ medium permeability values, when $\alpha \ne 0^{\circ }$. It shows that the minimum entropy generation is found in the aspect ratio $A= 0.5$ and 1, for ${Da}=10^{-2}$ and $10^{-4}$, respectively. However, Malashetty et al. [12] studied the fully developed convective flow and heat transfer in an inclined channel bounded by two rigid plates, containing porous layer saturated with a fluid and a clear viscous fluid layer using the Darcy–Brinkman equation model. Hooman and Gurgency [13] numerically investigated the forced convection with viscous dissipation in a parallel-plate channel filled by a saturated porous medium. He examined the effect of various viscous dissipation models on the thermal aspects. It shows that, the three models lead to similar Nusselt number values when Darcy number is low, however, for high Darcy number values only the model of Al-Hadhrami et al. [14] claimed to be valid. Hooman et al. [15] numerically investigated the entropy generation due to forced convection in a parallel-plate channel filled by a saturated porous medium. It was observed that the increase in the medium aspect ratio provokes an increase of the irreversibility degree in the studied system. However, Chinyoka and Makinde [16] analyzed the flow and heat transfer inside a uniformly porous vertical pipe. They presented the entropy generation number, irreversibility distribution ratio, and Bejan number. Entropy generation in an unsteady flow through a porous pipe with suction was investigated numerically by Makinde and Chinyoka [17].

The prime objective of this study is to consider the effect of viscous dissipation term for the flow and heat transfer in a horizontal channel filled with porous media in different inclination angles. The investigation is carried out from the numerical solutions of complete Navier–Stokes and energy equations by the finite volume method. In this study the porosity, the Reynolds, the Prandtl number, the Rayleigh, and the modified Brinkman numbers are fixed at 0.5, 10, 0.7, $10^{4}$, and $10^{-3}$, respectively. The Brinkman number, the Darcy number, and the inclination angle of the channel are in the following ranges: $10^{-5}\le Br\le 10^{-2}$; $10^{-6}\le Da \le 10$; $0^{\circ }\le \beta \le 180^{\circ }$.

2 Mathematical Modeling

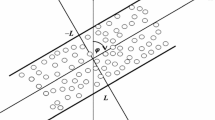
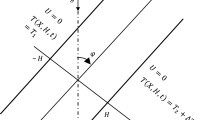
The schematic of the system under consideration is shown in Fig. 1. It consists of a laminar two-dimensional mixed convective flow inside an inclined channel saturated by porous medium. The inclination angle of the channel is defined as the angle between the hot wall, which coincides with the x-axis, and the horizontal plane. The fluid is assumed to be incompressible, Newtonian, and viscous. The porous medium is supposed to be isotropic, homogeneous, and in thermodynamic equilibrium with the fluid. The homogeneity and isotropy of the porous medium leads us to believe that pores have same size and form. The capillary force is assumed to be negligible.

Fig. 1

Mathematical model

The thermophysical properties of the fluid and the solid matrix are supposed to be constant, except for the fluid density which satisfies the Boussinesq approximation such as:

$$\begin{aligned} \rho =\rho _0\left[ {1-\beta _\mathrm{T}(T-T_0)}\right] \end{aligned}$$

(1)

In the equation above, $\rho _{0}$, $T_{0}$, and $\beta _\mathrm{T}$ are the fluid density, the reference temperature, and the thermal volumetric expansion coefficient, respectively. The latter is given by:

$$\begin{aligned} \beta _\mathrm{T} =\frac{1}{\rho _0}{\left( {\frac{\partial \rho }{\partial T}}\right) }_p \end{aligned}$$

(2)

Using the Darcy Brinkman model and in two-coordinate system, the governing equations of the flow under consideration are:

Dimensional continuity equation:

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(3)

Dimensional momentum equation in x-axis:

$$\begin{aligned} \rho _0 \left[ {\frac{1}{\varepsilon }\frac{\partial u}{\partial t}+\frac{1}{\varepsilon ^{2}}u\frac{\partial u}{\partial x}+\frac{1}{\varepsilon ^{2}}v\frac{\partial u}{\partial y}} \right] =-\frac{\partial p}{\partial x}-\frac{\eta }{\mu }u+\eta _{{\mathrm{eff}}} \left( {\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}} \right) -\rho g {\cdot } \sin \beta \nonumber \\, \end{aligned}$$

(4)

Dimensional momentum equation in y-axis:

$$\begin{aligned} \rho _0 \left[ {\frac{1}{\varepsilon }\frac{\partial v}{\partial t}+\frac{1}{\varepsilon ^{2}}u\frac{\partial v}{\partial x}+\frac{1}{\varepsilon ^{2}}v\frac{\partial v}{\partial y}} \right] =-\frac{\partial p}{\partial y}-\frac{\eta }{\mu }v+\eta _{{\mathrm{eff}}} \left( {\frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}} \right) -\rho g{\cdot }\cos \beta \nonumber \\, \end{aligned}$$

(5)

Dimensional energy equation with viscous dissipation:

$$\begin{aligned} \sigma \frac{\partial T}{\partial t}+\left[ {u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}} \right] =\alpha _{{\mathrm{eff}}} \left( {\frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}} \right) +\frac{\varPhi }{\left( {\rho c}\right) _\mathrm{f}}, \end{aligned}$$

(6)

where $\eta _{{\mathrm{eff}}}$ is the effective viscosity, $\eta$ is the fluid dynamic viscosity, $\mu$ is the permeability, and $\varepsilon$ is the medium porosity. In Eq. 6, the term $\varPhi$ is the viscous dissipation which appears as an internal heat source in the porous media, which was defined by Al-Hadhrami et al. [14]:

$$\begin{aligned} \varPhi =\frac{\eta }{\mu }\left( {u^{2}+v^{2}} \right) +\eta _{{\mathrm{eff}}} \left[ {2\left( {\frac{\partial u}{\partial x}}\right) ^{2}+2\left( {\frac{\partial v}{\partial y}} \right) ^{2}+\left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}}\right) ^{2}} \right] \end{aligned}$$

(7)

Following the work of Bejan [18], only the first term of Eq. 7 will be considered as the viscous dissipation contribution in the energy Eq. 6. Details of the alternative viscous dissipation models for flow through a porous media can be found in Nield [19–21], Nield et al. [22] and Magyari et al. [23].

The terms $\sigma$ and $\alpha _\mathrm{eff}$ refer to the specific heat capacity ratio and the effective thermal diffusivity, respectively and they are defined by:

$$\begin{aligned} \alpha _{{\mathrm{eff}}} =\frac{\lambda _\mathrm{m}}{(\rho c)_\mathrm{f}};\quad \sigma =\frac{(\rho c)_\mathrm{m}}{(\rho c)_\mathrm{f}}, \end{aligned}$$

(8)

where $(\rho c)_\mathrm{m}$ and $(\rho c)_\mathrm{f}$ are the specific heat capacity per unit volume of the porous medium and the specific heat capacity of the fluid, respectively. The effective thermal conductivity of a porous medium $\lambda _\mathrm{m}$ depends in a complex manner on the geometry of the medium and on the way how heat conduction in the solid and fluid phases occurs. The local thermal equilibrium model is used, therefore the considered effective conductivity can be written as the weighted arithmetic mean of the solid phase and the fluid phase conductivities:

$$\begin{aligned} \lambda _\mathrm{m} =(1-\varepsilon )\lambda _\mathrm{s} +\varepsilon \lambda _\mathrm{f}, \end{aligned}$$

(9)

where $\lambda _\mathrm{f}$ and $\lambda _\mathrm{s}$ are the thermal conductivities of the fluid and solid, respectively.

The dimensionless variables are:

$$\begin{aligned} \tau =\frac{t}{h}u_0; \quad X=\frac{x}{h}; \quad Y=\frac{y}{h}; \quad U=\frac{u}{u_0}; \quad V=\frac{v}{u_0}; \quad P=\frac{p}{\rho _0 u_0^{2}};\quad \theta =\frac{T-T_\mathrm{c}}{T_\mathrm{h}-T_\mathrm{c}}\!\!\nonumber \\ \end{aligned}$$

(10)

Using the dimensionless variables mentioned above, the governing equations can be written in dimensionless form as:

$$\begin{aligned}&\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial U}{\partial \tau }+\mathrm{div}\left( {J_U } \right) =-\varepsilon \frac{\partial P}{\partial X}-\frac{\varepsilon }{Da{\cdot }{Re}}U+\frac{Ra{\cdot }\varepsilon }{{Re}{\cdot } Pe}\theta {\cdot }\sin \beta , \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\partial V}{\partial \tau }+\mathrm{div}\left( {J_V } \right) =-\varepsilon \frac{\partial P}{\partial Y}-\frac{\varepsilon }{Da{\cdot }{Re}}V+\frac{Ra{\cdot }\varepsilon }{{Re}{\cdot } Pe}\theta {\cdot }\cos \beta , \end{aligned}$$

(13)

$$\begin{aligned}&\sigma \frac{\partial \theta }{\partial \tau }+\mathrm{div}\left( {J_\theta } \right) =c{\cdot }\frac{Br}{{Re}{\cdot }Pr\cdot Da}({U^{2}+V^{2}}), \end{aligned}$$

(14)

where $J_U =\frac{1}{\varepsilon }U{\cdot }\mathbf{V}-\frac{\Lambda \varepsilon }{{Re}}\mathrm{grad}(U)$, $J_V =\frac{1}{\varepsilon }V{\cdot }\mathbf{V}-\frac{\Lambda \varepsilon }{{Re}}\mathrm{grad}(V)$, $J_\theta =\theta {\cdot }\mathbf{V}-\frac{1}{{Re}{\cdot }Pr}\mathrm{grad}(\theta ).$

In Eq. 14, the term c is taken equal to one or zero in the presence or absence of viscous dissipation effect, respectively.

The boundary and initial conditions appropriate to laminar flow within the differential heated channel are:

$$\begin{aligned} \begin{array}{l} 0\le X\le l/h; \quad Y=0; \quad U=V=0;\quad \theta =1 \\ 0\le X\le l/h;\quad Y=1;\quad U=V=0;\quad \theta =0 \\ X=0;\quad 0\le Y\le 1;\quad U=6Y(1-Y);\quad V=0;\quad \theta =1-Y \\ X=l/h;\quad 0\le Y\le 1;\quad \frac{\partial \varphi }{\partial \tau }+\frac{\partial \varphi }{\partial X}=0,\quad \int \limits _0^1 {UdY} =1, \quad (\varphi =U,V) \\ \hbox {At}\;\tau =0;\quad U=V=0;\quad P=0;\quad \theta =0.5-Y .\\ \end{array} \end{aligned}$$

(15)

3 Entropy Generation

For the flow in porous medium, entropy generation per unit volume can be written as follows (Bejan [24]):

$$\begin{aligned} {\varvec{s}}= & {} \frac{\lambda _\mathrm{m}}{T_0^2}\left[ {\left( {\frac{\partial T}{\partial x}}\right) ^{2}+\left( {\frac{\partial T}{\partial y}} \right) ^{2}} \right] +\frac{\eta }{T_0{\cdot }\mu }\left( {u^{2}+v^{2}}\right) \nonumber \\&+\,\frac{\eta }{T_0}\left[ {2\left( {\frac{\partial u}{\partial x}} \right) ^{2}+2\left( {\frac{\partial v}{\partial y}} \right) ^{2}+\left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}} \right) ^{2}} \right] . \end{aligned}$$

(16)

Using the dimensionless variables listed in Eq. 15, dimensionless entropy generation equation is given in compact form by Tasnim et al. [25], Mahmud and Fraser [26], and Hooman and Gurgency [13]:

$$\begin{aligned} {\varvec{s}}_\mathrm{l,a} ={\varvec{s}}_\mathrm{l,a,H}+{\varvec{s}}_\mathrm{l,a,D}+{\varvec{s}}_\mathrm{l,a,F} \end{aligned}$$

(17)

On the right-hand side of Eq. 17, the first term represents the heat transfer entropy generation $({\varvec{s}}_\mathrm{l,a,H})$, the second is the Darcy viscous entropy generation $({\varvec{s}}_\mathrm{l,a,D})$, and the third represents the clear fluid viscous entropy generation $({\varvec{s}}_\mathrm{l,a,F})$. They are given by:

$$\begin{aligned} {\varvec{s}}_\mathrm{l,a,H}= & {} \left( {\frac{\partial \theta }{\partial X}} \right) ^{2}+\left( {\frac{\partial \theta }{\partial Y}} \right) ^{2}, \end{aligned}$$

(18)

$$\begin{aligned} {\varvec{s}}_\mathrm{l,a,D}= & {} \frac{Br^{*}}{Da}\left( {U^{2}+V^{2}} \right) , \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{s}}_\mathrm{l,a,F}= & {} Br^{*}\left[ {2\left( {\frac{\partial U}{\partial X}} \right) ^{2}+2\left( {\frac{\partial V}{\partial Y}} \right) ^{2}+\left( {\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}} \right) ^{2}} \right] , \end{aligned}$$

(20)

where $Br^{*}$ is defined as the modified Brinkman number, it is given by:

$$\begin{aligned} Br^{*}=\frac{Br}{\varOmega }. \end{aligned}$$

(21)

Br and $\varOmega$ are the Brinkman number and the dimensionless temperature difference, respectively. They are given by:

$$\begin{aligned} Br=\frac{u_0^2{\cdot }\eta }{\lambda _\mathrm{m}{\cdot }\Delta T},\quad \varOmega =\frac{\Delta T}{T_0}. \end{aligned}$$

(22)

The dimensionless total entropy generation for the entire channel is obtained by integrating Eq. 17:

$$\begin{aligned} {\varvec{s}}_\mathrm{t}=\int \limits _0^1{\int \limits _0^{l/h}{{\varvec{s}}_\mathrm{l,a}\mathrm{d}X\mathrm{d}Y}}. \end{aligned}$$

(23)

The time-averaged total entropy generation can be evaluated using the following equation:

$$\begin{aligned} \left\langle {{\varvec{s}}_\mathrm{t}} \right\rangle =\frac{1}{\varTheta }\int \limits _0^\varTheta {{\varvec{s}}_\mathrm{t}\mathrm{d}\tau }. \end{aligned}$$

(24)

The thermal heat flux exchanged between the walls and the flow is characterized by the space-averaged Nusselt number evaluated as follows:

$$\begin{aligned} \overline{Nu} =\frac{1}{l/h}\int \limits _0^{l/h} {\left| {\frac{\partial \theta }{\partial Y}} \right| \mathrm{d}X}. \end{aligned}$$

(25)

The space- and time-averaged Nusselt number is defined as:

$$\begin{aligned} \left\langle {\overline{Nu}}\right\rangle =\frac{1}{\varTheta }\int \limits _0^\varTheta {\overline{Nu}\mathrm{d}\tau }, \end{aligned}$$

(26)

where $\varTheta$ is the period of oscillations of the space-averaged Nusselt number $\overline{Nu}$.

The Bejan number is defined as:

$$\begin{aligned} Be=\frac{\left\langle {\mathbf{s}_\mathrm{l,a,H}}\right\rangle }{\left\langle {\mathbf{s}_\mathrm{t}}\right\rangle }. \end{aligned}$$

(27)

The Bejan number compares the magnitude of entropy generation due to heat transfer with the magnitude of the total entropy generation. When $Be\ge 1/2$, the irreversibility due to heat transfer dominates, while for $Be\le 1/2$ the irreversibility due to viscous effects dominates. For $Be\cong 1/2$, entropy generation due to heat transfer is almost of the same magnitude as that due to viscous effects.

4 Numerical Procedure

A modified version of control volume finite-element method (CVFEM) of Saabas and Baliga [27] is adapted to the standard staggered grid in which pressure and velocity components are stored at different points. The SIMPLER algorithm was applied to resolve the pressure–velocity coupling in conjunction with an alternating direction implicit (ADI) scheme for performing the time evolution.

Our code was validated with other works as seen in the Tables 1, 2, and 3.

Table 1 Space- and time-averaged Nusselt number for $Re=10$; $Ra=10^{4}$; $Pr=0.7$, $Da=1$

This table shows a good agreement between our results and those of the previous study.

In order to assess the accuracy of our numerical technique, our results are compared with those of the laminar flow in a horizontal porous channel reported by Mahmud and Fraser [26] and the laminar flow in a vertical porous channel given by Karamallah et al. [28]. A good agreement between our results and the previous ones as illustrated in Table 2.

Table 2 Maximum dimensionless velocity component in X direction for $Pr=0.7$; $Re=100$

Another test of the accuracy of the present numerical study has been performed by comparing the average values of Nusselt number with the numerical and analytical works given by Mahmud and Fraser [26]. Nusselt numbers are calculated for six selected values of Darcy numbers in Table 3. Also, there is a good agreement between our results and those of Mahmud and Fraser [26].

Table 3 Averaged Nusselt number for $Pr=0.7$; $Re=1$

Details of the code used in this study can be found in Abbassi et al. [29, 30].

Imposed global and local convergence criteria are taken into account, and should respectively satisfy the following:

$$\begin{aligned} \left( {\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}} \right) \le 10^{-5},\quad \max \left| {\frac{\phi ^{\tau +\Delta \tau }-\phi ^{\tau }}{\phi ^{\tau +\Delta \tau }}} \right| \le 10^{-5}, \end{aligned}$$

(28)

where $\varPhi$ is the dependent variable $(\varPhi =U,\,V,\,\theta )$. This means that the continuity equation should verify the first convergence criterion at each time step of calculation, and the dependent variable $\varPhi$ should verify the second criterion at each point of the channel and at each time step. The transient study is carried out with a time step $\Delta \tau =10^{-3}$.

The averaged Nusselt number at the top wall is used for the grid independence analysis. Grid refinement tests have been performed for the case $Re=10$, $Pe=20/3$, and $Ra=10^{4}$ using three uniform grids $70\times 20$, $101\times 26$, and $131\times 31$. Results show that when we pass from a grid of $70\times 20$ to a grid of $101\times 26$, the averaged Nusselt number undergoes an increase of 7.1 %. When we pass from the grid of $101\times 26$ to the grid of $131\times 31$, it undergoes an increase of only 1.6 %. We conclude that the grid $101\times 26$ is sufficient to carry out a numerical study of this flow. This grid is retained for all the following investigations.

5 Results and Discussion

Given the large number of variables related to this study, some of them will be considered constants. Then, the porosity, Reynolds, Prandtl, Rayleigh, and the modified Brinkman numbers are fixed at 0.5, 10, 0.7, $10^{4}$, and $10^{-3}$, respectively. Also, the viscosity ratio and the specific heat capacity ratio are fixed to unity. An optimization study of the entropy generation according to the inclination angle of the channel ranging between $0^{\circ }$ and $180^{\circ }$ will be conducted.

Fig. 2

Transient entropy generation versus inclination angle

Figure 2 shows the transient entropy generation versus the inclination angle of the porous channel. From this figure, it can be seen that the entropy generation fluctuations are periodic at inclination angle $\beta =0^{\circ }$. The total entropy generation oscillates around average value close to 10 with dimensionless period $\varTheta =2.6$. These periodic fluctuations, which persist in time, lead us to believe in the presence of dissipative structure in the channel flow. This structure, highlighted by the plot of the stream lines in Fig. 3, is characterized by the presence of thermo-convective cells near the bottom and the top walls. This dissipative structure, present in the channel and maintained by energy dissipation, is characterized by three convective cells (Fig. 3) which appear in alternation near the bottom and the top walls of the main flow as cylinders turning without translation on walls. The bottom one turns in the clockwise direction, while the two other cells turn in the anticlockwise direction. In point of view of thermodynamics of irreversible processes this configuration maintained by energy dissipation and known as dissipative structure, corresponds to a rotation of the system around the steady state. This latter is far from equilibrium one, and consequently the system evolves in the non-linear domain of the thermodynamics of irreversible processes, since the Prigogine’s theorem of minimum entropy generation is unverified. In the following, we have tried to investigate the effect of the channel inclination on the entropy generation fluctuations and eventually the presence of dissipative structures. Results show that, when the inclination angle of the channel increases from $0^{\circ }$, the dissipative structure is immediately lost since the periodic fluctuations of the entropy generation are absent. Also, it can be seen in general case that, when the inclination angle increases the entropy generation takes an important initial value at the very beginning of mixed convection, then it decreases as dimensionless time proceeds with slight fluctuations before reaching the steady state. This latter corresponds to a constant value of the total entropy generation, where its dependence on the channel inclination angle will be studied later. These small fluctuations can be the effect of the birth of cells downstream of the channel that is rapidly lost. It is important to note that, at inclination angle equal to $180^{\circ }$, the entropy generation diminishes with time devoid of any fluctuation and tends asymptotically towards a constant and minimum value, which characterizes the steady state of mixed convection. In fact, this case corresponds to a heating from the top and a cooling from the bottom of the porous enclosure, then all the driving thermodynamic forces are minimum. Therefore the convective phenomena are practically absent and the obtained entropy generation is minimal. In a thermodynamic view point, in this case the steady state is sufficiently close to equilibrium one, thus the system tends directly towards the steady state. Consequently, the Prigogine’s theorem of minimum entropy generation for processes which are linear on a global scale is verified and the system evolves in the linear branch of the thermodynamics of irreversible processes in which the relations between thermodynamic forces and fluxes are linear.

Fig. 3

Stream lines of the flow configuration

Figure 4a illustrates the variation of the total entropy generation, at steady state, with the inclination angle of the porous channel for different values of Brinkman number. As can be seen from this figure, the total entropy generation begins with a small value at inclination angle equal to $0^{\circ }$, then it increases, reaches a maximum close to $70^{\circ }$ and decreases to reach a minimum value at $180^{\circ }$. Remark that, the inclination angle has more pronounced effect on the entropy generation as the Brinkman number increases.

Fig. 4

Variation of (a) the averaged total entropy generation and (b) Bejan number versus inclined angle for different Brinkman number at $Re=10$, $Ra=10^{4}$, and $Br^{*}=10^{-3}$

Figure 4b illustrates the variation of Bejan number versus the inclination angle for different values of Brinkman number. It can be seen that, when the Brinkman number is greater than $10^{-3}$, the Bejan number is always higher than 0.5. Therefore irreversibility due to heat transfer dominates for all inclination angle ranging between $0^{\circ }$ and $180^{\circ }$. Also the same figure shows that, at fixed inclination angle, the Bejan number decreases when the Brinkman number decreases, which implies that heat transfer irreversibility begins to lose its dominance. One can notice that, the Bejan number is maximum at inclination angles $0^{\circ }$ and $180^{\circ }$, whereas it is minimum at $90^{\circ }$. Results show that when the Brinkman number decreases from $10^{-3}$, heat transfer irreversibility is dominantly close to the selected limit angles ($0^{\circ }$ and $180^{\circ }$), whereas one can observe a dominance of the viscous fluid irreversibility in the vicinity of inclination angle $90^{\circ }$. Figures 5 and 6 illustrate the evolution of the streamlines and the isothermal lines respectively for $Pr=0.7$, $Da=10^{-2}$, $Br^{*}=10^{-3}$, $Br=10^{-3}$ and inclination angle ranging between $0^{\circ }$ and $180^{\circ }$. Figure 5 shows the existence of dissipative structure at $\beta =0^{\circ }$ which is characterize by three thermo-convective cells as explained before. The existence of this dissipative structure proves that convection is present in the channel and consequently irreversibility is mainly due to the convective heat transfer. As the inclination angle increases from $0^{\circ }$ to $90^{\circ }$, the flow structure undergoes a change from three thermo-convective cells to one convective cell, which occupies practically all the channel domain. Simultaneously, as shown in Fig. 6, the distortion of isotherms, which is marked at inclination angle $0^{\circ }$ mostly in the right half of the channel, becomes increasingly less pronounced when the inclination angle increases, indicating a decrease of the thermal gradients. In parallel total entropy generation increases (Fig. 4a, for $Br=10^{-3}$) whereas the Bejan number decreases and may even take values less than 0.5, which indicate that the thermal irreversibility dominance diminishes to give way to the viscous one (Fig. 4b, for $Br=10^{-3}$). This means that, when increasing the inclination angle in the range cited above, the change in the flow configuration is mainly accompanied by an increase in the velocity gradients. This augmentation in the velocity gradients increases the total entropy generation via essentially the viscous irreversibility, which becomes dominant as the inclination angle exceeds practically the value $45^{\circ }$. As inclination angle increases from $90^{\circ }$ to $180^{\circ }$ the Bejan number increases, indicating that the dominance of the viscous irreversibility is gradually lost. When inclination angle approaches $180^{\circ }$, stream lines and isotherms become practically parallel and the flow is stratified. In this case the irreversibility is minimal and limited to the thermal conduction one.

Fig. 5

Evolution of stream lines versus inclination angle at $\varepsilon =0.5$; $Re=10$; $Ra=10^{4}$; $Pr=0.7$; $Br^{*}=10^{-3}$; $Da=10^{-2}$; and $Br=10^{-3}$

Fig. 6

Evolution of isothermal lines versus inclination angle at $\varepsilon =0.5$; $Re=10$; $Ra=10^{4}$; $Pr=0.7$; $Br^{*}=10^{-3}$; $Da=10^{-2}$; and $Br=10^{-3}$

This section is a brief comment related to the experimental validation of the numerical results concerning the porous media. In fact, the experimental validation can be conducted according to two aspects. The first is related to the observation and the second concerns the calculation. Regarding the first aspect, the observation of the flow structure behavior in the porous medium, when flow parameters change is relatively difficult. This is due to the nature of the porous medium, eventually its opacity, and the diffusion of light by its porous matrix (this light diffusion can occur even when the porous medium is transparent). The second aspect is technically possible and the numerical prediction of entropy generation can be experimentally verified using the entropy balance over the entire porous medium in the stationary state. This requires the measurement of the inlet and outlet temperatures and flow rates of the fluid and also the heat transfer fluxes through the two isothermal walls. In my opinion, experimental validation of the numerical calculation encounters two problems. The first is that the experimental calculation of entropy generation can only concern the global level (entire system) and consequently cannot be applied at local level, which is the highlight of the numerical calculation. The second one is the necessity to make a dimensional numerical study (with real values and in the same condition with experiment), which presents the weakness of the numerical calculation even with traditional numerical code. In this context the use of industrial numerical calculation software is indispensable to approach experimental conditions with real fluid and real dimensions of flow configuration.

6 Conclusion

This work concerns the influence of the channel inclination angle on the irreversibility at steady and transient states. It was found that the existence of periodic fluctuations of the entropy generation at inclination angle $\beta =0^{\circ }$, corresponds from a thermodynamic point of view, to a rotation of the system around the steady state. This steady state is therefore far from equilibrium one and the system evolves in the non-linear domain of the thermodynamics of irreversible processes. When the inclination angle of the channel increases from $0^{\circ }$, the periodic fluctuations of the entropy generation are lost. The entropy generation takes important initial value at the very beginning of mixed convection, and then it decreases and takes practically a constant value in the steady state, which is minimal at inclination angle equal to $180^{\circ }$. In this case, the Prigogine’s theorem of minimum entropy generation for processes which are linear on a global scale is verified and the system evolves in the linear branch of the thermodynamics of irreversible processes. The investigation of the steady-state irreversibility with the inclination angle of the porous channel, for different values of Brinkman number, showed that the total entropy generation is maximum at inclination angle close to $70^{\circ }$, and insignificant at inclination angle equal to $0^{\circ }$ and $180^{\circ }$. The study of Bejan number with the inclination angle, illustrated a dominance of heat transfer irreversibility for all inclination angle, when the Brinkman number is greater than $10^{-3}$. Whereas, when the Brinkman number decreases from $10^{-3}$, a dominance of the viscous fluid irreversibility is remarked in the vicinity of inclination angle $90^{\circ }$.