1 Introduction

Rare earth aluminate perovskites have been studied extensively for their interesting ferroelectric and piezoelectric properties [1]. The crystal structure of scandium aluminate \((\hbox {ScAlO}_{3})\) was refined for the first time by Reid and Ringwood [2], and a single- crystal diffraction experiment was performed by Sinclair et al. [3] confirmed the \(\hbox {GdFeO}_{3}\)-type structure of \(\hbox {ScAlO}_{3}\). The structural stability of ABO\(_{3}\)- or \(\hbox {GdFeO}_{3}\)-type perovskites has been investigated by many researchers [4–8]. Ross [6] used single-crystal X-ray diffraction for pressures below 5 GPa. Also, Magyari-Köpe et al. [7] showed that the orthorhombic Pbnm structure remains stable relative to the cubic structure for pressures up to 150 GPA by using an ab initio total energy method. Wu and Neumann [8] investigated the high-pressure phase stability and elasticity based on density functional theory and showed that a phase transition occurs at 53 GPa and 0 K from the Pbnm to the Cmcm structure. There have been few studies of the thermal properties of the \(\hbox {ScAlO}_{3}\) perovskite. The thermal expansion has been reported by Hill and Jackson [9] and Yamanaka et al. [1]. The temperature dependence of the shear modulus and bulk modulus was investigated by Jackson and Kung up to 1000 K at 300 MPa [10]. Kung et al. [11] determined the elasticity of \(\hbox {ScAlO}_{3}\) up to 3 GPa at room temperature and the temperature dependence of the elastic moduli between 300 K and 600 K [12]. It is important to study the physical properties of materials under high pressures and temperatures for microscopic understanding as well as technological applications. In this paper, we report a theoretical study of both the pressure and temperature dependence of the thermal properties of \(\hbox {ScAlO}_{3}\) perovskite. The results of Debye calculations are reported in two sections. In the first section, the results of three approaches, the Slater, Dugdale–MacDonald (DM), and Vaschenko–Zubarev (VZ) approaches, are compared with available experimental data. The approach that leads to the best results was taken into account to calculate the temperature and pressure dependence of the bulk modulus, thermal expansion, thermal expansion coefficient, and the heat capacity at constant volume and constant pressure, and the results are presented in the second section. In Fig. 1 the unit cell of \(\hbox {ScAlO}_{3}\) perovskite is shown.

Fig. 1
figure 1

Unit cell of ScAlO\(_{3}\) perovskite

Full size image

2 Theoretical Method

2.1 First-Principles Calculations

The ab initio calculations were performed within density functional theory (DFT), using the plane-wave pseudo-potential method as implemented in the Quantum-ESPRESSO package [13] with ultrasoft Vanderbilt pseudo-potentials [14]. For the exchange and correlation terms in the electron–electron interaction, the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) [15] has been used. The plane-wave energy cutoff was 60 Ry, and the k-grids used in the total energy were \(12\times 12 \times 12\) Monkhorst–Pack (MP) meshes [16]. The self-consistent threshold value for convergence was \(10^{-12}\) Ry, and the first-order Methfessel–Paxton method [17] was used with a smearing width of 0.05 Ry.

2.2 Quasi-harmonic Approximation

In the quasi-harmonic Debye model, the non-equilibrium Gibbs function \(G^{*}\) is taken in a form,

$$\begin{aligned} G^{*}\left( {V,p,T} \right) =E\left( V \right) +pV+A_{\hbox {vib}} (V,T), \end{aligned}$$
(1)

where \(E\left( V \right) \) is the total energy per unit cell, and \(pV\) corresponds to the constant hydrostatic pressure condition. \(A_\mathrm{vib}\) is the vibrational Helmholtz-free energy given by the Debye model, which can be written as [18]

$$\begin{aligned} A_{\hbox {vib}} \left( {\theta _\mathrm{D} ,T} \right) =nk_\mathrm{B} T\left[ {\frac{9}{8}\frac{\theta _\mathrm{D} }{T}+3\hbox {ln}\left( {1-\exp \left( {-\frac{\theta _\mathrm{D} }{T}} \right) } \right) -D\left( {\frac{\theta _\mathrm{D} }{T}} \right) } \right] , \end{aligned}$$
(2)

where \(\theta _\mathrm{D} \) is the Debye temperature, \(n\) is the number of atoms per formula unit, \(k_\mathrm{B} \) is the Boltzmann constant, and \(D\) is the Debye function, which is defined as

$$\begin{aligned} D_y =\frac{3}{y^{3}}\int _{0}^{y} \frac{x^{3}}{\mathrm{e}^{x}-1}\hbox {d}x. \end{aligned}$$
(3)

The volume dependence enters by way of \(\theta _\mathrm{D} \) through the relation [19],

$$\begin{aligned} \theta _\mathrm{D} \left( V \right) =f\left( \sigma \right) \frac{\hbar }{k_\mathrm{B} \sqrt{rm}}\left( {6\pi ^{2}N} \right) ^{\frac{1}{3}}V^{\frac{2}{3}}\left[ {-\frac{\partial P\left( V \right) }{\partial V}-\frac{2\left( {\lambda +1} \right) }{3}\frac{P\left( V \right) }{V}} \right] ^{\frac{1}{2}}, \end{aligned}$$
(4)

where \(r\) is the number of atoms in the chemical formula of the material, \(m\) is an effective atomic mass defined as the logarithmic average of all masses in the formula, and \(P\left( V \right) =-\frac{\partial E\left( V \right) }{\partial V}\). The \(f\left( \sigma \right) \)function is

$$\begin{aligned} f\left( \sigma \right) =\left[ {\frac{2}{3}\left[ {\frac{2(1+\sigma )}{3(1-2\sigma )}} \right] ^{\frac{3}{2}}+\frac{1}{3}\left[ {\frac{1+\sigma }{3(1-\sigma )}} \right] ^{\frac{3}{2}}} \right] ^{-\frac{1}{3}}, \end{aligned}$$
(5)

where \(\sigma \) is Poisson’s ratio at the equilibrium geometry. When \(\lambda =-1,0,\) and +1, one obtains the Slater [20] model that assumes a pressure-independent Poisson ratio, and the Dugdale–MacDonald (DM) [21] and Vaschenko–Zubarev (VZ) [22] approaches, respectively. In order to calculate the thermal properties of \(\hbox {ScAlO}_{3}\), we used all three approaches as implemented in the GIBBS code [23].The default value of \(\sigma \) in GIBBS is \(\sigma = 0.25\), corresponding to a Cauchy solid.

To evaluate \(E\left( V \right) \), the calculated static energy versus volume was fitted to the finite-strain isothermal third-order Birch–Murnaghan [24] equation of state (EOS). By minimizing the non-equilibrium Gibbs function with respect to volume \(V\), one can obtain the thermal equation of state (EOS) for \(V (P,\; T)\). The specific heat capacity \((C_{V})\) at constant volume, isothermal bulk modulus \((B_{T})\), coefficient of volume thermal expansion \((\alpha )\), heat capacity at constant pressure (\(C_{P})\), and adiabatic bulk modulus \((B_{S})\) can be expressed as [23]

$$\begin{aligned} C_V= & {} 3nk\left[ {4D\left( {\frac{\theta _\mathrm{D} }{T}} \right) -\frac{3\frac{\theta _\mathrm{D} }{T}}{\hbox {e}^{\frac{\theta _\mathrm{D} }{T}}-1}} \right] ,\end{aligned}$$
(6)
$$\begin{aligned} B_T= & {} V\left( {\frac{\partial ^{2}G}{\partial V^{2}}} \right) _T ,\end{aligned}$$
(7)
$$\begin{aligned} \alpha= & {} -\frac{\gamma C_V }{B_T V},\end{aligned}$$
(8)
$$\begin{aligned} C_p= & {} C_V \left( {1+\gamma \alpha T} \right) ,\end{aligned}$$
(9)
$$\begin{aligned} B_S= & {} B_T \left( {1+\gamma \alpha T} \right) , \end{aligned}$$
(10)

where \(\gamma \) is the Grüneisen ratio, which is defined as

$$\begin{aligned} \gamma =-\frac{\hbox {d}\ln \theta _\mathrm{D} }{\hbox {d}\ln V}. \end{aligned}$$
(11)

In the Debye–Grüneisen model such as the DM or VZ formula, an approximate Grüneisen ratio is chosen to correct quasi-harmonicity introduced by assuming that the Poisson ratio does not change with volume. In the DM model, the material is modeled as a simple cubic lattice undergoing one-dimensional harmonic oscillations. In the VZ model the Grüneisen parameter is derived from free-volume theory based on anharmonic central pairwise potentials between nearest-neighbor atoms in a three-dimensional cubic lattice. This model incorporates the volume dependence of Poisson’s ratio and reduces to the DM approach for one-dimensional vibrations [25].

Also, the empirical energy corrections (EECs) are applied to the results of the three models to correct the systematic errors introduced by the functional in the calculation of equilibrium volumes [23]. The corrected static energy (\(E_\mathrm{s})\) is defined as follows:

$$\begin{aligned} \tilde{E}_\mathrm{s} \left( V \right) =E_\mathrm{s} \left( {V_0 } \right) +\frac{B_{\mathrm{exp}} V_{\mathrm{exp}} }{B_0 V_0 }\left[ {E_\mathrm{s} \left( {V\frac{V_0 }{V_{\mathrm{exp}} }} \right) -E_\mathrm{s} (V_0 )} \right] , \end{aligned}$$
(12)

where \(V_0 \) and \(B_0 \) are chosen so that the experimental room-temperature equilibrium volume and bulk modulus are reproduced. The calculation procedure is described in more detail in [23].

3 Results and Discussion

\(\hbox {ScAlO}_{3}\) perovskite has an orthorhombic structure (space group \(Pbnm)\). The equilibrium lattice parameters calculated by using a PBE functional for bulk \(\hbox {ScAlO}_{3}\) are \(a= 4.971\) Å, \(b= 5.263\) Å, and \(c= 7.305\) Å, compared with experimental values of \(a= 4.9355\) Å, \(b= 5.2313\) Å, and \(c= 7.2003\) Å [1]. In order to compare the results of the Slater, Dugdale–MacDonald (DM), and Vaschenko–Zubarev (VZ) approaches, we used the three models with the same parameters for electronic calculations. Also, in order to obtain more reasonable results, the empirical energy corrections are applied to the results of all three models. The equilibrium volume and bulk modulus at room temperature that have been used for empirical energy corrections were set to 186 Å\(^{3}\) [1] and 222 GPa [10]. Variations of static energies with the unit cell volume before and after the empirical energy corrections (EEC) are presented in Fig. 2.

Fig. 2
figure 2

Empirical energy correction (EEC) to the static energy; dashed lines denote equilibrium volumes for each curve

Full size image

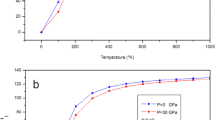
The results of the quasi-harmonic analysis after empirical energy corrections together with all available experimental data are presented in Table 1 and plotted in Fig. 3a–d. In the figures, the results of the three models are plotted together for comparison. In Fig. 3a, the temperature dependence of the unit cell volume at zero pressure is compared with experimental data. As can be seen from the figure, the best agreement with experiment is obtained by the VZ approximation. Calculated and experimental results for the pressure dependence of the unit cell volume are plotted in Fig. 3b. The results of the three models at zero temperature are identical and in excellent agreement with experimental data [6]. The results for the bulk modulus are shown in Fig. 3c. As can be seen from the figure, the VZ approach gives the results which are in better agreement with the experimental data [10], but none of the models is really close to the experimental data, especially at high temperatures. The origin of this difference is mainly due to the neglect of intrinsic anharmonic effects in the quasi-harmonic approximation. On the other hand, by applying the empirical energy correction, the volume-energy curve is changed in a way that reproduces the experimental room-temperature bulk modulus which may also lead to a change in the slope of the bulk modulus versus temperature.

Fig. 3
figure 3

Calculated unit cell volume as a function of (a) temperature and (b) pressure, (c) temperature dependence of bulk modulus and (d) coefficient of volume thermal expansion with Slater, Dugdale–MacDonald (DM), and Vaschenko–Zubarev (VZ) approaches. Experimental data are also displayed for comparison

Full size image
Table 1 Calculated and experimental results for expansion, CVTE, and bulk modulus
Full size table

To obtain the experimental coefficient of the volume thermal expansion (CVTE), experimental results obtained by Hill and Jackson [9] and Yamanaka et al. [1] for unit cell expansion are altogether fitted to a third-order polynomial using the least-squares method. The unit cell volume change with temperature does not show a linear expansion but is well represented with the equation,

$$\begin{aligned} V(T)=185.157+0.001556T+3.2188 \times 10^{-6} T^{2}-7.9797 \times 10^{-10} T^{3}.\qquad \quad \end{aligned}$$
(13)

The results together with the calculated results for CVTE are shown in Fig. 3d. The results of the VZ approximation are lower than Slater and DM analysis and are clearly in reasonable agreement with experiment. Differences between calculated and experimental values 1 [9] of the coefficient of volume thermal expansion at 298 K are about 3.3 %, 29.7 %, and 56.6 % for VZ, DM, and Slater approaches, respectively. These values at 1000 K are about 2.3 %, 31.4 %, and 62.3 %.

As mentioned in Sect. 2.2, in the VZ approach, the anharmonicity is taken into account as an anharmonic central pairwise potential between nearest-neighbor atoms. Therefore, it is expected that the results obtained with the VZ approach are in better agreement with experiment. On the other hand, as can be seen, the maximum deviation occurs for the Slater approach. This is because in the Slater model, Poisson’s ratio is volume-independent. Although the variation of Poisson’s ratio with pressure is usually very small [26], the volume derivatives of the shear mode and the longitudinal mode are different. Therefore, failure of Slater’s assumption must be the reason that the results of the Slater approach are in less agreement with experimental data than the other two approaches. The results of the DM approach are located between the Slater and VZ approaches.

The results obtained after applying the VZ approach to the corrected static energy are presented in Figs. 4 and 5. In Fig. 4a–e, the temperature dependence of the unit cell volume, bulk modulus, CVTE, and the heat capacity at constant volume \((C_{V})\) and constant pressure \((C_{P})\), up to 1400 K at different pressures \((P=0 \hbox { GPa},\; 5 \hbox { GPa},\; 10 \hbox { GPa},\; \hbox { and } 20 \hbox { GPa})\) are, respectively, plotted. The results for the bulk modulus at different pressures (Fig. 4b) show that at \(T < 100 \hbox { K}\), the bulk modulus is nearly constant, but it drops at higher temperatures. As can be seen from Fig. 4c, the thermal expansion coefficient increases with nearly \(T^{3}\) at low temperatures and then approaches a linear increase at high temperatures. Also, the results show that \(C_{V}\) and \(C_{P}\) (Fig. 4d and e) decrease with pressure, especially at high temperatures.

The pressure dependence of the unit cell volume, CVTE, the bulk modulus, and \(C_{V}\) and \(C_{P}\) at different temperatures (T \(=\) 0 K, 298 K, 600 K, and 1400 K) are plotted in Fig. 5a–e, respectively. The EOS curves at different temperatures are shown in Fig. 5a. The results for the bulk modulus are shown in Fig. 5b. The results show that the bulk modulus increases almost linearly with pressure but it decreases with increasing temperature. As it can be seen from Fig. 5c, CVTE drops rapidly with increasing pressure up to 30 GPa, especially at very high temperature (at 1400 K, it becomes half at 30 GPa). As can be seen in Figs. 5d and e both \(C_{V}\) and \(C_{P}\) decrease almost linearly with increasing pressure. Also, it can be seen that the variation of \(C_{V}\) in the range of 0 GPa to 30 GPa decreases with increasing temperature, as shown in Fig. 5d. This is not true for \(C_{P}\) at very high temperatures.

Fig. 4
figure 4

Results of Debye–Grüneisen VZ approach after empirical energy correction for temperature dependence of (a) unit cell volume, (b) bulk modulus, (c) coefficient of volume thermal expansion and heat capacities of copper at (d) constant volume and (e) constant pressure at different pressures

Full size image
Fig. 5
figure 5

Results of Debye–Grüneisen VZ approach after empirical energy correction for pressure dependence of (a) unit cell volume, (b) bulk modulus, (c) coefficient of volume thermal expansion, and heat capacities of copper at (d) constant volume and (e) constant pressure at different temperatures

Full size image

4 Conclusions

Thermodynamic properties of ScAlO\(_{3}\) perovskite are determined from first principles in the temperature range from 0 K to 1400 K. The pressure effect is studied in the 0 to 30 GPa range.

The basic thermodynamic quantities such as the bulk modulus, the heat capacity at constant volume and constant pressure, the thermal expansion, and the coefficient of volume thermal expansion have been calculated based on the Debye–Grüneisen model with Slater, Dugdale–MacDonald (DM), and Vaschenko–Zubarev (VZ) approaches. The empirical energy corrections are applied to the results of the three models to correct the systematic errors introduced by the functional. The best agreement between the calculated and experimental data was obtained for VZ calculations. Differences between calculated and experimental values for the coefficient of volume thermal expansion in the range of 283 K to 1273 K are not more than about 8.4 % for the VZ analysis. Comparing the results of the VZ calculations with the experimental data shows that by applying the empirical energy corrections, this method can be used to determine thermodynamic properties of \(\hbox {ScAlO}_{3}\) perovskite with reasonable accuracy.