Equation of State for the Lennard-Jones Truncated and Shifted Model Fluid

Abstract

An equation of state is developed for the Lennard-Jones model fluid, truncated and shifted at $r_{\mathrm{c}} = 2.5\sigma$. The underlying dataset contains thermodynamic properties at 706 state points including pressure, residual internal energy, first volume derivative of the residual internal energy, and residual isochoric heat capacity as a function of temperature and density. The equation of state is explicit in terms of the Helmholtz energy, allowing the determination of any thermodynamic property by differentiation. It is valid for temperatures $0.6<T/T_{\mathrm{c}}<10$ and pressures $p/p_{\mathrm{c}}<70$. High accuracy and good extrapolation behavior of the equation of state are established.

1 Introduction

Molecular modeling and simulation have become widely accepted tools in the applied sciences for detailed understanding of thermophysical processes. Molecular models (force fields) can be used as powerful tools for thermodynamic data prediction. The truncated and shifted Lennard-Jones (LJTS) potential [1] is one of the most basic and computationally inexpensive molecular models available. Nonetheless, it is still sufficiently realistic to represent nonpolar spherical molecules. It is defined by

$$\begin{aligned} {u(r)}_{\mathrm{LJTS}} =\left\{ \begin{array}{ll} u_{\mathrm{LJ}} \left( r \right) -u_{\mathrm{LJ}} \left( {r=r_{\mathrm{c}}} \right) &{}\quad \hbox {for }\;r\le r_{\mathrm{c} } \\ 0 &{}\quad \hbox {for }\; r>r_{\mathrm{c}} \\ \end{array}\right. , \end{aligned}$$

(1)

with

$$\begin{aligned} u_{\mathrm{LJ} }(r)=4\varepsilon \left[ {\left( {\frac{\sigma }{r}} \right) ^{12} -\left( {\frac{\sigma }{r}} \right) ^{6}} \right] , \end{aligned}$$

(2)

where $\varepsilon$ and $\sigma$ are the energy and size parameters of the Lennard-Jones (LJ) potential, $r$ is the distance between two particles, and $r_{\mathrm{c}}$ is a cut-off radius, which is $r_{\mathrm{c}} = 2.5\sigma$ here. Truncation leads to inexpensive simulation and avoids long-range corrections. The LJ fluid differs significantly from the LJTS fluid. For example, the critical temperature of the Lennard-Jones fluid is about $T_{\mathrm{c,LJ}} = 1.31$, whereas the critical temperature of the truncated and shifted version is about $T_{\mathrm{c,LJTS}} = 1.08$. The LJTS potential has been employed in numerous theoretical studies on phase coexistence [2–13] as well as in applications to noble gases and methane [14], where e.g., the vapor–liquid surface tension of the noble gases was predicted within 10 % of the experimental data. For the full Lennard-Jones fluid, several equations of state were published, e.g., Nicholas et al. [15], Johnson et al. [16], Kolafa and Nezbeda [17], Mecke et al. [18, 19], and May and Mausbach [20]. To our knowledge, no fundamental equation of state (FEOS) has been developed prior to this work for the LJTS model fluid. There is only a general approach how to convert a FEOS for the full Lennard-Jones model fluid into a FEOS for a truncated and shifted potential as published by Johnson et al. [16].

2 Molecular Simulation

The underlying dataset was generated by NVT molecular dynamics using the molecular simulation tool ms2 [21]. Newton’s equations of motion were solved using a fifth-order Gear predictor-corrector numerical integrator [1]. The temperature was kept constant using isokinetic velocity scaling [1]. Thermodynamic properties at 706 state points include pressure $p$, residual internal energy $u^{\mathrm{r}}$, first volume derivative of the residual internal energy ($\partial u^{\mathrm{r}}/\partial v)_{T}$, and residual isochoric heat capacity $c_{v}^{\mathrm{r}}$ as a function of temperature $T$ and density $\rho =N/V$. At each state point, $N=1372$ particles were sufficiently equilibrated and sampled for 2 to 5 million production time steps of $\Delta t (\varepsilon /m)^{1/2}/{\sigma }=0.001$, where $m$ is the molecular mass. Figure 1 shows the dataset in the $T$, $\rho$ plane. The energy and size parameters $\varepsilon$ and $\sigma$ of the potential were used to reduce all properties to dimensionless numbers of order unity: temperature $T^{*}=Tk_{\mathrm{B}}/\varepsilon$, density $\rho ^{*}=\rho \sigma ^{3}$, internal energy $u^{*}=u/\varepsilon$, enthalpy $h^{*}=h/\varepsilon$, or pressure $p^{*}= p\sigma ^{3}/\varepsilon$. For brevity, asterisks are omitted in the following with the understanding that reduced quantities are used. Results were validated with simulations of $N=2048$ and 3072 particles and no significant system size dependence was found (cf. Supplementary Material D). Statistical uncertainties of all results were estimated by a block averaging method [22].

Fig. 1

Simulation dataset used in the present FEOS development. Four independent thermodynamic properties were measured at each state point: pressure, residual internal energy, first volume derivative of the residual internal energy, and residual isochoric heat capacity

3 Equation of State

The present FEOS is written in terms of the reduced molar Helmholtz energy $\alpha$ as a function of temperature and density. The equation is decomposed into an ideal-gas contribution (superscript ${}^{\mathrm{o}}$) and a residual contribution due to the intermolecular interactions (superscript ${}^{\mathrm{r}}$)

$$\begin{aligned} \alpha \left( {\tau ,\delta } \right) =\frac{A\left( {T,\rho } \right) }{Nk_{\mathrm{B}} T}=\frac{a^{\mathrm{o}}\left( {T,\rho } \right) +a^{\mathrm{r}}\left( {T,\rho } \right) }{k_{\mathrm{B}} T}=\alpha ^{\mathrm{o}}\left( {\tau ,\delta } \right) +\alpha ^{\mathrm{r}}\left( {\tau ,\delta } \right) , \end{aligned}$$

(3)

where $k_{\mathrm{B}}$ is Boltzmann’s constant, $\tau =T_{\mathrm{c}}/T$, and $\delta =\rho /\rho _{\mathrm{c}}$ with $T_{\mathrm{c}} = 1.086$ and $\rho _{\mathrm{c}}= 0.319$. The critical parameters were determined during the fitting process. See Sect. 4.2.

As the LJTS model fluid is a classical monatomic model, the isobaric heat capacity of the ideal gas is $c_{p}^{\mathrm{o}}/k_{\mathrm{B}}=2.5$. Integration yields the ideal-gas contribution

$$\begin{aligned} \alpha ^{\mathrm{o}}=\ln \delta +1.5\ln \tau +c_1 \tau +c_2. \end{aligned}$$

(4)

The constants $c_{1}$ and $c_{2}$ were arbitrarily adjusted so that $h_{0}^{\mathrm {o}}=0$ and $s_{0}^{\mathrm {o}}=0$ at $T_{0}=0.8$, $p_{0}=0.001$, and the corresponding density of the ideal gas is $\rho _{0}=p_{0}/T_{0}$.

A common form for the residual part of the Helmholtz energy consists of polynomial, exponential, Gaussian bell-shaped, and non-analytic terms [23]. Polynomial and exponential terms capture the overall features of the FEOS. The Gaussian bell-shaped terms, introduced by Setzmann and Wagner [24] for methane, improve the representation of the properties in the critical region. Originally, these terms were used to yield significant contributions only near the critical point. However, with moderate parameters, they may also improve the Helmholtz energy surface over the entire fluid range [25]. Non-analytic terms were used only for the FEOS of water [26] and carbon dioxide [27]. These terms allow modeling the isochoric heat capacity and the speed of sound very close to the critical point. However, they require very accurate data in that region [23] which are not well accessible by molecular simulation.

The functional form of the present FEOS has 21 terms: 6 polynomials, 6 exponentials, and 9 Gaussian’s

$$\begin{aligned} \alpha ^{\mathrm{r}}\left( {\delta ,\tau } \right)&=\sum _{i=1}^6 {n_i \delta ^{d_i }\tau ^{t_i }} +\sum _{i=7}^{12} {n_i \delta ^{d_i }\tau ^{t_i }\exp \left( {-\delta ^{l_i }} \right) } \nonumber \\&\quad +\sum _{i=13}^{21} {n_i \delta ^{d_i }\tau ^{t_i }\exp \left( {-\eta _i \left( {\delta -\varepsilon _i } \right) ^{2}-\beta _i \left( {\tau -\gamma _i } \right) ^{2}} \right) }. \end{aligned}$$

(5)

The correlation is valid for temperatures $0.64<T<11$ and pressures $p<6.8$, corresponding to $0.6< T/T_{\mathrm{c}} <10$ and $p/p_{\mathrm{c}} <70$. No accurate triple-point temperature $T_{\mathrm{tr,LJTS}}$ of the Lennard-Jones truncated and shifted model fluid is available in the literature. Therefore, the well-known triple-point temperature of the Lennard-Jones fluid, which is about $T_{\mathrm{tr,LJ}} = 0.68$ [28], has been used as an estimate for the triple-point temperature $T_{\mathrm{tr,LJTS}} = 0.56$ by naive corresponding states estimation. To ensure that all simulations are located in the fluid region, the value was increased to $T = 0.64$. The coefficients, temperature and density exponents, as well as the Gaussian bell-shaped parameters are listed in Table 1.

Table 1 Parameters and coefficients of the residual part of the FEOS correlation, Eq. 5

The simultaneous determination of coefficients and parameters requires a non-linear fit algorithm which was provided by E. W. Lemmon from the National Institute of Standards and Technology (NIST). During the fit, simulation data were augmented by several thermodynamic constraints to ensure reasonable physical behavior of the FEOS results. Recent FEOS correlations for real substances, e.g., R-125 [29], propane [25], or propylene [30], show that correct FEOS behavior can be enforced for properties and regions where no data are available. Special attention was given to the vapor–liquid equilibrium (VLE) curves, rectilinear diameter, heat capacities, speed of sound, Gruneisen coefficient, the phase identifier parameter [31] (which significantly influences heat capacities and speed of sound), virial coefficients up to the fourth order, and ideal curves.

Figure 2 shows VLE in the critical region. The rectilinear diameter from the present FEOS exhibits a sudden bend very close to the critical point, which is not common for real fluids. Molecular simulation does most likely not allow for a verification of the effect. Therefore, it is at least not ruled out that the bend is correct.

Fig. 2

VLE in the critical region. Dashed line: saturated vapor density $\rho ^{\prime \prime }$, solid line: saturated liquid density $\rho '$, dashed-dotted line: rectilinear diameter $( \rho ' + \rho ^{\prime \prime })/2$

The virial coefficients $B$, $C$, and $D$ ensure a correct transition from the ideal-gas into the real fluid. They are calculated from the FEOS as

$$\begin{aligned} B\left( T \right)&= {\mathop {\lim }\limits _{\rho \rightarrow 0} \left( {{\partial \alpha ^{\mathrm{r}}}/{\partial \delta }} \right) _\tau }/{\rho _{\mathrm{r}} },\end{aligned}$$

(6)

$$\begin{aligned} C\left( T \right)&= {\mathop {\lim }\limits _{\rho \rightarrow 0} \left( {{\partial ^{2}\alpha ^{\mathrm{r}}}/{\partial \delta ^{2}}} \right) _\tau }/{\rho _{\mathrm{r}}^2 },\end{aligned}$$

(7)

$$\begin{aligned} D\left( T \right)&= {\mathop {\lim }\limits _{\rho \rightarrow 0} \left( {{\partial ^{3}\alpha ^{\mathrm{r}}}/{\partial \delta ^{3}}} \right) _\tau }/{\rho _{\mathrm{r}}^3 }. \end{aligned}$$

(8)

As the limit is $\rho \rightarrow 0$, they also determine the ideal curves, which prove a correct extrapolation behavior of the correlation for high temperatures, pressures, and densities. See Sect. 5.

Figure 3 is deduced from the virial equation,

$$\begin{aligned} Z=1+B\rho +C\rho ^{2}+D\rho ^{3}+\cdots . \end{aligned}$$

(9)

For $\rho \rightarrow 0$, intercepts with the ordinate are $B$, the slopes of the isotherms correspond to $C$, and the curvatures are $D$. As $D$ can be neglected for densities $\rho \,{<}\, {\approx } 0.2 \rho _{\mathrm{c}}$, the isotherms are nearly straight lines for low densities. The absolute values for $B$, $C$, and $D$ are shown in Fig. 4. The second virial coefficient $B$ passes through zero at the Boyle temperature $T_{\mathrm{BL}}$, reaches a maximum at the Joule-Thomson inversion temperature $T_{\mathrm{JT}}$, and approaches zero for high temperatures [32]. Not only the qualitative but also the quantitative behavior of the virial coefficients is correct. Therefore, calculated virial coefficients of Shaul et al. [33], Wheatley [33, 34], Hellmann [36], and this work were considered to validate the FEOS. All computed data for $B$ (Shaul et al. [33], Wheatley [35], and this work) are consistent and represented very well by the new FEOS. The data for $C$ of the same authors are also reproduced well. Only in the critical region, the FEOS calculations for $C$ are too low. For $D$, the behavior is quite similar to $C$ and qualitatively correct. Three computed datasets of Hellmann [36], Wheatley [35], and this work agree very well. Although no data for $D$ were used in the fit, the FEOS represents all of them qualitatively as well as quantitatively. For $C$, there is an unusual change in curvature for $3<T<100$. For $D$, a second maximum occurs at $T\approx 5$ in both the FEOS and data from direct numerical integration. These phenomena appear to exist for this model fluid, although they are not common in real fluids.

Fig. 3

$(Z-1)/ \rho$ as a function of $\rho$ along isotherms ($T=0.2$ to 2.8)

Fig. 4

Second, third, and fourth virial coefficients ($B$, $C$, and $D)$ as functions of temperature. The dashed line indicates the critical temperature. The dashed-dotted line indicates the Boyle temperature ($T_{\mathrm{BL}} = 2.784$), and the dotted line the Joule-Thomson inversion temperature ($T_{\mathrm{JT}}=20.09$)

Heat capacities and speed of sound are illustrated in Fig. 5. The residual isochoric heat capacity of the saturated liquid and vapor phase meet in an absolute maximum at the critical point. Compared to real fluids (water [26] or carbon dioxide [27]), the maximum of the present FEOS is less pronounced. Obviously, the critical region is described less accurately than for water [26] and carbon dioxide [27], which is a consequence of insufficient data in the critical region and the neglect of non-analytic terms. However, the critical region was not the main focus of this work. The speed of sound should exhibit a steep decrease in the critical region. Again, the effect is not as distinctive as for water [26] or carbon dioxide [27]. Nevertheless, the speed of sound of the saturated liquid as well as the isobars show a linear trend with negative slope, which indicates proper extrapolation behavior.

Fig. 5

Typical plots of residual isochoric heat capacity $c^{\mathrm{r}}_{v}$ (left) and speed of sound $w$ (right) as functions of temperature along isobars ($0.02<p_c <0.2$)

Further qualitative physical behavior of other thermodynamic properties is described by Lemmon and Jacobsen [29], Lemmon and Wagner [30], and Lemmon [37].

4 Simulation Data and Comparison to the Equation of State

Table 2 gives an overview of which property and how many data points were published. In this work, all literature data were used for comparison purposes only. As mentioned before, the only available data from the literature are VLE data (69 state points in total). This dataset was extended by nine VLE state points and 706 state points in the homogeneous fluid phase (cf. Fig.  1).

Table 2 VLE simulation data of the LJTS model fluid with $r_{\mathrm{c}}=2.5\sigma$ from the literature

4.1 Vapor–Liquid Equilibrium

Prior work mainly focused on VLE data. In this work, a FEOS valid for the entire fluid region was developed and used to set up ancillary equations for vapor pressure, saturated liquid density, and saturated vapor density. Although ancillary equations are not required when a full FEOS is available, they are useful for estimates in the iterative procedures to find the saturation states. They should not be used for calculating proper VLE data.

The vapor pressure, $p_\mathrm{{v}}$, may be represented by a modified Wagner equation [38],

$$\begin{aligned} \ln \left( {\frac{p_{\mathrm{v}} }{p_{\mathrm{c}} }} \right) =\frac{T_{\mathrm{c}} }{T}\left[ {N_1 \theta +N_2 \theta ^{1.5}+N_3 \theta ^{3.25}+N_4 \theta ^{4.85}+N_5 \theta ^{6.63}} \right] , \end{aligned}$$

(10)

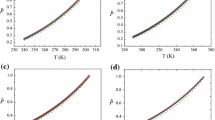
where $N_{1}=-6.21, N_{2}=1.5, N_{3}=-1.92, N_{4}=2.2, N_{5}=-4.76$, and $\theta =(1-T/T_{\mathrm{c}})$. The values of the critical parameters are given in Sect. 4.2. Comparison with simulation data and the present FEOS is presented in Fig. 6. Except for the data of Mareschal et al. [8], the agreement is within $\pm 2.5~\%$.

Fig. 6

Comparison with vapor pressure data from the literature. The FEOS is represented by the zero line, the ancillary equation by the solid line, and error bars are simulation uncertainties (if given by the authors)

The saturated liquid density $\rho '$ was represented by the ancillary equation

$$\begin{aligned} \frac{\rho {\prime }}{\rho _{\mathrm{c}} }=1+N_1 \theta ^{0.334}+N_2 \theta ^{0.667}+N_3 \theta ^{1.25}+N_4 \theta ^{1.92}, \end{aligned}$$

(11)

where $N_{1}= 1.45, N_{2}=-0.172, N_{3}=-0.298$, and $N_{4}=0.295$. Comparison with simulation data and the present FEOS is presented in Fig. 7. Except for 6 data points out of 77, the agreement is within ${\pm }1~\%$.

Fig. 7

Comparison with saturated liquid density data from the literature. The FEOS is represented by the zero line, the ancillary equation by the solid line, and error bars are simulation uncertainties (if given by the authors)

The saturated vapor density $\rho ^{\prime \prime }$ may be represented by the ancillary equation

$$\begin{aligned} \ln \left( {\frac{\rho {\prime \prime }}{\rho _{\mathrm{c}} }} \right) =N_1 \theta ^{1}+N_2 \theta ^{1.5}+N_3 \theta ^{5.94}+N_4 \theta ^{0.41452}, \end{aligned}$$

(12)

where $N_{1}= 1.59809, N_{2}=-0.09975, N_{3}=-0.4774$, and $N_{4}=-2.33736$. Comparison with simulation data and the present FEOS is presented in Fig. 8. Except for the dataset of Adams and Henderson [2], Dunikov et al. [5], and Mareschal et al. [8], agreement is within $\pm 3~\%$.

Fig. 8

Comparison with saturated vapor density data from the literature. The FEOS is represented by the zero line, the ancillary equation by the solid line, and error bars are simulation uncertainties (if given by the authors)

4.2 Critical Point

Critical parameters from the literature are given in Table 3. The critical values for temperature and density of Vrabec et al. [14] were taken as a starting point for setting up the present FEOS. As both parameters were included in the fitting process (not constrained), their influence on thermodynamic properties was monitored carefully. Special attention was given to the first and second derivatives of pressure with respect to density, which vanish at the critical point. The critical temperature $T_{\mathrm{c}} = 1.086$ and the critical density $\rho _{\mathrm{c}} = 0.319$ were found which are within the uncertainties of the data by Dunikov et al. [5] and Smit [13]. The critical pressure $p_{\mathrm{c}} = 0.101$ can then be calculated from the present FEOS.

Table 3 Critical parameters of the LJTS model fluid with $r_{\mathrm{c}}=2.5\sigma$ from the literature

4.3 Homogenous Fluid States

In this work, a comprehensive dataset for the homogenous fluid regions was simulated to set up the FEOS which is valid for a wide range of temperature, density, and pressure. The numerical values of the simulation data are given in the Supplementary Material B.

The accuracy of the FEOS was determined by relative deviations of all properties at all state points depicted in Fig. 9 along randomly selected isotherms. Comparisons using the complete dataset can be found in Supplementary Material C. Thermodynamic consistency was verified and most of the simulation data were represented within their statistical uncertainty.

Fig. 9

Comparison of the present molecular simulation data with the FEOS as a function of density along selected isotherms

The uncertainty of density calculated with the present FEOS is $\pm 0.2~\%$. In the extended critical region ($1 < T <1.5$), the deviations increase to $\pm 1~\%$. The uncertainty in the residual internal energy is $\pm 0.3~\%$, up to $\pm 0.5~\%$ for high temperatures. Deviations for the residual isochoric heat capacity and the first volume derivative of the residual internal energy at constant temperature are less than $\pm 5~\%$. For higher temperatures, the deviations for the residual isochoric heat capacity are below $\pm 2~\%$. Deviations of total isochoric heat capacity are also shown. Agreement is within $\pm 2~\%$ and less than $\pm 0.5~\%$ for higher temperatures. Thus, the new FEOS can be classified as a technical equation of state [23].

5 Extrapolation Behavior

Although the range of validity of the FEOS for the LJTS model fluid is defined by $0.6<T/T_{\mathrm{c}}<10$ and $p/p_{\mathrm{c}}<70$ (based on the available molecular simulation data), the FEOS can be extended in all directions (higher temperatures, pressures, densities, and lower temperatures), while maintaining a physically reasonable behavior. As explained in Sect. 3, this was achieved by applying proper constraints to the fit, based on experience from past FEOS fitting work on real substances [25, 28, 29]. Good extrapolation behavior is also beneficial within the range of validity. Poor extrapolation usually causes incorrect slopes in the validity range for properties such as the heat capacities. The investigation of the extrapolation behavior includes four different aspects: the representation of simulation data outside the given range of validity, the functional form, the representation of ideal curves, and physically reasonable behavior of different thermodynamic properties such as speed of sound or heat capacities.

To study the extrapolation capability, additional data points were simulated along the isochore $\rho =0.5$ ($15 < T< 19$) and the isotherm $T=20$ ($0.1 < \rho <0.6$) outside the range of validity. Figure 10 shows that for densities up to $\rho =0.6$, the data can be represented within $\pm 0.05\,\%$. The isochore $\rho =0.5$ is predicted within $\pm 0.05\,\%$, too.

Fig. 10

Comparison of additional molecular simulation data with the extrapolated FEOS at isotherm $T = 20$ (left) and isochore $\rho = 0.5$ (right). These data were not used for the development of the FEOS

A reasonable behavior can be observed along the saturated liquid line for the speed of sound, which is a straight line down to a reduced temperature of about $T/T_{\mathrm{c}}=0.04$. The residual isochoric heat capacity (Fig. 5) shows an upward trend in the liquid phase at low temperatures, which is common for many real fluids and has been validated experimentally [25]. Pressure versus density to extreme conditions is presented in Fig. 11 on the left. Obviously, extrapolation is smooth to extremely high temperatures, pressures, and densities, which is controlled by the functional form of the FEOS. As discussed in detail by Span and Wagner [32], the extrapolation to high temperatures and pressures is mainly influenced by polynomial and exponential terms with power $l_{i}=1$. In the investigated region, $\delta = \rho /\rho _{\mathrm{c}}$ reaches a high value, whereas $\tau =T_{\mathrm{c}}/T$ is decreasing. Therefore, the density exponent $d_{i}$ must be high (but not too high to prevent overestimation of the curvature) and the temperature exponent must be low. The first polynomial term of the present FEOS with exponents $t_{1}=1$ and $d_{1}=4$, which were found to be an effective combination by Lemmon and Jacobsen [29], accounts for the correct behavior of the investigated isotherms. The density exponent $d_{1}$ is high enough to model the increasing temperature at increasing pressure and density, but avoids unreasonably pronounced curvature of isotherms. The temperature exponent $t_{1}$ ensures that intersecting isotherms are avoided and isotherms converge towards each other. Additionally, the corresponding coefficient $n_{1}$ has to be positive so that no negative pressures occur.

Fig. 11

Pressure versus density diagram along isotherms (left) and ideal curves (right). $p_\mathrm{v}$: vapor pressure curve; ID: ideal curve $\left( {\frac{\partial \alpha ^{\mathrm{r}}}{\partial \delta }} \right) _\tau =0$, BL: Boyle curve $\left( {\frac{\partial \alpha ^{\mathrm{r}}}{\partial \delta }} \right) _\tau +\delta \left( {\frac{\partial ^{2}\alpha ^{\mathrm{r}}}{\partial \delta ^{2}}} \right) _\tau =0$, JTI: Joule-Thomson inversion curve $\left( {\frac{\partial \alpha ^{\mathrm{r}}}{\partial \delta }} \right) _\tau +\delta \left( {\frac{\partial ^{2}\alpha ^{\mathrm{r}}}{\partial \delta ^{2}}} \right) _\tau +\tau \left( {\frac{\partial ^{2}\alpha ^{\mathrm{r}}}{\partial \delta \partial \tau }} \right) =0$, JI: Joule inversion curve $\left( {\frac{\partial ^{2}\alpha ^{\mathrm{r}}}{\partial \delta \partial \tau }} \right) =0$

Finally, some ideal curves were investigated. Figure 11 shows the Boyle curve, the Joule-Thomson inversion curve, the Joule inversion curve, and the ideal curve. Shapes are similar to those of real fluids [32] without unreasonable inflection points or deformations. Thus, these ideal curves indicate a qualitatively correct extrapolation behavior of the FEOS extending to high temperatures and pressures.

6 Conclusion

Based on molecular simulation data, a new FEOS was developed for the LJTS model fluid. The equation is expressed in terms of the Helmholtz energy, can be implemented easily in common software packages, and can be used to calculate all thermodynamic properties, e.g., density, VLE data, heat capacities, speed of sound, or internal energy by differentiation only. It is valid for temperatures $0.64<T<11$ and for pressures $p<6.8$, corresponding to $0.6<T/T_{\mathrm{c}}<10$ and $p/p_{\mathrm{c}}<70$. Uncertainties of the FEOS were studied by comparison to simulation data. The uncertainty in density is $\pm 0.2~\%$. In the extended critical region ($1 < T < 1.5$), deviations increase to $\pm 1~\%$. The uncertainty in the residual internal energy is 0.3 % to 0.5 % for high temperatures, and 1 % for the residual enthalpy. Deviations for the residual isochoric heat capacity and the first derivative of the residual internal energy with respect to volume at constant temperature are less than $\pm 5~\%$. For higher temperatures, deviations for the residual isochoric heat capacity are below $\pm 2~\%$.

Reference values are given in Table 4 to verify a computer implementation of the FEOS. Additionally, the FEOS is given as a source code in the Supplementary Material D.

Table 4 Calculated properties for computer implementation verification

This work is a first step to show that molecular simulation data can be used to set up FEOS correlations for a wide temperature and pressure range. Work on a new equation of state for the Lennard-Jones model is in progress.