1 Introduction

According to its definition, the binary diffusion coefficients (BDCs) or interdiffusion coefficients of gases characterize the velocity of spontaneous interpenetration of the substances due to inhomogeneity of composition. Nowadays, the BDC are widely used in the calculation of various heat and mass transfer setups, processes of chemical kinetics and combustion, as well as to obtain data needed for the calculation of the parameters of the intermolecular interaction of diverse molecules. Considering the application of these coefficients in thermodynamic calculations, it is crucial to investigate their dependences on temperature and pressure.

At present, the temperature dependence of the BDCs at elevated pressures is an insufficiently explored area. As a rule, the pressure dependence of the BDCs is measured and analyzed at a fixed temperature. In a few existing papers on the temperature dependence of BDCs, studies have been carried out at different pressures, mainly at low temperatures [1–4]: from a temperature of 350 K and below in the narrow temperature range from 100 K to 150 K.

On the other hand, in the rarefied gases the temperature dependence of BDCs can be evaluated within the framework of the rigorous kinetic theory by generalizing experimental data and restoring the parameters of an interaction potential, for example, using the weighted least-squares method [5], or a variety of semi-empirical methods based on the rigorous or elementary kinetic theories [6, 7]. The accumulated extensive experimental data of studies on the temperature dependence of the BDCs in the rarefied gases show that a simple power law gives sufficient accuracy [6–9].

The power dependence of the BDCs on temperature corresponds to the potential of point centers of force [10]. The exponent in the temperature dependence of the BDCs is not a constant, but a function of temperature; that should be considered in calculations. Therefore, the range of temperatures in which it is possible to use the obtained function of the temperature dependence of the BDCs should be listed along with the exponent.

2 Experimental Setup and Technique

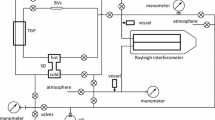
A well-established steady-flow method [11, 12] was used for the measurements of BDCs with the use of the diffusion apparatus [13], which allows implementation of this method to measure BDCs in dense gases. A general diffusion cell apparatus is shown in Fig. 1. Two channels 1 and 2 were connected by a set of thin narrow tubes—capillary \(K\) with length of \(L\) and cross-sectional area \(S\). Channels were blown with gases \(A\) and \(B\) at the same flow rate. The resistance of the gap (capillary K) was much greater than the channel resistance. As a result of diffusion through the capillary, there were no pure gases at the outlet of the cell, just mixtures. It was necessary that there was no pressure difference between the channels, so that the mass transfer was due to a process of diffusion. Gases in channels 1 and 2 were supplied and taken away with the help of two cylinders with pistons of the same diameter, so that the gas volume flow rate \(\upsilon \) in the two channels was the same before and after the capillary. Hence, measurements of the BDCs were carried out in the average volume frame of reference.

Fig. 1
figure 1

Diffusion cell in a steady-flow method

Full size image

Earlier we used the setup to measure the BDCs in the dense gases with the use of a steady-flow method; it is described previously [14] in detail. As an analyzer of the gas mixture, the Rayleigh interferometer was used. The length of the cuvette was 1 m, and it had been scaled by changing the argon pressure in the right half of the cell. So after the experiment had been finished, the numerical fraction of the diffused gas was measured by the Rayleigh interferometer. Further, the volume fraction was calculated, using the value of the numerical fraction and the compressibility factors of pure gases. The total error of calculation was less than 1 %. In our experiments, the volume fraction of impurity was rather small in the range from 0.005 to 0.025. Moreover, it is known that when the change of the volume fraction is comparatively small, the BDC is almost independent of concentration (volume fraction) or depends slightly [2, 15].

Calculations of the diffusion coefficient were evaluated using the known formula [12] of the steady-flow method:

$$\begin{aligned} D_{12} =\frac{c \upsilon L_\mathrm{eff} }{S\left( {1-c} \right) }, \end{aligned}$$
(1)

where \(c\) is the volume fraction of the diffusing gas, \(L_{\mathrm{eff}}\) is the effective length of the capillary tube, \(S\) is the cross-sectional area of the capillary tubes, and \(\upsilon \) is a gas volume flow rate. The values of the flow rate were adjusted in each experiment based on the following conditions: the volume fraction of the second component in the gas blown through the channel should not exceed 0.01 to 0.03. Thereby, the effects of mixing can be neglected [9]. The effects of mixing consist of the pressure changes in the vessels due to non-equivalence of the compressibility of the mixture and of the pure gases. However, the increase of this pressure at low pressures remains negligible within the error of the pressure measurement. Our own studies have shown that the changes in the diffused gas volume fraction within 0.005 to 0.025 had no effect on the measured value of the diffusion coefficient.

In [16] it was found that when an open end of the capillary tube was blowing, the diffusing substance was washing out to a depth of \(l_{i}\). The value of the depth of washing out \(l_{i}\) depends on the Reynolds number and the capillary diameter \(d\), and at Re \(<20\) is defined as follows:

$$\begin{aligned} {l_i }/d=1.35\times 10^{-2}+1.69\times 10^{-1}{Re}+1.3\times 10^{-2}{Re}^{2}+\ldots , \end{aligned}$$
(2)

where the Reynolds number is determined as

$$\begin{aligned} {Re}=\frac{Ux\rho }{\eta }, \end{aligned}$$

where \(U\) is the velocity of the gas in the channel, \(x\) is a characteristic linear dimension, here it is the height of the gap, \(\eta \) is the dynamic viscosity of gas, and \(\rho \) is the density of gas. That is, the effective length of the capillary tube is shorter than the actual one by the value of \( l_{i }\) on each side of the tube, respectively. Our experiments had shown that the Reynolds number in our setups varied from 0.1 to 20.

We used two more cells with geometrical parameters presented in Table 1, different from those two described in [14]. These four cells allowed us to measure the BDCs in the pressure range from 0.1 MPa to 15 MPa and the temperature range from 250 K to 900 K. The experimental error of the measurement of temperature was in the limits of 0.03 % and of pressure was in the range from 0.02 % to 0.7 %.

Table 1 Geometrical dimensions of additional diffusion cells used to measure the BDC by steady-flow method
Full size table

Additional studies showed that the measured values of the BDCs obtained with the use of four cells under the same experimental conditions were consistent with each other within the experimental error.

With a reliability of \(\alpha = 0.95\), the total error of the experiment remained the same: from 1 % to 2 % for the whole set of the experimental data for all the examined systems of gases. The error was estimated as a sum of a random measurement uncertainty and a systematic measurement uncertainty.

3 Results of Measurements and Calculation of the BDCs

In the apparatus described above with the use of different diffusion cells, the experimental study of the temperature dependence of the BDCs was carried out for the following five binary mixtures of gases: \(\mathrm{H}_{2}{-}\mathrm{N}_{2}, \mathrm{H}_{2}{-}\mathrm{CO}, \mathrm{H}_{2}{-}\mathrm{CH}_{4}, \mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\), and \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\). The measurements were obtained in the temperature range from 250 K to 900 K and the pressure range from 0.1 MPa to 15 MPa. Samples of high purity were taken: \(\mathrm{N}_{2}\)—99.996 %, \(\mathrm{H}_{2 }\)—99.994 %, \(\mathrm{CH}_{4}\)—99.9 %, \(\mathrm{C}_{2}\mathrm{H}_{6}\)—99.5 %, \(\mathrm{C}_{3}\mathrm{H}_{8}\)—99.97 %, and \(\mathrm{CO}\)—99.8 %.

The results of the measurements are shown in Tables 2, 3, 4, 5, and 6.

Table 2 Temperature dependence of the binary diffusion coefficients of \(\mathrm{H}_{2}{-}\mathrm{N}_{2}\) at different pressures
Full size table
Table 3 Temperature dependence of the binary diffusion coefficients of \(\mathrm{H}_{2}{-}\mathrm{CO}\) at different pressures
Full size table
Table 4 Temperature dependence of the binary diffusion coefficients of \(\mathrm{H}_{2}{-}\mathrm{CH}_{4}\) at different pressures
Full size table
Table 5 Temperature dependence of the binary diffusion coefficients of \(\mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\) at different pressures
Full size table
Table 6 Temperature dependence of binary diffusion coefficients of \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\) at different pressures
Full size table

To determine the exponents of the temperature dependence at the pressure of 0.1 MPa, the experimental data for the BDCs of these gaseous systems obtained by other authors [8, 17–20] were also processed, in addition to the values given in Tables 2, 3, 4, 5, and 6. A well-known empirical formula for the BDC dependence on temperature in the rarefied gases was used for evaluating the exponent \(n\) of a power law:

$$\begin{aligned} D_{1 2 }^T =D_{1 2 }^0 \left( {\frac{T}{T^{0}}} \right) ^{n} , \end{aligned}$$
(3)

where \(D_{1 2}^T \) represents the value of the BDC at pressure \(P^{0}\) and at temperature T, \(D_{1 2}^0 \) represents the experimental value of the BDC at pressure \(P^{0}\) and temperature \(T^{0}\), and \(n\) is the exponent of the generalized temperature dependence.

It is helpful to present Eq. 3 in a logarithmic form for additional analysis:

$$\begin{aligned} \mathrm{lg}\left( {D_{1 2 }^T } \right) =n\cdot \lg (T)+\left( {\lg \left( {D_{1 2 }^0 }\right) -n\cdot \lg ({T^{0}})}\right) . \end{aligned}$$
(4)

As initial data for the calculations, only those values of the BDCs were taken that had been obtained with the use of the following direct methods of measuring of the BDC: Loschmidt’s cell, two-bulb, and steady-flow methods. The data calculated on the base of experimental studies of other thermophysical properties of substances were not taken into account. Single measurements which significantly deviated from the calculated generalized dependences were also removed from the study. Table 7 shows the generalized empirical dependences of the BDCs on temperature for the examined systems at of 0.1 MPa. Table 7 also includes information about the temperature range in which the study was done, the number of experimental points and references, as well as the average deviation of the experimental values from this dependence. The calculation was performed with the use of an ordinary least-squares method.

Table 7 The power dependence of the BDC at pressure of 0.1 MPa for systems \(\mathrm{H}_{2}{-}\mathrm{N}_{2}, \mathrm{H}_{2}{-}\mathrm{CO}, \mathrm{H}_{2}{-}\mathrm{CH}_{4}, \mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\), and \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\)
Full size table

In [21] within the framework of the elementary kinetic theory with the use of the equation of molecular mass transfer obtained by Laranjeira [22], the following formula for calculating the value of the BDCs at different pressures has been obtained:

$$\begin{aligned} \overline{D_{1 2 }^{P,T} } =\frac{D_{1 2 }^T P^{0}}{P}z_1 z_2 A, \end{aligned}$$
(5)

where \(\overline{D_{1 2}^{P,T} } \) represents the integral value of the BDC at pressure \(P\) and temperature \(T\) in the given range of the volume-fraction changes and \(P^{0}\) is the pressure of the gas when the compressibility factor \(z_{i}\) is equal to unity. The multiplier \(A\) here is a dimensionless value that depends on the volume fraction. It is an integral characteristic in the given range of the volume-fraction changes in the process of gas diffusion, the formula for its calculation is given in [14, 21].

The compressibility factor of the gas can be defined by the following equation:

$$\begin{aligned} z_i =PV_i /RT, \end{aligned}$$

where \(R\) is the gas constant, \(P\) is the gas pressure; and \(V_{i}\) is the molar volume of gas \(i\) at a given temperature \(T\) and pressure \(P\).

Since the BDC dependence on temperature in the rarefied gases can be submitted as shown in Eq. 3, Eq. 5 can be rewritten as follows:

$$\begin{aligned} \overline{D_{1 2 }^{P,T} } =D_{1 2 }^0 \left( {\frac{T}{T^{0}}} \right) ^{n}\frac{P^{0}}{P}z_1 z_2 A. \end{aligned}$$
(6)

According to the results of our calculations, for all the studied systems, when the changes of the volume fraction of the diffusing component were within limits of 0.03, the value of the multiplier \(A\) differed from unity by less than 1 %. That fact helps to simplify the calculations by taking the ratio \(A\) equal to unity \((A = 1)\). The calculation error of the BDCs using Eq. 6 varies from 1 % to 3 % taking measurement uncertainties and uncertainties in the calculation of the compressibility factors \(z_{1}\) and \(z_{2}\) into account.

In [1] authors proposed to describe the dependence of diffusion coefficients on temperature and pressure with a power law in the form of the product of powers \(( {T/{T^{0}}})^{n}\) and \(( {{P^{0}}/P})^{m}\). As the authors stated, there is good agreement with experiment at low temperatures for three pairs of gases. However, according to our calculations, our experimental data are in good agreement with the values of the BDCs calculated by the proposed formula in [1] which is valid only in a narrow temperature range. Obviously, this is because exponent \(m\) changes its value depending on temperature.

Figure 2 shows graphs of the temperature dependence of the BDCs at different pressures: 0.1 MPa, 4.0 MPa, 7.0 MPa, 10.0 MPa, and 15.0 MPa. Our experimental values of the BDC are marked with symbols, while the ones calculated with the use of Eq. 6 are presented as curves. For easier analysis the graphs are drawn in the following form: \(\lg ({{D_{12}^{P,T} }\big /{D_{1 2 }^P }})=f( {\lg ( {T\big /T^{0}} )} )\). It can be seen that there is a good agreement between the measured and calculated values of the BDC of the gases. It should be noted that temperature dependence of the BDC becomes rather complicated at pressures greater than 0.1 MPa. The law of this dependence is determined by the individual properties of the gases, in particular by the dependence of the compressibility factor on temperature.

Fig. 2
figure 2

Temperature dependence of the experimental (symbols) and calculated (curves) values of the BDC at different pressures for binary systems: (a) \(\mathrm{H}_{2}{-}\mathrm{N}_{2}\), (b) \(\mathrm{H}_{2}{-}\mathrm{CO}\), (c) \(\mathrm{H}_{2}{-}\mathrm{CH}_{4}\), (d) \(\mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\), and (e) \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\)

Full size image

In Fig. 3, the graphs of the temperature dependences of the BDC values are presented at the same pressure of 7 MPa in the temperature range from 400 K to 900 K for all five systems studied. The graphs exhibit that the temperature dependence is practically reduced to a power law for the systems \(\mathrm{H}_{2}{-}\mathrm{N}_{2}\) and \(\mathrm{H}_{2}{-}\mathrm{CO}\), while it becomes more complex for systems \(\mathrm{H}_{2}{-}\mathrm{CH}_{4}\), \(\mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\), and \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\). The last one is described neither by a power law (4) nor by the formula suggested in [1]. However, at higher temperatures (600 K or higher) the dependence is getting closer to a power law. It suggests that it is determined by the nature of the dependence of the compressibility factor on temperature for these gases (\(\mathrm{H}_{2}, \mathrm{CH}_{4}, \mathrm{C}_{2}\mathrm{H}_{6}\), and \(\mathrm{C}_{3}\mathrm{H}_{8})\).

Fig. 3
figure 3

Temperature dependence of the experimental (symbols) and calculated (curves) values of the BDC at the same pressure of 7.0 MPa for binary systems: \(\mathrm{H}_{2}{-}\mathrm{N}_{2}\), \(\mathrm{H}_{2}{-}\mathrm{CO}\), \(\mathrm{H}_{2}{-}\mathrm{CH}_{4}\), \(\mathrm{H}_{2}{-}\mathrm{C}_{2}\mathrm{H}_{6}\), and \(\mathrm{H}_{2}{-}\mathrm{C}_{3}\mathrm{H}_{8}\)

Full size image