An iterated-tabu-search heuristic for a variant of the partial set covering problem

Abstract

In this paper, we propose a heuristic algorithm to solve a new variant of the partial set covering problem. In this variant, each element $e_i$ has a gain $g_i$ (i.e., a positive profit), each set $s_j$ has a cost $c_j$ (i.e., a negative profit), and each set $s_j$ is part of a unique group $G_k$ that has a fixed cost $f_k$ (i.e., a negative profit). The objective is to maximize profit and it is not necessary to cover all of the elements. We present an industrial application of the model and propose a hybrid heuristic algorithm to solve it; the proposed algorithm is an iterated-local-search algorithm that uses two levels of perturbations and a tabu-search heuristic. Whereas the first level of perturbation diversifies the search around the current local optimum, the second level of perturbation performs long jumps in the search space to help escape from local optima with large basins of attraction. The proposed algorithm is evaluated on thirty real-world problems and compared to a memetic algorithm. Computational results show that most of the solutions found by ITS are either optimal or very close to optimality.

1 Introduction

The set covering problem (SCP) is an NP-hard optimization problem (Garey and Johnson 1979) that has been extensively studied in operations research and combinatorial optimization. The SCP can be defined as follows: let $E=\{e_1,\dots ,e_m\}$ be a universe of elements and $S=\{s_1,\dots ,s_n\}$ be a collection of subsets $s_j \subset E$, where $\bigcup {s_j}=E$, with $j$ = 1 ...$n$. Each set $s_j$ covers at least one element of $E$ and has a cost $c_j>0$. The objective is to find a sub-collection of sets $X \subseteq S$ that covers all of the elements in $E$ at a minimal cost. The SCP has been applied to a wide range of industrial applications including scheduling, manufacturing, service planning and location problems (Caprara et al. 1999; Lan et al. 2007; Balas 1983).

To address the specific needs of some applications, the partial set covering problem (PSCP) has been introduced. The PSCP is a generalization of the SCP where it is either not necessary or not possible to cover all of the elements of $E$ because of other objectives or constraints. Several variants of the PSCP have been proposed in the literature. In the k-set covering variant (Athanassopoulos et al. 2009), the aim is to cover at least $k$ elements at a minimal cost. In the facility location variant (Farahani and Hekmatfar 2009), the total number of facilities (i.e., total budget) allowed to cover the demand points (i.e., the elements) is usually limited, and as a result, some demand points cannot be covered. The budgeted maximum coverage location problem (Khuller et al. 1999) is a particular case of facility location problems and it involves choosing a subset of sets from a collection of sets of weighted elements, to maximize the total weight that is covered under a given budget constraint. Another variant of the PSCP called the prize-collecting set cover problem has been proposed in (Könemann et al. 2006). In this variant, a profit $p_j$ is associated with each element $e_i \in E$. The objective is to find a minimum cost subset of $S$ such that the total profit of the covered elements is greater than or equal to a specified profit bound.

In order to solve an industrial problem (which is described in Sect. 2.1), we introduce a profit-maximization variant of the partial set covering problem (PMSCP). In this variant, each element $e_{i}$ has a gain $g_{i}$ (i.e., a positive profit), each set $s_j$ has a cost $c_j$ (i.e., a negative profit), and each set $s_j$ is part of a unique group $G_k$ that has a fixed cost $f_k$ (i.e., a negative profit). The fixed cost of a group is paid only once, namely, whenever a set of the group is added to the solution. The objective is to maximize the total profit represented by the total gain of the covered elements minus the total cost of the sets and groups that are used in the solution. The profit-maximization objective encapsulates the idea that when the additional cost that is required to cover certain uncovered elements is higher than the additional revenue ($\sum {g_i}$) associated with these elements, it is better to leave these elements out of the cover.

To solve the PMSCP, we propose an iterated-tabu-search (ITS) algorithm (ITS) that is an iterated-local-search (ILS) algorithm, where a tabu-search heuristic (TS) is used for local-search. An important characteristic of our algorithm is the use of a second perturbation operator in the ILS framework that helps escaping from local optima and hence, increases the chances of reaching optimal solutions.

Because the PMSCP is a new problem that has not previously been solved in the literature, there are no existing algorithms to which we can compare our heuristic. Instead, we adapted one of the best heuristics that has been developed for the SCP (which is a very similar problem) and compared our heuristic to it. The adapted algorithm has been developed by Beasley and Chu (1996) and is described in Sect. 4. The two algorithms are compared on 30 real world test problems (Sect. 5). Additionally, limited experiments using the general purpose solver CPLEX are performed to validate our results.

The main contributions of this work are the use of tabu-search and a second perturbation operator in the ILS framework. To our knowledge, iterated-local-search has not previously been used to solve the partial or standard set covering problem. In addition, we present a new variant of the PSCP and a new practical application of it.

2 Modeling a mining-industry application with the PMSCP

2.1 The mining application

We originally developed our profit-maximization variant of the PMSCP to solve a mining-industry problem called drillholes placement. The first steps in the mining cycle are exploration and feasibility. In the exploration stage, geologists start by estimating the potential locations of mineral deposits. Then, they drill many long holes inside the mine and extract samples from these potential sites for analysis and to confirm or adjust their estimations. Because drilling is expensive, geologists and mining engineers try to position their holes to cover most potential sites with a minimum amount of drilling. Minimizing the amount of drilling involves choosing the number, location, orientation and length of each drill hole to minimize the total cost of drilling. In addition to the cost of drilling, moving the drill-platform from one location to another is also expensive. The locations where the drill-platform can be positioned are called drill stations.

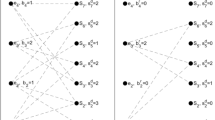
Usually, geologists express their estimations in the form of a 3D model; in the mining industry, this model is often called a block model. A block model is a set of cubic blocks of equal size where each block is characterized by the estimated grade of the minerals it may contain. Using this block model and the available drill stations, it is possible to create a set that contains all of the potential drill holes that can be drilled inside the mine. In this set of drill holes, each drill hole can have any length and orientation that is feasible using the drill, which can be rotated both horizontally and vertically. In addition, each drill hole covers at least one block and the drill holes are grouped by drill stations. A block is said to be covered by a given drill hole if the orthogonal distance from the center of the block to the drill hole is smaller than a given value. Figure 1 shows an example of a set of potential drill holes in a 2-D block model where only two drill stations are shown for illustration purposes. To illustrate the drill hole coverage, the blocks covered by one of the drill hole (highlighted in bold) are shown in gray.

Fig. 1

Set of potential drill holes

Each drill hole has a cost that is proportional to its length and each block has a gain that is proportional to the importance of covering that block. Because the blocks are only explored (not extracted) in the exploration stage, the gain attributed to each block is the highest cost that we would find it worthwhile to pay to cover that block (not the value of the minerals that are inside that block). A geostatistical classification method can be used to separate important blocks from less important ones, which makes the attribution of the gains easier. For instance, the classification method proposed by Pan (1995) allows separating the blocks into five different categories.

From the set of all possible drill holes, we want to choose a subset of drill holes that maximizes the profit represented by $\sum {\text{ gains } \text{(blocks } \text{ covered) }} - \sum {\text{ costs } \text{(drill } \text{ holes } \text{ selected) }} - \sum {\text{ costs } \text{(drill } \text{ relocation) }}$.

In order to solve this problem with our PMSCP model, we need to generalize the concepts of drill holes, blocks and drill stations. Because a drill hole covers a set of blocks and because the drill holes are grouped by drill stations, a block can be modeled as an element $(e_i)$, a drill hole can be modeled as a set of elements $(s_j)$ and a drill station can be modeled as a group of sets $(G_k)$. Moreover, each element has a gain $(g_i)$, each set has a cost $(c_j)$ and each group has a fixed cost $(f_k)$. Because the cost of moving the drill to a new location is paid exactly once, the cost of a group $f_k$ is modeled as a fixed cost.

2.2 The PMSCP model

The PMSCP is a maximization problem that can be formulated as follows. Let

• $A^{m\times n}$ be a zero-one matrix where $a_{ij}=1$ if the element $e_i$ is covered by the set $j$, and $a_{ij} = 0$ otherwise.

• $B^{l\times n}$ be a zero-one matrix where $b_{kj}=1$ if the set $s_j$ is part of the group $G_k$, and $b_{kj} = 0$ otherwise.

• $X=\{x_1,x_2,\dots ,x_n\}$ where $x_j=1$ if the set $s_j$ (with cost $c_j>0$) is part of the solution, and $x_j=0$ otherwise.

• $Y=\{y_1,y_2,\dots ,y_m\}$ where $y_i=1$ if the element $e_i$ (with a gain $g_i>0$) is covered in the solution, and $y_i=0$ otherwise.

• $GR=\{gr_1,gr_2, \dots ,gr_l\}$ where $gr_k=1$ if at least one set of the group $G_k$ (with a cost $f_k>0$) is part of the solution, and $gr_k=0$ otherwise.

Maximize

$$\begin{aligned} \sum \limits _{i = 1}^m {{g_i}{y_i}} - \sum \limits _{j = 1}^n {{c_j}{x_j}} - \sum \limits _{k = 1}^l {{f_k}{gr_k}} \end{aligned}$$

(1)

subject to

$$\begin{aligned}&{y_i} \le \sum \limits _{j = 1}^n {{a_{ij}}{x_j}}, \quad i = 1,\dots ,m \end{aligned}$$

(2)

$$\begin{aligned}&{b_{kj}}{x_j} \le {gr_k}, \quad j=1,\dots ,n; \quad k = 1,\dots ,l \end{aligned}$$

(3)

$$\begin{aligned}&{x_j},{y_i},{gr_k} \in \{ 0,1\}&\end{aligned}$$

(4)

Each set is part of exactly one group and each group must contain at least one set. Constraint (2) implies that an element is covered if at least one of the sets that covers it is part of the solution, and constraint (3) implies that a group is part of the solution if at least one of the sets that it contains is part of the solution. In fact, the purpose of constraints (2) and (3) is to keep track of which elements are covered and which groups are used in a given configuration.

Throughout all this paper, the term solution or configuration refers to the collection of selected sets (i.e, all of the sets $s_j$ such that $x_j = 1$).

3 The proposed ITS algorithm

In this work, we propose a hybrid heuristic algorithm to solve the PMSCP. The proposed algorithm is hybrid because it combines two metaheuristics: iterated-local-search (ILS) and tabu-search (TS).

Iterated-local-search is a simple but very effective metaheuristic that has been successfully applied to many difficult optimization problems, such as the traveling salesman problem (Martin et al. 1991; Johnson 1990; Johnson and McGeoch 1997; Katayama et al. 1999), scheduling problems (Congram et al. 2002; Stützle 1998; Lourenço and Zwijnenburg 1996; Balas and Vazacopoulos 1998; Kreipl 2000), graph partitioning (Martin and Otto 1995, 1996) and MAX-SAT (Battiti and Protasi 1997). The aim of iterated-local-search is to explore the space of local optima in an efficient and effective way. ILS manipulates a single solution using two main operators: a local-search operator and a perturbation operator. In each iteration, a new starting point is created using the perturbation operator and a new local optimum is found using the local-search operator. The new local optimum is kept if it passes a given acceptance criterion; otherwise, a new iteration is performed using the previous local optimum.

The perturbation and local-search operators must be carefully designed to work well together. Furthermore, the perturbation must be large enough to ensure that it is not negated by the local-search operator and small enough to avoid a random-restart behavior. A complete description and guide for building effective iterated-local-search algorithms is presented in (Lourenço et al. 2002).

Tabu-search (TS) is a local-search algorithm that uses a search history to escape from local optima and cycles. The search history of TS is saved in a list, which is called the tabu-list. Whenever a move is performed, the reverse move is added to the tabu-list. A move stays in the tabu-list for a limited number of iterations (equal to the length of the tabu-list). A move is forbidden as long as it is part of the tabu-list. Another important component of tabu-search is the aspiration criterion that allows a tabu move to be performed in some circumstances. A typical aspiration criterion, which is actually used in this paper, allows a tabu move to be performed when the resulting solution is better than the current best solution. A full description of tabu-search can be found in (Glover et al. 1989; Glover and Taillard 1993; Zäpfel et al. 2010).

To achieve better results, many authors have combined iterated-local-search with other heuristics such as the genetic algorithm (Azim and Ben Othman 2010), variable neighborhood descent (VND) (Chen et al. 2008), GENIUS (Subramanian 2011) and tabu-search (TS) (Misevičius et al. 2006; Smyth et al. 2003; Misevičius 2004; Palubeckis 2007). When tabu-search is used as the local-search operator in ILS, the resulting ILS algorithm is often called iterated-tabu-search.

The algorithm proposed in our paper is an ITS algorithm with two levels of perturbations: whereas the first level of perturbation diversifies the search around the current local optimum, the second level of perturbation performs long jumps in the search space to help escape from local optima with large basins of attraction. In each iteration, the first perturbation operator is invoked; then, a short run of tabu-search is performed. The second perturbation operator is invoked if the current best solution is not improved after $stag_{(ITS)}$ iterations, where $stag_{(ITS)}$ is a parameter. The acceptance criterion that is used only allows a better solution to replace the current local optimum at the end of each iteration. The algorithm stops after a limited computation time.

3.1 Solution-representation and objective function

We use a binary-string solution representation in ITS where the $i$th bit is equal to one if set $i$ is part of the solution, and the $i$th bit is equal to zero otherwise.

Let $X$ be a given configuration, $S_X$ be the sets used in $X$, $E_X$ be the elements covered by $X$ and $G_X$ be the groups used in $X$. Then, the objective-score of $X$ can be calculated as follows:

$$\begin{aligned} \mathrm {score}(X) = \sum \limits _{e \in {E_X}} {\mathrm {gain}(e)} - \sum \limits _{s \in {S_X}} {\mathrm {cost}(s)} - \sum \limits _{g \in {G_X}} {\mathrm {cost}(g)} \end{aligned}$$

3.2 Perturbation operators

As mentioned earlier, we use two perturbation operators in ITS. The first perturbation operator (see Algorithm 1) diversifies the search around the current best solution by randomly removing sets from (or adding sets to) the current configuration. This operator iterates over the bits of value 1 and flips each bit to 0 with a probability $p$. Afterward, if $n$ bits have been flipped from 1 to 0, $n$ new bits are randomly chosen and flipped from 0 to 1 (if a bit is already equal to one, it is left at 1). The goal is to ensure that the number of bits that have been flipped from 0 to 1 is less than or equal to the number of bits that have been flipped from 1 to 0; the reason is that if too many bits are flipped from 0 to 1, most of the sets will be redundant and the local-search operator will spend excessive time removing redundant sets. This behavior only occurs if the density of ones in a redundant-free solution is small, which is in fact the case for our test problems. The probability $p$ (or the strength of the perturbation operator) must be low enough to avoid a random-restart behavior but high enough to ensure that the perturbation is not immediately canceled by the local-search operator.

The analysis of the execution traces that were produced in preliminary testing revealed that ITS have difficulties escaping from certain local optima because of the fixed cost that is associated with the groups (these difficulties have also been confirmed by the experimental results presented in Tables 6 and 7). In fact, when few groups are added to the solution, their associated fixed costs are paid; then, ITS tends to keep adding sets to (or removing sets from) the solution using these groups instead of exploring new groups. This happens because the costs of the selected groups have already been paid, and as a result, it is more expensive to pay for other unvisited groups and explore their sets. Therefore, certain regions of the search space, that may in fact contain the global optimum become difficult to reach. To overcome this weakness of ITS, a second perturbation operator that performs long jumps in the search space is used. This operator is invoked when the search is stagnant for a given number of iterations [$stag_{(ITS)}$ in Algorithm 4]. The long jumps consist of forcing a group into or out of the solution for a fixed number of iterations ($F$ in Algorithm 2). If the solution is not improved, the group is released and another group is forced (only one group is forced at a time). When a new best solution is found, the forced group is released, the stagnancy counter is reset and the search is continued (see Algorithm 4).

Let $M$ be a very large constant such that $M>\sum (g_i)$. To force a group out of the solution, we remove all of its sets from the solution and increase its fixed cost by $M$ to make it unaffordable. Similarly, to force a group into the solution, we decrease its fixed cost by $M$ to make it very attractive (the cost of the group becomes negative, and therefore, adding any set from the group to the solution increases the objective score). To release a group, we restore its original cost. During evaluation, if a group was forced into the solution, the original cost of the group must be used instead of the modified cost.

The pseudo-code of the second perturbation operator is presented in Algorithm 2, where $F$ is the number of iterations during which a group is forced into (or out of) the solution.

3.3 Local-search operator

As mentioned earlier, tabu-search has been used to perform local-search in our ITS algorithm. In each iteration of ITS, a short run of TS is performed. In addition, the tabu-list is cleared at the beginning of each run of TS.

As mentioned in Sect. 3.1, a binary-string solution representation is used in ITS. In the TS operator, a neighbor of a given solution is obtained by adding a set to (or removing a set from) the solution.

Let $X$ be a given configuration, $S_X$ be the sets used in $X$, $E_X$ be the elements covered by $X$ and $G_X$ be the groups used in $X$. The score of $X^{+j}$, which is the neighbor of $X$ that is obtained by adding the set $j$ to the configuration, and the score of $X^{-j}$, which is the neighbor of $X$ that is obtained by removing the set $j$ from the configuration, can be calculated as follows:

$$\begin{aligned} \mathrm {score}({X^{+j}})&= \mathrm{score}(X) + \sum {\mathrm{gain}(E_{X^{+j}}{\textbackslash }E_X)} - c_j - \mathrm{cost}(G_{X^{+j}}{\textbackslash }G_X) \end{aligned}$$

(5)

$$\begin{aligned} \mathrm{score}(X^{-j})&= \mathrm{score}(X) - \sum {\mathrm{gain}(E_X{\textbackslash }E_{X^{-j}})} + c_j + \mathrm{cost}(G_X{\textbackslash }G_{X^{-j}}) \end{aligned}$$

(6)

In each iteration, the best possible non-tabu move is performed and the reverse move is added to the tabu-list; the best move is the move that replaces the current solution with its best neighbor, i.e, the neighbor with the greatest score. The algorithm stops if the solution is not improved after $stag_{(TS)}$ iterations, where $stag_{(TS)}$ is a parameter. The tabu-list is used to avoid adding a set that was recently removed or removing a set that was recently added, and the aspiration criterion allows adding or removing such a set if the resulting solution is better than all of the solutions that have been visited so far. The pseudo-code of TS is given in Algorithm 3. The procedure find-next-move returns either the best non-tabu move or a tabu move that passes the aspiration criterion.

A separate tabu-list is used for each type of move (namely, add and remove) to allow the use of a different tabu-list size for each type of move. Our experiments have shown that using a tabu-list for remove moves slows down the convergence of TS toward the optimal solution. This behavior can be explained by the fact that remove moves usually eliminate the redundant sets from the solution and open new possibilities for add moves. For this reason, remove moves should not be postponed for very long during the search. Instead of discarding the tabu-list for remove moves, a short list was used.

3.4 Resulting ITS algorithm

The pseudo-code of the resulting ITS algorithm is presented in Algorithm 4.

Figure 2 illustrates how the use of the two levels of perturbation helps ITS to reach the global optimum. The first level of perturbation (perturb$_{1}$) and the local-search operator allow the algorithm to jump from one local optimum to another in the same region until the best local optimum of the region is reached. Because the strength of the first perturbation operator is relatively small, it is difficult to reach new regions in the search space. By forcing a group into (or out of) the solution, the second perturbation operator (perturb$_{2}$) performs a long jump in the search space and reaches a new region (as shown in Fig. 2). Then, the first perturbation operator and the local-search operator are reused to find the best local optimum of the new region. The global optimum of the problem is the best local optimum of all regions.

Fig. 2

The use of two levels of perturbation increases the chances of reaching the global optimum

Figure 3 illustrates how the use of tabu-search as an improvement operator in ILS increases the chances of reaching the global optimum. In this case, if a simple descent heuristic is used instead of tabu-search, the basin of attraction of the global optimum that is located between the two dashed lines is very small. For this reason, the probability that the perturbation operator attains the basin of attraction of the global optimum is very low and as a result, the global optimum will be difficult to reach. In contrast, tabu-search can escape from local optima located on small hills, which increases the size of the basin of attraction of the global optimum. In addition, the use of tabu-search has the effect of merging small and adjacent hills into bigger hills, which considerably reduces the total number of hills (i.e., the total number of local optima to explore). As a result, the chances of reaching the global optimum are increased as shown in Fig. 3. On the other hand, it is important to note that the runs of tabu-search must be short enough to avoid a significant reduction of the overall number of iterations of the ILS algorithm.

Fig. 3

The use of tabu-search in ILS increases the probability of reaching the global optimum

4 The adaptation of a memetic algorithm

To evaluate the performance of the proposed algorithm, we compare it to a memetic algorithm that was proposed by Beasley and Chu (1996) to solve the SCP. A memetic algorithm is a genetic algorithm (GA) that has been hybridized with an exact or heuristic algorithm (Radcliffe and Surry 1994). Generally, a local-search-improvement heuristic is incorporated into the GA to improve the quality of each individual before it is evaluated.

We transposed as accurately as possible the memetic algorithm developed by Beasley and Chu (BCMA) from the SCP domain to the PMSCP domain. We used the same solution representation (binary string), the same way of managing the population (selection and replacement), the same crossover operator (fusion crossover), but different initialization, mutation and evaluation operators. In the following material, BCMA is briefly presented and the adapted operators are described. The reader is referred to (Beasley and Chu 1996) for a complete description of the original BCMA. The resulting memetic algorithm for the PMSCP is called MA-PMSCP.

In each generation of BCMA, only one child is created (i.e., BCMA is an incremental GA). Two parents are selected using the tournament selection method and combined using the fusion crossover operator. Then, the newly generated child is mutated and added to the population by replacing a randomly chosen individual, although a below-average individual is more likely to be replaced. If the newly generated child is identical to an existing member of the population, the child is discarded and a new generation is performed.

Unlike other known crossover operators (e.g., one-point, two-point and uniform), the fusion crossover operator produces only one child. When two parents are combined with the fusion operator, the resulting child has more chances to inherit genes from its fittest parent.

The initialization operator of BCMA creates a feasible solution to the SCP (i.e., all of the elements are covered) by randomly selecting a set to cover each element. For a given element, a set is randomly selected from the five cheapest sets (which are called elite sets) that cover this element. This initialization operator is not compatible with the PMSCP because the cost of a set is also influenced by the fixed cost of the group that contains the set, and as a result, the concept of elite sets is not applicable. We replaced the initialization operator of BCMA with a simple operator that randomly assigns a value of 0 or 1 to each bit.

The mutation operator of BCMA randomly flips each bit at a given mutation rate. Only elite sets are considered for mutation. Because the concept of elite sets is not applicable to the PMSCP, the adapted mutation operator considers all of the bits for mutation. As in BCMA, a variable mutation rate is used as follows: the mutation rate is low at the beginning of the search to allow high intensification using the crossover operator and is increased as the GA converges to escape from local optima.

In BCMA, a repair operator is used to ensure the feasibility of the solutions generated by the GA. In addition, a redundancy-removal operator is used to enhance the quality of the repaired solutions. The concept of feasibility is not applicable to PMSCP’s because it is not necessary to cover all of the elements. We replace the repair and redundancy removal operators of BCGA with a best improvement (or steepest descent) operator that enhances the quality of the solutions produced by the GA. The best improvement operator (BI) is executed on the newly created individuals immediately before the evaluation step of MA-PMSCP; moreover, this operator uses the same neighborhood that is used in the tabu-search operator 3.3. As in TS, the best possible move is performed in each iteration. BI starts from a given configuration and performs a sequence of moves on it until the solution is locally optimal. Redundant sets are automatically removed because a configuration that contains one or more redundant sets will always have a better neighbor, which can be obtained by removing a redundant set: if $X$ is a configuration containing a redundant set $j, X^\prime = X - \{j\}$ is a better neighbor than $X$ because score($X^\prime$) = score$(X) + {c_{j}}$ (see Eq. 6). As a result, a solution that is improved with BI is devoid of redundant sets.

5 Computational results

In this section, we perform experimental analysis on the proposed ITS algorithm and compare it to a memetic algorithm (MA-PMSCP). Experiments are performed on thirty test problems that stem from the mining industry; these test problems contain twenty small-scale and medium-scale problems, and ten large-scale problems. The algorithms were implemented in C++ and compiled with the GNU-C++-Compiler(G++). The experiments were performed on an Intel(R)Xeon(R) X7550@2.00GHz processor with up to 1 TB of RAM.

The test problems have been generated using real geometrical data (block models and drill holes) from the mining industry. The cost associated with each set is proportional to the length of the corresponding drill hole. The gain attributed to each block is proportional to the highest cost that one would pay to cover that block. The same fixed cost is used for all groups because the cost of positioning the drill is invariable for our test problems. The objective score of a solution has no physical interpretation and is used for comparison purposes. The characteristics of the test problems are presented in Tables 1 and 2 where the best-known solutions that are presented are the best results that were obtained in all our experiments (including CPLEX runs, which are discussed below). The density is the percentage of ones in the matrix $A^{m\times n}$ defined in Sect. 2.2.

Table 1 Small and medium problems characteristics

Table 2 Large problems characteristics

We use the mathematical programming solver CPLEX (version 12.2) to determine the quality of the solutions found by ITS and MA-PMSCP. By running CPLEX for a sufficiently long computation time (up to 9 days per instance), we obtain optimal or near-optimal solutions and an optimality gap. The optimality gap is an upper bound of the percentage deviation from the optimal solution. Some of the CPLEX runs were stopped due to RAM limitation; which was up to 173 GB but varied for each run depending on the traffic in the test machine. The results obtained by CPLEX are presented in Table 3. Whereas a solution with an optimality gap of zero is optimal, a solution with an optimality gap that is close to zero is near-optimal and may in fact be optimal. The total time spend by CPLEX is presented in days (d), hours (h) or seconds (s). The tree size is the size of the branching tree used in the branch and bound algorithm of CPLEX; this tree is stored in memory. Note that the large problems have not been solved with CPLEX. In fact, because of the size of these problems, CPLEX was not able to start branching after up to 24 h.

Table 3 Optimal or near-optimal solutions obtained with CPLEX

Five trials of ITS and MA-PMSCP are performed for each test problem. The parameters used in ITS are as follows: $stag_{(ITS)} = 200$, $stag_{(TS)} = 1000$, $F=50$ for small and medium-size problems, and $F=1$ for large problems ($F$ is decreased for large problems because the overall number of iterations is lower and as a result, the second perturbation operator is invoked fewer times). The length of the tabu-list that is used for add moves is equal to the number of sets in the problem that is being solved and the length of the tabu-list that is used for remove moves is equal to one. These parameters where chosen based on preliminary computational experiments. For MA-PMSCP, we use a population size of fifty individuals and a variable mutation rate that varies between 0.1 and 0.3. As in BCGA, the crossover operator is invoked in each generation (i.e., the crossover probability is 1).

The detailed results of ITS are presented in Tables 4 and 5. The minimum, maximum and average solutions are presented in columns $S_{(min)}$, $S_{(max)}$ and $S_{(avg)}$, respectively. The cases where ITS was able to find the optimal solution or a solution that is better than the near-optimal solution that was found by CPLEX are highlighted in bold. The other columns contain the average of the following values that correspond to a given run: $T$ is the time in seconds when the best solution was first found, $Iters$ is the total number of iterations that were performed, $Imp$ is the number of times the solution has been improved, $P2$ is the number of times that stagnancy has been detected in ITS (and resulted in the use of the second perturbation operator), and $P2\text{- }Imp$ is the number of times in which the use of the second perturbation operator has allowed ITS to escape from local optima and improve the current best solution. Note that if the optimal solution is found early in a run, $P2$ will be high because the solution will be stagnant and $P2\text{- }Imp$ will be low because the solution is already optimal and cannot be improved.

Table 4 Detailed results for ITS on small and medium problems

Table 5 Detailed results for ITS on large problems

In Tables 6 and 7, ITS and MA-PMSCP are compared. In addition, we experiment with two variants of ITS. The first variant (called ITS without perturb$_{2}$) is ITS without the second perturbation operator and the second variant (called ILS + perturb$_{2}$) is ITS where the TS operator has been replaced with a steepest descent operator (the steepest descent operator is similar to TS but stops when a local optimum is reached). The column $\sigma _{(avg)}$ contains the percentage deviation of the average solution from the best-known solution, the column $\sigma _{(best)}$ contains the percentage deviation of the best solution from the best-known solution and the column $T_{(avg)}$ contains the average solution-time (in seconds unless otherwise specified) for each algorithm. The total execution time for each instance is the same for all algorithms and is presented in the last column of the tables.

Table 6 Comparison of ITS, ITS without perturb$_{2}$, ILS + perturb$_{2}$ and MA-PMSCP on small and medium problems

Table 7 Comparison of ITS, ITS without perturb$_{2}$, ILS + perturb$_{2}$ and MA-PMSCP on large problems

From the presented tables, we observe the following:

• From Tables 4 and 5, we observe that ITS performs consistently better than MA-PMSCP on all test problems (between 0.47 and 7.26 % better on small-scale and medium-scale problems, and between 2.41 and 9.4 % better on large-scale problems).

• From Tables 3 and 4, we observe that ITS is able to find equal or better solutions than the long CPLEX runs for 17 of the 20 small and medium-scale problems. Given the small optimality gap of CPLEX solutions and the long duration of CPLEX runs, we deduce that most of the solutions found by ITS (the bests of the five trials) are optimal or very close to optimality.

• Even though the differences between the solutions found by ITS and the solutions found by the two variants of ITS are small (Tables 6 and 7), ITS performs consistently better when both the second perturbation operator and TS are used (except for A5 where ILS + perturb$_{2}$ performs better). In addition, given the long CPLEX runs results, we observe that the use of both operators allows ITS to reach the optimal solution more frequently.

• Finally, we notice that the percentage deviations of ITS from MA-PMSCP are larger for large-scale problems than the percentage deviations that were found for small and medium-scale problems. Thus ITS is both better and more scalable than MA-PMSCP.

6 Conclusions and future work

In this work, we proposed a new variant of the partial set covering problem, a mining-industry application to it and a heuristic algorithm to solve it. The analysis of our computational results shows that the proposed algorithm is very effective and scalable for solving the PMSCP. We showed that most of the solutions found by ITS are either optimal or very close to optimality.

In addition, we theoretically discussed how the use of tabu-search and a second perturbation operator in ITS can help escape from the local optimum located on small hills and the local optima that have large basins of attraction. Furthermore, we experimentally showed that the use of both the second perturbation operator and tabu-search allows the algorithm to reach the optimal solution more frequently.

We end this paper by motivating the use of multiple perturbation operators in ILS. Even though we used two perturbation operators to target the sets and the groups of the PMSCP, other applications can benefit from the use of more perturbation operators. In addition, each perturbation operator can have a frequency that is dependent on the strength of the perturbation; where the frequency is used to determine how frequently an operator will be invoked. For instance, in our case, the first perturbation operator is invoked in each iteration (i.e. has a frequency of one) while the second perturbation operator (that has a higher strength) is invoked in each $stag_{(ITS)}$ iterations (i.e. has a frequency of $stag_{(ITS)}$). Similarly, the use of multiple local-search operators in ILS can be an interesting subject for future research.