Kerr–Newman–AdS black hole with quintessence and cloud of strings

Abstract

We obtain the solution corresponding to a Kerr–Newman–anti de Sitter black hole with quintessence and a spherically symmetric cloud of strings by using the Newman–Janis algorithm slightly modified. We analyze the horizon structure and the ergoregions, study the thermodynamics and the Hawking radiation as well. We discuss the role played by the different sources, namely, the quintessence, cosmological constant and cloud of strings on the horizons, ergoregions, thermodynamic quantities and in the flux of scalar particles associated to the Hawking radiation.

1 Introduction

The observational confirmation concerning the accelerated expansion of the universe is one of the most important discoveries made recently connected with modern cosmology [1]. This fact leads us to conclude that, at the cosmological scale, there is a gravitationally repulsive energy component corresponding to a negative pressure responsible for this accelerated expansion. Thus, it is natural to ask about the possible origins of this negative pressure. One of the possible answers is to assume that this expansion is produced by a fluid that permeates all the universe, which is termed quintessence dark energy [2,3,4]. It is worth calling attention to the fact that, also in the astrophysical scenario, quintessence should be important when surrounding a black hole.

Another possibility for this energy responsible for the accelerated cosmic expansion is the cosmological constant which is associated with the vacuum energy, assuming the same value in all space and being homogeneous. It seems that this constant has an important role also in some astrophysical scenarios [5].

Motivated by the fact that nature can be represented more appropriately by a collection of extended objects, like one-dimensional strings instead of point particles, Letelier [6] developed a formalism to consider these extended structures and obtained a solution corresponding to the Schwarzschild black hole surrounded by a spherically symmetric cloud of strings, whose presence alters the horizon of this black hole as compare with the Schwarzschild one.

Thus, all these possibilities concerning different sources, as the quintessential fluid, the cosmological constant or the cloud of strings have some profound astrophysical consequences and, therefore, it seems to be important to obtain solutions of Einstein equations for black holes surrounded by quintessence and cloud of strings, and, additionally, taking into account the cosmological constant.

The analysis of the black holes as thermodynamic systems with physical temperature, entropy, heat capacity and so on is one of the most interesting studies realized since the early 1970s with the aim to establish a statistical explanation for their thermodynamical properties. On the other hand, black holes can radiate with a black body spectrum and it constitutes one of the most important consequences of the existence of quantum fields in gravitational fields. Therefore, we can conclude that the study of thermodynamics as well as of the Hawking radiation in general scenario with a charged rotating black hole with cosmological constant and surrounded by quintessence and a cloud of strings seems to be important in order to know the role played by each component of the source and form this reason we decided to do this in this paper.

There is a method developed by Newman and Janis [7] which permits to obtain solutions of the Einstein equations corresponding to stationary spacetimes from their static counterpart, as, for example, in the computation of Kerr–Newman black hole solution taking the Reissner–Nordström one as a seed [8]. From that time up to now, this method became a powerful tool to obtain rotating black hole solutions. However, this method contains an ambiguity in which concerns the complexification of the radial coordinate, a question that was overcomed by dropping the complexification of this coordinate [9]. Following the Newman–Janis algorithm with the modification introduced by Azreg-Aïnou [9] a series of rotating solutions were obtained [9,10,11,12,13,14].

In this paper, we adopt the Newman–Janis algorithm [7] with the modification introduced by Azreg-Aïnou to construct a solution that corresponds to a charged rotating black hole with quintessence, cosmological constant and a spherically symmetric cloud of strings. We show that the obtained metric is a solution of Einstein’s field equations for these sources, generalizing a solution already obtained in the literature [11]. Then, we study and discuss some characteristics and consequences of this black hole spacetime, namely, the existence and nature of the horizons, the ergoregions, the thermodynamic quantities such as energy, Hawking temperature and heat capacity, as well as the flux of scalar particles emitted by the black hole under consideration.

The motivation to include the quintessence and the cloud of strings is connected with the fact that it is important to investigate the role of each source on the properties of the black hole. Otherwise, to include a cloud of strings is equivalent to have a solid deficit angle, as the global monopole has [15]. Thus, we can see this solution as a KNAdS black hole with a topological defect surrounded by quintessence. In this paper, we will, then, study how the quintessence affects the geometrical and topological properties of the KNAdS spacetime with a solid deficit angle.

This paper is organized as follows. In Sect. 2, we obtain the solution and study the black hole horizons and ergoregions. In Sect. 3, we investigate different aspects of its thermodynamics. In Sect. 4, the Hawking radiation of scalar particles is investigated. Finally, in Sect. 5, we present our conclusions.

2 Black holes surrounded by a cloud strings and quintessence

In recent years, Kiselev has obtained the solution corresponding to a static and spherically symmetric black hole surrounded by quintessence, whose metric is given by [16]

$$\begin{aligned} ds^2= & {} -\left( 1 -\frac{2 M}{r} - \frac{\alpha }{r^{3\omega _q+1}}\right) dt^2 \nonumber \\&+\left( 1 -\frac{2 M}{r} - \frac{\alpha }{r^{3\omega _q+1}}\right) ^{-1}dr^2 + r^2d \varOmega ^2, \end{aligned}$$

(1)

where M is the black hole mass, $\alpha$ is the quintessence parameter, $\omega _q$ is the quintessential state parameter and we are adopting the metric signature $(-,+,+,+)$.

The pressure and the density associated with the quintes-sence, respectively, $p_q$ and $\rho _q$, obey the equation of state $p_q = \omega _q \rho _q$, and where

$$\begin{aligned} \rho _q = - \frac{\alpha }{2} \frac{3 \omega _q}{r^{3 ( \omega _q +1)}} . \end{aligned}$$

(2)

In a scenario where the accelerated expansion is present, we have that $\omega _q$ should satisfy the inequality $- 1<\omega _q< - 1/3$. The parameter $\alpha$ assumes positive values and measures how intense is the quintessence field.

The stress-energy tensor related to the quintessence is given by [16]

$$\begin{aligned} T^t_{t}= & {} T^r_{r} = \rho _q \end{aligned}$$

(3)

$$\begin{aligned} T^\theta _{\theta }= & {} T^\phi _{\phi } = -\frac{1}{2} \rho _q (3 \omega _q+1), \end{aligned}$$

(4)

Another extra source was considered by Letelier which corresponds to a gauge-invariant and spherically symmetric cloud of strings surrounding the black hole, whose stress-energy tensor is given by [6]

$$\begin{aligned} T^t_{t}= & {} T^r_{r} = \rho _c = \frac{b}{r^2}, \end{aligned}$$

(5)

$$\begin{aligned} T^\theta _{\theta }= & {} T^\phi _{\phi } = 0, \end{aligned}$$

(6)

where $\rho _c$ is the energy density associated with the cloud of strings and b is a constant which takes care of the presence of the cloud of strings, as well as measures its intensity. Considering this mass-energy distribution, Letelier [6] solved Einstein’s equations determining the spacetime metric concerning a black hole surrounded by a cloud of strings, which can be written as

$$\begin{aligned} ds^2= & {} -\left( 1 -b-\frac{2 M}{r}\right) dt^2 \nonumber \\&+\left( 1 -b-\frac{2 M}{r} \right) ^{-1}dr^2 + r^2 d \varOmega ^2 \end{aligned}$$

(7)

Now, let us assume a static and spherically symmetric black hole surrounded by both extra sources of energy, namely, the quintessence and the cloud of strings. Assuming that the total stress-energy tensor is a superposition of the one associated with the quintessence as well as to the one that describes the cloud of strings, we can write

$$\begin{aligned} T^t_{t}= & {} T^r_{r} = \rho _c +\rho _q= \frac{b}{r^2}- \frac{\alpha }{2} \frac{3 \omega _q}{r^{3 ( \omega _q +1)}}, \end{aligned}$$

(8)

$$\begin{aligned} T^\theta _{\theta }= & {} T^\phi _{\phi } = -\frac{1}{2} \rho _q (3 \omega _q+1), \end{aligned}$$

(9)

In this case, the corresponding metric is given by [17]

$$\begin{aligned} ds^2= & {} -\left( 1 -b-\frac{2 M}{r} - \frac{\alpha }{r^{3\omega _q+1}}\right) dt^2 \nonumber \\&+\left( 1 -b -\frac{2 M}{r} - \frac{\alpha }{r^{3\omega _q+1}}\right) ^{-1}dr^2 +r^2 d \varOmega ^2. \end{aligned}$$

(10)

Additionally, we can consider an extra source corresponding to an electromagnetic field due to an electrical charge Q in the black hole [18]. Thus, the resulting metric is given by

$$\begin{aligned} ds^2= & {} -\left( 1 -b-\frac{2 M}{r}+\frac{Q^2}{r^2} - \frac{\alpha }{r^{3\omega _q+1}}\right) dt^2 \nonumber \\&\quad +\left( 1 -b -\frac{2 M}{r} +\frac{Q^2}{r^2} - \frac{\alpha }{r^{3\omega _q+1}}\right) ^{-1}dr^2 +r^2 d \varOmega ^2. \end{aligned}$$

(11)

Now, let us perform the following transformation in the metric given by Eq. (11)

$$\begin{aligned} t= & {} (1-b)^{-1/2} T, \nonumber \\ r= & {} (1-b)^{1/2} R, \nonumber \\ M= & {} (1-b)^{-1/2} M, \nonumber \\ \alpha= & {} (1-b)^{3(\omega _q+1)/2} \bar{\alpha }. \end{aligned}$$

(12)

Thus, Eq. (11) can be written as

$$\begin{aligned} ds^2= & {} -\left( 1 -\frac{2 m}{R}+\frac{Q^2}{R^2} - \frac{\bar{\alpha }}{R^{3\omega _q+1}}\right) dT^2 \nonumber \\&+\left( 1 -\frac{2 m}{R} +\frac{Q^2}{R^2} - \frac{\bar{\alpha }}{R^{3\omega _q+1}}\right) ^{-1}dR^2 \nonumber \\&+\,(1-a)R^2 d \varOmega ^2. \end{aligned}$$

(13)

We can note that the effect of a cloud of strings is equivalent to the one produced by a solid deficit angle [15].

Using the Newman–Janis algorithm [7] with a modification about this method performed by Azreg-Aïnou [9], we can obtain the solution corresponding to a rotating black hole surrounded by quintessence and a cloud of strings. Firstly, let we write the metric given by Eq. (11) in the following form

$$\begin{aligned} ds^2= -f(r) dt^2+\frac{1}{g(r)}dr^2 + h^2 d \varOmega ^2, \end{aligned}$$

(14)

where $f(r)=g(r)=\left( 1 -b-\frac{2 M}{r} - \frac{\alpha }{r^{3\omega _q+1}}\right)$. Thus, performing the transformation

$$\begin{aligned} du = dt-\frac{dr}{\sqrt{fg}}, \end{aligned}$$

(15)

we can write Eq. (14) in the Eddington–Finkelstein (EF) coordinates as [10]

$$\begin{aligned} ds^2 = -f du^2- \sqrt{\frac{f}{g}} du dr + h^2 d\varOmega ^2. \end{aligned}$$

(16)

Now, if we adopt the null tetrad basis given by

$$\begin{aligned} l^\mu= & {} \delta ^{\mu }_{1}, \end{aligned}$$

(17a)

$$\begin{aligned} n^\mu= & {} \sqrt{\frac{g}{f}} \delta ^{\mu }_{0} - \frac{f}{2} \delta ^{\mu }_{1}, \end{aligned}$$

(17b)

$$\begin{aligned} m^\mu= & {} \frac{1}{\sqrt{2} h} \left( \delta ^{\mu }_{2} + \frac{i}{sin \theta } \delta ^{\mu }_{3} \right) , \end{aligned}$$

(17c)

$$\begin{aligned} \bar{ m}^\mu= & {} \frac{1}{\sqrt{2} h} \left( \delta ^{\mu }_{2} - \frac{i}{sin \theta } \delta ^{\mu }_{3} \right) , \end{aligned}$$

(17d)

from which we can obtain the relations $l_{\mu }l^{\nu }{=}m_{\mu } m^{\mu }{=} n_{\nu } n^{\nu } {=}0$, $l_{\mu } m^{\mu } {=} n_{\mu } m^{\mu } {=} 0$ and $l_{\mu } n^{\mu } = - m_{\mu } \bar{m}^{\mu } = 0$. Thus, it is possible to write Eq. (16) as

$$\begin{aligned} g^{\mu \nu } = -l^{\mu } n^{\nu } - l^{\nu } n^{\mu } + m^{\mu }\bar{m}^{\nu } + m^{\nu } \bar{m}^{\mu }. \end{aligned}$$

(18)

At this stage, we can make a complex transformation in the (u, r) plane such as $u \rightarrow u - ia \cos \theta$ and $r \rightarrow r - ia \cos \theta$. We also adopt the changes $f(r) \rightarrow F(r, a, \theta )$, $g(r) \rightarrow G(r, a, \theta )$ and $h \rightarrow \varSigma (r, a, \theta )$ [9]. Thus, the null tetrades will assume the form [10]

$$\begin{aligned} l^\mu= & {} \delta ^{\mu }_{1}, \end{aligned}$$

(19a)

$$\begin{aligned} n^\mu= & {} \sqrt{\frac{G}{f}} \delta ^{\mu }_{0} - \frac{F}{2} \delta ^{\mu }_{1}, \end{aligned}$$

(19b)

$$\begin{aligned} m^\mu= & {} \frac{1}{\sqrt{2} \varSigma } \left[ \delta ^{\mu }_{2} +ia sin \theta (\delta ^\mu _0-\delta ^\mu _1)+ \frac{i}{sin \theta } \delta ^{\mu }_{3} \right] , \end{aligned}$$

(19c)

$$\begin{aligned} \bar{ m}^\mu= & {} \frac{1}{\sqrt{2} \varSigma } \left[ \delta ^{\mu }_{2} -ia sin \theta (\delta ^\mu _0-\delta ^\mu _1)- \frac{i}{sin \theta } \delta ^{\mu }_{3} \right] . \end{aligned}$$

(19d)

Then, the new metric components in the Eddington–Finkelstein coordinates are

$$\begin{aligned} g_{00}= & {} -F, \nonumber \\ g_{01}= & {} g_{10} = - \sqrt{\frac{G}{F}}, \nonumber \\ g_{22}= & {} \varSigma ^2, \nonumber \\ g_{33}= & {} sin^2 \theta \left[ \varSigma ^2+ a^2 \left( 2 \sqrt{\frac{F}{G}} -F \right) \sin ^2 \theta \right] , \nonumber \\ g_{03}= & {} g_{30} = a \left( F - \sqrt{\frac{F}{G}} \right) \sin ^2 \theta , \nonumber \\ g_{13}= & {} g_{31} =a \sin ^2 \theta \sqrt{\frac{F}{G}}. \end{aligned}$$

(20)

Finally, we write the metric back in the Boyer–Lindquist coordinates by using the transformation [9]

$$\begin{aligned} du \rightarrow dt + \lambda (r) dr, \quad d \phi \rightarrow d \phi + \chi (r) dr, \end{aligned}$$

(21)

with

$$\begin{aligned} \lambda (r)= & {} - \frac{k(r)+a^2}{g(r) h(r) +a^2}, \end{aligned}$$

(22)

$$\begin{aligned} \chi (r)= & {} - \frac{a}{g(r) h(r) +a^2}, \end{aligned}$$

(23)

$$\begin{aligned} k(r)= & {} \sqrt{\frac{g(r)}{f(r)}} h(r). \end{aligned}$$

(24)

The functions given by Eqs. (22)–(24) were chosen such that all the non-diagonal components of the metric tensor are null, with exception for $g_{03}$ and $g_{30}$. Additionally, we can write

$$\begin{aligned} F(r, \theta )= & {} \frac{(g h+ a^2 \cos ^2 \theta ) \varSigma }{(k +a^2 \cos ^2 \theta )^2}, \nonumber \\ G(r,\theta )= & {} \frac{gh+ a^2 \cos ^2 \theta }{\varSigma }. \end{aligned}$$

(25)

In the case under consideration, $f(r) = g(r)$ and $h(r) = r^2$. Thus, $k(r)=h(r)$ and

$$\begin{aligned} \varSigma = r^2 + a^2 \cos ^2 \theta . \end{aligned}$$

(26)

Finally, using Eq. (21) we find the metric corresponding to a charged rotating black hole surrounded by quintessence and a cloud of strings, which is given by

$$\begin{aligned} ds^2= & {} -\frac{\varDelta - a^2 sin^2 \theta }{\varSigma }dt^2 \nonumber +\frac{\varSigma }{\varDelta }dr^2 \nonumber \\&\quad 0 2 a sin^2 \theta \left( 1 - \frac{\varDelta - a^2 sin^2 \theta }{\varSigma } \right) dt d\phi + \varSigma d \theta ^2 \nonumber \\&\quad +\,sin^2 \theta \left[ \varSigma + a^2 sin^2 \theta \left( 2 - \frac{\varDelta - a^2 sin^2 \theta }{\varSigma } \right) \right] d\phi ^2, \end{aligned}$$

(27)

where a can be understood as the black hole angular momentum per unit mass and

$$\begin{aligned} \varDelta = (1-b)r^2 + a^2+Q^2 - 2Mr - \alpha r^{-3 \omega _q +1}. \end{aligned}$$

(28)

The Einstein tensor, $G_{\mu \nu }$, associated with the solution given by Eq. (27) can be determined by using the package RGTC of the software Mathematica and its components can be written as

$$\begin{aligned} G_{tt}= & {} \frac{2 \left( r^4 - 2 r^3\rho + a^2 r^2 - a^4 \sin ^2 \theta \cos ^2 \theta \right) \rho '}{\varSigma ^3} \nonumber \\&-\,\frac{a^2 r \sin ^2 \theta }{\varSigma ^2}, \end{aligned}$$

(29a)

$$\begin{aligned} G_{t \phi }= & {} \frac{2 a \sin ^2 \theta \left[ (r^2+ a^2) (a^2 \cos ^2 \theta - r^2)+ 2 r^2 \rho \right] \rho '}{\varSigma ^3} \nonumber \\&+\,\frac{a^2 r \sin ^2 \theta (r^2+ a^2) \rho ''}{\varSigma ^2}, \end{aligned}$$

(29b)

$$\begin{aligned} G_{rr}= & {} - \frac{2 r^2 \rho '}{\varSigma \varDelta }, \end{aligned}$$

(29c)

$$\begin{aligned} G_{\theta \theta }= & {} -\frac{2 a^2 \cos ^2 \theta \rho }{\varSigma } - r \rho '' \end{aligned}$$

(29d)

$$\begin{aligned} G_{\phi \phi }= & {} - \frac{ a \sin ^2 \theta \left[ (r^2+ a^2) (a^2 +(2 r^2 + a^2)\cos 2 \theta )+ 2 r^2 \rho \right] \rho '}{\varSigma ^3}\nonumber \\&-\,\frac{2 a^2 r^3 \sin ^4 \theta \rho \rho '}{\varSigma ^3} -\frac{ r \sin ^2 \theta (r^2+ a^2)^2 \rho ''}{\varSigma ^2}, \end{aligned}$$

(29e)

where $2 \rho = 2 M +br+ \alpha r^{-3 \omega _q}-\frac{Q^2}{r}$. Using the standard tetrade basis

$$\begin{aligned} e^{\mu }_t= & {} \frac{1}{\sqrt{\varSigma \varDelta }}(r^2+a^2,0,0,a), \nonumber \\ e^{\mu }_r= & {} \sqrt{\frac{\varDelta }{\varSigma }} (0,1,0,0), \nonumber \\ e^\mu _\theta= & {} \frac{1}{\sqrt{\varSigma }} \left( 0,0,1,0 \right) , \nonumber \\ e^{\mu }_\phi= & {} - \frac{1}{\sqrt{\varSigma \sin ^2 \theta }}(a^2 \sin ^2 \theta ,0,0,1), \end{aligned}$$

(30)

we can write the stress-tensor $T_{\mu \nu }$ in the form $T_{\mu \nu } = \left( \epsilon , p_r, p_\theta , p_\phi \right)$ [10], where

$$\begin{aligned} \epsilon= & {} - \frac{1}{8 \pi } e^{\mu }_t e^{\nu }_t G_{\mu \nu } = \frac{2 \rho ' r^2}{8 \pi \varSigma ^2}, \nonumber \\ p_r= & {} \frac{1}{8 \pi } e^{\mu }_r e^{\nu }_r G_{\mu \nu } = - \frac{2 \rho ' r^2}{8 \pi \varSigma ^2}, \nonumber \\ p_\theta= & {} \frac{1}{8 \pi } e^{\mu }_\theta e^{\nu }_\theta G_{\mu \nu } = p_r- \frac{ \rho '' r +2 \rho '}{8 \pi \varSigma }, \nonumber \\ p_\phi= & {} \frac{1}{8 \pi } e^{\mu }_\phi e^{\nu }_\phi G_{\mu \nu } = p_r- \frac{ \rho '' r +2 \rho '}{8 \pi \varSigma }. \end{aligned}$$

(31)

Thus, we can conclude that the proposed solution is physically valid, as long as it obeys Einstein’s field equations with a stress-energy tensor with the quintessential fluid and a cloud of strings around the rotating black hole whose form is known in the literature [10].

Furthermore, we can note that the stress tensor with components given by Eq. (31) satisfies the weak energy condition (WEC), depending on the values of the parameters associated with the quintessence and the cloud of strings. Indeed, if $u^\mu$ is a timelike unity vector, $T_{\mu \nu } u^\mu u^\nu \ge 0$, for any value of the coordinates, for the correct values of b, $\alpha$ and $\omega _q$.

The next step is to add the cosmological constant, following the procedure adopted in [11]. Doing this, we get

$$\begin{aligned} ds^2= & {} \frac{\varSigma }{\varDelta _r}dr^2 + \frac{\varSigma }{\varDelta _\theta } d \theta ^2 + \frac{\varDelta _\theta sin^2 \theta }{\varSigma }\left[ a \frac{dt}{\varXi } - \left( r^2+a^2\right) \frac{d\phi }{\varXi } \right] ^2 \nonumber \\&-\,\frac{\varDelta _r}{\varSigma }\left( \frac{dt}{\varXi } -a sin^2 \theta \frac{d \phi }{\varXi } \right) ^2, \end{aligned}$$

(32)

where

$$\begin{aligned} \varDelta _r= & {} (1-b)r^2 + a^2+Q^2 - 2Mr - \frac{\varLambda }{3} r^2 \left( r^2 + a^2 \right) \nonumber \\&-\,\alpha r^{1 - 3 \omega _q}, \end{aligned}$$

(33)

$$\begin{aligned} \varDelta _\theta= & {} 1 + \frac{\varLambda }{3} a^2 cos^2 \theta ,\end{aligned}$$

(34)

$$\begin{aligned} \varXi= & {} 1 + \frac{\varLambda }{3} a^2, \end{aligned}$$

(35)

and the electromagnetic potential generated by the charge in the black hole is given by

$$\begin{aligned} A_{\mu } = - \frac{Qr}{\varSigma } \left( \delta ^t_{\mu } - \frac{a sin^2 \theta }{\varXi } \delta ^{\phi }_{\mu } \right) . \end{aligned}$$

(36)

With the metric given by Eq. (32), we can calculate the components of Einstein’s tensor $G_{\mu \nu }$ using once again, the RGTC package of Mathematica and obtain

$$\begin{aligned} G_{tt}= & {} \frac{2 \left( r^4 - 2 r^3\rho + a^2 r^2 - a^4 \sin ^2 \theta \cos ^2 \theta \right) \rho '}{\varSigma ^3} \nonumber \\&-\,\frac{a^2 r \sin ^2 \theta }{\varSigma ^2}+ \varLambda \frac{a^2 \sin ^2 \theta }{\varSigma ^2}, \end{aligned}$$

(37a)

$$\begin{aligned} G_{t \phi }= & {} \frac{2 a \sin ^2 \theta \left[ (r^2+ a^2) (a^2 \cos ^2 \theta - r^2)+ 2 r^2 \rho \right] \rho '}{\varSigma ^3} \nonumber \\&+\,\frac{a^2 r \sin ^2 \theta (r^2+ a^2) \rho ''}{\varSigma ^2} \nonumber \\&+\varLambda 2 a \sin ^2 \theta \frac{r^2+ a^2- \varDelta }{\varSigma }, \end{aligned}$$

(37b)

$$\begin{aligned} G_{rr}= & {} - \frac{2 r^2 \rho '}{\varSigma \varDelta }+ \varLambda \frac{\varSigma ^2}{\varDelta _r}, \end{aligned}$$

(37c)

$$\begin{aligned} G_{\theta \theta }= & {} -\frac{2 a^2 \cos ^2 \theta \rho }{\varSigma } - r \rho '' \nonumber \\ G_{\phi \phi }= & {} - \frac{ a \sin ^2 \theta \left[ (r^2+ a^2) (a^2 +(2 r^2 + a^2)\cos 2 \theta ) \right] \rho '}{\varSigma ^3} \nonumber \\&- \,\frac{ a \sin ^2 \theta 2 r^2 \rho \rho '}{\varSigma ^3} \nonumber \\&-\,\frac{2 a^2 r^3 \sin ^4 \theta \rho \rho '}{\varSigma ^3} -\frac{ r \sin ^2 \theta (r^2+ a^2)^2 \rho ''}{\varSigma ^2} \nonumber \\&+\,\varLambda \frac{sin^2 \theta [(r^2+a^2)^2 - a^2 \varDelta _r]}{\varSigma ^2}. \end{aligned}$$

(37d)

This result permit us to conclude that the metric (32) is a solution for the Einstein equation with cosmological constant, namely

$$\begin{aligned} G_{\mu \nu } = R_{\mu \nu } - \frac{1}{2}R g_{\mu \nu }+ \varLambda g_{\mu \nu } = 8 \pi T_{\mu \nu }. \end{aligned}$$

(38)

In order to give to the coordinate t the unit of time, we can use the substitution $t \rightarrow t' / \varXi$. Thus, we obtain the following form of the metric

$$\begin{aligned} ds^2= & {} \frac{\varSigma }{\varDelta _r}dr^2 - \frac{\varSigma }{\varDelta _\theta } d \theta ^2 - \frac{\varDelta _\theta sin^2 \theta }{\varSigma }\left[ a dt - \left( r^2+a^2\right) \frac{d\phi }{\varXi } \right] ^2 \nonumber \\&+\,\frac{\varDelta _r}{\varSigma }\left( dt -a sin^2 \theta \frac{d \phi }{\varXi } \right) ^2, \end{aligned}$$

(39)

which is more appropriate to do the analysis which follows. This metric generalizes the ones obtained in the literature [11] with respect to the addition of an extra source corresponding to a spherically symmetric cloud of strings.

2.1 Black hole horizons

The black hole horizons are determined by the condition

$$\begin{aligned} \varDelta _r= & {} (1-b)r^2 + a^2+Q^2 - 2Mr \nonumber \\&-\,\frac{\varLambda }{3} r^2 \left( r^2 + a^2 \right) - \alpha r^{1 - 3 \omega _q}=0. \end{aligned}$$

(40)

which can be factorized as

$$\begin{aligned} (r-r_+)(r-r_-)(r-r_q) (r-r_c)= 0, \end{aligned}$$

(41)

where $r_q$ is the cosmological horizon related to the quintes-sence, $r_c$ is a cosmological horizon due to the cosmological constant, $r_+$ is the black hole event horizon and $r_-$ is the internal (Cauchy) horizon.

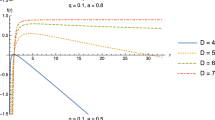
In Fig. 1, we represent the function $\varDelta _r = \varDelta _r(r)$ for different values of the cloud of string parameter b. In the graphs, we have fixed the values of the quintessence parameter as well as of the quintessential state parameter and varied the parameter which codifies the presence of the cloud of strings. The figures show the role played by these quantities with emphasis on the effect associated with the cloud of strings. Due to the small value of the cosmological constant, the cosmological horizon $r_c$ will be negative and, thus, there can be only three positive horizons, as can be seen in the figure.

Fig. 1

$\varDelta _ r$ for different values of the parameter b and for fixed values of $\alpha$ and $\omega _q$

2.2 Ergorregions

The static surfaces of the black hole are determined by the equation $g_{tt} = 0$. Thus, we obtain

$$\begin{aligned} \varDelta _r = a^2 \sin ^2 \theta \varDelta _\theta . \end{aligned}$$

(42)

The region located between the static surfaces and the black hole horizons are called ergoregions and no reference frame can be at rest in it. In Figs. 2 and 3, we represent the black hole ergoregions for different values of the string cloud parameter b. Note that the case $b=0$ is shown and this permits us to compare with the cases for $b \ne 0$, and conclude what is the role played by the cloud of strings with respect to the boundaries of the ergoregions.

Fig. 2

The black hole ergoregions for different values of the string cloud parameter b. The dashed lines correspond to the black hole horizons, while the solid lines represent the static surfaces

Fig. 3

The black hole ergoregions for different values of the string cloud parameter b. The dashed lines correspond to the black hole horizons, while the solid lines represent the static surfaces

3 Black hole thermodynamics

As a function of the black hole horizon, the energy of the system can be defined as [19]

$$\begin{aligned} E= & {} \frac{M}{\varXi } \nonumber \\= & {} \frac{(1-b) r_h^2 +a^2 + Q^2-\frac{\varLambda }{3} r_h^2( r_h^2+a^2) - \alpha r_h^{1-3 \omega _q }}{2 \varXi r_h} \end{aligned}$$

(43)

The Hawking temperature [20,21,22] of the black hole is given by

$$\begin{aligned}&T =\frac{\kappa _h}{2 \pi } = \frac{1}{4 \pi } \frac{\varDelta '_r \left( r_h \right) }{r^2_h +a^2} \nonumber \\&\,\quad =\frac{(1-b) r_h^2-a^2-Q^2-\frac{\varLambda }{3} r_h^2 \left( 3 r_h^2+a^2 \right) +3 \omega _q r_h^{1-3 \omega _q} }{4 \pi r_h \left( r_h^2 + a^2 \right) }, \end{aligned}$$

(44)

with $\kappa _h=\frac{1}{2}\frac{1}{r^2_h + a^2}\frac{d \varDelta }{d r} \big |_{r=r_h}$ being the gravitational acceleration nearby the black hole horizon. The area of the horizon is given by

$$\begin{aligned} A_h = \int \int \sqrt{-g} d \theta d \phi {\Big |}_{r=r_h} = \frac{4 \pi }{\varXi } \left( r_h^2 +a^2\right) , \end{aligned}$$

(45)

and, through the area law [23, 24], the entropy of the black hole is calculated according to

$$\begin{aligned} S = \frac{A_H}{4} = \frac{\pi \left( r_h^2 +a^2\right) }{\varXi }. \end{aligned}$$

(46)

Thus, as a function of the entropy, S, we can write the energy, E, as

$$\begin{aligned} E= & {} \frac{(1-b) \left( S \varXi /\pi -a^2 \right) +a^2 + Q^2 }{2 \varXi \sqrt{S \varXi /\pi - a^2}}\nonumber \\&\quad -\,\frac{\frac{\varLambda }{3}\left( S \varXi /\pi -a^2 \right) S \varXi /\pi + \alpha \left( S \varXi /\pi -a^2 \right) ^{(1-3 \omega _q )/2} }{2 \varXi \sqrt{S \varXi /\pi - a^2}}, \end{aligned}$$

(47)

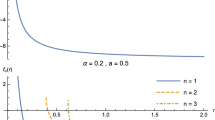
whose behavior is represented in Fig. 4 for fixed values of $\omega _q$ and different values of $\alpha$ and b with emphasis to the role played by the cloud of strings.

Fig. 4

The energy, E, as a function of the entropy, S, for diffenrent values of b and $\alpha$ and fixed value of $\omega _q$

Similarly, we can write the Hawking temperature as a function of the entropy, as follows

$$\begin{aligned} T= & {} \frac{(1-b)\left( S \varXi /\pi -a^2 \right) -a^2-Q^2 }{4 \sqrt{S \varXi /\pi - a^2} S \varXi } \nonumber \\&-\,\frac{\frac{\varLambda }{3} \left( S \varXi /\pi -a^2 \right) \left( 3 S \varXi /\pi -2a^2 \right) }{4 \sqrt{S \varXi /\pi - a^2}S \varXi }\nonumber \\&+\,\frac{3 \omega _q \alpha \left( S \varXi /\pi -a^2 \right) ^{(1-3 \omega _q)/2} }{4 \sqrt{S \varXi /\pi - a^2}S \varXi }. \end{aligned}$$

(48)

The behavior of T as a function of S is represented in Fig. 5. Note the quantitative and qualitative behaviors of the Hawking temperature in terms of the entropy.

Fig. 5

The Hawking temperature, T, as a function of the entropy, S, for diffenrent values of b and $\alpha$ and fixed value of $\omega _q$

We can observe in Fig. 5 that the Hawking temperature of the black hole can be negative depending on the values of the parameter related to the quintessence and the cloud of strings. In fact, it was already discussed in the literature the possibility of negative Hawking temperatures of black holes with some added matter-energy content, like quintessence, higher dimensional spacetimes and modified gravity theories [25]. The Hawking temperature, which is associated with the quantum fields in thermal equilibrium with the black holes, being negative means that the black hole mass can increase with the decrease of the entropy of the system. This fact is associated with the existence of the quintessence and the cloud of strings surrounding the black hole.

The angular velocity of the black hole horizon is given by

$$\begin{aligned} \varOmega _h = - \frac{g_{03}}{g_{33}} {\Bigg |}_{r=r_h}= \frac{ a \varXi }{r_h^2 + a^2}. \end{aligned}$$

(49)

Thus, we can write the first law of black hole thermodynamics as

$$\begin{aligned} dE = T dS + \varOmega _h d J + \phi _h dq, \end{aligned}$$

(50)

for which

$$\begin{aligned} J= & {} \frac{Ma}{{\varXi }^2}, \end{aligned}$$

(51a)

$$\begin{aligned} q= & {} \frac{Q}{\varXi }, \end{aligned}$$

(51b)

$$\begin{aligned} \phi _h= & {} \frac{Q r_h}{r^2_h + a^2}, \end{aligned}$$

(51c)

Fig. 6

The heat capacity as a function of the entropy, S

with $\phi _h$ being the electric potential.

Finally, the heat capacity is calculated through the relation

$$\begin{aligned} C_{J,q} = T\frac{\partial S}{\partial T}\bigg |_{J,q} = \frac{\partial E}{\partial T}\bigg |_{J,q}, \end{aligned}$$

(52)

whose behavior is represented in Fig. 6. From the graphs of this figure, we can verify that there are values of the parameters for which the system is thermodynamically stable ($C>0$), as well as there are values for which the black hole is thermodynamically unstable ($C<0$). It is worth calling attention to the fact that these behaviors are strongly related to the presence of the cloud of strings.

4 Hawking radiation

In this section, we will study the emission of scalar particles near the black hole horizons. To do this, we start by writing the covariant Klein–Gordon equation in the background spacetime under consideration.

4.1 Klein–Gordon equation

For a charged scalar particle, in a curved spacetime, the covariant Klein–Gordon equation can be written as

$$\begin{aligned} \frac{1}{\sqrt{-g}} \left[ \left( \frac{\partial }{\partial x^\mu } - i e A_{\mu }\right) \sqrt{-g} g^{\mu \nu } \left( \frac{\partial }{\partial x^\nu } - i e A_{\nu }\right) \right] \varPsi - \mu _0^2 \varPsi = 0, \end{aligned}$$

(53)

where e is the electric charge and $\mu _0$ its mass. Thus, for the metric corresponding to a Kerr–Newman–anti-de Sitter black hole with quintessence and a cloud of strings given by Eq. (39), the Klein–Gordon equation is written as

$$\begin{aligned}&\frac{1}{\varDelta _r \varDelta _\theta } \left[ \varDelta _\theta \left( r^2+a^2 \right) ^2 - \varDelta _r a^2 \sin ^2 \theta \right] \frac{\partial ^2 \varPsi }{\partial t^2} \nonumber \\&\quad +\,2i \frac{eQr}{\varDelta _r} \left[ a \varXi \frac{\partial }{\partial \phi } +\left( r^2+a^2 \right) \frac{\partial }{\partial t} \right] \varPsi \nonumber \\&\quad -\,\frac{\varXi ^2}{\varDelta _r \varDelta _\theta sin^2 \theta } \left( \varDelta _r - \varDelta _\theta a^2 sin^2 \theta \right) \frac{\partial ^2 \varPsi }{\partial \phi ^2} \nonumber \\&\quad +\,\frac{2 \varXi a}{\varDelta _r \varDelta _\theta } \left[ \varDelta _\theta \left( r^2+a^2 \right) ^2 - \varDelta _r \right] \frac{\partial ^2 \varPsi }{\partial t \partial \phi } - \frac{\partial }{\partial r} \varDelta _r \frac{\partial \varPsi }{\partial r} \nonumber \\&\quad -\,\frac{1}{sin \theta } \frac{\partial }{\partial \theta } \left( sin\theta \varDelta _\theta \right) \frac{\partial \varPsi }{\partial \theta } = \left( -\mu _0^2 \varSigma + e^2 Q^2 r^2 \frac{1}{\varDelta _r}\right) \varPsi . \end{aligned}$$

(54)

Considering the symmetry of the problem, we can write the solution $\varPsi (t, r, \theta , \phi )$ as

$$\begin{aligned} \varPsi (t, r, \theta , \phi ) = e^{- i \omega t}e^{i m \phi } \psi (r, \theta ), \end{aligned}$$

(55)

and, thus, we get

$$\begin{aligned}&-\omega ^2 \frac{\varXi ^2}{\varDelta _r \varDelta _\theta } \left[ \varDelta _\theta \left( r^2+a^2 \right) ^2 - \varDelta a^2 sin^2 \theta \right] \psi \nonumber \\&+\,2\frac{eQr}{\varDelta _r}\varXi \left[ \left( r^2+a^2 \right) \omega - a m \right] \psi \nonumber \\&+\,m^2 \frac{\varXi ^2}{\varDelta _r \varDelta _\theta sin^2 \theta } \left( \varDelta _r - \varDelta _\theta a^2 sin^2 \theta \right) \psi \nonumber \\&+\,m \omega \frac{2 \varXi ^2 a}{\varDelta _r \varDelta _\theta } \left[ \varDelta _\theta \left( r^2+a^2 \right) ^2 - \varDelta _r \right] \psi - \frac{\partial }{\partial r} \varDelta \frac{\partial \psi }{\partial r} \nonumber \\&-\,\frac{1}{sin \theta } \frac{\partial }{\partial \theta } \left( sin\theta \varDelta _\theta \right) \frac{\partial \psi }{\partial \theta } = \left( -\mu _0^2 \varSigma + e^2 Q^2 r^2 \frac{1}{\varDelta _r}\right) \psi . \end{aligned}$$

(56)

Now, let us suppose that $\psi (r, \theta ) = R(r) \chi (\theta )$. Thus, we find the following equations for the angular and radial variables

$$\begin{aligned}&\frac{1}{sin \theta } \frac{d}{d \theta } \left[ sin\theta \varDelta _\theta \frac{d \chi (\theta )}{d \theta }\right] \nonumber \\&\quad =\left[ \frac{1}{\varDelta _\theta }\left( \omega a sin \theta - \frac{m}{sin \theta }\right) ^2 +\mu ^2_0 a^2 cos^2 \theta - \lambda \right] \chi (\theta ), \end{aligned}$$

(57)

$$\begin{aligned}&\frac{d}{d r} \varDelta _r \frac{d R(r)}{d r} = \left\{ \lambda +\mu ^2_0 r^2 \right. \nonumber \\&\qquad \left. -\frac{1}{\varDelta _r} \left[ \omega \left( r^2+a^2 \right) - a m \varXi - e Q r\right] ^2 \right\} R(r), \end{aligned}$$

(58)

with $\lambda$ being a separation constant and $\omega$ the particle energy. The Eq. (58) can be written in the tortoise coordinates, $r_*$, which are defined by

$$\begin{aligned} dr_*= & {} \frac{1}{\varDelta _r} \left( r^2 + a^2\right) dr, \end{aligned}$$

(59a)

$$\begin{aligned} \frac{d}{dr}= & {} \frac{\left( r^2 + a^2\right) }{\varDelta _r} \frac{d}{dr_*}. \end{aligned}$$

(59b)

Defining $K = \omega \left( r^2+a^2 \right) - a m \varXi - e Q r$, we get

$$\begin{aligned} \left( r^2 + a ^2\right) ^2\frac{d^2 R}{d r_*^2} + 2 r \varDelta _r \frac{d R}{d r_*} = \left[ \varDelta _r \left( \lambda +\mu ^2_0 r^2 \right) - K^2\right] R. \end{aligned}$$

(60)

This is a more appropriate form of the equation for the radial function, R(r), to investigate the radiation of scalar particles emitted by the black hole.

4.2 Black hole radiation and analytic continuation

In the black hole horizon, we get $\varDelta _r(r_+) = 0$. In this region, Eq. (60) turns into

$$\begin{aligned} \frac{d^2 R}{d r^2} + \left( \omega - \omega _0 \right) ^2 R=0, \end{aligned}$$

(61)

where

$$\begin{aligned} \omega _0 = m \varOmega _+ + e \phi _+. \end{aligned}$$

(62)

Thus, the radial solution of the Klein–Gordon equation near the black hole horizon will be written in the form

$$\begin{aligned} R \sim e^{\pm i \left( \omega - \omega _0 \right) r_*}, \end{aligned}$$

(63)

and, therefore, we can write

$$\begin{aligned} \varPsi \sim e^{-i \omega t \pm i \left( \omega - \omega _0 \right) r_*}. \end{aligned}$$

(64)

In the exterior region of the event horizon, the ingoing and outgoing solutions will be given by [19]

$$\begin{aligned} \varPsi _{in}= & {} e^{-i \omega t - i \left( \omega - \omega _0 \right) t} = e^{-i \omega (t + \hat{r})} = e^{- i \omega \nu }, \end{aligned}$$

(65)

$$\begin{aligned} \varPsi _{out} (r>r_+)= & {} e^{-i \omega t + i \left( \omega - \omega _0 \right) t}= e^{- i \omega \nu } e^{2 i \omega \hat{r}} \nonumber \\= & {} e^{- i \omega \nu } (r-r_+)e^{\frac{ i}{\kappa _+} (\omega - \omega _0)}, \end{aligned}$$

(66)

where

$$\begin{aligned} \hat{r} = \frac{\omega - \omega _0}{\omega }r_* , \quad \nu = t+\hat{r} \end{aligned}$$

(67)

are the Eddington–Finkelstein coordinates. We can verify that, in the black hole horizon region, we can write [19]

$$\begin{aligned} ln (r-r_+)=\frac{1}{r_+^2 + a^2}\frac{d \varDelta }{dr} \Bigg |_{r=r_+} r_* = 2 \kappa _+ r_*. \end{aligned}$$

(68)

By analytic continuation, we can determine a real damped part for the solution $\varPsi _{out}$, which is not analytic at the horizon, namely, $r=r_+$. Using the Damour-Ruffini method [26], and performing a $- \pi$ rotation, we get

$$\begin{aligned} (r-r_+) \rightarrow |r-r_+|e^{-i\pi }=(r_+-r)e^{-i\pi }. \end{aligned}$$

(69)

Thus, we obtain the wave function in the interior of the horizon, which is given by

$$\begin{aligned} \varPsi _{out} (r<r_+) = e^{-i \omega \nu } (r_+-r)^{\frac{i}{\kappa _+}(\omega -\omega _0)}e^{\frac{\pi }{\kappa _+}(\omega -\omega _0)}. \end{aligned}$$

(70)

Therefore, the emission rate of particles by the black hole horizon will, so, be written as

$$\begin{aligned} \varGamma _+ = \Bigg |\frac{\varPsi _{out} (r>r_+)}{\varPsi _{out} (r<r_+)} \Bigg |^2 = e^{-\frac{2 \pi }{\kappa _+}(\omega - \omega _0)}, \end{aligned}$$

(71)

which represents the probability of creation of particles/antiparticles out the horizon and is represented in Fig. 7.

Fig. 7

The rate, $\varGamma$, as a function of the entropy, S, for diffenrent values of b

4.3 Black body spectrum and Hawking flux

Assuming that the black hole horizon irradiates particles with energy $\omega$, electric charge e and angular momentum m, there will be a reduction in the thermodynamical parameters of the black hole, in such a way that $M/{\varXi } \rightarrow M/\varXi - \omega$, $Q \rightarrow Q - e$ and $J \rightarrow J - m$, which should be reflected in the spacetime metric. Assuming that the energy, electric charge and angular momentum of the universe are conserved, we must impose that

$$\begin{aligned} - \omega= & {} \varDelta E, \end{aligned}$$

(72a)

$$\begin{aligned} - e= & {} \varDelta Q, \end{aligned}$$

(72b)

$$\begin{aligned} - m= & {} \varDelta J, \end{aligned}$$

(72c)

with $\varDelta E$, $\varDelta Q$ and $\varDelta J$ being, respectively, variations in the energy, charge and angular momentum in the black hole horizon due to the emission of radiation. Substituting these quantities into Eq. (71), and using the first law of black hole thermodynamics, we get

$$\begin{aligned} \varGamma _+ = e^{-\frac{2 \pi }{\kappa _+}(-\varDelta E - m \varOmega _+ - e \phi _+)} = e^{-\frac{2 \pi }{\kappa _+}(-T_+ \varDelta S_+)} = e^{\varDelta S_+}, \end{aligned}$$

(73)

where $\varDelta S_+$ represents the change of the entropy near the black hole horizon due to the particle emission. Similarly, near the cosmological horizon, we can write

$$\begin{aligned} \varGamma _c = e^{\varDelta S_c}. \end{aligned}$$

(74)

The average number of particles emitted in a given mode, $\bar{N}_{\omega }$, is related to the probability of emission, $\varGamma _+$, through [19, 27]

$$\begin{aligned} \bar{N}_{\omega } = \frac{\varGamma _+}{1-\varGamma _+} = \frac{1}{e^{\frac{\hbar (\omega - \omega _0)}{k_B T_+}}-1} \end{aligned}$$

(75)

Note that, in Eq. (75), we reinserted the Planck and Boltzmann constants. Performing the integration of $\bar{N}_{\omega }$ in the range of all spectrum of emission, we get the Hawking flux, $\varPhi$, corresponding to emitted particles, which will be given by

$$\begin{aligned} \varPhi= & {} \frac{1}{2 \pi } \int _0^{\infty } \bar{N}_{\omega } \omega d \omega = \frac{1}{2 \pi } \int _0^{\infty } \frac{\omega }{e^{\frac{2 \pi }{\kappa _+}(\omega - \omega _0)} - 1} d \omega \nonumber \\= & {} \frac{1}{2 \pi } \left( \frac{\kappa _+}{2 \pi } \right) ^2 \left\{ \frac{\pi ^2}{6} + log (e^{\frac{2 \pi }{\kappa _+} \omega _0} ) \right. \nonumber \\&-\, log (e^{\frac{2 \pi }{\kappa _+} \omega _0} ) log[- log (e^{\frac{2 \pi }{\kappa _+} \omega _0} ) ] \nonumber \\&\left. + \sum ^{\infty }_{j=2} \frac{log^j (e^{\frac{2 pi}{\kappa _+} \omega _0} ) \zeta (j-2)}{j!} \right\} , \end{aligned}$$

(76)

where $\zeta$ is the Riemann zeta function. Note that there are dependencies on the quintessence as well as on the cloud of strings. If we consider the Schwarzschild black hole, $\omega _0 = 0$, we obtain the known result $\varPhi = \frac{\kappa _+}{48 \pi }$.

5 Concluding remarks

Firstly, we obtained the Kerr–Newman black hole with quintessence and a cloud of strings by using the Newman–Janis algorithm [7] with a modification introduced by Azreg-Aïnou [9] and, then, the cosmological constant term was added appropriately, following the procedure adopted by Xu and Wang [11]. In the analysis of the horizon structure, we showed in Fig. 1, how the parameter that codifies the cloud of strings determines the number and nature of the horizons, as well as how the intensity of the quintessence does this. The ergoregions are affected also by the presence of the quintessence and cloud of strings as shown in Figs. 2 and 3, where the effects associated with the intensity of these sources are shown.

The thermodynamics quantities, namely, the energy (see Fig. 4), the Hawking temperature (see Fig. 5) and the heat capacity (see Fig. 6) are affected by the cloud of strings, as well as by the presence of the quintessence. In particular, for fixed values of the intensity of quintessence, the energy as a function of entropy decreases when the parameter that codifies the presence of the cloud of strings increases. With respect to the intensity of quintessence, when it decreases, the energy has a behavior slightly different. The Hawking temperature increases when the intensity of the cloud of strings decreases, for fixed values of the intensity of the quintessence parameter. As to the heat capacity, its graphs showed in Fig. 6 indicate the existence of phase transitions for different values of the quintessence state parameter. These phase transitions also depend on the intensity of the cloud of strings. Thus, the thermodynamic stability of the system is affected by the presence of the cloud of strings as well.

The Hawking radiation is strongly correlated with the presence of both sources, the quintessence and the cloud of strings. The rate of particle production increases when the parameter associated with the cloud of strings increases, for fixed values of $\alpha$ and $\omega _q$.

In summary, the number and the structure of the horizons, the ergoregions, the forms of the ergoregions, as well as the thermodynamical quantities analyzed, namely, energy, Hawking temperature and heat capacity, and the flux of scalar particles emitted depend on the intensity of the quintessential dark energy and of the cloud of strings.