Time-like geodesic structure in massive gravity

Abstract

In the present paper we analyze the geodesic structure of black hole spacetime in massive gravity with the scalar charge Q representing the modification to Einstein’s general relativity. By solving the geodesic equation and analyzing the behavior of effective potential, we investigate the time-like geodesic types of the test particle around a black hole in massive gravity. At the same time, all kinds of orbits, which are allowed according to the energy levels of the effective potential, are numerically simulated in detail.

1 Introduction

Many test gravitational effects have been predicted by the general relativity, such as bending of light, precession of planetary orbits, gravitational time-delay and gravitational red-shift, etc. The structure of geodesics helps us to understand different gravitational effects of a gravitational source. Recently the geodesics of different gravitational sources have been studied in Refs. [1–5]. The time-like geodesic structure of the Schwarzschild black hole (anti) de Sitter black hole was studied by Jaklitsch et al. [6] and Cruz et al. [7]. Podolsky [8] investigated all possible geodesic motions in the extreme Schwarzschild-de Sitter spacetime. By solving the Hamilton–Jacobi partial differential equation, Kraniotis [9] investigated the geodesic motion of the massive particle in the Kerr and Kerr (anti) de Sitter gravitational field. The analysis of the effective potential for null geodesics in the Reissner-Nordström-de Sitter and Kerr-de Sitter spacetime was carried out in Refs. [10, 11]. Chen and Wang [12, 13] have investigated the time-like geodesic motion of test particle in Schwarzschild spacetime surrounded by quintessence and in Ho r̆ ava–Lifshitz spacetime by analyzing the behavior of the effective potential for the particle. Zhou et al. [14] analyzed the effective of massless and massive test particles in Bardeen spacetime and numerically simulated all possible orbits corresponding to all kinds of energy levels. And he also investigated all geodesic types of the test particle and the photon in JNW spacetime by solving the geodesic equation and analyzing the behavior of effective potential [15].

Several theories [16–22] have been proposed to generalize general relativity in order to get an agreement with the observations that the universe is going through a phase of the accelerated expansion [23, 24] without requiring the existence of the cosmological constant or dark energy and dark matter. One class of these models is called massive gravity [25] which is a well-developed case in the infrared modification of gravity, and that all of these points are nicely illustrated. Fierz and Pauli [26] do the first attempt to include mass for the graviton in 1939. After that, the massive gravity theory was not concerned until the vigorous development of quantum field theory in the early 1970s. Especially, in recent years many significant massive gravity models as a modified Einstein gravity theory (see the excellent reviews on the subject [27–29]) have been proposed. For example, a great of scientists constructed the massive gravity fulfilling Lorentz invariance [30] and proved to be free from ghosts and instabilities at a full nonperturbative level, even though there are very few known solutions for such models [31, 32]. Lorentz violation, which are formulated in a nonperturbative way, makes the study of black holes possible [22, 25]. Fortunately the massive gravity theory with a Lorentz violation gave us an asymptotically flat spherically symmetric space [33, 34] with finite total energy, featuring an asymptotic behavior slower than 1 / r and generically of the form $1/r^{\lambda }$, which makes the black hole solutions be far richer than in general relativity due to the presence of “hair” $\lambda$. Last years Sharmanthie Fernando [35, 36] studied quasinormal modes of scalar and massless Dirac perturbations of this theory. Capela and Tinyakov [37] and Capela and Nardini [38] has checked the validity of the laws of thermodynamics in massive gravity by making use of the exact black hole solution and equilibrium states and phase structures of such a solution enclosed in a spherical surface kept at a fixed temperature.

In this paper we mainly focus on the geodesic structure of a black hole in massive gravity which has different effective potential characterized by the scalar charge Q representing the modification to Einstein’s general relativity due to the presence of graviton with a mass. The present paper is organized as follows: In Sect. 2 we give a brief review on the black hole spacetime in massive gravity, then we study the geodesic equation and its effective potential of the black hole in massive gravity. In Sect. 3 we analyze the orbit types of test particle to the corresponding effective potential and the effect of the parameters $Q, L, \lambda$ on the orbit structure of a black hole in massive gravity. A brief conclusion is given in the last section.

2 Geodesic equation and effective potential

It is well known that the massive gravity is a hot topic in theoretical physics in recent years. The theory of massive gravity is described by the following action

$$\begin{aligned} S=\int d^{4}x\sqrt{-g} \left[ \frac{R}{16\pi }+\Lambda ^4 \Theta (X,W^{ij})\right] , \end{aligned}$$

(1)

where R is the scalar curvature and $\Theta$ is a function of scalar fields $\phi ^0, \phi ^i$. The functions X and $W^{ij}$ are defined as:

$$\begin{aligned} X= & {} \frac{\partial ^{\mu }\phi ^{0}\partial _{\mu }\phi ^{0}}{\Lambda ^{4}},\end{aligned}$$

(2)

$$\begin{aligned} W^{ij}= & {} \frac{\partial ^{\mu }\phi ^{i}\partial _{\mu }\phi ^{j}}{\Lambda ^{4}}- \frac{\partial ^{\mu }\phi ^{i}\partial _{\mu }\phi ^{0}\partial ^{\nu }\phi ^{j} \partial _{\nu }\phi ^{0}}{\Lambda ^{8}X}. \end{aligned}$$

(3)

Now we present static spherically symmetric black hole solution to the action in Eq. (1) which a detailed derivation is given in Refs. [22, 29]. So the metric is given by

$$\begin{aligned} ds^2=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) , \end{aligned}$$

(4)

where

$$\begin{aligned} f(r)=1-\frac{2M}{r}-\frac{Q}{r^{\lambda }}. \end{aligned}$$

(5)

The scalar fields are given by

$$\begin{aligned} \phi ^{0}=\Lambda ^{2}(t+h(r)),\quad \phi ^{i}=\Lambda ^{2}x^{i}, \end{aligned}$$

(6)

where

$$\begin{aligned} h(r)=\pm \int \frac{dr}{\alpha (r)}\left[ 1-\alpha (r) \left( \frac{Q\lambda (\lambda -1)}{12m^{2}} \frac{1}{r^{\lambda +2}}+1\right) ^{-1}\right] ^{\frac{1}{2}}. \end{aligned}$$

(7)

Where m is the mass of the graviton. The solution (4) has an attractive behavior at infinity with positive M. However when M is negative, the corresponding Newton potential is repulsive at large distances and attractive near the horizon. This situation does not have a corresponding case in GR, so we only consider the case $M>0$. Q is a scalar charge which reflects the modification of the gravitational interaction as compared to general relativity. We will get standard Schwarzschild when $Q=0$. For $Q>0$, the modified black hole has attractive gravitational potential at all distances and the horizon size is larger than 2GM. For $Q<0$, the horizon exists only for sufficiently small Q. But When the horizon exists, the gravitational field is attractive all the way to the horizon while the attraction is weaker than in the case of the usual Schwarzschild black hole of mass M, and the horizon size is smaller. Here $\lambda$ is constant. When $\lambda <0$, the solution does not describe asymptotically flat space. And when $0<\lambda <1$, the Arnowitt–Deser–Misner (ADM) mass will be infinite. For $\lambda >1$, the solution recovers standard Schwarzschild term at infinity and the ADM mass is equal to M. Moreover, we forbid naked singularities, i.e. f(r) must have real roots and the largest of them determines the radius of the event horizon. In the following we will limit ourselves to the case $\lambda >1$, so we choose $\lambda =4$ as a test numerical example to simulate in the following sections.

In order to investigate the time-like geodesics of a test particle around the black hole in massive gravity, we firstly set up the geodesic equations and its constraint equations which are given by

$$\begin{aligned}&\displaystyle \ddot{x}^{\mu }+\Gamma ^{\mu }_{\nu \lambda }\dot{x}^{\nu }\dot{x}^{\lambda }=0,\end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }=\varepsilon . \end{aligned}$$

(9)

Here $\dot{x}$ denotes the differentiation with respect to the affine parameter $\tau$ and $x^{\mu }$ are the space time coordinates. $\varepsilon =0$ and $-1$ correspond to null and time-like geodesics, respectively. For convenience we only choose $\varepsilon =-1$ for time-like geodesics to investigate as an example.

The geodesic equations for the metric we considered take the following forms

$$\begin{aligned}&\displaystyle \ddot{t}+\frac{f'(r)}{f(r)}\dot{t}\dot{r}=0,\end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \ddot{r}+\frac{1}{2}f(r)f'(r)\dot{t}^{2}-\frac{f'(r)}{2f(r)}\dot{r}^{2}-rf(r)(\dot{\theta }^{2}+\dot{\varphi }^{2}\sin ^{2}\theta )=0,\end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \ddot{\theta }+\frac{2}{r}\dot{r}\dot{\theta }-\sin \theta \cos \theta \dot{\varphi }^{2}=0,\end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \ddot{\varphi }+\frac{2}{r}\dot{r}\dot{\varphi }+2\dot{\theta }\dot{\varphi }\cot \theta =0. \end{aligned}$$

(13)

The time-like constraint on the trajectories is given by

$$\begin{aligned} -f(r)\dot{t}^{2}+\frac{1}{f(r)}\dot{r}^{2}+r^{2}\dot{\theta }^{2} +r^{2}\sin ^{2}\theta \dot{\varphi }^{2}=-1. \end{aligned}$$

(14)

Now we consider the equatorial plan ($\theta =\frac{\pi }{2}$), so the geodesic equations and its constraint equation can be rewritten as

$$\begin{aligned}&\displaystyle \ddot{t}+\frac{f'(r)}{f(r)}\dot{t}\dot{r}=0,\end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle \ddot{r}+\frac{1}{2}f(r)f'(r)\dot{t}^{2}-\frac{f'(r)}{2f(r)}\dot{r}^{2}-rf(r)\dot{\varphi }^{2}=0,\end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \ddot{\varphi }+\frac{2}{r}\dot{r}\dot{\varphi }=0,\end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle -f(r)\dot{t}^{2}+\frac{1}{f(r)}\dot{r}^{2}+r^{2}\dot{\varphi }^{2}=-1. \end{aligned}$$

(18)

By integrating Eqs. (15, 17) leads to

$$\begin{aligned} \dot{t}= & {} \frac{C_{1}}{f(r)},\end{aligned}$$

(19)

$$\begin{aligned} \dot{\varphi }= & {} \frac{C_{2}}{r^{2}}, \end{aligned}$$

(20)

where the integrating constants $C_{1}$ and $C_{2}$ correspond to the conserved total energy E and the conserved angular momentum L of the test particle, respectively.

Substituting Eqs. (19, 20) into Eq. (18), we can obtain

$$\begin{aligned} -\frac{E^{2}}{f(r)}+\frac{\dot{r}^{2}}{f(r)}+\frac{L^{2}}{r^{2}}=-1. \end{aligned}$$

(21)

Now we solve the above equation for $\dot{r}^{2}$ in order to obtain the radial equation, which allows us to characterize possible moments of the test particle without an explicit solution of the motion equation in an invariant plane

$$\begin{aligned} \dot{r}^{2}=E^{2}-f(r)\left( 1+\frac{L^{2}}{r^{2}}\right) . \end{aligned}$$

(22)

We can rewrite the above equation in one-dimension form

$$\begin{aligned} \dot{r}^{2}=E^{2}-V_{eff}^{2}, \end{aligned}$$

(23)

so we can define the effective potential $V_{eff}^{2}$ as

$$\begin{aligned} V_{eff}^{2}=f(r)\left( 1+\frac{L^{2}}{r^{2}}\right) = \left( 1-\frac{2M}{r}-\frac{Q}{r^{\lambda }}\right) \left( 1+\frac{L^{2}}{r^{2}}\right) . \end{aligned}$$

(24)

3 Effective potential and corresponding orbit

For the above Eq. (24), the effective potential $V_{eff}$ is relevant to the parameters Q, L and $\lambda$. Firstly, we will analyze the impact of scalar charge Q to the potential energy, and then analyze the impact of angular moment L and $\lambda$ to the effective potential.

Fig. 1

The $V_{eff}$ versus r and the corresponding time-like geodesic structure of the test particle around a black hole in massive gravity for the parameters $Q=1, \lambda =4$ and $L=40$

3.1 $Q>0$ case

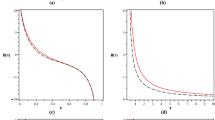
When $Q>0$, at all distances, the gravitational potential is attractive and stronger than the usual Schwarzschild black hole potential. Therefore, the event horizon radius $r_{+}$ is never smaller than in the standard case. According to the equation of motion (Eq. 22) and Fig. 1a, we can divide the time-like geodesics into several cases according to different levels of E as follows:

(1) When $E^{2}>E_{1}^{2}$, The particle with enough energy will directly fall into the center from a finite distance. So we expect a plunge orbit which the particle comes from infinity and then plunges into the center. In Fig. 1b we have simulated the fall-into orbit for the energy E corresponding to $E^{2}>E_{1}^{2}$.

(2) When $E^{2}=E_{1}^{2}$, the particle has an unstable circular orbit. For $r<r_{A}$ ($r_{A}$ is the radius corresponding to $E_{1}$), the particle will fall into the center from $r_{A}$. For $r>r_{A}$, the particle will escape from $r_{A}$ to infinity. These two kinds of unstable circular orbits are showed in Fig. 1c, d.

(3) When $E_{1}^{2}>E^{2}>E_{2}^{2}$, the particle has two different kinds of orbits. If $r<r_{B}$, the particle will fall into the center from $r_{B}$. For $r>r_{C}$, the particle will rebound from $r_{C}$ to infinity. The corresponding orbits are showed in Fig. 1e, f.

Fig. 2

The effective potential $V_{eff}$ versus r of the test particle around a black hole in massive gravity for the parameters Q, $\lambda$ and L

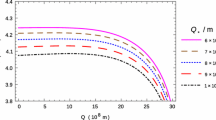
In order to analyze the effect of the parameters $Q>0,\lambda$ and L on the effective potential energy, we numerically showed the situation of the effective potential with different values of the parameters Q, L and $\lambda$ in Fig. 2, in detail.

Figure 2a shows the effective potential for different values of scalar charge Q. The maximum value of effective potential decreases with scalar charge Q increasing. We find that the scalar charge Q mainly take effect on the orbit near the black hole and take no effect on the orbit far away from the center. In Fig. 2b we showed the effective potential energy with parameter $\lambda$. With increasing of the parameter $\lambda$, the effective potential energy move to the left and the maximum value of effective potential energy increases. Figure 2c showed the effective potential energy with angular momentum L, it is easy to see that the maximum value of effective potential energy increases as the angular momentum L increases. All in all, we find the parameters $Q,\lambda$ and L don’t change the styles of the orbits of the test particle around the black hole spacetime in massive gravity.

Fig. 3

The $V_{eff}$ versus r and the corresponding time-like geodesic structure of the test particle around a black hole in massive gravity for the parameters $Q=-1.7, \lambda =4$ and $L=40$

3.2 $Q<0$ case

In this case the Newton potential is always attractive until reaching the horizon, but the attraction is weaker (which makes the event horizon radius $r_{+}$ smaller) than in the Schwarzschild case. Now we investigate, in detail, the orbits of the radial particle in several styles according to different values of E for $Q<0$ case in Fig. 3.

(1) When $E^{2}=E_{2}^{2}$, the particle circles around the center with a constant radius $r=r_{D}$. This particle circles around the center with a constant radius $r=r_{D}$ which is showed in Fig. 3b.

(2) When $E^{2}=E_{1}^{2}$, the particle has an unstable circular orbit. For $r<r_{A}$ ($r_{A}$ is the radius corresponding to $E_{1}$), the particle will fall into the center from $r_{A}$. For $r>r_{A}$, the particle in this kind of orbit escape from $r_{A}$ to infinity. They are simulated in Fig. 3c, d, respectively.

(3) When $E_{1}^{2}>E^{2}>E_{2}^{2}$, the particle has two different kinds of orbits. If $r_{B}<r<r_{C}$, the particle moves in a bound orbit in a range $r_{B}<r<r_{C}$ as Fig. 3e, where $r_{B}$ and $r_{C}$ are the perihelion and aphelion distances, respectively. If $r>r_{C}$, the particle will rebound from $r_{C}$ to infinity, which is showed in Fig. 3f.

(4) When $E^{2}>E_{1}^{2}$, the particle with enough energy will escape from $r=r_{B}$ to infinity, seeing Fig. 3g.

Fig. 4

The effective potential $V_{eff}$ versus r of the test particle around a black hole in massive gravity for the parameters Q, $\lambda$ and L

In order to analyze the effect of $Q,\lambda$ and L on the effective potential energy, we numerically study the effective potential with different values of the parameters $Q<0,\lambda$ and L in Fig. 4.

Figure 4a shows the effective potential for different values of the scalar charge $Q<0$. We find that the scalar charge Q mainly take effect on the orbit near the black hole and take no effect on the orbit far away from the center. We also can see that the bound orbit gap becomes narrow and the energy of particle becomes low as the scalar charge Q increases. In Fig. 4b we show the effective potential for different values of the parameter $\lambda$. With increasing of parameter $\lambda$, the effective potential energy move to the left and the maximum value of effective potential energy increases. Figure 4c shows the effective potential for different values of the angular momentum L, we can see that the maximum value of effective potential energy increases as the angular momentum L increases.

4 Conclusion

In this paper we have solved the geodesic equation and analyzed the behavior of effective potential to investigate the motion of massive particles and study the geodesic structure of a black hole in massive gravity. By using numerical technique, we have found that for a test particle: (1) When the scalar charge $Q>0$, there exist two kinds of fall into orbit, two kinds of unstable circular orbits, a rebound orbit; (2) When the scalar charge $Q<0$, the test particle will move on an escape orbit, two kinds of unstable circular orbits, a bound orbit, or a rebound orbit, an stable circular orbit when the particle energy reaches a minimum. We also have found that the parameters $\lambda$ and L don’t change the styles of the orbits of the test particle around the black hole spacetime in massive gravity.

Appendix

In this section we give a brief review about how the solution Eq. (4) meets the solar system tests, in particular what limits these tests put on the parameter $\lambda$. In order to describe the star system, (see Ref. [22]), the metric should be an asymptotically flat space, and the masses of fluctuations around flat space are

$$\begin{aligned} m^{2}_{0}= & {} \frac{3}{4}\left( \bar{\alpha }_{1}-4\bar{\alpha }_{2}+6\bar{\alpha }_{3}-\bar{\beta }_{1}+4\bar{\beta }_{2}-6\bar{\beta }_{3}\right) m^{2},\nonumber \\ m^{2}_{1}= & {} 0, m^{2}_{2}=\frac{1}{2}\left( \bar{\alpha }_{1}-2\bar{\alpha }_{2}+\bar{\beta }_{1}-2\bar{\beta }_{2}\right) m^{2},\nonumber \\ m^{2}_{3}= & {} \frac{1}{4}\left( \bar{\alpha }_{1}-6\bar{\alpha }_{3}-\bar{\beta }_{1}+8\bar{\beta }_{2}-18\bar{\beta }_{3}\right) m^{2},\nonumber \\ m^{2}_{4}= & {} \frac{1}{4}\left( \bar{\alpha }_{1}-4\bar{\alpha }_{2}+6\bar{\alpha }_{3}-3\bar{\beta }_{1}+12\bar{\beta }_{2}-18\bar{\beta }_{3}\right) m^{2}, \end{aligned}$$

(25)

where $\bar{\alpha }_{i}$ and $\bar{\beta }_{i}$ are constants [22]. By defining another parameter

$$\begin{aligned} \mu ^{2}\equiv m^{2}_{2}\frac{3m^{4}_{4}-m^{2}_{0}\left( m^{2}_{2}-3m^{2}_{3}\right) }{m^{4}_{4}-m^{2}_{0}\left( m^{2}_{2}-m^{2}_{3}\right) }, \end{aligned}$$

(26)

we can obvious find that the limit on $\mu ^{2}$ can be interpreted as a limit on the graviton mass scale $m^{2}$.

Considering a star as a source, the gravitational mass of the body can be written as

$$\begin{aligned} M=M_{0}\left[ 1-\frac{8\mu ^{2}R^{2}}{5(\lambda -1)(\lambda +2)}\right] , \end{aligned}$$

(27)

where $M_{0}$ is the bare mass of the star and R is the radius of the star. The pressure at the center of the star is

$$\begin{aligned} P(0)\simeq \frac{GM_{0}\rho _{0}}{2R} \left[ 1+\frac{16\mu ^{2}R^{2}(11+2\lambda )}{5(2\lambda +1)(\lambda +4)(\lambda +2)}\right] , \end{aligned}$$

(28)

and the derivative of the pressure is

$$\begin{aligned} P^{'}(R)\simeq -\frac{GM_{0}\rho _{0}}{2R}\left[ 1-\frac{16\mu ^{2}R^{2}(\lambda -2)}{5(2\lambda +1)(\lambda +4)(\lambda +2)}\right] . \end{aligned}$$

(29)

In order to ensure the stability of the matter system, so $M>0, P(0)>0, P^{'}(R)<0$ and $\mu ^{2}\le \frac{o(1)}{R^{2}}$. Comelli et al. [22] discussed earlier that the limit on $\mu ^{2}$ can be interpreted as a limit on the graviton mass scale $m^{2}$. Therefore for $\lambda >1$, the typical real stars with $R\sim \times 10^5$ km, require $m<\times 10^{-11}$ eV. Considering the Sun with $R\simeq 7\times 10^{5}$ km and the central pressure not deviating more than few percent from the standard value [42, 43], the graviton mass will be $m<\times 10^{-13}$ eV [39–41]. In fact, larger objects give rise to stranger limits, for instance, the stability of the largest bound states in the universe, $R\simeq 1/10$ Mpc, gives a limit $m<\times 10^{-28/29}$ eV [22]. So we can see that the star system tests, in particular, the solar system tests, limit the parameter $\lambda >1$ in the black hole solution Eq. (4) in massive gravity.