1 Introduction

Thermodynamical properties of the AdS black hole has been a subject of intense study for the past decades. In terms of the AdS/CFT correspondence, the thermodynamics of black holes in AdS space can be identified with that of dual strong coupled conformal field theory (CFT) in the boundary of the AdS space [1]. The thermodynamic properties in AdS black holes were reported in [2], which represented the existence for a certain phase transition (Hawking-Page phase transition) in the phase space of the Schwarzschild AdS black hole.

Recently, the analogy between four dimensional RN-AdS black holes and the Van der Waals fluid-gas system has been completed in this extended phase space [3], where the cosmological constant is treated as a thermodynamic pressure with

$$\begin{aligned} P=-\frac{\Lambda }{8\pi } \end{aligned}$$
(1)

in the geometric units \(G_N=\hbar =c=k=1\). There exist some more meaningful reasons to regard the cosmological constant as a variable [3]. Firstly, some more fundamental theories could be considered, where physical quantities, such as Yukawa coupling, gauge constant, Newton’s constant, or cosmological constant may not be fixed values, but can vary arising from the vacuum expectation energy. Moreover, the lack of the cosmological constant \(\Lambda \) term in the first law of black hole thermodynamics can not lead to a consistent Smarr relation for the black hole thermodynamics. In the extended phase space, however, the Smarr relation is satisfied in addition to the first law of thermodynamics from the aspect of the scaling arguments. In addition, based on the mathematical analogies, the \(\beta \)–\(r_+\) and \(Q\)–\(\Phi \) diagrams of the fixed charge RN-AdS black holes are found to be similar to the \(P\)–\(V\) diagram of the Van der Waals fluid-gas system. Nevertheless, these analogies are only an identification of similar physical quantities. This analogy becomes more natural in this extended phase space. Until now, these critical behaviour of a lot of black hole systems in this extended phase space are under discussion in this direction [5–18]. It is worth to noting that, in four-dimensional Born–Infeld AdS black holes [4], the impact of the nonlinearity can bring the new phenomenon of reentrant phase transition which was observed in rotating AdS holes [19, 20], while this reentrant phase transition does not occur for higher dimensional Born–Infeld AdS black holes [21].

So far, the black holes including these two gauge fields (Maxwell field and YM field) are coupled through gravity have been considered in general relativity [22–29] and higher order derivative gravities [30–32]. From physics standpoint, electromagnetism has long range effects and dominates outside the nuclei of natural matter, while YM field is confined to act inside nuclei. In this paper we will turn to study the black holes in the Einstein–Maxwell–power-Yang–Mills (EMPYM) gravity. Whether the critical behaviour of black hole with two gauge fields still exist? It is interesting to explore. We will find that the existence for the Van der Waals like small-large black hole phase transition depends on dimension \(N\), various values of parameter \(q\), charges \(Q\) and \(C\) of the YM and Maxwell fields. However, this reentrant phase transition will not emerge for the black holes with two gauge fields.

This paper is organized as follows. In Sect. 2, we examine the critical behaviors of the EMPMY black holes. Then, we will study the critical exponents near critical point in Sect. 3. By using the Ehrenfest equations, we will evaluate the phase transition of the EMPMY black holes at the critical point in Sect. 4. Finally, Sect. 5 is devoted to the closing remarks.

2 Critical behavior of Einstein–Maxwell–power-Yang–Mills black holes

The \(N\)-dimensional action for Einstein–Maxwell–power-Yang–Mills gravity with a cosmological constant \(\Lambda \) is given by

$$\begin{aligned} \mathcal{I}=\frac{1}{2}\int dx^N \sqrt{-g}\left( R-\frac{(N-1)(N-2)}{3}\Lambda -F_{\mu \nu }F^{\mu \nu }-(\mathbf Tr (F^{(a)}_{\mu \nu }F^{(a)\mu \nu }))^q\right) , \nonumber \\ \end{aligned}$$
(2)

where \(\mathbf Tr (.)=\sum _{a=1}^{(N-1)(N-2)/2}(.)\), \(R\) is the Ricci scalar, \(q\) is a positive real parameter, YM and Maxwell fields are defined respectively as

$$\begin{aligned}&F_{\mu \nu }^{(a)}=\partial _{\mu }A_{\nu }^{(a)}-\partial _{\nu }A_{\mu }^{(a)} +\frac{1}{2\sigma }C_{(b)(c)}^{(a)}A_{\mu }^{b}A_{\nu }^{c},\end{aligned}$$
(3)
$$\begin{aligned}&F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }. \end{aligned}$$
(4)

Here \(C_{(b)(c)}^{(a)}\) represents the structure constants of \((N-1)(N-2)/2\) parameter Lie group \(G\) and \(\sigma \) is a coupling constant, \(A_{\mu }^{(a)}\) are the \(SO(N-1)\) gauge group YM potentials, and \(A_{\mu }\) is the usual Maxwell potential.

Our metric ansatz for \(N\) dimensional spherically symmetric line element is chosen as

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2d\Omega _n^2 \end{aligned}$$
(5)

with the line element of a unit \(n\)-sphere \(d\Omega _n^2\). Depending on different dimensions \(N\) and values of \(q\), the action Eq. (2) admits various black hole solutions. As we known, the black hole solutions in the standard Einstein–Maxwell–Yang–Mills theory with \(q=1\) [30] and Einstein–power-Yang–Mills theory [32] have been investigated. Here we present the black hole solutions in the Einstein–Maxwell–power-Yang–Mills theory, and then discuss the thermodynamics and critical behavior for each possible black hole solution in the extended phase space.

2.1 \(N(=n+2)\ge 4,~ q\ne (n+1)/4\)

The solution of \(N\)-dimensional EMPYM black hole with negative cosmological constant under the condition of \(q\ne (n+1)/4\) is given by

$$\begin{aligned} f(r)=1-\frac{2m}{r^{n-1}}-\frac{\Lambda }{3}r^2+\frac{2(n-1)C^2}{nr^{2n-2}} +\frac{Q_1}{r^{4q-2}},\quad Q_1=\frac{[(n-1)nQ^2]^q}{n(4q-n-1)},\quad \quad \end{aligned}$$
(6)

where the integration constant \(m\) denotes the mass parameter of black hole, \(C\) and \(Q\) are the charges of Maxwell field and Yang–Mills field respectively. Note in order to keep the power Yang-Mils term satisfying the weak energy condition (WEC), one must take \(q>0\) [32], which is discussed in detailed in what follows. In case of \(q=1\), Eq. (6) reduces to the black hole solution in the Einstein–Maxwell–Yang–Mills gravity [30].

In term of the black hole radius \(r_+\), the Hawking temperature, mass and entropy of black hole in the extended phase space read as

$$\begin{aligned}&T=\frac{f'(r_+)}{4\pi }=\frac{n-1}{4\pi r_+}+\frac{2(n+1)P}{3}r_+-\frac{(4q-n-1)Q_1}{4\pi r_+^{4q -1}}-\frac{(n-1)^2C^2}{2\pi n r_+^{2n-1}}, \quad \quad \quad \end{aligned}$$
(7)
$$\begin{aligned}&M=\frac{n\omega _n}{48\pi }\left( 8\pi P r_+^{n+1}+3r_+^{n-4q+1}Q_1+3r_+^{n-1} +\frac{6(n-1)C^2}{nr_+^{n-1}} \right) ,\quad \quad \quad \quad \end{aligned}$$
(8)
$$\begin{aligned}&S=\frac{\omega _n r_+^n}{4} , \end{aligned}$$
(9)

and the YM potential \(\Phi _Q\) and the electromagnetic potential \(\Phi _C\) can be written as

$$\begin{aligned}&\Phi _Q=\frac{\omega _n q[(n-1)nQ^2]^{q}}{8\pi (4q-n-1)Q}r_+^{n-4q+1},\end{aligned}$$
(10)
$$\begin{aligned}&\Phi _C=\frac{\omega _n (n-1)C}{4\pi r_+^{n-1}}, \end{aligned}$$
(11)

where \(\omega _n=\frac{2\pi ^{(n+1)/2}}{\Gamma (\frac{n+1}{2})}\) is the volume of the unit \(n\)-sphere. Moreover, the free energy \(F\) of black hole can be written as

$$\begin{aligned} F&= M-T\cdot S. \end{aligned}$$
(12)

From Eqs. (7–9), these thermodynamic quantities obey the first law of black hole thermodynamics in the extended phase space

$$\begin{aligned} \,\mathrm {d}\,M=T\,\mathrm {d}\,S+\Phi _Q\,\mathrm {d}\,Q+\Phi _C\,\mathrm {d}\,C+V\,\mathrm {d}\,P, \end{aligned}$$
(13)

where \(V\) denotes the thermodynamic volume with \(V=(\frac{\partial M}{\partial P})_{S,\Phi _Q,\Phi _C}\). By the scaling argument, we can obtain the generalized Smarr relation for the EMPYM black hole in the extended phase space

$$\begin{aligned} M=\frac{n}{n-1}TS+\Phi _C C+\frac{2q-1}{(n-1)q}\Phi _Q Q-\frac{2}{n-1}VP. \end{aligned}$$
(14)

By rewriting the Eq. (7), we can get the equation of state of the black hole

$$\begin{aligned} P=\frac{3T}{2(n+1)r_+}+\frac{3(n-1)^2C^2}{4\pi n(n+1)r_+^{2n}}+\frac{3(4q-n-1)Q_1}{8\pi (n+1)r_+^{4q}}-\frac{3(n-1)}{8\pi (n+1)r_+^2}. \quad \quad \quad \end{aligned}$$
(15)

To compare with the Van der Waals fluid equation, we can translate the “geometric” equation of state to physical one by identifying the specific volume \(v\) of the fluid with the horizon radius of the black hole as \(v=\frac{4r_+}{n}\) such that we will just use the horizon radius in the equation of state for the black hole hereafter in this paper.

The critical point should satisfy the following condition

$$\begin{aligned} \frac{\partial P}{\partial r_+}\Big |_{T=T_c, r_+=r_c} =\frac{\partial ^2 P}{\partial r_+^2}\Big |_{T=T_c, r_+=r_c}=0, \end{aligned}$$
(16)

which leads to the critical temperature

figure a

and the equation for the critical horizon radius

$$\begin{aligned} r_c^{4q-2}-2(2n-1)(n-1)C^2 r_c^{4q-2n}-\frac{2q(4q-1)(4q-n-1)Q_1}{n-1}=0. \end{aligned}$$
(18)

The physical solutions of Eq. (18) crucially depend on the dimensions \(n\), parameter \(q\) and charges \(Q\) and \(C\) of the YM and Maxwell fields. Further, The existence of the critical behavior is also determined by the positive critical pressure \(P_c\) and critical temperature \(T_c\).

It is worth to note that Eq. (6) becomes the RN-AdS black hole solution when \(Q=0(Q_1=0)\). The \(P\)–\(V\) criticality of RN-AdS black hole has been investigated in [3, 4]. Then we only focus on the cases of \(Q\ne 0\) below.

2.1.1 \(C=0\)

In the case of \(C=0\), Eq. (18) with \(q=\frac{1}{2}\) or \(q\le \frac{1}{4}\) does not exhibit any real positive root \(r_c\), which implies disappearance of critical behavior of black hole in these cases. Otherwise Eq. (18) can be solved as

$$\begin{aligned} r_c=\left[ \frac{2q(4q-1)[(n-1)nQ^2]^q}{n(n-1)} \right] ^\frac{1}{4q-2}. \end{aligned}$$
(19)

Plugging it into Eq. (17), the critical temperature and pressure are given by

figure b

This also gives the following ratio relation

$$\begin{aligned} \rho _c=\frac{P_c v_c}{T_c}=\frac{3(4q-1)}{4nq(n+1)}, \end{aligned}$$
(21)

where the ratio \(\rho _c\) is independent with the charge \(Q\) of the YM field. If taking \(q=1\), the system reduces especially to the EYM black hole, and the critical quantities of EYM black hole are given by

$$\begin{aligned} r_c=\sqrt{6}Q,\quad T_c=\frac{n-1}{3\sqrt{6}\pi Q}, \quad P_c=\frac{n-1}{32\pi (n+1)Q^2}. \end{aligned}$$
(22)

The ratio here becomes \(\rho _c=\frac{P_c v_c}{T_c}=\frac{9}{4n(n+1)}\).

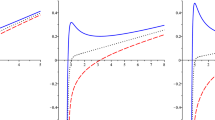
The “\(P\)–\(r_+\) diagrams” of black hole in four dimensions for \(q=1\) and \(q\ne 1\) are respectively depicted in Fig. 1. These diagrams are exactly the same as the \(P\)–\(V\) diagram of the Van der Waals liquid-gas system [3]. For a fixed temperature lower than the critical one \(T_c\), we have two branches whose pressure decreases as the increase of horizon radius, one is in the small radius region (corresponding to fluid phase) and the other is in the large radius region (corresponding to the gas phase). However, the black holes are always in the gas phase and no phase transition happens above the critical temperature \(T_c\). In addition, the pictures for free energy shown in Eq. (12) as a function of temperature with different pressure are plotted in Fig. 2. One can see that these figure develops a “swallow tail” for \(P<P_c\), which denotes a first order phase transition and this “swallow tail” vanishes at \(P>P_c\) and \(P=P_c\) (critical point). Moreover, the corresponding “\(P\)–\(r_+\)” and “\(F\)–\(T\)” diagrams of black hole in higher dimensions are also qualitatively similar.

Fig. 1
figure 1

The \(P\)–\(r_+\) diagrams of the EMPYM black hole with \(N=4, Q=0.5, C=0\). Here these black, dashed and dotdashed curves correspond to the isotherm \(T=0.8T_c\), \(T=T_c\), \(T=1.2T_c\) respectively. a \(q=1\), b \(q=2\)

Full size image
Fig. 2
figure 2

The \(F\)–\(T\) diagrams of the EMPYM black hole with \(N=4, Q=0.5, C=0\). Here these black, dashed and dotdashed curves correspond to the isopiestic \(P=0.5P_c\), \(P=P_c\), \(P=1.5P_c\) respectively. a \(q=1\), b \(q=2\)

Full size image

2.1.2 \(C\ne 0\)

Generally, it is hard to exactly solve the Eq. (18) for \(C\ne 0\). However, what we are interested in is whether the phase transition happens or not, which is equivalent to study the existence of positive solution \(r_c\) of Eq. (18). We introduce a function

$$\begin{aligned} H(r_c)&= r_c^{4q-2}-A r_c^{4q-2n}-B\nonumber \\&= r_c^{4q-2}\left( 1-\frac{A}{r_c^{2n-2}}\right) -B \end{aligned}$$
(23)

with \(A=2(2n-1)(n-1)C^2\) and \(B=\frac{2q(4q-1)[(n-1)nQ^2]^q}{n(n-1)}\). Obviously the critical radius is determined by \(H(r_c)=0\). It is clear that \(r_c=A^{1/(2n-2)}\) is a solution if \(B=0\) (\(q=1/4\)). For generic \(q\), the derivative of \(H(r_c)\)

$$\begin{aligned} H'(r_c)=(4q-2)-A\left( 4q-2n\right) r_c^{2-2n} \end{aligned}$$
(24)

vanishes at \(r_c\equiv r_g=\left[ \frac{2(2n-1)(n-1)C^2\left( 2q-n\right) }{2q-1}\right] ^{\frac{1}{2n-2}}\) when \(q>\frac{n}{2}\) or \(q<\frac{1}{2}\), while always maintains positive in the region of \(\frac{1}{2}<q\le \frac{n}{2}\) and negative for \(q=\frac{1}{2}\).

Now, we return to analyse the existence of the critical behaviours based on the values of \(q\).

  1. 1.

    \(\mathbf {q<\frac{1}{4}}\), the function \(H(r_c)\) tends to \(-\infty \) as \(r_c\rightarrow 0\) and \(H(r_c)\rightarrow (-B)>0\) when \(r_c\rightarrow +\infty \), and Eq. (24) has one solution \(r_g\). This implies that just one positive critical radius \(r_c\) makes \(H(r_c)=0\). Meanwhile, the positive condition of \(T_c,P_c>0\) gives a constrain on the Maxwell field charge \(C\)

    $$\begin{aligned} \frac{n}{2n-1}\cdot \frac{(1-2q)}{2(n-2q)(n-1)}r_c^{2n-2}<C^2<\frac{(1-2q)}{2(n-2q)(n-1)}r_c^{2n-2}. \end{aligned}$$
    (25)
  2. 2.

    \(\mathbf {\frac{1}{4}<q<\frac{1}{2}}\), the function \(H(r_c)\) reaches a negative number \((-B)\) as \(r_c\rightarrow +\infty \), and approaches \(-\infty \) if \(r_c\rightarrow 0\), and Eq. (24) has one solution \(r_g\). Hence \(H(r_c)=0\) admits one or two critical radius solutions \(r_c\) which are determined by the cases of \(H(r_g)=0\) and \(H(r_g)>0\). As to the asymptotic behavior of the critical temperature \(T_c\) [Eq. (16a)] and the critical pressure \(P_c\) [Eq. (16b)], we find the temperature function \(T_c(r_c)\) tends to \(+\infty \) as \(r_c\rightarrow +\infty \), \(T_c(r_c)\rightarrow 0\) from the negative direction when \(r_c\rightarrow 0\) and vanishes at

    $$\begin{aligned} r_c\equiv r_t=\left[ \frac{2(n-1)\left( n-2q\right) C^2}{1-2q}\right] ^{\frac{1}{2n-2}}; \end{aligned}$$
    (26)

    the pressure function \(P_c(r_c)\) has the same asymptotic behavior with the temperature function and vanished at

    $$\begin{aligned} r_c\equiv r_p=\left[ \frac{2(n-1)(2n-1)\left( n-2q\right) C^2}{n(1-2q)}\right] ^{\frac{1}{2n-2}}, \end{aligned}$$
    (27)

    which also gives the inequality \(\frac{r_t}{r_g}<\frac{r_p}{r_g}<1\).

    When \(H(r_g)=0\), the critical temperature \(T_c(r_g)\) is always negative, there is no phase transition. If \(H(r_g)>0\), the equation \(H(r_c)=0\) has two positive solutions \(r_1<r_2~\) satisfying \(r_1<r_g<r_2\). Taking account of the signs of \(T_c\) and \(P_c\) at \(r_1\) and \(r_2\), one can find that the phase transition happens at \(r_1\) under condition

    $$\begin{aligned} C^2<\Big [\frac{n(n-1)^2}{2q(n-2q)[(n-1)nQ^2]^q} \Big ]^{\frac{n-1}{1-2q}}\cdot \frac{1-2q}{2(n-2q)(n-1)}. \end{aligned}$$
    (28)
  3. 3.

    \(\mathbf {\frac{1}{2}<q<\frac{n}{2}}\), the function \(H(r_c)\) reaches positive infinity as \(r_c\rightarrow +\infty \) and approaches \(-\infty \) when \(r_c\rightarrow 0\). Since \(H'(r_c)\) is a monotonic increasing function, Eq. (23) only admits just one positive critical radius solution \(r_c\). Meanwhile, the critical temperature \(T_c\) and the critical pressure \(P_c\) are always positive in this case.

  4. 4.

    \(\mathbf {q>\frac{n}{2}}\), the function \(H(r_c)\) approaches \(+\infty \) as \(r_c\rightarrow +\infty \) and tends to a negative number \((-B)\) as \(r_c\rightarrow 0\). Hence, \(H(r_c)=0\) always admits just one positive root, and then the charge \(C\) satisfies Eq. (25) on account of \(T_c,P_c>0\).

  5. 5.

    \(\mathbf {q=\frac{1}{4}}\), critical radius \(r_c\) equals to \(\big [2(2n-1)(n-1)C^2 \big ]^\frac{1}{2n-2}\), and the critical temperature and pressure read

    figure c

    which leads to \(C^2<2^{2n-3}\frac{(n-1)^{\frac{7n-9}{2}}n^{\frac{3(n-1)}{2}}}{(2n-1)^{2n-1}Q^{n-1}}\) based on \(T_c>0\) and \(P_c>0\).

  6. 6.

    \(\mathbf {q=\frac{1}{2}}\), the solution of Eq. (18) is

    $$\begin{aligned} r_c={\left[ \frac{2(2n-1)(n-1)C^2}{1-Q_1} \right] }^{\frac{1}{2n-2}}. \end{aligned}$$
    (30)

    However, the critical pressure \(P_c\) always disappears, there is no phase transition.

  7. 7.

    \(\mathbf {q=\frac{n}{2}}\), the critical quantities can be written as

    figure d

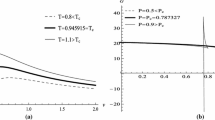
Therefore, excepting \(q=1/2\), there exists a Van der Waals phase transition under proper conditions, the “\(P\)–\(r_+\)” and “\(F\)–\(T\)” diagrams of black holes are similar, which are depicted in Figs. 3 and 4. with \(N=4\). Moreover, the behaviour of black holes in higher dimensions are also qualitatively similar.

Fig. 3
figure 3

The \(P\)–\(r_+\) diagrams of the EMPYM black hole with \(N=4, Q=1, C=0.1\). Here these black, dashed and dotdashed curves correspond to the isotherm \(T=0.8T_c\), \(T=T_c\), \(T=1.2T_c\) respectively. a \(q=1/8\), b \(q=1/3\)

Full size image
Fig. 4
figure 4

The \(F-T\) diagrams of the EMPYM black hole with \(N=4, Q=1, C=0.1\). Here these black, dashed and dotdashed curves correspond to the isopiestic \(P=0.5P_c\), \(P=P_c\), \(P=1.5P_c\) respectively. a \(q=1/8\). b \(q=1/3\)

Full size image

2.2 \(N(=n+2)\ge 4, ~q=(n+1)/4\)

In this case, the solution of \(N\)-dimensional EMPYM black hole is given by

$$\begin{aligned}&f(r)=1-\frac{2m}{r^{n-1}}-\frac{\Lambda }{3}r^2+\frac{2(n-1)C^2}{nr^{2n-2}} -\frac{Q_2\ln {r}}{r^{n-1}},\nonumber \\&Q_2=\frac{1}{n}\big [(n-1)nQ^2 \big ]^{\frac{n+1}{4}} . \end{aligned}$$
(34)

When the power exponent \(q\) takes 1, Eq. (34) will reduce to the EMYM black hole where the dimension \(n=5\) [30].

The temperature \(T\), mass and entropy of this EMPYM black hole in the extended phase space can be derived as

$$\begin{aligned}&T=\frac{n-1}{4\pi r_+}+\frac{2(n+1)Pr_+}{3}-\frac{Q_2}{4\pi r_+^n}-\frac{(n-1)^2C^2}{2\pi n r_+^{2n-1}}, \end{aligned}$$
(35)
$$\begin{aligned}&M=\frac{n\omega _n}{8\pi }\left( \frac{r_+^{n-1}}{2}-\frac{\Lambda r_+^{n+1}}{6}-\frac{Q_2\ln {r_+}}{2}+\frac{(n-1)C^2}{nr_+^{n-1}}\right) ,\end{aligned}$$
(36)
$$\begin{aligned}&S=\frac{\omega _n r_+^n}{4}. \end{aligned}$$
(37)

with the pressure \(P=-\frac{\Lambda }{8\pi }\). This gives the equation of state

$$\begin{aligned} P=\frac{3T}{2(n+1)r_+}+\frac{3Q_2}{8\pi (n+1)r_+^{n+1}}+\frac{3(n-1)^2C^2}{4\pi n(n+1)r_+^{2n}} -\frac{3(n-1)}{8\pi (n+1)r_+^2}. \end{aligned}$$
(38)

By adopting the Eq. (16), we can obtain the critical temperature

figure e

and the equation for the critical horizon radius

$$\begin{aligned} r_c^{2n-2}-\frac{n(n+1)Q_2}{2(n-1)}r_c^{n-1}-2(2n-1)(n-1)C^2=0, \end{aligned}$$
(40)

which leads to

$$\begin{aligned} r_c=\left[ \frac{n(n+1)Q_2}{4(n-1)}+\sqrt{\frac{n^2(n+1)^2Q_2^2}{16(n-1)^2} +2(2n-1)(n-1)C^2} \right] ^{\frac{1}{n-1}}. \end{aligned}$$
(41)

Obviously the critical temperature and pressure are always positive, and then the critical behaviour also exist in this case. The system reduces to the EMYM black hole with \(q=1\) in five dimensions. Following the same procedure above, we can also discuss the free energy \(F\) of black hole and the first order phase transition and this “swallow tail” will also appear in the \(F\)–\(T\) diagrams.

3 Critical exponents near critical point

Now we turn to compute the critical exponents \(\alpha \), \(\beta \), \(\gamma \), \(\delta \) for the black hole system, which characterize the behaviors of physical quantities in the vicinity of the critical point \((r_+=r_c, v=v_c, T=T_c, P=P_c)\) for the black hole. Firstly, we define

$$\begin{aligned} p=\frac{P}{P_c};~~\nu =\frac{v}{v_c};~~\tau =\frac{T}{T_c}. \end{aligned}$$
(42)

Near the critical point, critical exponents are defined as follows [3]

$$\begin{aligned}&C_v=T\frac{\partial S}{\partial T}\Big |_v\propto \left( -\frac{T-T_c}{T_c}\right) ^{-\alpha },\nonumber \\&\eta =\frac{v_s-v_l}{v_c}\propto \left( -\frac{T-T_c}{T_c}\right) ^{\beta },\nonumber \\&\kappa _T=-\frac{1}{v}\frac{\partial v}{\partial P}\Big |_T\propto \left( -\frac{T-T_c}{T_c}\right) ^{-\gamma },\nonumber \\&P-P_c \propto (v-v_c)^{\delta }, \end{aligned}$$
(43)

where \(``c''\) denotes the quantity at the critical point of the system.

In order to compute the critical exponent \(\alpha \), we rewrite the entropy of black hole as \(S=\frac{(n+1)\pi ^{\frac{n+1}{2}}r_+^n}{4\Gamma (\frac{n+3}{2})}\). Obviously this entropy \(S\) is independent of \(T\) for the constant value of specific volume \(v\), so we conclude that the critical exponent \(\alpha =0\). To obtain the other exponents, we introduce the expansion parameters

$$\begin{aligned} \tau =t+1, \quad \nu =\omega +1, \end{aligned}$$
(44)

and expand this equation of state near the critical point we can get

$$\begin{aligned} p=1+a_{10}t+a_{11}t\omega +a_{03}\omega ^3 +\mathcal {O}(t\epsilon ^2,\epsilon ^4). \end{aligned}$$
(45)

During the phase transition, the pressure remains constant

$$\begin{aligned}&p=1+a_{10}t+a_{11}t\omega _s+a_{03}\omega _s^3=1+a_{10}t+a_{11}t \omega _l+a_{03}\omega _l^3,\nonumber \\&\quad \Rightarrow a_{11}t\left( \omega _s-\omega _l\right) +a_{03} \left( \omega _s^3-\omega _l^3\right) =0, \end{aligned}$$
(46)

where \(\omega _s\) and \(\omega _l\) denote the ‘volume’ of small and large black holes.

Using Maxwell’s area law, we obtain

$$\begin{aligned} \int ^{\omega _s}_{\omega _l}\omega \frac{dp}{d\omega }d\omega =0 \Rightarrow a_{11}t\left( \omega _s^2-\omega _l^2\right) +\frac{3}{2}a_{03}\left( \omega _s^4-\omega _l^4\right) =0. \end{aligned}$$
(47)

With Eqs. (46, 47), the nontrivial solutions appear only when \(a_{11}a_{03}t<0\). Then we can get

$$\begin{aligned} \omega _s=\frac{\sqrt{-a_{11}a_{03}t}}{3|a_{03}|}, \quad \omega _l=-\frac{\sqrt{-a_{11}a_{03}t}}{3|a_{03}|}. \end{aligned}$$
(48)

Table.1 is the different values of \(a_{10},~a_{11},~a_{03}\) in Eq. (46) corresponding to the different situations.

Table 1 Coefficient
Full size table

Therefore, we have

$$\begin{aligned} \eta =\omega _s-\omega _l=2\omega _s\propto \sqrt{-t}\Rightarrow \beta =1/2. \end{aligned}$$
(49)

The isothermal compressibility can be computed as

$$\begin{aligned} \kappa _T=-\frac{1}{v}\frac{\partial v}{\partial P}\Big |_{v_c}\propto -\frac{1}{\frac{\partial p}{\partial \omega }}\Big |_{\omega =0}=-\frac{1}{a_{11}t}, \end{aligned}$$
(50)

which indicates that the critical exponent \(\gamma =1\). Moreover, the shape of the critical isotherm \(t=0\) is given by

$$\begin{aligned} p-1=-\omega ^3\Rightarrow \delta =3. \end{aligned}$$
(51)

Evidently these critical exponents of the black holes coincide with those of the Van der Waals liquid-gas system [3].

4 Phase transition at the critical point and Ehrenfest’s equations

For Van der Waals liquid-gas system, the liquid-gas structure does not change suddenly but undergoes the second order phase transition at the critical point \((V=V_c, T=T_c, P=P_c)\). This is described by the Ehrenfest’s description [34, 35]. In conventional thermodynamics, Ehrenfest’s description consists of the first and second Ehrenfest’s equations [36, 37]

$$\begin{aligned}&\frac{\partial P}{\partial T}\Big |_S=\frac{C_{P2}-C_{P1}}{TV(\zeta _2-\zeta _1)} =\frac{\Delta C_P}{TV\Delta \zeta },\end{aligned}$$
(52)
$$\begin{aligned}&\frac{\partial P}{\partial T}\Big |_V=\frac{\zeta _2-\zeta _1}{\kappa _{T2}-\kappa _{T1}} =\frac{\Delta \zeta }{\Delta \kappa _{T}}. \end{aligned}$$
(53)

For a genuine second order phase transition, both of these equations have to be satisfied simultaneously. Here \(\zeta \) and \(\kappa _T\) denote the volume expansion and isothermal compressibility coefficients of the system respectively

$$\begin{aligned} \zeta =\frac{1}{V}\frac{\partial V}{\partial T}\Big |_P,\quad \kappa _T=-\frac{1}{V}\frac{\partial V}{\partial P}\Big |_T. \end{aligned}$$
(54)

Let us concentrate on the \(N\)-dimensional EMPYM black hole. From Eq. (54), we can obtain

$$\begin{aligned} V\zeta =\frac{\partial V}{\partial T}\Big |_P =\frac{\partial V}{\partial S}\Big |_P\times \frac{\partial S}{\partial T}\Big |_P =\frac{\partial V}{\partial S}\Big |_P\times \frac{C_P}{T}. \end{aligned}$$
(55)

The right hand side of Eq. (52) can be expressed into

$$\begin{aligned} \frac{\Delta C_P}{TV\Delta \zeta }=\left[ \frac{\partial S}{\partial V}\Big |_P\right] _{r_+=r_c} =\frac{3}{2(n+1)r_c}, \end{aligned}$$
(56)

where the thermodynamic volume \(V\) is described above and the subscript denotes the physical quantities at the critical point. From Eqs. (15) and (38), the left hand side of Eq. (52) at the critical point can be got as

$$\begin{aligned} \left[ \frac{\partial P}{\partial T}\Big |_S\right] _{r_+=r_c} =\frac{3}{2(n+1)r_c}. \end{aligned}$$
(57)

Therefore, the first of Ehrenfest’s equations can be satisfied at the critical point.

Now let’s examine the second of Ehrenfest’s equations. In order to compute \(\kappa _T\), we make use of the thermodynamic identify

$$\begin{aligned} \frac{\partial V}{\partial P}\Big |_T\times \frac{\partial P}{\partial T}\Big |_V \times \frac{\partial T}{\partial V}\Big |_P=-1. \end{aligned}$$
(58)

Considering Eq. (54), we can have

$$\begin{aligned} \kappa _T V=-\frac{\partial V}{\partial P}\Big |_T=\frac{\partial T}{\partial P}\Big |_V \times \frac{\partial V}{\partial T}\Big |_P =\frac{\partial T}{\partial P}\Big |_V V\zeta . \end{aligned}$$
(59)

which reveals the validity of the second Ehrenfest equations at the critical point. Moreover, the right hand side of Eq. (53) is given by

$$\begin{aligned} \frac{\Delta \zeta }{\Delta \kappa _T}=\left[ \frac{\partial P}{\partial T}\Big |_V\right] _{r_+=r_c} =\frac{3}{2(n+1)r_c}. \end{aligned}$$
(60)

Using Eqs. (56) and (60), the Prigogine-Defay (PD) ratio \((\Pi )\) [38] is

$$\begin{aligned} \Pi =\frac{\Delta C_P\Delta \kappa _T}{Tv(\Delta \zeta )^2}=1. \end{aligned}$$
(61)

Hence, this phase transition at the critical point in the \(N\)-dimensional EMPYM black hole is of the second order in both cases of \(q=(n+1)/4\) and \(q\ne (n+1)/4\). These results are also consistent with the nature of the liquid-gas phase transition at the critical point.

5 closing remarks

In this paper we have studied the phase transition and critical behavior of \(N\)-dimensional AdS black holes in the Einstein–Maxwell–power-Yang–Mills gravity, where the cosmological constant appears as a dynamical pressure of the system and its conjugate quantity is the thermodynamic volume of the black hole. It shows that for the case of \(q\ne (n+1)/4\), excepting \(q=1/2\), there exists a Van der Waals phase transition under proper constraint conditions of the charges \(C\),\(Q\) of Maxwell and Yang–Mills fields and the dimension \(n\). For the case of \(q=(n+1)/4\), the P-V criticality and the small/large black hole phase transition always exist with no constraint condition.

In the case of \(q\ne (n+1)/4\), the power Yang–Mills term contributes a positive term or a negative term to the metric function Eq. (6), which depends on the range of the power exponent \(q\). However, the contribution of the YM term in the equation of state Eq. (15) is always positive. Comparing Eq. (15) with the equation of state in Ref.[3, 4], we can find that the first and last terms in Eq. (15) are standard and the middle terms are both positive monotonically decreasing functions of radius \(r\), which means the equation of state can at most produce a single minimum and a single maximum. This discussion is consistent with the results we calculated, which shows that there is at most one critical point in the system. This is why no re-entrant behaviour is observed and only the Van der Waals behaviour may exist. For the same reason, we can only observed the Van der Waals behaviour in the case of \(q=(n+1)/4\).

We have also calculated the critical exponents at the critical point and found in all cases the critical exponents coincide with those of the Van der Waals fluid. Finally, both of the Ehrenfest’s equations have been verified to hold at the critical point, which shows that in resemblance with the liquid-gas phase transition, the phase transition of the EMPYM black hole at the critical point is of the second order.