Elastic Impedance Variation with Angle and Azimuth Inversion for Brittleness and Fracture Parameters in Anisotropic Elastic Media

Abstract

Young’s modulus, Poisson’s ratio, and fracture excess compliances, which are related to rock brittleness and natural fractures, can be used to evaluate the hydraulic fracturing and infer the optimized sweet spots in unconventional reservoirs. We aim to characterize the elastic properties of rock brittleness and compliance from the observable wide-azimuth seismic data via the inversion of Young’s modulus, Poisson’s ratio, and excess compliances. Using the linear slip model, we first derive the perturbations in stiffness components in terms of Young’s modulus, Poisson’s ratio, and excess compliances for the case of weak anisotropy and small contrasts in elastic properties across the interface. Based on the relationship between scattering function and reflection coefficient in weakly anisotropic media, we then derive a linearized PP-wave reflection coefficient and an azimuthal elastic impedance (EI) equation as a function of Young’s modulus, Poisson’s ratio, density, and excess compliances. Finally, we develop an EI variation with incident angle and azimuth inversion method to estimate the Young’s modulus, Poisson’s ratio, and excess compliances in a Bayesian framework. The approach is implemented in a two-step inversion: azimuthal EI inversion and estimation of model parameters. A synthetic test demonstrates that the model parameter can be reasonably estimated even containing moderate noise. A field data set test reveals that the inversion results agree well with the well log interpretation.

1 Introduction

Young’s modulus and Poisson’s ratio, related to mineral, porosity, total organic carbon (TOC) content, and rock strength, are treated as an indicator of rock brittleness, which play significant roles in seismic reservoir characterization to evaluate hydraulic fracturing and infer sweet spots of unconventional reservoirs (Harris et al. 2011; Sena et al. 2011). Young’s modulus and Poisson’s ratio are usually estimated from surface seismic data indirectly with the computation of P- and S-wave velocities and density to perform the “sweet spot” discrimination and optimization of horizontal well placement (Sena et al. 2011). There, however, exist two difficulties. Firstly, when computing the Young’s modulus, the density needed is more problematic than the inversion of P- and S-wave velocities even with the seismic data containing the information of large incident angles or offsets (de Nicolao et al. 1993; Debski and Tarantola 1995; Downton 2005; Kabir et al. 2006). Secondly, the indirect computation of Young’s modulus and Poisson’s ratio accumulates errors and causes much more bias in parameter estimation (Zong et al. 2013a, b; Yin and Zhang 2014). In this paper, we demonstrate an approach of direct inversion for Young’s modulus, Poisson’s ratio, and density from surface seismic data to avoid the indirect estimation and accumulated errors.

Fractures are the storage and migration of hydrocarbon, and the detection of fractures also plays an important role in seismic reservoir characterization (Narr et al. 2006; Bachrach et al. 2009; Liu and Martinez 2013; Pan et al. 2018a). Fractured rock-physics model relates the seismic characterization to the fracture properties (fracture porosity, aspect ratio, fracture density, fracture fillings, etc.), which is usually used to describe the fractures (Hudson 1980, 1981; Schoenberg 1980, 1983). Based on the linear slip (LS) model, the normal and tangential excess compliances ($Z_{\text{N}}$ and $Z_{\text{T}}$) are used to characterize the rotationally invariant fractures (Schoenberg and Douma 1988). Schoenberg and Sayers (1995) suggest using the normal-to-tangential excess compliance ratio (${{Z_{\text{N}} } \mathord{\left/ {\vphantom {{Z_{\text{N}} } {Z_{\text{T}} }}} \right. \kern-0pt} {Z_{\text{T}} }}$) to indicate the fluids filling the fractures. Bakulin et al. (2000a) use the approximate excess compliance ratio as a fracture fluid indicator (FFI), which is a product of the square of the S- and P-wave velocity ratio and the normal-to-tangential weakness ratio (${{\Delta_{\text{N}} } \mathord{\left/ {\vphantom {{\Delta_{\text{N}} } {\Delta_{\text{T}} }}} \right. \kern-0pt} {\Delta_{\text{T}} }}$). Similarly, the indirect estimation of excess compliance ratio results in more bias in computing the fluid indicator (Pan et al. 2017a, 2018b). In this paper, we derive a linearized PP-wave reflection coefficient in terms of excess compliances and present a direct approach to estimate the excess compliances to compute the fluid indicator and detect the fractures from observable azimuthal seismic data.

A rock permeated by a single set of fractures can be treated as a horizontal transverse isotropy (HTI) medium (Bakulin et al. 2000a; Koren et al. 2010; Ravve and Koren 2010; Tsvankin and Grechka 2011). Rüger (1997, 1998) derives the linearized PP-wave reflection coefficient for an HTI medium as a function of background isotropic elastic parameters and Thomsen’s (1986) anisotropic parameters. Based on the work of Rüger (1997, 1998), much work has been done to estimate the anisotropic parameters and detect the fractures using the amplitude variation with offset and azimuth (AVOAz) data (Mallick et al. 1998; Gray and Head 2000; Chen et al. 2005; Shaw and Sen 2006; Goodway et al. 2007; Bachrach et al. 2009; Far et al. 2014; Downton and Roure 2015; Pan et al. 2017b). In addition, elastic impedance (EI) has been widely studied in the literature because of its practicability (Connolly 1999; Duffaut et al. 2000; Mallick 2001, 2007; Whitcombe 2002; Morozov 2010). Martins (2006) extends the EI to the case of weakly anisotropic media. Zhang and Li (2016) derive the EI of qP- and qS-waves for the transversely isotropic medium to characterize the unconventional reservoir with strong seismic anisotropy. Pan et al. (2017a) use the azimuthally anisotropic EI to estimate the approximate excess compliance ratio as a fluid indicator in a carbonate reservoir. In the present study, the EI variation with incident angle and azimuth (EIVAZ) inversion for Young’s modulus, Poisson’s ratio, and excess compliances in a horizontal transversely isotropic medium can be divided into two main steps: azimuthally anisotropic EI inversion from partial angle-stack azimuthal seismic data, and estimation of model parameters from inverted azimuthal EI data.

Unlike the method proposed by Rüger (1997, 1998), Shaw and Sen (2004, 2006) derive the linearized reflection coefficients for weakly anisotropic media using the asymptotic ray theory and the method of stationary phase. Following Shaw and Sen (2004, 2006), we first derive the perturbations in stiffness components in terms of Young’s modulus, Poisson’s ratio, and excess compliances for the case of an interface separating two media containing a single set of fractures based on the linear slip (LS) model. Based on the relationship between scattering function and reflection coefficient in weakly anisotropic media, we then derive a linearized PP-wave reflection coefficient and an azimuthal elastic impedance (EI) equation as a function of Young’s modulus, Poisson’s ratio, density, and excess compliances. We develop a two-step EIVAZ inversion method to estimate the Young’s modulus, Poisson’s ratio, and excess compliances in a Bayesian framework: azimuthal EI inversion and Bayesian estimation of model parameters. We apply the EIVAZ inversion approach to synthetic and field data sets to illustrate its feasibility and stability.

2 Theory and Method

2.1 Perturbations in Stiffnesses in Terms of Young’s Modulus, Poisson’s Ratio, and Excess Compliances

The homogeneous and isotropic host rock permeated by a set of vertical, aligned fractures can be described by the linear slip model, which is characterized by a compliance matrix ${\varvec{S}}$ of fractured rock (Schoenberg and Douma 1988; Schoenberg and Sayers 1995)

$$\varvec{S} = \varvec{S}_{b} + \varvec{S}_{f} ,$$

(1)

where $\varvec{S}_{b}$ denotes the compliance matrix of the isotropic host rock, and $\varvec{S}_{f}$ denotes the excess compliance matrix caused by the presence of fractures.

In this paper, the fractures are assumed to be rotationally invariant, which is normal to the fracture plane. The host compliance and excess compliance expressed by Young’s modulus $E$ and Poisson’s ratio $\sigma$ for the horizontally transverse isotropic (HTI) rock containing a set of parallel fractures are given by (Pan et al. 2017c)

$$\varvec{S}_{b} = \left[ {\begin{array}{*{20}c} {\frac{1}{E}} & { - \frac{\sigma }{E}} & { - \frac{\sigma }{E}} & 0 & 0 & 0 \\ { - \frac{\sigma }{E}} & {\frac{1}{E}} & { - \frac{\sigma }{E}} & 0 & 0 & 0 \\ { - \frac{\sigma }{E}} & { - \frac{\sigma }{E}} & {\frac{1}{E}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{\mu }} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{\mu }} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{\mu }} \\ \end{array} } \right],$$

(2)

and

$$\varvec{S}_{f} = \left[ {\begin{array}{*{20}c} {Z_{\text{N}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {Z_{\text{T}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {Z_{\text{T}} } \\ \end{array} } \right],$$

(3)

where $Z_{\text{N}}$ and $Z_{\text{T}}$ denote the normal and tangential excess compliances due to the presence of fractures.

The inverse of compliance matrix ${\varvec{S}}$ yields the stiffnesses $\varvec{C}$ in terms of excess compliances, and the stiffness components $C_{ij}$ are given by

$$\begin{aligned} C_{11} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - {{\left( {\frac{{E^{2} \left( {1 - \sigma } \right)^{2} Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E^{2} \left( {1 - \sigma } \right)^{2} Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}, \\ C_{13} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - {{\left( {\frac{{E^{2} \sigma \left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E^{2} \sigma \left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}, \\ C_{22} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - {{\left( {\frac{{E^{2} \sigma^{2} Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E^{2} \sigma^{2} Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}, \\ C_{23} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - {{\left( {\frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}} \right)} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{E\left( {1 - \sigma } \right)Z_{\text{N}} }}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}} \right)}}, \\ C_{44} & = \frac{E}{{2\left( {1 + \sigma } \right)}},\quad {\text{ and}} \\ C_{55} & = \frac{E}{{2\left( {1 + \sigma } \right)}} - {{\left( {\frac{{E^{2} Z_{\text{T}} }}{{4\left( {1 + \sigma } \right)^{4} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E^{2} Z_{\text{T}} }}{{4\left( {1 + \sigma } \right)^{4} }}} \right)} {\left( {1 + \frac{{EZ_{\text{T}} }}{{2\left( {1 + \sigma } \right)}}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{EZ_{\text{T}} }}{{2\left( {1 + \sigma } \right)}}} \right)}}. \\ \end{aligned}$$

(4)

For the case of small excess compliances (i.e., $Z_{\text{N}} \ll 1$ and $Z_{\text{T}} \ll 1$, neglecting $O\left( {Z^{2} } \right)$ terms), we apply the first-order Taylor series expansion to the excess compliances (i.e., $\frac{xZ}{1 + xZ} \approx xZ + O\left( {Z^{2} } \right)$, where $x$ represents the arbitrary parameters), and derive the stiffnesses in terms of Young’s modulus $E$ and Poisson’s ratio $\sigma$

$$\begin{aligned} C_{11} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \left( {1 - \sigma } \right)^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} , \\ C_{13} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} , \\ C_{22} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} , \\ C_{23} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} , \\ C_{44} & = \frac{E}{{2\left( {1 + \sigma } \right)}},\quad {\text{and}} \\ C_{55} & = \frac{E}{{2\left( {1 + \sigma } \right)}} - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}Z_{\text{T}} . \\ \end{aligned}$$

(5)

We then assume that the contrasts of the plane horizontal reflector between two half-spaces with given properties are small, for example, $\left| {\Delta E} \right| = \left| {E_{2} - E_{1} } \right| \ll 1$ with $E_{2}$ and $E_{1}$ being Young’s modulus across the interface, are further assume the normal and tangential excess compliances to be small, ignoring the items that proportional to $\Delta E\left( {Z_{\text{N}} + \Delta Z_{\text{N}} } \right)$, $\Delta \sigma \left( {Z_{\text{N}} + \Delta Z_{\text{N}} } \right)$, $\Delta E\left( {Z_{\text{T}} + \Delta Z_{\text{T}} } \right)$, $\Delta \sigma \left( {Z_{\text{T}} + \Delta Z_{\text{T}} } \right)$, $\left( {\Delta E} \right)^{2}$ or $\left( {\Delta \sigma } \right)^{2}$, we finally derive the perturbations in stiffnesses

$$\begin{aligned}\Delta C_{11} & = \frac{{\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{2E\sigma \left( {2 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \left( {1 - \sigma } \right)^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} , \\\Delta C_{22} & = \frac{{\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{2E\sigma \left( {2 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} , \\\Delta C_{13} & = \frac{\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{E\left( {2\sigma^{2} + 1} \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} , \\\Delta C_{23} & = \frac{\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{E\left( {2\sigma^{2} + 1} \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} , \\\Delta C_{44} & = \frac{1}{{2\left( {1 + \sigma } \right)}}\Delta E - \frac{E}{{2\left( {1 + \sigma } \right)^{2} }}\Delta \sigma ,\text{ }\quad {\text{and}} \\\Delta C_{55} & = \frac{1}{{2\left( {1 + \sigma } \right)}}\Delta E - \frac{E}{{2\left( {1 + \sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}\Delta Z_{\text{T}} , \\ \end{aligned}$$

(6)

where $\Delta E$, $\Delta \sigma$, $\Delta Z_{\text{N}}$, and $\Delta Z_{\text{T}}$ denote the contrasts in Young’s modulus, Poisson’s ratio, and excess compliances across the interface.

2.2 Linearized PP-Wave Reflection Coefficient and Azimuthal Elastic Impedance

Following Shaw and Sen (2004, 2006), we use the scattering function and perturbations in stiffnesses in terms of Young’s modulus and Poisson’s ratio to derive a linearized reflection coefficient for a weak HTI medium. The linearized PP-wave reflection coefficient is given by

$$R_{\text{PP}} = \frac{1}{{4\rho \cos^{2} \theta }}\left( {\Delta \rho \cos 2\theta + \sum\limits_{i = 1,j = 1}^{i = 6,j = 6} {\Delta C_{ij} \cdot \eta_{ij} } } \right),$$

(7)

where $\rho$ denotes density, and $\Delta \rho$ denotes the perturbation in density, and $\theta$ is the angle of incidence, and where $\eta_{11} = {{\sin^{4} \theta \cos^{4} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \cos^{4} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{12} = {{\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{13} = {{\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{22} = {{\sin^{4} \theta \sin^{4} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \sin^{4} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{23} = {{\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{33} = {{\cos^{4} \theta } \mathord{\left/ {\vphantom {{\cos^{4} \theta } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{33} = {{ - 4\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } \mathord{\left/ {\vphantom {{ - 4\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{55} = {{ - 4\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } \mathord{\left/ {\vphantom {{ - 4\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, $\eta_{66} = {{4\sin^{4} \theta \sin^{2} \varphi \cos^{2} \phi } \mathord{\left/ {\vphantom {{4\sin^{4} \theta \sin^{2} \varphi \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}$, in which $\phi$ is azimuth, and $\alpha^{2} = {{E\left( {1 - \sigma } \right)} \mathord{\left/ {\vphantom {{E\left( {1 - \sigma } \right)} {\left[ {\rho \left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)} \right]}}} \right. \kern-0pt} {\left[ {\rho \left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)} \right]}}$ denotes the square of P-wave velocity of the isotropic host rock.

Combining Eqs. (6)–(7), we derive the linearized PP-wave reflection coefficient.

$$R_{\text{PP}} (\theta ,\phi ) = a\left( \theta \right)\frac{{\Delta E}}{{\bar{E}}} + b\left( \theta \right)\frac{{\Delta \sigma }}{{\bar{\sigma }}} + c\left( \theta \right)\frac{{\Delta \rho }}{{\bar{\rho }}} + d\left( {\theta ,\phi } \right)\Delta Z_{\text{N}} + e\left( {\theta ,\phi } \right)\Delta Z_{\text{T}} ,$$

(8)

where $a\left( \theta \right) = \frac{{\sec^{2} \theta }}{4} - 2g\sin^{2} \theta$, $b\left( \theta \right) = \frac{{\sec^{2} \theta }}{4}\frac{{\left( {2g - 3} \right)\left( {2g - 1} \right)^{2} }}{{g\left( {4g - 3} \right)}} + 2g\sin^{2} \theta \frac{1 - 2g}{3 - 4g}$, $c\left( \theta \right) = \frac{1}{2} - \frac{{\sec^{2} \theta }}{4}$, $d\left( {\theta ,\phi } \right) = - \frac{{\bar{E}\left( {1 - \bar{\sigma }} \right)}}{{\left( {1 + \bar{\sigma }} \right)\left( {1 - 2\bar{\sigma }} \right)}}\frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2}$, and $e\left( {\theta ,\phi } \right) = \frac{{\bar{E}g}}{{2\left( {1 + \bar{\sigma }} \right)}}\sin^{2} \theta \cos^{2} \phi \left( {1 - \tan^{2} \theta \sin^{2} \phi } \right)$, and where $\bar{E}$, $\bar{\sigma }$, and $\bar{\rho }$ denote the averages over the interface, and $g = {{\left( {1 - 2\bar{\sigma }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - 2\bar{\sigma }} \right)} {\left( {2 - 2\bar{\sigma }} \right)}}} \right. \kern-0pt} {\left( {2 - 2\bar{\sigma }} \right)}}$, $\Delta E$, $\Delta \sigma$, $\Delta \rho$, $\Delta Z_{\text{N}}$, and $\Delta Z_{\text{T}}$ denote the corresponding contrasts.

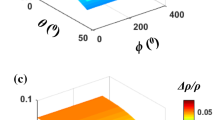
Figure 1 shows the effects of perturbations in background isotropic Young’s modulus, Poisson’s ratio, and density on the PP-wave reflection coefficient. We see that the Young’s modulus reflectivity ${{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} {\bar{E}}}} \right. \kern-0pt} {\bar{E}}}$ almost contributes to the reflection coefficient over the full range of angles of incidence or offsets with a similar weight (Fig. 1a). Therefore, the ${{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} {\bar{E}}}} \right. \kern-0pt} {\bar{E}}}$ parameter can be easily and perfectly estimated. The Poisson’s ratio reflectivity ${{\Delta \sigma } \mathord{\left/ {\vphantom {{\Delta \sigma } {\bar{\sigma }}}} \right. \kern-0pt} {\bar{\sigma }}}$ contributes to the reflection coefficient over the full range of angles of incidence or offsets (Fig. 1b). However, it is most sensitive at the far angles. The density reflectivity ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}}$ contributes to the reflection coefficient mostly at the near angles of incidence or offsets (Fig. 1c). Comparison of Fig. 1b, c illustrates that the contributions of ${{\Delta \sigma } \mathord{\left/ {\vphantom {{\Delta \sigma } {\bar{\sigma }}}} \right. \kern-0pt} {\bar{\sigma }}}$ and ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}}$ to the PP-wave reflection coefficient are complementary to each other, so the reflectivities of ${{\Delta \sigma } \mathord{\left/ {\vphantom {{\Delta \sigma } {\bar{\sigma }}}} \right. \kern-0pt} {\bar{\sigma }}}$ and ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}}$ are usually coupled and they can decoupled at the far angles of incidence or offsets. In this case, we require good-quality high-angle information to estimate the ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}}$ parameter, even though it contributes mostly at the near angles of incidence.

Fig. 1

Effects of perturbations in background isotropic Young’s modulus, Poisson’s ratio, and density on the PP-wave reflection coefficient, where a shows the change only in Young’s modulus reflectivity ${{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} {\bar{E}}}} \right. \kern-0pt} {\bar{E}}}$ from − 0.3 to 0.3, b shows the change only in Poisson’s ratio reflectivity ${{\Delta \sigma } \mathord{\left/ {\vphantom {{\Delta \sigma } {\bar{\sigma }}}} \right. \kern-0pt} {\bar{\sigma }}}$ from − 0.3 to 0.3, and c shows the change only in density reflectivity ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}}$ from − 0.3 to 0.3

Figure 2 shows the effects of perturbations only in excess compliances on the PP-wave reflection coefficient. We can find that both the perturbations in the normal and tangential excess compliances contribute to the reflection coefficient not only at angles of incidence but also at azimuths. In addition, the perturbation in normal excess compliance $\Delta Z_{\text{N}}$ contributes to the reflection coefficient over the full range of angles of incidence (Fig. 2a), but it is most sensitive at the far angles. However, the perturbation in tangential excess compliance $\Delta Z_{\text{T}}$ contributes to the reflection coefficient at the far angles of incidence (Fig. 2b), so we also require good-quality high-angle information to estimate the $\Delta Z_{\text{T}}$ parameter well.

Fig. 2

Effects of perturbations in excess compliances on the PP-wave reflection coefficient, where a shows the change only in normal excess compliance $\Delta Z_{\text{N}}$ from − 0.3 to 0.3, and b shows the change only in tangential excess compliance $\Delta Z_{\text{T}}$ from − 0.3 to 0.3

Following the relationship between the reflection coefficient and azimuthal elastic impedance (EI) (Martins 2006), we obtain

$$\frac{{\Delta {{EI}}\left( {\theta ,\phi } \right)}}{{\overline{{EI}} }} \approx 2R_{{\text{PP}}} (\theta ,\phi ) = 2a\left( \theta \right)\frac{\Delta E}{{\bar{E}}} + 2b\left( \theta \right)\frac{\Delta \sigma }{{\bar{\sigma }}} + 2c\left( \theta \right)\frac{\Delta \rho }{{\bar{\rho }}} + 2d\left( {\theta ,\phi } \right)\Delta Z_{\text{N}} + 2e\left( {\theta ,\phi } \right)\Delta Z_{\text{T}} ,$$

(9)

We substitute the relative contrasts in Eq. (10) with ${{\Delta {{EI}}} \mathord{\left/ {\vphantom {{\Delta {{EI}}} {{EI}}}} \right. \kern-0pt} {{EI}}} \approx \Delta \left[ {\ln {{EI}}} \right]$, ${{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} {\bar{E}}}} \right. \kern-0pt} {\bar{E}}} \approx \Delta \left[ {\ln E} \right]$, ${{\Delta \sigma } \mathord{\left/ {\vphantom {{\Delta \sigma } {\bar{\sigma }}}} \right. \kern-0pt} {\bar{\sigma }}} \approx \Delta \left[ {\ln \sigma } \right]$, and ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\bar{\rho }}}} \right. \kern-0pt} {\bar{\rho }}} \approx \Delta \left[ {\ln \rho } \right]$, in which $\ln \left( \cdot \right)$ represents a natural logarithm. We then use the assumption of continuous variation in elastic and anisotropic properties of fractured rocks, i.e., $\Delta \left[ {\ln {{EI}}} \right] \approx d\left[ {\ln {{EI}}} \right]$, $\Delta \left[ {\ln E} \right] \approx d\left[ {\ln E} \right]$, $\Delta \left[ {\ln \sigma } \right] \approx d\left[ {\ln \sigma } \right]$, $\Delta \left[ {\ln \rho } \right] \approx d\left[ {\ln \rho } \right]$, $\Delta Z_{\text{N}} \approx d\left( {Z_{\text{N}} } \right)$, and $\Delta Z_{\text{T}} \approx d\left( {Z_{\text{T}} } \right)$, in which $d\left( \cdot \right)$ represents a differential operator. We finally evaluate an integral of Eq. (10), yielding the logarithmic azimuthal EI which incorporates the effects of anisotropy

$$\ln {{EI}}\left( {\theta ,\phi } \right) = 2a\left( \theta \right)\ln E + 2b\left( \theta \right)\ln \sigma + 2c\left( \theta \right)\ln \rho + 2d\left( {\theta ,\phi } \right)Z_{\text{N}} + 2e\left( {\theta ,\phi } \right)Z_{\text{T}} .$$

(10)

We express the final azimuthal EI equation as

$${{EI}}\left( {\theta ,\phi } \right) = \left( E \right)^{2a\left( \theta \right)} \left( \sigma \right)^{2b\left( \theta \right)} \left( \rho \right)^{2c\left( \theta \right)} \exp \left[ {2d\left( {\theta ,\phi } \right)Z_{\text{N}} + 2e\left( {\theta ,\phi } \right)Z_{\text{T}} } \right],$$

(11)

where $\exp \left( \cdot \right)$ represents an exponential function.

In Appendix 1, we also derive the linearized PP-wave reflection coefficient and azimuthal EI equation in an orthorhombic anisotropic medium.

2.3 EIVAZ Inversion for Young’s Modulus, Poisson’s Ratio, and Excess Compliances

There exist two implementation steps of anisotropic elastic impedance inversion for Young’s modulus, Poisson’s ratio, and excess compliances with the derived anisotropic EI in Eq. (12): the anisotropic EI inversion from partial angle-stack seismic data and the estimation of Young’s modulus, Poisson’s ratio, and excess compliances from inverted anisotropic EI data.

The first process of azimuthal EI inversion from partial angle-stack seismic data is generally implemented incorporating the seismic wavelets at different incident angles and azimuths convoluted with the normal-incidence reflection coefficient, in which the inversion algorithm used in this process is the same as that of post-stack seismic inversion (Russell and Hampson 1991). In this study, we implement the second process of azimuthal EI inversion for Young’s modulus, Poisson’s ratio, and excess compliances in a Bayesian framework proposed by Pan et al. (2017a).

Using the logarithmic anisotropic EI in Eq. (10), we express the relationship between the logarithmic azimuthal EI and model parameters (i.e., Young’s modulus, Poisson’s ratio, density, and excess compliances) in the matrix form with $K$ incident angles, $M$ azimuths, and $J$ interfaces

$${\varvec{d = Gm}},$$

(12)

where

$$\varvec{d} = \left[ {\begin{array}{*{20}c} {\varvec{LEI}\left( {\theta_{1} ,\phi_{1} } \right)} & \cdots & {\varvec{LEI}\left( {\theta_{K} ,\phi_{1} } \right)} & \cdots & {\varvec{LEI}\left( {\theta_{1} ,\phi_{M} } \right)} & \cdots & {\varvec{LEI}\left( {\theta_{K} ,\phi_{M} } \right)} \\ \end{array} } \right]_{KMJ \times 1}^{\text{T}} ,$$

$$\varvec{m} = \left[ {\begin{array}{*{20}c} {\varvec{L}_{\text{E}} } \\ {\varvec{L}_{\sigma } } \\ {\varvec{L}_{\rho } } \\ {\varvec{Z}_{\text{N}} } \\ {\varvec{Z}_{\text{T}} } \\ \end{array} } \right]_{5J \times 1} ,\,{\text{and}}\quad \varvec{G} = \left[ {\begin{array}{*{20}c} {\varvec{A}\left( {\theta_{1} } \right)} & {\varvec{B}\left( {\theta_{1} } \right)} & {\varvec{C}\left( {\theta_{1} } \right)} & {\varvec{D}\left( {\theta_{1} ,\phi_{1} } \right)} & {\varvec{E}\left( {\theta_{1} ,\phi_{1} } \right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\varvec{A}\left( {\theta_{K} } \right)} & {\varvec{B}\left( {\theta_{K} } \right)} & {\varvec{C}\left( {\theta_{K} } \right)} & {\varvec{D}\left( {\theta_{K} ,\phi_{1} } \right)} & {\varvec{E}\left( {\theta_{K} ,\phi_{1} } \right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\varvec{A}\left( {\theta_{1} } \right)} & {\varvec{B}\left( {\theta_{1} } \right)} & {\varvec{C}\left( {\theta_{1} } \right)} & {\varvec{D}\left( {\theta_{1} ,\phi_{M} } \right)} & {\varvec{E}\left( {\theta_{1} ,\phi_{M} } \right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {\varvec{A}\left( {\theta_{K} } \right)} & {\varvec{B}\left( {\theta_{K} } \right)} & {\varvec{C}\left( {\theta_{K} } \right)} & {\varvec{D}\left( {\theta_{K} ,\phi_{M} } \right)} & {\varvec{E}\left( {\theta_{K} ,\phi_{M} } \right)} \\ \end{array} } \right]_{KMJ \times 5J} ,$$

and where $\varvec{LEI} = \left[ {\ln {{EI}}^{1} , \ldots ,\ln {{EI}}^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{L}_{\text{E}} = \left[ {\ln E^{1} , \ldots ,\ln E^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{L}_{\sigma } = \left[ {\ln \sigma^{1} , \ldots ,\ln \sigma^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{L}_{\rho } = \left[ {\ln \rho^{1} , \ldots ,\ln \rho^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{Z}_{\text{N}} = \left[ {Z_{\text{N}}^{1} , \ldots ,Z_{\text{N}}^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{Z}_{\text{T}} = \left[ {Z_{\text{T}}^{1} , \ldots ,Z_{\text{T}}^{J} } \right]_{J \times 1}^{\text{T}}$, $\varvec{A}\left( {\theta_{i} } \right) = {\text{diag}}\left[ {a^{1} \left( {\theta_{i} } \right), \ldots ,a^{J} \left( {\theta_{i} } \right)} \right]_{J \times J}$, $\varvec{B}\left( {\theta_{i} } \right) = {\text{diag}}\left[ {b^{1} \left( {\theta_{i} } \right), \ldots ,b^{J} \left( {\theta_{i} } \right)} \right]_{J \times J}$, $\varvec{C}\left( {\theta_{i} } \right) = {\text{diag}}\left[ {c^{1} \left( {\theta_{i} } \right), \ldots ,c^{J} \left( {\theta_{i} } \right)} \right]_{J \times J}$, $\varvec{D}\left( {\theta_{i} ,\phi_{j} } \right) = {\text{diag}}\left[ {d^{1} \left( {\theta_{i} ,\phi_{j} } \right), \ldots ,d^{J} \left( {\theta_{i} ,\phi_{j} } \right)} \right]_{J \times J}$, and $\varvec{E}\left( {\theta_{i} ,\phi_{j} } \right) = {\text{diag}}\left[ {e^{1} \left( {\theta_{i} ,\phi_{j} } \right), \ldots ,e^{J} \left( {\theta_{i} ,\phi_{j} } \right)} \right]_{J \times J}$.

Here the superscript $T$ represents the transpose of a matrix, and the symbol ${\text{diag}}$ represents a diagonal matrix. The subscripts $i$ and $j$ represent the $i$th angle of incidence and the $j$th angle of azimuth, respectively.

To decorrelate the model parameters, we re-express Eq. (12) using the decorrelated coefficient matrix ${\varvec{G}}^{{\prime }}$ and model parameter vector ${\varvec{m}}^{{\prime }}$

$${\varvec{d}} = {\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} ,$$

(13)

where ${\varvec{G}}^{{\prime }} = {\varvec{G}}\varvec{U}$, and ${\varvec{m}}^{{\prime }} = \varvec{U}^{ - 1} {\varvec{m}}$, and $\varvec{U}^{ - 1}$ represents the inverse of the decorrelation matrix $\varvec{U}$ (see Appendix 2).

Following Pan et al. (2017a), we use Eq. (13) as a forward equation, and a Cauchy probability distribution as the prior probability density function (PDF) $p\left( {{\varvec{m}}^{{\prime }} } \right)$ (Sacchi and Ulrych 1995; Alemie and Sacchi 2011; Zong et al. 2013a), and a Gaussian probability distribution as the likelihood function $p\left( {{\varvec{d}}\left| {{\varvec{m}}^{{\prime }} } \right.} \right)$ (Downton 2005). The posterior PDF $p\left( {{\varvec{m}}^{{\prime }} \left| {\varvec{d}} \right.} \right)$ can be solved as a joint PDF of the prior PDF and the likelihood function, which is given by

$$p\left( {{\varvec{m}}^{{\prime }} \left| {\varvec{d}} \right.} \right) \propto p\left( {{\varvec{m}}^{{\prime }} } \right)p\left( {{\varvec{d}}\left| {{\varvec{m}}^{{\prime }} } \right.} \right) = \prod\limits_{j = 1}^{5J} {\left[ {\frac{1}{{1 + {{m_{j}^{{{\prime }2}} } \mathord{\left/ {\vphantom {{m_{j}^{{{\prime }2}} } {\sigma_{{{\varvec{m^{\prime}}}}}^{2} }}} \right. \kern-0pt} {\sigma_{{{\varvec{m^{\prime}}}}}^{2} }}}}} \right]} \cdot \exp \left[ { - \frac{{\left( {{\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} - {\varvec{d}}} \right)^{\text{T}} \left( {{\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} - {\varvec{d}}} \right)}}{{2\sigma_{n}^{2} }}} \right],$$

(14)

where $p\left( \cdot \right)$ represents a PDF, and $\exp \left( \cdot \right)$ represents an exponential function; $\sigma_{n}^{2}$ indicates the noise variance, and $\sigma_{{{\varvec{m}}^{{\prime }} }}^{2}$ indicates the variance of model parameter vector. Maximizing Eq. (14), and combining the initial model regularization (Pan et al. 2017a, 2018a), the objective function can be expressed as

$$\begin{aligned} F\left( {{\varvec{m}}^{{\prime }} } \right) & = \left( {{\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} - {\varvec{d}}} \right)^{\text{T}} \left( {{\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} - {\varvec{d}}} \right) + 2\sigma_{n}^{2} \sum\limits_{j = 1}^{5J} {\ln \left( {1 + {{m_{j}^{{{\prime }2}} } \mathord{\left/ {\vphantom {{m_{j}^{{{\prime }2}} } {\sigma_{{{\varvec{m}}^{{\prime }} }}^{2} }}} \right. \kern-0pt} {\sigma_{{{\varvec{m}}^{{\prime }} }}^{2} }}} \right)} \\ & \quad + \,\omega_{E} \left( {\ln E - \ln E_{0} } \right)^{\text{T}} \left( {\ln E - \ln E_{0} } \right) \\ & \quad + \,\omega_{\sigma } \left( {\ln \sigma - \ln \sigma_{0} } \right)^{\text{T}} \left( {\ln \sigma - \ln \sigma_{0} } \right) + \omega_{\rho } \left( {\ln \rho - \ln \rho_{0} } \right)^{\text{T}} \left( {\ln \rho - \ln \rho_{0} } \right) \\ & \quad \text{ + }\,\omega_{{Z_{\text{N}} }} \left( {Z_{\text{N}} - Z_{{{\text{N}}0}} } \right)^{\text{T}} \left( {Z_{\text{N}} - Z_{{{\text{N}}0}} } \right) + \omega_{{Z_{\text{T}} }} \left( {Z_{\text{T}} - Z_{{{\text{T}}0}} } \right)^{\text{T}} \left( {Z_{\text{T}} - Z_{{{\text{T}}0}} } \right), \\ \end{aligned}$$

(15)

where $\omega_{{\varvec{m}}}$ represents the regularization coefficients of initial model parameters, and the subscript $0$ represents the initial model parameters. In this study, we construct the initial model of excess compliances using the known well log data of elastic parameters (Young’s modulus and Poisson’s ratio) and fracture density (see Appendix 3).

The introduction of Cauchy-sparse and initial model regularization terms makes Eq. (15) become nonlinear, but it can be solved iteratively by using the iteratively reweighted least-square (IRLS) optimization algorithm (Scales and Smith 2000; Bissantz et al. 2009).

3 Examples

3.1 Synthetic Examples

A well log data are used to test the feasibility of the proposed Bayesian EIVAZ inversion for Young’s modulus, Poisson’s ratio, density, and excess compliances. The original logging Young’s modulus, Poisson’s ratio, density, and excess compliances are displayed in blue in Fig. 3. The synthetic seismic gathers with different angles of incidence and azimuth are generated using the convolution and a 35-Hz Ricker wavelet, including four azimuths ($\phi_{1}$ = 30°, $\phi_{2}$ = 60°, $\phi_{3}$ = 90°, and $\phi_{4}$ = 120°, respectively) and three angles of incidence ($\theta_{1}$ = 5° stacked over a range 0°–10°, $\theta_{2}$ = 15° stacked over a range 10°–20°, and $\theta_{3}$ = 25° stacked over a range 20°–30°, respectively). Then we implement the Bayesian EIVAZ inversion for Young’s modulus, Poisson’s ratio, density, and excess compliances using the synthetic seismic gathers with twelve angles of incidence and azimuth. The initial model parameters are displayed in green in Fig. 3, and the corresponding inverted results of model parameters are displayed in red in Fig. 3. From the inversion results, we find that the Young’s modulus, Poisson’s ratio, density, and excess compliances can be inverted reasonably even with quite smooth models. Figure 4 shows the relative errors of inverted model parameters, and we see that the relative errors of Young’s modulus, Poisson’s ratio, and density are all within 5%, and the errors of normal and tangential excess compliances are both within 20%. To further verify the stability of the proposed Bayesian EIVAZ inversion approach, we add the Gaussian random noise with different signal-to-noise ratios (SNRs) (SNRs are 5 and 2, respectively) to the synthetic gathers and then implement the inversion using the noisy data. Figure 5 shows the comparison between the true and inverted well log of model parameters with SNR being 5, and Fig. 6 shows the corresponding relative prediction errors. We find that the Young’s modulus, Poisson’s ratio, density, and excess compliances can also be inverted reasonably using moderate noisy gathers. Similarly, Figs. 7 and 8 show the inverted results and relative prediction errors with SNR being 2, respectively. As in the case of bigger noises, reasonable estimates of Young’s modulus, Poisson’s ratio, and density are obtained, and the relative errors are still small. However, the inversion errors of excess compliances are relative high but still feasible for the application.

Fig. 3

Comparison between true (blue) and inverted (red) values of model parameters using synthetic gathers without noise, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

Fig. 4

Relative prediction errors of model parameters without noise, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

Fig. 5

Comparison between true (blue) and inverted (red) values of model parameters using synthetic gathers with SNR = 5, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

Fig. 6

Relative prediction errors of model parameters with SNR = 5, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

Fig. 7

Comparison between true (blue) and inverted (red) values of model parameters using synthetic gathers with SNR = 2, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

Fig. 8

Relative prediction errors of model parameters with SNR = 2, where a shows the Young’s modulus, Poisson’s ratio, density, and b shows the normal and tangential excess compliances

3.2 Field Data Example

Real data acquired in southwest China are employed to implement Bayesian EIVAZ inversion for Young’s modulus, Poisson’s ratio, density, and excess compliances to verify the proposed approach. For the data, the angle range of incidence for each common-midpoint-profile (CMP) gather is 1°–30°. We then stack the seismic angle gathers over different angle ranges of incidence to obtain the seismic profiles of the near angle of incidence ($\theta_{1}$ = 5° stacked over a range 0°–10°), the middle angle of incidence ($\theta_{2}$ = 15° stacked over a range 10°–20°), and the far angle of incidence ($\theta_{3}$ = 25° stacked over a range 20°–30°), respectively. Figure 9 shows the seismic angle gathers with four azimuths ($\phi_{1}$ = 22.5° stacked over a range 0°–45°, $\phi_{2}$ = 67.5° stacked over a range 45°–90°, $\phi_{3}$ = 112.5° stacked over a range 90°–135°, and $\phi_{4}$ = 157.5° stacked over a range 135°–180°, respectively).

Fig. 9

Stacked seismic gathers with different azimuths, where a $\phi_{1}$ = 22.5°, b $\phi_{2}$ = 67.5°, c $\phi_{3}$ = 112.5°, and d $\phi_{4}$ = 157.5°

Red lines in Fig. 9a indicate the position of well log, and the red circles indicate the location of target gas-filled reservoir. We can find amplitude anomaly in the red circles at the well position. Then, we implement the anisotropic EI inversion from partial angle-stack seismic data with four azimuths. Figure 10 shows the EI inversion results with four azimuths, and the red lines and circles are also the well log position and target reservoir. From the inversion results, we find that the inverted anisotropic EI profiles show low values in the target reservoir. After obtaining the inverted anisotropic EI data, we then perform the estimates of Young’s modulus, Poisson’s ratio, and excess compliances from inverted anisotropic EI data. Figure 11 shows the inversion results of Young’s modulus, Poisson’s ratio, and density, and Fig. 12 shows the corresponding comparison between the inverted results and true well log curves. Similarly, Fig. 13 shows the inversion results of normal and tangential excess compliances, and Fig. 14 shows the corresponding comparison between the inverted results and true well log curves.

Fig. 10

Inverted anisotropic EI with different azimuths, where a $\phi_{1}$ = 22.5°, b $\phi_{2}$ = 67.5°, c $\phi_{3}$ = 112.5°, and d $\phi_{4}$ = 157.5°

Fig. 11

Estimation of Young’s modulus, Poisson’s ratio, and density inverted from inverted anisotropic EI data, where a shows the Young’s modulus, b shows the Poisson’s ratio, and c shows the density

Fig. 12

Comparison between the inverted results (red) and true well log curves (blue) of Young’s modulus, Poisson’s ratio, and density

Fig. 13

Estimation of excess compliances inverted from inverted anisotropic EI data, where a shows the normal excess compliance, and b shows the tangential excess compliance

Fig. 14

Comparison between the inverted results (red) and true well log curves (blue) of normal and tangential excess compliances

From Figs. 11 and 12, we can see that the inversion results of Young’s modulus, Poisson’s ratio, and density agree well with the well log curves at the target reservoir. From the inversion results of excess compliances shown in Figs. 13 and 14, we find that both the normal and tangential excess compliances show high values at the target reservoir, which also have a good match with the well log curves of excess compliances. Therefore, the reasonable matches between inversion results of model parameters and well log curves further demonstrate our proposed Bayesian EIVAZ inversion approach to estimate the Young’s modulus, Poisson’s ratio, and excess compliances.

4 Discussion and Conclusions

Our goal in the presented methodology is to estimate the Young’s modulus, Poisson’s ratio, and excess compliances to characterize the rock brittleness and compliance from the observable wide-azimuth seismic data in a fractured reservoir containing a single set of fractures. Based on the linear slip model, we first derive the perturbations in stiffness components in terms of Young’s modulus, Poisson’s ratio, and excess compliances. We then derive the linearized PP-wave reflection coefficient using the scattering function and perturbations in stiffness components in an HTI medium, and derive the elastic impedance variation with incident angle and azimuth (EIVAZ) equation to couple the Young’s modulus, Poisson’s ratio, density, and excess compliances. Next, we develop a two-step Bayesian EIVAZ inversion approach, which involves the anisotropic EI inversion using partial angle-stack seismic gathers with different azimuths, and the estimates of Young’s modulus, Poisson’s ratio, density, and excess compliances using the inverted azimuthal EI data. Finally, we apply the proposed approach to the synthetic and real data sets, and the inversion results demonstrate the feasibility and reasonability of our approach.

Appendices

Appendix 1: Linearized PP-Wave Reflection Coefficient and Azimuthal Elastic Impedance in an Orthorhombic Anisotropic Medium

A horizontally layered rock permeated by a single set of aligned, vertical fractures is equivalent to an orthorhombic anisotropic medium (Schoenberg and Helbig 1997; Bakulin et al. 2000b). Following Pan et al. (2018a), we derive the stiffness components of an orthorhombic anisotropic medium based on weak-anisotropy assumption in terms of Young’s modulus, Poisson’s ratio, and excess compliances

$$\begin{aligned} C_{11} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \left( {1 - \sigma } \right)^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\varepsilon_{b} , \\ C_{12} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\varepsilon_{b} - \frac{2E}{{\left( {1 + \sigma } \right)}}\gamma_{b} , \\ C_{13} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} + \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\delta_{b} , \\ C_{22} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\varepsilon_{b} , \\ C_{23} & = \frac{E\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} + \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\delta_{b} , \\ C_{33} & = \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}} - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}Z_{\text{N}} \\ C_{44} & = \frac{E}{{2\left( {1 + \sigma } \right)}},\text{ }\quad {\text{and}} \\ C_{55} & = \frac{E}{{2\left( {1 + \sigma } \right)}} - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}Z_{\text{V}} \text{,}\quad {\text{and}} \\ C_{66} & = \frac{E}{{2\left( {1 + \sigma } \right)}} - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}Z_{\text{H}} - \frac{E}{{\left( {1 + \sigma } \right)}}\gamma_{b} , \\ \end{aligned}$$

(16)

where $Z_{\text{N}}$, $Z_{\text{V}}$, and $Z_{\text{H}}$ denote the normal, vertical, and horizontal tangential excess compliances, respectively, and $\varepsilon_{b}$, $\delta_{b}$, and $\gamma_{b}$ denote the Thomsen’s (1986) weak-anisotropy (WA) parameters, which are used to characterize the vertical horizontally isotropic (VTI) medium.

Using the derived stiffnesses in Eq. (16), we ignore the items that proportional to $\Delta E\left( {Z_{\text{N}} + \Delta Z_{\text{N}} } \right)$, $\Delta \sigma \left( {Z_{\text{N}} + \Delta Z_{\text{N}} } \right)$, $\Delta E\left( {Z_{\text{V}} + \Delta Z_{\text{V}} } \right)$, $\Delta \sigma \left( {Z_{\text{V}} + \Delta Z_{\text{V}} } \right)$, $\Delta E\left( {Z_{\text{H}} + \Delta Z_{\text{H}} } \right)$, $\Delta \sigma \left( {Z_{\text{H}} + \Delta Z_{\text{H}} } \right)$, $\Delta E\left( {\varepsilon_{b} + \Delta \varepsilon_{b} } \right)$, $\Delta \sigma \left( {\varepsilon_{b} + \Delta \varepsilon_{b} } \right)$, $\Delta E\left( {\delta_{b} + \Delta \delta_{b} } \right)$, $\Delta \sigma \left( {\delta_{b} + \Delta \delta_{b} } \right)$, $\Delta E\left( {\gamma_{b} + \Delta \gamma_{b} } \right)$, $\Delta \sigma \left( {\gamma_{b} + \Delta \gamma_{b} } \right)$, $\left( {\Delta E} \right)^{2}$ or $\left( {\Delta \sigma } \right)^{2}$, we further derive the perturbations in stiffnesses in terms of Young’s modulus, Poisson’s ratio, and excess compliances for the case of weak anisotropy, weak excess compliances, and small contrasts in elastic properties across the interface

$$\begin{aligned} \Delta C_{11} & = \frac{{\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{2E\sigma \left( {2 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \left( {1 - \sigma } \right)^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta \varepsilon_{b} , \\ \Delta C_{12} & = \frac{\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{E\left( {2\sigma^{2} + 1} \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta \varepsilon_{b} - \frac{2E}{{\left( {1 + \sigma } \right)}}\Delta \gamma_{b} , \\ \Delta C_{13} & = \frac{\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{E\left( {2\sigma^{2} + 1} \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma \left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} + \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta \delta_{b} , \\ \Delta C_{22} & = \frac{{\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{2E\sigma \left( {2 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} + \frac{{2E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta \varepsilon_{b} , \\ \Delta C_{23} & = \frac{\sigma }{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{E\left( {2\sigma^{2} + 1} \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} + \frac{{E\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta \delta_{b} , \\ \Delta C_{33} & = \frac{{\left( {1 - \sigma } \right)}}{{\left( {1 + \sigma } \right)\left( {1 - 2\sigma } \right)}}\Delta E + \frac{{2E\sigma \left( {2 - \sigma } \right)}}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} \sigma^{2} }}{{\left( {1 + \sigma } \right)^{2} \left( {1 - 2\sigma } \right)^{2} }}\Delta Z_{\text{N}} \\ \Delta C_{44} & = \frac{1}{{2\left( {1 + \sigma } \right)}}\Delta E - \frac{E}{{2\left( {1 + \sigma } \right)^{2} }}\Delta \sigma ,\text{ } \\ \Delta C_{55} & = \frac{1}{{2\left( {1 + \sigma } \right)}}\Delta E - \frac{E}{{2\left( {1 + \sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}\Delta Z_{\text{V}} \quad {\text{and}} \\ \Delta C_{66} & = \frac{1}{{2\left( {1 + \sigma } \right)}}\Delta E - \frac{E}{{2\left( {1 + \sigma } \right)^{2} }}\Delta \sigma - \frac{{E^{2} }}{{4\left( {1 + \sigma } \right)^{2} }}\Delta Z_{\text{H}} - \frac{E}{{\left( {1 + \sigma } \right)}}\Delta \gamma_{b} , \\ \end{aligned}$$

(17)

where $\Delta E$, $\Delta \sigma$, $\Delta \varepsilon_{b}$, $\Delta \delta_{b}$, $\Delta \gamma_{b}$, $\Delta Z_{\text{N}}$, $\Delta Z_{\text{V}}$, and $\Delta Z_{\text{H}}$ denote the contrasts in Young’s modulus, Poisson’s ratio, Thomsen’s WA parameters, and excess compliances across the interface.

Similarly, we then derive the linearized PP-wave reflection coefficient of an orthorhombic anisotropic medium

$$\begin{aligned} R_{\text{PP}}^{\text{ORT}} (\theta ,\phi ) & = \left( {\frac{{\sec^{2} \theta }}{4} - 2g\sin^{2} \theta } \right)\frac{\Delta E}{{\bar{E}}} + \left( {\frac{{\sec^{2} \theta }}{4}\frac{{\left( {2g - 3} \right)\left( {2g - 1} \right)^{2} }}{{g\left( {4g - 3} \right)}} + 2g\sin^{2} \theta \frac{1 - 2g}{3 - 4g}} \right)\frac{\Delta \sigma }{{\bar{\sigma }}} \\ & \quad + \,\left( {\frac{1}{2} - \frac{{\sec^{2} \theta }}{4}} \right)\frac{\Delta \rho }{{\bar{\rho }}} + \frac{{\sin^{2} \theta \tan^{2} \theta }}{2}\Delta \varepsilon_{b} + \frac{{\sin^{2} \theta }}{2}\Delta \delta_{b} \\ & \quad - \,\left( {\frac{{\bar{E}\left( {1 - \bar{\sigma }} \right)}}{{\left( {1 + \bar{\sigma }} \right)\left( {1 - 2\bar{\sigma }} \right)}}\frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} } \right)\Delta Z_{\text{N}} \\ & \quad + \,\left( {\frac{{\bar{E}g}}{{2\left( {1 + \bar{\sigma }} \right)}}\sin^{2} \theta \cos^{2} \phi } \right)\Delta Z_{\text{V}} - \left( {\frac{{\bar{E}g}}{{2\left( {1 + \bar{\sigma }} \right)}}\sin^{2} \theta \tan^{2} \theta \sin^{2} \phi \cos^{2} \phi } \right)\Delta Z_{\text{H}} , \\ \end{aligned}$$

(18)

where $\bar{E}$, $\bar{\sigma }$, and $\bar{\rho }$ represent the averages over the interface, and $g = {{\left( {1 - 2\bar{\sigma }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - 2\bar{\sigma }} \right)} {\left( {2 - 2\bar{\sigma }} \right)}}} \right. \kern-0pt} {\left( {2 - 2\bar{\sigma }} \right)}}$.

In a similar way, we also derive the azimuthal EI equation in an orthorhombic anisotropic medium

$$\begin{aligned} {\text{EI}}_{\text{PP}}^{\text{ORT}} \left( {\theta ,\phi } \right) & = \left[ E \right]^{{\frac{{\sec^{2} \theta }}{2} - 4g\sin^{2} \theta }} \left[ \sigma \right]^{{\frac{{\sec^{2} \theta }}{2}\frac{{\left( {2g - 3} \right)\left( {2g - 1} \right)^{2} }}{{g\left( {4g - 3} \right)}} + 4g\sin^{2} \theta \frac{1 - 2g}{3 - 4g}}} \left[ \rho \right]^{{1 - \frac{{\sec^{2} \theta }}{2}}} \\ & \quad \cdot \exp \left[ \begin{array}{l} \left[ {\sin^{2} \theta \tan^{2} \theta } \right]\varepsilon_{b} + \left[ {\sin^{2} \theta } \right]\delta_{b} \hfill \\ - \left\{ {\frac{{\bar{E}\left( {1 - \bar{\sigma }} \right)}}{{\left( {1 + \bar{\sigma }} \right)\left( {1 - 2\bar{\sigma }} \right)}}\frac{{\sec^{2} \theta }}{2}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} } \right\}Z_{\text{N}} \hfill \\ + \left[ {\frac{{\bar{E}g}}{{\left( {1 + \bar{\sigma }} \right)}}\sin^{2} \theta \cos^{2} \phi } \right]Z_{\text{V}} - \left[ {\frac{{\bar{E}g}}{{\left( {1 + \bar{\sigma }} \right)}}\sin^{2} \theta \tan^{2} \theta \sin^{2} \phi \cos^{2} \phi } \right]Z_{\text{H}} \hfill \\ \end{array} \right]. \\ \end{aligned}$$

(19)

Appendix 2: Decorrelation of Model Parameters

To decorrelate the model parameters, we first calculate the covariance matrix ${\varvec{C}}_{{\varvec{m}}}$ of model parameters

$${\varvec{C}}_{{\varvec{m}}} = \left[ {\begin{array}{*{20}c} {\sigma_{{L_{E} }}^{2} } & {\sigma_{{L_{E} L_{\sigma } }} } & {\sigma_{{L_{E} L_{\rho } }} } & {\sigma_{{L_{E} Z_{N} }} } & {\sigma_{{L_{E} Z_{T} }} } \\ {\sigma_{{L_{E} L_{\sigma } }} } & {\sigma_{{L_{\sigma } }}^{2} } & {\sigma_{{L_{\sigma } L_{\rho } }} } & {\sigma_{{L_{\sigma } Z_{N} }} } & {\sigma_{{L_{\sigma } Z_{T} }} } \\ {\sigma_{{L_{E} L_{\rho } }} } & {\sigma_{{L_{\sigma } L_{\rho } }} } & {\sigma_{{L_{\rho } }}^{2} } & {\sigma_{{L_{\rho } Z_{N} }} } & {\sigma_{{L_{\rho } Z_{T} }} } \\ {\sigma_{{L_{E} Z_{N} }} } & {\sigma_{{L_{\sigma } Z_{N} }} } & {\sigma_{{L_{\rho } Z_{N} }} } & {\sigma_{{Z_{N} }}^{2} } & {\sigma_{{Z_{N} Z_{T} }} } \\ {\sigma_{{L_{E} Z_{T} }} } & {\sigma_{{L_{\sigma } Z_{T} }} } & {\sigma_{{L_{\rho } Z_{T} }} } & {\sigma_{{Z_{N} Z_{T} }} } & {\sigma_{{Z_{T} }}^{2} } \\ \end{array} } \right],$$

(20)

where the diagonal elements denote the variances $\sigma_{{L_{E} }}^{2}$, $\sigma_{{L_{\sigma } }}^{2}$, $\sigma_{{L_{\rho } }}^{2}$, $\sigma_{{Z_{N} }}^{2}$, and $\sigma_{{Z_{T} }}^{2}$ of model parameters, and the off-diagonal elements or covariances characterize the correlation of model parameters. Using the singular value decomposition (SVD) method, the parameter covariance matrix ${\varvec{C}}_{{\varvec{m}}}$ is decomposed as (Downton 2005)

$${\varvec{C}}_{{\varvec{m}}} = \varvec{u\sum u}^{\text{T}} = \varvec{u}\left[ {\begin{array}{*{20}c} {\sigma_{1}^{2} } & 0 & 0 & 0 & 0 \\ 0 & {\sigma_{2}^{2} } & 0 & 0 & 0 \\ 0 & 0 & {\sigma_{3}^{2} } & 0 & 0 \\ 0 & 0 & 0 & {\sigma_{4}^{2} } & 0 \\ 0 & 0 & 0 & 0 & {\sigma_{5}^{2} } \\ \end{array} } \right]\varvec{u}^{\text{T}} ,$$

(21)

where $\varvec{u}$ represents the eigenvector, and $\varvec{\sum }$ represents the diagonal matrix of eigenvalues, in which all the values are real and positive (and can be presented as real numbers squared $\sigma_{i}^{2} ,\text{ }i = 1,2, \ldots ,5$).

We define the inverse of single-interface eigenvector $\varvec{u}$ as

$$\varvec{u}^{ - 1} = \left[ {\begin{array}{*{20}c} {u_{11} } & {u_{12} } & {u_{13} } & {u_{14} } & {u_{15} } \\ {u_{21} } & {u_{22} } & {u_{23} } & {u_{24} } & {u_{25} } \\ {u_{31} } & {u_{32} } & {u_{33} } & {u_{34} } & {u_{35} } \\ {u_{41} } & {u_{42} } & {u_{43} } & {u_{44} } & {u_{45} } \\ {u_{51} } & {u_{52} } & {u_{53} } & {u_{54} } & {u_{55} } \\ \end{array} } \right].$$

(22)

For the case of $J$ interfaces, the single-interface eigenvector $\varvec{u}$ can be extended as

$$\varvec{U}^{ - 1} = \left[ {\begin{array}{*{20}c} {u_{11} } & 0 & \cdots & {u_{12} } & 0 & \cdots & {u_{13} } & 0 & \cdots & {u_{14} } & 0 & \cdots & {u_{15} } & 0 & \cdots \\ 0 & {u_{11} } & 0 & 0 & {u_{12} } & 0 & 0 & {u_{13} } & 0 & 0 & {u_{14} } & 0 & 0 & {u_{15} } & 0 \\ {} & {} & {} & {} & {} & {} & {} & \cdots & {} & {} & {} & {} & {} & {} & {} \\ {u_{21} } & 0 & \cdots & {u_{22} } & 0 & \cdots & {u_{23} } & 0 & \cdots & {u_{24} } & 0 & \cdots & {u_{25} } & 0 & \cdots \\ 0 & {u_{21} } & 0 & 0 & {u_{22} } & 0 & 0 & {u_{23} } & 0 & 0 & {u_{24} } & 0 & 0 & {u_{25} } & 0 \\ {} & {} & {} & {} & {} & {} & {} & \cdots & {} & {} & {} & {} & {} & {} & {} \\ {u_{31} } & 0 & \cdots & {u_{32} } & 0 & \cdots & {u_{33} } & 0 & \cdots & {u_{34} } & 0 & \cdots & {u_{35} } & 0 & \cdots \\ 0 & {u_{31} } & 0 & 0 & {u_{32} } & 0 & 0 & {u_{33} } & 0 & 0 & {u_{34} } & 0 & 0 & {u_{35} } & 0 \\ {} & {} & {} & {} & {} & {} & {} & \cdots & {} & {} & {} & {} & {} & {} & {} \\ {u_{41} } & 0 & \cdots & {u_{42} } & 0 & \cdots & {u_{43} } & 0 & \cdots & {u_{44} } & 0 & \cdots & {u_{45} } & 0 & \cdots \\ 0 & {u_{41} } & 0 & 0 & {u_{42} } & 0 & 0 & {u_{43} } & 0 & 0 & {u_{44} } & 0 & 0 & {u_{45} } & 0 \\ {} & {} & {} & {} & {} & {} & {} & \cdots & {} & {} & {} & {} & {} & {} & {} \\ {u_{51} } & 0 & \cdots & {u_{52} } & 0 & \cdots & {u_{53} } & 0 & \cdots & {u_{54} } & 0 & \cdots & {u_{55} } & 0 & \cdots \\ 0 & {u_{51} } & 0 & 0 & {u_{52} } & 0 & 0 & {u_{53} } & 0 & 0 & {u_{54} } & 0 & 0 & {u_{55} } & 0 \\ {} & {} & {} & {} & {} & {} & {} & \cdots & {} & {} & {} & {} & {} & {} & {} \\ \end{array} } \right]_{5J \times 5J} .$$

(23)

Here $\varvec{U}^{ - 1}$ is the inverse of decorrelation matrix $\varvec{U}$ of multiple interfaces. Using the transformation of the coefficient matrix ${\varvec{G}}$ and model parameter vector ${\varvec{m}}$

$$\left\{ {\begin{array}{*{20}l} {{\varvec{G}}^{{\prime }} = {\varvec{G}}\varvec{U}} \hfill \\ {{\varvec{m}}^{{\prime }} = \varvec{U}^{ - 1} {\varvec{m}}} \hfill \\ \end{array} } \right.,$$

(24)

and Eq. (12) yields

$$\varvec{d} = {\varvec{G}}^{{\prime }} {\varvec{m}}^{{\prime }} .$$

(25)

The covariance matrix ${\varvec{C}}_{{{\varvec{m^{\prime}}}}}$ after the transformation then becomes

$${\varvec{C}}_{{{\varvec{m^{\prime}}}}} = \left[ {\begin{array}{*{20}c} {\sigma_{1}^{2} } & 0 & 0 & 0 & 0 \\ 0 & {\sigma_{2}^{2} } & 0 & 0 & 0 \\ 0 & 0 & {\sigma_{3}^{2} } & 0 & 0 \\ 0 & 0 & 0 & {\sigma_{4}^{2} } & 0 \\ 0 & 0 & 0 & 0 & {\sigma_{5}^{2} } \\ \end{array} } \right],$$

(26)

where all the off-diagonal elements become to be zero, which indicates that the model parameters after decorrelation are mutually independent.

Appendix 3: Calculation of Excess Compliances Using Fracture Density

According to the relationship between the excess compliances and fracture density (Bakulin et al. 2000a), we derive the gas-filled, or dry, excess compliances expressed by Young’s modulus $E$, Poisson’s ratio $\sigma$, and fracture density $e$

$$Z_{\text{N}} = \frac{{16e\left( {1 - \sigma^{2} } \right)}}{3E},$$

(27)

and

$$Z_{\text{T}} = \frac{{32e\left( {1 - \sigma^{2} } \right)}}{{3E\left( {2 - \sigma } \right)}}.$$

(28)