Azimuthal Seismic Amplitude Variation with Offset and Azimuth Inversion in Weakly Anisotropic Media with Orthorhombic Symmetry

Abstract

Seismic amplitude variation with offset and azimuth (AVOaz) inversion is well known as a popular and pragmatic tool utilized to estimate fracture parameters. A single set of vertical fractures aligned along a preferred horizontal direction embedded in a horizontally layered medium can be considered as an effective long-wavelength orthorhombic medium. Estimation of Thomsen’s weak-anisotropy (WA) parameters and fracture weaknesses plays an important role in characterizing the orthorhombic anisotropy in a weakly anisotropic medium. Our goal is to demonstrate an orthorhombic anisotropic AVOaz inversion approach to describe the orthorhombic anisotropy utilizing the observable wide-azimuth seismic reflection data in a fractured reservoir with the assumption of orthorhombic symmetry. Combining Thomsen’s WA theory and linear-slip model, we first derive a perturbation in stiffness matrix of a weakly anisotropic medium with orthorhombic symmetry under the assumption of small WA parameters and fracture weaknesses. Using the perturbation matrix and scattering function, we then derive an expression for linearized PP-wave reflection coefficient in terms of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses in such an orthorhombic medium, which avoids the complicated nonlinear relationship between the orthorhombic anisotropy and azimuthal seismic reflection data. Incorporating azimuthal seismic data and Bayesian inversion theory, the maximum a posteriori solutions of Thomsen’s WA parameters and fracture weaknesses in a weakly anisotropic medium with orthorhombic symmetry are reasonably estimated with the constraints of Cauchy a priori probability distribution and smooth initial models of model parameters to enhance the inversion resolution and the nonlinear iteratively reweighted least squares strategy. The synthetic examples containing a moderate noise demonstrate the feasibility of the derived orthorhombic anisotropic AVOaz inversion method, and the real data illustrate the inversion stabilities of orthorhombic anisotropy in a fractured reservoir.

1 Introduction

Existing geophysical and geological data demonstrate that orthorhombic media with a horizontal symmetry plane are rather common for naturally fractured reservoirs (Bakulin et al. 2000). A set of parallel vertical fractures aligned along a preferred horizontal direction embedded in a transverse isotropic background with a vertical symmetry axis (VTI medium), or two orthogonal sets of rotationally invariant vertical fractures embedded in a purely isotropic or VTI background can combine to form an effective long-wavelength orthorhombic medium (Schoenberg and Helbig 1997; Bakulin et al. 2000, 2002). It needs to be stressed that we mainly discussed an effective orthorhombic model formed by a single set of aligned vertical fractures embedded in a VTI background medium in the text, and the other orthorhombic models were involved in the appendices.

In a fractured reservoir, WA parameters and fracture weaknesses play a vital role in the characterization of orthorhombic media, and an analytical expression for linearized PP-wave reflection coefficient in terms of WA parameters and fracture weaknesses is far difficult to derive due to the complexity of seismic wave propagation in such an orthorhombic media. Pšenčik and Vavryčuk (1998) derived weak contrast PP-wave reflection/transmission coefficients in weakly anisotropic media. Shaw and Sen (2004) introduced a novel method of scattering function to derive the linearized PP- and PS-wave reflection coefficients in weakly anisotropic media integrating the Born integral with stationary phase. Bachrach (2015) derived a linearized reflection coefficient approximation varying with offset and azimuth for orthorhombic media following the notation of Pšenčik and Martins (2001). Schoenberg and Helbig (1997) defined the stiffness matrix of a fracture-induced orthorhombic model formed by vertical fractures perpendicular to the x axis and horizontal fine layers with a vertical z axis as the symmetry axis using the stiffness tensor of the VTI background medium and the dimensionless fracture weaknesses, which has fewer number of parameters compared with the general orthorhombic model (one parameter less). Bakulin et al. (2000, 2002) described the estimation of fracture parameters in all three orthorhombic models integrating the relations between the Thomsen’s (1986) weak-anisotropy (WA) parameters (Rüger 1997, 1998; Tsvankin 1997) and fracture weaknesses (Schoenberg and Helbig 1997). Stating from the stiffness matrix of orthorhombic media derived by Schoenberg and Helbig (1997), and using the perturbation matrix and scattering function, we derive an expression for linearized PP-wave reflection coefficient in terms of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses in an orthorhombic medium with weak anisotropy and small weaknesses.

In an orthorhombic fractured reservoir, the azimuthal anisotropy of observable seismic data can be used to perform better seismic fracture characterization incorporating the amplitude variations with offset and azimuth (AVOaz) inversion (Mallick et al. 1998; Shaw and Sen 2006; Downton and Roure 2015; Bachrach 2015; Chen et al. 2017; Pan et al. 2017a, b). However, the estimated orthorhombic anisotropic parameters are usually unstable due to the seismic amplitude severely affected by noise and ill-conditioned inverse problems (Sacchi and Ulrych 1995; Downton 2005). In this paper, we implemented the orthorhombic anisotropic AVOaz inversion in a Bayesian framework, and Cauchy and Gaussian probability density function (PDF) are utilized for the a priori information of model parameters and the likelihood function, respectively, to enhance the resolution of the inversion results for model parameters in a weakly anisotropic medium with orthorhombic symmetry. The nonlinear iteratively reweighted least squares (IRLS) strategy is finally used to solve the maximum a posteriori solutions of model parameters to improve the inversion stability. We finish with synthetic and real data case studies to illustrate the feasibility of proposed orthorhombic anisotropic AVOaz equation and inversion approach in a fractured reservoir.

2 Theory and Method

2.1 Effective Elastic Stiffness Tensor in a Weakly Anisotropic Medium with Orthorhombic Symmetry

A system of aligned vertical fractures embedded in a VTI background can be considered as an effective long-wavelength orthorhombic medium. In the case that fracture faces are perpendicular to the x axis (shown in Fig. 1a), and using the linear-slip theory with physically intuitive relations between stress and discontinuity in displacement across the fractures, the effective elastic stiffness tensor C _OA in such an orthorhombic medium can be expressed as (Schoenberg and Helbig 1997)

$${\mathbf{C}}_{\text{OA}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{C}}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\tilde{\mathbf{C}}}_{2} } \\ \end{array} } \right],$$

(1)

where 0 represents the 3 × 3 zero matrix, and ${\tilde{\mathbf{C}}}_{1}$ and ${\tilde{\mathbf{C}}}_{2}$ are given by

$${\tilde{\mathbf{C}}}_{1} = \left[ {\begin{array}{*{20}l} {C_{{11{\text{b}}}} \left( {1 - \Delta_{\text{N}} } \right)} \hfill & {C_{{12{\text{b}}}} \left( {1 - \Delta_{\text{N}} } \right)} \hfill & {C_{{13{\text{b}}}} \left( {1 - \Delta_{\text{N}} } \right)} \hfill \\ {C_{{12{\text{b}}}} \left( {1 - \Delta_{\text{N}} } \right)} \hfill & {C_{{11{\text{b}}}} \left( {1 - \Delta_{\text{N}} \frac{{C_{{12{\text{b}}}}^{2} }}{{C_{{11{\text{b}}}}^{2} }}} \right)} \hfill & {C_{{13{\text{b}}}} \left( {1 - \Delta_{\text{N}} \frac{{C_{{12{\text{b}}}} }}{{C_{{11{\text{b}}}} }}} \right)} \hfill \\ {C_{{13{\text{b}}}} \left( {1 - \Delta_{\text{N}} } \right)} \hfill & {C_{{13{\text{b}}}} \left( {1 - \Delta_{\text{N}} \frac{{C_{{12{\text{b}}}} }}{{C_{{11{\text{b}}}} }}} \right)} \hfill & {C_{{33{\text{b}}}} \left( {1 - \Delta_{\text{N}} \frac{{C_{{13{\text{b}}}}^{2} }}{{C_{{11{\text{b}}}} C_{{33{\text{b}}}} }}} \right)} \hfill \\ \end{array} } \right],$$

(2)

and

$${\tilde{\mathbf{C}}}_{2} = \left[ {\begin{array}{*{20}c} {C_{{44{\text{b}}}} } & 0 & 0 \\ 0 & {C_{{44{\text{b}}}} \left( {1 - \Delta_{\text{V}} } \right)} & 0 \\ 0 & 0 & {C_{{66{\text{b}}}} \left( {1 - \Delta_{\text{H}} } \right)} \\ \end{array} } \right].$$

(3)

Fig. 1

Schematic diagram of orthorhombic media, where a is formed by a single set of vertical fractures aligned yz-plane embedded in a VTI background, b is formed by two orthogonal vertical fracture sets embedded in an isotropic background, and c is formed by two orthogonal vertical fracture sets embedded in a VTI background

Here C _ijb represents the stiffness elements of a VTI background medium, which is constrained by $C_{{12{\text{b}}}} = C_{{11{\text{b}}}} - 2C_{{66{\text{b}}}}$ and related to the P- and S-wave moduli M = C _33b and $\mu = C_{{44{\text{b}}}}$. $\delta_{\text{N}}$, $\delta_{\text{V}}$, and $\delta_{\text{H}}$ denote the dimensionless normal, vertical and horizontal tangential fracture weaknesses, respectively, which change from zero for the case of no fractures to unity for the case of extreme fracturing (Bakulin et al. 2000), and can be expressed as (Schoenberg and Helbig 1997)

$$0 \le \delta_{\text{N}} \equiv \frac{{Z_{\text{N}} \rho C_{{11{\text{b}}}} }}{{1 + Z_{\text{N}} \rho C_{{11{\text{b}}}} }} < 1,$$

(4)

$$0 \le \delta_{\text{V}} \equiv \frac{{Z_{\text{V}} \rho C_{{44{\text{b}}}} }}{{1 + Z_{\text{V}} \rho C_{{44{\text{b}}}} }} < 1,$$

(5)

and

$$0 \le \delta_{\text{H}} \equiv \frac{{Z_{\text{H}} \rho C_{{66{\text{b}}}} }}{{1 + Z_{\text{H}} \rho C_{{66{\text{b}}}} }} < 1,$$

(6)

where Z _N, Z _V, and Z _H denote the nonnegative normal, vertical, and horizontal tangential fracture compliances, respectively, and ρ represents the density term of a homogenous isotropic background. Meanwhile, the normal fracture weakness $\delta_{\text{N}}$ depends on fluid content filling the fractures and possible fluid flow between the fractures and pore space, whereas the tangential fracture weaknesses $\delta_{\text{V}}$ and $\delta_{\text{H}}$ give a direct measure of fracture density (Schoenberg and Douma 1988).

Under the weak-anisotropy assumption, the dimensionless Thomsen’s (1986) WA parameters can be written in terms of stiffness elements of VTI background as

$$\varepsilon_{\text{b}} \equiv \frac{{C_{{11{\text{b}}}} - C_{{33{\text{b}}}} }}{{2C_{{33{\text{b}}}} }},$$

(7)

$$\text{ }\gamma_{\text{b}} \equiv \frac{{C_{{66{\text{b}}}} - C_{{44{\text{b}}}} }}{{2C_{{44{\text{b}}}} }},$$

(8)

and

$$\delta_{\text{b}} \equiv \frac{{\left( {C_{{13{\text{b}}}} + C_{{44{\text{b}}}} } \right)^{2} - \left( {C_{{33{\text{b}}}} - C_{{44{\text{b}}}} } \right)^{2} }}{{2C_{{33{\text{b}}}} \left( {C_{{33{\text{b}}}} - C_{{44{\text{b}}}} } \right)}} \approx \frac{{C_{{13{\text{b}}}} + 2C_{{44{\text{b}}}} - C_{{33{\text{b}}}} }}{{C_{{33{\text{b}}}} }},$$

(9)

where $\varepsilon_{\text{b}}$, $\text{ }\gamma_{\text{b}}$, and $\delta_{\text{b}}$ represent the three Thomsen’s WA parameters of VTI background.

In order to derive the perturbation in stiffness tensor of an orthorhombic medium expressed using the dimensionless Thomsen’s WA parameters and fracture weaknesses, we rewrite the expressions for the stiffness tensor of an orthorhombic medium.

Under the assumption of small WA parameters and fracture weaknesses, i.e., $\delta_{\text{N}} ,\,{\text{etc}} \ll 1$ (Shaw and Sen 2006), we neglected the terms that contain $\delta_{\text{N}}^{2}$, $\varepsilon_{\text{b}}^{2}$, $\gamma_{\text{b}}^{2}$, $\delta_{\text{b}}^{2}$, $\varepsilon_{\text{b}} \delta_{\text{N}}$, $\gamma_{\text{b}} \delta_{\text{N}}$, $\delta_{\text{b}} \delta_{\text{N}}$, and $\gamma_{\text{b}} \delta_{\text{H}}$, and thus, a new expression of WA approximate effective elastic stiffness tensor in terms of Thomsen’s WA parameters and fracture weaknesses in a weakly anisotropic medium with orthorhombic symmetry can be derived. Thus, the stiffness tensor for such a medium is given by

$${\mathbf{C}}_{\text{OA}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right],$$

(10)

where

$$C_{11} \approx M + 2M\varepsilon_{\text{b}} - M\delta_{\text{N}} ,$$

(11)

$$C_{12} \approx \lambda + 2M\varepsilon_{\text{b}} - 4\mu \gamma_{\text{b}} - \lambda \delta_{\text{N}} ,$$

(12)

$$C_{13} \approx \lambda + M\delta_{\text{b}} - \lambda \delta_{\text{N}} ,$$

(13)

$$C_{22} \approx M + 2M\varepsilon_{\text{b}} - M\chi^{2} \delta_{\text{N}} ,$$

(14)

$$C_{23} \approx \lambda + M\delta_{\text{b}} - \lambda \chi \delta_{\text{N}} ,$$

(15)

$$C_{33} \approx M - M\chi^{2} \delta_{\text{N}} ,$$

(16)

$$C_{44} = \mu ,$$

(17)

$$C_{55} \approx \mu - \mu \delta_{\text{V}} ,$$

(18)

and

$$C_{66} \approx \mu - 2\mu \gamma_{\text{b}} - \mu \delta_{\text{H}} .$$

(19)

Here $\lambda = M - 2\mu$ represents the first Lamé parameter of background medium, and $\chi = {\lambda \mathord{\left/ {\vphantom {\lambda M}} \right. \kern-0pt} M}$. $\varepsilon_{\text{b}}$, $\text{ }\gamma_{\text{b}}$, and $\delta_{\text{b}}$ represent the three Thomsen’s WA parameters of a VTI medium, and $\delta_{\text{N}}$, $\delta_{\text{V}}$, and $\delta_{\text{H}}$ represent the three fracture weaknesses of aligned vertical fractures.

2.2 Linearized PP-Wave Reflection Coefficient for a Weakly Anisotropic Medium with Orthorhombic Symmetry

Considering the small perturbations in P- and S-wave moduli and Lamé parameters across the interface, and neglecting the terms that contain $\Delta M\delta_{\text{N}}$, $\Delta \lambda \delta_{\text{N}}$, $\Delta M\varepsilon_{\text{b}}$, $\Delta M\delta_{\text{b}}$, $\Delta \mu \gamma_{\text{b}}$, $\Delta \mu \delta_{\text{V}}$, and $\Delta \mu \delta_{\text{H}}$ for the case of small WA parameters and fracture weaknesses, we can derive the perturbations over a weakly anisotropic medium with orthorhombic symmetry expressed as

$$\Delta C_{11} \approx \Delta M + 2M\Delta \varepsilon_{\text{b}} - M\Delta \delta_{\text{N}} ,$$

(20)

$$\Delta C_{12} \approx \Delta \lambda + 2M\Delta \varepsilon_{\text{b}} - 4\mu \Delta \gamma_{\text{b}} - \lambda \Delta \delta_{\text{N}} ,$$

(21)

$$\Delta C_{13} \approx \Delta \lambda + M\Delta \delta_{\text{b}} - \lambda \Delta \delta_{\text{N}} ,$$

(22)

$$\Delta C_{22} \approx \Delta M + 2M\Delta \varepsilon_{\text{b}} - M\chi^{2} \Delta \delta_{\text{N}} ,$$

(23)

$$\Delta C_{23} \approx \Delta \lambda + M\Delta \delta_{\text{b}} - \lambda \chi \Delta \delta_{\text{N}} ,$$

(24)

$$\Delta C_{33} \approx \Delta M - M\chi^{2} \Delta \delta_{\text{N}} ,$$

(25)

$$\Delta C_{44} = \Delta \mu ,$$

(26)

$$\Delta C_{55} \approx \Delta \mu - \mu \Delta \delta_{\text{V}} ,$$

(27)

and

$$\Delta C_{66} \approx \Delta \mu - 2\mu \Delta \gamma_{\text{b}} - \mu \Delta \delta_{\text{H}} ,$$

(28)

where ∆M, $\Delta \mu$, $\Delta \lambda$, $\Delta \varepsilon_{\text{b}}$, $\Delta \gamma_{\text{b}}$, $\Delta \delta_{\text{b}}$, $\Delta \delta_{\text{N}}$, $\Delta \delta_{\text{V}}$, and $\Delta \delta_{\text{H}}$ represent the perturbations in P- and S-wave moduli, Lamé parameter, Thomsen’s WA parameters, and fracture weaknesses between the layers separated by the interface, respectively.

The perturbations in stiffness tensor depend linearly on Thomsen’s WA parameters and fracture weaknesses, which quantify the orthorhombic anisotropy in a weakly anisotropic medium. Combining the perturbations in stiffness tensor and scattering function (Shaw and Sen 2004, 2006), the linearized PP-wave reflection coefficient for a weakly anisotropic medium with orthorhombic symmetry can be thus derived to characterize the orthorhombic anisotropy incorporating wide-azimuth seismic data and inversion method.

Shaw and Sen (2004, 2006) proposed a novel approach to derive the linearized reflection coefficients using the perturbations in stiffness tensor and the slowness and polarization vectors in weakly anisotropic media. For a weakly anisotropic medium with orthorhombic symmetry, the linearized PP-wave reflection coefficient is given by

$$R_{\text{PP}} = \frac{1}{{4\rho \cos^{2} \theta }}S,$$

(29)

where θ represents the angle between the normal to the interface and the phase vector normal to the incident wave front, and the scattering function is written as

$$S = \Delta \rho \xi + \sum\limits_{I = 1}^{6} {\sum\limits_{J = 1}^{6} {\Delta C_{IJ} \eta_{IJ} } } ,$$

(30)

where $\Delta \rho$ represents the perturbation in the density, $\xi = \left. {t_{i} t_{i}^{\prime } } \right|_{{r = r_{0} }}$, and $\eta_{IJ} = \left. {t_{i}^{\prime } p_{j}^{\prime } t_{k} p_{l} } \right|_{{r = r_{0} }}$. Here the parameters p and t represent the slowness and polarization vectors, respectively, and the position vector r ₀ represents the point on the horizontal interface separating two weakly isotropic or anisotropic media satisfying Snell’s law of reflection. The subscripts I and J refer to Voigt’s concise notation, I takes values over i and j, whereas J takes values over k and l with i, j, k, l = 1, 2, 3. The expressions for $\xi$ and $\eta_{IJ}$ are shown in Appendix 1.

Combining Eqs. (20)–(30), we derived a new linearized PP-wave reflection coefficient in terms of background elastic moduli, density, Thomsen’s WA parameters, and fracture weaknesses (in Appendix 1) to characterize the orthorhombic anisotropy. Thus, the derived linearized PP-wave reflection coefficient over a weakly anisotropic medium with orthorhombic symmetry can be expressed as

$$\begin{aligned} R_{\text{PP}} \left( {\theta ,\phi } \right) & = a_{M} \left( \theta \right)\frac{\Delta M}{M} + a_{\mu } \left( \theta \right)\frac{\Delta \mu }{\mu } + a_{\rho } \left( \theta \right)\frac{\Delta \rho }{\rho } + a_{{\varepsilon_{\text{b}} }} \left( \theta \right)\Delta \varepsilon_{\text{b}} + a_{{\delta_{\text{b}} }} \left( \theta \right)\Delta \delta_{\text{b}} \\ & \quad + \,a_{{\delta_{\text{N}} }} \left( {\theta ,\phi } \right)\Delta \delta_{\text{N}} + a_{{\delta_{\text{V}} }} \left( {\theta ,\phi } \right)\Delta \delta_{\text{V}} + a_{{\delta_{\text{H}} }} \left( {\theta ,\phi } \right)\Delta \delta_{\text{H}} , \\ \end{aligned}$$

(31)

where $a_{M} \left( \theta \right) = {{\sec^{2} \theta } \mathord{\left/ {\vphantom {{\sec^{2} \theta } 4}} \right. \kern-0pt} 4}$, $a_{\mu } \left( \theta \right) = - 2g\sin^{2} \theta$, $a_{\rho } \left( \theta \right) = {{\left( {1 - {{\sec^{2} \theta } \mathord{\left/ {\vphantom {{\sec^{2} \theta } 2}} \right. \kern-0pt} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {{\sec^{2} \theta } \mathord{\left/ {\vphantom {{\sec^{2} \theta } 2}} \right. \kern-0pt} 2}} \right)} 2}} \right. \kern-0pt} 2}$, $a_{{\varepsilon_{b} }} \left( \theta \right) = {{\sin^{2} \theta \tan^{2} \theta } \mathord{\left/ {\vphantom {{\sin^{2} \theta \tan^{2} \theta } 2}} \right. \kern-0pt} 2}$, $a_{{\delta_{\text{b}} }} \left( \theta \right) = {{\sin^{2} \theta } \mathord{\left/ {\vphantom {{\sin^{2} \theta } 2}} \right. \kern-0pt} 2}$, $a_{{\delta_{\text{N}} }} \left( {\theta ,\phi } \right) = - {{\sec^{2} \theta } \mathord{\left/ {\vphantom {{\sec^{2} \theta } 4}} \right. \kern-0pt} 4}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2}$, $a_{{\delta_{\text{V}} }} \left( {\theta ,\phi } \right) = g\sin^{2} \theta \cos^{2} \phi$, $a_{{\delta_{\text{H}} }} \left( {\theta ,\phi } \right) = - g\sin^{2} \theta \tan^{2} \theta \sin^{2} \phi \cos^{2} \phi$, $g = {\mu \mathord{\left/ {\vphantom {\mu M}} \right. \kern-0pt} M}$, and where $\phi$ represents the azimuthal phase angle ($\phi = 0$ for the direction along the fracture orientation), and the denominators of ∆M/M, ${{\Delta \mu } \mathord{\left/ {\vphantom {{\Delta \mu } \mu }} \right. \kern-0pt} \mu }$, and ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0pt} \rho }$ denote the average values of the corresponding P- and S-wave moduli and density parameters of the upper and lower layers.

The derived Eq. (31) depends linearly on P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, which quantifies the seismic reflection response of an orthorhombic medium to estimate the elastic and anisotropic parameters from observable azimuthal seismic reflection data in a fractured reservoir. Of course, the accuracy of derived AVOaz equation can be simply verified compared with Eq. (16) derived by Zong et al. (2012) for the case of isotropy, and with Eq. (6) derived by Chen et al. (2017) for the case of transverse isotropy with a vertical symmetry axis (HTI) anisotropy. For other cause of orthorhombic media, the corresponding linearized PP-wave reflection coefficient can be derived in a similar way (shown in Appendix 1).

Based on the derived linearized PP-wave reflection coefficient in such an orthorhombic medium, we can characterize the effects of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weakness parameters on the PP-wave reflection, and further implement the inversion for elastic moduli and fracture properties using the azimuthal seismic data.

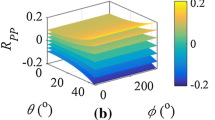
Figure 2 shows the effects of changes in model parameters on PP-wave reflection coefficient. Form Fig. 2a, c, we find that both the reflectivities of P-wave moduli and density term have contributions to the reflection coefficient at small angles of incidence, which indicates that seismic data of large angles of incidence are necessary to be used to discriminate the effects of P-wave moduli and density on PP-wave reflection coefficient. Compared with the changes of the reflectivities of P-wave moduli and density, the change of the reflectivity of S-wave moduli shown in Fig. 2b makes no contribution to the reflection coefficient at small angles of incidence and contributes more at large angles of incidence. From Fig. 2d, e, we can see that the changes of Thomsen’s WA parameters contribute the reflection coefficient similarly, and this may lead to uncertainties in estimating the Thomsen’s WA parameters. From Fig. 2f, g, h, we can see that the changes in fracture weaknesses contribute to the variation of reflection coefficient with not only angles but also azimuths, and the contributions of the normal weakness are more than the other weakness parameters. To invert the Thomsen’s WA parameters and fracture weaknesses in a weakly anisotropic medium with orthorhombic symmetry, we develop an AVOaz inversion method in a Bayesian framework incorporating the constraints of Cauchy a priori probability distribution and smooth initial models of model parameters.

Fig. 2

Effects of changes in model parameters on PP-wave reflection coefficient, where a shows the effect of change only in ∆M/M from −0.2 to 0.2 on reflection coefficients, b shows the effect of change only in ${{\Delta \mu } \mathord{\left/ {\vphantom {{\Delta \mu } \mu }} \right. \kern-0pt} \mu }$ from −0.2 to 0.2 on reflection coefficients, c shows the effect of change only in ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0pt} \rho }$ from −0.2 to 0.2 on reflection coefficients, d shows the effect of change only in $\Delta \varepsilon_{\text{b}}$ from −0.2 to 0.2 on reflection coefficients, e shows the effect of change only in $\Delta \varepsilon_{\text{b}}$ from −0.2 to 0.2 on reflection coefficients, f shows the effect of change only in $\Delta \delta_{\text{N}}$ from −0.2 to 0.2 on reflection coefficients, g shows the effect of change only in $\Delta \delta_{\text{V}}$ from −0.2 to 0.2 on reflection coefficients, and h shows the effect of change only in $\Delta \delta_{\text{T}}$ from −0.2 to 0.2 on reflection coefficients

2.3 AVOaz Inversion for Thomsen’s WA Parameters and Fracture Weaknesses

The relative contrasts of elastic moduli and density in Eq. (31) can be substituted by ${{\Delta M} \mathord{\left/ {\vphantom {{\Delta M} M}} \right. \kern-0pt} M} \approx \Delta \left( {\ln M} \right)$, ${{\Delta \mu } \mathord{\left/ {\vphantom {{\Delta \mu } \mu }} \right. \kern-0pt} \mu } \approx \Delta \left( {\ln \mu } \right)$, and ${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0pt} \rho } \approx \Delta \left( {\ln \rho } \right)$, where ln(∙) denotes the natural logarithm, and the symbol ∆ indicates small perturbations across the interface, i.e., $\left| {{{\Delta M} \mathord{\left/ {\vphantom {{\Delta M} M}} \right. \kern-0pt} M}} \right| \ll 1$, $\left| {{{\Delta \mu } \mathord{\left/ {\vphantom {{\Delta \mu } \mu }} \right. \kern-0pt} \mu }} \right| \ll 1$, and $\left| {{{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } \rho }} \right. \kern-0pt} \rho }} \right| \ll 1$. Combining Eq. (31) and convolution model gives us the forward model which relates the azimuthal seismic traces to the logarithm of P- and S-wave moduli, density, and to the Thomsen’s WA parameters and fracture weaknesses:

$$\begin{aligned} T\left( {\theta ,\phi } \right) & = Wa_{M} \left( \theta \right)D\ln M + Wa_{\mu } \left( \theta \right)D\ln \mu + Wa_{\rho } \left( \theta \right)D\ln \rho \\ & \quad + \,Wa_{{\varepsilon_{\text{b}} }} \left( \theta \right)D\varepsilon_{\text{b}} + Wa_{{\delta_{\text{b}} }} \left( \theta \right)D\delta_{\text{b}} \\ & \quad + \,Wa_{{\delta_{\text{N}} }} \left( {\theta ,\phi } \right)D\delta_{\text{N}} + Wa_{{\delta_{\text{V}} }} \left( {\theta ,\phi } \right)D\delta_{\text{V}} + Wa_{{\delta_{\text{H}} }} \left( {\theta ,\phi } \right)D\delta_{\text{H}} . \\ \end{aligned}$$

(32)

Here W represents the wavelet matrix, and D represents the derivative matrix given by (Hampson et al. 2005)

$$D = \left[ {\begin{array}{*{20}c} { - 1} & 1 & 0 & \cdots \\ 0 & { - 1} & 1 & \ddots \\ 0 & 0 & { - 1} & \ddots \\ \vdots & \ddots & \ddots & \ddots \\ \end{array} } \right].$$

(33)

Equation (32) can be written in matrix form as

$${\mathbf{d}} = {\mathbf{Gm}},$$

(34)

where d represents the observable azimuthal seismic data vector, G represents the forward operator, and m is the model parameter vector given by

$${\mathbf{m}} = \left( {\ln M,\ln \mu ,\ln \rho ,\varepsilon_{\text{b}} ,\delta_{\text{b}} ,\delta_{\text{N}} ,\delta_{\text{V}} ,\delta_{\text{H}} } \right).$$

(35)

In this paper, we implement the AVOaz inversion in a Bayesian scheme (Pan et al. 2017a), which combines the model parameters with any prior information. The a posteriori probability distribution function (PDF) of estimated model parameters (p(m|d)) in Eq. (34) can be solved as a joint PDF of a priori PDF (p(m)) and a likelihood function (p(d|m)) given by

$$p\left( {{\mathbf{m}}\left| {\mathbf{d}} \right.} \right) = \frac{{p\left( {\mathbf{m}} \right)p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right)}}{{\int {p\left( {\mathbf{d}} \right)d{\mathbf{m}}} }} \propto p\left( {\mathbf{m}} \right)p\left( {{\mathbf{d}}\left| {\mathbf{m}} \right.} \right),$$

(36)

where p(·) represents the probability density. We chose a convolution operator as a forward solver expressed by Eq. (32), and a Cauchy PDF as the prior PDF due to its high-resolution solution (Sacchi and Ulrych 1995; Downton 2005). Thus, the a posteriori PDF of estimated model parameters combined a Gaussian PDF for the likelihood function with a Cauchy PDF for the a priori PDF can be expressed as

$$p\left( {{\mathbf{m}}\left| {\mathbf{d}} \right.} \right) \propto \prod\limits_{i = 1}^{N} {\left[ {\frac{1}{{1 + {{m_{i}^{2} } \mathord{\left/ {\vphantom {{m_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}}}} \right] \cdot \exp \left[ { - \frac{{\left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)}}{{2\sigma_{d}^{2} }}} \right]} ,$$

(37)

where $\sigma_{d}^{2}$ and $\sigma_{m}^{2}$ represent the variances of seismic noise and model parameters, respectively, and N represents the sample numbers of seismic data. After some algebraic operation, the objective function of model parameters for the maximum a posteriori inverse solution of Eq. (34) can be thus written as

$$F\left( {\mathbf{m}} \right) = \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right) + 2\sigma_{d}^{2} \sum\limits_{i = 1}^{N} {\ln \left( {1 + {{m_{i}^{2} } \mathord{\left/ {\vphantom {{m_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}} \right)} ,$$

(38)

where F(·) represents the objective function.

Incorporating the initial model regularization, Eq. (38) then gives

$$F\left( {\mathbf{m}} \right) = \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right)^{\text{T}} \left( {{\mathbf{d}} - {\mathbf{Gm}}} \right) + 2\sigma_{d}^{2} \sum\limits_{i = 1}^{N} {\ln \left( {1 + {{m_{i}^{2} } \mathord{\left/ {\vphantom {{m_{i}^{2} } {\sigma_{m}^{2} }}} \right. \kern-0pt} {\sigma_{m}^{2} }}} \right)} +\Gamma _{\bmod } ,$$

(39)

where

$$\begin{aligned}\Gamma _{\bmod } & = \omega_{M} \left( {\ln M - \ln M_{0} } \right)^{\text{T}} \left( {\ln M - \ln M_{0} } \right) + \omega_{\mu } \left( {\ln \mu - \ln \mu_{0} } \right)^{\text{T}} \left( {\ln \mu - \ln \mu_{0} } \right) \\ & \quad + \,\omega_{\rho } \left( {\ln \rho - \ln \rho_{0} } \right)^{\text{T}} \left( {\ln \rho - \ln \rho_{0} } \right) + \omega_{{\varepsilon_{\text{b}} }} \left( {\varepsilon_{\text{b}} - \varepsilon_{{{\text{b}}0}} } \right)^{\text{T}} \left( {\varepsilon_{\text{b}} - \varepsilon_{{{\text{b}}0}} } \right) \\ & \quad +\, \omega_{{\delta_{\text{b}} }} \left( {\delta_{\text{b}} - \delta_{{{\text{b}}0}} } \right)^{\text{T}} \left( {\delta_{\text{b}} - \delta_{{{\text{b}}0}} } \right) + \omega_{{\delta_{\text{N}} }} \left( {\delta_{\text{N}} - \delta_{{{\text{N}}0}} } \right)^{\text{T}} \left( {\delta_{\text{N}} - \delta_{{{\text{N}}0}} } \right) \\ & \quad +\, \omega_{{\delta_{\text{V}} }} \left( {\delta_{\text{V}} - \delta_{{{\text{V}}0}} } \right)^{\text{T}} \left( {\delta_{\text{V}} - \delta_{{{\text{V}}0}} } \right) + \omega_{{\delta_{\text{H}} }} \left( {\delta_{\text{H}} - \delta_{{{\text{H}}0}} } \right)^{\text{T}} \left( {\delta_{\text{H}} - \delta_{{{\text{H}}0}} } \right). \\ \end{aligned}$$

(40)

In Eq. (40), ω _i represent the initial model regularization parameters of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, respectively, and the subscript 0 represents the initial model parameters.

Equation (39) is nonlinear due to the introduction of Cauchy-sparse and initial model regularization, which can be solved using the IRLS strategy (Scales and Smith 1994). After a few iterations, reasonable inversion results can be obtained.

3 Examples

3.1 Synthetic Examples

To test the feasibility of the proposed AVOaz inversion for Thomsen’s WA parameters and fracture weaknesses proposed in this paper, we use a well log data in a gas-bearing fractured field as model parameters. The logging Thomsen’s WA parameters and fracture weaknesses are calculated by using well logs and rock physics analysis results (Pan et al. 2017a, b). In Fig. 3, we present a process of constructing the effective rock physics model with orthorhombic symmetry used to estimate the Thomsen’s WA parameters and fracture weaknesses by using the conventional well logs, including the rock minerals and their volume fraction, the porosity of matrix pores, the pore fluid types and water saturation, and the fracture density (Backus 1962; Hill 1952; Hornby et al. 1994; Hudson 1981; Schoenberg and Muir 1989). The original P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses of a well are displayed in blue in Fig. 4. The synthetic azimuthal seismic data are simulated with the convolution model of the linearized PP-wave reflection coefficient and seismic wavelet (Richer wavelets are utilized here). Azimuths are 30°, 60°, 90°, and 120°, and the incidence phase angles are 0°–34°. We implement the orthorhombic anisotropic AVOaz inversion on the synthetic data. The initial models (in green) and inverted results (in red) of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses are displayed in green and red in Fig. 4, respectively. Figure 5 shows the relative prediction errors (the difference values between real and estimated values divided by real values) of model parameters without noise. From Figs. 4 and 5, we find that the elastic moduli and orthorhombic anisotropic parameters can be estimated reasonably even with fairly smoothing initial models. The errors of P- and S-wave moduli and density are about within 5%, and the errors of Thomsen’s WA parameters and fracture weaknesses are about 10%. To further demonstrate the stability of proposed AVOaz inversion for a weakly anisotropic medium with orthorhombic symmetry, we add a Gaussian random noise to the true synthetic seismic data with different signal-to-noise ratios (SNR) being 5:1 and 2:1, respectively. The inverted results and corresponding relative prediction errors are shown in Figs. 6, 7, 8, and 9, respectively. As is in the case of noises, reasonable estimates of model parameters can be obtained, and the errors of background elastic moduli are within 10%, and the errors of orthorhombic anisotropic parameters are about 20%, which are feasible for our application. However, the estimation precisions of Thomsen’s WA parameters and fracture weaknesses are not as good as those of P- and S-wave moduli and density, which may result from the differences of contributions of model parameters on PP-wave reflection coefficient shown in Fig. 2.

Fig. 3

Process of constructing effective rock physics model with orthorhombic symmetry

Fig. 4

Model parameter estimation without noise, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses. Note that the blue lines represent the true values, the green lines represent the initial models, and the red lines represent the estimated values

Fig. 5

Prediction errors of the model parameters without noise, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses

Fig. 6

Model parameter estimation with SNR = 5, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses

Fig. 7

Prediction errors of the model parameters with SNR = 5, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses

Fig. 8

Model parameter estimation with SNR = 2, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses

Fig. 9

Prediction errors of the model parameters with SNR = 2, where a represents the estimated P- and S-wave moduli, density parameters, b represents the estimated Thomsen’s WA parameters, and c represents the estimated fracture weaknesses

3.2 Field Data Example

The proposed azimuthally anisotropic EI inversion approach has been tested on the real data set from Gaoshiti area, which is located in the Sichuan Basin, China. A series of tectonic gas-bearing reservoirs exit in this work area, and formation micro-imaging (FMI) interpretation shows the gas is trapped in the Sinian Dengying formation. The lateral continuity of reservoir is better, and a large amount of vertical or near-vertical fractures is well developed in the low-porosity and low-permeability reservoir. In this work area, we assume that the gas-bearing reservoir can be treated as an orthorhombic medium formed by a single set of vertically aligned fractures embedded in a horizontal layer (Fig. 1a). Before implementing the AVOaz inversion, the observable seismic data are processed by a contractor to preserve the amplitudes of the true subsurface reflection interfaces as correctly as possible. After processing, the wave-mode conversions, inter-bed multiples, and anisotropic moveout are assumed to be neglected. To further enhance the SNR of observable seismic data, we used the angle-stack trace gathers, and the four azimuthal seismic data are 22.5°, 67.5°, 112.5°, and 157.5° shown in Fig. 10, and the average angles for the near, mid- and far stacks are 5° (and a range of 0°–10°), 15° (and a range of 10°–20°) and 25° (and a range of 20°–30°), respectively. Black lines in the figures represent the well log position, and red circles in each profile indicate the location of gas-bearing fractured reservoirs. We observed that there was amplitude anomaly in the location of the reservoirs.

Fig. 10

Azimuthal observable seismic data at different phase angles of azimuth, where a shows an average angle of 22.5° (and a range of 0°–45°), b shows an average angle of 67.5° (and a range of 45°–90°), c shows an average angle of 112.5° (and a range of 90°–135°), and c shows an average angle of 157.5° (and a range of 135°–180°)

We construct the initial models of model parameters by using the constructed rock physics model with orthorhombic symmetry (Fig. 2). The estimated Thomsen’s WA parameters and fracture weakness parameters are smoothed under the constraint of horizons, and the smooth results are treated as the initial models of model parameters. Then, we perform the AVOaz inversion with the constraints of Cauchy a priori probability distribution and smooth initial models of model parameters to enhance the inversion resolution. According to the nonlinear IRLS strategy, we estimate the Thomsen’s WA parameters and fracture weakness parameters iteratively. Figures 11, 12, and 13 show the inversion results of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, where the white dashed ellipses in well A indicate the target reservoir zones and the white lines are the corresponding inverted results of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, and the red rectangles in well B show the response of gas-bearing fractured reservoir. Note that well A is used to establish the initial model of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, and well B is used to demonstrate the inversion results dissociating from the establishment of the initial model. We find that the estimated P- and S-wave moduli, density, and Thomsen’s WA parameters show anomalously low value, while the estimated fracture weaknesses show anomalously high value at the position of gas-bearing fractured reservoir. The fracture weaknesses indicate the fracture development of the layer, and the inverted fracture weaknesses may be used to characterize the fracture-developed target. Moreover, there is a good match between the estimated results with the response of gas-bearing fractured reservoir in well B.

Fig. 11

Estimated P- and S-wave moduli, and density parameters using the AVOaz inversion, where a shows the estimated P-wave modulus M, b shows the estimated S-wave modulus $\mu$, and c shows the estimated density $\rho$

Fig. 12

Estimated Thomsen’s WA parameters using the AVOaz inversion, where a shows the estimated $\varepsilon_{\text{b}}$, and b shows the estimated $\delta_{\text{b}}$

Fig. 13

Estimated fracture weakness parameters using the AVOaz inversion, where a shows the estimated normal fracture weakness ∆_N, b shows the estimated vertical tangential fracture weakness ∆_V, and c shows the estimated horizontal tangential fracture weakness ∆_H

In order to test the reliability of the inversed P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses, we firstly present the comparisons between the true well logs estimated by using the well log interpretations and rock physics analysis (black) and inverted results (red) at well location in Fig. 14. We can see that the inverted results are reasonably consistent with the true well logs, which indicates that our proposed inversion method can make a reliable inversion for elastic moduli and orthorhombic parameters. Then, we use the inversed parameters to create the synthetic seismic data with extracted wavelets and show the comparisons between the synthetic and real traces in Fig. 15. A good match between the traces can be seen, and it further demonstrates the accuracy of our proposed AVOaz inversion for orthorhombic anisotropy.

Fig. 14

Comparison of well curves in time domain (blue) and inverted results (red) at well location, where a shows the estimated P- and S-wave moduli, density parameters, b shows the estimated Thomsen’s WA parameters, and c shows the estimated fracture weaknesses

Fig. 15

Comparisons between real (blue) and synthetic (red) stack traces at different azimuths, where a shows the azimuth of 22.5°, b shows the azimuth of 67.5°, c shows the azimuth of 112.5°, and d shows the azimuth of 157.5°

4 Discussion and Conclusions

The presented methodology aims to simultaneously estimate the P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses in a gas-bearing fractured reservoir directly from wide-azimuth observable seismic reflection data. Combining Thosmen’s (1986) WA theory with linear-slip model, we derived a new expression for stiffness elements of a weakly anisotropic medium with orthorhombic symmetry formed by a single set of aligned vertical fractures embedded in a VTI background, and then using the perturbation matrix and scattering function, we derived the linearized PP-wave reflection coefficient in terms of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses to describe the relationship between the orthorhombic anisotropy and azimuthal seismic reflection data. Combing the derived AVOaz equation and Bayesian seismic inversion with regularization constraints, the elastic and anisotropic parameters were reasonably estimated demonstrated using both synthetic and real data in a gas-bearing fractured reservoir.

In Appendix 2, under the assumption of weak anisotropy and small weaknesses, we also derived the linearized PP-wave reflection coefficients in terms of P- and S-wave moduli, density, Thomsen’s WA parameters, and fracture weaknesses in an another orthorhombic medium formed by two orthogonal vertical fracture sets with rotationally invariant properties embedded in an isotropic or VTI background. During the derivation of AVOaz equation in orthorhombic media, weak anisotropy, small fracture weaknesses, and small perturbations in parameters should be satisfied.

Appendices

Appendix 1: Derivation for Linearized PP-Wave Reflection Coefficient in a Weakly Anisotropic Medium with Orthorhombic Symmetry Formed by a Single Set of Aligned Vertical Fractures Embedded in a VTI Background

The relationships between the subscripts (I, J) and (i, j, k, l) in Eq. (30) are given by Shaw and Sen (2006)

$$I = i\delta_{ij} + \left( {9 - i - j} \right)\left( {1 - \delta_{ij} } \right),$$

(41)

and

$$J = k\delta_{kl} + \left( {9 - k - l} \right)\left( {1 - \delta_{kl} } \right),$$

(42)

where $\delta_{ij}$ and $\delta_{kl}$ both denote the Kronecker delta.

For the case of P-wave incidence and reflection, the polarization and slowness vectors are given by

$$t\text{ = }\left[ {\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta } \right],$$

(43)

$$t^{\prime } = \left[ { - \sin \theta \cos \phi , - \sin \theta \sin \phi ,\cos \theta } \right],$$

(44)

$$p = {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }\left[ {\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta } \right],$$

(45)

and

$$p^{\prime } = {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }\left[ { - \sin \theta \cos \phi , - \sin \theta \sin \phi ,\cos \theta } \right],$$

(46)

where α represents the background P-wave velocity, and $\phi$ represents the azimuthal phase angle.

Substituting Eqs. (43) and (44) into Eq. (30), the expression of $\xi$ is then given by

$$\xi = \cos^{2} \theta - \sin^{2} \theta = \cos 2\theta .$$

(47)

Substituting Eqs. (43)–(47) into Eq. (30), the expression of $\eta_{IJ}$ is then given by

$$\begin{aligned} \eta_{11} & = {{\sin^{4} \theta \cos^{4} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \cos^{4} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{12} = {{\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{13} = {{\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}, \\ \eta_{22} & = {{\sin^{4} \theta \sin^{4} \phi } \mathord{\left/ {\vphantom {{\sin^{4} \theta \sin^{4} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{23} = {{\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } \mathord{\left/ {\vphantom {{\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{33} = {{\cos^{4} \theta } \mathord{\left/ {\vphantom {{\cos^{4} \theta } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }}, \\ \eta_{44} & = {{ - 4\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } \mathord{\left/ {\vphantom {{ - 4\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{55} = {{ - 4\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } \mathord{\left/ {\vphantom {{ - 4\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\text{ } \\ \eta_{66} & = {{4\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } \mathord{\left/ {\vphantom {{4\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi } {\alpha^{2} }}} \right. \kern-0pt} {\alpha^{2} }},\quad \eta_{21} = \eta_{12} \text{,}\quad \eta_{31} = \eta_{13} \text{,}\quad \eta_{32} = \eta_{23} . \\ \end{aligned}$$

(48)

The calculation of Eq. (30) then yields

$$\begin{aligned} S & = \Delta \rho \xi + \sum\limits_{I = 1}^{6} {\sum\limits_{J = 1}^{6} {\Delta C_{IJ} \eta_{IJ} } } \\ & = \Delta \rho \cos 2\theta + \frac{{\sin^{4} \theta \cos^{4} \phi }}{{\alpha^{2} }}\left[ {\Delta M - M\Delta \delta_{\text{N}} + 2M\Delta \varepsilon_{\text{b}} } \right] \\ & \quad +\, \frac{{2\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi }}{{\alpha^{2} }}\left[ {\Delta \lambda - \lambda \Delta \delta_{\text{N}} + 2M\Delta \varepsilon_{\text{b}} - 4\mu \Delta \gamma_{\text{b}} } \right] \\ & \quad + \,\frac{{2\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi }}{{\alpha^{2} }}\left[ {\Delta \lambda - \lambda \Delta \delta_{\text{N}} + M\Delta \delta_{\text{b}} } \right] + \frac{{\sin^{4} \theta \sin^{4} \phi }}{{\alpha^{2} }}\left[ {\Delta M - M\chi^{2} \Delta \delta_{\text{N}} + 2M\Delta \varepsilon_{\text{b}} } \right] \\ & \quad + \,\frac{{2\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi }}{{\alpha^{2} }}\left[ {\Delta \lambda - \lambda \chi \Delta \delta_{\text{N}} + M\Delta \delta_{\text{b}} } \right] \\ & \quad +\, \frac{{\cos^{4} \theta }}{{\alpha^{2} }}\left[ {\Delta M - M\chi^{2} \Delta \delta_{\text{N}} } \right]- \frac{{4\sin^{2} \theta \cos^{2} \theta \sin^{2} \phi }}{{\alpha_{0}^{2} }}\Delta \mu \\ & \quad - \frac{{4\sin^{2} \theta \cos^{2} \theta \cos^{2} \phi }}{{\alpha^{2} }}\left[ {\Delta \mu - \mu \Delta \delta_{\text{V}} } \right] + \frac{{4\sin^{4} \theta \sin^{2} \phi \cos^{2} \phi }}{{\alpha^{2} }}\left[ {\Delta \mu - \mu \Delta \delta_{\text{H}} - 2\mu \Delta \gamma_{\text{b}} } \right] \\ & = \frac{1}{{\alpha^{2} }}\Delta M - \frac{{\sin^{2} \theta \cos^{2} \theta }}{{\alpha^{2} }}\Delta \mu + \cos 2\theta \Delta \rho + \frac{{2M\sin^{4} \theta }}{{\alpha^{2} }}\Delta \varepsilon_{\text{b}} + \frac{{2M\sin^{2} \theta \cos^{2} \theta }}{{\alpha^{2} }}\Delta \delta_{\text{b}} \\ & \quad - \,\frac{M}{{\alpha^{2} }}\left[ {2\frac{\mu }{M}\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{\text{N}} + \frac{{4\mu \sin^{2} \theta \cos^{2} \phi }}{{\alpha^{2} }}\Delta \delta_{\text{V}} \\ & \quad-\, \frac{{4\mu \sin^{4} \theta \sin^{2} \phi \cos^{2} \phi }}{{\alpha^{2} }}\Delta \delta_{\text{H}} . \\ \end{aligned}$$

(49)

Combining Eq. (49), the calculation of Eq. (29) finally gives

$$\begin{aligned} R_{\text{PP}} \left( {\theta ,\phi } \right) & = \frac{{\sec^{2} \theta }}{4M}\Delta M - \frac{{2\sin^{2} \theta }}{M}\Delta \mu + \frac{1}{2\rho }\left( {1 - \frac{{\sec^{2} \theta }}{2}} \right)\Delta \rho \\ & \quad + \,\frac{{\sin^{2} \theta \tan^{2} \theta }}{2}\Delta \varepsilon_{\text{b}} + \frac{{\sin^{2} \theta }}{2}\Delta \delta_{\text{b}} - \frac{{\sec^{2} \theta }}{4}\left[ {2\frac{\mu }{M}\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{\text{N}} \\ & \quad + \,\frac{\mu }{M}\sin^{2} \theta \cos^{2} \phi \Delta \delta_{\text{V}} - \frac{\mu }{M}\sin^{2} \theta \tan^{2} \theta \sin^{2} \phi \cos^{2} \phi \Delta \delta_{\text{H}} , \\ \end{aligned}$$

(50)

Appendix 2: Derivation for Linearized PP-Wave Reflection Coefficients in a Weakly Anisotropic Medium with Orthorhombic Symmetry Formed by Two Orthogonal Vertical Fracture Sets Embedded in an Isotropic or VTI Background

Two orthogonal vertical fracture sets embedded in an isotropic or VTI background can be both considered as an effective long-wavelength orthorhombic medium (Bakulin et al. 2000, 2002). To further simplify the procedure of parameter estimation, the fracture sets are assumed to be rotationally invariant. For such a weakly anisotropic medium with orthorhombic symmetry formed by two orthogonal vertical fracture sets embedded in an isotropic background, where the first fracture set is perpendicular to the x axis (shown in Fig. 1b), neglecting the terms that contain $\delta_{{{\text{N}}1}} \delta_{{{\text{N}}2}}$ and $\delta_{{{\text{T}}1}} \delta_{{{\text{T}}2}}$ for the case of small fracture weaknesses, an expression for the effective elastic stiffness tensor can be approximated as

$${\mathbf{C}}_{\text{OA}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right] \approx \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{C}}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\hat{\mathbf{C}}}_{2} } \\ \end{array} } \right],$$

(51)

where 0 represents the 3 × 3 zero matrix, and ${{\hat{\mathbf{C}}}}_{1}$ and ${{\hat{\mathbf{C}}}}_{2}$ are given by

$${{\hat{\mathbf{C}}}}_{1} = \left[ {\begin{array}{*{20}l} {M\left( {1 - \delta_{{{\text{N}}1}} - \chi^{2} \delta_{{{\text{N}}2}} } \right)} \hfill & {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right)} \hfill & {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \chi \delta_{{{\text{N}}2}} } \right)} \hfill \\ {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right)} \hfill & {M\left( {1 - \chi^{2} \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right)} \hfill & {\lambda \left( {1 - \chi \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right)} \hfill \\ {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \chi \delta_{{{\text{N}}2}} } \right)} \hfill & {\lambda \left( {1 - \chi \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right)} \hfill & {M\left( {1 - \chi^{2} \delta_{{{\text{N}}1}} - \chi^{2} \delta_{{{\text{N}}2}} } \right)} \hfill \\ \end{array} } \right],$$

(52)

and

$${{\hat{\mathbf{C}}}}_{2} = \left[ {\begin{array}{*{20}c} {\mu \left( {1 - \delta_{{{\text{T}}2}} } \right)} & 0 & 0 \\ 0 & {\mu \left( {1 - \delta_{{{\text{T}}1}} } \right)} & 0 \\ 0 & 0 & {\mu \left( {1 - \delta_{{{\text{T}}1}} - \delta_{{{\text{T}}2}} } \right)} \\ \end{array} } \right].$$

(53)

Here $\delta_{{{\text{N}}i}} = {{Z_{{{\text{N}}i}} M} \mathord{\left/ {\vphantom {{Z_{{{\text{N}}i}} M} {\left[ {1 + Z_{{{\text{N}}i}} M} \right]}}} \right. \kern-0pt} {\left[ {1 + Z_{{{\text{N}}i}} M} \right]}}$ and $\delta_{{{\text{T}}i}} = {{Z_{{{\text{T}}i}} \mu } \mathord{\left/ {\vphantom {{Z_{{{\text{T}}i}} \mu } {\left[ {1 + Z_{{{\text{T}}i}} \mu } \right]}}} \right. \kern-0pt} {\left[ {1 + Z_{{{\text{T}}i}} \mu } \right]}}$ represent the normal and tangential weaknesses of two orthogonal vertical fracture sets related to the corresponding normal and tangential fracture compliances Z _Ni and Z _Ti .

Following a similar derivation method for the case of small fracture weaknesses, the expression for linearized PP-wave reflection coefficient in such an orthorhombic medium can be expressed as

$$\begin{aligned} R_{\text{PP}} \left( {\theta ,\phi } \right) & = \frac{{\sec^{2} \theta }}{4}\frac{\Delta M}{M} - 2g\sin^{2} \theta \frac{\Delta \mu }{\mu } + \left( {\frac{1}{2} - \frac{{\sec^{2} \theta }}{4}} \right)\frac{\Delta \rho }{\rho } \\ & \quad - \frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{{{\text{N}}1}} \\ & \quad+ g\sin^{2} \theta \cos^{2} \phi \left( {1 - \tan^{2} \theta \sin^{2} \phi } \right)\Delta \delta_{{{\text{T}}1}} \\ & \quad - \frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \cos^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{{{\text{N}}2}} \\ & \quad+ g\sin^{2} \theta \sin^{2} \phi \left( {1 - \tan^{2} \theta \cos^{2} \phi } \right)\Delta \delta_{{{\text{T}}2}} . \\ \end{aligned}$$

(54)

Similarly, for such an orthorhombic medium formed by two orthogonal vertical fracture sets embedded in a VTI background (shown in Fig. 1c), neglecting the terms that contain $\varepsilon_{\text{b}} \delta_{{{\text{N}}1}}$, $\varepsilon_{\text{b}} \delta_{{{\text{N}}2}}$, $\varepsilon_{\text{b}} \delta_{{{\text{N}}1}} \delta_{{{\text{N}}2}}$, $\gamma_{\text{b}} \delta_{{{\text{N}}1}}$, $\gamma_{\text{b}} \delta_{{{\text{N}}2}}$, $\gamma_{\text{b}} \delta_{{{\text{N}}1}} \delta_{{{\text{N}}2}}$,$\delta_{\text{b}} \delta_{{{\text{N}}1}}$, $\delta_{\text{b}} \delta_{{{\text{N}}2}}$, $\delta_{\text{b}} \delta_{{{\text{N}}1}} \delta_{{{\text{N}}2}}$, $\gamma_{\text{b}} \delta_{{{\text{T}}1}}$, $\gamma_{\text{b}} \delta_{{{\text{T}}2}}$, and $\gamma_{\text{b}} \delta_{{{\text{T}}1}} \delta_{{{\text{T}}2}}$ for the case of weak anisotropy and small fracture weaknesses, an expression for the effective elastic stiffness tensor can be approximated as

$${\mathbf{C}}_{\text{OA}} = \left[ {\begin{array}{llllll} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right] \approx \left[ {\begin{array}{*{20}c} {\hat{\hat{{\mathbf{C}}}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\hat{{\mathbf{C}}}}_{2} } \\ \end{array} } \right],$$

(55)

where 0 represents the 3 × 3 zero matrix, and ${\hat{\hat{\mathbf{C}}}}_{1}$ and ${\hat{\hat{\mathbf{C}}}}_{2}$ are given by

$${\hat{\hat{\mathbf{C}}}}_{1} = \left[ {\begin{array}{*{20}l} {M\left( {1 - \delta_{{{\text{N}}1}} - \chi^{2} \delta_{{{\text{N}}2}} } \right) + 2M\varepsilon_{\text{b}} } \hfill & {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right) + 2M\varepsilon_{\text{b}} - 4\mu \gamma_{\text{b}} } \hfill & {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \chi \delta_{{{\text{N}}2}} } \right) + M\delta_{\text{b}} } \hfill \\ {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right) + 2M\varepsilon_{\text{b}} - 4\mu \gamma_{\text{b}} } \hfill & {M\left( {1 - \chi^{2} \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right) + 2M\varepsilon_{\text{b}} } \hfill & {\lambda \left( {1 - \chi \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right) + M\delta_{\text{b}} } \hfill \\ {\lambda \left( {1 - \delta_{{{\text{N}}1}} - \chi \delta_{{{\text{N}}2}} } \right) + M\delta_{\text{b}} } \hfill & {\lambda \left( {1 - \chi \delta_{{{\text{N}}1}} - \delta_{{{\text{N}}2}} } \right) + M\delta_{\text{b}} } \hfill & {M\left( {1 - \chi^{2} \delta_{{{\text{N}}1}} - \chi^{2} \delta_{{{\text{N}}2}} } \right)} \hfill \\ \end{array} } \right],$$

(56)

and

$${\hat{\hat{\mathbf{C}}}}_{2} = \left[ {\begin{array}{*{20}c} {\mu \left( {1 - \Delta \delta_{{{\text{T}}2}} } \right)} & 0 & 0 \\ 0 & {\mu \left( {1 - \delta_{{{\text{T}}1}} } \right)} & 0 \\ 0 & 0 & {\mu \left( {1 - \delta_{{{\text{T}}1}} - \delta_{{{\text{T}}2}} } \right) - 2\mu \gamma_{\text{b}} } \\ \end{array} } \right].$$

(57)

Following a similar derivation method for the case of weak anisotropy and small fracture weaknesses, the expression for linearized PP-wave reflection coefficient in such an orthorhombic medium can be expressed as

$$\begin{aligned} R_{\text{PP}} \left( {\theta ,\phi } \right) & = \frac{{\sec^{2} \theta }}{4}\frac{\Delta M}{M} - 2g\sin^{2} \theta \frac{\Delta \mu }{\mu } + \left( {\frac{1}{2} - \frac{{\sec^{2} \theta }}{4}} \right)\frac{\Delta \rho }{\rho } + \frac{{\sin^{2} \theta \tan^{2} \theta }}{2}\Delta \varepsilon_{\text{b}} + \frac{{\sin^{2} \theta }}{2}\Delta \delta_{\text{b}} \\ & \quad - \,\frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \sin^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{{{\text{N}}1}} \\ & \quad+ g\sin^{2} \theta \cos^{2} \phi \left( {1 - \tan^{2} \theta \sin^{2} \phi } \right)\Delta \delta_{{{\text{T}}1}} \\ & \quad - \,\frac{{\sec^{2} \theta }}{4}\left[ {2g\left( {\sin^{2} \theta \cos^{2} \phi + \cos^{2} \theta } \right) - 1} \right]^{2} \Delta \delta_{{{\text{N}}2}} \\ & \quad+ g\sin^{2} \theta \sin^{2} \phi \left( {1 - \tan^{2} \theta \cos^{2} \phi } \right)\Delta \delta_{{{\text{T}}2}} . \\ \end{aligned}$$

(58)