The residual set dimension of a generalized apollonian packing

Abstract

We view space-filling circle packings as subsets of the boundary of hyperbolic space subject to symmetry conditions based on a discrete group of isometries. This allows for the application of counting methods which admit rigorous upper and lower bounds on the Hausdorff dimension of the residual set of a generalized Apollonian circle packing. This dimension (which also coincides with a critical exponent) is strictly greater than that of the Apollonian packing.

1 Introduction

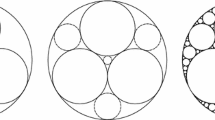
The Apollonian packing is an infinite collection of circles whose corresponding discs cover a region almost everywhere (see Fig. 1). The residual set (the space not covered) is a Cantor-like set with Hausdorff dimension satisfying

$$\begin{aligned} 1.302327< \delta _{\mathcal {A}} < 1.310876. \end{aligned}$$

(1)

The main result of this paper is that the Hausdorff dimension of a non-Apollonian packing to be introduced briefly satisfies

$$\begin{aligned} 1.327266< \delta < 1.348771. \end{aligned}$$

(2)

This is the first set of rigorous bounds on the residual set dimension for a packing other than the Apollonian packing.

The genesis of circle packings can be traced back to the works of Apollonius of Perga (ca 262-190 BC). In Apollonius’ book Tangencies, he solved the following problem: given three circles in the plane, construct the tangent circles. Variations include the cases when one or more of the given circles has radius zero (a point), or radius infinity (a line). Kasner [15] described an iterative construction process which yielded what we now refer to as the Apollonian packing; and also proved that the Apollonian packing is complete, meaning the residual set occupies zero area. The techniques and notation introduced in Kasner’s paper were furthered in later works such as [7, 26, 27].

Given a connected open region $\Omega \subseteq \mathbb {R}^2$, we will refer to a circle packing, or just packing, ${\mathcal {P}}$, as a disjoint union of open discs in $\Omega$. The residual set is ${\mathcal {R}} = \Omega - {\mathcal {P}}$. We say that a given packing is complete if $\textrm{Vol}({\mathcal {R}}) = 0$. We will call a packing bounded if $\Omega$ is a bounded subset of $\mathbb {R}^2$. Associated to a bounded circle packing is a sequence of radii $\{r_n\}_{n=1}^\infty$ which can be reordered to decrease to zero. Consider the “L-function"

$$\begin{aligned} L(t) = \sum _{n=1}^\infty r_n^t. \end{aligned}$$

(3)

Notice that $L(2) = \frac{1}{\pi } \textrm{Vol}({\mathcal {P}})$. If $t = 1$, the sequence of partial sums represents a sum of circumferences apart from a factor of $\frac{1}{2 \pi }$. For the Apollonian packing, this full series diverges [20, 26]. It is then natural to study the critical exponent

$$\begin{aligned} \begin{aligned} S = \inf \left\{ t : \sum _{n=1}^\infty r_n^t < \infty \right\} = \sup \left\{ t : \sum _{n=1}^\infty r_n^t = \infty \right\} . \end{aligned} \end{aligned}$$

(4)

For the Apollonian and generalized (or non-Apollonian) packing to be described briefly, the Hausdorff dimension of the residual set coincides with the critical exponent [16].

It has been known for some time that there are non-Euclidean aspects to packing problems [18]. David Boyd’s “separation" formula [9] (which can be traced back to Darboux [11] and Clifford [10]) is used to determine a polyspherical coordinate system for packed spheres. With the machinery of hyperbolic (or Lobackevsky) geometry, we may interpret the separation of two spheres as the minimal distance connecting two disjoint hyperbolic planes. We will use the pseudosphere or vector model of hyperbolic geometry. See [1,2,3, 12, 21] for additional introductory information.

Lorentz (or Minkowski) space ${\mathbb {R}}^{3,1}$ is defined as the set of vectors in ${\mathbb {R}}^4$ together with the Lorentz product

$$\begin{aligned} \vec {x}\circ \vec {y}= x_1y_1 + x_2y_2+x_3y_3 - x_4y_4. \end{aligned}$$

(5)

More generally, any symmetric $4 \times 4$ matrix J of signature (3, 1) will define, up to a change of basis, a Lorentz product via $\vec {x}\circ \vec {y}= \vec {x}^tJ\vec {y}$. The surface cut by the equation $\vec {x}\circ \vec {x}= -1$ is a hyperboloid of two sheets. The top or forward sheet

$$\begin{aligned} {\mathcal {H}} = \left\{ \vec {x}: \quad \vec {x}\circ \vec {x}= -1, \quad x_4>0 \right\} \end{aligned}$$

together with the metric d where

$$\begin{aligned} \vec {x}\circ \vec {y}= ||\vec {x}|| ||\vec {y}|| \cosh d(\vec {x},\vec {y}) = - \cosh d(\vec {x},\vec {y}) \end{aligned}$$

(6)

is a model of hyperbolic geometry, ${\mathbb {H}}^{3}$. The linear maps preserving the Lorentz product, called Lorentz transformations can be identified with the matrix group

$$\begin{aligned} \begin{aligned} {\mathcal {O}}_J(\mathbb {R}) = \{ T\in {M_{4 \times 4}(\mathbb {R})}: T \vec {x}\circ T \vec {y}= \vec {x}\circ \vec {y}\quad \text { for all } \vec {x}, \vec {y}\in {\mathbb {R}^4} \}, \end{aligned} \end{aligned}$$

(7)

and the group of isometries of the model ${\mathcal {H}}$ can be identified with

$$\begin{aligned} {\mathcal {O}}_J^+(\mathbb {R}) = \{ T\in {{\mathcal {O}}_J(\mathbb {R})}: T {\mathcal {H}} = {\mathcal {H}} \}. \end{aligned}$$

(8)

Reflection through the plane $\vec {n} \circ \vec {x}= 0$ is

$$\begin{aligned} R_{\vec {n}}(\vec {x}) = \vec {x} - 2 \cdot \textrm{Proj}_{\vec {n}}(\vec {x}) = \vec {x}- 2 \frac{\vec {x}\circ \vec {n}}{\vec {n}\circ \vec {n}}\vec {n}. \end{aligned}$$

(9)

A subgroup of interest is the discrete group ${\mathcal {O}}_J^+(\mathbb {Z})$ and, generally speaking, the symmetries of a packing (often reflections) may be represented by a subgroup of finite index in ${\mathcal {O}}_J^+(\mathbb {Z})$. Fix the standard basis $\{\vec {e}_1,\vec {e}_2,\vec {e}_3,\vec {e}_4 \}$. The matrix

$$\begin{aligned} J = (\vec {e}_i \circ \vec {e}_j) = -\begin{pmatrix} -1 &{} 1 &{} 1 &{} 1 \\ 1 &{} -1 &{} 1 &{} 1 \\ 1 &{} 1 &{} -1 &{} 1 \\ 1 &{} 1 &{} 1 &{} -1 \end{pmatrix} \end{aligned}$$

(10)

diagonalizes with eigenvalues $\{2,2,2,-2\}$. Thus, the bilinear form $(\vec {x},\vec {y}) \mapsto \vec {x}^t J \vec {y}= \vec {x}\circ \vec {y}$ provides a model of Lorentzian $4-$space, which is isometrically equivalent to the Poincaré upper half space model [4]. With the interpretation that $\vec {e}_j$ represents a normal vector to the plane $\vec {x}\circ \vec {e}_j = 0$, then in view of formula (6), J conveys to us that the configuration of basis vectors represents mutually tangent planes. Since planes intersect the boundary $\partial {\mathbb {H}}^3$ in Euclidean circles or planes, J defines a configuration of 4 mutually tangent circles on the boundary. It is then, in general, a non-trivial problem to identify a subgroup $\Gamma \le {\mathcal {O}}_J^+(\mathbb {Z})$ which acts on these four planes (or faces) whose orbit is a complete packing (in this case, the Apollonian packing.)

Fig. 1

An initial configuration of the four basis vectors along with some symmetries (dotted lines) as visualized on the boundary of the model of hyperbolic space induced by the circulant J above. $\vec {e}_1$ and $\vec {e}_2$ represent the two large circles while $\vec {e}_3$ and $\vec {e}_4$ the horizontal lines

2 The separation-3 (or boyd/mallows) packing

In the case of the Apollonian packing, the basis vectors $\{\vec {e}_1, \vec {e}_2,\vec {e}_3,\vec {e}_4 \}$ may be chosen to represent mutually tangent circles, which in turn implies that the separation matrix has the above circulant form. Boyd [6] showed the existence of several packings which do not possess the mutually tangent condition. One such set of examples begins if the disks represented by $\vec {e}_1$ and $\vec {e}_2$ are disjoint [5]. Let $r_1$ and $r_2$ be the radii of $\vec {e}_1$ and $\vec {e}_2$ on the boundary and s the distance between their centers. The separation formula [9]

$$\begin{aligned} \cosh d(\vec {e}_1,\vec {e}_2) = \frac{s^2-r_1^2-r_2^2}{2r_1r_2} \end{aligned}$$

(11)

implies that if $r_1 = r_2 = \frac{1}{2}$ and $s = \sqrt{2}$, then we get a separation of 3; and via (6), $- (\vec {e_1} \circ \vec {e_2}) = 3$. This leads to using the matrix

$$\begin{aligned} J = -\begin{pmatrix} -1&{}3&{}1&{}1\\ 3&{}-1&{}1&{}1\\ 1&{}1&{}-1&{}1\\ 1&{}1&{}1&{}-1\\ \end{pmatrix} \end{aligned}$$

to define a Lorentz product as well as a packing of disks with some distinct differences compared to the Apollonian packing. It is also possible to choose $-J$ above and all the results are the same modulo minus signs. The existence of this particular packing was first shown in [6]. Although Boyd provides the separation matrix and a general description of the construction process, it was likely not until [17] that pictures of this packing were published. Additional analysis was done in [14].

Fig. 2

A region of a Boyd/Mallows packing with integer curvatures

Fig. 3

A set of generating symmetries (dotted lines/circles) for the Boyd/Mallows packing which intersect tangentially

This packing may be generated by taking the image of

$$\begin{aligned} \Gamma = \left\langle R_{\vec {n}_1},R_{\vec {n}_2},R_{\vec {n}_3},R_{\vec {n}_4},R_{\vec {n}_5} \right\rangle \end{aligned}$$

acting on the faces

$$\begin{aligned} \{ \vec {e}_1,\vec {e}_2,\vec {e}_3,\vec {e}_4,\vec {e}_1+\vec {e}_2-\vec {e}_4 \} \end{aligned}$$

where $\vec {n}_1 = (-1,1,2,2)$, $\vec {n_2} = (1,-1,2,2)$, $\vec {n}_3 = (1,1,-2,0)$, $\vec {n}_4 = (3,1,2,-2)$, and $\vec {n}_5 = (1,3,2,-2)$.

Let $\{r_n\}$ be a sequence of radii of the disks packed within a bounded region of a Boyd/Mallows or separation-3 packing. We wish to bound the new critical exponent $S_{\text {Boyd/Mallows}} = \delta _{\text {Boyd/Mallows}} = \delta$ defined by (4), which coincides with the Hausdorff dimension of the residual set [24]. Let $\vec {k}= (a,b,c,d) = (\vec {e}_1 \circ \vec {E}, \vec {e}_2 \circ \vec {E}, \vec {e}_3 \circ \vec {E}, \vec {e}_4 \circ \vec {E})$, with $\vec {E}$ the point at infinity. Writing $\vec {k}^t J^{-1} \vec {k}= 0$ gives an analogue of the Descarte’s quadruple relationship

$$\begin{aligned} -\frac{1}{8}(a^2+b^2)-\frac{1}{2}(c^2+d^2)+\frac{1}{4}ab+\frac{1}{2}(a+b)(c+d)= 0. \end{aligned}$$

(12)

Define the quadratic form

$$\begin{aligned} K(\vec {k}) = \vec {k}^t J^{-1}\vec {k}\end{aligned}$$

and define $c_n$ as being the smaller of the two solutions to $K(c_n,c_{n-1},a,b) = 0$. The sequence $\{c_n\}$ is the set of curvatures of “center disks" down the necklace opposite the triangle from the bounding circle C of curvature $c=c_0$ in Fig. 4. By symmetry, $\{ b_n \}$ and $\{a_n\}$ are the curvatures of the center tails of circles in necklaces opposite bounding circles B and A, respectively. To solve for $a_1$, we know that the the disks corresponding to a and $a_1$ are disjoint, so solving $K(a_1,a,b,c) = 0$ results in $a_1 = a+2b+2c\pm \sqrt{8}\sqrt{ab+ac+bc}$. Similarly, $b_1 = 2a+b+2c \pm \sqrt{8}\sqrt{ab+ac+bc}$, and also, $c_1 = 2a+2b+c\pm \sqrt{8}\sqrt{ab+ac+bc}$.

Lemma 1

Let A, B, and C be three pairwise externally tangent circles with curvatures a, b,  and $c = c_0$. Let $\{C_n \}$ be the sequence of disks in which $C_1$ is the smaller of the disks tangent to A and B, and at a separation of 3 from C. Let $C_n$ be the smaller of the disks tangent to A and B at a separation of 3 from $C_{n-1}$. Then, for all $n\in {{\mathbb {N}}}$,

$$\begin{aligned} c_n = c+2n^2(a+b)+n\sqrt{8}d \end{aligned}$$

(13)

where $d = \sqrt{ab+ac+bc}$.

Proof

: Let $\{ \vec {e}_1,\vec {e}_2,\vec {e}_3,\vec {e}_4 \}$ be the standard basis with the above separation matrix and let

$$\begin{aligned} \vec {k}&= (\text {curv}(\vec {e}_1), \text {curv}(\vec {e}_2),\text {curv}(\vec {e}_3),\text {curv}(\vec {e}_4)) \\&= (\vec {e}_1 \circ \vec {E}, \vec {e}_2 \circ \vec {E}, \vec {e}_3 \circ \vec {E}, \vec {e}_4 \circ \vec {E}) = (c,c_1,a,b) \end{aligned}$$

(curvature is Lorentz product with $\vec {E}$ [4].) Consider the reflections $R_1 = R_{(1,-1,2,2)}$ and $R_2 = R_{(1,-1,0,0)}$. Then, $R_2R_1 = P$ is a parabolic translation moving $\vec {e}_1$ to $\vec {e}_2$ and

$$\begin{aligned} P^n = \begin{pmatrix} 1-n&{}-n&{}0&{}0\\ n&{}n+1&{}0&{}0\\ 2n(n-1)&{}2n(n+1)&{}1&{}0\\ 2n(n-1)&{}2n(n+1)&{}0&{}1\\ \end{pmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} c_n&= \text {curv}(P^n\vec {e}_1) = \text {curv}(1-n,n,2n(n-1),2n(n-1)) \\&= (1-n) (\vec {e}_1 \circ \vec {E}) + n(\vec {e}_2 \circ \vec {E}) + 2n(n-1)((\vec {e}_3 + \vec {e}_4) \circ \vec {E}) \\&= (1-n)c + nc_1+2n(n-1)(a+b). \end{aligned}$$

Note that, based on Fig. 4 which uses curvatures a, b, c and $c_1$, the point at infinity is not $\vec {e}_3 + \vec {e}_4$. Using $c_1 = 2a+2b+c+\sqrt{8}d$ gives the desired result. $\square$

For example, using T(0, 1, 2) pictured above, we have $c_1 = 8$, $c_2 = 18$, $c_3 = 32$ etc. Since the necklace opposite the curvilinear triangle from either A, B or C has three “tails", we need formulas for the curvatures of the circles in the “left" and “right" tails.

Lemma 2

Let A, B, and C be three pairwise externally tangent circles with curvatures a, b,  and c. Let $\{C_{n,r} \}$ be the sequence of circles in which $C_{1,r}$ is the smaller of the circles tangent to $C_1$ and $C_2$, and at a separation of 3 from A. Let $C_{n,l}$ be the smaller of the circles tangent to $C_{n+1}$ and $C_n$ at a separation of 3 from B. Then, for all $n\in {{\mathbb {N}}}$,

$$\begin{aligned} c_{n,r} = a + 2b+2c+4(n^2+n)(a+b)+(2n+1)\sqrt{8}d \end{aligned}$$

(14)

and

$$\begin{aligned} c_{n,l} = 2a+b+2c+4(n^2+n)(a+b)+(2n+1)\sqrt{8}d. \end{aligned}$$

(15)

Proof

: As before, let $\vec {k}= (\vec {e}_1 \circ \vec {E}, \vec {e}_2 \circ \vec {E}, \vec {e}_3 \circ \vec {E}, \vec {e}_4 \circ \vec {E}) = (c,c_1,a,b)$. Consider the reflection $R_{\vec {n}_3} = R_{(1,1,-2,0)}$. Then, $R_{\vec {n}_3}(\vec {e}_3) = (1,1,-1,0)$ and

$$\begin{aligned} P^n(1,1,-1,0) = (1-2n,1+2n,4n^2-1,4n^2) \end{aligned}$$

implying

$$\begin{aligned} c_{n,r} = (1-2n)c + (1+2n)c_1+(4n^2-1)a+4n^2b. \end{aligned}$$

Substituting in $c_1 = 2a+2b+c+\sqrt{8}d$ gives the desired result for $c_{n,r}$. Interchanging a and b gives $c_{n,l}$. $\square$

Let T(a, b, c) be the curvilinear (or triply asymptotic) triangle bounded by three mutually externally tangent circles A, B, C of curvatures a, b, c, with $0 \le a \le b \le c$, and $b>0$. The condition $b>0$ guarantees that T(a, b, c) has finite area even if $a = 0$, in which case A is a line. For $t>0$, define

$$\begin{aligned} M(a,b,c;t) = \sum _{n=1}^\infty r_n^t \end{aligned}$$

(16)

where the $r_n$ are the radii of the disks in the Boyd/Mallows packing within T(a, b, c) and the equality holds in the extended sense. To save writing space, we may suppress the variable t, writing M(a, b, c) . First note that based on the symmetries $\Gamma$, M is symmetric in the three variables a, b, c.

Lemma 3

M(a, b, c; t) is decreasing in each variable a, b, c. M is strictly decreasing if $t > \delta$, and $M(a,b,c;t)= + \infty$ if $t < \delta$, where $\delta =S$ is the critical exponent.

Note that, apriori, $\delta$ may depend on (a, b, c) . We will see shortly that this is not the case.

Proof

: If $t < \delta$, equality holds trivially in the extended sense $(\infty = \infty )$. Next let $t > \delta$ and $\epsilon > 0$. If we replace $c \mapsto c+ \epsilon$ then by Lemmas 1 and 2, $a_n,a_{n,l},a_{n,r},b_n,b_{n,l},b_{n,r},c_n,c_{n,l},c_{n,r}$ strictly increase. We now expand M(a, b, c) by writing M(a, b, c) as a sum of 3 necklaces (each with 3 bands of circles), four central triangles, and 18 sub-triangle bands (6 from each necklace):

$$\begin{aligned} M(a,b,c)&= \sum _{n=1}^\infty \left( a_n^{-t} + a_{n,l}^{-t} + a_{n,r}^{-t} + b_n^{-t} + b_{n,l}^{-t} + b_{n,r}^{-t} + c_n^{-t} + c_{n,l}^{-t} + c_{n,r}^{-t} \right) \nonumber \\&\quad + M(a,c_1,b_1)+M(b,c_1,a_1)+M(c,b_1,a_1)+M(c_1,b_1,a_1) \nonumber \\&\quad + \sum _{n = 1}^\infty ( M(b,a_n,a_{n,l}) + M(b,a_{n+1},a_{n,l}) + M(a_n,a_{n,l},a_{n,r}) \nonumber \\&\quad + M(a_{n+1},a_{n,l},a_{n,r}) + M(c,a_n,a_{n,r})+M(c,a_{n+1},a_{n,r}) \nonumber \\&\quad + M(c,b_n,b_{n,l})+M(c,b_{n+1},b_{n,l})+M(b_n,b_{n,r},b_{n,l}) \nonumber \\&\quad +M(b_{n+1},b_{n,r},b_{n,l})+ M(a,b_n,b_{n,r})+M(a,b_{n+1},b_{n,r}) \nonumber \\&\quad + M(a,c_n,c_{n,l})+M(a,c_{n+1},c_{n,l})+ M(c_n,c_{n,l},c_{n,r}) \nonumber \\&\quad +M(c_{n+1},c_{n,l},c_{n,r})+ M(b,c_n,c_{n,r})+M(b,c_{n+1},c_{n,r})) \end{aligned}$$

(17)

(see Fig. 4). Since $t>\delta$, $M(a,b,c+\epsilon ;t) < M(a,b,c;t)$. Since M is symmetric in each of a, b, c, it follows that M is strictly decreasing in each variable. $\square$

Note that since $0 \le a \le b \le c$ and $b>0$, then $c_1 \le b_1 \le a_1$, $a_{n+1} \le a_{n,l} \le a_{n,r}$, $b_{n+1} \le b_{n,r} \le b_{n,l}$, and $c_{n+1} \le c_{n,l} \le c_{n,r}$, the above sums with $M(\cdot ,\cdot ,\cdot )$ in (17) are written in increasing curvature.

Fig. 4

The $0^{\text {th}}$ iteration necklace of the Boyd/Mallows packing

If T(a, b, c) is dilated by a factor of $\frac{1}{\alpha }$, where $\alpha > 0$, then the radii $r_n$ are replaced by $\frac{1}{\alpha } r_n$ and a, b, c are scaled by $\alpha$. So, M is homogenous of degree $-t$:

$$\begin{aligned} M(\alpha a, \alpha b, \alpha c;t) = \alpha ^{-t} M(a,b,c;t). \end{aligned}$$

(18)

Remark 1

The Boyd/Mallows packing in T(0, 1, 1) is not an integer packing since, for instance $c_n = 1+2n^2+\sqrt{8}n$. The packing in Fig. 2 contains triangles T(0, 1, 2) but not T(0, 1, 1).

Lemma 4

Let M be defined by (16) and $0 \le a \le b \le c$ with $b>0$. Then,

$$\begin{aligned}{} & {} (a+c)^{-t}M(0,1,1;t) \le \left( a+\frac{b+c}{2} \right) ^{-t} M(0,1,1;t) \le M(a,b,c;t), \nonumber \\{} & {} \quad M(a,b,c;t) \le \frac{1}{2}((a+b)^{-t}+c^{-t})M(0,1,1;t) \le b^{-t}M(0,1,1;t) \end{aligned}$$

(19)

with the inequality holding in the extended sense when $t < S = \delta$.

Sketch of proof: The outermost inequalities are immediate as $(a+c)^{-t} \le (a+(b+c)/2)^{-t}$ and $\frac{1}{2}((a+b)^{-t}+c^{-t}) \le b^{-t}$. Using Lemmas 1 and 2 and (17), a curvature occurring in T(a, b, c) may be written as

$$\begin{aligned} \textrm{curv} = w_1 a + w_2 b + w_3 c + w_4 d \end{aligned}$$

with $w_j > 0$. This, along with M being homogenous, decreasing in each variable, and symmetric in each variable, we may repeat the arguments in [8] and the claim follows.

Lemma 4 shows that $M(a,b,c;t) < \infty$ if and only if $M(0,1,1;t) < \infty$, allowing us to analyze the Boyd/Mallows packing within T(0, 1, 1) . Moreover, $\delta$ is independent of (a, b, c).

To help us understand the forthcoming definitions, we will first exhibit one way to craft a self-similar inequality for M. Based on (17), define

$$\begin{aligned} h_0(t) = \sum _{n=1}^\infty \left( a_n^{-t} + a_{n,l}^{-t} + a_{n,r}^{-t} + b_n^{-t} + b_{n,l}^{-t} + b_{n,r}^{-t} + c_n^{-t} + c_{n,l}^{-t} + c_{n,r}^{-t} \right) . \end{aligned}$$

Applying the more coarse but simpler inequality $M(a,b,c;t) \le b^{-t}M(0,1,1;t)$ to (17),

$$\begin{aligned}&M(a,b,c) \le h_0(t) + 2M(0,1,1)\Bigl ( c_1^{-t}+b_1^{-t} \nonumber \\&\quad + \sum _{n=1}^\infty (a_n^{-t}+a_{n+1}^{-t}+a_{n,l}^{-t} + b_n^{-t}+b_{n+1}^{-t} +b_{n,r}^{-t} + c_n^{-t}+c_{n+1}^{-t}+c_{n,l}^{-t})\Bigl ). \end{aligned}$$

(20)

If we write

$$\begin{aligned} {\tilde{f}}_0(t)&= 2(c_1^{-t}+b_1^{-t} \\&\quad + \sum _{n=1}^\infty (a_n^{-t}+a_{n+1}^{-t}+a_{n,l}^{-t} + b_n^{-t}+b_{n+1}^{-t}+b_{n,r}^{-t} + c_n^{-t}+c_{n+1}^{-t}+c_{n,l}^{-t})) \end{aligned}$$

and let $(a,b,c) = (0,1,1)$, then

$$\begin{aligned} M(0,1,1;t) \le h_0(t) + M(0,1,1;t){\tilde{f}}_0(t). \end{aligned}$$

(21)

If ${\tilde{\mu }}_0$ satisfies ${\tilde{f}}_0({\tilde{\mu }}_0) = 1$, then Theorem 1 will show that ${\tilde{\mu }}_0 > S$. Similarly, applying $(a+c)^{-t}M(0,1,1;t) \le M(a,b,c;t)$ gives

$$\begin{aligned} M(a,b,c)&\ge h_0(t) \nonumber \\&\quad + M(0,1,1)\big ((a+b_1)^{-t}+(b+a_1)^{-t}+(c+a_1)^{-t}+(c_1+a_1)^{-t} \nonumber \\&\quad + \sum _{n=1}^\infty (2(b+a_{n,l})^{-t}+ 2(c+a_{n,r})^{-t} + (a_n+a_{n,r})^{-t} + (a_{n+1}+a_{n,r})^{-t} \nonumber \\&\quad + 2(c+b_{n,l})^{-t} + 2(a+b_{n,r})^{-t} + (b_n+b_{n,l})^{-t} + (b_{n+1}+b_{n,l})^{-t} \nonumber \\&\quad + 2(a+c_{n,l})^{-t}+2(b+c_{n,r})^{-t}+(c_n+c_{n,r})^{-t} + (c_{n+1}+c_{n,r})^{-t}) \big ). \end{aligned}$$

(22)

Letting ${\tilde{g}}_0(t)$ be the function to the right of M(0, 1, 1) above with $(a,b,c) = (0,1,1)$, we can write

$$\begin{aligned} M(0,1,1) \ge h_0(t) + M(0,1,1){\tilde{g}}_0(t). \end{aligned}$$

Theorem 1 will also show that if ${\tilde{g}}_0({\tilde{\lambda }}_0) = 1$, then ${\tilde{\lambda }}_0 < S$.

We now define functions similar to ${\tilde{f}}_0,{\tilde{g}}_0$, and $h_0$, but based on the tighter inside inequalities of (19). First define a set-valued function $\tau$ which collects the triples of curvatures (x, y, z) when T(x, y, z) occurs as a sub-triangle per Fig. 4. Define

$$\begin{aligned} \tau (a,b,c)&= \{ (a,c_1,b_1),(b,c_1,a_1),(c,b_1,a_1),(c_1,b_1,a_1) \} \cup \nonumber \\&\quad \bigcup _{n=1}^\infty \{ (b,a_n,a_{n,l}) , (b,a_{n+1},a_{n,l}) , (a_n,a_{n,l},a_{n,r}), \nonumber \\&\quad (a_{n+1},a_{n,l},a_{n,r}), (c,a_n,a_{n,r}), (c,a_{n+1},a_{n,r}), \nonumber \\&\quad (c,b_n,b_{n,l}),(c,b_{n+1},b_{n,l}),(b_n,b_{n,r},b_{n,l}), \nonumber \\&\quad (b_{n+1},b_{n,r},b_{n,l}),(a,b_n,b_{n,r}),(a,b_{n+1},b_{n,r}), \nonumber \\&\quad (a,c_n,c_{n,l}),(a,c_{n+1},c_{n,l}),(c_n,c_{n,l},c_{n,r}), \nonumber \\&\quad (c_{n+1},c_{n,l},c_{n,r}),(b,c_n,c_{n,r}),(b,c_{n+1},c_{n,r}) \}. \end{aligned}$$

(23)

Define

$$\begin{aligned} {\tilde{f}}_0(\kappa ;a,b,c;t)&= \sum _{(x,y,z) \in {\tau (a,b,c)}} y^{-t}, \end{aligned}$$

(24)

$$\begin{aligned} {\tilde{g}}_0(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {\tau (a,b,c)}} (x+z)^{-t}, \end{aligned}$$

(25)

$$\begin{aligned} f_0(\kappa ;a,b,c;t)&= \sum _{(x,y,z) \in {\tau (a,b,c)}} \frac{1}{2}((x+y)^{-t}+z^{-t}), \end{aligned}$$

(26)

$$\begin{aligned} g_0(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {\tau (a,b,c)}} \left( x+\frac{y+z}{2}\right) ^{-t}, \end{aligned}$$

(27)

$$\begin{aligned} h_0(\kappa ;a,b,c;t)&= \sum _{n=1}^\infty \left( a_n^{-t} + a_{n,l}^{-t} + a_{n,r}^{-t} + b_n^{-t} + b_{n,l}^{-t} + b_{n,r}^{-t} + c_n^{-t} + c_{n,l}^{-t} + c_{n,r}^{-t} \right) . \end{aligned}$$

(28)

For $\kappa \ge 0$ and a set l consisting of curvature triples, define

$$\begin{aligned} {\mathscr {S}}(\kappa ;l) = l \cup \bigcup _{\begin{array}{c} (x,y,z)\in {l}\\ y< \kappa \end{array}} \tau (x,y,z) - \lbrace (p,q,r)\in {l}: q < \kappa \rbrace \end{aligned}$$

(29)

and ${\mathscr {S}}^0( \kappa ;l) = l$. Define iterates of ${\mathscr {S}}$ as

$$\begin{aligned} {\mathscr {S}}^2(\kappa ;l)&= {\mathscr {S}}(\kappa ; {\mathscr {S}}(\kappa ;l)) \\ {\mathscr {S}}^3(\kappa ;l)&= {\mathscr {S}}(\kappa ; {\mathscr {S}}(\kappa ;{\mathscr {S}}(\kappa ;l))) \end{aligned}$$

etc. For $m \ge 1$, define

$$\begin{aligned} {\tilde{f}}_m(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}} y^{-t}, \end{aligned}$$

(30)

$$\begin{aligned} {\tilde{g}}_m(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}} (x+z)^{-t}, \end{aligned}$$

(31)

$$\begin{aligned} f_m(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}} \frac{1}{2}((x+y)^{-t}+z^{-t}) \end{aligned}$$

(32)

$$\begin{aligned} g_m(\kappa ;a,b,c;t)&= \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}} \left( x+\frac{y+z}{2}\right) ^{-t} \end{aligned}$$

(33)

$$\begin{aligned} h_m(\kappa ;a,b,c;t)&= h_{m-1}(\kappa ;a,b,c;t) \nonumber \\&\quad + \sum _{\begin{array}{c} (x,y,z)\in {{\mathscr {S}}^{m-1}(\kappa ;\tau (a,b,c))}\\ y < \kappa \end{array}} h_0(\kappa ;x,y,z;t) \end{aligned}$$

(34)

For fixed $\kappa ,a,b,c$, and m, the functions $f_m,g_m,$ and $h_m$ above are defined when $t > \frac{1}{2}$. At $t = \frac{1}{2}$, they are harmonic-type series since $c_n \asymp n^2$. If $c_1 > 1$, they are positive, continuous, strictly monotone decreasing functions of t, tending to $\infty$ as $t \rightarrow \frac{1}{2}^+$ and 0 as $t \rightarrow \infty$. Based on the above definitions of $f_m,g_m,$ and $h_m$, if $\kappa$ is smaller than all sub-triangle curvatures, we expect that the iteration should terminate; in other words, $f_m=f_{m+1}= \cdots$. The following lemma establishes that the breaking of necklace triangles into sub-triangles occurs with curvatures which grow at an exponential rate (Fig. 5).

Fig. 5

A first iteration of the necklace packing for any $c_1 < \kappa \le b_1$. The green/gray disks are added because those four sub-triangles have a middle curvature smaller than $\kappa$

Lemma 5

If $\kappa \le 5^{n+1}b$, then

$$\begin{aligned} {\mathscr {S}}^{n+1}(\kappa ;\tau (a,b,c)) = {\mathscr {S}}^n(\kappa ;\tau (a,b,c)) \quad \text { for all } n \ge 0. \end{aligned}$$

Proof

: On any triangle triple (a, b, c) with $0 \le a \le b \le c$ and $b>0$, we have

$$\begin{aligned} \min \{ y: (x,y,z)\in {\tau (a,b,c)} \} = c_1 \end{aligned}$$

and

$$\begin{aligned} c_1 = c+2a+2b+\sqrt{8}\sqrt{ab+ac+bc} \ge 3b + \sqrt{8}\sqrt{b^2} > 5b. \end{aligned}$$

So, if $\kappa \le 5b < c_1$, then by (29),

$$\begin{aligned} {\mathscr {S}}(\kappa ;\tau (a,b,c)) = {\mathscr {S}}^0(\kappa ;\tau (a,b,c)) = \tau (a,b,c). \end{aligned}$$

If true for $1,...,n-1$, then by choosing $\kappa \le 5^{n+1}b$, the union and set exclusion on the right hand side of (29) for ${\mathscr {S}}^{n+1}$ will be empty, and the claim follows. $\square$

Corollary 1

Fix $n \ge 0$ and let $m \ge 0$. If $\kappa \le 5^{n+1}b$ then

$$\begin{aligned} f_m(\kappa ;a,b,c;t)&= f_{n}(\kappa ;a,b,c;t) \quad (m \ge n) \\ g_m(\kappa ;a,b,c;t)&= g_{n}(\kappa ;a,b,c;t) \quad (m \ge n) \\ h_m(\kappa ;a,b,c;t)&= h_{n}(\kappa ;a,b,c;t) \quad (m \ge n). \end{aligned}$$

When $(a,b,c) = (0,1,1)$, $c_1 = 3+\sqrt{8}$. Let $\beta _0 = 3+\sqrt{8}$. Iterating $c_1 = 2a+2b+c+\sqrt{8}\sqrt{ab+ac+bc}$ by replacing $(a,b,c) \rightarrow (0,\beta _0^m,\beta _0^m)$,

$$\begin{aligned} \min \{y:(x,y,z) \in {{\mathscr {S}}^m(\infty ;\tau (0,1,1))} \}&= 2(0)+2\beta _0^m+\beta _0^m+\sqrt{8}\sqrt{\beta _0^{2m}} \\&= (3+\sqrt{8})\beta _0^m = \beta _0^{m+1}. \end{aligned}$$

The $\kappa$-cutoff values in Table 1 are $\lfloor \beta _m \rfloor$ where $\beta _m = \beta _0^{m+1}$.

Theorem 1

Let S be the critical exponent of the Boyd/Mallows packing. Let $\kappa > 0$, $m \ge 0$, and $t > \frac{1}{2}$. Let $\mu _m(\kappa )$ and $\lambda _m(\kappa )$ satisfy $f_m(\kappa ;0,1,1;\mu _m(\kappa )) = 1$ and $g_m(\kappa ;0,1,1;\lambda _m(\kappa )) = 1$. Then,

$$\begin{aligned} \lambda _m(\kappa ) \le S \le \mu _m(\kappa ). \end{aligned}$$

(35)

Moreover, if $1 < \kappa \le (3+2 \sqrt{2})^{m+1}$, then

$$\begin{aligned} 0< \mu _m(\kappa ) - \lambda _m(\kappa ) < \frac{2.3}{\log \kappa }. \end{aligned}$$

(36)

Proof

: With $(a,b,c) = (0,1,1)$, $c_1 = 3+2\sqrt{2} > 1$, so $f_m$ and $g_m$ are strictly decreasing, continuous functions. Thus, $\mu _m(\kappa )$ and $\lambda _m(\kappa )$ are unique. Define

$$\begin{aligned} M_j(a,b,c;t) = \sum _{q \le c_1^j} q^{-t}, \end{aligned}$$

(37)

where the sum is over curvatures q occurring in T(a, b, c). We will first show that

$$\begin{aligned} M_j(0,1,1;t) \le h_m(\kappa ;0,1,1;t) + M_j(0,1,1;t)f_m(\kappa ;0,1,1;t). \end{aligned}$$

(38)

Let $m = 0$, fix $\kappa > 0$, and $t > \frac{1}{2}$. Using (19) applied to $M_j$,

$$\begin{aligned} M_j(a,b,c;t)&< h_0(\kappa ;a,b,c;t) + \sum _{\begin{array}{c} (x,y,z)\in {\tau (a,b,c)}\\ \end{array}} M_j(x,y,z;t) \nonumber \\&\le h_0(\kappa ;a,b,c;t) + \sum _{(x,y,z)\in {\tau (a,b,c)}} \frac{1}{2}((x+y)^{-t}+z^{-t})M_j(0,1,1;t) \nonumber \\&= h_0(\kappa ;a,b,c;t) + f_0(\kappa ;a,b,c;t)M_j(0,1,1;t). \end{aligned}$$

(39)

If also true for $1,...,m-1$, then using the definitions of $f_m$ and $h_m$,

$$\begin{aligned}&M_j(a,b,c;t) \quad \quad \nonumber \\< h_0(\kappa ;a,b,c;t)&+ \sum _{\begin{array}{c} (x,y,z)\in {\tau (a,b,c)}\\ y< \kappa \end{array}} M_j(x,y,z;t) \nonumber \\&\qquad + \sum _{\begin{array}{c} (x,y,z)\in {\tau (a,b,c)}\\ \kappa \le y \end{array}} M_j(x,y,z;t) \nonumber \\< h_0(\kappa ;a,b,c;t)&\nonumber \\ + \sum _{\begin{array}{c} (x,y,z)\in {\tau (a,b,c)}\\ y< \kappa \end{array}}&\quad (h_{m-1}(\kappa ;x,y,z;t)+f_{m-1}(\kappa ;x,y,z;t)M_j(0,1,1;t)) \nonumber \\ + \sum _{\begin{array}{c} (x,y,z)\in {\tau (a,b,c)}\\ \kappa \le y \end{array}}&\frac{1}{2}((x+y)^{-t}+z^{-t}) M_j(0,1,1;t) \nonumber \\ < h_m(\kappa ;a,b,c;t&) + M_j(0,1,1;t)f_m(\kappa ;a,b,c;t). \end{aligned}$$

(40)

This establishes (38) by induction. Now let $t>\mu _m(\kappa )$, making $f_m(\kappa ;0,1,1;t) < 1$. Then,

$$\begin{aligned} M_j(0,1,1;t) < \frac{h_m(\kappa ;0,1,1;t)}{1-f_m(\kappa ;0,1,1;t)}. \end{aligned}$$

(41)

Since $M_j \nearrow M$, letting $j \rightarrow \infty$, shows that when $t > \mu _m(\kappa )$, M(0, 1, 1; t) is bounded above by the finite quantity $h_m(\kappa ;0,1,1;t)/(1-f_m(\kappa ;0,1,1;t))$. Thus $\mu _m(\kappa ) \ge S$.

Using (17) and (19), we may write M(a, b, c; t) as a sum of $h_m$ “tails" and remaining sub-triangle packings:

$$\begin{aligned} M(a,b,c;t)&= h_m(\kappa ;a,b,c;t) + \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ; \tau (a,b,c))}} M(x,y,z;t) \\&\ge h_m(\kappa ;a,b,c;t) + \sum _{(x,y,z)\in {{\mathscr {S}}^m(\kappa ; \tau (a,b,c))}} \left( x+\frac{y+z}{2}\right) ^{-t} M(0,1,1;t) \\&= h_m(\kappa ;a,b,c;t) + g_m(\kappa ;a,b,c;t)M(0,1,1;t). \end{aligned}$$

Letting $(a,b,c) = (0,1,1)$ establishes

$$\begin{aligned} \frac{h_m(\kappa ;0,1,1;t)}{1-g_m(\kappa ;0,1,1;t)} \le M(0,1,1;t). \end{aligned}$$

If $t > \lambda _m(\kappa )$ then $g_m < 1$ since $g_m$ is decreasing. Since

$$\begin{aligned} \lim _{t \rightarrow \lambda _m(\kappa )^+}g_m(\kappa ;0,1,1;t) = 1 \end{aligned}$$

and

$$\begin{aligned} \lim _{t \rightarrow \lambda _m(\kappa )^+} \frac{h_m(\kappa ;0,1,1;t)}{1-g_m(\kappa ;0,1,1;t)} \le \lim _{t \rightarrow \lambda _m(\kappa )^+} M(0,1,1;t) = M(0,1,1;\lambda _m(\kappa )) \end{aligned}$$

then $M(0,1,1;\lambda _m(\kappa )) = \infty$, which shows that $\lambda _m(\kappa ) \le S$.

Next, we show that for fixed $\kappa ,a,b,c,t$,

$$\begin{aligned} g_m \ge {\tilde{g}}_m \ge 5.5^{-t}{\tilde{f}}_m \ge 5.5^{-t}f_m. \end{aligned}$$

(42)

The outermost inequalities follow from (19). For the inside inequality, with $m = 0$, we compare $x+z$ to y for $(x,y,z) \in {\tau (a,b,c)}$. For instance, if $(x,y,z) = (c,a_n,a_{n,r})$ (the 9th necklace term in $\tau (a,b,c)$) then

$$\begin{aligned} c+a_{n,r}&= 2a+b(1+4n+4n^2)+c(3+4n+4n^2)+\sqrt{8}d(2n+1) \\&\le 5.5( a+b(2n^2) + c(2n^2) + \sqrt{8}dn) = 5.5a_n. \end{aligned}$$

The 11th and 21st terms in $\tau (a,b,c)$ can also be compared with the constant 5.5, while the other terms can be compared with constants (also independent of $\kappa$ and m) ranging between 2 and 5. Thus, $(x+z)^{-t} \ge 5.5^{-t}y^{-t}$ for all $(x,y,z)\in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}$, establishing (42).

Now let $1 < \kappa \le \beta _m$. By Corollary 1, $\lambda _m(\kappa ) = \lambda _{m+1}(\kappa ) =...$ and $\mu _m(\kappa ) = \mu _{m+1}(\kappa ) =...$ and $y \ge \kappa$ for all $(x,y,z) \in {{\mathscr {S}}^m(\kappa ;\tau (a,b,c))}$. Let $\epsilon > 0$ be given. Since $\frac{\kappa }{\beta _m} \le 1$, if q is a curvature occurring in the expression of ${\tilde{f}}_m(\kappa ;0,1,1;t)$, then $q \ge \beta _m$, so $\frac{\kappa }{q} \le 1$. Thus, $\left( \frac{\kappa }{q} \right) ^\epsilon \le 1^\epsilon = 1$ and so

$$\begin{aligned} {\tilde{f}}_m(\kappa ;0,1,1;t) = \sum _{n=1}^\infty q_n^{-t} \ge \sum _{n = 1}^\infty \kappa ^\epsilon q_n^{-t-\epsilon } = \kappa ^\epsilon {\tilde{f}}_m(\kappa ;0,1,1;t+\epsilon ). \end{aligned}$$

(43)

Numerical computation (see next section) showed that $\mu _5(39201) = 1.348771$, so $\lambda _m(\kappa ) \le 1.348771$ for all $\kappa$ and m. Thus, $5.5^{-\lambda _m(\kappa )} \ge 5.5^{-1.348771} = 0.100327$. Using (42), (43), setting ${\mathcal {C}} = 0.100327$, $\epsilon = \mu _m(\kappa )-\lambda _m(\kappa )$, and $\kappa >1$ to ensure $\log \kappa > 0$,

$$\begin{aligned} 1&= g_m(\kappa ;0,1,1;\lambda _m{(\kappa )}) \nonumber \\&\ge 5.5^{- \lambda _m(\kappa )}{\tilde{f}}_m(\kappa ;0,1,1;\lambda _m(\kappa )) \nonumber \\&\ge {\mathcal {C}} \kappa ^\epsilon {\tilde{f}}_m(\kappa ;0,1,1; \lambda _m(\kappa ) + \epsilon ) \nonumber \\&\ge {\mathcal {C}} \kappa ^{\epsilon } f_{m}(\kappa ;0,1,1; \lambda _m(\kappa )+\epsilon ) \nonumber \\&= {\mathcal {C}} \kappa ^{{\mu _m(\kappa ) - \lambda _m(\kappa )}} f_m(\kappa ;0,1,1; \mu _m(\kappa )) \nonumber \\&= {\mathcal {C}} \kappa ^{{\mu _m(\kappa ) - \lambda _m(\kappa )}}. \end{aligned}$$

(44)

This proves (36) and concludes the proof of the theorem. $\square$

Remark 2

The above condition $1 < \kappa \le \beta _m$ is necessary in establishing the multiplicative inequality (43). For example, if $m=0$ and $\kappa = 6 > \beta _0 = 3 + \sqrt{8}$, then $\tau (0,1,1)$ includes $(0,3+\sqrt{8},3+\sqrt{8})$ so the property $\kappa / q \le 1$ fails. If $0 < \kappa \le 1$, then $\log \kappa \le 0$ and the inequalities leading to (44) flip and give no useful information. If $\kappa = 1$, (43) degrades to the (already known) monotonic decreasing property of ${\tilde{f}}_m$. $0 < \kappa \le 1$ could be treated as a separate case, but in our computations we seek values of $\kappa > 10^4$.

Remark 3

It is likely possible to prove (42) without ${\tilde{f}}_m$ and ${\tilde{g}}_m$. For comparison, ${\tilde{\mu }}_m$ and ${\tilde{\lambda }}_m$, are included in Table 1.

3 Numerical results

The functions $\tau , {\mathscr {S}}, f_m$, and $g_m$ were incorporated into a computer program written using Sage mathematics software [23]. All computations were run on personal computers with 8 Gigabytes of random access memory and a single central processor unit. Table 1 provides the computed upper and lower bounds. The convergence rate with both sets of inequalities appears to be roughly $\frac{1}{\log \kappa }$. The functions $\lambda _{m}$ and $\mu _{m}$ provide closer starting values ($\lambda _{0}(\kappa )$ and $\mu _{0}(\kappa )$) to S as compared to ${\tilde{\lambda }}_m$ and ${\tilde{\mu }}_m$. As suggested by Theorem 1, the approximate slope of $f_m,g_m,{\tilde{f}}_m,$ and ${\tilde{g}}_{m}$ is $-\log \kappa$. A numerical root-finding algorithm incorporating a Newton type map $x_0 \mapsto -\frac{A}{\log \kappa }(1-f_0(\kappa ;0,1,1,x_0)) + x_0$ was employed using a constant approximate slope. The value of $A \approx 1.5$ as well as the initial guess for $x_0$ can be adjusted to offer faster or slower convergence to the root of $f_m-1$, $g_m-1$, ${\tilde{f}}_{m}-1$, or ${\tilde{g}}_{m}-1$. Iterations of the Newton type map were done until $|f_m(\kappa ;0,1,1;x_n) - 1| < 10^{-7}$, $x_n = x_0,x_1,x_2,...$ and similar for $g_m$, ${\tilde{f}}_{m}$, ${\tilde{g}}_{m}$.

Table 1 Table of upper and lower bounds of $S = \delta$ for various $\kappa$ and m of the Boyd/Mallows packing

The $\kappa$ values of 33, 197, 1153, 6725, and 39201 were rounded down from the cutoff values of $\beta _1 = \beta _0^2 \approx 33.97$, $\beta _2 = \beta _0^3 \approx 197.99$ etc., where $\beta _0 = 3 + 2 \sqrt{2} \approx 5.82$. The other values of 16 and 100 were inserted to illustrate that further refinement can happen even with the same number of iterations. The fact that $\lambda _{1}(16) = 1.316674> 1.310876 > \delta _{{\mathcal {A}}}$ proves that the critical exponent of the Boyd/Mallows packing is strictly greater than the critical exponent of the Apollonian packing. The longest calculations took approximately 6 h to complete. The above values are truncated, not rounded.

To obtain bounds for the critical exponent of the Apollonian packing, $\delta _{{\mathcal {A}}}$, analogous functions $f_{m, {\mathcal {A}}},g_{m,{\mathcal {A}}},\lambda _{m,{\mathcal {A}}},\mu _{m,{\mathcal {A}}},$ were created. A $\kappa$-cutoff value of 166464 was used to provide 6 levels of iteration. Obtaining the roots $\lambda _{6,{\mathcal {A}}}$ and $\mu _{6,{\mathcal {A}}}$ yielded (1).

The author has also computed a heuristic estimate of $S = \delta$ by methods which originate in [9, 13, 19]. Since each generator of ${\mathcal {O}}_J^+(\mathbb {Z})$ has a matrix representation, the problem of estimating $\delta$ is equivalent to determining the average growth rate of the orbit of a vector under random products of certain non-commuting matrices. After a similarity transformation, these integer matrices correspond to Lorentz transformations (see [25] or [22]) which generate a discrete subgroup of the full Lorentz group $O_{3,1}(\mathbb {R})$. Define the “height" function

$$\begin{aligned} h(\vec {x}) = \vec {x}\circ \vec {D}= 4x_1+4x_2+2x_3+2x_4. \end{aligned}$$

(45)

Again let $\Gamma = \left\langle R_{\vec {n}_1},R_{\vec {n}_2},R_{\vec {n}_3},R_{\vec {n}_4},R_{\vec {n}_5} \right\rangle$ and consider the image of $\Gamma$ on the faces $\{ \vec {e}_1,\vec {e}_2,\vec {e}_3,\vec {e}_4,\vec {e}_1+\vec {e}_2-\vec {e}_4 \}$ (see Fig. 3). A finite subset of this image was created with these 5 faces as a “seed". There were calculated to be 13, 244, 370 vectors with a height below $2^{19}$. These vectors were then sorted according to height and then fit by linear least-squares regression to the curve $y = ax^b$. The resulting growth rate of 1.33544546879 fits between the rigorous bounds displayed in Table 1 and is merely 0.002573 off from the arithmetic average of the lower and upper bounds $\lambda _{5}(39201)$ and $\mu _{5}(39201)$.