An arithmetic property of the set of angles between closed geodesics on hyperbolic surfaces of finite type

Abstract

For a hyperbolic surface S of finite type we consider the set A(S) of angles between closed geodesics on S. Our main result is that there are only finitely many rational multiples of $\pi$ in A(S).

1 Introduction

Geometry of two dimensional manifolds, surfaces, have been in the center of mathematical research for centuries. Hyperbolic metrics on surfaces has been a very important testing ground for different geometric curiosities. In particular, lengths of closed geodesics on these surfaces have been an important topic of research for years (see [3,4,5, 8, 10]). This article is on a related geometric quantity, the angles between pairs of closed geodesics.

Let S be a hyperbolic surface of finite type. We denote the set of angles between pairs of closed geodesics on S by $\mathcal {A}(S)$. A fixed angle may appear at many different intersections. We call this number of distinct appearances the multiplicity of the angle. We denote the set of angles in $\mathcal {A}(S)$ forgetting their multiplicities by A(S) and call $\mathcal {A}(S)$ and A(S) by angle spectrum and angle set respectively.

We begin by specifying a way of measuring these angles. Let $\gamma$ and $\delta$ be two closed geodesics on S that intersect each other at p. Let $\dot{\gamma }_p$ and $\dot{\delta }_p$ respectively denote the tangent vectors to to $\gamma$ and $\delta$ at p. We measure the angle of intersection $\theta (\gamma , \delta , p)$ between $\dot{\gamma }_p$ and $\dot{\delta }_p$ in the counter clockwise direction from $\gamma$ to $\delta$. In particular $\theta (\gamma , \delta , p) = \pi - \theta (\delta , \gamma , p)$.

Remark 1.1

For $\gamma , \delta$ and $\theta = \theta (\gamma , \delta , p)$ as above $\cos ^2(\theta )$ depends on $\gamma$ and $\delta$ but not on the direction in which the angle is measured.

In this article we focus on qualitative properties of the two collections $\mathcal {A}(S)$ and A(S). For any hyperbolic surface S of finite type A(S) is a countable infinite set and it follows from [9] that A(S) is dense in $[0, \pi ]$. The main question that we address in this paper is the following.

Question 1.2

How many angles in $\mathcal {A}(S)$ can be a rational multiple of $\pi$?

Surprisingly the author’s motivation to study this question came from a seemingly unrelated field. In the paper [6] we have studied eigenfunctions of the Laplacian on hyperbolic surfaces. Let $\phi$ be an eigenfunction of the Laplacian on $\mathbb {H}^2$. Let $\Gamma _\phi$ denote the subgroup of isometries of $\mathbb {H}^2$ that leaves $\phi ^2$ invariant. In [6] we have observed (motivated by a similar observation in [1]) that if $\phi$ vanishes on a geodesic $\gamma$ then it is odd with respect to the reflection isometry $R_\gamma$ along $\gamma$ of $\mathbb {H}^2$ i.e. $\phi \circ R_\gamma = - \phi$. In particular, $R_\gamma \in \Gamma _\phi$. An important property of any non-constant eigenfunction $\phi$ is that the subgroup $\Gamma _\phi$ is discrete (see if it contains a co-finite subgroup [6]).

Now consider two intersecting geodesics $\gamma , \delta$ on $\mathbb {H}^2$ and consider the subgroup $\Gamma (\gamma , \delta )$ of SL$(2, \mathbb {R})$ generated by the reflections $R_\gamma , R_\delta$ along $\gamma$ and $\delta$ respectively. Let $\gamma , \delta$ intersect each other at p and let $\theta = \theta (\gamma , \delta , p)$. Then $\Gamma (\gamma , \delta )$ contains an elliptic isometry of $\mathbb {H}^2$ which is a rotation about p by an angle equal to $\theta$. Let $\phi$ be a non-constant eigenfunction that vanish on both $\gamma$ and $\delta$. Then by the last paragraph $\Gamma (\gamma , \delta ) \subset \Gamma _\phi$. In particular, if $\Gamma _\phi$ is discrete, so is $\Gamma (\gamma , \delta )$ implying that $\theta$ must be a rational multiple of $\pi$.

It is not difficult to construct eigenfunctions that vanish on two intersecting geodesics, even on closed hyperbolic surfaces (see [6]). In general the answer to Question 1.2 is ‘infinite’. In the last section we construct examples of surfaces for which there are infinitely many distinct intersections between pairs of closed geodesics such that the angle of intersection is $\pi /2$. The main result of this article is that, in general, there are infinitely many rational multiples of $\pi$ in $\mathcal {A}(S)$ if and only if one of these rational multiples of $\pi$ has infinite multiplicity in $\mathcal {A}(S)$.

Theorem 1.3

For any hyperbolic surface S of finite type there are only finitely many angles in A(S) that are rational multiples of $\pi$.

1.1 Structure of the article

In the first section we consider a complete hyperbolic surface S of finite type. Using uniformization theorem we consider a Fuchsian group $\Gamma$ such that $S = \mathbb {H}^2/\Gamma$, up to isometry. For two intersecting closed geodesics $\gamma$ and $\delta$ on S we fix an intersection point p. In Sect.1 we consider $M_\gamma , M_\delta \in \Gamma$ representing $\gamma$ and $\delta$ respectively and use the matrix entries of $M_\gamma$ and $M_\delta$ to get a formula for $\cos ^2 (\theta )$ where $\theta = \theta (\gamma , \delta , p)$.

We prove Theorem 1.3 in Sect. 2. In the first step of the proof we consider the field $\mathbb {F}_\Gamma$ obtained by attaching the matrix entries of all the elements in $\Gamma$ to $\mathbb {Q}$. Using the fact that $\Gamma$ is finitely generated it follows that $\mathbb {F}_\Gamma$ is a finitely generated field extension of $\mathbb {Q}$. Using the expression for $\cos ^2(\theta )$ obtained in Sect.1 we deduce that $\cos ^2(\theta ) \in \mathbb {F}_\Gamma$ for any angle $\theta \in A(\mathbb {H}^2 /\Gamma )$.

The final arguments of the proof go follows. For simplicity, assume that $\mathbb {F}_\Gamma$ is algebraic over $\mathbb {Q}$. Since $\mathbb {F}_\Gamma$ is finitely generated over $\mathbb {Q}$ we obtain that the degree of extension $\mathbb {F}_\Gamma |_{\mathbb {Q}}$ is finite. Now let $\frac{p}{q}\pi$ be in $A(\mathbb {H}^2 /\Gamma )$ and so $\cos ^2(\frac{p}{q}\pi ) \in \mathbb {F}_\Gamma$. Then there is a field extension $\mathbb {F}(q)$ of $\mathbb {F}_\Gamma$ with degree of extension at most two that contain a primitive q-th root of unity. In particular, the degree of extension $\mathbb {F}(q)|_\mathbb {Q}$ is uniformly bounded independent of q. Finally we observe that the degree of extension $\mathbb {F}(q)|_\mathbb {Q}$ is at least $\phi (q)$ where $\phi$ is the Euler’s $\phi$-function that counts the number of distinct positive integers less than and co-prime with q. Since $\phi (q)$ goes to infinity as q goes to infinity [2, Theorem 328], we reach our desired contradiction.

2 Formula for the cosine of an angle

Let $\Gamma$ be a finitely generated Fuchsian group. This usually means that $\Gamma \subset \text {PSL}(2, \mathbb {R})$. By taking the pre-image of $\Gamma$ under the quotient map $\Pi : \text {SL}(2, \mathbb {R}) \rightarrow \text {PSL}(2, \mathbb {R})$ we can always think of $\Gamma \subset \text {SL}(2, \mathbb {R})$. This identification will be assumed in the article from now on. It is a standard fact that every closed geodesic on S corresponds to a conjugacy class of elements in $\pi _1(S) = \Gamma$. Let $\gamma , \delta$ be two closed geodesics on S and let $M_\gamma , M_\delta \in \Gamma$ be two representatives of $\gamma , \delta$ respectively. Let us denote

$$\begin{aligned} M_\gamma = \left( \begin{array}{c@{\quad }c} a_\gamma &{} b_\gamma \\ c_\gamma &{} d_\gamma \ \end{array} \right) , \quad M_\delta = \left( \begin{array}{c@{\quad }c} a_\delta &{} b_\delta \\ c_\delta &{} d_\delta \ \end{array} \right) . \end{aligned}$$

Recall that $\gamma$ and $\delta$ are the projections of the axes of $M_\gamma$ and $M_\delta$ respectively, under the covering map: $\mathbb {H}^2 \rightarrow \mathbb {H}^2 /\Gamma$. Since $\gamma$ and $\delta$ are closed geodesics, $M_\gamma$ and $M_\delta$ are hyperbolic linear fractional transformations. Thus the axes of $M_\gamma$ and $M_\delta$ are either semi-circles or vertical straight lines that intersect $\mathbb {R}$ orthogonally. Here $\mathbb {R}\cup \{\infty \}$ is identified with the boundary $\partial {\mathbb {H}^2}$ of $\mathbb {H}^2$.

Observe that in both the cases it is possible to determine the axis of $M_\gamma$ (or $M_\delta$) from the points where they intersect $\mathbb {R}$. Now these last set of points are just the fixed points of $M_\gamma$ (or $M_\delta$). The fixed points of $M_\gamma$ can be computed simply as follows. There are two cases.

Case I First let the axis of $M_\gamma$ (or $M_\delta$) be a semi-circle. Then both the points of intersections are finite real numbers that satisfy

$$\begin{aligned} M_\gamma (z) = z \Rightarrow \frac{a_\gamma z + b_\gamma }{c_\gamma z + d_\gamma } = z \Rightarrow c_\gamma z^2 + \left( d_\gamma - a_\gamma \right) z - b_\gamma = 0. \end{aligned}$$

Hence the two points of intersections of the axis of $M_\gamma$ with the real line are the two roots of the equation

$$\begin{aligned} c_\gamma z^2 + \left( d_\gamma - a_\gamma \right) z - b_\gamma = 0. \end{aligned}$$

(2.1)

Denote these by $\alpha _\gamma$ and $\beta _\gamma$ with $\alpha _\gamma < \beta _\gamma$. In terms of matrix coefficients of $M_\gamma$ we have

$$\begin{aligned} \alpha _\gamma = \frac{\left( a_\gamma - d_\gamma \right) - \sqrt{\left( a_\gamma - d_\gamma \right) ^2 + 4c_\gamma b_\gamma }}{2 c_\gamma }, \quad \beta _\gamma = \frac{\left( a_\gamma - d_\gamma \right) + \sqrt{\left( a_\gamma - d_\gamma \right) ^2 + 4c_\gamma b_\gamma }}{2 c_\gamma }. \end{aligned}$$

(2.2)

Using $\det {M_\gamma } = 1$ they take the form:

$$\begin{aligned} \alpha _\gamma = \frac{\left( a_\gamma - d_\gamma \right) - \sqrt{{\text {tr}}{M_\gamma }^2 - 4}}{2 c_\gamma }, \quad \beta _\gamma = \frac{\left( a_\gamma - d_\gamma \right) + \sqrt{{\text {tr}}{M_\gamma }^2 - 4}}{2 c_\gamma }. \end{aligned}$$

(2.3)

In particular, the center and the Euclidean radius of the axis of $M_\gamma$ are respectively

$$\begin{aligned} m_\gamma = \left( \frac{a_\gamma - d_\gamma }{2c_\gamma }, 0\right) \quad \text {and} \quad r_\gamma = \frac{\sqrt{{\text {tr}}{M_\gamma }^2 - 4}}{2c_\gamma }. \end{aligned}$$

(2.4)

Case II The axis of $M_\gamma$ is a vertical straight line. In particular, $c_\gamma = 0$. Then the only point of intersection between the axis of $M_\gamma$ and $\mathbb {R}$ is $\left( \frac{b_\gamma }{d_\gamma - a_\gamma }, 0\right)$.

Fig. 1

Cosine of the angle

2.1 Cosine of the angle

Consider two intersecting closed geodesics $\gamma$ and $\delta$ on S. Fix one point of their intersection p. Choose two representatives $M_\gamma , M_\delta$ for $\gamma , \delta$ respectively such that the point of intersection $\tilde{p}$ between the axis of $M_\gamma$ and the axis of $M_\delta$ is a lift of p under the covering map $\pi : \mathbb {H}^2 \rightarrow \mathbb {H}^2/\Gamma =S$. Let $\theta = \theta (\gamma , \delta , p)$. Hence $\theta$ is the angle between the axis of $M_\gamma$ and the axis of $M_\delta$ at $\tilde{p}$. Now we have two cases depending on the nature of the axes of $M_\gamma$ and $M_\delta$. We treat them separately.

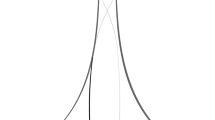
Case I First let us assume that both $M_\gamma$ and $M_\delta$ have semi-circle axes. This situation is explained in the top picture in Fig. 1. Let $\psi$ be the angle between the normals to the the axis of $M_\gamma$ and the axis of $M_\delta$ at $\tilde{p}$. Then $\psi = \pi - \theta$.

Now consider the Euclidean triangle on $\mathbb {H}^2$ with the following three vertices: the centre of the (semi-circle) axis of $M_\gamma$, the centre of the (semi-circle) axis of $M_\delta$ and $\tilde{p}$ the point of intersection of the two axes. Let us denote the distance between the two centres by $d_{\gamma ,\delta }$. Hence

$$\begin{aligned} d_{\gamma , \delta } = \left| \frac{a_\gamma - d_\gamma }{2c_\gamma } - \frac{a_\delta - d_\delta }{2c_\delta }\right| . \end{aligned}$$

(2.5)

Using Euclidean geometry for the above described triangle we obtain

$$\begin{aligned} \cos (\pi -\theta ) = \frac{r_\gamma ^2 + r_\delta ^2 - d_{\gamma , \delta }^2}{2r_\gamma r_\delta }. \end{aligned}$$

Thus

$$\begin{aligned} \cos ^2\left( \theta \right) = \frac{\left( r_\gamma ^2 + r_\delta ^2 - d_{\gamma , \delta }^2\right) ^2}{4r_\gamma ^2 r_\delta ^2}. \end{aligned}$$

(2.6)

Case II Now we assume that the axis of $M_\gamma$ is a vertical straight line. Since $\gamma$ and $\delta$ intersect each other, the axis of $M_\delta$ must be a semi-circle. This situation is explained in the bottom picture of Fig. 1. Consider the normal $N_\delta$ to the axis of $M_\delta$ at $\tilde{p}$. Let $\psi$ be the angle between the boundary $\partial {\mathbb {H}^2} = \mathbb {R}$ and $N_\delta$. Observe that $\psi = \theta$. Now we consider the Euclidean triangle with vertices: the center of the axis of $M_\delta$, the point of intersection between axis of $M_\gamma$ and $\partial {\mathbb {H}^2} = \mathbb {R}$ and $\tilde{p}$. By the definition of the cosine function and the last equality $\psi = \theta$ we get

$$\begin{aligned} \cos ^2(\theta ) = \left( \frac{\bigg |\frac{b_\gamma }{d_\gamma - a_\gamma } - \frac{a_\delta - d_\delta }{2c_\delta }\bigg |}{\frac{\sqrt{{\text {tr}}{M_\delta }^2 - 4}}{2c_\delta }}\right) ^2. \end{aligned}$$

(2.7)

Lemma 2.1

From the above two expressions it is clear that $\cos ^2(\theta )$ is expressible as rational functions in the matrix entries $a_\gamma , b_\gamma , c_\gamma , d_\gamma$ of $M_\gamma$ and $a_\delta , b_\delta , c_\delta , d_\delta$ of $M_\delta$.

Remarks 2.2

• 1. The two expressions (2.6) and (2.7) are not original. Some variant of these expressions are most likely known to experts. The author was informed by the anonymous referee that an expression similar to these is implicitly used in [7].

• 2. It was pointed out to the author by the anonymous referee that it is possible to deduce the same conclusion as in Lemma 2.1 by staying entirely in hyperbolic framework (avoiding Euclidean geometry). This approach is in fact a little shorter than ours. We are sticking to this approach mainly because of the last part of the proof our main result, which in the other approach becomes a bit complicated.

3 Proof of Theorem 1.3

Consider the field

$$\begin{aligned} \mathbb {F}_\Gamma = \mathbb {Q}\left( a_\gamma , b_\gamma , c_\gamma , d_\gamma : M_\gamma = \left( \begin{array}{c@{\quad }c} a_\gamma &{} b_\gamma \\ c_\gamma &{} d_\gamma \ \end{array} \right) \in \Gamma \right) \end{aligned}$$

generated by the entries of the matrices in $\Gamma \subset \text {SL}(2, \mathbb {R})$. Observe that this is a finitely generated field. This is clear because $\Gamma$ is a finitely generated group and so adjoining the matrix entries of a generating subset of $\Gamma$ is enough.

Now we have two cases depending on whether $\mathbb {F}_\Gamma$ is algebraic over $\mathbb {Q}$ or not. In the latter case, since $\mathbb {F}_\Gamma$ is finitely generated over $\mathbb {Q}$, there is a purely transcendental extension ${\mathbb {T}_\Gamma }{|_\mathbb {Q}} \subset \mathbb {F}_\Gamma$ such that $\mathbb {F}_\Gamma$ is algebraic over $\mathbb {T}_\Gamma$. To treat the two cases at the same time let ${\mathbb {T}_\Gamma }$ denote $\mathbb {Q}$ when $\mathbb {F}_\Gamma$ is algebraic over $\mathbb {Q}$. In both the cases $\mathbb {F}_\Gamma$ is finitely generated over $\mathbb {T}_\Gamma$. Hence the degree $[\mathbb {F}_\Gamma : \mathbb {T}_\Gamma ]$ of the extension ${\mathbb {F}_\Gamma }{|_{\mathbb {T}_\Gamma }}$ is finite.

Now from Lemma 2.1 we have for $\theta = \theta (\gamma , \delta , p)$ the value $\cos ^2(\theta )$ is in $\mathbb {F}_\Gamma$. Hence the degree of the field extension $\mathbb {F}_\Gamma \left( e^{2i\theta }\right) _{|{\mathbb {F}_\Gamma }}$

$$\begin{aligned} \left[ \mathbb {F}_\Gamma \left( e^{2i\theta }\right) :{\mathbb {F}_\Gamma }\right] \le 2. \end{aligned}$$

This implies that the degree of the extension $\mathbb {T}_\Gamma \left( e^{2i\theta }\right) _{|{\mathbb {T}_\Gamma }}$

$$\begin{aligned} \left[ \mathbb {T}_\Gamma \left( e^{2i\theta }\right) : \mathbb {T}_\Gamma \right] \le \left[ \mathbb {F}_\Gamma \left( e^{2i\theta }\right) : \mathbb {T}_\Gamma \right] = \left[ \mathbb {F}_\Gamma \left( e^{2i\theta }\right) :{\mathbb {F}_\Gamma }\right] \cdot \left[ \mathbb {F}_\Gamma : \mathbb {T}_\Gamma \right] \le 2\left[ \mathbb {F}_\Gamma : \mathbb {T}_\Gamma \right] . \end{aligned}$$

Now recall that $\mathbb {T}_\Gamma$ is a purely transcendental extension of $\mathbb {Q}$ and so for $\theta$ rational multiple of $\pi$ (since $e^{2i\theta }$ is algebraic over $\mathbb {Q}$) we always have

$$\begin{aligned} \left[ \mathbb {T}_\Gamma \left( e^{2i\theta }\right) : \mathbb {T}_\Gamma \right] = \left[ \mathbb {Q}\left( e^{2i\theta }\right) : \mathbb {Q}\right] . \end{aligned}$$

Let $\theta = \frac{p}{q}\pi$. It is a known fact that, in this case, the degree

$$\begin{aligned} \left[ \mathbb {Q}\left( e^{2i\theta }\right) : \mathbb {Q}\right] = \left[ \mathbb {Q}\left( e^{\frac{2i\pi p }{q}}\right) : \mathbb {Q}\right] = \phi (q) \end{aligned}$$

(3.1)

where $\phi$ is the Euler $\phi$-function. Thus combining the above inequalities we have

$$\begin{aligned} \phi (q) \le 2\left[ \mathbb {F}_\Gamma : \mathbb {T}_\Gamma \right] . \end{aligned}$$

Hence there are only finitely many choices for q by [2, Theorem 328].

Remarks 3.1

• (i) Observe that the field $\mathbb {F}_\Gamma$ depends explicitly on $\Gamma$ where $A(\mathbb {H}^2/\Gamma )$ depends only on the conjugacy class of $\Gamma$ because conjugate groups produce isometric surfaces. Hence we conclude that for any $\frac{p}{q} \pi \in A(\mathbb {H}^2 /\Gamma )$

  $$\begin{aligned} \phi (q) \le 2 \cdot \min _{\gamma \in \text {PSL}(2, \mathbb {R})} \left[ \mathbb {F}_{\gamma \Gamma {\gamma ^{-1}}}, \mathbb {T}_{\gamma \Gamma {\gamma ^{-1}}}\right] . \end{aligned}$$

  This can be used to give an explicit bound on the size of $A(\mathbb {H}^2 /\Gamma ) \cap \mathbb {Q}\cdot \pi .$

• (ii) For the modular surface $\mathbb {H}^2/ \text {PSL}(2, \mathbb {Z})$ the group $\Gamma$ is $\text {PSL}(2, \mathbb {Z})$ and so the field $\mathbb {F}_\Gamma$ is just $\mathbb {Q}$. Hence for any $\frac{p}{q} \pi \in A(\mathbb {H}^2/\text {PSL}(2, \mathbb {Z}))$ we have $\phi (q) \le 2$ i.e. $q \le 6.$ A simple computation provides that the possible angles are $\pi /6, \pi /4$ and $\pi /3$.

4 Some questions and examples

Let $\Gamma$ be a Fuchsian group as above and $S = \mathbb {H}^2/\Gamma$. Given an angle $\theta \in A(S)$ one may consider the map $\Theta : A(S) \rightarrow \mathbb {F}_\Gamma ^1$ given by $\Theta (\theta ) = \cos ^2(\theta )$, where $\mathbb {F}_\Gamma ^1 \subset \mathbb {F}_\Gamma$ is the set of elements with norm $< 1$.

Question 4.1

What is the image of this map?

Since A(S) is dense in $[0, \pi ]$ the image is dense in $[-\,1, 1]$ and hence in $\mathbb {F}_\Gamma ^1$. It is not clear if it equals $\mathbb {F}_\Gamma ^1$ though.

4.1 Angles with infinite multiplicity

Now we show that for $m < n$ there are closed hyperbolic surfaces S such that the angle $m\pi /n$ has infinite multiplicity in $\mathcal {A}(S)$. Let S be a hyperbolic surface that has an isometry $\tau _n$ of order 2n that fixes exactly two points $x_1, x_2$ of S and such that $S/<\tau _n>$ is not homeomorphic to the sphere. Clearly $S/<\tau _n>$ has exactly two cone points with cone angle equal to $\pi /n$. Since $S/<\tau _n>$ is not homeomorphic to the sphere there are infinitely many geodesic arcs on $S/<\tau _n>$ that joins the two cone points. Let $\gamma$ be one such arc and let $\tilde{\gamma }$ be a lift of $\gamma$ that joins $x_1, x_2$. It is not that difficult to see that $\tilde{\gamma }$ and $\tau _n^n(\tilde{\gamma })$ forms a closed geodesic $\hat{\gamma }$ that contains $\tilde{\gamma }$. It is now easy to see that for any $m < n$ the angle between $\hat{\gamma }$ and $\tau ^m_n(\hat{\gamma })$ at $x_1$ (or $x_2$) equals $m\pi /n$.

It was pointed out by the referee that the above example can be modified to construct a closed hyperbolic surface $S'$ such that the angle $m\pi /n$ has infinite multiplicity in $\mathcal {A}(S')$ but $S'$ has no isometry.

Our last question is the following:

Question 4.2

What angles in $\mathcal {A}(S)$ can have infinite multiplicity? In particular, can irrational multiples of $\pi$ have infinite multiplicity?