Seismic Active Earth Pressure on Walls Using a New Pseudo-Dynamic Approach

Abstract

Seismic active soil thrust, soil pressure distribution and overturning moment are obtained in closed form using a new pseudo-dynamic approach based on standing shear and primary waves propagating on a visco-elastic backfill overlying rigid bedrock subjected to both harmonic horizontal and vertical acceleration. Seismic waves respect the zero stress boundary condition at the soil surface, backfill is modeled as a Kelvin–Voigt medium and a planar failure surface is assumed in the analysis. Effects of a wide range of parameters such as amplitude of base accelerations, soil shear resistance angle, soil wall friction angle, damping ratio are discussed. Results of the parametric study indicate that amplitude of the horizontal base acceleration and soil shear resistance angle are the factors most influencing active pressure distribution whereas the presence of the vertical acceleration always results in a quite small increase in seismic active thrust. Damping ratio is important mainly close to the fundamental frequency of shear wave where seismic active thrust is maximum. Unlike the original pseudo-dynamic approach the effect of a different frequency for S-wave and P-wave is considered in the analysis. Seismic active thrust is found to increase when the frequency of P-wave is greater than that of S-wave. The results obtained by the proposed approach are found to be in agreement with previous studies, provided that the seismic input is adapted to include amplification effects.

1 Introduction

Design of retaining walls under seismic conditions is a very important topic in geotechnical engineering.

Among various approaches available the finite element methods coupled with advanced constitutive models allow to well describe the complex dynamic behavior of geo-structures. However the use of such sophisticated methods requires both a proper selection of several parameters and a specific knowledge of earthquake geotechnical engineering that is not so commonly diffused in technical community.

In current practice simplified methods are still used in which seismic analysis of retaining walls is obtained as a function of few parameters relatively easy to estimate. The most popular simplified method is the pseudo-static method or Mononobe–Okabe method, developed in the 1920s as an extension of the static Coulomb theory (Okabe 1926; Mononobe and Matsuo 1929). It is widely recognized that a pseudo-static analysis considers the dynamic nature of earthquakes in a very approximate manner and does not account for the effects of time.

To overcome this drawback Steedman and Zeng (1990) proposed a simple pseudo-dynamic analysis of seismic active earth thrust that incorporates phase difference and amplification effects in a dry elastic backfill behind a vertical retaining wall subjected only to horizontal acceleration that varies along the face of the wall. Further improvements of the original pseudo-dynamic method were proposed in the literature in order to consider vertical acceleration, non vertical walls, inclined or submerged backfill (Choudhury and Nimbalkar 2006; Ghosh 2008, 2010; Kolathayar and Ghosh 2009; Bellezza et al. 2012).

The pioneering pseudo-dynamic method was also extended to passive case (Choudhury and Nimbalkar 2005; Ghosh 2007; Ghosh and Kolathayar 2011). The same framework was utilized to estimate seismic displacements (Choudhury and Nimbalkar 2007, 2008) and to design retaining structures also with reinforced backfill (Nimbalkar et al. 2006; Nimbalkar and Choudhury 2007; Choudhury and Ahmad 2008; Ahmad and Choudhury 2008a, b, 2009).

Despite its various applications, a careful review of the original pseudo-dynamic method highlighted some critical aspects; in particular it considers only incident waves travelling upward throughout a linear elastic backfill, resulting in a violation of the free-surface boundary condition (Bellezza et al. 2012, 2014; Choudhury et al. 2014a, b).

Recently in the literature various approaches have been presented to overcome this shortcoming. Some studies considered Rayleigh waves to calculate both active and passive earth pressure on retaining walls (Choudhury and Katdare 2013; Choudhury et al. 2014a).

Bellezza (2014) proposed a new pseudo-dynamic approach based on a standing shear wave in a visco-elastic backfill overlying a rigid base subject to harmonic shaking. Maintaining other hypotheses of the existing pseudo-dynamic method—including absence of water, homogeneous backfill and planar failure surface—closed form expressions for the horizontal inertia force, seismic active thrust, active pressure distribution and overturning moment were derived in dimensionless form as a function of the normalized frequency of shear wave and damping ratio.

In this paper a more complete study is presented in which the seismic active thrust is obtained including also the vertical acceleration. Unlike the pioneering pseudo-dynamic approach a different angular frequency for S-wave and P-wave is accounted for.

2 Wave Equation for a Visco-Elastic Soil

For the purposes of viscoelastic wave propagation, soils are usually modeled as Kelvin–Voigt materials represented by a purely elastic spring and a purely viscous dashpot connected in parallel (Kramer 1996). The same model is also used by ASTM D4015 (2007) to analyze resonant column test results.

The constitutive equation of the Kelvin–Voigt visco-elastic medium is given by:

$$\sigma_{ij} = 2G\varepsilon_{ij} + 2\eta \frac{{\partial \varepsilon_{ij} }}{\partial t}$$

(1)

where σ _ij is a stress ε _ij is a strain G is the shear modulus and η is a viscosity.

The motion equation of the Kelvin–Voigt visco-elastic medium can be written in vectorial form as (see for example Yuan et al. 2006):

$$\rho \frac{{\partial^{2} {\mathbf{u}}}}{{\partial t^{2} }} = \left\{ {\left( {\lambda + G} \right) + \left( {\eta_{1} + \eta_{s} } \right)\frac{\partial }{\partial t}} \right\}grad\left( \theta \right) + \left( {G + \eta_{s} \frac{\partial }{\partial t}} \right)\nabla^{2} {\mathbf{u}}$$

(2)

where ρ is the density of the material, λ and G are the Lamè constant, η ₁ and η _s are viscosities, ${\mathbf{u}}$ is the displacement vector of components u _x , u _y and u _z and $\theta = div\left( {\mathbf{u}} \right)$.

If the plane wave solution of a wave propagating along the z-axis in a Kelvin–Voigt homogeneous medium is considered, then (2) can be simplified as:

$$\rho \frac{{\partial^{2} u_{h} }}{{\partial t^{2} }} = G\frac{{\partial^{2} u_{h} }}{{\partial z^{2} }} + \eta_{s} \frac{{\partial^{3} u_{h} }}{{\partial t\partial z^{2} }}$$

(3)

$$\rho \frac{{\partial^{2} u_{v} }}{{\partial t^{2} }} = \left( {\lambda + 2G} \right)\frac{{\partial^{2} u_{v} }}{{\partial z^{2} }} + \left( {\eta_{1} + 2\eta_{s} } \right)\frac{{\partial^{3} u_{v} }}{{\partial t\partial z^{2} }}$$

(4)

where u _h  = u _x and u _v  = u _z .

2.1 Horizontal Displacement and Acceleration

For a harmonic horizontal base shaking of angular frequency ω _s and period T _s (=2π/ω _s ) the solution of (3) is obtained by Bellezza (2014) as a function of damping ratio D _s (=η _s ω _s /2G) and normalized frequency of S-wave (ω _s H/V _s ). Assuming a base displacement u _bh  = u _h0 cos(ω _s t) the horizontal displacement within a layer of thickness H is given by:

$$u_{h} \left( {z,t} \right) = \frac{{u_{h0} }}{{C_{S}^{2} + S_{S}^{2} }}\left[ {\left( {C_{S} C_{sz} + S_{S} S_{sz} } \right)\text{cos}\left( {\omega_{s} t} \right) + \left( {S_{S} C_{sz} - C_{S} S_{sz} } \right)\text{sin}\left( {\omega_{s} t} \right)} \right]$$

(5)

Defining a _h0 = −ω ² _s u _h0, the horizontal acceleration is easily obtained as:

$$a_{h} \left( {z,t} \right) = \frac{{a_{h0} }}{{C_{S}^{2} + S_{S}^{2} }}\left[ {\left( {C_{S} C_{sz} + S_{S} S_{sz} } \right)\text{cos}\left( {\omega_{s} t} \right) + \left( {S_{S} C_{sz} - C_{S} S_{sz} } \right)\text{sin}\left( {\omega_{s} t} \right)} \right]$$

(6)

where:

$$C_{sz} = \text{cos}\left( {y_{S1} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)\text{cosh}\left( {y_{S2} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)$$

(7a)

$$S_{sz} = - \text{sin}\left( {y_{S1} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)\text{sinh}\left( {y_{S2} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)$$

(7b)

$$C_{S} = \text{cos}\left( {y_{S1} } \right)\text{cosh}\left( {y_{S2} } \right)$$

(7c)

$$S_{S} = - \text{sin}\left( {y_{S1} } \right)\text{sinh}\left( {y_{S2} } \right)$$

(7d)

$$y_{S1} = k_{s1} H = \frac{{\omega_{s} H}}{{V_{s} }}\sqrt {\frac{{\sqrt {1 + 4D{}_{s}^{2} } + 1}}{{2\left( {1 + 4D_{s}^{2} } \right)}}} = \frac{{\omega_{s} H}}{{\sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0pt} \rho }} }}\sqrt {\frac{{\sqrt {1 + 4D{}_{s}^{2} } + 1}}{{2\left( {1 + 4D_{s}^{2} } \right)}}}$$

(8a)

$$y_{S2} = k_{s2} H = - \frac{{\omega_{s} H}}{{V_{s} }}\sqrt {\frac{{\sqrt {1 + 4D_{s}^{2} } - 1}}{{2\left( {1 + 4D_{s}^{2} } \right)}}} = - \frac{{\omega_{s} H}}{{\sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0pt} \rho }} }}\sqrt {\frac{{\sqrt {1 + 4D_{s}^{2} } - 1}}{{2\left( {1 + 4D_{s}^{2} } \right)}}}$$

(8b)

where k _s1 and k _s2 are the real and imaginary part of the complex wave number k ^* _s , defined as a function of the complex shear modulus G ^*; in particular $k_{s}^{*} = \omega_{s} \sqrt {{\rho \mathord{\left/ {\vphantom {\rho {G^{*} }}} \right. \kern-0pt} {G^{*} }}} = k_{s1} + ik_{s2}$ and G ^* = G(1 + 2iD _s ). Further details about the complex wave number and complex shear modulus appear in many text books (e.g. Kolsky 1963; Kramer 1996).

2.2 Vertical Displacement and Acceleration

Equation (4) can be written in a form similar to Eq. (3) provided that u _h , G and η _s are replaced by u _v , E _c (=λ + 2G) and η _p  = (η ₁  + 2η _s ), respectively.

Considering a harmonic vertical shaking of the base u _vb  = u _v0 cos(ω _p t)and by imposing that at the free surface (z = 0) the normal stress is null (σ _zz  = 0) and that at z = H the displacement coincides with that of the rigid base, the solution of (4) can be expressed as a function of damping ratio D _p (=η _p ω _p /2E _c ) and normalized frequency of P-wave (ω _p H/V _p ). Then, the vertical displacement within a layer of thickness H can be calculated as:

$$u_{v} \left( {z,t} \right) = \frac{{u_{v0} }}{{C_{P}^{2} + S_{P}^{2} }}\left[ {\left( {C_{P} C_{pz} + S_{P} S_{pz} } \right)\text{cos}\left( {\omega_{p} t} \right) + \left( {S_{P} C_{pz} - C_{P} S_{pz} } \right)\text{sin}\left( {\omega_{p} t} \right)} \right]$$

(9)

Defining a _v0 = −ω ² _p u _v0, the vertical acceleration is given by:

$$a_{v} \left( {z,t} \right) = \frac{{a_{v0} }}{{C_{P}^{2} + S_{P}^{2} }}\left[ {\left( {C_{P} C_{pz} + S_{P} S_{pz} } \right)\text{cos}\left( {\omega_{p} t} \right) + \left( {S_{P} C_{pz} - C_{P} S_{pz} } \right)\text{sin}\left( {\omega_{p} t} \right)} \right]$$

(10)

where:

$$C_{pz} = \text{cos}\left( {y_{p1} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)\text{cosh}\left( {y_{p2} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)$$

(11a)

$$S_{pz} = - \text{sin}\left( {y_{p1} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)\text{sinh}\left( {y_{p2} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)$$

(11b)

$$C_{P} = \text{cos}\left( {y_{p1} } \right)\text{cosh}\left( {y_{p2} } \right)$$

(11c)

$$S_{P} = - \text{sin}\left( {y_{p1} } \right)\text{sinh}\left( {y_{p2} } \right)$$

(11d)

$$y_{p1} = \frac{{\omega_{p} H}}{{V_{p} }}\sqrt {\frac{{\sqrt {1 + 4D_{p}^{2} } + 1}}{{2\left( {1 + 4D_{p}^{2} } \right)}}} = \frac{{\omega_{p} H}}{{\sqrt {{E_{c} \mathord{\left/ {\vphantom {E_{c}\rho }} \right. \kern-0pt} \rho }} }}\sqrt {\frac{{\sqrt {1 + 4D_{p}^{2} } + 1}}{{2\left( {1 + 4D_{p}^{2} } \right)}}}$$

(12a)

$$y_{p2} = - \frac{{\omega_{p} H}}{{V_{p} }}\sqrt {\frac{{\sqrt {1 + 4D_{p}^{2} } - 1}}{{2\left( {1 + 4D_{p}^{2} } \right)}}} = - \frac{{\omega_{p} H}}{{\sqrt {{E_{c} \mathord{\left/ {\vphantom {E_{c} \rho }} \right. \kern-0pt} \rho }} }}\sqrt {\frac{{\sqrt {1 + 4D_{p}^{2} } - 1}}{{2\left( {1 + 4D_{p}^{2} } \right)}}}$$

(12b)

It is worthy to note that soil accelerations described by (6) and (10) automatically incorporate amplification effects within the soil layer without introducing an amplification factor as needed in the original pseudo-dynamic approach (Steedman and Zeng 1990; Choudhury and Nimbalkar 2007, 2008; Nimbalkar and Choudhury 2007).

The ratio between the amplitude of horizontal and vertical acceleration at the ground surface and at the base of the layer can be calculated as:

$$f_{ah} = \frac{{max\left\{ {a_{h} \left( {z = 0,t} \right)} \right\}}}{{max\left\{ {a_{h} \left( {z = H,t} \right)} \right\}}} = \frac{{{{a_{h0} } \mathord{\left/ {\vphantom {{a_{h0} } {\sqrt {C_{S}^{2} + S_{S}^{2} } }}} \right. \kern-0pt} {\sqrt {C_{S}^{2} + S_{S}^{2} } }}}}{{a_{h0} }} = \frac{1}{{\sqrt {\text{cos}^{2} y_{s1} + \text{senh}^{2} y_{s2} } }}$$

(13)

$$f_{av} = \frac{{max\left\{ {a_{v} \left( {z = 0,t} \right)} \right\}}}{{max\left\{ {a_{v} \left( {z = H,t} \right)} \right\}}} = \frac{{{{a_{v0} } \mathord{\left/ {\vphantom {{a_{v0} } {\sqrt {C_{P}^{2} + S_{P}^{2} } }}} \right. \kern-0pt} {\sqrt {C_{P}^{2} + S_{P}^{2} } }}}}{{a_{v0} }} = \frac{1}{{\sqrt {\text{cos}^{2} y_{p1} + \text{senh}^{2} y_{p2} } }}$$

(14)

3 Pseudo-Dynamic Inertial Forces

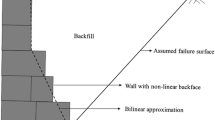
Considering a planar surface inclined at an angle α with respect to the horizontal plane (Fig. 1), the mass of a thin element of the wedge at depth z is given by given by:

$$m\left( z \right) = \frac{{\gamma \left( {H - z} \right)}}{{g\text{tan}\alpha }}\text{d}z$$

(15)

where γ is the unit weight of soil.

Fig. 1

Scheme of forces acting on soil wedge

The horizontal inertial force of the wedge Q _h , which is assumed to be positive if directed towards the wall, can be calculated as:

$$Q_{h} \left( {t,\alpha } \right) = \int\limits_{z = 0}^{z = H} {a_{h} \left( {z,t} \right)m\left( z \right)} = \int\limits_{z = 0}^{z = H} {a_{h} \left( {z,t} \right)\frac{{\gamma \left( {H - z} \right)}}{{g\text{tan}\alpha }}\text{d}z}$$

(16)

Considering (6), (7) and (8) Bellezza (2014) developed Eq. (16) obtaining:

$$Q_{h} \left( {t,\alpha } \right) = \frac{{a_{h,avg} \left( t \right)}}{g}W\left( \alpha \right) \cdot$$

(17)

where W is the weight of soil wedge (W = 0.5γH ²/tanα) and a _h,avg is the weighted average horizontal acceleration within the wedge:

$$a_{h,avg} = \frac{1}{{{{0.5H^{2} } \mathord{\left/ {\vphantom {{0.5H^{2} } {\text{tan}\alpha }}} \right. \kern-0pt} {\text{tan}\alpha }}}}\int\limits_{0}^{H} {\frac{{a_{h} \left( {H - z} \right)}}{{\text{tan}\alpha }}dz} = 2a_{h0} \left[ {A_{h} \text{cos}\left( {\omega_{s} t} \right) + B_{h} \text{sin}\left( {\omega_{s} t} \right)} \right]$$

(18)

with

$$A_{h} = \frac{{2y_{s1} y_{s2} \text{sin}(y_{s1} )\text{sinh}(y_{s2} ) + \left( {y_{s1}^{2} - y_{s2}^{2} } \right)\left\{ {\text{cos}(y_{s1} )\text{cosh}(y_{s2} ) - \text{cos}^{2} (y_{s1} ) - \text{sinh}^{2} (y_{s2} )} \right\}}}{{\left( {\text{cos}^{2} \left( {y_{s1} } \right) + \text{sinh}^{2} \left( {y_{s2} } \right)} \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)^{2} }}$$

(19a)

$$B_{h} = \frac{{2y_{s1} y_{s2} \left\{ {\text{cos}\left( {y_{s1} } \right)\text{cosh}\left( {y_{s2} } \right) - \text{cos}^{2} (y_{s1} ) - \text{sinh}^{2} (y_{s2} )} \right\} - \left( {y_{s1}^{2} - y_{s2}^{2} } \right)\text{sin}(y_{s1} )\text{sinh}(y_{s2} )}}{{\left( {\text{cos}^{2} \left( {y_{s1} } \right) + \text{sinh}^{2} \left( {y_{s2} } \right)} \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)^{2} }}$$

(19b)

Similarly, the vertical inertial force of the wedge Q _v , which is assumed to be positive if directed upward, can be calculated as:

$$Q_{v} \left( {t,\alpha } \right) = \int\limits_{z = 0}^{z = H} {a_{v} \left( {z,t} \right)m\left( z \right)} = \int\limits_{z = 0}^{z = H} {a_{v} \left( {z,t} \right)\frac{{\gamma \left( {H - z} \right)}}{{g\text{tan}\alpha }}\text{d}z}$$

(20)

After substituting (10) into (20) and solving the integral, Q _v can be written in a form similar to (17):

$$Q_{v} \left( {t,\alpha } \right) = \frac{{a_{v,avg}(t) }}{g}W(\alpha)$$

(21)

where a _v,avg is the weighted average vertical acceleration within the wedge:

$$a_{v,avg} = \frac{1}{{{{0.5H^{2} } \mathord{\left/ {\vphantom {{0.5H^{2} } {\text{tan}\alpha }}} \right. \kern-0pt} {\text{tan}\alpha }}}}\int\limits_{0}^{H} {\frac{{a_{v} \left( {H - z} \right)}}{{\text{tan}\alpha }}\text{d}z} = 2a_{v0} \left[ {A_{v} \text{cos}\left( {\omega_{p} t} \right) + B_{v} \text{sin}\left( {\omega_{p} t} \right)} \right]$$

(22)

and A _v and B _v are dimensionless coefficients dependent on y _p1 and y _p2 :

$$A_{v} = \frac{{2y_{p1} y_{p2} \text{sin}(y_{p1} )\text{sinh}(y_{p2} ) + \left( {y_{p1}^{2} - y_{p2}^{2} } \right)\left\{ {\text{cos}(y_{p1} )\text{cosh}(y_{p2} ) - \text{cos}^{2} (y_{p1} ) - \text{sinh}^{2} (y_{p2} )} \right\}}}{{\left( {\text{cos}^{2} \left( {y_{p1} } \right) + \text{sinh}^{2} \left( {y_{p2} } \right)} \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)^{2} }}$$

(23a)

$$B_{v} = \frac{{2y_{p1} y_{p2} \left\{ {\text{cos}\left( {y_{p1} } \right)\text{cosh}\left( {y_{p2} } \right) - \text{cos}^{2} (y_{p1} ) - \text{sinh}^{2} (y_{p2} )} \right\} - \left( {y_{p1}^{2} - y_{p2}^{2} } \right)\text{sin}(y_{p1} )\text{sinh}(y_{p2} )}}{{\left( {\text{cos}^{2} \left( {y_{p1} } \right) + \text{sinh}^{2} \left( {y_{p2} } \right)} \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)^{2} }}$$

(23b)

It is easy to demonstrate that the maximum values of a _h,avg and a _v,avg are given by:

$$a_{h,avg,max} = 2\left| {a_{h0} } \right|\sqrt {A_{h}^{2} + B_{h}^{2} }$$

(24)

$$a_{v,avg,max} = 2\left| {a_{v0} } \right|\sqrt {A_{v}^{2} + B_{v}^{2} }$$

(25)

Equations (24) and (25) indicate that a _h,avg,max and a _v,avg,max depend on the normalized frequency (ω _s H/V _s and ω _p H/V _p ) and damping ratio (D _s and D _p ) as well as the amplitudes of base accelerations a _h0 and a _v0 .

In Fig. 2 values of the ratios a _h,avg,max /a _h0 and a _v,avg,max /a _v0 are plotted against the normalized frequency of the S-wave (ω _s H/V _s ) for D = D _s  = D _p  = 10 % assuming V _p /V _s  = 1.87. This latter hypothesis is generally accepted in the literature for dry soils (Das 1993; Kramer 1996) and it occurs when Poisson’s ratio is equal to 0.3.

Fig. 2

Influence of normalized frequency of S-wave on maximum weighted average accelerations within the soil wedge for D = 10 %

It is evident that all curves of Fig. 2 show a similar trend with the same maximum value which depends on damping ratio; the curves are shifted as the maximum average horizontal acceleration peaks when the S-wave reaches its fundamental frequency (ω _s H/V _s  = π/2) whereas the P-wave peaks for ω _p H/V _p  = π/2, at which corresponds ω _s H/V _s  = π/2(V _p /V _s )(ω _s /ω _p ). It can be observed that for ω _p /ω _s >1 the curve of the vertical acceleration tends to move left-hand with a complete superimposition to the curve relevant to horizontal acceleration for ω _p  = 1.87 ω _s .

For a rigid soil (i.e. for V _s  → ∞ V _p  → ∞) the ratios a _h,avg,max /a _h0 and a _v,avg,max /a _v0 tend to the unit (i.e. A _h  = A _v  = 0.5 B _v  = B _h  = 0).

For values of normalized frequencies (ω _s H/V _s and ω _p H/V _p ) less than the fundamental frequencies the ratios a _h,avg,max /a _h0 and a _v,avg,max /a _v0 are always greater than the unit. In this range soil accelerations are in phase at all depth of soil layer and this results in a significant increase in a _h,avg and a _v,avg .

After the peak for increasing values of normalized frequencies part of the wedge can be subjected to an acceleration in one direction while the other one part can accelerate in the opposite direction and this results in a reduction of the average acceleration of the soil wedge with values of the ratios a _h,avg,max /a _h0 and a _v,avg,max /a _v0 even less than the unity.

Equations (18) and (22) indicate that a _h,avg and a _v,avg follow a harmonic trend of period T _s and T _p , respectively. Consequently, for an assigned angle α, also the inertial forces Q _h and Q _v calculated by (17) and (21) follow the same trend versus time. Considering (18), (22), (24) and (25) the following expressions hold:

$$\frac{{Q_{h} \left( t \right)}}{{Q_{h,max} }} = \frac{{a_{h,avg} \left( t \right)}}{{a_{h,avg,max} }} = \frac{{a_{h0} \left[ {A_{h} \text{cos}\left( {\omega_{s} t} \right) + B_{h} \text{sin}\left( {\omega_{s} t} \right)} \right]}}{{\left| {a_{h0} } \right|\sqrt {A_{h}^{2} + B_{h}^{2} } }}$$

(26)

$$\frac{{Q_{v} \left( t \right)}}{{Q_{v,max} }} = \frac{{a_{v,avg} \left( t \right)}}{{a_{v,avg,max} }} = \frac{{a_{v0} \left\{ {A_{v} \text{cos}\left( {\omega_{p} t} \right) + B_{v} \text{sin}\left( {\omega_{p} t} \right)} \right\}}}{{\left| {a_{v0} } \right|\sqrt {A_{v}^{2} + B_{v}^{2} } }}$$

(27)

Figure 3 shows an example of the trend versus time of the ratios Q _h /Q _h,max and Q _v /Q _v,max obtained for a _h0  > 0; ω _s H/V _s  = 2; D = D _s  = D _p  = 10 %; ω _p /ω _s  = 1. The ratio Q _v /Q _v,max is calculated by assuming both positive and negative value of a _v0 . It is clear that Q _h and Q _v peak at a different times; the time at which the inertia forces reach their maximum depends on the values of normalized frequency (ω _s H/V _s and ω _p H/V _p ) and damping ratio (D _S and D _p ). Complete expressions to calculate the time at which Q _h is maximum are provided by Bellezza (2014). Similar expressions can be derived for the vertical inertial force Q _v .

Fig. 3

Example of trend of normalized inertia forces in the period of shaking for D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

4 Pseudo-Dynamic Active Thrust

By assuming that the dry cohesionless soil is in the limit condition along the planar failure plane (Fig. 1) and imposing the vertical and horizontal equilibrium of the wedge, the total (static + dynamic) active thrust P _AE can be obtained as:

$$P_{AE} \left( {\alpha ,t} \right) = \frac{{W\text{sin}(\alpha - \varphi ) + Q_{h} \text{cos}(\alpha - \varphi ) - Q_{v} \text{sin}(\alpha - \varphi )}}{{\text{cos}\left( {\varphi + \delta - \alpha } \right)}}$$

(28)

where W = weight of the wedge, φ = backfill shear resistance angle; δ = friction angle between the wall and backfill.

The active thrust is taken as the maximum value of P _AE with respect to α and t.

Substituting (17) and (21) into (28) gives:

$$\frac{{P_{AE,max} }}{{\gamma H^{2} }} = max\left\{ \begin{gathered} \frac{{\text{sin}(\alpha - \varphi )}}{{2\text{tan}\alpha \text{cos}\left( {\varphi + \delta - \alpha } \right)}} + \frac{{\text{cos}(\alpha - \varphi )}}{{\text{tan}\alpha \text{cos}\left( {\varphi + \delta - \alpha } \right)}}\frac{{a_{h0} }}{g}\left[ {A_{h} \text{cos}\left( {\omega_{s} t} \right) + B_{h} \text{sin}\left( {\omega_{s} t} \right)} \right] \hfill \\ - \frac{{\text{sin}(\alpha - \varphi )}}{{\text{tan}\alpha \text{cos}\left( {\varphi + \delta - \alpha } \right)}}\frac{{a_{v0} }}{g}\left[ {A_{v} \text{cos}\left( {\omega_{p} t} \right) + B_{v} \text{sin}\left( {\omega_{p} t} \right)} \right] \hfill \\ \end{gathered} \right\}$$

(29)

Similarly to Steedman and Zeng (1990) and Choudhury and Nimbalkar (2006), it is possible to define a pseudo-dynamic coefficient of active thrust:

$$\begin{aligned} K_{AE} = \frac{{2P_{AE,max} }}{{\gamma H^{2} }} & = \frac{{\text{sin}(\alpha_{m} - \varphi )}}{{\text{tan}\alpha_{m} \text{cos}\left( {\varphi + \delta - \alpha_{m} } \right)}} + \frac{{2\text{cos}(\alpha_{m} - \varphi )}}{{\text{tan}\alpha_{m} \text{cos}\left( {\varphi + \delta - \alpha_{m} } \right)}}\frac{{a_{h0} }}{g}\left[ {A_{h} \text{cos}\left( {\omega_{s} t_{m} } \right) + B_{h} \text{sin}\left( {\omega_{s} t_{m} } \right)} \right] \\ & \quad - \frac{{2\text{sin}(\alpha_{m} - \varphi )}}{{\text{tan}\alpha_{m} \text{cos}\left( {\varphi + \delta - \alpha_{m} } \right)}}\frac{{a_{v0} }}{g}\left[ {A_{v} \text{cos}\left( {\omega_{p} t_{m} } \right) + B_{v} \text{sin}\left( {\omega_{p} t_{m} } \right)} \right] \\ \end{aligned}$$

(30)

where α _m and t _m are the values of α and t that maximize K _AE . In this study the values of K _AE are obtained by an optimization procedure in which the magnitudes of the variables α and t/T _s have been varied independently at an interval of 0.1° and 0.01, respectively.

The value of t _m depends on various factors including α _m , φ, ω _s , ω _p , a _ho and a _v0 . Moreover it can be observed that the maximum active thrust is generally achieved for a time at which Q _h and Q _v do not reach their maximum values (i.e. a _h,avg,tm  < a _h,avg,max and a _v,avg,tm  < a _v,avg,max ).

From a mathematical point of view the time t _m is the solution of the following equation:

$$\begin{aligned} \frac{\partial }{\partial t}\left( {\frac{{2P_{AE,max} }}{{\gamma H^{2} }}} \right) & = \frac{{2\text{cos}(\alpha_{m} - \varphi )}}{{\text{tan}\alpha_{m} \text{cos}\left( {\varphi + \delta - \alpha_{m} } \right)}}\frac{{a_{h0} }}{g}\left[ { - \omega_{s} A_{h} \text{sin}\left( {\omega_{s} t_{m} } \right) + \omega_{s} B_{h} \text{cos}\left( {\omega_{s} t_{m} } \right)} \right] \\ & \quad - \frac{{2\text{sin}(\alpha_{m} - \varphi )}}{{\text{tan}\alpha_{m} \text{cos}\left( {\varphi + \delta - \alpha_{m} } \right)}}\frac{{a_{v0} }}{g}\left[ { - \omega_{p} A_{v} \text{sin}\left( {\omega_{p} t_{m} } \right) + \omega_{p} B_{v} \text{cos}\left( {\omega_{p} t_{m} } \right)} \right] = 0 \\ \end{aligned}$$

(31)

A closed form expression for the time t _m is derived only for ω _p  = ω _s  = ω, i.e. when S-wave and P-wave have the same period T = T _s = T _p . In this case Eq. (31) can be written in a simplified form:

$$\left( {A_{h} - \beta A_{v} } \right)\text{tan}\left( {\omega t_{m} } \right) = B_{h} - \beta B_{v}$$

(32)

where β = tan(α _m  − φ)a _v0/a _h0.

For a _h0  > 0 the solution of (32) that maximizes K _AE is given by:

$$\left( {\frac{{t_{m} }}{T}} \right) = \frac{1}{2\pi }\text{arctan}\frac{{B_{h} - \beta B_{v} }}{{A_{h} - \beta A_{v} }}\quad \text{for }A_{h} {-}\beta A_{v} > \, 0 \, \text{and }B_{h} {-}\beta B_{v} > \, 0$$

(33a)

$$\left( {\frac{{t_{m} }}{T}} \right) = 1 + \frac{1}{2\pi }\text{arctan}\frac{{B_{h} - \beta B_{v} }}{{A_{h} - \beta A_{v} }}\quad \text{for }A_{h} {-}\beta A_{v} > \, 0 \, \text{and }B_{h} {-}\beta B_{v} < \, 0$$

(33b)

$$\left( {\frac{{t_{m} }}{T}} \right) = \frac{1}{2\pi }\text{arctan}\frac{{B_{h} - \beta B_{v} }}{{A_{h} - \beta A_{v} }} + \frac{1}{2}\quad \text{for }A_{h} {-}\beta A_{v} < \, 0$$

(33c)

5 Soil Active Pressure Distribution

It is well known that Coulomb approach does not directly provide the distribution of soil active pressures. However, the seismic active earth pressure distribution can be obtained by writing P _AE for a generic z instead of H and then differentiating P _AE with respect to z (e.g. Steedman and Zeng 1990; Choudhury and Nimbalkar 2006; Ghosh 2010; Bellezza et al. 2012; Bellezza 2014):

$$p_{ae} \left( {\it{\alpha ,t,z}} \right) = \frac{{\partial P_{AE} }}{\partial z} = \frac{\partial }{\partial z}\left\{ {\frac{{W\left( {\alpha ,z} \right)\text{sin}(\alpha - \varphi ) + Q_{h} \left( {\it{\alpha ,t,z}} \right)\text{cos}(\alpha - \varphi ) - Q_{v} \left({\it {\alpha ,t,z}} \right)\text{sin}(\alpha - \varphi )}}{{\text{cos}\left( {\varphi + \delta - \alpha } \right)}}} \right\}$$

(34)

where:

$$W\left( {\alpha ,z} \right) = \frac{{\gamma z^{2} }}{{2\text{tan}\alpha }}$$

(35)

$$Q_{h} \left( {\alpha ,t,z} \right) = \int\limits_{\zeta = 0}^{\zeta = z} {a_{h} \left( {\zeta ,t} \right)\frac{{\gamma \left( {z - \zeta } \right)}}{{g\text{tan}\alpha }}\text{d}\zeta = \frac{\gamma }{{g\text{tan}\alpha }}} \int\limits_{\zeta = 0}^{\zeta = z} {a_{h} \left( {\zeta ,t} \right)\left( {z - \zeta } \right)\text{d}\zeta }$$

(36)

$$Q_{V} \left( {\alpha ,t,z} \right) = \int\limits_{\zeta = 0}^{\zeta = z} {a_{v} \left( {\zeta ,t} \right)\frac{{\gamma \left( {z - \zeta } \right)}}{{g\text{tan}\alpha }}\text{d}\zeta } = \frac{\gamma }{{g\text{tan}\alpha }}\int\limits_{\zeta = 0}^{\zeta = z} {a_{v} \left( {\zeta ,t} \right)\left( {z - \zeta } \right)\text{d}\zeta }$$

(37)

Developing (34) taking into account of (35)–(37) the seismic active soil pressure can be expressed in a normalized form as a function of the normalized depth z _n (z _n  = z/H):

$$\begin{aligned} \frac{{p_{ae} }}{\gamma H} & = \frac{{\text{sin}(\alpha - \phi )}}{{\text{tan}\alpha \text{cos}\left( {\phi + \delta - \alpha } \right)}}z_{n} + \frac{{\text{cos}(\alpha - \phi)}}{{\text{tan}\alpha \text{cos}\left( {\phi + \delta - \alpha } \right)}}\frac{{a_{h0} }}{g}\left[ {A_{ph} \text{cos}\left( {\omega_{s} t} \right) + B_{ph} \text{sin}\left( {\omega_{s} t} \right)} \right] \\ & \quad - \frac{{\text{sin}(\alpha - \phi )}}{{\text{tan}\alpha \text{cos}\left( {\phi + \delta - \alpha } \right)}}\frac{{a_{v0} }}{g}\left[ {A_{pv} \text{cos}\left( {\omega_{p} t} \right) + B_{pv} \text{sin}\left( {\omega_{p} t} \right)} \right] \\ \end{aligned}$$

(38)

where:

$$A_{ph} = \frac{{\left( {C_{S} y_{s2} + S_{S} y_{s1} } \right)\text{cos}\left( {y_{s1} z_{n} } \right)\text{sinh}\left( {y_{s2} z_{n} } \right) + \left( {C_{S} y_{s1} - S_{S} y_{s2} } \right)\text{sin}\left( {y_{s1} z_{n} } \right)\text{cosh}\left( {y_{s2} z_{n} } \right)}}{{\left( {C_{S}^{2} + S_{S}^{2} } \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)}}$$

(39a)

$$B_{ph} = \frac{{\left( {S_{S} y_{s2} - C_{S} y_{s1} } \right)\text{cos}\left( {y_{s1} z_{n} } \right)\text{sinh}\left( {y_{s2} z_{n} } \right) + \left( {S_{S} y_{s1} + C_{S} y_{s2} } \right)\text{sin}\left( {y_{s1} z_{n} } \right)\text{cosh}\left( {y_{s2} z_{n} } \right)}}{{\left( {C_{S}^{2} + S_{S}^{2} } \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)}}$$

(39b)

$$A_{pv} = \frac{{\left( {C_{p} y_{p2} + S_{p} y_{p1} } \right)\text{cos}\left( {y_{p1} z_{n} } \right)\text{sinh}\left( {y_{p2} z_{n} } \right) + \left( {C_{p} y_{p1} - S_{p} y_{p2} } \right)\text{sin}\left( {y_{p1} z_{n} } \right)\text{cosh}\left( {y_{p2} z_{n} } \right)}}{{\left( {C_{p}^{2} + S_{p}^{2} } \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)}}$$

(40a)

$$B_{pv} = \frac{{\left( {S_{p} y_{p2} - C_{p} y_{p1} } \right)\text{cos}\left( {y_{p1} z_{n} } \right)\text{sinh}\left( {y_{p2} z_{n} } \right) + \left( {S_{p} y_{p1} + C_{p} y_{p2} } \right)\text{sin}\left( {y_{p1} z_{n} } \right)\text{cosh}\left( {y_{p2} z_{n} } \right)}}{{\left( {C_{p}^{2} + S_{p}^{2} } \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)}}$$

(40b)

The distribution of active soil pressure described by (38)–(40) is clearly non-linear.

The total seismic pressure p _ae can be viewed as the sum of three components, the first one is independent of seismic accelerations, the second and third dependent on the horizontal and vertical acceleration, respectively.

The first component, although independent of a _ho and a _v0 , does not represent the active pressure in static conditions (i.e. for a _h0  = a _v0  = 0) because the value of α _m in static conditions is greater than α _m in seismic conditions.

The point of application (h _p ) of total seismic active thrust can be calculated on the basis of the overturning moment respect to the wall base:

$$h_{P} = \frac{M}{{P_{AE} \text{cos}\delta }} = \frac{{\int\limits_{z = 0}^{z = H} {p_{ae} \text{cos}\delta } \left( {H - z} \right)\text{d}z}}{{0.5K_{AE} \gamma H^{2} \text{cos}\delta }}$$

(41)

After substituting (38) into (41) and solving the integral the normalized point of application is given by:

$$\frac{{h_{P} }}{H} = \frac{{{M \mathord{\left/ {\vphantom {M {\gamma H^{3} }}} \right. \kern-0pt} {\gamma H^{3} }}}}{{0.5K_{AE} \text{cos}\delta }}$$

(42)

where

$$\frac{M}{{\gamma H^{3} }} = \frac{{\text{cos}\delta }}{{\text{tan}\alpha \;\text{cos}\left( {\phi + \delta - \alpha } \right)}}\left\{ \begin{gathered} \frac{1}{6}\text{sin}\left( {\alpha - \phi } \right) + \text{cos}\left( {\alpha - \phi } \right)\frac{{a_{h0} }}{g}\left\{ {A_{mh} \text{cos}\left( {\omega_{s} t} \right) + B_{mh} \text{sin}\left( {\omega_{s} t} \right)} \right\} \hfill \\ - \text{sin}\left( {\alpha - \phi } \right)\frac{{a_{v0} }}{g}\left\{ {A_{mv} \text{cos}\left( {\omega_{p} t} \right) + B_{mv} \text{sin}\left( {\omega_{p} t} \right)} \right\} \hfill \\ \end{gathered} \right\}$$

(43)

$$A_{mh} = \int\limits_{0}^{1} {A_{ph} \left( {1 - z_{n} } \right)\text{d}z_{n} } = \frac{{\left[ \begin{gathered} \left( {y_{s2}^{3} - 3y_{s1}^{2} y_{s2} } \right)\text{sinh}\left( {y_{s2} } \right)\text{cosh}\left( {y_{s2} } \right) + \left( {3y_{s1} y_{s2}^{2} - y_{s1}^{3} } \right)\text{sin}\left( {y_{s1} } \right)\text{cos}\left( {y_{s1} } \right) \hfill \\ + 2y_{s1} y_{s2} \left( {y_{s1}^{2} + y_{s2}^{2} } \right)\text{sin}\left( {y_{s1} } \right)\text{sinh}\left( {y_{s2} } \right) + \left( {y_{s1}^{4} - y_{s2}^{4} } \right)\text{cos}\left( {y_{s1} } \right)\text{cosh}\left( {y_{s2} } \right) \hfill \\ \end{gathered} \right]}}{{\left( {\text{cos}^{2} \left( {y_{s1} } \right) + \text{sinh}^{2} \left( {y_{s2} } \right)} \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)^{3} }}$$

(44a)

$$B_{mh} = \int\limits_{0}^{1} {B_{ph} \left( {1 - z_{n} } \right)\text{d}z_{n} } = \frac{{\left[ \begin{gathered} \left( {y_{s1}^{3} - 3y_{s1} y_{s2}^{2} } \right)\text{sinh}\left( {y_{s2} } \right)\text{cosh}\left( {y_{s2} } \right) + \left( {y_{s2}^{3} - 3y_{s1}^{2} y_{s2} } \right)\text{sin}\left( {y_{s1} } \right)\text{cos}\left( {y_{s1} } \right) \hfill \\ - \left( {y_{s1}^{4} - y_{s2}^{4} } \right)\text{sin}\left( {y_{s1} } \right)\text{sinh}\left( {y_{s2} } \right) + 2y_{s1} y_{s2} \left( {y_{s1}^{2} + y_{s2}^{2} } \right)\text{cos}\left( {y_{s1} } \right)\text{cosh}\left( {y_{s2} } \right) \hfill \\ \end{gathered} \right]}}{{\left( {\text{cos}^{2} \left( {y_{s1} } \right) + \text{sinh}^{2} \left( {y_{s2} } \right)} \right)\left( {y_{s1}^{2} + y_{s2}^{2} } \right)^{3} }}$$

(44b)

$$A_{mv} = \int\limits_{0}^{1} {A_{pv} \left( {1 - z_{n} } \right)\text{d}z_{n} } = \frac{{\left[ \begin{gathered} \left( {y_{p2}^{3} - 3y_{p1}^{2} y_{p2} } \right)\text{sinh}\left( {y_{p2} } \right)\text{cosh}\left( {y_{p2} } \right) + \left( {3y_{p1} y_{p2}^{2} - y_{p1}^{3} } \right)\text{sin}\left( {y_{p1} } \right)\text{cos}\left( {y_{p1} } \right) \hfill \\ + 2y_{p1} y_{p2} \left( {y_{p1}^{2} + y_{p2}^{2} } \right)\text{sin}\left( {y_{p1} } \right)\text{sinh}\left( {y_{p2} } \right) + \left( {y_{p1}^{4} - y_{p2}^{4} } \right)\text{cos}\left( {y_{p1} } \right)\text{cosh}\left( {y_{p2} } \right) \hfill \\ \end{gathered} \right]}}{{\left( {\text{cos}^{2} \left( {y_{p1} } \right) + \text{sinh}^{2} \left( {y_{p2} } \right)} \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)^{3} }}$$

(45a)

$$B_{mv} = \int\limits_{0}^{1} {B_{pv} \left( {1 - z_{n} } \right)\text{d}z_{n} } = \frac{{\left[ \begin{gathered} \left( {y_{p1}^{3} - 3y_{p1} y_{p2}^{2} } \right)\text{sinh}\left( {y_{p2} } \right)\text{cosh}\left( {y_{p2} } \right) + \left( {y_{p2}^{3} - 3y_{p1}^{2} y_{p2} } \right)\text{sin}\left( {y_{p1} } \right)\text{cos}\left( {y_{p1} } \right) \hfill \\ - \left( {y_{p1}^{4} - y_{p2}^{4} } \right)\text{sin}\left( {y_{p1} } \right)\text{sinh}\left( {y_{p2} } \right) + 2y_{p1} y_{p2} \left( {y_{p1}^{2} + y_{p2}^{2} } \right)\text{cos}\left( {y_{p1} } \right)\text{cosh}\left( {y_{p2} } \right) \hfill \\ \end{gathered} \right]}}{{\left( {\text{cos}^{2} \left( {y_{p1} } \right) + \text{sinh}^{2} \left( {y_{p2} } \right)} \right)\left( {y_{p1}^{2} + y_{p2}^{2} } \right)^{3} }}$$

(45b)

The angle α in (43) is the same one (α _m ) that maximizes the active thrust P _AE , as the uniqueness of the planar failure surface in seismic conditions is assumed (i.e. the failure surface, once formed, does not change thereafter).

As noted by Bellezza (2014) the maximum overturning moment is reached at a slightly different time to when the active thrust is maximum; in other words, the soil pressure distribution which gives the maximum soil thrust does not exactly coincide with that producing the maximum moment. However, the difference between the maximum overturning moment and the moment produced by P _AE is found to be very small and negligible for practical purposes.

6 Results and Discussion

6.1 Applicability of the Pseudo-Dynamic Method

It is well established (e.g. Okabe 1926; Mononobe and Matsuo 1929; Kramer 1996) that using the traditional pseudo-static approach, for a vertical wall retaining a horizontal backfill (Fig. 1), the coefficient K _AE is given by:

$$K_{AE} = \frac{{\text{cos}^{2} \left( {\varphi - \psi } \right)}}{{\text{cos}\psi \text{cos}\left( {\delta + \psi } \right)\left[ {1 + \sqrt {\frac{{\text{sin}\left( {\varphi + \delta } \right)\text{sin}\left( {\varphi - \psi } \right)}}{{\text{cos}\left( {\delta + \psi } \right)}}} } \right]^{2} }}$$

(46)

where ψ = arctan(k _h /(1 − k _v )); k _h  = horizontal seismic coefficient. k _v  = vertical seismic coefficient.

The inclination of the planar slip surface that maximizes the active thrust can be calculated by a rather complex expression as a function of φ, δ and ψ (e.g. Kramer 1996).

It can be demonstrated that the values of K _AE obtained by the pseudo-dynamic method are linked to those obtained by the pseudo-static method. In particular:

$$K_{AE} = K_{AE,ps} \left( {1 - {{a_{v,avg,tm} } \mathord{\left/ {\vphantom {{a_{v,avg,tm} } g}} \right. \kern-0pt} g}} \right)$$

(47)

where K _AE,ps is the active coefficient calculated by (46) provided $\text{tan}\psi = \frac{{{{a_{h,avg.tm} } \mathord{\left/ {\vphantom {{a_{h,avg.tm} } g}} \right. \kern-0pt} g}}}{{\left( {1 - {{a_{v,avg.tm} } \mathord{\left/ {\vphantom {{a_{v,avg.tm} } g}} \right. \kern-0pt} g}} \right)}}$

The form of (46) indicates that the maximization procedure only yields results if φ > ψ, i.e. when:

$$\frac{{{{a_{h,avg,tm} } \mathord{\left/ {\vphantom {{a_{h,avg,tm} } g}} \right. \kern-0pt} g}}}{{1 - {{a_{v,avg,tm} } \mathord{\left/ {\vphantom {{a_{v,avg,tm} } g}} \right. \kern-0pt} g}}} \le \text{tan}\varphi$$

(48)

6.2 Effect of Vertical Acceleration

Figure 4 shows the combined effect on K _AE of the normalized frequency ω _s H/V _s and vertical acceleration assuming D = D _S  = D _p  = 10 %; a _h0  = 0.1 g; φ = 40°; δ = 20°; ω _p /ω _s  = 1.

Fig. 4

Influence of the vertical acceleration and normalized frequency of S-wave on seismic active soil coefficient K _AE for φ = 40°; δ = 20°; a _h0 /g = 0.1; D = 10 %; ω _p /ω _s  = 1

In particular the curve relevant to absence of vertical acceleration (a _v0  = 0) is compared with those obtained for a _v0  = 0.5a _h0 and a _{v 0}  = −0.5a _h0 .

The trend of K _AE versus ω _s H/V _s is not monotonic and two main parts of the curves can be distinguished. For low values of ωH/V _s , K _AE sharply increases with ωH/V _s reaching a local maximum, while in the second part the K _AE trend is generally a downwards one, even if a second local maximum of K _AE occurs in the presence of the vertical acceleration. The first local maximum of K _AE occurs when ω _s H/V _s is close to π/2 i.e. when the backfill is subjected to the fundamental frequency of S-wave and the average weighted horizontal acceleration is maximum (see Fig. 2). The second local maximum of K _AE occurs when the average weighted vertical acceleration is maximum; this occurs for ω _p H/V _p  = π/2 at which corresponds ω _s H/V _s  = 2.93 in the hypothesis that V _p  = 1.87 V _s and ω _p /ω _s  = 1, as shown in Fig. 2.

For the overall range of ω _s H/V _s , except close to the fundamental frequency, the effect of the vertical acceleration is appreciable; in other words the curves relevant to a _v0  ≠ 0 are different to that obtained for a _v0  = 0 and the values of K _AE obtained for a _v0  > 0 differ from those obtained for a _v0  < 0.

This difference can be explained with the phase difference between Q _h and Q _v . Provided that the maximum active thrust is achieved when Q _h is close to its maximum, the different sign of a _v0 implies that when Q _h is close to its positive peak, Q _v can be directed upward or downward (see Fig. 3) and this results in different values of K _AE . As explained later, the effect of phase difference between Q _h and Q _v is magnified in the hypothesis that S-wave and P-wave have the same period.

It can be observed that also for a rigid soil (ω _s H/V _s  → 0) the values of K _AE are found to be slightly dependent on both value and sign of a _v0 . As noted previously, the values of K _AE obtained by the pseudo-dynamic approach are correlated with those obtained with the pseudo-static method according to (47).

For a rigid soil (47) becomes

$$K_{AE} = K_{AE,ps} \left( {1 - {{a_{v0} } \mathord{\left/ {\vphantom {{a_{v0} } g}} \right. \kern-0pt} g}} \right).$$

(49)

Considering that most technical codes (e.g. Eurocode 8 (2005)) recommend to assume vertical inertia force both upward and downward, in the followings of the paper the value of K _AE is assumed as the maximum K _AE obtained for a _v0  > 0 and a _v0  < 0. Similarly to the pseudo-static approach (Fang and Chen 1995), it is not assured a priori if the maximum K _AE is reached for a _v0  > 0 or for a _v0  < 0. This is evident also in Fig. 4 where for the same input parameters the maximum K _AE is obtained for a _v0  > 0 in certain ranges of ω _s H/V _s and for a _v0  < 0 in other ones.

Figure 5 shows normalized distribution of active seismic pressure for three different value of a _v0 with a _h0 /g = 0.1; ω _s H/V _s  = 2; ω _p /ω _s  = 1; D = 10 %; φ = 40°; δ = 20°.

Fig. 5

Normalized seismic active earth pressure distribution for different values of vertical acceleration for φ = 40°; δ = 20°; a _h0 /g = 0.1; D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

It can be noted that as a _v0 increases active earth pressure also increases. When a _v0 changes from 0 to 0.5a _h0 seismic active earth thrust increases by about 4.6 %. Similarly when a _vo changes from 0.5a _h0 to a _h0 seismic active earth thrust increases by about 4.7 %.

6.3 Effect of Horizontal Acceleration

Figure 6 shows the typical normalized pressure distribution for different values of a _h0 with |a _vo | = 0.5a _h0 ; φ = 40°; δ = 20°; ω _s H/V _s  = 2; ω _p /ω _s  = 1. As expected, it is evident that as a _h0 increases, seismic active earth pressure also increases. This results in a significant increase in active soil thrust. As an example K _AE increases by about 45 % when a _h0 changes from 0.1 g to 0.2 g.

Fig. 6

Normalized seismic active earth pressure distribution for different values of amplitude of base horizontal acceleration for φ = 40°; δ = 20°; |a _v0 |/a _h0  = 0.5; D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

From Fig. 6 it is also clear that degree of non-linearity of the curves increases with a _h0 . The point of application of P _AE calculated by (42) is found to slightly increase from 0.343H for a _h0  = 0.05 g to 0.367H for a _h0  = 0.20 g.

6.4 Effect of Soil Shear Resistance Angle and Soil-Wall Friction Angle

Figure 7 shows the normalized pressure distribution for different values of soil shear resistance angle φ with a _h0  = 0.1 g; |a _v0 | = 0.5a _ho , ω _s H/V _s  = 2; D = 10 %; δ = φ/2. As expected, seismic active earth pressure shows significant decrease with the increase in the value of φ. When φ changes from 30° to 35° seismic active earth pressure decreases by about 16 % at mid-height and by about 17 % at the bottom of the wall. Similarly when φ changes from 35° to 40° seismic active earth pressure decreases by about 16.3 % at mid-height and by about 17.3 % at the bottom of the wall. Finally when φ changes from 40° to 45° seismic active earth pressure decreases by about 16.7 % at mid-height and by about 17.9 % at the bottom of the wall.

Fig. 7

Normalized seismic active earth pressure distribution for different values of soil shear resistance angle for δ/φ = 0.5; a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

Figure 8 shows the normalized pressure distribution for different values of soil-wall friction angle δ with a _h0 /g = 0.1, |a _v0 | = 0.5a _h0 , ω _s H/V _s  = 2; D = 10 %; φ = 40°. The effect of δ is quite marginal.

Fig. 8

Normalized seismic active earth pressure distribution for different values of soil wall friction angle for φ = 40°; a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

For the same input parameters Fig. 9 shows the combined effect on K _AE of φ and δ/φ for four different values of φ. It is clear that the effect of δ on K _AE is generally small if compared with that of φ. In the investigated ranges of φ (φ = 30°–45°) the trend of K _AE versus δ/φ is not monotonic with a minimum value of K _AE for δ/φ in the range 0.25–0.50. The maximum value of K _AE is reached in most cases for δ = φ, except the case of φ = 30° when the maximum is obtained for δ = 0. The range of variability of K _AE is found to increase at increasing φ; the percent difference between the maximum value of K _AE and the value obtained for δ = φ/2 varies from about 6 % for φ = 30° to about 19 % for φ = 45°.

Fig. 9

Effect of wall-backfill friction angle for different values of soil shear resistance angle for a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; D = 10 %; ω _s H/V _s  = 2; ω _p /ω _s  = 1

6.5 Effect of Damping Ratio

The analysis presented in the previous sections allows to consider a different damping ratio for S-wave and P-wave. However, for a sake of simplicity it is here assumed that D = D _s  = D _p .

Figure 10 shows the values of K _AE at varying ω _s H/V _s obtained for D = 5, 10 and 15 %, all other input parameters being equal (φ = 40°; δ = 20°; a _h0  = 0.1 g; |a _v0 | = 0.5a _h0 ). The trend of the three curves is similar with a maximum of K _AE when ω _s Η/V _s is close to π/2. For the lower damping ratio (D = 5 %) the first peak does not exist as the condition expressed by (46) is not satisfied; a second local maximum is found when P-wave reaches its fundamental frequency (i.e. for ω _s H/V _s  = 2.93) and a third local maximum is visible when ω _s Η/V _s is close to 1.5π. For D = 10 % and D = 15 % the second and the third local maxima are not appreciable. In the analyzed case the effect on K _AE of soil damping varying in the range 5–15 % is found to be negligible for ω _s H/V _s ranging between 0 and 1 and very small in the range 3.5–5 in which the values of K _AE differ <3.5 %.

Fig. 10

Effect of damping ratio and normalized frequency of S-wave on seismic active soil coefficient K _AE for φ = 40°; δ = 20°; a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; ω _s H/V _s  = 2; ω _p /ω _s  = 1

On the contrary, the damping ratio is found to have a great effect on the first peak of K _AE . For ω _s H/V _s  = π/2 K _AE decreases of about 50 % when D varies from 10–15 %.

Figure 11 shows that a lower damping ratio implies a greater non-linearity of active pressure distribution and a slight rise of the application point of the active thrust (h _p /H = 0.357 for D = 15 % and h _p /H = 0.373 for D = 10 %).

Fig. 11

Normalized seismic active earth pressure distribution for different values of damping ratio for φ = 40°; δ = 20°; a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; ω _s H/V _s  = 2; ω _p /ω _s  = 1

6.6 Effect of Frequency Ratio

Previous studies based on the original pseudo-dynamic method assumed that angular frequency of S-wave coincide with angular frequency of P-wave (Choudhury and Nimbalkar 2006, 2007, 2008; Nimbalkar and Choudhury 2007, Choudhury and Ahmad 2008; Nimbalkar et al. 2006; Ghosh 2007, 2010; Bellezza et al. 2012). In this study a different frequency for S- and P-wave is considered by the ratio ω _p /ω _s .

A value of ω _p /ω _s (=T _s /T _p ) different from the unit implies that Q _h and Q _v have the same pair of values after a period T _sp generally greater than T _s and/or T _p . As an example for ω _p /ω _s  = 0.8 T _sp  = 5T _s  = 4T _p whereas for ω _p /ω _s  = 1.5 T _sp  = 2T _s  = 3T _p , as shown in Fig. 12. Consequently, for ω _p /ω _s  ≠ 1 the seismic active thrust follows no longer a sinusoidal trend but a cyclic trend of period T _sp (Fig. 13).

Fig. 12

Normalized values of inertia forces in the overall period for D = 10 %; ω _s H/V _s  = 2 (a) ω _p /ω _s  = 0.8; (b) ω _p /ω _s  = 1.5

Fig. 13

Values of the normalized soil active thrust versus normalized time in the overall period T _sp for different values of ω _p /ω _s for φ = 40°; δ = 20°; a _h0 /g = 0.1; |a _v0 |/a _h0  = 0.5; D = 10 %; ω _s H/V _s  = 2

Figure 14 shows the values of K _AE as a function of ω _p /ω _s for two different values ω _s H/V _s , all other parameters being equal. In the same figure the open symbols represents the maximum values of K _AE obtained for a _h,avg  = a _h , _avg,max and a _v,avg  = a, _v,avg,max (i.e. assuming that horizontal and vertical inertia forces peak at the same instant). Generally the difference between the calculated K _AE and K _AEmax are found to be very small (<1 %). Greatest differences are found for ω _s H/V _s  = 2 and ω _p /ω _s  = 1 and 1.5, i.e. at the lowest values of the overall period T _sp when it is more likely that Q _h and Q _v do not peak simultaneously.

Fig. 14

Effect of frequency ratio ω _p /ω _s on seismic active soil coefficient for φ = 40° δ = 20° a _h0 /g = 0.1 |a _v0 |/a _h0  = 0.5; D = 10 % (a) ω _s H/V _s  = 1; b ω _s H/V _s  = 2. Solid symbols refer to K _AE obtained by optimization procedure; open symbols and line refer to K _AE obtained assuming maxima inertia forces

Moreover it can be observed that in the investigated range of ω _p /ω _s (0.6–2) the trend of K _AE versus ω _p /ω _s depends on the value of the normalized frequency of S-wave; in particular for ω _s H/V _s  = 1 the trend is monotonically increasing (Fig. 14a), whereas for ω _s H/V _s  = 2 the trend shows a peak for ω _p /ω _s  = 1.45 (Fig. 14b). This different trend is due to the different amplification of vertical acceleration within the soil wedge, plotted as dashed curve in Fig. 14. Indeed, in the hypothesis that V _p  = 1.87V _s , for ω _s H/V _s  = 1 the normalized frequency of P-wave ω _p H/V _p ranges between 0.32 and 1.07, far from its fundamental frequency. On the contrary for ω _s H/v _s  = 2 ω _p H/v _p varies between 0.64 and 2.14, i.e. in a range containing the fundamental frequency of P-wave.

6.7 Comparison of Results

It has been previously noted that the new pseudo-dynamic method automatically includes amplification effects within the soil and that the average seismic accelerations through the soil wedge (a _h,avg and a _v,avg ) are generally greater than amplitude of accelerations at the base of the wall (a _h0 , a _v0 ), as shown in Fig. 2. Consequently, it is obvious that the values of K _AE obtained by the present method can be much higher than those obtained with the pseudo-static approach using k _h  = a _h0 /g and k _v  = a _v0 /g, especially close to the fundamental frequency of S-wave.

Similarly, the present method overestimates the values of K _AE in comparison with the values obtained using other pseudo-dynamic methods which neglect amplification effect. The recent procedure based on Rayleigh waves (Choudhury et al. 2014a, b) belongs to this category.

A meaningful comparison can be made only with the existing pseudo-dynamic method, provided that amplification factors are included in the analysis for both S-wave and P-wave, by assuming that amplitudes of seismic accelerations vary linearly from the base of the layer to the ground surface (Steedman and Zeng 1990; Choudhury and Nimbalkar 2007, 2008; Nimbalkar and Choudhury 2007; Kolathayar and Ghosh 2009). To make the seismic input uniform, two different amplification factors are considered for S-wave and P-wave (i.e. f _ah  ≠ f _av ), according to Eqs. (13)–(14).

In Tables 1 and 2 a comparison of active earth pressure coefficients is presented for two different values of ω _s H/V _s varying the base horizontal acceleration (a _h0  = 0.05–0.25 g) and soil shear resistance angle (φ = 30; φ = 40°), assuming the same damping ratio (D = 10 %) and the same frequency (ω _s  = ω _p ) for S-wave and P-wave.

Table 1 Comparison of seismic active earth coefficient (K _AE ) obtained by the present study with those from the existing pseudo-dynamic method for ω _s H/V _s  = 1; ω _p  = ω _s ; D = 10 % φ/δ = 0.5; a _v0  = 0.5a _h0

Table 2 Comparison of seismic active earth coefficient (K _AE ) obtained by the present study with those from the existing pseudo-dynamic method for ω _s H/V _s  = 2; ω _p  = ω _s ; D = 10 % φ/δ = 0.5; |a _v0 | = 0.5a _h0

Data shown in Table 1 indicate that for a normalized frequency ω _s H/V _s  = 1 the present method is more conservative than the existing pseudo-dynamic method. The differences between the values of K _AE increase at increasing base horizontal acceleration, from about 5 % for a _h0 /g = 0.15 to about 9 % for a _h0 /g = 0.25.

For a higher normalized frequency ω _s H/V _s  = 2 (Table 2) the present approach gives values of K _AE practically coincident with those of the existing pseudo-dynamic approach, with differences not exceeding 2 %.

It is well recognized that most of the available methods assume a constant acceleration in the soil using seismic coefficient k _h and k _v obtained from the maximum acceleration expected at the soil surface taking into account of stratigraphic amplification (see for example Eurocode 8):

$$k_{h} = \alpha_{h} a_{h,max} / g.\quad k_{v} = \pm \alpha_{v} k_{h}$$

(50)

where $\alpha_{h} \le 1\quad 1/ 3 \le \alpha_{v} \le 1/ 2$.

Therefore a more comprehensive comparison can be made assuming the same maximum acceleration instead of the same base acceleration. With this aim the seismic input must be adapted; in particular the present method requires to calculate the base acceleration considering amplification factors f _ah and f _av and Eq. (50), i.e. a _h0 = k _h g/(f _ah α _h ) and a _v0 = k _v g/(f _av α _h ).

Table 3 shows the numerical results for seismic active earth coefficient K _AE obtained from the present solution and some established solutions in the literature. For sake of simplicity the comparison is made neglecting the vertical acceleration for two different values of α _h (α _h  = 1 α _h  = 2/3). For the proposed and the existing pseudo-dynamic methods a normalized frequency of 1.885 (i.e. H/V _s T _s  = 0.3) is assumed, according to previous studies on similar topic (Choudhury and Nimbalkar 2005, 2006; Ghosh 2007, 2010; Kolathayar and Ghosh 2009; Ghosh and Kolathayar 2011).

Table 3 Comparison of seismic active earth coefficient (K _AE ) obtained by the present study with those from some available theories for φ/δ = 0.5; k _v  = a _v0  = 0; ω _s H/V _s  = 1.885; ω _p  = ω _s ; D = 10 %

Results are in reasonable good agreement (largest discrepancy 16 %). As expected, the predictions given by the present method underestimate K _AE when α _h  = 1 because in other methods the acceleration is assumed to have its maximum amplitude through the entire wedge. On the contrary, the proposed approach leads to slightly conservative predictions of K _AE when the available approaches assume α _h  = 2/3 to calculate k _h from the maximum acceleration. In this case the present approach can be more suitable for practical applications. Indeed it should be emphasized that the present method, unlike pseudo-static method and Mylonakis et al. analysis, allows to consider effect of time, as well as to predict a not linear pressure distribution along the back of the wall, according to experimental observations (e.g. Steedman and Zeng 1990).

7 Conclusions

The new pseudo-dynamic approach proposed by Bellezza (2014) has been extended taking into account both horizontal and vertical acceleration.

The proposed approach represents an improvement of the pioneering pseudo-dynamic approach for two main reasons: (1) standing seismic S-wave and P-wave respect the zero stress boundary condition at the ground surface and therefore both horizontal and vertical accelerations are naturally amplified within the backfill without the need of introducing an amplification factor; (2) a more realistic behavior of soil is accounted for by modeling the backfill as a visco-elastic medium.

Maintaining some hypotheses of the existing pseudo-dynamic method—including absence of water, homogeneous backfill and planar failure surface—inertia forces, seismic active thrust, active pressure distribution and overturning moment were derived in dimensionless form as a function of the normalized frequencies ω _s H/V _s and ω _p H/V _p and damping ratio D, assumed to be the same for both shear and primary wave.

The range of applicability of the pseudo-dynamic approach and the correlations with pseudo-static method have been also discussed by introducing the concept of weighted average acceleration.

The results of the parametric study substantially confirm the results previously obtained in the absence of the vertical acceleration; soil active thrust and pressure distribution are very sensitive to variation of amplitude of base horizontal acceleration, soil shear resistance angle and normalized frequency of shear wave, especially close to its fundamental frequency where the effect of damping is magnified. The effect of soil-wall friction angle is generally small.

Unlike the pioneering pseudo-dynamic approach, the effect of a different frequency for S- and P-wave has been investigated, highlighting that soil active thrust generally increases when P-wave have a frequency greater than that of S-wave.

The results obtained by the proposed method are found to be in agreement with previous studies, provided that the seismic input is adapted to include amplification effects.